In the last several weeks, I’ve given talks about innovation, mobile technology, mathematics and philosophy. Last week I gave a talk at the Bio–IT World conference in Boston.

At the beginning I covered many of my favorite topics: Wolfram|Alpha, Mathematica, A New Kind of Science. But then I turned more specifically to biomedicine, and talked about quite a few topics that I’ve never discussed in public before.

Here’s an edited transcript.

OK. Well. I’m going to talk about some pretty ambitious things here today.

Both in technology and in science.

I’m going to talk about what we can know, and what we can compute, in biomedicine.

And about how we can make use of that.

I’m going to talk both about some practical technology and some basic science that I’ve been involved in building, that tries to address those things.

Many of you I hope will have seen and used Wolfram|Alpha, which has been off entertaining us in the background there.

Let me start with that.

You know–when computers, and I, were a lot younger, it used to be a common assumption that one day one would just be able to walk up to a computer and ask it anything.

And that if what one asked could somehow be answered on the basis of any knowledge that had been accumulated in our civilization, then the computer would be able to figure it out.

Well, 30 years ago I started wondering what it would take to actually do this.

And at first I have to say I thought the only possibility was to build a whole artificial intelligence—a whole brain-like thing that somehow thinks like a human.

And that seemed really hard.

But gradually I realized that actually, that might not be the right direction at all.

And that we might not want to build sort of the analog of a bird—but rather the analog of an airplane.

And that computation—and a bunch of ideas around it—might be the key.

Well, by that point I’d assembled a pretty big stack of technology and science, and organizational capability.

And a little more than five years ago I decided it was time to try a serious assault on the problem—of making the world’s knowledge computable.

Well, the result was Wolfram|Alpha. Which is a very long-term project.

But already gets used every day by millions of people, who manage effectively just to walk up to it and have it answer all kinds of things.

So, let’s give it a try here.

The basic idea is: you ask it a question; it gives you an answer.

[Check out Wolfram|Alpha here.]

OK. So how does all this work?

There are really four big pieces.

First, one has to get all the underlying data.

And one can’t somehow just forage that from the web.

One has to do a lot of work, going to primary sources for every domain.

But just having raw data is only a very first step.

There’s a whole curation pipeline that we’ve developed for taking that data and really making it computable.

So that it’s not just blobs of data—but actually something where questions can be answered from it.

The curation process is an interesting mixture of automation and human effort.

We’ve steadily been tuning it. But one thing I’ve noticed is that unless one injects real human domain experts into it, one won’t get the right answers.

So, OK, let’s say across thousands of domains we have nice curated data.

Well, now we have to compute actual answers from it.

And the second big piece of Wolfram|Alpha is to implement all the methods and models and algorithms for computing things that we’ve learned from science, and engineering, and all sorts of other areas.

Well, that’s a big job, and inside Wolfram|Alpha today there are about 10 million lines of Mathematica code devoted to it, covering a very wide range of areas.

Well, OK, so we can compute lots of answers.

But how can we ask questions?

Well, what we want is for humans to just be able to walk up to Wolfram|Alpha and immediately do that.

So that means we have to be able to understand their natural language utterances.

Of course, people have been trying to get computers to understand natural language for many decades.

But usually the problem has been: here are a million pages of documents. Computer: go understand them.

Our problem is different: we want to take short utterances that people enter, and figure out what they’re telling us to compute.

And it turned out that we were able to make some great breakthroughs in that, that allow Wolfram|Alpha to be remarkably successful at understanding all sorts of weird linguistic things that people feed it.

Well, OK. So we can ask Wolfram|Alpha questions. And it can compute all sorts of answers.

The fourth big issue is deciding what to actually compute, and how to present it.

We have to automate computational aesthetics, and have all sorts of algorithms and heuristics to decide just what a human is likely to find useful in an answer.

But the result is that for all sorts of kinds of questions—and more every week—you really can just walk up to Wolfram|Alpha, and have it give you answers.

And of course, every answer it gives you, it computed.

It’s not like a web search engine where it’s looking up text people have put on the web—and giving you pointers to where that is.

Wolfram|Alpha is computing specific answers to specific questions you ask it, whether or not those questions have ever been asked before.

It’s not doing something like IBM’s Watson Jeopardy system, where it’s pulling out snippets of text from a corpus.

It’s actually understanding questions, turning them into an internal computable form, and using its built-in computable knowledge to compute answers.

In effect what we’re trying to do is to automate—for everyone—the process of getting expert-level knowledge.

Right now if you want to get an expert-level question answered… well, you typically have to actually go and ask a human expert.

The point of Wolfram|Alpha is steadily to capture all that expert knowledge, all those methods and algorithms, and so on. And automate the process of delivering it whenever it’s needed.

You know, when you look inside Wolfram|Alpha, there are a lot of moving parts.

I think Wolfram|Alpha might actually be by many measures the most complex software system that’s ever been assembled.

And more than anything else, what’s made it possible is Mathematica—the algorithmic language and system that we’ve been developing for nearly 25 years.

Mathematica gets used for all kinds of things in the world today.

Pretty much wherever top-of-the-line R&D is happening across every industry.

All over technical education. And so on.

But it’s interesting. Even though Mathematica first appeared 23 years ago, I think it’s still in some ways an artifact from the future.

You know, in designing Mathematica I’ve always thought it was a little like doing natural science.

Starting from all those computations one might want to do, and then drilling down to see what’s underneath—what primitives one can use to build them all up.

And underneath Mathematica is a very general idea: the idea of symbolic programming.

The idea that everything one manipulates—whether it be data, or a document, or a graph, or a program—can always be represented as a symbolic expression.

And then manipulated using a coherent set of primitive operations.

Well, it’s taken me decades to understand just how general and powerful the idea of symbolic programming is.

It’s brought us all sorts of innovations—and it’s a core part of what’s made Wolfram|Alpha possible.

You know, from the very beginning of designing I had some fundamental principles—which have continued to guide our development ever since.

One was: automate as much as possible.

We want the human to define what they want to do. But then we want Mathematica to take over and be able to automatically figure out as much as possible.

Whether it’s which of a hundred possible algorithms to use in a particular case. Or how best to lay out a graph, or set up an interface. Or whatever.

Because it’s by automating as much as possible that we as humans get the most leverage out of the system.

Now, another principle—which I have to say I’ve personally put many years of my life into—is unity of design.

Making sure that all of the many capabilities of Mathematica all consistently fit together.

And I have to say that particularly in recent years this has paid off so incredibly.

Not only for people learning and using the Mathematica language.

But for building the system itself.

Our principle in Mathematica has been to build in essentially any general algorithmic procedure.

Whether it’s for graphics. Or statistics. Or image processing. Or control theory. Or sequence alignment. Or whatever.

And by now we certainly have by far the world’s largest and broadest web of algorithms—many of which we’ve actually invented ourselves.

But the point is that everything fits together. So when you want to add something in one particular area, we immediately get to leverage anything in any other area.

And it’s been exciting for us internally to see the sort of exponential development process that that’s allowing—and that for example made possible Wolfram|Alpha.

Well, Mathematica has been used for lots of industrial-scale applications over the years.

And it’s got very robust development and deployment mechanisms. Which for the whole supercomputer-class infrastructure of Wolfram|Alpha we basically just had to turn on.

You know, from a user point of view, it’s interesting to compare Mathematica and Wolfram|Alpha.

Mathematica is this very precise language, where you can build arbitrarily deep structures.

Wolfram|Alpha is this very broad system, that handles and knows about all the messiness of the world.

It’s pretty interesting to bring these things together.

So, for example, now inside Mathematica you can call on Wolfram|Alpha capabilities.

So you can type free-form natural language—and have it automatically translated into precise Mathematica code.

I think it’s a pretty exciting development—especially for areas like biology.

Because it really breaks down the barrier between programmers and non-programmers.

And lets anyone build up programs step by step, just using free-form natural language.

Right now we’re in sort of a remarkable situation.

We’ve got oodles of technology that we’ve been assembling for 25 years. And it all seems to be coming together at once. And letting us do fascinating things.

Like our new CDF—Computable Document Format.

Where we use symbolic programming to make it incredibly easy to create computable, interactive, documents.

Here’s a site with about 7,000 examples.

And what we’re seeing is that now papers—and reports—can be made interactive.

It’s a situation a bit like what happened with typesetting of documents 20 years ago.

It went from a thing that one had to have a specialist do for one.

To something that a typical person could do for themselves.

Well, that’s what CDF makes possible now for interactivity and computability.

You don’t just have a static curve. You have something where you can drill down, adjust the model, and so on.

And the real kicker is that you can start creating that interactivity using Wolfram|Alpha technology—just entering free-form natural language.

Oh yes, and by the way, you’ll be able to have your data uploaded to the Wolfram cloud to be accessed in CDF and Wolfram|Alpha—as well as through the whole Mathematica language.

You know, I think this is a pivotal year for the computer industry. With all sorts of new methods and platforms and so on coming online.

Cloud computing is one thing.

But something that’s becoming possible with Wolfram|Alpha is what I call knowledge-based computing.

Usually one thinks of constructing software sort of from raw computational primitives.

But with Wolfram|Alpha in the loop one gets to start in effect from the knowledge of the world, and then build software from there.

And there are lots of interesting products in the pipeline doing that.

Notably for example in mobile computing.

Where this whole idea of immediately being able to get exactly the knowledge one needs—without rooting around or searching or whatever—is particularly important.

It’s interesting: with each new platform there are new ideas.

Here’s an example from our spinoff company Touch Press, which I’m happy to say has published the #1 bestselling highly interactive ebooks on the iPad to date.

Here’s one about the Solar System.

In a couple of months we’re having a rather unexpected bio-related title coming out.

I might say, by the way, that the whole image processing and animation pipeline here is built in Mathematica, and we use Wolfram|Alpha for the background data, and so on.

Well, OK. There’s lots more to say about technology.

But I want to turn now to basic science.

And after that I’m going to try to bring all these things together and talk a bit about what they mean for the bio future.

So, OK. About science.

You know, I started out at a young age doing physics. And physics is in a sense a very arrogant science—that somehow expects to find fundamental theories for everything.

Well, what I realized at some point is that when the systems I looked at were complex—not least in areas like biology—the methods I knew just didn’t seem to make much progress.

And what I began to think—about 30 years ago now—is that if one was going to make progress one would have to take a whole different approach.

You know, in physics, there’s really one big idea—about 300 years old. That one can use things like mathematical equations to model the natural world.

Well, if there’s going to be any kind of theory for a system, the system had better be based on some kind of rules.

But what I began wondering is whether there are more general kinds of rules than the ones we’ve got from mathematics.

Well, fortunately in modern times we have a framework for thinking about such things: programs.

One can think of any kind of definite rule as corresponding to a program.

But if one’s interested in systems in nature, the question is: what kinds of programs correspond to what it does?

Well, when we use programs in practice, we’re used to building up very complicated programs—maybe from millions of lines of code—that do very specific things.

But the question I got interested in a long time ago is a basic science one.

If one somehow looks at the kind of computational universe of all possible programs, what do they typically do?

Well, the best way to find that out is to do an experiment.

And for me it was a question of taking my sort of computational telescope—Mathematica—and pointing it at the computational universe.

Well, OK, here’s what I saw.

I started off looking at a very simple kind of program called a cellular automaton.

That consists of a bunch of idealized cells, each either black or white, arranged on a line.

And the idea is that at each step, the color of each cell is determined by a simple rule from the colors of the cells on the step before.

OK, so here’s an example of what happens.

That little icon at the bottom represents the rule.

And now starting from a single black cell at the top, it just makes this simple pattern.

OK. Nothing surprising. A simple rule makes a simple pattern.

Well, let’s try changing the rule a bit.

Now we get a checkerboard.

Now we get a nested pattern.

Which is pretty intricate. But in a sense still somehow has a regularity that reflects the simplicity of the rule that made it.

But now the question is: what else can happen in the computational universe of possible programs?

Well, we can just run a little Mathematica experiment to find out.

Let’s try running all possible rules that have icons like the ones I was showing.

Well, here’s the result.

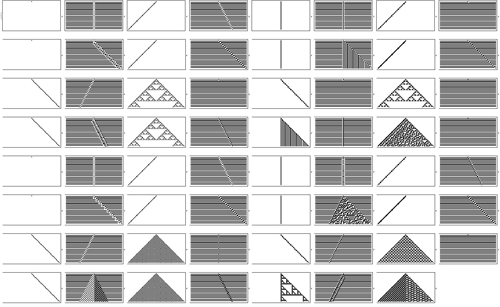
Each little picture corresponds to a different rule. And we can see there’s quite a lot of diversity in what happens.

But mostly it’s pretty simple.

Well, at least until one gets to the 30th rule in the list.

Let’s look at that one in more detail.

Simple rule. Simple initial state.

But look at what it does.

One can see a little regularity over on the left. But mostly, this is just really complicated. In many ways quite random.

Well, when I first saw this back in the early 1980s it was a real shock to my intuition.

I mean, from doing engineering and so on, we’re used to the idea that to make something complicated should take a lot of effort.

But here, out in the computational universe, it seems to sort of just be happening for free.

And I think this is something very fundamental.

I mean, when we look at systems in nature, there often seems to be some secret that they have that lets them make stuff that’s just incredibly much more complicated than anything we as humans typically make.

Well, I think this rule 30 phenomenon is at the heart of that secret of nature.

And really what it is is that out in the computational universe—when one isn’t constrained by somehow having to foresee what the systems one’s setting up are going to do—it’s actually pretty common to have even very simple rules that produce immensely complex behavior.

Well, I’ve spent years understanding what this really means, and trying to build up—as the title of the big book I wrote about this says—a new kind of science based on it.

I found lots of longstanding mysteries in science that one could start to make progress on. Lots of new kinds of models of things—in biology, in mathematics, even in the most fundamental levels of physics.

And some new general kinds of principles.

The biggest is probably what I call the Principle of Computational Equivalence.

Here’s how it works.

Let’s look at all these systems—cellular automata, systems in nature, whatever.

In sort of a modern paradigm we can think of them all as doing computations.

They get set up in some way, then they run, and they produce some kind of result.

Well, an important question is how all these computations compare.

Well, one might have thought that every system would somehow do a fundamentally different computation.

But here’s the first big point—that’s been known actually since the 1930s.

That there exist universal computers—systems that, when fed appropriate programs, can do any possible computation.

And of course that’s an important idea—because it’s the idea that made software possible, and led to the whole computer revolution.

Well, it turns out there’s more. And that’s what the Principle of Computational Equivalence is about.

Because it says that out in the computational universe, when one gets beyond really trivial systems, essentially every system achieves a sort of maximal computational sophistication.

You don’t have to build up all that technology and detail to get sophisticated computation.

Zillions of systems just lying around the computational universe already do it.

And this has all kinds of consequences.

One of them is that if you actually want to make a computer, you can expect to do it out of much simpler components than you thought.

And, like, if you’re trying to do nanotechnology, it suggests that instead of having to shrink down large-scale mechanisms, we should be working the other way.

Just starting from simple molecular forms, and understanding how to assemble them—a bit like a cellular automaton—to be able to compute.

There’s also a very important theoretical implication of the Principle of Computational Equivalence, that has implications for biomedicine.

It’s what I call computational irreducibility.

Traditional physics, for example, has tended to pride itself on being able to predict things.

And when you’re making a prediction, what you’re really saying is that you as the predictor—with your mathematics or whatever—are so much smarter than the system you’re predicting, that you can work out what it will do with a lot less computational effort than it takes the system itself.

Well, the Principle of Computational Equivalence says that you often won’t be able to do that.

Because the system itself will be just as computationally sophisticated as you are yourself.

So its behavior will seem computationally irreducible to you. And the only way you’ll be able to work out what the system does is effectively by explicitly tracing every step in its evolution.

Well, we often think it’s convenient to simulate the behavior of systems.

But what computational irreducibility means is that simulation is not just convenient, it’s fundamentally necessary. That’s really the only way to find out what the systems will do.

And knowing one has to simulate each step, it puts a lot of pressure on having the computationally best possible underlying model.

Having the most minimal representation of the system, so one can take the computations of the simulations as far as possible.

Well, OK, so there’s a lot to learn from studying the computational universe.

But let’s talk about how it relates to biological systems.

I suppose the big issue there is just how much theory there can ever be for biology.

I mean: it could be that sort of everything we see in a modern biological system is just frozen history of natural selection.

And with the traditional intuition that whenever you see something complex, it must be the result of something somehow correspondingly complex—like the whole history of biological evolution—this seems reasonable.

But once we’ve seen things like rule 30, well, then we might start thinking that some of this complicated stuff we see in biological systems might actually have much simpler causes.

Let me mention one case that I happen to have studied in some detail: it happens to have to do with molluscs.

Molluscs have shells that in effect grow a line at a time.

And on the growing lip there’s a line of cells that secrete pigment.

And you can make a model of that using a cellular automaton.

But what cellular automaton? What rule?

Well, how about trying all the possibilities?

Well, here’s the remarkable thing. Abstractly looking at the computational universe of possible cellular automata, one sees a few classes of behavior.

And if one looks at the actual molluscs of the earth, their pigmentation patterns turn out to fall into the exact same classes.

It doesn’t seem that there’s a whole elaborate chain of natural selection that shapes the patterns.

It’s just as if the molluscs of the earth try out each possible program—and then we get to see the outputs from those programs printed on the molluscs’ shells.

There’s a curious predictive biology that happens here.

In addition to simple stripes and spots, knowing about the abstract computational universe can tell one that, yes, there will be elaborate triangle patterns too.

It’s not like with natural selection, where one predicts that there should be a “missing link”—a smooth interpolation—between two forms.

It’s something that’s based on the strange intuition of the computational universe—understanding the kind of abstract diversity that we know exists there.

Well, so how can we use intuition from the computational universe to think about biological systems in general?

Let me perhaps start painting some pictures.

One big question is how we should think about mechanisms in biology.

I mean, 50 years ago there was the big idea that ultimately biology is based on digital information—in the genome.

But what about biological processes? How should we think of those?

Is it all mathematical equations? Is it like logic?

Or is it something more like simple programs? A whole diverse collection of those.

Let’s say it is like simple programs. What does that mean?

Well, all those issues like computational irreducibility are going to come up.

If you say: is such-and-such a structure going to grow forever in a biological system, that may be an irreducible—an undecidable—question.

Somehow a lot of biological explanations still sound very mechanical.

The level of this goes up, so the level of that goes down. And so on. Like a mechanical lever.

Well, in the computational universe, it’s more like: this will be computationally irreducible, so it will seem random. Or there are pockets of reducibility here, that we can use to control the system. Or whatever.

It’s a different paradigm.

And, by the way, it applies not only at the molecular or chemical level, but also at the structural level.

I’ve spent a lot of time trying to understand how all sorts of biological structures grow.

It’s a bit like with the mollusc pigmentation patterns. All over the place—whether it’s shapes of plant leaves or human biometrics—one finds that a whole space of possible forms is covered.

But there’s lots of unexpected stuff in that space. It’s not something smooth, with just one bone getting longer, and another shorter.

It’s full of surprises, but completely predictable just from the abstract structure of the computational universe.

Well, OK. So some aspects of biological—some specific subsystems—may correspond to pretty simple programs.

But by the time you’ve got a whole human or something, it’s a big collection of different systems.

So how should one think about that?

Well, in engineering there’s been gradual progress in trying to model systems with lots of parts—like cars and planes and chemical plants and things.

And actually just recently we’ve announced a big new initiative in this direction.

.

Let’s talk first about systems modeled with traditional mathematical equations.

Like Newton’s equations, or Kirchhoff’s laws for circuits, or whatever.

Well, it turns out there’s a very definite structure to these kinds of equations—even if one might need 100,000 of them to make a decent model of something like a car.

Well, in the past it’s been pretty much impossible to do an accurate job of solving all these equations and the constraints that come with them.

And it turns out that the key to making progress is having a really broad algorithm base.

Because this isn’t just a numerical computation problem. It’s also a graph theory problem. And it’s also, as it turns out, an algebraic computation problem.

Well, after 25 years of development, we’re finally at the point with Mathematica where we can actually do this—actually work with models with hundreds of thousands of equations.

We just acquired a company—MathCore—that’s been developing related technology based on Mathematica for many years. And we’re going to start the process of integrating all of this into Mathematica.

Actually, it’s interesting. In the modern world of Wolfram|Alpha what we realize is that getting all the models for components is just another curation problem.

And then deploying is also a Wolfram|Alpha thing. Being able to run models for large-scale systems within the Wolfram|Alpha cloud, and being able to ask questions about them using free-form linguistics, getting results on mobile devices, or whatever.

You might do this if you were trying to debug a gas turbine in the field.

But maybe you might also do this if you were trying to do something medical in the field.

Of course, to do that you’d have to have the underlying model.

And it’s not like a car or a plane, where we’ve specifically engineered a system with a model in mind.

We’ve now got a system in nature.

Well, of course, lots of work has been done trying to figure out pathways and networks for biochemical processes.

And indeed in Wolfram|Alpha we already know about lots of those.

And for some systems one can already expect to use the systems-modeling technology that we’re building.

But ultimately I think it’s going to take a combination of this methodology, with methodology that we get from studying the computational universe.

In biology—with all the new measurement technologies that are coming online—we’re gradually starting to get oodles of data on things.

Now the question is how we’re going to make sense of it, what models we’re going to use for it.

A traditional approach has been in effect to set up mechanisms and formulas, then to use statistics and so on to fit parameters.

Well, our new kind of science—NKS—gives a different idea.

Because in the computational universe it’s giving us this immense collection of possible models.

Models that do simple things, models that do complex things—lots of diversity.

With pre-NKS intuition we might have assumed that the only way to get reasonable models was somehow explicitly to construct them.

But what NKS shows us is that there’s something different to do: we can just search the computational universe to find models that fit whatever phenomenon we’re looking at.

Well, I’ve certainly done this a lot over the years. And there are all kinds of methodological things to learn.

But it’s remarkable how well it can work. And out in the computational universe one routinely discovers the most surprising—kind of creative—models.

There needs to be a lot more done on this in biomedicine, but I think it’s a pretty interesting direction.

And even before we know the details, there are already things we can start to see.

General phenomena. For example related to computational irreducibility.

You know, it’s interesting to compare a biological system with a big computer program. Like an operating system.

Both of them are set up in a certain way, then have to respond to all sorts of stimuli.

Both of them gradually build up more and more cruft. And eventually die.

Only to be restarted, or reborn in the next generation.

In medicine, we’ve classified things that can go wrong—we’ve got our ICD-9 codes, or whatever.

We could imagine doing the same kind of thing for an operating system.

Diseases of the display subsystem. Memory allocation failure. And so on.

In the operating system we do, at least in principle, know how all the underlying pieces work.

But actually, at a diagnostic level, it’s still large-scale classes of behavior that seem most relevant.

One thing we realize, though, is how complicated the identification of “diseases” can be.

Maybe we’ll know that the disease is localized to some particular piece of code.

But usually there’s going to be an immense story about interactions with other pieces of code and so on. And an almost infinite number of variants.

It’ll be something that at some level is describable in algorithmic form. But it’s not going to fit neatly in an ICD-9 code, or whatever.

No doubt it’s the same in medicine. Ultimately there aren’t just discrete diseases and so on most of the time.

But that’s the way we have to set things up this way, because ultimately we only have a discrete set of possible actions—treatments—that we can apply.

One day this is all going to change.

Whether it’s through ubiquitous real-time sensors, and control systems based on those.

Or at a much more microscopic level. By not just having a drug that binds to some particular fixed active site.

But actual algorithmic drugs. Where individual molecules—or other nanoscale objects—can do computations and figure out what to do in real time.

Maybe—at least for a while—it’ll be convenient to package these things in complete synthetic organisms.

But one of the big lessons of studying the computational universe is that there are always lots of ways to do things.

So going through the whole scheme of current biology is unlikely to be necessary.

Instead, we’ll be able to get our computations and algorithms to run on much simpler nano-infrastructure.

Of course, that doesn’t mean that programming these things will be any easier.

In fact, I’ve no doubt the big issue all over the place will be computational irreducibility.

That even when we’ve carefully set up all the microscopic rules, knowing what their overall consequences are will be irreducibly hard.

You know, in the world of practical computing, we’re already used to a version of this phenomenon.

Because that’s why debugging is hard. Even if we can read the code, it can be fundamentally difficult to figure out how it will end up behaving.

Now, of course, that hasn’t stopped us building very large and successful software systems.

And nor will it stop us building analogous systems in biomedicine.

I shudder to think what all the regulatory aspects will be.

But in software we’ve developed all kinds of strategies for handling things.

For example, recognizing that there will always be bugs, and just managing all their priorities, and having pipelines for fixing, retesting, and so on.

I must say that in the future, as we have more medical information, I expect our own medical situations will look a lot more like that.

We’ll all know we have lots of little things wrong with us.

We’ll be getting priorities assigned to our bugs, and fixing the ones that aren’t too hard, and so on.

Actually, there’ll be a little more to it.

In software, we occasionally study how a particular system degrades when it runs longer—fragments its memory, or whatever.

But we’re usually pretty happy to reboot. In effect, force the system to die and restart.

Well, not with people.

So we need to study a lot more about how things evolve during the lifetime of the person.

Right now an awful lot looks like it’s just probabilities.

Given this or that genetic feature, or lab finding, there’s just a certain probability to have this or that go wrong.

It sounds a bit like in the financial markets. Where at first blush there’s a lot of randomness.

And the best one can do is try to get ahead of the probabilities, by analyzing fundamentals, hedging, and so on.

Well, perhaps we’ll do a little of that in medicine.

But I suspect that—despite computational irreducibility—we’re going to be able to do considerably better in making predictions.

There’ll come a time when all of us have giant health dashboards, with all kinds of measurements and their histories.

And then in effect simulations going on of what will happen, and what the effects of different choices or circumstances will be.

There’ll be a whole giant quant-like industry of automated and human advice about how to optimize this.

Computational irreducibility pretty much guarantees that there won’t be “one right answer”; there’ll be all sorts of detailed cases, that depend on unknowable future circumstances and so on.

Well, OK. So what does this look like in the shorter term?

It’s interesting to see what we’ve managed to do with Wolfram|Alpha so far.

For example, we’ve taken large public health studies, and made them computable.

So that we can ask all sorts of questions, and if the information is there, be able to compute answers to them.

And—though it’s been a very tricky business—we’re also soon going to be able to do the best Bayesian kind of thing going backward from symptoms to diagnoses.

There are many problems.

The most obvious are that data isn’t that clean. And there isn’t enough of it.

Actually, it’s very frustrating for us in a way.

You see, an important part of our business with Wolfram|Alpha is curating internal data for organizations, to set up custom Wolfram|Alpha experiences, often with onsite Wolfram|Alpha appliances and so on.

Well, we’ve now done that in lots of industries. Including healthcare.

And that means we’ve seen much more extensive health data.

But of course we can’t use it in our public system.

And at some level that’s always going to be necessary to protect privacy.

But what we need is a nice streamlined way to be able to have all the detailed data inside the system, so we can compute whatever is asked from it—but then have definite protocols for fuzzing things out to protect privacy.

I have to say that in completely different domains there are similar—though simpler—issues with secrecy and security, where the problems are solved.

So I’m hopeful that it’ll happen for medical data too.

Now of course what may happen—and we’re starting to see this—is that there will be things closer to social networks that build up. And it won’t be the medical establishment that’s getting us the next generation of medical information.

It’ll be individual people, motivated for all sorts of reasons to upload data.

Of course the data will be a bit messy, just as it always is. With wrong diagnoses, oversimplified coding, all kinds of biases, whatever.

But just having vastly more data will help so much.

And, you know, the data quality issue is going to solve itself.

Because increasingly what we’ll upload will come from automated sensors.

From a whole bunch of devices we wear and interact with.

It’s becoming so easy to store—and measure—so much.

I mean, someone like me has been an informational packrat for years. Archiving everything. Like measuring every keystroke I’ve typed in the last couple of decades.

And all sorts of other strange things, medical and otherwise.

There’s a whole industry of personal analytics that I think is going to grow up.

Ingesting data like that—in some cases curating it. Then computing things from it.

So we learn more about ourselves. So we can predict and optimize what we’re doing. Or at least be amused by it.

Soon image processing and video acquisition are going to get to the point where we can routinely get data that way too.

There’ll be a competition between instrumentation—RFID, QR codes, location-based systems—and analyzing images. Say to work out the nutrition content of something we’re eating.

But the end result of it all is that it’s going to become trivial for us to have amazing amounts of data—that effectively give us medical information.

There’s our genomes too. I got my whole genome sequenced last year, and so far I’ve been a bit disappointed by how little I’ve been able to figure out from it.

I don’t know what all the motivations will be yet, but somehow though, as the cost of sequencing goes way down, we’re going to find lots of people getting sequences, and uploading them.

No doubt we’ll be able to extrapolate to past generations, and compare with genealogical records, and gradually fill in all sorts of things.

Right now if we want to know the effects of different kinds of interventions, pretty much all we can do is to mine the medical literature, hopefully as automatically as possible.

And for extreme interventions that’ll probably be all we ever have—though in each case there’ll be vastly more raw data collected.

But for milder interventions… well, there we should be able to see what’s going on in much more of a crowdsourced way.

Now, let’s say each of us is collecting all this ongoing data on ourselves.

How do we figure out what it means? We can do it as sort of a lookup, comparing with existing data. Or we can actually try to compute, with models.

In time, I’m sure the models will win out. And there’ll be a lot of pressure to have them, because that’ll be the only way to assess possible interventions and courses of action.

You know, in the short term, I think what you’ll see is that when you enter symptoms in Wolfram|Alpha, if you’ve also uploaded personal analytics data, then the probabilities for different things will get a little narrower.

Eventually, there’ll be all sorts of detailed predictions and scenarios that can be described.

At first, it’ll just be tweaks to known approaches and treatments.

But I’m guessing that as we know more, we’ll see more and more “custom situations”. So we’ll really be forced to compute things—to mass customize, and to automate the process of coming up with new, creative, discoveries.

In biomedicine, we’ve seen a certain amount of things like random screening of possible drug candidates and so on.

But from understanding the computational universe, we realize there’s vastly more that can be done.

Actually, in building Wolfram|Alpha, and even the current Mathematica, we’ve routinely been doing “algorithm discovery”: in effect just searching the computational universe, and finding programs that we can mine to use for particular purposes.

And that’s the kind of approach that we should be able to use with what amount to the procedures as well as the materials of biomedicine.

Well, I think I’ve already gone on too long; I’d better stop here.

But I hope I’ve been able to give you a little flavor of how I currently see the bio–IT world.

There are a lot of exciting developments ahead. And I’m pleased that it seems as if—between Wolfram|Alpha, Mathematica, and the science of the computational universe—we’re going to be able to make some contributions to what can be done.

Thanks very much.

Photo courtesy of Mark Gabrenya, Bio-IT World.