Towards a Science of Metamathematics
One of the many surprising things about our Wolfram Physics Project is that it seems to have implications even beyond physics. In our effort to develop a fundamental theory of physics it seems as if the tower of ideas and formalism that we’ve ended up inventing are actually quite general, and potentially applicable to all sorts of areas.
One area about which I’ve been particularly excited of late is metamathematics—where it’s looking as if it may be possible to use our formalism to make what might be thought of as a “bulk theory of metamathematics”.
Mathematics itself is about what we establish about mathematical systems. Metamathematics is about the infrastructure of how we get there—the structure of proofs, the network of theorems, and so on. And what I’m hoping is that we’re going to be able to make an overall theory of how that has to work: a formal theory of the large-scale structure of metamathematics—that, among other things, can make statements about the general properties of “metamathematical space”.
Like with physical space, however, there’s not just pure underlying “geometry” to study. There’s also actual “geography”: in our human efforts to do mathematics over the last few millennia, where in metamathematical space have we gone, and “colonized”? There’ve been a few million mathematical theorems explicitly published in the history of human mathematics. What does the “empirical metamathematics” of them reveal? Some of it presumably reflects historical accidents, but some may instead reflect general features of metamathematics and metamathematical space.
I’ve wondered about empirical metamathematics for a long time, and tucked away on page 1176 at the end of the Notes for the section about “Implications for Mathematics and Its Foundations” in A New Kind of Science is something I wrote more than 20 years ago about it:
This note is mostly about what a descriptive theory of empirical metamathematics might be like—for example characterizing what one might mean by a powerful theorem, a deep theorem, a surprising theorem and so on. But at the end of the note is a graph: an actual piece of quantitative empirical metamathematics, based on the best-known structured piece of mathematics in history—Euclid’s Elements.
The graph shows relationships between theorems in the Elements: a kind of causal graph of how different theorems make use of each other. As presented in A New Kind of Science, it’s a small “footnote item” that doesn’t look like much. But for more than 20 years, I’ve kept wondering what more there might be to learn from it. And now that I’m trying to make a general theory of metamathematics, it seemed like it was a good time to try to find out…
The Most Famous Math Book in History
Euclid’s Elements is an impressive achievement. Written in Greek around 300 BC (though presumably including many earlier results), the Elements in effect defined the way formal mathematics is done for more than two thousand years. The basic idea is to start from certain axioms that are assumed to be true, then—without any further “input from outside”—use purely deductive methods to establish a collection of theorems.
Euclid effectively had 10 axioms (5 “postulates” and 5 “common notions”), like “one can draw a straight line from any point to any other point”, or “things which equal the same thing are also equal to one another”. (One of his axioms was his fifth postulate—that parallel lines never meet—which might seem obvious, but which actually turns out not to be true for physical curved space in our universe.)
On the basis of his axioms, Euclid then gave 465 theorems. Many were about 2D and 3D geometry; some were about arithmetic and numbers. Among them were many famous results, like the Pythagorean theorem, the triangle inequality, the fact that there are five Platonic solids, the irrationality of ![]() and the fact that there are an infinite number of primes. But certainly not all of them are famous—and some seem to us now pretty obscure. And in what has remained a (sometimes frustrating) tradition of pure mathematics for more than two thousand years, Euclid never gives any narrative about why he’s choosing the theorems he does, out of all the infinitely many possibilities.
and the fact that there are an infinite number of primes. But certainly not all of them are famous—and some seem to us now pretty obscure. And in what has remained a (sometimes frustrating) tradition of pure mathematics for more than two thousand years, Euclid never gives any narrative about why he’s choosing the theorems he does, out of all the infinitely many possibilities.
We don’t have any original Euclids, but versions from a few centuries later exist. They’re written in Greek, with each theorem explained in words, usually by referring to a diagram. Mathematical notation didn’t really start getting invented until the 1400s or so (i.e. a millennium and a half later)—and even the notation for numbers in Euclid’s time was pretty unwieldy. But Euclid had basically modern-looking diagrams, and he even labeled points and angles with (Greek) letters—despite the fact that the idea of variables standing for numbers wouldn’t be invented until the end of the 1500s.
There’s a stylized—almost “legalistic”—way that Euclid states his theorems. And so far as we can tell, in the original version, all that was done was to state theorems; there was no explanation for why a theorem might be true—no proof offered. But it didn’t take long before people started filling in proofs, and there was soon a standard set of proofs, in which each particular theorem was built up from others—and ultimately from the axioms.
There’ve been more than a thousand editions of Euclid printed (probably more than any other book except the Bible), and reading Euclid was until quite recently part of any serious education. (At Eton—where I went to high school—it was only in the 1960s that learning “mathematics” began to mean much other than reading Euclid, in the original Greek of course.) Here’s an edition of Euclid from the 1800s that I happen to own, with the proof of every theorem giving little references to other theorems that are used:

But so what about the metamathematics of Euclid? Given all those theorems—and proofs—can we map out the structure of what Euclid did? That’s what the graph in A New Kind of Science was about. A few years ago, we put the data for that graph into our Wolfram Data Repository—and I looked at it again, but nothing immediately seemed to jump out about it; it still just seemed like a complicated mess:
What else happened? One thing is that we added automated theorem proving to Mathematica and the Wolfram Language. Enter a potential theorem, and axioms from which to derive it, and FindEquationalProof will try to generate a proof. This works well for “structurally simple” mathematical systems (like basic logic), and indeed one can generate proofs with complex networks of lemmas that go significantly beyond what humans can do (or readily understand):

✕
FindEquationalProof[p\[CenterDot]q == q\[CenterDot]p, \!\(
\*SubscriptBox[\(\[ForAll]\), \({a, b,
c}\)]\(\((\((a\[CenterDot]b)\)\[CenterDot]c)\)\[CenterDot]\((a\
\[CenterDot]\((\((a\[CenterDot]c)\)\[CenterDot]a)\))\) ==
c\)\)]["ProofGraph"]
|
It’s in principle possible to use these methods to prove theorems in Euclidean geometry too. But it’s a different problem to make the proofs readily understandable to humans (like the step-by-step solutions of Wolfram|Alpha). So at least for now—even after 2000 years—the most effective source of information about the empirical metamathematics of proofs of Euclid’s theorems is still basically going to be Euclid’s Elements.
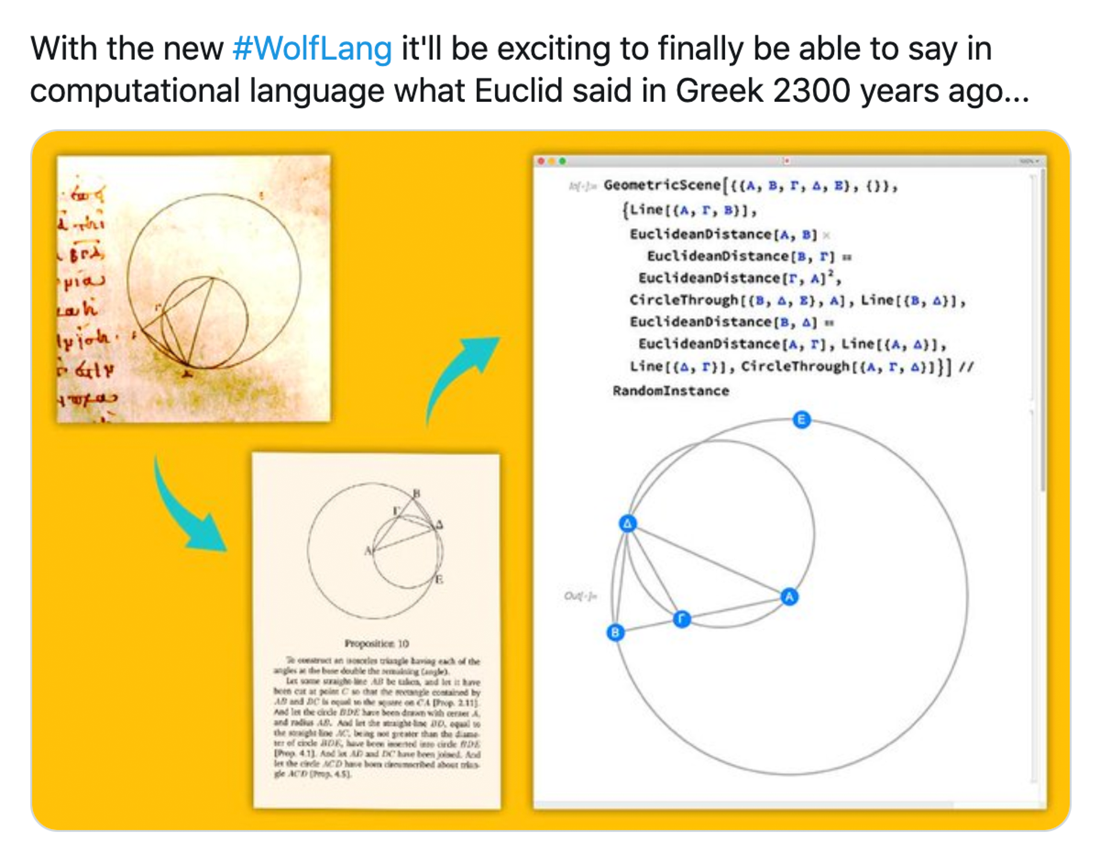
But when it comes to representing Euclid’s theorems there’s something new. The whole third-of-a-century story of the Wolfram Language has been about finding ways to represent more and more things in the world computationally. I had long wondered what it would take to represent Euclid-style geometry computationally. And in April I was excited to announce that we’d managed to do it:
Basic Statistics of Euclid
Euclid’s Elements is divided into 13 “books”, containing a total of 465 theorems (and 131 definitions):

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; Module[{g, h},
g[expr_] := Style[Row[{"(", expr, ")"}], Italic, Gray, 10];
h[expr_] := Style[expr, Italic, FontFamily -> "Source Sans Pro"];
Text[Grid[
MapIndexed[
Prepend[#,
Style[{"subjects", "books", "theorems", "totals", "definitions",
"totals"}[[First[#2]]], Italic,
FontFamily -> "Source Sans Pro"]] &, {{h[
"2D geometry"], \[SpanFromLeft], \[SpanFromLeft], \
\[SpanFromLeft], \[SpanFromLeft], \[SpanFromLeft],
h["numbers"], \[SpanFromLeft], \[SpanFromLeft], \[SpanFromLeft],
h["3D geometry"], \[SpanFromLeft], \[SpanFromLeft]},
Style[#, Italic, Smaller] & /@ Range[13], {48, 14, 37, 16, 25,
33, 39, 27, 36, 115, 39, 18,
18}, {g[173], \[SpanFromLeft], \[SpanFromLeft], \
\[SpanFromLeft], \[SpanFromLeft], \[SpanFromLeft],
g[217], \[SpanFromLeft], \[SpanFromLeft], \[SpanFromLeft],
g[75], \[SpanFromLeft], \[SpanFromLeft]}, {23, 2, 11, 7, 18, 4,
22, 0, 0, 16, 28, 0,
0}, {g@
65, \[SpanFromLeft], \[SpanFromLeft], \[SpanFromLeft], \
\[SpanFromLeft], \[SpanFromLeft],
g@38, \[SpanFromLeft], \[SpanFromLeft], \[SpanFromLeft],
g@28, \[SpanFromLeft], \[SpanFromLeft]}}],
Background -> {Prepend[
Composition[Lighter[#, 0.4] &, bookColor] /@ Range[13],
GrayLevel[0.9]], None}, Frame -> All]]]
|
Stating the theorems takes 9589 words (about 60k characters) of Greek (about 13,000 words in a standard English translation). (The 10 axioms take another 115 words in Greek or about 140 in English, and the definitions another 2369 words in Greek or about 3300 in English.)
A typical theorem (or “proposition”)—in this case Book 1, Theorem 20—is stated as:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; GreekEnglishShort[<| "Book" -> 1, "Theorem" -> 20|>] |
(This is what we now call the triangle inequality. And of course, to make this statement we have to have defined what a triangle is, and Euclid does that earlier in Book 1.)
If we look at the statements of Euclid’s theorems in Greek (or in English), there’s a distribution of lengths (colored here by subjects, and reasonably fit by a Pascal distribution):

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; GraphicsRow[
MapThread[
Function[{t, l}, Module[{dataE = WordCount[#[t]] & /@ eus, dataG},
dataG =
GroupBy[If[MissingQ[#[[1]]["Book"]],
0 -> #[[2]], #[[1]]["Book"] -> #[[2]]] & /@ Normal[dataE],
First -> Last];
Histogram[
Flatten[Join[Values[dataG[[Key /@ #]]]]] & /@ {{0}, {1, 2, 3, 4,
5, 6}, {7, 8, 9, 10}, {11, 12, 13}}, {1}, Frame -> True,
PlotRange -> All, FrameLabel -> {l, None},
FrameTicks -> {Automatic, None}, ChartLayout -> "Stacked",
ChartBaseStyle -> Opacity[1],
ChartStyle -> {bookColorIntense /@ {0, 6, 10, 13},
EdgeForm[Directive[Thin, GrayLevel[0.15]]]}]]], {{"GreekText",
"Text"}, {"Greek words", "English words"}}]]
|
The “outlier” longest-to-state theorem (in both Greek and English) is the rather unremarkable 103-Greek-word 3.8

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; GreekEnglish[<|"Book" -> 3, "Theorem" -> 8|>, 12] |
which can be illustrated as:

✕
GeometricScene[
{A, B, C, D, E, F, G, H, K, L, M},
{
GeometricAssertion[{D}, {"Outside", CircleThrough[{A, B, C}, M]}],
GeometricAssertion[{A, B, C, E, F, G, H, K, L}, "Distinct"],
Line[{D, G, M, A}],
Line[{{D, K, E}, {D, L, F}, {D, H, C}}],
CircleThrough[{A, B, C, E, F, G, H, K, L}, M],
GeometricAssertion[{A, E, F, C, H, L, K, G, B},
"CyclicallyOrdered"],
Style[{Line[{M, K}], Line[{M, L}], Line[{M, H}], Line[{M, C}],
Line[{M, F}], Line[{M, E}]}, Dashed],
PlanarAngle[{D, M, B}] == PlanarAngle[{D, M, K}],
Line[{D, B}]
}(*,
{
EuclideanDistance[D,A]>EuclideanDistance[D,E]>EuclideanDistance[D,
F]>EuclideanDistance[D,C],
EuclideanDistance[D,G]<EuclideanDistance[D,K]<EuclideanDistance[D,
L]<EuclideanDistance[D,H],
EuclideanDistance[D,B]==EuclideanDistance[D,K]
}*)
] // RandomInstance
|
(The runner-up, at about two-thirds the length, is the also rather unremarkable 11.35.)
The nominally shortest-to-state theorems are in Book 10, Theorems 85 through 90, and all have just 4 Greek words:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; GreekEnglish[<|"Book" -> 10, "Theorem" -> 85|>] |
⋮

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; GreekEnglishShort[<|"Book" -> 10, "Theorem" -> 90|>] |
The shortness of these theorems is a bit of a cheat, since the successive “apotomes” (pronounced /əˈpɒtəmi/ like “hippopotamus”) actually have quite long definitions that are given elsewhere. And, yes, some emphasis in math has changed in the past 2000+ years; you don’t hear about apotomes these days. (An apotome is a number x – y where ![]() isn’t rational, but
isn’t rational, but ![]() is—as for
is—as for ![]() , y = 1. It’s difficult enough to describe even this without math notation. But then for a “first apotome” Euclid added the conditions that both
, y = 1. It’s difficult enough to describe even this without math notation. But then for a “first apotome” Euclid added the conditions that both ![]() and x must be rational—all described in words.)
and x must be rational—all described in words.)
At five words, we’ve got one more familiar theorem (3.30) and another somewhat obscure one (10.26):
|
✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; GreekEnglishShort[<|"Book" -> 3, "Theorem" -> 30|>] |
|
✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; GreekEnglishShort[<|"Book" -> 10, "Theorem" -> 26|>] |
In our modern Wolfram Language representation, we’ve got a precise, symbolic way to state Euclid’s theorems. But Euclid had to rely on natural language (in his case, Greek). Some words he just assumed people would know the meanings of. But others he defined. Famously, he started at the beginning of Book 1 with his Definition 1—and in a sense changing how we think about this is what launched our whole Physics Project:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; GreekEnglishShort[<|"Book" -> 1, "Definition" -> 1|>] |
There is at least an implicit network of dependencies among Euclid’s definitions. Having started by defining points and lines, he moves on to defining things like triangles, and equilaterality, until eventually, for example, by Book 11 Definition 27 he’s saying things like “An icosahedron is a solid figure contained by twenty equal and equilateral triangles”.
Of course, Euclid didn’t ultimately have to set up definitions; he could just have repeated the content of each definition every time he wanted to refer to that concept. But like words in natural language—or functions in our computational language—definitions are an important form of compression for making statements. And, yes, you have to pick the right definitions to make the things you want to say easy to say. And, yes, your definitions will likely play at least some role in determining what kinds of things you choose to talk about. (Apotomes, anyone?)
The Interdependence of Theorems
All the theorems Euclid states represent less than 10,000 words of Greek. But the standard proofs of them are perhaps 150,000 words of Greek. (They’re undoubtedly not minimal proofs—but the fact that the same ones are being quoted after more than 2000 years presumably tells us at least something.)
Euclid is very systematic. Every theorem throughout the course of his Elements is proved in terms of earlier theorems (and ultimately in terms of his 10 axioms). Thus, for example, the proof of 1.14 (i.e. Book 1, Theorem 14) uses 1.13 as well as the axioms P2 (i.e. Postulate 2), P4, CN1 (i.e. Common Notion 1) and CN3. By the time one’s got to 12.18 the proof is written only in terms of other theorems (in this case 12.17, 12.2, 5.14 and 5.16) and not directly in terms of axioms.
The total number of theorems (or axioms) directly referenced in a given proof varies from 0 (for axioms) to 21 (for 12.17, which is about inscribing polyhedra in spheres); the average is 4.3:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Histogram[
Module[{vod = # -> VertexOutDegree[euc, #] & /@ VertexList[euc],
dataG}, dataG =
GroupBy[If[MissingQ[#[[1]]["Book"]],
0 -> #[[2]], #[[1]]["Book"] -> #[[2]]] & /@ vod, First -> Last];
Flatten[Join[Values[dataG[[Key /@ #]]]]] & /@ {{0}, {1, 2, 3, 4, 5,
6}, {7, 8, 9, 10}, {11, 12, 13}}
], {1}, Frame -> True,
FrameLabel -> {"number of theorems directly referenced"},
ChartLayout -> "Stacked", ChartBaseStyle -> Opacity[1],
ChartStyle -> {bookColorIntense /@ {0, 6, 10, 13},
EdgeForm[Directive[Thin, GrayLevel[0.15]]]}]
|
If we put Euclid’s axioms and theorems in order, we can represent which axioms or theorems occur in a given proof by an arrangement of dots across the page. For example, for 1.12 through 1.17 we have:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
With[{axiomcol = bookColorDarker[0], geom2dcol = bookColor[1]},
Grid[With[{head =
Composition[Text, Style[#, 13] &, EuclidVertexName] /@
Take[SortBy[VertexList[euc], Length], 26]},
Prepend[Table[
Prepend[If[
MemberQ[Rest[
VertexOutComponent[euc, <|"Book" -> 1, "Theorem" -> n|>,
1]], #], Style["\[FilledCircle]", 10], ""] & /@
Take[SortBy[VertexList[euc], Length], 25],
Text[Style[EuclidVertexName[<|"Book" -> 1, "Theorem" -> n|>],
13]]], {n, 12, 17}], Prepend[head, ""]]],
Background -> {1 -> GrayLevel[.9],
1 -> GrayLevel[.9], {{{2, -1}, {2, 11}} ->
axiomcol, {{2, -1}, {12, -1}} -> geom2dcol}}, Frame -> All,
FrameStyle -> GrayLevel[.7], ItemSize -> All,
Spacings -> {0.2, 0.2}]]
|
Doing this for all the theorems we get:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"key", "=",
RowBox[{"MapIndexed", "[",
RowBox[{
RowBox[{
RowBox[{"#", "\[Rule]",
RowBox[{"First", "[", "#2", "]"}]}], "&"}], ",",
RowBox[{
RowBox[{"GatherBy", "[",
RowBox[{
RowBox[{"VertexList", "[", "euc", "]"}], ",", "Length"}],
"]"}], "[",
RowBox[{"[", "1", "]"}], "]"}]}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"bookmarkers", "=",
RowBox[{"Append", "[",
RowBox[{
RowBox[{"First", "/@",
RowBox[{"Table", "[",
RowBox[{
RowBox[{"FirstPosition", "[",
RowBox[{
RowBox[{"First", "/@", "key"}], ",",
RowBox[{"<|",
RowBox[{
RowBox[{"\"\<Book\>\"", "\[Rule]", "b"}], ",",
RowBox[{"\"\<Theorem\>\"", "\[Rule]", "_"}]}], "|>"}]}],
"]"}], ",",
RowBox[{"{",
RowBox[{"b", ",", "13"}], "}"}]}], "]"}]}], ",",
RowBox[{"Length", "[", "key", "]"}]}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"ListPlot", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{"1", ",",
RowBox[{"-", "1"}]}], "}"}], "*", "#"}], "&"}], "/@",
RowBox[{"DeleteCases", "[",
RowBox[{
RowBox[{"Reverse", "/@",
RowBox[{"(",
RowBox[{"List", "@@@",
RowBox[{"(",
RowBox[{
RowBox[{"EdgeList", "[", "euc", "]"}], "/.", "key"}],
")"}]}], ")"}]}], ",",
RowBox[{"{",
RowBox[{"x_", ",", "x_"}], "}"}]}], "]"}]}], ",",
RowBox[{"PlotStyle", "\[Rule]", "Black"}], ",",
RowBox[{"AspectRatio", "\[Rule]", "1"}], ",",
RowBox[{"GridLines", "\[Rule]",
RowBox[{"{",
RowBox[{"bookmarkers", ",",
RowBox[{"-", "bookmarkers"}]}], "}"}]}], ",",
RowBox[{"Ticks", "\[Rule]", "None"}], ",",
RowBox[{"PlotRange", "->",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"-", "10"}], ",", "460"}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"-", "468"}], ",",
RowBox[{"-", "10"}]}], "}"}]}], "}"}]}], ",", " ",
RowBox[{"Epilog", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"MapIndexed", "[",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"Style", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"Text", "[",
RowBox[{
RowBox[{"#2", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"Mean", "[", "#1", "]"}], ",", "5"}],
"}"}]}], "]"}], ",",
RowBox[{"Text", "[",
RowBox[{
RowBox[{"#2", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"-", "5"}], ",",
RowBox[{"-",
RowBox[{"Mean", "[", "#1", "]"}]}]}], "}"}]}],
"]"}]}], "}"}], ",", "14"}], "]"}], ",",
RowBox[{"bookColorDarker", "[",
RowBox[{"#2", "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}], ",",
RowBox[{"Opacity", "[", ".3", "]"}], ",",
RowBox[{"Rectangle", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"#1", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"-", "465"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"#1", "[",
RowBox[{"[", "2", "]"}], "]"}], ",", "0"}], "}"}]}],
"]"}], ",",
RowBox[{"Rectangle", "[",
RowBox[{
RowBox[{"{",
RowBox[{"0", ",",
RowBox[{"-",
RowBox[{"#1", "[",
RowBox[{"[", "2", "]"}], "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{"465", ",",
RowBox[{"-",
RowBox[{"#1", "[",
RowBox[{"[", "1", "]"}], "]"}]}]}], "}"}]}], "]"}]}],
"}"}], "&"}], ",",
RowBox[{"Partition", "[",
RowBox[{"bookmarkers", ",", "2", ",", "1"}], "]"}]}], "]"}],
",",
RowBox[{"GrayLevel", "[", ".6", "]"}], ",",
RowBox[{"Opacity", "[", ".3", "]"}], ",",
RowBox[{"Rectangle", "[",
RowBox[{
RowBox[{"{",
RowBox[{"0", ",", "0"}], "}"}], ",",
RowBox[{"{",
RowBox[{"465", ",", "20"}], "}"}]}], "]"}], ",",
RowBox[{"Rectangle", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"-", "10"}], ",",
RowBox[{"-", "465"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{"0", ",", "0"}], "}"}]}], "]"}]}], "}"}]}]}],
"]"}]], "Input"]
}, Open ]]
|
We can see there’s lots of structure here. For example, there are clearly “popular” theorems near the beginning of Book 6 and Book 10, to which lots of at least “nearby” theorems refer. There are also “gaps”: ranges of theorems that no theorems in a given book refer to.
At a coarse level, something we can do is to look at cross-referencing within and between books:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"books", "=",
RowBox[{"{",
RowBox[{
RowBox[{"\"\<Book\>\"", "\[Rule]", "1"}], ",",
RowBox[{"\"\<Book\>\"", "\[Rule]", "2"}], ",",
RowBox[{"\"\<Book\>\"", "\[Rule]", "3"}], ",",
RowBox[{"\"\<Book\>\"", "\[Rule]", "4"}], ",",
RowBox[{"\"\<Book\>\"", "\[Rule]", "5"}], ",",
RowBox[{"\"\<Book\>\"", "\[Rule]", "6"}], ",",
RowBox[{"\"\<Book\>\"", "\[Rule]", "7"}], ",",
RowBox[{"\"\<Book\>\"", "\[Rule]", "8"}], ",",
RowBox[{"\"\<Book\>\"", "\[Rule]", "9"}], ",",
RowBox[{"\"\<Book\>\"", "\[Rule]", "10"}], ",",
RowBox[{"\"\<Book\>\"", "\[Rule]", "11"}], ",",
RowBox[{"\"\<Book\>\"", "\[Rule]", "12"}], ",",
RowBox[{"\"\<Book\>\"", "\[Rule]", "13"}]}], "}"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"vertexweights", "=",
RowBox[{"Select", "[",
RowBox[{
RowBox[{"Tally", "[",
RowBox[{
RowBox[{
RowBox[{"First", "[",
RowBox[{"Normal", "[", "#", "]"}], "]"}], "&"}], "/@",
RowBox[{"VertexList", "[", "euc", "]"}]}], "]"}], ",",
RowBox[{
RowBox[{"MemberQ", "[",
RowBox[{"books", ",",
RowBox[{"First", "[", "#", "]"}]}], "]"}], "&"}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"edgeweights", "=",
RowBox[{"Select", "[",
RowBox[{
RowBox[{"Tally", "[",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"Normal", "[", "#", "]"}], "[",
RowBox[{"[",
RowBox[{"1", ",", "1"}], "]"}], "]"}], ",",
RowBox[{
RowBox[{"Normal", "[", "#", "]"}], "[",
RowBox[{"[",
RowBox[{"2", ",", "1"}], "]"}], "]"}]}], "}"}], "&"}], "/@",
RowBox[{"EdgeList", "[", "euc", "]"}]}], "]"}], ",",
RowBox[{
RowBox[{"MemberQ", "[",
RowBox[{"books", ",",
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "2"}], "]"}], "]"}]}], "]"}], "&"}]}],
"]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"bookweights", "=",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"Last", "[",
RowBox[{"First", "[", "#", "]"}], "]"}], ",",
RowBox[{"Last", "[", "#", "]"}]}], "}"}], "&"}], "/@",
"vertexweights"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"edgesout", "=",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "1", ",", "1", ",", "2"}], "]"}], "]"}],
",",
RowBox[{"Total", "[",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "]"}]}], "}"}], "&"}], "/@",
RowBox[{"(",
RowBox[{"Transpose", "/@",
RowBox[{"GatherBy", "[",
RowBox[{"edgeweights", ",",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "1"}], "]"}], "]"}], "&"}]}], "]"}]}],
")"}]}]}], ";"}]], "Input"],
Cell[BoxData[{
RowBox[{
RowBox[{
RowBox[{"normalizededgeweights", "=",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"DirectedEdge", "[",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "1", ",", "2"}], "]"}], "]"}], ",",
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "2", ",", "2"}], "]"}], "]"}]}], "]"}],
"\[Rule]",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "/",
RowBox[{"edgesout", "[",
RowBox[{"[",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "1", ",", "2"}], "]"}], "]"}], ",",
"2"}], "]"}], "]"}]}]}], "&"}], "/@", "edgeweights"}]}],
";"}], "\n"}], "\[IndentingNewLine]",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"diskedLine", "[",
RowBox[{"{",
RowBox[{"line_", ",", "radii_"}], "}"}], "]"}], ":=",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"RegionIntersection", "[",
RowBox[{
RowBox[{"Line", "[", "line", "]"}], ",",
RowBox[{"Circle", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"radii", "[",
RowBox[{"[", "1", "]"}], "]"}]}], "]"}]}], "]"}], "[",
RowBox[{"[",
RowBox[{"1", ",", "1"}], "]"}], "]"}], ",",
RowBox[{
RowBox[{"RegionIntersection", "[",
RowBox[{
RowBox[{"Line", "[", "line", "]"}], ",",
RowBox[{"Circle", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"[", "2", "]"}], "]"}], ",",
RowBox[{"radii", "[",
RowBox[{"[", "2", "]"}], "]"}]}], "]"}]}], "]"}], "[",
RowBox[{"[",
RowBox[{"1", ",", "1"}], "]"}], "]"}]}], "}"}]}], ";"}],
"\n"}], "\[IndentingNewLine]",
RowBox[{
RowBox[{
RowBox[{"weightedArrow", "[",
RowBox[{"line_", ",", "weight_"}], "]"}], ":=",
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
"len", ",", "start", ",", "end", ",", "angle", ",", "thick",
",", "rec", ",", "mid"}], "}"}], ",",
RowBox[{
RowBox[{"start", "=",
RowBox[{"line", "[",
RowBox[{"[", "1", "]"}], "]"}]}], ";",
RowBox[{"end", "=",
RowBox[{"line", "[",
RowBox[{"[", "2", "]"}], "]"}]}], ";",
RowBox[{"mid", "=",
RowBox[{"Mean", "[", "line", "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"len", "=",
RowBox[{"EuclideanDistance", "[",
RowBox[{"start", ",", "end"}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"angle", "=",
RowBox[{"Arg", "[",
RowBox[{
RowBox[{"(",
RowBox[{"start", "-", "end"}], ")"}], ".",
RowBox[{"{",
RowBox[{"1", ",", "I"}], "}"}]}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"thick", "=",
RowBox[{"weight", "/", "len"}]}], ";", "\[IndentingNewLine]",
RowBox[{"rec", "=",
RowBox[{
RowBox[{
RowBox[{"#", "+", "mid"}], "&"}], "/@",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"RotationMatrix", "[", "angle", "]"}], ".", "#"}],
"&"}], "/@",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"-", "len"}], "/", "2"}], ",",
RowBox[{
RowBox[{"-", "thick"}], "/", "2"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"len", "/", "2"}], ",",
RowBox[{
RowBox[{"-", "thick"}], "/", "2"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"len", "/", "2"}], ",",
RowBox[{"thick", "/", "2"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"-", "len"}], "/", "2"}], ",",
RowBox[{"thick", "/", "2"}]}], "}"}]}], "}"}]}],
")"}]}]}], ";", "\[IndentingNewLine]",
RowBox[{"Polygon", "[", "rec", "]"}]}]}], "]"}]}],
";"}]}], "Input"],
Cell[BoxData[
RowBox[{"Labeled", "[",
RowBox[{
RowBox[{"Graph", "[",
RowBox[{
RowBox[{"Range", "[", "13", "]"}], ",",
RowBox[{"First", "/@", "normalizededgeweights"}], ",",
RowBox[{"EdgeStyle", "\[Rule]",
RowBox[{"Thread", "[",
RowBox[{
RowBox[{"First", "/@", "normalizededgeweights"}], "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"AbsoluteThickness", "[",
RowBox[{"15", " ",
RowBox[{"Last", "[", "#", "]"}]}], "]"}], ",",
RowBox[{"bookColorIntense", "[",
RowBox[{"First", "[",
RowBox[{"First", "[", "#", "]"}], "]"}], "]"}], ",",
RowBox[{"Arrowheads", "[",
RowBox[{
RowBox[{"Last", "[", "#", "]"}], "/", "15"}], "]"}]}],
"}"}], "&"}], "/@", "normalizededgeweights"}], ")"}]}],
"]"}]}], ",",
RowBox[{"VertexSize", "\[Rule]",
RowBox[{"Thread", "[",
RowBox[{
RowBox[{"First", "/@", "bookweights"}], "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"1.5", " ",
RowBox[{
RowBox[{"Sqrt", "[", "#", "]"}], "/", "20"}]}], "&"}], "/@",
RowBox[{"(",
RowBox[{"Last", "/@", "bookweights"}], ")"}]}], ")"}]}],
"]"}]}], ",",
RowBox[{"VertexStyle", "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "#", "]"}], ",",
RowBox[{"EdgeForm", "[",
RowBox[{"Darker", "[",
RowBox[{
RowBox[{"bookColorIntense", "[", "#", "]"}], ",",
".2"}], "]"}], "]"}]}], "}"}]}], "&"}], "/@",
RowBox[{"Range", "[", "13", "]"}]}], ")"}]}], ",",
RowBox[{"GraphLayout", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{
"\"\<VertexLayout\>\"", "\[Rule]", " ",
"\"\<SpringElectricalEmbedding\>\""}], ",",
RowBox[{"\"\<SelfLoopRadius\>\"", "\[Rule]", " ", "1"}]}],
"}"}]}], ",",
RowBox[{"VertexLabels", "\[Rule]",
RowBox[{"Placed", "[",
RowBox[{"Automatic", ",", "Center"}], "]"}]}], ",",
RowBox[{"PerformanceGoal", "\[Rule]", "\"\<Quality\>\""}], ",",
RowBox[{"BaseStyle", "\[Rule]", "13"}]}], "]"}], ",",
RowBox[{"Row", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"Row", "[",
RowBox[{"#", ",",
RowBox[{"Spacer", "[", "0.005", "]"}]}], "]"}], "&"}], "/@",
RowBox[{"Transpose", "[",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "/@",
RowBox[{"{",
RowBox[{"6", ",", "10", ",", "13"}], "}"}]}], ",",
RowBox[{
RowBox[{
RowBox[{"Style", "[",
RowBox[{"#", ",",
RowBox[{
"FontFamily", "\[Rule]", "\"\<Source Sans Pro\>\""}],
",",
RowBox[{"GrayLevel", "[", "0.3", "]"}], ",",
RowBox[{"FontSize", "\[Rule]", "16"}]}], "]"}], "&"}], "/@",
RowBox[{"{",
RowBox[{
"\"\<2D geometry\>\"", ",", " ", "\"\<numbers\>\"", ",",
"\"\<3D geometry\>\""}], "}"}]}]}], "}"}], "]"}]}], ",",
RowBox[{"Spacer", "[", "20", "]"}]}], "]"}]}], "]"}]], "Input"]
}, Open ]]
|
The size of each node represents the number of theorems in each book. The thickness of each arrow represents the fraction of references in the proofs of those theorems going to different books. The self-loops are from theorems in a given book that refer to theorems in the same book. Needless to say, the self-loop is large for Book 1, since it doesn’t have any previous book to refer to. Book 7 again has a large self-loop, because it’s the first book about numbers, and doesn’t refer much to the earlier books (which are about 2D geometry).
It’s interesting to see that Books 7, 8 and 9—which are about numbers rather than geometry—“keep to themselves”, even though Book 10, which is also about numbers, is more central. It’s also interesting to see the interplay between the books on 2D and 3D geometry over on the right-hand side of the graph.
But, OK, what about individual theorems? What is their network of dependencies?
Here’s 1.5, whose proof is given in terms of 1.3 and 1.4, as well as the axioms P1, P2 and CN3:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; EuclidGraphLarge[ Subgraph[euc, VertexOutComponent[euc, <|"Book" -> 1, "Theorem" -> 5|>, 1]]] |
But now we can continue this, and show what 1.3 and 1.4 depend on—all the way down to the axioms:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; EuclidGraphLarge[ Subgraph[euc, VertexOutComponent[euc, <|"Book" -> 1, "Theorem" -> 5|>, 2]]] |
Later theorems depend on much more. Here are the direct dependencies for 12.18:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; EuclidGraphLarge[ Subgraph[euc, VertexOutComponent[euc, <|"Book" -> 12, "Theorem" -> 18|>, 1]]] |
Here’s what happens if one goes another step:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; EuclidGraphLarge[ Subgraph[euc, VertexOutComponent[euc, <|"Book" -> 12, "Theorem" -> 18|>, 2]], VertexSize -> .9, BaseStyle -> 8, AspectRatio -> 1/3] |
Here’s 3 steps:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; EuclidGraphSmall[ Subgraph[euc, VertexOutComponent[euc, <|"Book" -> 12, "Theorem" -> 3|>, 3]], "Intense"] |
And here’s what happens if one goes all the way down to the axioms (which in this case takes 5 steps):

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; EuclidGraphSmall[ Subgraph[euc, VertexOutComponent[ euc, <|"Book" -> 12, "Theorem" -> 3|>]], "Intense"] |
Things look a little simpler if we consider the transitive reduction of this graph. We’re no longer faithfully representing what’s in the text of Euclid, but we’re still capturing the core dependency information. If theorem A in Euclid refers to B, and B refers to C, then even if in Euclid A refers to C we won’t mention that. And, yes, graph theoretically A→C is just the transitive closure of A→B and B→C. But it could still be that the pedagogical structure of the proof of theorem A makes it desirable to refer to theorem B, even if in principle one could rederive theorem B from theorem C.
Here’s the original 1-step graph for 12.18, along with its transitive reduction:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Row[Riffle[
EuclidGraphLarge[#[
Subgraph[euc,
VertexOutComponent[euc, <|"Book" -> 12, "Theorem" -> 18|>,
1]]], ImageSize -> {Automatic, 180}] & /@ {Identity,
TransitiveReductionGraph}, Spacer[50]]]
|
And here, by the way, is also the “fully pedantic” transitive closure, including all indirect connections, whether they’re mentioned by Euclid or not:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
EuclidGraphLarge[
TransitiveClosureGraph[
Subgraph[euc,
VertexOutComponent[euc, <|"Book" -> 12, "Theorem" -> 18|>, 1]]],
ImageSize -> {Automatic, 200}]
|
And now here’s the transitive reduction of the full 12.8 dependency graph, all the way down to the axioms:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
EuclidGraphSmall[
TransitiveReductionGraph[
Subgraph[euc,
VertexOutComponent[
euc, <|"Book" -> 12, "Theorem" -> 18|>]]], "Intense"]
|
And what all these graphs show is that even to prove one theorem, one’s making use of lots of other theorems. To make this quantitative, we can plot the total number of theorems that appear anywhere in the “full proof” of a given theorem, ultimately working all the way down to the axioms:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Module[{dataA =
If[MissingQ[#[["Book"]]],
Nothing, #[["Book"]] -> Length[VertexOutComponent[euc, #]]] & /@
VertexList[euc], vals, acc, xval},
vals = CountsBy[dataA, First];
acc = Association[
MapIndexed[First[#2] -> #1 &,
Accumulate[Values[CountsBy[dataA, First]]]]];
xval = Association[#[[1]] -> (#[[2]] - vals[#[[1]]]/2) & /@
Normal[acc]];
Show[{ListLinePlot[Values[dataA], Axes -> {False, True},
Frame -> True,
FrameLabel -> {"theorems by book", "theorems in full proof"},
FrameTicks -> {{True,
False}, {{#[[2]], #[[1]], {0, 0}} & /@ Normal[xval], False}},
Filling -> Axis, ColorFunctionScaling -> False,
ColorFunction ->
Function[{x, y},
Piecewise[{{bookColorIntense[6],
x <= acc[6]}, {bookColorIntense[10],
x <= acc[10]}, {bookColorIntense[13], x <= acc[13]}}]],
PlotRange -> All ],
Graphics[{GrayLevel[0.5],
Line[{{#, -5}, {#, 300}} & /@ Values[acc]]}]
}]]
|
At the beginnings of many of the books, there tend to be theorems that are proved more directly from the axioms, so they don’t depend on as much. But as one progresses through the books, one’s relying on more and more theorems—sometimes, as we saw above, in the same book, and sometimes in earlier books.
From the picture above, we can see that Euclid in a sense builds up to a “climax” at the end—with his very last theorem (13.18) depending on more theorems than anything else. We’ll be discussing “Euclid’s last theorem” some more below...
The Graph of All Theorems
OK, so what is the full interdependence graph for all the theorems in Euclid? It’s convenient to go the opposite way than in our previous graphs—and put the axioms at the top, and show how theorems below are derived from them. Here’s the graph one gets by doing that:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Labeled[ReverseGraph[euc,
GraphLayout -> {"LayeredDigraphEmbedding", "RootVertex" -> axioms},
AspectRatio -> 1/2, EdgeStyle -> GrayLevel[.5, .5],
VertexStyle -> (# -> EuclidVertexStyle[#, "Intense"] & /@
VertexList[euc]), VertexSize -> 6,
VertexLabels -> (# -> EuclidVertexName[#] & /@ VertexList[euc])],
Row[Row[#, Spacer[0.005]] & /@
Transpose[{bookColorIntense /@ {0, 6, 10, 13},
Style[#, FontFamily -> "Source Sans Pro", GrayLevel[0.3],
FontSize -> 11] & /@ {"axioms", "2D geometry", "numbers",
"3D geometry"}}], Spacer[20]]]
|
One can considerably simplify this by looking just at the transitive reduction graph (the full graph has 2054 connections; this reduction has 974, while if one went “fully pedantic” with transitive closure, one would have 25,377 connections):

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Graph[TransitiveReductionGraph[ReverseGraph[euc]],
GraphLayout -> {"LayeredDigraphEmbedding", "RootVertex" -> axioms},
AspectRatio -> 1/2, EdgeStyle -> GrayLevel[.5, .5],
VertexStyle -> (# -> EuclidVertexStyle[#, "Intense"] & /@
VertexList[euc]), VertexSize -> 1.7,
VertexLabels -> (# ->
Style[EuclidVertexName[#], Background -> Opacity[.4, White]] & /@
VertexList[euc])]
|
What can we see from this? Probably the most obvious thing is that the graphs start fairly sparse, then become much denser. And what this effectively means is that one starts off by proving certain “preliminaries”, and then after one’s done that, it unlocks a mass of other theorems. Or, put another way, if we were exploring this metamathematical space starting from the axioms, progress might seem slow at first. But after proving a bunch of preliminary theorems, we’d be able to dramatically speed up.
Here’s another view of this, plotting how many subsequent theorems depend on each different theorem:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Module[{dataA =
If[MissingQ[#[["Book"]]],
Nothing, #[["Book"]] -> Length[VertexInComponent[euc, #]]] & /@
VertexList[euc], vals, acc, xval},
vals = CountsBy[dataA, First];
acc = Association[
MapIndexed[First[#2] -> #1 &,
Accumulate[Values[CountsBy[dataA, First]]]]];
xval = Association[#[[1]] -> (#[[2]] - vals[#[[1]]]/2) & /@
Normal[acc]];
Show[{ListLinePlot[Values[dataA], Axes -> {False, True},
Frame -> True,
FrameLabel -> {"theorems by book", "dependent theorems"},
Filling -> Axis,
FrameTicks -> {{True,
False}, {{#[[2]], #[[1]], {0, 0}} & /@ Normal[xval], False}},
ColorFunctionScaling -> False,
ColorFunction ->
Function[{x, y},
Piecewise[{{bookColorIntense[6],
x <= acc[6]}, {bookColorIntense[10],
x <= acc[10]}, {bookColorIntense[13], x <= acc[13]}}]],
PlotRange -> All ],
Graphics[{GrayLevel[0.5],
Line[{{#, -5}, {#, 400}} & /@ Values[acc]]}]}]]
|
In a sense, this is complementary to the plot we made above, that showed how many theorems a given theorem depends on. (From a graph-theoretical point of view they’re very directly complementary: this plot involves VertexInComponent; the previous one involved VertexOutComponent.)
And what the plot shows is that there are a bunch of early theorems (particularly in Book 1) that have lots of subsequent theorems depending on them—so that they’re effectively foundational to much of what follows. The plot also shows that in most of the books the early theorems are the most “foundational”, in the sense that the most subsequent theorems depend on them.
By the way, we can also look at the overall form of the basic dependency graph, not layering it starting from the axioms:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Graph[euc,
VertexStyle -> (# -> EuclidVertexStyle[#, "Intense"] & /@
VertexList[euc]), VertexSize -> 3, EdgeStyle -> GrayLevel[.5, .5],
VertexLabels -> (# ->
Style[EuclidVertexName[#], GrayLevel[.3],
Background -> Opacity[.4, White]] & /@ VertexList[euc]),
AspectRatio -> 1]
|
The transitive reduction is slightly easier to interpret:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Graph[ReverseGraph[TransitiveReductionGraph[ReverseGraph[euc]]],
VertexStyle -> (# -> EuclidVertexStyle[#, "Intense"] & /@
VertexList[euc]), VertexSize -> 8, EdgeStyle -> GrayLevel[.5, .5],
VertexLabels -> (# ->
Style[EuclidVertexName[#], GrayLevel[.1],
Background -> Opacity[.4, White]] & /@ VertexList[euc]),
AspectRatio -> 1]
|
And the main notable feature is the presence of “prongs” associated, for example, with Book 9 theorems about the properties of even and odd numbers.
The Causal Graph Analogy
Knowing about the Wolfram Physics Project, there’s an obvious analog of theorem dependency graphs: they’re like causal graphs. You start from a certain set of “initial events” (the “big bang”), corresponding to the axioms. Then each subsequent theorem is like an event, and the theorem dependency graph is tracing out the causal connections between these events.
Just like the causal graph, the theorem dependency graph defines a partial ordering: you can’t write down the proof of a given theorem until the theorems that will appear in it have been proved. Like in the causal graph, one can define light cones: there’s a certain set of “future” theorems that can be affected by any given theorem. Here is the “future light cone” of Book 1, Theorem 5:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
HighlightGraph[ReverseGraph[euc, EdgeStyle -> GrayLevel[.5, .5]],
Subgraph[ReverseGraph[euc],
VertexOutComponent[
ReverseGraph[euc], <|"Book" -> 1, "Theorem" -> 5|>]],
GraphLayout -> {"LayeredDigraphEmbedding", "RootVertex" -> axioms},
AspectRatio -> 1/2]
|
And here is the corresponding transitive reduction graph:

✕
TransitiveReductionGraph[%] |
But now let’s think about the notion of time in the theorem dependency graph. Imagine you were rederiving the theorems in Euclid in a series of “time steps”. What would you have to do at each time step? The theorem dependency graph tells you what you will have to have done in order to derive a particular theorem. But just like for spacetime causal graphs, there are many different foliations one can use to define consistent time steps.
Here’s an obvious one, effectively corresponding to a “cosmological rest frame” in which at each step one “does as much as one consistently can at that step”:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/KXgcRNRJ\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"GraphPlot", "[",
RowBox[{
RowBox[{"ReverseGraph", "[", "euc", "]"}], ",",
RowBox[{"GraphLayout", "\[Rule]",
RowBox[{"{",
RowBox[{"\"\<LayeredDigraphEmbedding\>\"", ",",
RowBox[{"\"\<RootVertex\>\"", "\[Rule]", "axioms"}]}], "}"}]}],
",",
RowBox[{"AspectRatio", "\[Rule]",
RowBox[{"1", "/", "2"}]}], ",",
RowBox[{"VertexStyle", "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", "\[Rule]",
RowBox[{"EuclidVertexStyle", "[",
RowBox[{"#", ",", "\"\<Intense\>\""}], "]"}]}], "&"}], "/@",
RowBox[{"VertexList", "[", "euc", "]"}]}], ")"}]}], ",",
RowBox[{"VertexSize", "\[Rule]", "4"}], ",",
RowBox[{"EdgeStyle", "\[Rule]",
RowBox[{"GrayLevel", "[",
RowBox[{".5", ",", ".5"}], "]"}]}], ",",
RowBox[{"Epilog", "\[Rule]",
RowBox[{"Scale", "[",
RowBox[{
RowBox[{"straightFoliationLines", "[",
RowBox[{
RowBox[{"{",
RowBox[{"0.43", ",", "0"}], "}"}], ",",
RowBox[{"{",
RowBox[{"0", ",", "0"}], "}"}], ",",
RowBox[{"#", "&"}], ",",
RowBox[{"{",
RowBox[{"45", ",", "3"}], "}"}]}], "]"}], ",", "4"}],
"]"}]}]}], "]"}]], "Input"]
}, Open ]]
|
And here are the number of theorems that appear on each slice (in effect each theorem appears on the slice determined by its longest path to any axiom):

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"longestpathlengths", "=",
RowBox[{"ParallelMap", "[",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"t", ",",
RowBox[{"t", "->",
RowBox[{
RowBox[{"Max", "[",
RowBox[{
RowBox[{
RowBox[{"Length", "[",
RowBox[{"FindLongestPath", "[",
RowBox[{"euc", ",", "t", ",", "#"}], "]"}], "]"}],
"&"}], "/@", "axioms"}], "]"}], "-", "1"}]}]}], "]"}],
",",
RowBox[{"VertexList", "[", "euc", "]"}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"layers", "=",
RowBox[{"Map", "[",
RowBox[{"First", ",",
RowBox[{"SortBy", "[",
RowBox[{
RowBox[{"GatherBy", "[",
RowBox[{"longestpathlengths", ",", "Last"}], "]"}], ",",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "2"}], "]"}], "]"}], "&"}]}], "]"}], ",",
RowBox[{"{", "2", "}"}]}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{"data", ",",
RowBox[{"max", "=",
RowBox[{"Length", "[", "layers", "]"}]}]}], "}"}], ",",
RowBox[{
RowBox[{"data", "=",
RowBox[{"Map", "[",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"u", ",",
RowBox[{"PadLeft", "[",
RowBox[{
RowBox[{"Reverse", "[",
RowBox[{
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{"MissingQ", "[",
RowBox[{"#", "[", "\"\<Book\>\"", "]"}], "]"}], ",",
"100", ",",
RowBox[{"#", "[", "\"\<Book\>\"", "]"}]}], "]"}],
"&"}], "/@", "u"}], "]"}], ",", "max"}], "]"}]}], "]"}],
",", "layers"}], "]"}]}], ";", "\[IndentingNewLine]",
RowBox[{"Show", "[",
RowBox[{
RowBox[{"ArrayPlot", "[",
RowBox[{
RowBox[{"Transpose", "[", "data", "]"}], ",",
RowBox[{"AspectRatio", "\[Rule]",
RowBox[{"1", "/", "4"}]}], ",",
RowBox[{"ColorRules", "->",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
"1", "|", "2", "|", "3", "|", "4", "|", "5", "|", "6"}], "->",
RowBox[{"bookColorIntense", "[", "6", "]"}]}], ",",
RowBox[{
RowBox[{"7", "|", "8", "|", "9", "|", "10"}], "->",
RowBox[{"bookColorIntense", "[", "10", "]"}]}], ",",
RowBox[{
RowBox[{"11", "|", "12", "|", "13"}], "->",
RowBox[{"bookColorIntense", "[", "13", "]"}]}], ",",
RowBox[{"100", "\[Rule]",
RowBox[{"bookColorIntense", "[", "0", "]"}]}]}],
"}"}]}]}], "]"}], ",",
RowBox[{"Frame", "\[Rule]", "True"}], ",",
RowBox[{"FrameTicks", "\[Rule]", "Automatic"}], ",", " ",
RowBox[{"FrameLabel", "\[Rule]",
RowBox[{"{",
RowBox[{
"\"\<longest path to axioms\>\"", ",", "\[IndentingNewLine]",
"\"\<number of theorems\>\""}], "}"}]}]}], "]"}]}]}],
"]"}]], "Input"]
}, Open ]]
|
But there are many other foliations that are possible, in which one for example concentrates first on a particular group of theorems, only doing others when one “needs to”.
Each choice of foliation can be thought of as corresponding to a different reference frame—and a different choice of how one explores the analog of spacetime in Euclid. But, OK, if the foliations define successive moments in time—or successive “simultaneity surfaces”—what is the analog of space? In effect, the “structure of space” is defined by the way that theorems are laid out on the slices defined by the foliations. And a convenient way to probe this is to look at branchial graphs, in which pairs of theorems on a given slice are connected by an edge if they have an immediate common ancestor on the slice before.
So here are the branchial graphs for all successive slices of Euclid in the “cosmological rest frame”:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"longestpathlengths", "=",
RowBox[{"ParallelMap", "[",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"t", ",",
RowBox[{"t", "->",
RowBox[{
RowBox[{"Max", "[",
RowBox[{
RowBox[{
RowBox[{"Length", "[",
RowBox[{"FindLongestPath", "[",
RowBox[{"euc", ",", "t", ",", "#"}], "]"}], "]"}],
"&"}], "/@", "axioms"}], "]"}], "-", "1"}]}]}], "]"}],
",",
RowBox[{"VertexList", "[", "euc", "]"}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"layers", "=",
RowBox[{"Map", "[",
RowBox[{"First", ",",
RowBox[{"SortBy", "[",
RowBox[{
RowBox[{"GatherBy", "[",
RowBox[{"longestpathlengths", ",", "Last"}], "]"}], ",",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "2"}], "]"}], "]"}], "&"}]}], "]"}], ",",
RowBox[{"{", "2", "}"}]}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"GraphicsGrid", "[",
RowBox[{
RowBox[{"Partition", "[",
RowBox[{
RowBox[{"Table", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"SimpleGraph", "[",
RowBox[{"#", ",",
RowBox[{"ImageSize", "\[Rule]", "Tiny"}], ",",
RowBox[{"EdgeStyle", "\[Rule]",
RowBox[{
RowBox[{
RowBox[{
"ResourceFunction", "[",
"\"\<WolframPhysicsProjectStyleData\>\"", "]"}], "[",
"\"\<BranchialGraph\>\"", "]"}], "[",
"\"\<EdgeStyle\>\"", "]"}]}]}], "]"}], "&"}], "@",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{
RowBox[{"Outer", "[",
RowBox[{"UndirectedEdge", ",", "#", ",", "#"}], "]"}],
"&"}], "[",
RowBox[{"Intersection", "[",
RowBox[{
RowBox[{"layers", "[",
RowBox[{"[",
RowBox[{"t", "+", "1"}], "]"}], "]"}], ",",
RowBox[{"VertexInComponent", "[",
RowBox[{"euc", ",", "#", ",", "1"}], "]"}]}], "]"}],
"]"}], "&"}], "/@",
RowBox[{"layers", "[",
RowBox[{"[", "t", "]"}], "]"}]}], "]"}]}], ",",
RowBox[{"{",
RowBox[{"t", ",",
RowBox[{
RowBox[{"Length", "[", "layers", "]"}], "-", "1"}]}],
"}"}]}], "]"}], ",",
RowBox[{"UpTo", "[", "8", "]"}]}], "]"}], ",",
RowBox[{"Frame", "\[Rule]", "All"}]}], "]"}]], "Input"]
}, Open ]]
|
And here are the branchial graphs specifically from slices 23 and 26:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"longestpathlengths", "=",
RowBox[{"ParallelMap", "[",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"t", ",",
RowBox[{"t", "->",
RowBox[{
RowBox[{"Max", "[",
RowBox[{
RowBox[{
RowBox[{"Length", "[",
RowBox[{"FindLongestPath", "[",
RowBox[{"euc", ",", "t", ",", "#"}], "]"}], "]"}],
"&"}], "/@", "axioms"}], "]"}], "-", "1"}]}]}], "]"}],
",",
RowBox[{"VertexList", "[", "euc", "]"}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"layers", "=",
RowBox[{"Map", "[",
RowBox[{"First", ",",
RowBox[{"SortBy", "[",
RowBox[{
RowBox[{"GatherBy", "[",
RowBox[{"longestpathlengths", ",", "Last"}], "]"}], ",",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "2"}], "]"}], "]"}], "&"}]}], "]"}], ",",
RowBox[{"{", "2", "}"}]}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"Function", "[",
RowBox[{"t", ",",
RowBox[{
RowBox[{
RowBox[{"Framed", "[",
RowBox[{"SimpleGraph", "[",
RowBox[{"#", ",",
RowBox[{"EdgeStyle", "->",
RowBox[{
RowBox[{
RowBox[{
"ResourceFunction", "[",
"\"\<WolframPhysicsProjectStyleData\>\"", "]"}], "[",
"\"\<BranchialGraph\>\"", "]"}], "[", "\"\<EdgeStyle\>\"",
"]"}]}], ",",
RowBox[{"VertexStyle", "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", "\[Rule]",
RowBox[{"EuclidVertexStyle", "[", "#", "]"}]}], "&"}], "/@",
RowBox[{"VertexList", "[", "euc", "]"}]}], ")"}]}], ",",
RowBox[{"VertexSize", "\[Rule]", ".4"}], ",",
RowBox[{"ImageSize", "\[Rule]",
RowBox[{"{",
RowBox[{"400", ",", "Automatic"}], "}"}]}], ",",
RowBox[{"VertexLabels", "->",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", "\[Rule]",
RowBox[{"EuclidVertexName", "[", "#", "]"}]}], "&"}], "/@",
RowBox[{"VertexList", "[", "euc", "]"}]}], ")"}]}]}],
"]"}], "]"}], "&"}], "@",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{
RowBox[{"Outer", "[",
RowBox[{"UndirectedEdge", ",", "#", ",", "#"}], "]"}],
"&"}], "[",
RowBox[{"Intersection", "[",
RowBox[{
RowBox[{"layers", "[",
RowBox[{"[",
RowBox[{"t", "+", "1"}], "]"}], "]"}], ",",
RowBox[{"VertexInComponent", "[",
RowBox[{"euc", ",", "#", ",", "1"}], "]"}]}], "]"}],
"]"}], "&"}], "/@",
RowBox[{"layers", "[",
RowBox[{"[", "t", "]"}], "]"}]}], "]"}]}]}], "]"}], "/@",
RowBox[{"{",
RowBox[{"23", ",", "26"}], "}"}]}]], "Input"]
}, Open ]]
|
How should we interpret these graphs? Just like in quantum mechanics, they effectively define a map of “entanglements”, but now these are “entanglements” not between quantum states but between theorems. But potentially we can also interpret these graphs as showing how theorems are laid out in a kind of “instantaneous metamathematical space”—or, in effect, we can use the graphs to define “distances between theorems”.
We can generalize our ordinary branchial graphs by connecting theorems that have common ancestors not just one slice back, but also up to δt slices back. Here are the results for slice 26 (in the cosmological rest frame):

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"longestpathlengths", "=",
RowBox[{"ParallelMap", "[",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"t", ",",
RowBox[{"t", "->",
RowBox[{
RowBox[{"Max", "[",
RowBox[{
RowBox[{
RowBox[{"Length", "[",
RowBox[{"FindLongestPath", "[",
RowBox[{"euc", ",", "t", ",", "#"}], "]"}], "]"}],
"&"}], "/@", "axioms"}], "]"}], "-", "1"}]}]}], "]"}],
",",
RowBox[{"VertexList", "[", "euc", "]"}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"layers", "=",
RowBox[{"Map", "[",
RowBox[{"First", ",",
RowBox[{"SortBy", "[",
RowBox[{
RowBox[{"GatherBy", "[",
RowBox[{"longestpathlengths", ",", "Last"}], "]"}], ",",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "2"}], "]"}], "]"}], "&"}]}], "]"}], ",",
RowBox[{"{", "2", "}"}]}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Transpose", "[",
RowBox[{"Table", "[",
RowBox[{
RowBox[{
RowBox[{"Function", "[",
RowBox[{"t", ",",
RowBox[{
RowBox[{
RowBox[{"Labeled", "[",
RowBox[{
RowBox[{"Framed", "[",
RowBox[{"SimpleGraph", "[",
RowBox[{"#", ",",
RowBox[{"EdgeStyle", "->",
RowBox[{
RowBox[{
RowBox[{
"ResourceFunction", "[",
"\"\<WolframPhysicsProjectStyleData\>\"", "]"}],
"[", "\"\<BranchialGraph\>\"", "]"}], "[",
"\"\<EdgeStyle\>\"", "]"}]}], ",",
RowBox[{"ImageSize", "\[Rule]", "300"}], ",",
RowBox[{"VertexLabels", "->",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", "\[Rule]",
RowBox[{"EuclidVertexName", "[", "#", "]"}]}],
"&"}], "/@",
RowBox[{"VertexList", "[", "euc", "]"}]}], ")"}]}],
",",
RowBox[{"VertexSize", "\[Rule]", ".4"}], ",",
RowBox[{"VertexStyle", "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", "\[Rule]",
RowBox[{"{",
RowBox[{"EuclidVertexStyle", "[", "#", "]"}],
"}"}]}], "&"}], "/@",
RowBox[{"VertexList", "[", "euc", "]"}]}], ")"}]}]}],
"]"}], "]"}], ",",
RowBox[{"Style", "[",
RowBox[{
RowBox[{
"\"\<\!\(\*StyleBox[\(\[Delta]\*StyleBox[\"t\",FontSlant-\
>\"Italic\"]\)]\) = \>\"", "<>",
RowBox[{"ToString", "[", "dt", "]"}]}], ",",
RowBox[{
"FontFamily", "\[Rule]", "\"\<Source Sans Pro\>\""}]}],
"]"}]}], "]"}], "&"}], "@",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{
RowBox[{"Outer", "[",
RowBox[{"UndirectedEdge", ",", "#", ",", "#"}], "]"}],
"&"}], "[",
RowBox[{"Intersection", "[",
RowBox[{
RowBox[{"Union", "@@",
RowBox[{"Table", "[",
RowBox[{
RowBox[{"layers", "[",
RowBox[{"[",
RowBox[{"t", "+", "i"}], "]"}], "]"}], ",",
RowBox[{"{",
RowBox[{"i", ",", "dt"}], "}"}]}], "]"}]}], ",",
RowBox[{"VertexInComponent", "[",
RowBox[{"euc", ",", "#", ",", "dt"}], "]"}]}], "]"}],
"]"}], "&"}], "/@",
RowBox[{"layers", "[",
RowBox[{"[", "t", "]"}], "]"}]}], "]"}]}]}], "]"}], "/@",
RowBox[{"{", "26", "}"}]}], ",",
RowBox[{"{",
RowBox[{"dt", ",", "1", ",", "3"}], "}"}]}], "]"}],
"]"}]], "Input"]
}, Open ]]
|
If we went all the way back to the axioms (the analog of the “big bang”) then we’d just get a complete graph, connecting all the theorems on slice 26. But here we’re seeing in effect “fuzzier and fuzzier” versions of how the theorems that exist at slice 26 can be thought of as being “metamathematically laid out”. The disconnected components in these branchial graphs represent theorems that have no recent shared history—so that in some sense they’re “causally disconnected”.
In thinking about “theorem search”, it’s interesting to try to imagine measures of “distance between theorems”—and in effect branchial distance captures some of this. And even for Euclid there are presumably things to learn about the “layout” of theorems, and what should count as “close to” what.
There are only 465 theorems in Euclid’s Elements. But what if there were many more? What might the “metamathematical space” they define be like? Just as for the hypergraphs—or, for that matter, the multiway graphs—in our models of physics we can ask questions about the limiting emergent geometry of this space. And—ironically enough—one thing we can immediately say is that it seems to be far from Euclidean!
But does it for example have some definite effective dimension? There isn’t enough data to say much about the branchial slices we just saw. But we can say a bit more about the complete theorem dependency graph—which is the analog of the multiway graph in our physics models. For example, starting with the axioms (the analog of the “big bang”) we can ask how many theorems are reached in successive steps. The result (counting the axioms) is:
|
✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Table[Length[Union @@ (VertexInComponent[euc, #, i] & /@ axioms)], {i,
0, 10}]
|
If we were dealing with something that approximated a d-dimensional manifold, we’d expect these numbers to be of order rd. Computing their logarithmic differences to fit for d gives

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
ListLinePlot[
ResourceFunction["LogDifferences"][
MeanAround /@
Transpose[
Table[Length[VertexInComponent[euc, #, i]], {i, 0, 10}] & /@
axioms]], Frame -> True,
FrameLabel -> {"graph distance", "effective dimension"}]
|
if one starts from the axioms, and

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
ListLinePlot[
ResourceFunction["LogDifferences"][
MeanAround /@
Transpose[
Table[Length[VertexInComponent[euc, #, i]], {i, 0, 10}] & /@
VertexList[euc]]], Frame -> True,
FrameLabel -> {"graph distance", "effective dimension"}]
|
if one starts from all possible theorems in the network.
One gets somewhat different results if one deals not with the actual theorem dependency graph in Euclid, but instead with its transitive reduction—removing all “unnecessary” direct connections. Now the number of theorems reached on successive steps is:
|
✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Table[Length[
Union @@ (VertexInComponent[TransitiveReductionGraph[euc], #, i] & /@
axioms)], {i, 0, 10}]
|
The “dimension estimate” based on theorems reached starting from the axioms is

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
ListLinePlot[
ResourceFunction["LogDifferences"][
MeanAround /@
Transpose[
Table[Length[
VertexInComponent[TransitiveReductionGraph[euc], #, i]], {i,
0, 20}] & /@ axioms]], Frame -> True]
|
while the corresponding result starting from all theorems is:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
ListLinePlot[
ResourceFunction["LogDifferences"][
MeanAround /@
Transpose[
Table[Length[
VertexInComponent[TransitiveReductionGraph[euc], #, i]], {i,
0, 20}] & /@ VertexList[euc]]], Frame -> True]
|
Euclid’s Elements represents far too little data to make a definite statement, but perhaps there’s a hint of 2-dimensional structure, with positive curvature.
The Most Difficult Theorem in Euclid
One way to assess the “difficulty” of a theorem is to look at what results have to have already been built up in order to prove the theorem. And by this measure, the most difficult theorem in Euclid’s Elements is the very last theorem in the last book—what one might call “Euclid’s last theorem”, the climax of the Elements—Book 13, Theorem 18, which amounts to the statement that there are five Platonic solids, or more specifically:
|
✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; Style[ Text[ Style[eus[<|"Book" -> 13, "Theorem" -> 18|>]["GreekText"], RGBColor["#333333"], FontSize -> 13]]] |
This theorem uses all 10 axioms, and 219 of the 464 previous theorems. Here’s its graph of dependencies:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Labeled[Subgraph[ReverseGraph[euc],
VertexInComponent[
ReverseGraph[euc], <|"Book" -> 13, "Theorem" -> 18|>],
GraphLayout -> {"LayeredDigraphEmbedding", "RootVertex" -> axioms},
AspectRatio -> 1/2, EdgeStyle -> GrayLevel[.5, .5], VertexSize -> 3,
VertexLabels -> (# -> EuclidVertexName[#] & /@ VertexList[euc]),
VertexStyle -> (# -> EuclidVertexStyle[#, "Intense"] & /@
VertexList[euc])],
Row[Row[#, Spacer[0.005]] & /@
Transpose[{bookColorIntense /@ {0, 6, 10, 13},
Style[#, FontFamily -> "Source Sans Pro", GrayLevel[0.3],
FontSize -> 12] & /@ {"axioms", "2D geometry", "numbers",
"3D geometry"}}], Spacer[20]]]
|
And here is the transitive reduction of this—notably with different subject areas being more obviously separated:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
TransitiveReductionGraph[
Subgraph[ReverseGraph[euc],
VertexInComponent[
ReverseGraph[euc], <|"Book" -> 13, "Theorem" -> 18|>],
GraphLayout -> {"LayeredDigraphEmbedding", "RootVertex" -> axioms},
AspectRatio -> 1/2, EdgeStyle -> GrayLevel[.5, .5],
VertexSize -> .8,
VertexLabels -> (# -> EuclidVertexName[#] & /@ VertexList[euc]),
VertexStyle -> (# -> EuclidVertexStyle[#, "Intense"] & /@
VertexList[euc])]]
|
This shows how 13.18 and its prerequisites (its “past light cone”) sit inside the whole theorem dependency graph:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
HighlightGraph[ReverseGraph[euc, EdgeStyle -> GrayLevel[.5, .5]],
Subgraph[ReverseGraph[euc],
VertexInComponent[
ReverseGraph[euc], <|"Book" -> 13, "Theorem" -> 18|>]],
GraphLayout -> {"LayeredDigraphEmbedding", "RootVertex" -> axioms},
AspectRatio -> 1/2]
|
If we started from the axioms, the longest chains of theorems we’d have to prove to get to 13.18 are:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Text[Column[(Style[
RightArrow @@ (Module[{text = EuclidVertexName[#]},
Framed[Style[text, 10, Black], RoundingRadius -> 4,
ImageSize -> {Automatic, 20},
Background ->
If[StringMatchQ[First[StringSplit[text, "."]],
NumberString],
bookColor[ToExpression[First[StringSplit[text, "."]]]],
bookColor[0]],
FrameStyle ->
If[StringMatchQ[First[StringSplit[text, "."]],
NumberString],
bookColor[ToExpression[First[StringSplit[text, "."]]]],
bookColorDarker[0]]]] & /@
FindLongestPath[
ReverseGraph[euc], #, <|"Book" -> 13, "Theorem" -> 18|>]),
Gray]) & /@ axioms, Frame -> All, FrameStyle -> GrayLevel[.7]]]
|
Or in other words, from CN1 and from P1 and P3 we’d have to go 33 steps to reach 13.18. If we actually look at the paths, however, we see that after different segments at the beginning, they all merge at Book 6, Theorem 1, and then are the same for the last 14 steps:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
HighlightGraph[ReverseGraph[euc, EdgeStyle -> GrayLevel[.5, .5]],
Style[PathGraph[
FindLongestPath[
ReverseGraph[euc], #, <|"Book" -> 13, "Theorem" -> 18|>],
DirectedEdges -> True], Red, Thick] & /@ axioms,
GraphLayout -> {"LayeredDigraphEmbedding", "RootVertex" -> axioms},
AspectRatio -> 1/2]
|
(Theorem 6.1 is the statement that both triangles and parallelograms that have the same base and same height have the same area, i.e. one can skew a triangle or parallelogram without changing its area.)
How much more difficult than other theorems is 13.18? Here’s a histogram of maximum path lengths for all theorems (ignoring cases to be discussed later where a particular theorem does not use a given axiom at all):

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"tlens", "=",
RowBox[{"ParallelMap", "[",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"t", ",",
RowBox[{"Max", "[",
RowBox[{
RowBox[{
RowBox[{"Length", "[",
RowBox[{"FindLongestPath", "[",
RowBox[{"euc", ",", "t", ",", "#"}], "]"}], "]"}], "&"}],
"/@", "axioms"}], "]"}]}], "]"}], ",",
RowBox[{"VertexList", "[", "euc", "]"}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"Histogram", "[",
RowBox[{
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"vod", "=",
RowBox[{"ParallelMap", "[",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"t", ",",
RowBox[{"t", "->",
RowBox[{"Max", "[",
RowBox[{
RowBox[{
RowBox[{"Length", "[",
RowBox[{"FindLongestPath", "[",
RowBox[{"euc", ",", "t", ",", "#"}], "]"}], "]"}],
"&"}], "/@", "axioms"}], "]"}]}]}], "]"}], ",",
RowBox[{"VertexList", "[", "euc", "]"}]}], "]"}]}], ",",
"dataG"}], "}"}], ",",
RowBox[{
RowBox[{"dataG", "=",
RowBox[{"GroupBy", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{"MissingQ", "[",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "[", "\"\<Book\>\"",
"]"}], "]"}], ",",
RowBox[{"0", "\[Rule]", " ",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}]}], ",",
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "[", "\"\<Book\>\"",
"]"}], "\[Rule]",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}]}]}], "]"}], "&"}], "/@",
"vod"}], ",",
RowBox[{"First", "\[Rule]", "Last"}]}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{
RowBox[{
RowBox[{"Flatten", "[",
RowBox[{"Join", "[",
RowBox[{"Values", "[",
RowBox[{"dataG", "[",
RowBox[{"[",
RowBox[{"Key", "/@", "#"}], "]"}], "]"}], "]"}], "]"}],
"]"}], "&"}], "/@",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
"1", ",", "2", ",", "3", ",", "4", ",", "5", ",", "6"}],
"}"}], ",",
RowBox[{"{",
RowBox[{"7", ",", "8", ",", "9", ",", "10"}], "}"}], ",",
RowBox[{"{",
RowBox[{"11", ",", "12", ",", "13"}], "}"}]}], "}"}]}]}]}],
"\[IndentingNewLine]", "]"}], ",",
RowBox[{"{", "1", "}"}], ",",
RowBox[{"Frame", "\[Rule]", "True"}], ",",
RowBox[{"ChartLayout", "\[Rule]", "\"\<Stacked\>\""}], ",",
RowBox[{"ChartBaseStyle", "\[Rule]",
RowBox[{"Opacity", "[", "1", "]"}]}], ",",
RowBox[{"ChartStyle", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "/@",
RowBox[{"{",
RowBox[{"6", ",", "10", ",", "13"}], "}"}]}], ",",
RowBox[{"EdgeForm", "[",
RowBox[{"Directive", "[",
RowBox[{"Thin", ",",
RowBox[{"GrayLevel", "[", "0.15", "]"}]}], "]"}], "]"}]}],
"}"}]}], ",",
RowBox[{"FrameLabel", "\[Rule]",
RowBox[{"{",
RowBox[{
"\"\<maximum path length\>\"", ",",
"\"\<number of theorems\>\""}], "}"}]}]}], "]"}]], "Input"]
}, Open ]]
|
And here’s how the maximum path length varies through the sequence of all 465 theorems:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Module[{dataA =
ParallelMap[
Function[t,
If[MissingQ[t["Book"]], Nothing,
t["Book"] ->
Max[Length[FindLongestPath[euc, t, #]] & /@ axioms] ]],
VertexList[euc]], vals, acc, xval},
vals = CountsBy[dataA, First];
acc = Association[
MapIndexed[First[#2] -> #1 &,
Accumulate[Values[CountsBy[dataA, First]]]]];
xval = Association[#[[1]] -> (#[[2]] - vals[#[[1]]]/2) & /@
Normal[acc]];
Show[{ListLinePlot[Values[dataA], Axes -> {False, True},
Frame -> True,
FrameTicks -> {{True,
False}, {{#[[2]], #[[1]], {0, 0}} & /@ Normal[xval], False}},
FrameLabel -> {"theorems by book", "maximum path length"},
Filling -> Axis, ColorFunctionScaling -> False,
ColorFunction ->
Function[{x, y},
Piecewise[{{bookColorIntense[6],
x <= acc[6]}, {bookColorIntense[10],
x <= acc[10]}, {bookColorIntense[13], x <= acc[13]}}]],
PlotRange -> All],
Graphics[{GrayLevel[0.5],
Line[{{#, -5}, {#, 35}} & /@ Values[acc]]}]}]]
|
In the causal graph interpretation, and using the “flat foliation” (i.e. the “cosmological rest frame”) what this basically shows is at what “time slice” a given theorem first emerges from Euclid’s proofs. Or, in other words, if one imagines exploring the “metamathematical space of Euclid” by going “one level of theorems at a time”, the order in which one will encounter theorems is:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"tlens", "=",
RowBox[{"ParallelMap", "[",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"t", ",",
RowBox[{"Max", "[",
RowBox[{
RowBox[{
RowBox[{"Length", "[",
RowBox[{"FindLongestPath", "[",
RowBox[{"euc", ",", "t", ",", "#"}], "]"}], "]"}], "&"}],
"/@", "axioms"}], "]"}]}], "]"}], ",",
RowBox[{"VertexList", "[", "euc", "]"}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"Column", "[",
RowBox[{
RowBox[{"Row", "/@",
RowBox[{"Map", "[",
RowBox[{
RowBox[{
RowBox[{"Text", "[",
RowBox[{
RowBox[{"Style", "[",
RowBox[{
RowBox[{"StringJoin", "[",
RowBox[{"\"\<\[ThinSpace]\>\"", ",",
RowBox[{"EuclidVertexName", "[",
RowBox[{"First", "[", "#", "]"}], "]"}], ",",
"\"\<\[ThinSpace]\>\""}], "]"}], ",", "11", ",",
RowBox[{"LineSpacing", "\[Rule]", " ",
RowBox[{"{",
RowBox[{"1", ",", "0"}], "}"}]}]}], "]"}], ",",
RowBox[{"Background", "\[Rule]",
RowBox[{"bookColorDarker", "[",
RowBox[{"Lookup", "[",
RowBox[{
RowBox[{"First", "[", "#", "]"}], ",", "\"\<Book\>\"",
",", "0"}], "]"}], "]"}]}]}], "]"}], "&"}], ",",
RowBox[{"SplitBy", "[",
RowBox[{
RowBox[{"SortBy", "[",
RowBox[{
RowBox[{"Transpose", "[",
RowBox[{"{",
RowBox[{
RowBox[{"VertexList", "[", "euc", "]"}], ",", "tlens"}],
"}"}], "]"}], ",", "Last"}], "]"}], ",", "Last"}], "]"}],
",",
RowBox[{"{", "2", "}"}]}], "]"}]}], ",",
RowBox[{"Frame", "\[Rule]", "All"}], ",",
RowBox[{"FrameStyle", "\[Rule]",
RowBox[{"GrayLevel", "[", ".8", "]"}]}]}], "]"}]], "Input"]
}, Open ]]
|
A question one might ask is whether “short-to-state” theorems are somehow “easier to prove” than longer-to-state ones. This shows the maximum path length to prove theorems as a function of the length of their statements in Euclid’s Greek. Remarkably little correlation is seen.

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Module[{dataA =
GroupBy[ParallelMap[
Function[t,
t["Book"] ->
Callout[{StringLength[eus[t]["GreekText"]],
Max[Length[FindLongestPath[euc, t, #]] & /@ axioms]},
EuclidVertexName[t]]], Complement[VertexList[euc], axioms]],
First -> Last]},
ListPlot[Values[dataA], ColorFunctionScaling -> False,
PlotStyle -> Table[bookColorIntense[i], {i, 1, 13}], Frame -> True,
FrameLabel -> {Style["Greek statement length", GrayLevel[.5]],
Style["maximum path", GrayLevel[.5]]} ]]
|
This plot shows instead the number of “prerequisite theorems” as a function of statement length:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Module[{dataA =
GroupBy[ParallelMap[
Function[t,
t["Book"] ->
Callout[{StringLength[eus[t]["GreekText"]],
Length[VertexOutComponent[euc, t]]}, EuclidVertexName[t]]],
Complement[VertexList[euc], axioms]], First -> Last]},
ListPlot[Values[dataA], ColorFunctionScaling -> False,
PlotStyle -> Table[bookColorIntense[i], {i, 1, 13}], Frame -> True,
FrameLabel -> {Style["Greek statement length", GrayLevel[.5]],
Style["dependencies", GrayLevel[.5]]} ]]
|
Once again there is poor correlation.
The Most Popular Theorems in Euclid
How often do particular theorems get used in the proofs of other theorems? The “most popular” theorems in terms of being directly quoted in the proofs of other theorems are:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Row[Text[Grid[#,
Background -> {None,
MapIndexed[
First[#2] ->
With[{bn =
StringCases[#1, b : (DigitCharacter ..) ~~ "." :> b]},
bookColorDarker[
If[Length[bn] == 1, FromDigits[First[bn]], 0]]] &, #[[All,
1]]]}, Frame -> All]] & /@
Partition[{EuclidVertexName[#],
Style[VertexInDegree[euc, #] - 1, Italic]} & /@
TakeLargestBy[VertexList[euc], VertexInDegree[euc, #] &, 50], 10],
Spacer[5]]
|
Notably, all but one of 10.11’s direct mentions are in other theorems in Book 10. Theorem 6.1 (which we already encountered above) is used in 4 books.
By the way, there is some subtlety here, because 26 theorems reference a particular theorem more than once in their proofs: for example, 10.4 references 10.3 three times, while 13.18 references both 13.17 and 13.16 twice:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
With[{g =
Select[EdgeList[euc],
First[#] == <|"Book" -> 13, "Theorem" -> 18|> &]},
Graph[g, VertexLabels -> (# ->
Placed[EuclidVertexName[#], Center] & /@ VertexList[g]),
VertexSize -> .75, EdgeStyle -> Gray,
VertexStyle -> (# -> EuclidVertexStyle[#] & /@ VertexList[g]),
GraphLayout -> "BalloonEmbedding", ImageSize -> 200]]
|
But looking simply at the distribution of the number of direct uses (here on a log scale), we see that the vast majority of theorems are very rarely used—with just a few being quite widely used:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Histogram[
Module[{vod = # -> Length[VertexInComponent[euc, #, 1]] & /@
VertexList[euc], dataG},
dataG = GroupBy[
If[MissingQ[#[[1]]["Book"]],
0 -> #[[2]], #[[1]]["Book"] -> #[[2]]] & /@ vod, First -> Last];
Flatten[Join[Values[dataG[[Key /@ #]]]]] & /@ {{0}, {1, 2, 3, 4, 5,
6}, {7, 8, 9, 10}, {11, 12, 13}}
], {1}, {"Log", "Count"}, PlotRange -> All, Frame -> True,
ChartLayout -> "Stacked",
FrameLabel -> {"number of direct uses", "number of theorems"},
ChartBaseStyle -> Opacity[1],
ChartStyle -> {bookColorIntense /@ {0, 6, 10, 13},
EdgeForm[Directive[Thin, GrayLevel[0.15]]]}]
|
Indicating the number of direct uses by size, here are the “directly popular” theorems:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
With[{vl = VertexList[euc]},
Labeled[Graph[ReverseGraph[euc],
VertexSize -> (# -> 4 Sqrt[VertexInDegree[euc, #]] & /@
VertexList[euc]),
VertexStyle -> (# -> EuclidVertexStyle[#] & /@ vl),
EdgeStyle -> GrayLevel[.5, .5],
VertexLabels -> (# ->
If[VertexInDegree[euc, #] > 10 ,
Placed[EuclidVertexName[#], Center], None] & /@
VertexList[euc]),
GraphLayout -> {"LayeredDigraphEmbedding", "RootVertex" -> axioms},
AspectRatio -> 1/2],
Row[Row[#, Spacer[0.005]] & /@
Transpose[{bookColorIntense /@ {0, 6, 10, 13},
Style[#, FontFamily -> "Source Sans Pro", GrayLevel[0.3],
FontSize -> 12] & /@ {"axioms", "2D geometry", "numbers",
"3D geometry"}}], Spacer[20]]]]
|
If we ask also about indirect uses, the results are as follows:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Row[Text[Grid[#,
Background -> {None,
MapIndexed[
First[#2] ->
With[{bn =
StringCases[#1, b : (DigitCharacter ..) ~~ "." :> b]},
bookColorDarker[
If[Length[bn] == 1, FromDigits[First[bn]], 0]]] &, #[[All,
1]]]}, Frame -> All]] & /@
Partition[{EuclidVertexName[#],
Style[Length[VertexInComponent[euc, #]] - 1, Italic]} & /@
TakeLargestBy[VertexList[euc],
Length[VertexInComponent[euc, #]] &, 50], 10], Spacer[5]]
|
Not too surprisingly, the axioms and early theorems are the most popular. But overall, the distribution of total number of uses is somewhat broader than the distribution of direct uses:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Histogram[
Module[{vod = # -> Length[VertexInComponent[euc, #]] & /@
VertexList[euc], dataG},
dataG = GroupBy[
If[MissingQ[#[[1]]["Book"]],
0 -> #[[2]], #[[1]]["Book"] -> #[[2]]] & /@ vod, First -> Last];
Flatten[Join[Values[dataG[[Key /@ #]]]]] & /@ {{0}, {1, 2, 3, 4, 5,
6}, {7, 8, 9, 10}, {11, 12, 13}}
], {3}, {"Log", "Count"}, PlotRange -> All, Frame -> True,
FrameLabel -> {"number of indirect uses", "number of theorems"},
ChartLayout -> "Stacked", ChartBaseStyle -> Opacity[1],
ChartStyle -> {bookColorIntense /@ {0, 6, 10, 13},
EdgeForm[Directive[Thin, GrayLevel[0.15]]]}]
|
This shows all theorems, with their sizes in the graph essentially determined by the sizes of their “future light cone” in the theorem dependency graph:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
With[{vl = VertexList[euc]},
Graph[ReverseGraph[euc],
VertexSize -> (# -> (Length[VertexInComponent[euc, #]]/8) & /@
VertexList[euc]),
VertexStyle -> (# -> EuclidVertexStyle[#] & /@ vl),
EdgeStyle -> GrayLevel[.5, .5],
VertexLabels -> (# ->
If[Length[VertexInComponent[euc, #]] > 10 ,
Placed[EuclidVertexName[#], Center], None] & /@
VertexList[euc]),
GraphLayout -> {"LayeredDigraphEmbedding", "RootVertex" -> axioms},
AspectRatio -> 1/2]]
|
In addition to asking about direct and indirect uses, one can also assess the “centrality” of a given theorem by various graph-theoretical measures. One example is betweenness centrality (the fraction of shortest paths that pass through a given node):

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
With[{vl = VertexList[euc], bw = BetweennessCentrality[euc],
reuc = ReverseGraph[euc]},
Graph[Part[VertexList[euc], Ordering[bw]], EdgeList[reuc],
VertexSize -> Thread[VertexList[euc] -> .05 bw],
VertexStyle -> (# -> EuclidVertexStyle[#] & /@ vl),
EdgeStyle -> GrayLevel[.5, .5],
VertexLabels ->
MapIndexed[# ->
If[bw[[First[#2]]] > 500 , Placed[EuclidVertexName[#], Center],
None] &, VertexList[euc]],
GraphLayout -> {"VertexLayout" -> {"LayeredDigraphEmbedding",
"RootVertex" -> axioms}, "RenderingOrder" -> "VertexFirst"},
AspectRatio -> 1/2]]
|
The theorems with top betweenness centralities are 1.31 (construction of parallel lines), 10.12 (transitivity of commensurability), 10.9 (commensurabilty in squares), 8.4 (continued ratios in lowest terms), etc.
For closeness centrality (average inverse distance to all other nodes) one gets:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
With[{vl = VertexList[euc], bw = ClosenessCentrality[euc]},
Graph[ReverseGraph[euc],
VertexSize -> Thread[VertexList[euc] -> 30 bw],
VertexStyle -> (# -> EuclidVertexStyle[#] & /@ vl),
EdgeStyle -> GrayLevel[.5, .5],
VertexLabels ->
MapIndexed[# ->
If[bw[[First[#2]]] > .7 , Placed[EuclidVertexName[#], Center],
None] &, VertexList[euc]],
GraphLayout -> {"VertexLayout" -> {"LayeredDigraphEmbedding",
"RootVertex" -> axioms}, "RenderingOrder" -> "VertexFirst"},
AspectRatio -> 1/2]]
|
What Really Depends on What?
Euclid’s Elements starts with 10 axioms, from which all the theorems it contains are derived. But what theorems really depend on what axioms? This shows how many of the 465 theorems depend on each of the Common Notions and Postulates according to the proofs given in Euclid:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Text[Grid[
Transpose[{EuclidVertexName[#],
Length[VertexInComponent[euc, #]] - 1} & /@ axioms],
Frame -> All, Background -> {None, {bookColorDarker[0], None}}]]
|
The famous fifth postulate (that parallel lines do not cross) has the fewest theorems depending on it. (And actually, for many centuries there was a suspicion that no theorems really depended on it—so people tried to find proofs that didn’t use it, although ultimately it became clear it actually was needed.)
Interestingly, at least according to Euclid, more than half (255 out of 465) of the theorems actually depend on all 10 axioms, though one sees definite variation through the course of the Elements:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Module[{dataA =
If[MissingQ[#[["Book"]]],
Nothing, #[["Book"]] ->
Length[Intersection[VertexOutComponent[euc, #], axioms]]] & /@
VertexList[euc], vals, acc, xval},
vals = CountsBy[dataA, First];
acc = Association[
MapIndexed[First[#2] -> #1 &,
Accumulate[Values[CountsBy[dataA, First]]]]];
xval = Association[#[[1]] -> (#[[2]] - vals[[#[[1]]]]/2) & /@
Normal[acc]];
Show[{ListLinePlot[Values[dataA], Axes -> {False, True},
Frame -> True,
FrameLabel -> {"theorems by book", "number of axioms used"},
FrameTicks -> {{True,
False}, {{#[[2]], #[[1]], {0, 0}} & /@ Normal[xval], False}},
Filling -> Axis, ColorFunctionScaling -> False,
ColorFunction ->
Function[{x, y},
Piecewise[{{bookColorIntense[6],
x <= acc[6]}, {bookColorIntense[10],
x <= acc[10]}, {bookColorIntense[13], x <= acc[13]}}]] ],
Graphics[{GrayLevel[0.5],
Line[{{#, -5}, {#, 11}} & /@ Values[acc]]}]}]]
|
The number of theorems depending on different numbers of axioms is:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Histogram[
Module[{vod = # ->
Length[Intersection[VertexOutComponent[euc, #], axioms]] & /@
Complement[VertexList[euc], axioms], dataG},
dataG = GroupBy[
If[MissingQ[#[[1]]["Book"]],
0 -> #[[2]], #[[1]]["Book"] -> #[[2]]] & /@ vod, First -> Last];
Flatten[Join[Values[dataG[[Key /@ #]]]]] & /@ {{0}, {1, 2, 3, 4, 5,
6}, {7, 8, 9, 10}, {11, 12, 13}}
], {1},
FrameLabel -> {"number of axioms used", "number of theorems"},
PlotRange -> All, Frame -> True, ChartLayout -> "Stacked",
ChartBaseStyle -> Opacity[1],
ChartStyle -> {bookColorIntense /@ {0, 6, 10, 13},
EdgeForm[Directive[Thin, GrayLevel[0.15]]]}]
|
Scattered through the Elements there are 86 theorems that depend only on one axiom, most often CN1 (which is transitivity of equality):

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Grid[Transpose[
List @@@ Normal[
KeyMap[EuclidVertexName,
ReverseSort[
Counts[Flatten[
Intersection[VertexOutComponent[euc, #], axioms] & /@
Select[Complement[VertexList[euc], axioms],
Length[Intersection[VertexOutComponent[euc, #], axioms]] ==
1 &]]]]]]], Frame -> All,
Background -> {None, {bookColorDarker[0], None}}]
|
In most cases, the dependence is quite direct, but there are cases in which it is actually quite elaborate, such as:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
TakeLargestBy[
With[{g = Subgraph[euc, VertexOutComponent[euc, #]]},
EuclidGraphLarge[g, BaseStyle -> 9,
ImageSize -> {300, Automatic}]] & /@
Select[Complement[VertexList[euc], axioms],
Length[Intersection[VertexOutComponent[euc, #], axioms]] == 1 &],
VertexCount, 5][[{1, 2, 4}]]
|
These get slightly simpler after transitive reduction:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
TransitiveReductionGraph /@
TakeLargestBy[
With[{g = Subgraph[euc, VertexOutComponent[euc, #]]},
EuclidGraphLarge[g, ImageSize -> {300, Automatic}]] & /@
Select[Complement[VertexList[euc], axioms],
Length[Intersection[VertexOutComponent[euc, #], axioms]] == 1 &],
VertexCount, 5][[{1, 2, 4}]]
|
We can now also ask the opposite question of how many theorems don’t depend on any given axiom (and, yes, this immediately follows from what we listed above):

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
Text[Grid[
Transpose[
Function[
a, {EuclidVertexName[a],
Length[Select[
VertexList[
euc], (! MemberQ[VertexOutComponent[euc, #], a]) &]]}] /@
axioms], Frame -> All,
Background -> {None, {bookColorDarker[0], None}}]]
|
And in general we can ask what subsets of the axioms different theorems depend on. Interestingly, of the 1024 possible such subsets, only 19 actually occur, suggesting some considerable correlation between the axioms. Here is a representation of the partial ordering of the subsets that occur, indicating in each case for how many theorems that subset of dependencies occurs:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
TransitiveReductionGraph[
Module[{ss = (First[
ToExpression[StringSplit[EuclidVertexName[#], "."]]] ->
Map[EuclidVertexName,
Intersection[VertexOutComponent[euc, #], axioms]] & /@
Complement[VertexList[euc], axioms]), sss, pieSet, disp},
sss = GroupBy[ss, Last -> First];
pieSet =
Association[(#[[1]] -> {Total[Table[Count[#[[2]], i], {i, 6}]],
Total[Table[Count[#[[2]], i], {i, 7, 10}]],
Total[Table[Count[#[[2]], i], {i, 11, 13}]]}) & /@
Normal[sss]];
disp = #[[1]] ->
PieChart[pieSet[#[[1]]],
ChartStyle -> bookColorDarker /@ {6, 10, 13}] & /@
Normal[sss];
SimpleGraph[
EuclidGraphLarge[Sort[Keys[sss]],
Catenate[
Table[If[SubsetQ[a, b], a -> b, Nothing], {a,
Sort[Keys[sss]]}, {b, Sort[Keys[sss]]}]],
VertexWeight -> (Length[sss[#]] & /@ Sort[Keys[sss]])],
VertexShape -> disp,
VertexLabels ->
Placed[Automatic, Automatic,
Grid[{#}, Frame -> All, FrameStyle -> LightGray,
Background -> bookColor[0]] &]]], VertexSize -> "VertexWeight",
AspectRatio -> 1/2, PerformanceGoal -> "Quality"]
|
The Machine Code of Euclid: All the Way Down to Axioms
Any theorem in Euclid can ultimately be proved just by using Euclid’s axioms enough times. In other words, the proofs Euclid gave were stated in terms of “intermediate theorems”—but we can always in principle just “compile things down” so we just get a sequence of axioms. And here for example is how that works for Book 1, Theorem 5:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"replacements", "=",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"First", "[",
RowBox[{"First", "[", "#", "]"}], "]"}], "\[Rule]",
RowBox[{"Last", "/@", "#"}]}], "&"}], "/@",
RowBox[{"GatherBy", "[",
RowBox[{
RowBox[{"Rule", "@@@",
RowBox[{"EdgeList", "[", "euc", "]"}]}], ",", "First"}],
"]"}]}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"repx", "=",
RowBox[{"replacements", "/.", " ",
RowBox[{"(",
RowBox[{"a_Association", " ", "\[RuleDelayed]", " ",
RowBox[{"EuclidVertexName", "[", "a", "]"}]}], ")"}]}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{"g", ",",
RowBox[{"i", "=", "1"}], ",", "vl", ",", "vs"}], "}"}], ",",
RowBox[{
RowBox[{
RowBox[{"vs", "[", "u_", "]"}], ":=",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorDarker", "[", "u", "]"}], ",",
RowBox[{"EdgeForm", "[",
RowBox[{"Darker", "[",
RowBox[{
RowBox[{"bookColorDarker", "[", "u", "]"}], ",", ".2"}],
"]"}], "]"}]}], "}"}]}], ";",
RowBox[{"g", "=",
RowBox[{"Map", "[",
RowBox[{
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{"MemberQ", "[",
RowBox[{
RowBox[{"EuclidVertexName", "/@", "axioms"}], ",", "#"}],
"]"}], ",",
RowBox[{"{",
RowBox[{"#", ",",
RowBox[{"i", "++"}]}], "}"}], ",", "#"}], "]"}], "&"}],
",",
RowBox[{"DeleteCases", "[",
RowBox[{
RowBox[{"Flatten", "[",
RowBox[{"Last", "[",
RowBox[{"Reap", "[",
RowBox[{"Nest", "[",
RowBox[{
RowBox[{
RowBox[{"(",
RowBox[{
RowBox[{"Sow", "[",
RowBox[{
RowBox[{
RowBox[{"Thread", "[",
RowBox[{"#", "\[Rule]",
RowBox[{"(",
RowBox[{"#", "/.", "repx"}], ")"}]}], "]"}],
"&"}], "/@", "#"}], "]"}], ";",
"\[IndentingNewLine]",
RowBox[{"Flatten", "[",
RowBox[{"#", "/.", "repx"}], "]"}]}], ")"}], "&"}],
",",
RowBox[{"{",
RowBox[{"EuclidVertexName", "[",
RowBox[{"<|",
RowBox[{
RowBox[{"\"\<Book\>\"", "\[Rule]", "1"}], ",",
RowBox[{"\"\<Theorem\>\"", "\[Rule]", "5"}]}],
"|>"}], "]"}], "}"}], ",", "4"}], "]"}], "]"}],
"]"}], "]"}], ",",
RowBox[{"x_", "\[Rule]", "x_"}]}], "]"}], ",",
RowBox[{"{",
RowBox[{"-", "1"}], "}"}]}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"vl", "=",
RowBox[{"VertexList", "[", "g", "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"EuclidGraphLarge", "[",
RowBox[{"g", ",",
RowBox[{
"GraphLayout", "\[Rule]", "\"\<LayeredDigraphEmbedding\>\""}],
",",
RowBox[{"VertexLabels", "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", "\[Rule]",
RowBox[{"Placed", "[",
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{"StringQ", "[", "#", "]"}], ",", "#", ",",
RowBox[{"First", "[", "#", "]"}]}], "]"}], ",",
"Center"}], "]"}]}], "&"}], "/@", "vl"}], ")"}]}], ",",
RowBox[{"VertexSize", "\[Rule]", ".5"}], ",",
RowBox[{"VertexStyle", "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", "\[Rule]",
RowBox[{"If", "[",
RowBox[{
RowBox[{"ListQ", "[", "#", "]"}], ",",
RowBox[{"vs", "[", "0", "]"}], ",",
RowBox[{"vs", "[",
RowBox[{"FromDigits", "[",
RowBox[{"First", "[",
RowBox[{"StringCases", "[",
RowBox[{"#", ",",
RowBox[{
RowBox[{
RowBox[{"b", ":",
RowBox[{"(",
RowBox[{"DigitCharacter", ".."}], ")"}]}], "~~",
"\"\<.\>\""}], "\[RuleDelayed]", "b"}]}], "]"}],
"]"}], "]"}], "]"}]}], "]"}]}], "&"}], "/@", "vl"}],
")"}]}]}], "]"}]}]}], "]"}],
"\[IndentingNewLine]"}]], "Input"]
}, Open ]]
|
Of course it’s much more efficient to “share the work” by using intermediate theorems:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; EuclidGraphLarge[ Subgraph[euc, VertexOutComponent[euc, <|"Book" -> 1, "Theorem" -> 5|>]]] |
This doesn’t change the “depth”—i.e. the length of any given path to get to the axioms. But it reduces the number of independent paths that have to be followed, because every time one reaches the same theorem (or axiom) one just “uses what one already knows about it”.
But to get a sense of the “axiomatic machine code” of Euclid we can just “compile” the proof of every theorem down to its underlying sequence of axioms. And for example if we do this for 3.18 the final sequence of axioms we get has length 835,416. These are broken down among the various axioms according to:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"replacements", "=",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"First", "[",
RowBox[{"First", "[", "#", "]"}], "]"}], "\[Rule]",
RowBox[{"Last", "/@", "#"}]}], "&"}], "/@",
RowBox[{"GatherBy", "[",
RowBox[{
RowBox[{"Rule", "@@@",
RowBox[{"EdgeList", "[", "euc", "]"}]}], ",", "First"}],
"]"}]}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"rep", " ", "=", " ", "replacements"}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Monitor", "[",
RowBox[{
RowBox[{"Do", "[", "\[IndentingNewLine]",
RowBox[{
RowBox[{
RowBox[{"rep", "[",
RowBox[{"[",
RowBox[{"n", ",", "2"}], "]"}], "]"}], "=",
RowBox[{"Sort", "[",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{"rep", "[",
RowBox[{"[",
RowBox[{"n", ",", "2"}], "]"}], "]"}], "/.", "rep"}],
"]"}], "]"}]}], ",", "\[IndentingNewLine]",
RowBox[{"{",
RowBox[{"n", ",", "1", ",",
RowBox[{"Length", "[", "rep", "]"}]}], "}"}]}], "]"}], ",",
"n"}], "]"}]], "Input"],
Cell[BoxData[
RowBox[{"Text", "[",
RowBox[{"Grid", "[",
RowBox[{
RowBox[{"Transpose", "[",
RowBox[{"KeyValueMap", "[",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"EuclidVertexName", "[", "#1", "]"}], ",", "#2"}],
"}"}], "&"}], ",",
RowBox[{"KeySort", "[",
RowBox[{"Counts", "[",
RowBox[{"rep", "[",
RowBox[{"[",
RowBox[{
RowBox[{"-", "1"}], ",", "2"}], "]"}], "]"}], "]"}],
"]"}]}], "]"}], "]"}], ",",
RowBox[{"Frame", "\[Rule]", "All"}], ",", " ",
RowBox[{"Background", "\[Rule]",
RowBox[{"{",
RowBox[{"None", ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorDarker", "[", "0", "]"}], ",", "None"}],
"}"}]}], "}"}]}]}], "]"}], "]"}]], "Input"]
}, Open ]]
|
Here is a plot of the lengths of axiom sequences for all the theorems, shown on a log scale:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"replacements", "=",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"First", "[",
RowBox[{"First", "[", "#", "]"}], "]"}], "\[Rule]",
RowBox[{"Last", "/@", "#"}]}], "&"}], "/@",
RowBox[{"GatherBy", "[",
RowBox[{
RowBox[{"Rule", "@@@",
RowBox[{"EdgeList", "[", "euc", "]"}]}], ",", "First"}],
"]"}]}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"rep", " ", "=", " ", "replacements"}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Monitor", "[",
RowBox[{
RowBox[{"Do", "[", "\[IndentingNewLine]",
RowBox[{
RowBox[{
RowBox[{"rep", "[",
RowBox[{"[",
RowBox[{"n", ",", "2"}], "]"}], "]"}], "=",
RowBox[{"Sort", "[",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{"rep", "[",
RowBox[{"[",
RowBox[{"n", ",", "2"}], "]"}], "]"}], "/.", "rep"}],
"]"}], "]"}]}], ",", "\[IndentingNewLine]",
RowBox[{"{",
RowBox[{"n", ",", "1", ",",
RowBox[{"Length", "[", "rep", "]"}]}], "}"}]}], "]"}], ",",
"n"}], "]"}]], "Input"],
Cell[BoxData[
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"dataA", "=",
RowBox[{
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{"MissingQ", "[",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "[", "\"\<Book\>\"",
"]"}], "]"}], ",", "Nothing", ",",
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "[", "\"\<Book\>\"",
"]"}], "\[Rule]",
RowBox[{"Length", "[",
RowBox[{"Last", "[", "#", "]"}], "]"}]}]}], "]"}], "&"}],
"/@", "rep"}]}], ",", "vals", ",", "acc", ",", "xval"}], "}"}],
",",
RowBox[{
RowBox[{"vals", "=",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"acc", "=",
RowBox[{"Association", "[",
RowBox[{"MapIndexed", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"First", "[", "#2", "]"}], "\[Rule]", "#1"}], "&"}],
",",
RowBox[{"Accumulate", "[",
RowBox[{"Values", "[",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}], "]"}], "]"}]}],
"]"}], "]"}]}], ";", "\[IndentingNewLine]",
RowBox[{"xval", "=",
RowBox[{"Association", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "-",
RowBox[{
RowBox[{"vals", "[",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}], "/", "2"}]}],
")"}]}], "&"}], "/@",
RowBox[{"Normal", "[", "acc", "]"}]}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"Show", "[",
RowBox[{"{",
RowBox[{
RowBox[{"ListLogPlot", "[",
RowBox[{
RowBox[{"Values", "[", "dataA", "]"}], ",",
RowBox[{"Axes", "\[Rule]",
RowBox[{"{",
RowBox[{"False", ",", "True"}], "}"}]}], ",",
RowBox[{"Filling", "\[Rule]", "Axis"}], ",",
RowBox[{"Frame", "\[Rule]", "True"}], ",",
RowBox[{"FrameLabel", "\[Rule]",
RowBox[{"{",
RowBox[{
"\"\<theorems by book\>\"", ",",
"\"\<length of axiom sequence\>\""}], "}"}]}], ",",
RowBox[{"FrameTicks", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"True", ",", "False"}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], ",",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"{",
RowBox[{"0", ",", "0"}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Normal", "[", "xval", "]"}]}], ",", "False"}],
"}"}]}], "}"}]}], ",",
RowBox[{"ColorFunctionScaling", "\[Rule]", "False"}], ",",
RowBox[{"ColorFunction", "\[Rule]",
RowBox[{"Function", "[",
RowBox[{
RowBox[{"{",
RowBox[{"x", ",", "y"}], "}"}], ",",
RowBox[{"Piecewise", "[",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "6", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "6", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "10", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "10", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "13", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "13", "]"}]}]}], "}"}]}], "}"}],
"]"}]}], "]"}]}], ",",
RowBox[{"Joined", "\[Rule]", "True"}]}], "]"}], ",",
RowBox[{"Graphics", "[",
RowBox[{"{",
RowBox[{
RowBox[{"GrayLevel", "[", "0.5", "]"}], ",",
RowBox[{"Line", "[",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"#", ",",
RowBox[{"-", "5"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{"#", ",",
RowBox[{"10", "^", "7"}]}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Values", "[", "acc", "]"}]}], "]"}]}], "}"}],
"]"}]}], "}"}], "]"}]}]}], "]"}]], "Input"]
}, Open ]]
|
Interestingly, 3.18 isn’t the theorem with the longest axiom sequence; it’s in 4th place, and the top 10 are (in gray are the results with intermediate theorems allowed):

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"replacements", "=",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"First", "[",
RowBox[{"First", "[", "#", "]"}], "]"}], "\[Rule]",
RowBox[{"Last", "/@", "#"}]}], "&"}], "/@",
RowBox[{"GatherBy", "[",
RowBox[{
RowBox[{"Rule", "@@@",
RowBox[{"EdgeList", "[", "euc", "]"}]}], ",", "First"}],
"]"}]}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"rep", " ", "=", " ", "replacements"}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Monitor", "[",
RowBox[{
RowBox[{"Do", "[", "\[IndentingNewLine]",
RowBox[{
RowBox[{
RowBox[{"rep", "[",
RowBox[{"[",
RowBox[{"n", ",", "2"}], "]"}], "]"}], "=",
RowBox[{"Sort", "[",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{"rep", "[",
RowBox[{"[",
RowBox[{"n", ",", "2"}], "]"}], "]"}], "/.", "rep"}],
"]"}], "]"}]}], ",", "\[IndentingNewLine]",
RowBox[{"{",
RowBox[{"n", ",", "1", ",",
RowBox[{"Length", "[", "rep", "]"}]}], "}"}]}], "]"}], ",",
"n"}], "]"}]], "Input"],
Cell[BoxData[
RowBox[{"Text", "[",
RowBox[{"Grid", "[",
RowBox[{
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"uu", "=",
RowBox[{
RowBox[{
RowBox[{"Length", "[",
RowBox[{"Last", "[", "#", "]"}], "]"}], "&"}], "/@",
"rep"}]}], ",", "vv"}], "}"}], ",",
RowBox[{
RowBox[{"vv", "=",
RowBox[{"(",
RowBox[{
RowBox[{"Complement", "[",
RowBox[{
RowBox[{"VertexList", "[", "euc", "]"}], ",", "axioms"}],
"]"}], "[",
RowBox[{"[",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{
RowBox[{"Position", "[",
RowBox[{"uu", ",", "#"}], "]"}], "&"}], "/@",
RowBox[{"TakeLargest", "[",
RowBox[{"uu", ",", "10"}], "]"}]}], "]"}], "]"}], "]"}],
")"}]}], ";",
RowBox[{"{",
RowBox[{
RowBox[{"EuclidVertexName", "/@", "vv"}], ",",
RowBox[{"TakeLargest", "[",
RowBox[{"uu", ",", "10"}], "]"}], ",",
RowBox[{
RowBox[{
RowBox[{"Style", "[",
RowBox[{
RowBox[{"Length", "[",
RowBox[{"VertexOutComponent", "[",
RowBox[{"euc", ",", "#"}], "]"}], "]"}], ",",
RowBox[{"GrayLevel", "[", ".6", "]"}], ",", "Italic"}],
"]"}], "&"}], "/@", "vv"}]}], "}"}]}]}], "]"}], ",",
RowBox[{"Frame", "\[Rule]", "All"}], ",",
RowBox[{"Background", "\[Rule]",
RowBox[{"{",
RowBox[{"None", ",", "None", ",",
RowBox[{"MapIndexed", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"Flatten", "[",
RowBox[{"{",
RowBox[{"1", ",", "#2"}], "}"}], "]"}], "\[Rule]",
RowBox[{"bookColorDarker", "[", "#1", "]"}]}], "&"}], ",",
RowBox[{"{",
RowBox[{
"10", ",", "12", ",", "12", ",", "13", ",", "10", ",", "10",
",", "10", ",", "10", ",", "10", ",", "10"}], "}"}]}],
"]"}]}], "}"}]}]}], "]"}], "]"}]], "Input"]
}, Open ]]
|
(10.72 is about addition of incommensurable medial areas, and is never referenced anywhere; 12.14 says the volumes of cones and cylinders with equal bases are proportional to their heights; 12.15 says the heights and bases of cones and cylinders with equal volumes are inversely proportional; etc.)
Here’s the distribution of the lengths of axiom sequences across all theorems:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"replacements", "=",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"First", "[",
RowBox[{"First", "[", "#", "]"}], "]"}], "\[Rule]",
RowBox[{"Last", "/@", "#"}]}], "&"}], "/@",
RowBox[{"GatherBy", "[",
RowBox[{
RowBox[{"Rule", "@@@",
RowBox[{"EdgeList", "[", "euc", "]"}]}], ",", "First"}],
"]"}]}]}], ";",
RowBox[{"rep", "=", "replacements"}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Monitor", "[",
RowBox[{
RowBox[{"Do", "[", "\[IndentingNewLine]",
RowBox[{
RowBox[{
RowBox[{"rep", "[",
RowBox[{"[",
RowBox[{"n", ",", "2"}], "]"}], "]"}], "=",
RowBox[{"Sort", "[",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{"rep", "[",
RowBox[{"[",
RowBox[{"n", ",", "2"}], "]"}], "]"}], "/.", "rep"}],
"]"}], "]"}]}], ",", "\[IndentingNewLine]",
RowBox[{"{",
RowBox[{"n", ",", "1", ",",
RowBox[{"Length", "[", "rep", "]"}]}], "}"}]}], "]"}], ",",
"n"}], "]"}]], "Input"],
Cell[BoxData[
RowBox[{"Histogram", "[",
RowBox[{
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"vod", "=",
RowBox[{
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "[", "\"\<Book\>\"",
"]"}], "->",
RowBox[{"Log", "[",
RowBox[{"10", ",",
RowBox[{"Length", "[",
RowBox[{"Last", "[", "#", "]"}], "]"}]}], "]"}]}],
"&"}], "/@", "rep"}]}], ",", "dataG"}], "}"}], ",",
RowBox[{
RowBox[{"dataG", "=",
RowBox[{"GroupBy", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{"MissingQ", "[",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}], ",",
RowBox[{"0", "\[Rule]", " ",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}]}], ",",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "\[Rule]",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}]}]}], "]"}], "&"}], "/@",
"vod"}], ",",
RowBox[{"First", "\[Rule]", "Last"}]}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{
RowBox[{
RowBox[{"Flatten", "[",
RowBox[{"Join", "[",
RowBox[{"Values", "[",
RowBox[{"dataG", "[",
RowBox[{"[",
RowBox[{"Key", "/@", "#"}], "]"}], "]"}], "]"}], "]"}],
"]"}], "&"}], "/@",
RowBox[{"{",
RowBox[{
RowBox[{"{", "0", "}"}], ",",
RowBox[{"{",
RowBox[{
"1", ",", "2", ",", "3", ",", "4", ",", "5", ",", "6"}],
"}"}], ",",
RowBox[{"{",
RowBox[{"7", ",", "8", ",", "9", ",", "10"}], "}"}], ",",
RowBox[{"{",
RowBox[{"11", ",", "12", ",", "13"}], "}"}]}], "}"}]}]}]}],
"\[IndentingNewLine]", "]"}], ",",
RowBox[{"{", ".2", "}"}], ",",
RowBox[{"Frame", "\[Rule]", "True"}], ",",
RowBox[{"FrameLabel", "\[Rule]",
RowBox[{"{",
RowBox[{
"\"\<length of axiom sequence\>\"", ",",
"\"\<number of theorems\>\""}], "}"}]}], ",",
RowBox[{"FrameTicks", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"None", ",", "None"}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"Table", "[",
RowBox[{
RowBox[{"{",
RowBox[{"n", ",",
RowBox[{"Superscript", "[",
RowBox[{"10", ",", "n"}], "]"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{"n", ",", "0", ",", "6"}], "}"}]}], "]"}], ",",
"Automatic"}], "}"}]}], "}"}]}], ",", "\n",
RowBox[{"ChartLayout", "\[Rule]", "\"\<Stacked\>\""}], ",",
RowBox[{"ChartBaseStyle", "\[Rule]",
RowBox[{"Opacity", "[", "1", "]"}]}], ",",
RowBox[{"ChartStyle", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "/@",
RowBox[{"{",
RowBox[{"0", ",", "6", ",", "10", ",", "13"}], "}"}]}], ",",
RowBox[{"EdgeForm", "[",
RowBox[{"Directive", "[",
RowBox[{"Thin", ",",
RowBox[{"GrayLevel", "[", "0.15", "]"}]}], "]"}], "]"}]}],
"}"}]}]}], "]"}]], "Input"]
}, Open ]]
|
We can get some sense of the dramatic value of “remembering intermediate theorems” by comparing the total number of “intermediate steps” obtained with and without merging different instances of the same theorem:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"(*",
RowBox[{
RowBox[{"unmerged", "=",
RowBox[{
RowBox[{
"ResourceFunction", "[", "\"\<ParallelMapMonitored\>\"", "]"}],
"[",
RowBox[{
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{"MissingQ", "[",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "[", "\"\<Book\>\"",
"]"}], "]"}], ",", "Nothing", ",",
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "[", "\"\<Book\>\"",
"]"}], "\[Rule]", " ",
RowBox[{"Length", "[",
RowBox[{"Flatten", "[",
RowBox[{"Most", "[",
RowBox[{"FixedPointList", "[",
RowBox[{
RowBox[{
RowBox[{"Sort", "[",
RowBox[{"Flatten", "[",
RowBox[{"#", "/.", "replacements"}], "]"}], "]"}],
"&"}], ",",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}]}], "]"}], "]"}], "]"}],
"]"}]}]}], "]"}], "&"}], ",", "replacements"}], "]"}]}],
";"}], "*)"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"unmerged", "=",
InterpretationBox[
DynamicModuleBox[{Typeset`open = False},
TemplateBox[{"List", "ListIcon",
GridBox[{{
RowBox[{
TagBox["\"Head: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["List", "IconizedItem"]}]}, {
RowBox[{
TagBox["\"Length: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["465", "IconizedItem"]}]}, {
RowBox[{
TagBox["\"Byte count: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["44760", "IconizedItem"]}]}},
GridBoxAlignment -> {"Columns" -> {{Left}}}, DefaultBaseStyle ->
"Column",
GridBoxItemSize -> {
"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}],
Dynamic[Typeset`open]},
"IconizedObject"]],
{1 -> 3, 1 -> 14, 1 -> 21, 1 -> 1, 1 -> 38, 1 -> 34, 1 -> 49, 1 ->
56, 1 -> 135, 1 -> 166, 1 -> 135, 1 -> 276, 1 -> 152, 1 -> 189,
1 -> 180, 1 -> 505, 1 -> 736, 1 -> 732, 1 -> 870, 1 -> 1173, 1 ->
1949, 1 -> 1352, 1 -> 1561, 1 -> 3172, 1 -> 3190, 1 -> 631, 1 ->
506, 1 -> 1048, 1 -> 397, 1 -> 409, 1 -> 2441, 1 -> 3723, 1 ->
1001, 1 -> 1126, 1 -> 1721, 1 -> 4210, 1 -> 6740, 1 -> 9647, 1 ->
9489, 1 -> 12396, 1 -> 8746, 1 -> 25067, 1 -> 1153, 1 -> 32185,
1 -> 67254, 1 -> 5654, 1 -> 18538, 1 -> 19567, 2 -> 4824, 2 ->
8367, 2 -> 8367, 2 -> 13531, 2 -> 16171, 2 -> 16171, 2 -> 10217,
2 -> 18320, 2 -> 30815, 2 -> 31376, 2 -> 43790, 2 -> 34158, 2 ->
30573, 2 -> 110990, 3 -> 425, 3 -> 2373, 3 -> 1503, 3 -> 2179, 3 ->
1, 3 -> 1, 3 -> 6562, 3 -> 9993, 3 -> 736, 3 -> 836, 3 -> 1932,
3 -> 1932, 3 -> 5454, 3 -> 23600, 3 -> 31939, 3 -> 2317, 3 ->
3412, 3 -> 2841, 3 -> 3164, 3 -> 3945, 3 -> 5119, 3 -> 9598, 3 ->
506, 3 -> 1506, 3 -> 3964, 3 -> 1520, 3 -> 7375, 3 -> 2455, 3 ->
8652, 3 -> 3201, 3 -> 16525, 3 -> 38820, 3 -> 72045, 3 -> 48485,
3 -> 41352, 3 -> 45657, 3 -> 63258, 4 -> 22, 4 -> 52390, 4 ->
15116, 4 -> 3961, 4 -> 17740, 4 -> 18540, 4 -> 3398, 4 -> 7955,
4 -> 118, 4 -> 177397, 4 -> 255297, 4 -> 309924, 4 -> 3975, 4 ->
210, 4 -> 27464, 4 -> 318652, 5 -> 1, 5 -> 1, 5 -> 2, 5 -> 3, 5 ->
2, 5 -> 2, 5 -> 1, 5 -> 2, 5 -> 3, 5 -> 6, 5 -> 1, 5 -> 2, 5 ->
1, 5 -> 15, 5 -> 6, 5 -> 30, 5 -> 4, 5 -> 30, 5 -> 48, 5 -> 19,
5 -> 19, 5 -> 25, 5 -> 73, 5 -> 63, 5 -> 87, 6 -> 19647, 6 ->
38284, 6 -> 43494, 6 -> 45195, 6 -> 53466, 6 -> 53154, 6 ->
55918, 6 -> 50428, 6 -> 41999, 6 -> 44331, 6 -> 42020, 6 ->
42020, 6 -> 68917, 6 -> 23520, 6 -> 20268, 6 -> 27795, 6 ->
28042, 6 -> 53253, 6 -> 87868, 6 -> 221525, 6 -> 2, 6 -> 233017,
6 -> 70041, 6 -> 39812, 6 -> 274404, 6 -> 43649, 6 -> 55229, 6 ->
458950, 6 -> 389781, 6 -> 434479, 6 -> 139565, 6 -> 60697, 6 ->
11752, 7 -> 1, 7 -> 2, 7 -> 6, 7 -> 3, 7 -> 1, 7 -> 2, 7 -> 2, 7 ->
3, 7 -> 6, 7 -> 15, 7 -> 8, 7 -> 6, 7 -> 16, 7 -> 23, 7 -> 7, 7 ->
8, 7 -> 23, 7 -> 35, 7 -> 89, 7 -> 34, 7 -> 46, 7 -> 24, 7 -> 1,
7 -> 219, 7 -> 220, 7 -> 220, 7 -> 442, 7 -> 1, 7 -> 1, 7 -> 204,
7 -> 1, 7 -> 2, 7 -> 178, 7 -> 444, 7 -> 1, 7 -> 456, 7 -> 8, 7 ->
8, 7 -> 499, 8 -> 118, 8 -> 783, 8 -> 2392, 8 -> 556, 8 -> 655,
8 -> 2743, 8 -> 2744, 8 -> 2928, 8 -> 1771, 8 -> 65, 8 -> 65, 8 ->
65, 8 -> 24, 8 -> 2895, 8 -> 3045, 8 -> 2896, 8 -> 3046, 8 -> 45,
8 -> 136, 8 -> 307, 8 -> 4336, 8 -> 308, 8 -> 4337, 8 -> 391, 8 ->
4768, 8 -> 1922, 8 -> 2068, 9 -> 3543, 9 -> 3586, 9 -> 7629, 9 ->
16551, 9 -> 16551, 9 -> 7941, 9 -> 1, 9 -> 4823, 9 -> 17840, 9 ->
20205, 9 -> 8, 9 -> 5315, 9 -> 10979, 9 -> 205, 9 -> 24438, 9 ->
89, 9 -> 114, 9 -> 180, 9 -> 181, 9 -> 2, 9 -> 1, 9 -> 2, 9 -> 6,
9 -> 1, 9 -> 2, 9 -> 2, 9 -> 2, 9 -> 2, 9 -> 7, 9 -> 7, 9 -> 8,
9 -> 10980, 9 -> 1, 9 -> 1, 9 -> 39, 9 -> 11724, 10 -> 1, 10 ->
1, 10 -> 2, 10 -> 9, 10 -> 32, 10 -> 102, 10 -> 103, 10 -> 33,
10 -> 226744, 10 -> 228716, 10 -> 323, 10 -> 878, 10 -> 879, 10 ->
279209, 10 -> 1, 10 -> 1, 10 -> 18725, 10 -> 20611, 10 -> 27267,
10 -> 27267, 10 -> 20502, 10 -> 319825, 10 -> 408640, 10 ->
440867, 10 -> 448859, 10 -> 381931, 10 -> 842497, 10 -> 880385,
10 -> 308650, 10 -> 605844, 10 -> 1738164, 10 -> 1738164, 10 ->
1915120, 10 -> 2359475, 10 -> 5485999, 10 -> 16108, 10 -> 30931,
10 -> 448389, 10 -> 2388459, 10 -> 2359505, 10 -> 6036076, 10 ->
434627, 10 -> 426484, 10 -> 876543, 10 -> 381932, 10 -> 2862054,
10 -> 890992, 10 -> 1172338, 10 -> 251225, 10 -> 251340, 10 ->
227826, 10 -> 250799, 10 -> 251340, 10 -> 202471, 10 -> 125054,
10 -> 480851, 10 -> 2548214, 10 -> 2530401, 10 -> 6116832, 10 ->
787216, 10 -> 957815, 10 -> 1264613, 10 -> 2965863, 10 ->
2930968, 10 -> 6557549, 10 -> 361925, 10 -> 1311832, 10 ->
3209590, 10 -> 2359506, 10 -> 6036077, 10 -> 6396519, 10 ->
23921481, 10 -> 12794, 10 -> 10237, 10 -> 1811901, 10 -> 1934358,
10 -> 10237, 10 -> 6039667, 10 -> 449303, 10 -> 824048, 10 ->
3247238, 10 -> 2406753, 10 -> 398170, 10 -> 7128494, 10 ->
246531, 10 -> 246531, 10 -> 246671, 10 -> 246531, 10 -> 246105,
10 -> 246671, 10 -> 417462, 10 -> 210228, 10 -> 2086447, 10 ->
2202068, 10 -> 137963, 10 -> 6226469, 10 -> 482928, 10 -> 944985,
10 -> 2795948, 10 -> 2566984, 10 -> 465701, 10 -> 6613882, 10 ->
357027, 10 -> 2844746, 10 -> 2271461, 10 -> 10238, 10 -> 6039668,
10 -> 3306126, 10 -> 367686, 10 -> 9155471, 10 -> 1294543, 10 ->
650467, 10 -> 398032, 10 -> 685229, 10 -> 27268, 11 -> 1, 11 ->
2, 11 -> 1, 11 -> 1141, 11 -> 1155, 11 -> 3010, 11 -> 2, 11 ->
2272, 11 -> 7397, 11 -> 9229, 11 -> 8457, 11 -> 14619, 11 -> 2,
11 -> 749, 11 -> 24506, 11 -> 2, 11 -> 38327, 11 -> 3801, 11 ->
144, 11 -> 7077, 11 -> 11179, 11 -> 6819, 11 -> 217077, 11 ->
11079, 11 -> 13954, 11 -> 26280, 11 -> 73198, 11 -> 1127, 11 ->
5890, 11 -> 5891, 11 -> 59453, 11 -> 160579, 11 -> 207420, 11 ->
309910, 11 -> 61474, 11 -> 177929, 11 -> 207421, 11 -> 11484, 11 ->
63945, 12 -> 367801, 12 -> 397182, 12 -> 119315, 12 -> 692504,
12 -> 1308299, 12 -> 1308630, 12 -> 1311835, 12 -> 1909305, 12 ->
1723450, 12 -> 3352109, 12 -> 5763932, 12 -> 5450959, 12 ->
5763933, 12 -> 15768375, 12 -> 15768176, 12 -> 4877, 12 ->
2243219, 12 -> 5009994, 13 -> 61824, 13 -> 41215, 13 -> 5655, 13 ->
36473, 13 -> 36561, 13 -> 856336, 13 -> 192, 13 -> 95131, 13 ->
92410, 13 -> 171606, 13 -> 2877566, 13 -> 67412, 13 -> 447778,
13 -> 65939, 13 -> 91391, 13 -> 3967013, 13 -> 1732990, 13 ->
14412576},
SelectWithContents->True,
Selectable->False]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"merged", "=",
RowBox[{
RowBox[{
RowBox[{"VertexCount", "[",
RowBox[{"Subgraph", "[",
RowBox[{"euc", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{"euc", ",", "#"}], "]"}]}], "]"}], "]"}], "&"}], "/@",
RowBox[{"Complement", "[",
RowBox[{
RowBox[{"VertexList", "[", "euc", "]"}], ",", "axioms"}],
"]"}]}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"dataA", "=", "unmerged"}], ",", "vals", ",", "acc", ",",
"xval"}], "}"}], ",", "\[IndentingNewLine]",
RowBox[{
RowBox[{"vals", "=",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}]}], ";",
RowBox[{"acc", "=",
RowBox[{"Association", "[",
RowBox[{"MapIndexed", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"First", "[", "#2", "]"}], "\[Rule]", " ", "#1"}],
"&"}], ",",
RowBox[{"Accumulate", "[",
RowBox[{"Values", "[",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}], "]"}], "]"}]}],
"]"}], "]"}]}], ";", "\[IndentingNewLine]",
RowBox[{"xval", "=",
RowBox[{"Association", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "-",
RowBox[{
RowBox[{"vals", "[",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}], "/", "2"}]}],
")"}]}], "&"}], "/@",
RowBox[{"Normal", "[", "acc", "]"}]}], "]"}]}], ";",
RowBox[{"Show", "[",
RowBox[{"{",
RowBox[{
RowBox[{"ListLogPlot", "[",
RowBox[{
RowBox[{"Values", "[", "dataA", "]"}], ",",
RowBox[{"ColorFunctionScaling", "\[Rule]", "False"}], ",",
RowBox[{"Filling", "\[Rule]", " ", "1"}], ",",
RowBox[{"FrameLabel", "\[Rule]",
RowBox[{"{",
RowBox[{
"\"\<theorems by book\>\"", ",",
"\"\<number of intermediate steps\>\""}], "}"}]}], ",",
RowBox[{"FrameTicks", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"True", ",", "False"}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], ",",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"{",
RowBox[{"0", ",", "0"}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Normal", "[", "xval", "]"}]}], ",", "False"}],
"}"}]}], "}"}]}], ",",
RowBox[{"ColorFunction", "\[Rule]", " ",
RowBox[{"Function", "[",
RowBox[{
RowBox[{"{",
RowBox[{"x", ",", "y"}], "}"}], ",",
RowBox[{"Piecewise", "[",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "6", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "6", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "10", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "10", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "13", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "13", "]"}]}]}], "}"}]}], "}"}],
"]"}]}], "]"}]}], " ", ",",
RowBox[{"Joined", "\[Rule]", "True"}], ",",
RowBox[{"Frame", "\[Rule]", "True"}]}], "]"}], ",",
RowBox[{"ListLogPlot", "[",
RowBox[{"merged", ",",
RowBox[{"Filling", "\[Rule]", " ", "1"}], " ", ",",
RowBox[{"FillingStyle", "\[Rule]", "LightGray"}], ",",
RowBox[{"Frame", "\[Rule]", "True"}], ",",
RowBox[{"Joined", "\[Rule]", "True"}]}], "]"}], ",",
RowBox[{"Graphics", "[",
RowBox[{"{",
RowBox[{
RowBox[{"GrayLevel", "[", "0.5", "]"}], ",",
RowBox[{"Line", "[",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"#", ",",
RowBox[{"-", "5"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{"#", ",",
RowBox[{"10", "^", "8"}]}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Values", "[", "acc", "]"}]}], "]"}]}], "}"}],
"]"}]}], "}"}], "]"}]}]}], "]"}]], "Input"]
}, Open ]]
|
For example, for 8.13, 229 steps are needed when intermediate theorems are remembered, while 14,412,576 steps are needed otherwise. (For 10.72, it’s 184 vs. 23,921,481 steps.)
Superaxioms, or What Are the Most Powerful Theorems?
Euclid’s 10 axioms are ultimately all we need in order to prove all the 465 theorems in the Elements. But what if we supplement these axioms with some of the theorems? Are there small sets of theorems we can add that will make the proofs of many theorems much shorter? To get a full understanding of this, we’d have to redo all the proofs. But we can get some sense of it just from the theorem dependency graph.
Consider the graph representing the proof of 1.12, with 1.7 highlighted:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"];
gg = With[{g =
Subgraph[euc,
VertexOutComponent[euc, <|"Book" -> 1, "Theorem" -> 12|>]]},
EuclidGraphLarge[g, GraphLayout -> "LayeredDigraphEmbedding",
VertexStyle -> (Flatten[{# -> {EuclidVertexStyle[#]} & /@
Complement[
VertexList[g], {<|"Book" -> 1, "Theorem" -> 7|>}], <|
"Book" -> 1, "Theorem" -> 7|> -> Opacity[.6, Red]}])]]
|
Now imagine adding 1.7 as a “superaxiom”. Doing this, we can get a smaller proof graph for 1.12—with 4 nodes (and 14 connections) fewer:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";",
RowBox[{
RowBox[{"PruneSubgraph", "[",
RowBox[{"graph_", ",", " ", "subgraph_"}], "]"}], " ", ":=", " ",
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
"subBranches", ",", " ", "branches", ",", " ", "prunecheck",
",", " ", "prunable"}], "}"}], ",", "\n", " ",
RowBox[{
RowBox[{"subBranches", " ", "=", " ",
RowBox[{"Sort", "[",
RowBox[{"Tally", "[",
RowBox[{"Last", " ", "/@", " ",
RowBox[{"Union", "[",
RowBox[{"EdgeList", "[", "subgraph", "]"}], "]"}]}], "]"}],
"]"}]}], ";", "\n", " ",
RowBox[{"branches", " ", "=", " ",
RowBox[{"Tally", "[",
RowBox[{"Last", " ", "/@", " ",
RowBox[{"Union", "[",
RowBox[{"EdgeList", "[", "graph", "]"}], "]"}]}], "]"}]}],
";", "\n", " ",
RowBox[{"prunecheck", " ", "=", " ",
RowBox[{"Sort", "[",
RowBox[{"Select", "[",
RowBox[{"branches", ",", " ",
RowBox[{
RowBox[{"MemberQ", "[",
RowBox[{
RowBox[{"First", " ", "/@", " ", "subBranches"}], ",",
" ",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}]}], "]"}], " ", "&"}]}],
"]"}], "]"}]}], ";", "\n",
RowBox[{"prunable", " ", "=", " ",
RowBox[{"Table", "[",
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"prunecheck", "[",
RowBox[{"[",
RowBox[{"n", ",", " ", "2"}], "]"}], "]"}], " ", "==",
" ",
RowBox[{"subBranches", "[",
RowBox[{"[",
RowBox[{"n", ",", " ", "2"}], "]"}], "]"}]}], ",", " ",
RowBox[{"prunecheck", "[",
RowBox[{"[",
RowBox[{"n", ",", " ", "1"}], "]"}], "]"}], ",", " ",
RowBox[{"Sequence", " ", "@@", " ",
RowBox[{"{", "}"}]}]}], "]"}], ",", " ",
RowBox[{"{",
RowBox[{"n", ",", " ", "1", ",", " ",
RowBox[{"Length", "[", "prunecheck", "]"}]}], "}"}]}],
"]"}]}], ";", "\n", " ",
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"Length", "[", "prunable", "]"}], " ", "==", " ",
"0"}], ",", " ", "\"\<Same graph\>\"", ",", "\n",
RowBox[{"Graph", "[",
RowBox[{"Select", "[",
RowBox[{
RowBox[{"EdgeList", "[", "graph", "]"}], ",", " ",
RowBox[{
RowBox[{
RowBox[{"Not", "[",
RowBox[{"MemberQ", "[",
RowBox[{"prunable", ",", " ",
RowBox[{"First", "[", "#", "]"}]}], "]"}], "]"}], " ",
"&&", " ",
RowBox[{"Not", "[",
RowBox[{
RowBox[{"First", "[", "#", "]"}], "\[Equal]",
RowBox[{"First", "[",
RowBox[{"VertexList", "[", "subgraph", "]"}], "]"}]}],
"]"}]}], " ", "&"}]}], "]"}], "]"}]}], "]"}]}]}],
"]"}]}]}]], "Input"],
Cell[BoxData[
RowBox[{"With", "[",
RowBox[{
RowBox[{"{",
RowBox[{"g", "=",
RowBox[{"PruneSubgraph", "[",
RowBox[{
RowBox[{"Subgraph", "[",
RowBox[{"euc", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{"euc", ",",
RowBox[{"\[LeftAssociation]",
RowBox[{
RowBox[{"\"\<Book\>\"", "\[Rule]", "1"}], ",",
RowBox[{"\"\<Theorem\>\"", "\[Rule]", "12"}]}],
"\[RightAssociation]"}]}], "]"}]}], "]"}], ",",
RowBox[{"Subgraph", "[",
RowBox[{"euc", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{"euc", ",",
RowBox[{"\[LeftAssociation]",
RowBox[{
RowBox[{"\"\<Book\>\"", "\[Rule]", "1"}], ",",
RowBox[{"\"\<Theorem\>\"", "\[Rule]", "7"}]}],
"\[RightAssociation]"}]}], "]"}]}], "]"}]}], "]"}]}],
"}"}], ",",
RowBox[{"EuclidGraphLarge", "[",
RowBox[{"g", ",",
RowBox[{
"GraphLayout", "\[Rule]", "\"\<LayeredDigraphEmbedding\>\""}],
",",
RowBox[{"VertexStyle", "\[Rule]",
RowBox[{"(",
RowBox[{"Flatten", "[",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "\[Rule]",
RowBox[{"{",
RowBox[{"EuclidVertexStyle", "[", "#", "]"}], "}"}]}],
"&"}], "/@",
RowBox[{"Complement", "[",
RowBox[{
RowBox[{"VertexList", "[", "g", "]"}], ",",
RowBox[{"{",
RowBox[{"\[LeftAssociation]",
RowBox[{
RowBox[{"\"\<Book\>\"", "\[Rule]", "1"}], ",",
RowBox[{"\"\<Theorem\>\"", "\[Rule]", "7"}]}],
"\[RightAssociation]"}], "}"}]}], "]"}]}], ",",
RowBox[{
RowBox[{"\[LeftAssociation]",
RowBox[{
RowBox[{"\"\<Book\>\"", "\[Rule]", "1"}], ",",
RowBox[{"\"\<Theorem\>\"", "\[Rule]", "7"}]}],
"\[RightAssociation]"}], "\[Rule]",
RowBox[{"Opacity", "[",
RowBox[{".6", ",", "Red"}], "]"}]}]}], "}"}], "]"}],
")"}]}], ",",
RowBox[{"AspectRatio", "\[Rule]",
RowBox[{"1", "/", "3"}]}]}], "]"}]}], "]"}]], "Input"]
}, Open ]]
|
What does adding 1.7 as a superaxiom do for the proofs of other theorems? Here’s how much it shortens each of them:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";",
RowBox[{
RowBox[{"PruneSubgraph", "[",
RowBox[{"graph_", ",", " ", "subgraph_"}], "]"}], " ", ":=", " ",
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
"subBranches", ",", " ", "branches", ",", " ", "prunecheck",
",", " ", "prunable"}], "}"}], ",", "\n", " ",
RowBox[{
RowBox[{"subBranches", " ", "=", " ",
RowBox[{"Sort", "[",
RowBox[{"Tally", "[",
RowBox[{"Last", " ", "/@", " ",
RowBox[{"Union", "[",
RowBox[{"EdgeList", "[", "subgraph", "]"}], "]"}]}], "]"}],
"]"}]}], ";", "\n", " ",
RowBox[{"branches", " ", "=", " ",
RowBox[{"Tally", "[",
RowBox[{"Last", " ", "/@", " ",
RowBox[{"Union", "[",
RowBox[{"EdgeList", "[", "graph", "]"}], "]"}]}], "]"}]}],
";", "\n", " ",
RowBox[{"prunecheck", " ", "=", " ",
RowBox[{"Sort", "[",
RowBox[{"Select", "[",
RowBox[{"branches", ",", " ",
RowBox[{
RowBox[{"MemberQ", "[",
RowBox[{
RowBox[{"First", " ", "/@", " ", "subBranches"}], ",",
" ",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}]}], "]"}], " ", "&"}]}],
"]"}], "]"}]}], ";", "\n",
RowBox[{"prunable", " ", "=", " ",
RowBox[{"Table", "[",
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"prunecheck", "[",
RowBox[{"[",
RowBox[{"n", ",", " ", "2"}], "]"}], "]"}], " ", "==",
" ",
RowBox[{"subBranches", "[",
RowBox[{"[",
RowBox[{"n", ",", " ", "2"}], "]"}], "]"}]}], ",", " ",
RowBox[{"prunecheck", "[",
RowBox[{"[",
RowBox[{"n", ",", " ", "1"}], "]"}], "]"}], ",", " ",
RowBox[{"Sequence", " ", "@@", " ",
RowBox[{"{", "}"}]}]}], "]"}], ",", " ",
RowBox[{"{",
RowBox[{"n", ",", " ", "1", ",", " ",
RowBox[{"Length", "[", "prunecheck", "]"}]}], "}"}]}],
"]"}]}], ";", "\n", " ",
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"Length", "[", "prunable", "]"}], " ", "==", " ",
"0"}], ",", " ", "\"\<Same graph\>\"", ",", "\n",
RowBox[{"Graph", "[",
RowBox[{"Select", "[",
RowBox[{
RowBox[{"EdgeList", "[", "graph", "]"}], ",", " ",
RowBox[{
RowBox[{
RowBox[{"Not", "[",
RowBox[{"MemberQ", "[",
RowBox[{"prunable", ",", " ",
RowBox[{"First", "[", "#", "]"}]}], "]"}], "]"}], " ",
"&&", " ",
RowBox[{"Not", "[",
RowBox[{
RowBox[{"First", "[", "#", "]"}], "\[Equal]",
RowBox[{"First", "[",
RowBox[{"VertexList", "[", "subgraph", "]"}], "]"}]}],
"]"}]}], " ", "&"}]}], "]"}], "]"}]}], "]"}]}]}],
"]"}]}]}]], "Input"],
Cell[BoxData[
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"dataA", "=",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"t", ",",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[", "\"\<Book\>\"", "]"}], "\[Rule]", " ",
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"Order", "[",
RowBox[{"#", ",", "t"}], "]"}], "\[NotEqual]",
RowBox[{"-", "1"}]}], ",", "0", ",",
RowBox[{"With", "[",
RowBox[{
RowBox[{"{",
RowBox[{"g", "=",
RowBox[{"Subgraph", "[",
RowBox[{"euc", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{"euc", ",", "#"}], "]"}]}], "]"}]}],
"}"}], ",",
RowBox[{"Catch", "[",
RowBox[{
RowBox[{"VertexCount", "[", "g", "]"}], "-",
RowBox[{"VertexCount", "[",
RowBox[{
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{"!",
RowBox[{"GraphQ", "[", "#", "]"}]}], ",",
RowBox[{"Throw", "[", "0", "]"}], ",", "#"}],
"]"}], "&"}], "[",
RowBox[{"PruneSubgraph", "[",
RowBox[{"g", ",",
RowBox[{"Subgraph", "[",
RowBox[{"euc", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{"euc", ",", "t"}], "]"}]}], "]"}]}],
"]"}], "]"}], "]"}]}], "]"}]}], "]"}]}], "]"}]}],
"&"}], "/@",
RowBox[{"Complement", "[",
RowBox[{
RowBox[{"VertexList", "[", "euc", "]"}], ",", "axioms"}],
"]"}]}]}], "]"}], "[",
RowBox[{"\[LeftAssociation]",
RowBox[{
RowBox[{"\"\<Book\>\"", "\[Rule]", "1"}], ",",
RowBox[{"\"\<Theorem\>\"", "\[Rule]", "7"}]}],
"\[RightAssociation]"}], "]"}]}], ",", "vals", ",", "acc",
",", "xval"}], "}"}], ",", "\[IndentingNewLine]",
RowBox[{
RowBox[{"vals", "=",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}]}], ";",
RowBox[{"acc", "=",
RowBox[{"Association", "[",
RowBox[{"MapIndexed", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"First", "[", "#2", "]"}], "\[Rule]", " ", "#1"}],
"&"}], ",",
RowBox[{"Accumulate", "[",
RowBox[{"Values", "[",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}], "]"}], "]"}]}],
"]"}], "]"}]}], ";", "\[IndentingNewLine]",
RowBox[{"xval", "=",
RowBox[{"Association", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "-",
RowBox[{
RowBox[{"vals", "[",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}], "/", "2"}]}],
")"}]}], "&"}], "/@",
RowBox[{"Normal", "[", "acc", "]"}]}], "]"}]}], ";",
RowBox[{"Show", "[",
RowBox[{"{",
RowBox[{
RowBox[{"ListStepPlot", "[",
RowBox[{
RowBox[{"Values", "[", "dataA", "]"}], ",",
RowBox[{"Axes", "\[Rule]",
RowBox[{"{",
RowBox[{"False", ",", "True"}], "}"}]}], ",",
RowBox[{"Joined", "\[Rule]", "True"}], ",",
RowBox[{"Frame", "\[Rule]", " ", "True"}], ",",
RowBox[{"FrameLabel", "\[Rule]",
RowBox[{"{",
RowBox[{
"\"\<theorems by book\>\"", ",", " ",
"\"\<shortening\>\""}], "}"}]}], ",",
RowBox[{"FrameTicks", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"True", ",", "False"}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], ",",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"{",
RowBox[{"0", ",", "0"}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Normal", "[", "xval", "]"}]}], ",", "False"}],
"}"}]}], "}"}]}], ",",
RowBox[{"Filling", "\[Rule]", "Axis"}], ",",
RowBox[{"ColorFunctionScaling", "\[Rule]", "False"}], ",",
RowBox[{"ColorFunction", "\[Rule]", " ",
RowBox[{"Function", "[",
RowBox[{
RowBox[{"{",
RowBox[{"x", ",", "y"}], "}"}], ",",
RowBox[{"Piecewise", "[",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "6", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "6", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "10", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "10", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "13", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "13", "]"}]}]}], "}"}]}], "}"}],
"]"}]}], "]"}]}], ",",
RowBox[{"PlotRange", "\[Rule]", "All"}]}], " ", "]"}], ",",
RowBox[{"Graphics", "[",
RowBox[{"{",
RowBox[{
RowBox[{"GrayLevel", "[", "0.5", "]"}], ",",
RowBox[{"Line", "[",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"#", ",",
RowBox[{"-", "5"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{"#", ",", "12"}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Values", "[", "acc", "]"}]}], "]"}]}], "}"}],
"]"}]}], "}"}], "]"}]}]}], "]"}]], "Input"]
}, Open ]]
|
(The largest shortening is for 1.8, followed by 4.1.)
So what are the “best” superaxioms to add? Here’s a plot of the average amount of shortening achieved by adding each possible individual theorem as a superaxiom:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"(*",
RowBox[{
RowBox[{"res", "=",
RowBox[{
RowBox[{
"ResourceFunction", "[", "\"\<ParallelMapMonitored\>\"", "]"}],
"[",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"t", ",",
RowBox[{"t", "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"Order", "[",
RowBox[{"#", ",", "t"}], "]"}], "\[NotEqual]",
RowBox[{"-", "1"}]}], ",", "0", ",",
RowBox[{"With", "[",
RowBox[{
RowBox[{"{",
RowBox[{"g", "=",
RowBox[{"Subgraph", "[",
RowBox[{"euc", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{"euc", ",", "#"}], "]"}]}], "]"}]}],
"}"}], ",",
RowBox[{"Catch", "[",
RowBox[{
RowBox[{"VertexCount", "[", "g", "]"}], "-",
RowBox[{"VertexCount", "[",
RowBox[{
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{"!",
RowBox[{"GraphQ", "[", "#", "]"}]}], ",",
RowBox[{"Throw", "[", "0", "]"}], ",", "#"}],
"]"}], "&"}], "[",
RowBox[{"PruneSubgraph", "[",
RowBox[{"g", ",",
RowBox[{"Subgraph", "[",
RowBox[{"euc", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{"euc", ",", "t"}], "]"}]}], "]"}]}],
"]"}], "]"}], "]"}]}], "]"}]}], "]"}]}], "]"}],
"&"}], "/@",
RowBox[{"Complement", "[",
RowBox[{
RowBox[{"VertexList", "[", "euc", "]"}], ",", "axioms"}],
"]"}]}], ")"}]}]}], "]"}], ",",
RowBox[{"Complement", "[",
RowBox[{
RowBox[{"VertexList", "[", "euc", "]"}], ",", "axioms"}],
"]"}]}], "]"}]}], ";"}], "*)"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"res", "=",
RowBox[{"{",
InterpretationBox[
DynamicModuleBox[{Typeset`open = False},
TemplateBox[{"Expression", "SequenceIcon",
GridBox[{{
RowBox[{
TagBox["\"Head: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["Sequence", "IconizedItem"]}]}, {
RowBox[{
TagBox["\"Length: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["465", "IconizedItem"]}]}, {
RowBox[{
TagBox["\"Byte count: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["5397840", "IconizedItem"]}]}},
GridBoxAlignment -> {"Columns" -> {{Left}}},
DefaultBaseStyle -> "Column",
GridBoxItemSize -> {
"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}],
Dynamic[Typeset`open]},
"IconizedObject"]],
Sequence[
Association["Book" -> 1, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 1, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIYWBgYmRnBLBoBFihNSztGNkAOWQCuDgKK
"],
Association["Book" -> 1, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKAgIWNhYWRbMDAQEABO5SG2cGAC2A1HdUq6gL8BoLt
I+w9agCI5xlgPibVSuTYAwDLWQPN
"],
Association["Book" -> 1, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKAgJERyhgFQx8AAJpGAn0=
"],
Association["Book" -> 1, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJAgJ2Tg5kJCBmZGJABEyoXC4ApwKuSHUozI+sYBfgB
M7mKAf41Ar4=
"],
Association["Book" -> 1, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLAgJWFgXaAHUoz4lU1CsgHyCELALB1Aow=
"],
Association["Book" -> 1, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIggJuVBQiZWRjhQoyMjCwsYAoqhFCMACwwmgVZFKgD
AiGAHVkxMxZTRgEDOKAZIGENxqwMMBY8SrBFAKYMAC5tAuc=
"],
Association["Book" -> 1, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKggJ0VBNmYmBihgImJiY0NTEGF4DJIgBWIGRiANCuy
KFAHBEIAO5JiRhZGJEvRABYLGFEEceokE+A3EGwfI3ZnURkALQKGMwM4rBmY
gJ5mAgcaKATh4Y81AjBlAC8MBBg=
"],
Association["Book" -> 1, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJggIOLjZOdgxEuxMjIyMEBpqBCyIphgAVGsyCLAnVA
IAQwQWlWEMGGxZRRwAAOaAZIWIMxFwOMBY8SbBEAAUxIbABHwQL7
"],
Association["Book" -> 1, "Theorem" -> 10] -> CompressedData["
1:eJydUUESgCAIXJjk0C/6Uk/wA721H4WIpJN1aB1hZhEWcMvHngnAWUxAVlkS
MzmYOSVzTkWkg+gF1EvPakY9kYj6uKgMmiMmAoTevaf+w3dB06NnW7VT7xdT
vo0Dum0bJBirHYPpnmG7BivJ0lYe+59+gEfgjWi9CwMwA+M=
"],
Association["Book" -> 1, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIQgJWXm4cRLsTIyMjDA6agQqiKIYAFRrMgiwJ1QCAE
MMHMR9YxCtAAKJwhYQ3GfAwwFjxKsEUABDAhsQFG6wL+
"],
Association["Book" -> 1, "Theorem" -> 12] -> CompressedData["
1:eJydUMERwzAIkxDpHlmpI2SBzNqNGsBpyKXNo7qz8XFCMpqX9bkQwCuuhkku
WYCkJPcsYgAC2BETj5wj3D8iW18MJnZ1GzU5wm+c1FtFmZE3s3/hXvDwq3Wb
f61f/8NI4yJWzSTiiOybfTy21PNkRLQp6BZh2p6f4YqRUeu8AY+BA1g=
"],
Association["Book" -> 1, "Theorem" -> 13] -> CompressedData["
1:eJy9kNENgCAMRHstfsIOruQILuCsbmSvoBKNfhlfCD2a0oOO8zLNEJGVW08u
Ztows5wVlAg8yJUEJhVpFxHMr0FFW5HGAgbqdOtxgg5hoxqrDvErvd+79xcP
88m3LxrtCifIk8//yeVIaJfcAMoOA2g=
"],
Association["Book" -> 1, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJQAB8zIxMUMDMz8vAwMTACAUQOQzEQsIBlmRhZWODK
gICZiZGJAQQhAEazgnVgMWUUAAEwvBkggQjGfKDwA7PgAYstAiCACYkNAFr6
AxM=
"],
Association["Book" -> 1, "Theorem" -> 15] -> CompressedData["
1:eJydUMENgCAM7NHCkx1cyRFYwFndyFJAUYMhHklTyvVabknbmkBEew53BJaK
EBCjgNk5GBxI+agodGHmHKUk9S149sin8Go/vOaQ98wTTfbSL1dq9XHrP8wJ
4rGPlSa0MumThz5Rv4ltkhmp1ov9XP0fTUDbxHXFAxB0A6o=
"],
Association["Book" -> 1, "Theorem" -> 16] -> CompressedData["
1:eJydUdsNwyAMvGKcWBBF+ckAXakjZIHO2o3qAyTSJs1HT8jY3Pkhc9+ej+0G
4EXzhWWacs5mNq+zqgldIWBA2IPqUVUBixodQBViTTFJQmolXSk8bkD6J2QH
D0Kot7Ssy9y/EC7Z3o+T0PbE4pctBLIMD8XqYxGir+ysPR0zRdkmFm+t0WSE
OmHD0FTxMGD7kY/HN8qGBSc=
"],
Association["Book" -> 1, "Theorem" -> 17] -> CompressedData["
1:eJytUMkNAjEMHF/JWvBgP/xpiRK2AWqlI+yEVWDJk4mUxNbYY89te9w3AvDM
6wj3pSxmdlovZsJn9yIJcgJ9IsmVRAAjU+ZIaPAYWCvHQX13jIwCEicZE8kd
WZ1IOURDin+8UdmqIvgzZvsPDD2iXIsGva/fXEhXOMOfZj3ZiBiWzeTzU4rA
muQ1nGA1VqSnrrrPcxSQPsJ32xf6SwRy
"],
Association["Book" -> 1, "Theorem" -> 18] -> CompressedData["
1:eJydUcENwzAIvMOBGsmVukJX6ghZoLN2oxocKZbS5NGTjMEcB8LP9f1aCeAT
5oBH8+bu93YTMbFaTQKoAGcEt5g74IVULcAgoqmqKHQT7C9Mi3TOIRN6QI47
zkhfFf+Dy2mmfjFJ2L0w/dwCIxvhQWw8JhH7yn61D8eMKEnpG+2CLjUV6rKc
TcvtRzAv5gvPEARC
"],
Association["Book" -> 1, "Theorem" -> 19] -> CompressedData["
1:eJydkNkNAyEMRD02GBYtRaSllLANpNZ0FB9SQs6PPCEzAh8Mp+NyPkBEVw/v
zDHHGHNvzE20dxUHHeAVGNJaIxoFULUgUqsAe9UqFRUJxxKQawsfhzqyYL2Y
bafUMUy+Vv4J/7yNefZa9+0vSMtpKXT8Avstp8dn8jAS8fiyNeEubJAqKGzS
FmLIFhm9lNfGS322peXwBoEJBTQ=
"],
Association["Book" -> 1, "Theorem" -> 20] -> CompressedData["
1:eJydUUESwjAIhAViGzvV8Qd+ySf0A77VH7nQquOMenAnISQQyG7Oy/WyqIjc
0nzA8XTofT/tgB6tNY+ENTMv1GJm4GRApJvqPDcIz+DAFGN4IMBaqMFDq9Ke
u2+IyFZrO9BJT1YfLBD+/ep/sJ/RpJbPTd7kb052G5J9WYrAJXL7im5wTzUq
EatyqLRnsj8uJbFhUKGOZjKahGrHKEqZ29qHUEuF359fn2FSVYQaQ+5i6QZJ
"],
Association["Book" -> 1, "Theorem" -> 21] -> CompressedData["
1:eJydUcERwjAMcyQrpL2DHViJEboAs7IRttsCD8oDXezYia2zkutyvy3NzB7p
vuE89z4mAZfh7l0JOumF2kgibJBmXa3N84BJUU1OPEU1iKBCLQdUzJ7ZEaJd
q0lIrthtjQFQftz6H/jzVjlyjJu6Q39K2pHqy6dKUpm+bzd4qPY6JtaXQ5W9
in1vSmG901oyWgRi65Rtb84dMH6OHHF9Bq1YDBHYEw8WBhY=
"],
Association["Book" -> 1, "Theorem" -> 22] -> CompressedData["
1:eJydUdsVQiEMa5u0esXjnwO4kiO4gLO6kaHXx4/6YQ6EQgqFcLpczxc3s9uk
jziOMfabiMO2qljVTGajB5JQU2S2wH0MwICITeY+h9alRYSkyZq6ubtyvha1
qqy1V0HBjGyNAbDy684/wZ+qiptBWZw3ERNPzNc3ywQNNadv9QG9GdnL7dO0
pNNeyfnclF0Nlu6kLbSCL7Ezl80VwRVOSPY3wr0/g9anOCh/7/RtByU=
"],
Association["Book" -> 1, "Theorem" -> 23] -> CompressedData["
1:eJydUclxAzEMoygAXI3XfqSDtJQS3EBqTUcGd51HZuI8Ag2hg5AgUe/3z4/7
iIivpt9xu62FzLcdQK5GoQw9oySBQpERO0Zer8TgzLxIS7s2Oj3n9CFplmaG
hwjkS9O1tlWOBuxY7uMc+xpc28ud/4T+zNo8Alapb2IWvtGvP1hw84NF9grJ
Th/kejkgT3TUrqo1rW9uQfetLRtVzeAYrqcYa46dlxg+FnPyxCCSzB84PyQO
vwQT4wEkUQik
"],
Association["Book" -> 1, "Theorem" -> 24] -> CompressedData["
1:eJydUcERwjAMs2TXoRwHb56sxAgswKxshBQ4eJUHSuo4ZzWSk8vtfr0hIh4O
Gziva5H7rirujJrI+iBJVi1LxGkHjtEEATS59r7HkgsToGiAQ4USKmxqtiAB
L822dFdoC039WmPb7n+o31WX5TbtSZeRaucNda+YAjSycqby6GYx78EkfWod
k5NvTsKcyai5cyKhMSAlFaM1gUMdXUa9ZOcpjvwCfgA/ULxc+eB4AhvDBf8=
"],
Association["Book" -> 1, "Theorem" -> 25] -> CompressedData["
1:eJydUdERQjEIIxDwPe88XcGVHMEFnNWNDFQ/9cO0TenBEaDX++N2h5k9m75h
3+l+LJK+NWQwGZk5BhnuLivNLhv8cCiHAyj3vY5VGekBuMLEIpqMEH2VLCHI
vsqrpYumJ7SVg/Wj3L/A3952q9romjSMUDtvqHtxCNAKxpirz74mKFMH0V1P
6IoJzEAmYF6dTkLbBinJaaUNnPLcbnDJThasUX6A+QB9kK2qRvwF+p8F9Q==
"],
Association["Book" -> 1, "Theorem" -> 26] -> CompressedData["
1:eJydUNsNwyAMPJuXSYUyQ1fqCFmgs3ajcJAqSEn56EkYPw6f8XN7vzYB8KH5
iTWHEDWXkpRAAWQEOSnmDJgL3nsHdCJW86YGOxrVjNBWAsRNFHVADUT6zdPL
s3H/wfT/gx4noT0fNr9tQVhleGnWk42Ic2V38nSWRRGb5IPSdYMJWgslhO88
N+Nf2+6XQgQ8
"],
Association["Book" -> 1, "Theorem" -> 27] -> CompressedData["
1:eJydUVEOwyAIfaC0xCzZfnaAXqlH6AV21t1oPuxil3V+7EURAXmAy/ZYNwHw
pPiNq9mkF3dTAg7IEQyZkxngyXLOqfkVuJdctKDseapFuGoAJA0I9YB6qbni
5G7uYbl/YNx/52MllP1h6DEFoVfkJFkzRiD6yM7oqbgrLChvpM6uM1Q43PfI
vtqX/Uc+jC9qmgQa
"],
Association["Book" -> 1, "Theorem" -> 28] -> CompressedData["
1:eJydUcERwzAIkwBfcsldM0NX6ghZoLN2oyKc9vypH9XDxkggbN/P5+MkgJeW
CVozP/ZtCcE2wki7wKpdoN3RogoySydvgfBg5Ik9K4Ku2Cd+chFkB+tmuWe3
aj+t/Qs2Zy9ac4QB5ECxiEwRdb2RHeoNJSxpVwwyG4N1DTRXdEDP5xnLZW/t
17TJ8vMTX7wBXgIEJA==
"],
Association["Book" -> 1, "Theorem" -> 29] -> CompressedData["
1:eJyVUEESwkAIS4BevfgCv+QT+oG+1R+VgDqd1daanYElwEL2Ni/3mQAeMke4
kuHuVnCCGyhAyOQtojhVyjn7NJJy2Ump4P7Q7H55Q8/IiIYn/2vdv3HuwdIw
Up9FX/rGCQPzjkqmdJboScGl5RP5/3vbWu9G2Ca9ArkiA3o=
"],
Association["Book" -> 1, "Theorem" -> 30] -> CompressedData["
1:eJy1UNsJgEAMS9rerzu4kiPcAs7qRvaBoIjn16VwzYWUlqx93zoBHPEMQZqK
MKHpfo6Y6+kq4t4wq7IqRUjMUticqw12lj373UVc+t+58zB/tSeETBotPkuw
KM/06wZ5EccJSdkDHQ==
"],
Association["Book" -> 1, "Theorem" -> 31] -> CompressedData["
1:eJyVUdtxAzAIA0s8TH/y0wG6UkfIAp01GwWc3PUr6VU2nM/CCPDX9ef7qiJy
G/cen2stflQvW2Z7527LHAsPYwEiQV17h2tf8FLl3AwQaUDvBTDTKFCl8LVo
1S4Pr4FVtUSFRBV6Ax7xZ7n/RL5lj960F5kVZt69PJHTGqzRDZoNeViSQx+H
vdtgnCH4AwFEx5+xDIk4sVNH55I+tihcyjTcBT3QHntnZXRmQkn9xVLN6K84
D0F1V8gdy+EINQ==
"],
Association["Book" -> 1, "Theorem" -> 32] -> CompressedData["
1:eJyVkLtxAzEMRPFbLInjXKDMoVtyCWrAtaojgedx4MDW+PEDAliCHLzfPz/u
KiKPvb0gwrGOqpWBPJhrTo4mswMIbI2LGuAhYWZvt5sp9JSSNckdIm0to5iq
CX9/tGrOZM5qoopkUVjlPd3B8/V3/wf/zu60bztGEUj4N+Q+o/Ee6ORXNrpd
21yiMXo52oHnBbKvtn5HtsA9L+2Q3WhIO4QYpFL9NHF2wW50g64crhH6A/Lo
v8j1ngbU5QmkvQgQ
"],
Association["Book" -> 1, "Theorem" -> 33] -> CompressedData["
1:eJyVUcERwjAMkxwTcr22O7ASI3QBZmUjLAe43HEUqkcSW1LsOJftdt0I4K7l
F9apuWALYaRbB9N7hvaCk6c2shLMDhlSqmw3WNG57NSUSVA5qIT8EQaRt/sf
7R6C7bNPWn24AeRAMYlIUbz2j4fJb0hhSrtikNl4aK2g5lyXmIR5iZKK1lq/
dRtX8fUTbzwATsQEIg==
"],
Association["Book" -> 1, "Theorem" -> 34] -> CompressedData["
1:eJyVUVsOwjAMS+xMG/3iD/HJlTjCLsBZuRF2i8bEBw9PnRLHkt30st6ua0bE
3b+vOLbJ4AlJYOYAkMKMqgjGVF0qFgUcGCzCHcRioOiaHzztYtgubaE61KZa
gfVL3H/Az1OP0/mVgZnjyh0KlyZE6fNN99NNpJNdmGMF2euXYCtk1BpjtiSa
NqFtFcLdeVmeefAe0Nn6S+zJB+pEBOc=
"],
Association["Book" -> 1, "Theorem" -> 35] -> CompressedData["
1:eJydUMENAjEMix0Tjr5gBFZihFuAWdmIJNyjAnFIpFLT1HZt9brebyvM7FHb
7xqhXDzDAvAIkiJae6Rk5nZQM70hntzcHTUxb7mV19l3jCQ1MbtSBZQ+R1M/
v6v9q7iPbnDlEKtPEBrIKxRe/eMzK7WsiU19MSaa5hxjuEVbjkQoT8tyuSzL
t7SJgvFm/ARWigQ1
"],
Association["Book" -> 1, "Theorem" -> 36] -> CompressedData["
1:eJyNUdsNAjEMs/No+YDPG4CVGOEWYFY2Is6dkPgA1ZWSNk6bOL3vz8dOAC+Z
BcSlVl4NbubuEWFBEsSsCGDIqDQyih3uWZRXghVOVxetQ47fRedMF2aBocfC
4ZHI1PPua+2uI/6yXY/y1ZJLBxu6GCUbkgWjtMkqu1keEisI8W3tHEbtj9H1
tj2pQpkTPiR0AmOEDVKDvG3bp1t+z65O9R8q03XZo30DroYEyA==
"],
Association["Book" -> 1, "Theorem" -> 37] -> CompressedData["
1:eJyNkM1tRCEMhP03NhghlHfey7aUEraB1JqOYoiinBK9DzECj6UxPF8f7y8m
os8td7geb4/Rsl8j11qZubL38OYm24awmLGziUi6CwdP6tQcQJVKWxMnYQbh
79A5R/fwPgsboyJGUIypc6oqYt4c9zb5rxtRokStZc4AHPpD5j7Xu6C1UOa3
a2bbPqJr1VbUBeoHhGqr/l3ZDapxevccVn8pyhlkoMlsLsTp6DiE7SiG8S/K
3NvVO+iEMpyVvgAy2Ain
"],
Association["Book" -> 1, "Theorem" -> 38] -> CompressedData["
1:eJyNkFtOBSEMhnsvBU5HdJ5N3JJLOBtwre7IcozxxZj5gKYtPxT6dv94vyMA
fG5ziafX9dxy5uw558js6R7SXGjvKiGJoJMQUWiFjgMcTJiNmZjVjAyYSOH7
yJ+cZ84WMc/C1jqOvgL6WrIOZvYYV597lf8vjCijAHNmnt0snH8YY/tecA0P
d/OdEakvs8pD1Hst9gqc2wOLnTHbbdHtcrCoalYhqcYQYzMQhRdErmZiVw+z
UqiJstYU/IURbyNvN4US7OoNGb4Av5UJbQ==
"],
Association["Book" -> 1, "Theorem" -> 39] -> CompressedData["
1:eJyNkMltQzEMRLkvWmxAp1zTkktwA641HYVSEOQU4z9BA4lDYCh9Pl+PJwLA
15ZrrI8eLe+9jbXGGGtkuoUJbVMJSQQNhYiaGaHjgIAwVa1SaQQJEKKC/B96
mz3NLWchfUd0B++T52Rm9XF53Iu0t657CVdXcXNVU/5ljH2udynX0jJ/XBHZ
9hFeqzZrXZTtoM4c1b8ru4HZT++eQ+ovidEbiMFEFCPACE09uOwoVME/GDHj
nqlwQlENGb4B98UIkA==
"],
Association["Book" -> 1, "Theorem" -> 40] -> CompressedData["
1:eJyNkFtSBCEMRRNuHqQ7Q4szNf9uySXMBlyrOzL4KH8sqw+QIg8I3JfH2+uD
ieh9mZM8PfeRmVuOkXPmdA/pLm3ltHETYW/SWgst13knJxPAgAaoWVNCK/N1
5E/ut5E9Im+FzetxbDNomxPzAOCxn3/uOf6/MKKMEh3HGPfNLBw/ZK69F6jh
4W6+IiL1Zah8F9WCl+Pon1gAG8yWLLqSCIiqjmokJUwDWycxujKjxORuHmZV
oSYKrSn8C5gve14uSlWwuncGfQCQ2glc
"],
Association["Book" -> 1, "Theorem" -> 41] -> CompressedData["
1:eJyVUNttBDEIBIaHDetd6TpISynhGkit6Sh4pShfiS5jgTAzYPDb8+P9yUT0
ud2rOEbl46jruirzzMwRM1Q2ZcKiyiEqIukuHLxo0nAzB8TMxhAniFiLf33i
XDU9fK6GHkdmVFDUwloALNY/xn0J9Scb0Q5EY1Sd0asYvlG1497L0MeabOuM
qm76djjPNlhfDH7DAhit35ktAOLW7jm0/1LAGaRGi1ldiNNtdu8uHepdxKb8
AzDnfGQa7W7G7gz6AsRHCHQ=
"],
Association["Book" -> 1, "Theorem" -> 42] -> CompressedData["
1:eJyVUUtOxTAMdPwZf1qVlsJjzZU4wrsAZ+VGON2wAj0mkjXyWDOJ837//LgP
Ivqa5WHg7TXTMzOqfFFdNJJltIepiBlDwMxmRgOjKAmi6qqsagZW0iY9/GvC
7aWiA+LczxPPx3HUllTbk2wlIpH1n+s+gvhTzeziRMuy77eKSJ/PlImI5uIN
6ePpjqsDYPZxDbU4VcwaF5Ai1bwN5BIlBW2ydxDzoMEEEBudNKR3SdbWqhG9
PxgHxHX8oJe/Vq4raOb2J8QQ+gYKUwj+
"],
Association["Book" -> 1, "Theorem" -> 43] -> CompressedData["
1:eJyVUMkRwkAMk2UxO2wHPGmJEtIAtdJRLIdHGIZM0GN9SD7W9+X5WALAy895
BDJiZNKIrh2UgMRFrTAl8ppIJVtYWW5Q2s+DmZI2ZQEe4foKoW5P/bXuCfCY
fdPeQ7TdUdFEpcK87dfHXE+0sKWbYifj3pkz65zuNOsSda0a6eg2xq9tq1XU
QT8Hr/f/A/0=
"],
Association["Book" -> 1, "Theorem" -> 44] -> CompressedData["
1:eJyVUMltBDEMk3VbtmceqSAtpYRtILWmo1D7yWsRLA0I1GHq+Hx8fz0GEf20
eQMfERYRWuWlepkny4CGqYgZ63BmVlUaPiYlGYtMd1hTcELKyPWl/lk1s2ru
s3fsfc5aRau2niNQqvneuP/j9SiNKpggWuu+z8qc0WtKQxVccIsQvKgIj464
e8f9WdTcn05IPuETa4CLJGJIwsPHuNFo4JLClElstGjIYCab27qPNxhSYfwH
Yb4qrsup+6Iwh9AvVKcIfg==
"],
Association["Book" -> 1, "Theorem" -> 45] -> CompressedData["
1:eJyVUclRBDAM8yHLTgaKoCVK2AaolY5QwoMXMKuZXPKtvD0+3h9uZp9newYc
FgkKwAJfAhFmQGZVwivcu8qjo53Ow0fEsTJgupZl/Jq+W24JtoC918Jqm9Ui
qg79ZLv/An9ab706J9kz03XHTBzUWQJKnNpjHeYKg+J1ITWLHilnXvRKNGYS
ozh8i6gkVCE/n5FWZQ5r98irLKQeXvcmdwCOqR+osuLXokE2eEpk/wJVLAeC
"],
Association["Book" -> 1, "Theorem" -> 46] -> CompressedData["
1:eJyVjzFyAzEIRUEfEMLs2I3XjRtfKUfwBXLW3CiwkxlXScavQIgPQv/x/Px4
MhF9dXiL87rd73m57Ju76zKMroJ4iLARxhhuxqwcNMlN1YChKu7DaJRA8vvS
TF/T54qMsFPhy8hWaqYq1OPd7/5H/qmaUXujiG3LtlJefsjs3ArYcZh6V0Sk
5SPgugM7rC6GeaATCJQXaDeUPo/erRbVJIERk4ZSMosJIaxHtDBRVrAKvwDz
Oj3WUupXpEYY9A2bpQiD
"],
Association["Book" -> 1, "Theorem" -> 47] -> CompressedData["
1:eJydUEFOBDEMS+PESaphpFmJEye+xBP2A7yVH5EWceCwSGC1bqs4VuPX+/vb
fYjIx6K/4WVW5ZyV59MxL4KjPaBDzez5dANmhKqrDwz61xMAaRC6Q+APzau8
nJFM0m/XdcVJibM8szs9H3f+E/PXKtlk6+yBgwziG5ncQ7ET2Me+Ap3CKm9C
VW/04K2JDRa2fvESrLW06x+qJmqdmCikbHiYuqm2p3ZwB30oOufxA0fWcbgs
tzkyBuQTW+EIDw==
"],
Association["Book" -> 1, "Theorem" -> 48] -> CompressedData["
1:eJytUFFKBUEMa9OknXXfzkPwAl7JI7wLeFZvZGcFeQoKgvmYmZBpGvJ8e325
uZm9reOPEFkkcx6Xy2NBgBkCHhFPk61uY8DlBFGK2DIRgSrRAv2b+NlbKUYw
mal5XI+YZZpqV6lGO/wztl/VqpVpxRpjZUh+oor3aKbz0S2c1714En2gvmk9
ufjoRe40LNZ1mtK7PwSjywuktFGOBOhfsIv7TluLH3yUh70DiBMHQA==
"],
Association["Book" -> 2, "Theorem" -> 1] -> CompressedData["
1:eJydkFFuhCEIhMGBEZRs/mQf+twr9Qh7gZ61N6qaJn3qJt0vEZUBdXx/fH48
VES+dvgv9/u83a6KCA+i7RREm5lS0FobEaquJSkjSAKNtDFaSFuC+N+XVkX2
6DlqDM5FJIVZXuUOj3rhuU+ZT1VStjfJrCq6by8/zLnX3PZ4JnrfGTPb8gm4
rjXAtSH6wTuQWF7gpwDop3YbW50CxVzf5FKq1k0wTosvaK4OddNfoJrjLdNl
n2JqVMg3M/MIKA==
"],
Association["Book" -> 2, "Theorem" -> 2] -> CompressedData["
1:eJydUEFOBDEMS+rETTqdQdobIw7wJZ6wH+Ct/Ih0hMSJlcCHtI1jpfbb/eP9
riLyucqf8XrcbudTRHgQbXUg2syUgtZakKquKZSgO4HmbhHNpBUh+H3pPiN7
9BxzDG5z2yIpzOlzusMj//PdR9gesqQsbzLnvu/LSnn5xnGsOwvgddD76pjZ
oq+C5xM4wXoQ/YJ3IFFe4Gug+H7N7rWolJUN+pBGmapGE1TIJfECzdWhbvoD
qOZ4yaxQS20lUcgXPpMIVQ==
"],
Association["Book" -> 2, "Theorem" -> 3] -> CompressedData["
1:eJydkEtOBDEMRO2UXbG7kx5pdrTYcCWOMBfgrNwIp4XEipHgLZxP2XHKb4+P
94eKyOcKf+e4389bRHgQbV1AtJkpBa21IFVdUyhBdwLN3SKaSStB8HvTOSJ7
9NzGtnEf+x5JYQ4fwx0e+a/vPmF/qpKyvMkYc85lpbx8cxxrzwK8FnpfN2a2
5Cvg5QROsA5Ev/AOJMoLfCWU3q/cWY2qsmaDvkmjDFWjCWrIVeIFzdWhbvoD
VHN7zayh1itWJQr5AgqqCDQ=
"],
Association["Book" -> 2, "Theorem" -> 4] -> CompressedData["
1:eJydUEGOAjEMSxynmc4gjtznSzyBD/DW/dE6u4DEAQ7jVlGVOE7q/Xa/3tzM
fjocAJljzlyD/lBwAekB4LRtYljq1CA7xUSVyhDJ4/PQHBtFj8qqYGQgaciB
TIkQeWzdz7h8rZIKMBujSgsAE0/su96cAifXVXdZO8OhL8udfkZvnViUWfjf
tsgNvkRUlD3is6wtDHPl0hAmARsaHoTam9s+/vX6G+LMCDib4BHS+AWRrQZv
"], Association["Book" -> 2, "Theorem" -> 5] -> CompressedData["
1:eJydkEtuwzAMREkOf4plu45WBbJpj9Qj5AI9a29Uyll0lS7yAI0wGlEffty/
v+5MRD9TXuFzvEd0j4BMK8Siyk4QkTBjNk4ycgUWMwHUXXTGU54ee+zrkq0t
676usb1t26UHZb/a9TCDt3zxuU+5/JtGlCjR7TbGkUV9DQ96j9IoEOcUnnNF
VU89N41RA1EmkCfeqiFwBxw6Q7RZoqMuqgICw5PEaWdWK5fuoWqFq7GpmPIf
YN56tclITWGiwaBfdowIww==
"],
Association["Book" -> 2, "Theorem" -> 6] -> CompressedData["
1:eJydkEtyAzEIRIFuQPL8MtbGXvpKOYIvkLPmRmFmkaychV+VkLpaCNDj+fX5
VBH5PsJbjHvmGpmwQ5mokRoCM0t3VdcmLkGgZxrACKM4SQFfvrpvy9R6n5Zt
WXL9WNfLnNLmq193d0Rv77b7isu/bmaF6vZ2G2NvES1rkBqpmOc6IwvkueXp
lk38XhqjFrJEop1EByZEAAEeJvqRwlGFKkGgiCYWsqnSS1XVJL0IujrNqX9A
dZ3rm1zohBtTIT9Hnwif
"],
Association["Book" -> 2, "Theorem" -> 7] -> CompressedData["
1:eJydUEFyAzEIAwtk8NrJsdcmT8oT8oG+tT8q3ulMT+khOmBjIbC4Pb8eTxWR
7x3ewzUiPIm2E4g2M6WgtRakqmsKJehOoLlbRIO0IgSvh64Z2aPnmGPwmMcR
SWFOn9MdHvn2d1/g+JclZXuTOdda20p5+cXlsu8sgOdB7/vFzDZ9BnzegTtY
CZEnvAOJ8gLfNcX3s3bVoFLWbtCHNMpUNZqgllwSL9BcHeqmf4Bqjo9qK7uL
lUQhP6JhCA8=
"],
Association["Book" -> 2, "Theorem" -> 8] -> CompressedData["
1:eJydkEFuAzEIRYEPfFtNPJ7FKOteKUfIBXLW3qh4qqqbtos8y19YHwzi/fG8
P1REPpa8CDmYHbZiEzV3DYGZMUI1tElIOtDcDfBM82Uv+fPPOWZPss/rnHHd
9q1tXdq2Y9+AINvr4/7O5V+39xIXud2OY7bMRnwzxopZoA47+eW6+6ln0px1
wXoQ7aQWhjdkAglfJvoq8aMaVYFAlV0sZagaTLUx6R5FemgkwvWHSh+XMUZI
VEs3p0I+AekaCFo=
"],
Association["Book" -> 2, "Theorem" -> 9] -> CompressedData["
1:eJylUMkRwkAMsyXLJNABP1qihDRArXSEzDAMD+ABStZeK/Gl03Y5bxkR1zG/
4lh7ISNdY6y9OPy6mC4/TIksElRI0ekwkvxYktzBheAMQipnIKodwijUH+O+
hb5+BWam8QDLpj3EeHg439kGm5LjQw+jWZmUr7wP7SQzzbpj5azxgtlz/nx0
s56FAIOJbEe0GtZ3OvqYnPcJy16Ly8Jau7f1TcYNy9kFaA==
"],
Association["Book" -> 2, "Theorem" -> 10] -> CompressedData["
1:eJylUNERQjEIgwRo6xau5AhvAWd1I0PP8/xQPzTtQZsCDZyP6+VwM7u1+Rm5
im6uGm3li02vmfDQomeS2mBappXrbE5+rEguqBCUQYxR0wcspq4QAvGP3Heo
r69Aa2oPMGRKItqjxYkrgcVMZK7NRLespnXkFq0kMcXYmNFtvEBloyMfv8Et
YKDR4aUbNQ3rmbHEiuz9hMZepygFKp7pqaHbHbzDBW8=
"],
Association["Book" -> 2, "Theorem" -> 11] -> CompressedData["
1:eJylUUtORDEMS+I4aSseaPROwJXmCHOBOSs3wn07JGABXliqm4/rvj+e94eb
2cemv+P1ZcUAzCIjq2pmJVDdHgx4eiHidhwRgWSGFQkL/jiQOTQJbHbzOM4b
3pb1IYUA58C/7H6D/vV2re3JbM4x5KircDkRdBDrzYWStsg5t6Kyi6+iXa/7
3twX5lLrpTe4ZSx1k0OL3PUb4aR5WoYrNXckYu+gMqFBaad/wTnqPNuo2Dpq
qPUTT5gHcw==
"],
Association["Book" -> 2, "Theorem" -> 12] -> CompressedData["
1:eJylUdsNAjEMS2yne7ASI9wCzMpG2D0kkBD84L7TxE3cy3G7Hl1V90x/YLGN
Ku6VizFK6pYbW0OOBNLWmiZQ7fENgJJRC+bwASXm5L3pzflfup+Yn7dMPcg6
g1S4p41JkRSSpKtyPy32lLj2lpGFDdlPz7AXw1bMirRD5sxj/8aSZfCrSLif
tmId4RTt7P7O4CtobXEcND0mrAcqpwSq
"],
Association["Book" -> 2, "Theorem" -> 13] -> CompressedData["
1:eJylUcENAzEIAxtIKt0SXakj3AKd9TaqyfVTVe3nrASsQIgh9/352N3MjjZX
AGemmQfluWVlRM4JBMjiTHK7TXHUyDACsMTPchEIlZIFxqjmMDDEqmIGL8r9
wv+CaKW5ZKGVQY20pgX0FkTadbiPV/ydtHohuosz5+zujDEX7aWr6zWXHqVo
nBbuClmX1B+xMreRGrZO/QOBHlMnYnhNp70AIrAFww==
"],
Association["Book" -> 2, "Theorem" -> 14] -> CompressedData["
1:eJylUMsNQjEMy99Nt2AlRmABZmUjnAcICQkuWGqSNq5j5XS5ni8qIrcJf8EO
BRU1M01TNa1MMbfUECAr2SnYAu/kmLh9VQNWWHg0uh1oeLdUoyiElch/7X5i
/exyuEhM3ns8FOKFtaYGEYiqrmKfL3nEeBC7eWJewA+DUVjkPxk9OVlsDrLZ
iwq3Jy5QVeduI9wzfe+ducXTfcUbNhY2jUk6Z2ukhd4BqdwHNw==
"],
Association["Book" -> 3, "Theorem" -> 1] -> CompressedData["
1:eJylUNsRgCAMa9J+eG7hSo7AAs7qRvYB6nmePwYoj5YQsrRtbRCRPcI/JIPK
PAGonXqnUCGDnWeZL+yDTB3Ugm/ImmNU+rfcB/iZHe8BoSTidTHXjMkbXaqn
szR/il4ULxAZE+XRcKqMQddhxk6bDppq3VUblr2pLdr7yQF9XQOY
"],
Association["Book" -> 3, "Theorem" -> 2] -> CompressedData["
1:eJylUNERglAMa9o8BJnClRyBBZzVjUxbuFM/+CEfvaMJL2ke2+u5wczeOS5i
vplx9rGuC+w+jRFkcNBDEC8LlwI+lZx24ukC/BfWOyCJ63H/DM9ZbwmZQXKi
k1SWnsrWiYO50fG55y5CssShUScA0bNIBML7MKnVloQGHZ0K1mcaH4+F+Xd9
3pVpXX75I+wDM5MEaQ==
"],
Association["Book" -> 3, "Theorem" -> 3] -> CompressedData["
1:eJy1UMENAjEMs+P0uAFYgJUY4RZgVjYicY+TTkLigYjaqErs2M1te9w3Anh2
+jWuQF6kdR2AUoI0Rg4sWjQRATAkixFfNN/tONdIxif436NUw8qdy0SwA3Y0
vU3HZa8b7h8gdjd4fNoIzuzypHh+L0imyMxEmpE1zY+6Om9v36+1sR+8AJNx
A44=
"],
Association["Book" -> 3, "Theorem" -> 4] -> CompressedData["
1:eJy1UMENwkAMs+Nc2zVYiRG6ALOyEYmPVqqExAeiu+gUx7Evt/1x3wng2ekH
kau0bQNQSpDGyIFFiyYcAEOyGPFF84DjWiMZn9r/HqUaVu5cJoIdsKPpbTou
ew0YP5vYaPD8tDs4s8uT4vm9IJkiMxNpRtY0P+rqur1jI62N98ELdBwDeQ==
"], Association["Book" -> 3, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 3, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 3, "Theorem" -> 7] -> CompressedData["
1:eJytUMkNwzAMo6RKcR55dYKu1BGyQGbtRiXloEAf7SsEJOuyTPOxH8/dALzk
rsBqXlUIN7NgWqOWjARTGFh1QAYE/PeaEDL7YOKuHdmx2rlcRPeDP1z0XtJR
ItL3SFoonhc9Tr4QO3Lsj7OulfOrzZpdb9/QberhetlUnur0/BjGKa0vdszu
tZlwm0VO8pSeXyARdzuFbrwBClUEVA==
"],
Association["Book" -> 3, "Theorem" -> 8] -> CompressedData["
1:eJytUNsNwkAMs53rlTVYiRG6ALOyEXHuWvUDEEL4pCS6OA/nut1vGwE8bP6C
iN4vZEukiVhDrbcmgGLZaAtyHKH3XWhMFxVz//XPp9Lf8IV+WZxXkWVQmtug
VnWL0URRi1b+IBVR3DlwooT5KtMnW0OmkMkc40Bc8p0GJSdcC74Axml9aTwB
pdQDwg==
"],
Association["Book" -> 3, "Theorem" -> 9] -> CompressedData["
1:eJy9UNsNgDAI5E4/XMOVHKELOKsbyQGNNTHxx0gaKMf71rZvDWZ2SH0jC+DN
KE1pGTJjMnBwkjO/zOxh3jFU+e9CzY4lYos8DuEnXBu7hy6ZgwQjsa7CIOwV
xZN/LJkLJudqfo2LjEf2MDw7ARBVAyI=
"],
Association["Book" -> 3, "Theorem" -> 10] -> CompressedData["
1:eJytUMERwzAIkwSLZKWMkAU6azcKWHbau17zin0GWzIg2I7XfhDAu81DKzMA
1YUSE1lOMlWOtREgmfxftGgO87XgY/Y5ubPgPUt/iWghbSe2tFifFSsaUUTj
ccVzPFZXPZGA7SBrNqKT1diwOsaY08zdBAzqR7HTgp/IEzliA1s=
"],
Association["Book" -> 3, "Theorem" -> 11] -> CompressedData["
1:eJytUEESwkAIg5Cs4/gBr37JJ/QDvrU/MlAPXvTUbJsuDIWQx/Z6bhkRe9NZ
uN8QqwCSWtdVoug05hGqpkod/QJZcxoHk07SPdGN60S5g/8NyaNkrRZi9nbl
F/2pgws+1lxUZyh1XlPUqjlB4bON7wsabqsAwf9WD5IicoY6ZOTKi6eTmTkl
3r7d+Jbs+/hkUxsB2t03n0AFSQ==
"],
Association["Book" -> 3, "Theorem" -> 12] -> CompressedData["
1:eJytUNEVwkAIgxDOp1u4kiN0AWd1IxPOD3/0q7k2PXgUQu7H83FkRLxMp+GG
WAWQ7HVd1Wwqi3kaVVPUjn6BrDnGZlJJqifcuM6Ua/xvSO6StSxErO1KL/yp
zQUdaS62M+x2vqfIqjlB4bON7gs9bKuAhv4tD+qOyBmqkJErL5pOZuaUaHu7
8S1Z9/FJphoByt03ePkFMA==
"],
Association["Book" -> 3, "Theorem" -> 13] -> CompressedData["
1:eJytUMERgCAMaxKOPVzJEVzAWd1I2oinH1+WIy2UljTLtq8bIuJI+NHQNaw1
jQVRzP4IRiig+kyf9cMKHhbezv5LN7l90/ETKYkkXneTi/mZMWs+KgeE7nrU
YU7FksJYyaEN4Wat4VYgfWd3TMuYMd/6cPrnPCdT2wN9
"],
Association["Book" -> 3, "Theorem" -> 14] -> CompressedData["
1:eJytUMERwjAMsyXbKceLBwOwEiN0AWZlI5QQjvYBr+qhc07SxdZtfdxXN7Nn
pwNxZWWRRDAQABO8nBeQnqwwAm6Jn/lQSvGRjVahBwwMTVGUeuy6ZvyrAm8L
hOikQzTFHD7ghnfIJHInkRvzEKc2f4PpSnNaJ3k5GjNU5sL0sYh/ke6B1ntR
b2h+aoq+AJ39BTE=
"],
Association["Book" -> 3, "Theorem" -> 15] -> CompressedData["
1:eJytUNsRgDAIS4BT13AlR+gCzupGQqmeH/auH80Hj5LQHHs5j0IAV4SZUDOj
QyAUz0pZt0U0OlPECDb+KVuI7Dsx2+6wh9dLRYfRFfOjZHY/uhj73dRjUhh1
0uSRa1uU8Gc0O3FYmN8INyjsAyk=
"],
Association["Book" -> 3, "Theorem" -> 16] -> CompressedData["
1:eJytkLERhTAMQ2UrR5GKFViJEViAWf9GX7JTUFHhS8zFxNZTjus+rwDwc/o0
9jmZSYayvqpIIoGZ3NMX5lu3eyJXhEInpLNPGvk17vvA0tNmm6Epmiuar3kX
MYtR1lXnulQOGPF0pbehc/3UquES2rZ+rIRNQ3UWwxijtQKl9gB0h8cTpefG
wB/gTQQu
"],
Association["Book" -> 3, "Theorem" -> 17] -> CompressedData["
1:eJytUEESAjEIIwGdXhyPnv2ST9gP+FZ/ZCDreNLT0k7aAg2B+/Z8bIiIV8Ox
drmCZKFwYiaCSRBY57pVx1fk78+QETaOw6v0LBEdLvc/4dSjZdky1VupwRY4
KL05ofh42AcH4eaNkxRfz0yGMbldqAou5u10XUpjHDIGmDuTBa5OYOwjSnHp
+gbVdAQS
"],
Association["Book" -> 3, "Theorem" -> 18] -> CompressedData["
1:eJytUMERwzAIQxL99pl/V8oIWaCzdqMKcNNX+4rskzHGQsfjeO4HIuJVdDE2
SBSEpJIBxwQzdWc9Z/D3XxjEoMswS75aFZfb/S/Y/Ti2BjZRRlgmh+1X/RSf
DOtgM+z55C6Kb4ZN0bXVKBPTbPaUO0hplGuYay4Lt2VyRiRrOXwDqMED5g==
"],
Association["Book" -> 3, "Theorem" -> 19] -> CompressedData["
1:eJytUMsVwzAMEoj03BW6UkfIAp21G1USTnrLKdgPf8A21mv/vHdExLfpbiCT
grAxlSgCCW35ZKuKvDhaIIxxw021VJZye9ZrtWU6llFfo0R2SHPlzZHi2GEP
HEZlPnlM8d/hUIy3H5Lgx9xtr4kyfTMDXHVZeKyQLlHZulo/nKgD4w==
"],
Association["Book" -> 3, "Theorem" -> 20] -> CompressedData["
1:eJytT8kNAjEM9DmOIyHYD39aooRtgFrpCHsBIR7wWsenZuJMLuvtujIR3Tvt
bueTsPFCB5rhbiLiQ+aUQcIs5L8fzczhwKialgkgQcjUclXDsrfU+IsClbRr
RMLMXd8W0b2XaR2Hd7RGs4btRapQr8E36kZXaHM2RjTSXeuo/VQDjMQowXoU
KnJ9G5+VXP5lKGV15QmasdIDpmQGpA==
"],
Association["Book" -> 3, "Theorem" -> 21] -> CompressedData["
1:eJytUDESwzAIA0uAr70M2bv0S3lCPtC39kcVuQxd2ik6DLaMjU7P/bXtbmbv
TtfjYUZbfPV1ZnKMkdOXhdPg7pa/h0YECVA1JgUQpmNGpID71Urj7y2gVIqS
HiiQWdVKJAgtSEgcBVHN8FBacTZpJZTPHjRTSTZfnRQs/a9B7jQM733ICbeb
KPkh/9hPCWc528MvMEo+ySTZ5hke9gFq8AaS
"],
Association["Book" -> 3, "Theorem" -> 22] -> CompressedData["
1:eJy1UNsNAkEI5DHccIm5DzuwJUu4BqzVjhwuGr/0SyfswDKwS7jst+vuZnYf
+gtg7Sc/ryQigotvG9oUu3V87KoqIBPytUJIpOnKKpJL8tdj1lc1U9Rm1P+V
siS7OdBFnALzcFmcDI5Ju55FOpTyqslDJTD5HpKhu2cOd1iGs2asKrfFwrUP
7Q/TinS0wnjDJekBqFGrqmDF4g9bKQa7
"],
Association["Book" -> 3, "Theorem" -> 23] -> CompressedData["
1:eJy1UNsNgDAI5GiNJPy4gis5QhdwVjeyUE3rI/1S0vIoBwed07okENFm6g/R
qKykR8REsBOyj9Ap40ZyABRrt6S/nrO/f+WzSUzXQvdhBpYFXpqVRwc6FHcE
WkeEaXDKyaij8EicExLOL3usjzLCte0OVh0Dbw==
"],
Association["Book" -> 3, "Theorem" -> 24] -> CompressedData["
1:eJy1ULENwzAMI0ULGTt06dqXckIeyK35KLJQ24WBdGoImBJoi5L83vZ1I4Cj
0i0oLz7xAEEzGoMhCpLJdVnFQNIUwwBWs3+P+duw9eMXgFglpWnergzfvB3c
9vkoGJTHnfFHNVtqaXF66oqGacv+vEFtNsSvqigidAJ/wQOf
"],
Association["Book" -> 3, "Theorem" -> 25] -> CompressedData["
1:eJy1UNsNwkAMy8MehJUYoQswazfCDqJUquhX69NZed3FyWN5PZeMiNV0D5o6
qExUiRvoThuJ/01JUIU08CGEDEW6W97VKnGedboty1LgEb7Y23YPEcOquT0Y
TMSlU73lPVjVXFITB6MgCrUtC4EXU9D2kD9on7Mn5PyYYHa8AW+eBWc=
"],
Association["Book" -> 3, "Theorem" -> 26] -> CompressedData["
1:eJy1UEEOgzAMsxMHrrvwgH1pT+ADe+t+RJpRKiFtJ7BUp3Ib1+lzfb9WAvg0
ugm24AGCZjTSDU6HZD7pZw8TRaeaBrDmdXXI//OTI1ZHDmZf6ZT3UIZvnQ7u
8+wKBtWKYP5R282tVcEo3fPBsuVxvcN7NmiSQlmhDWSRA5U=
"],
Association["Book" -> 3, "Theorem" -> 27] -> CompressedData["
1:eJy1UMsNQjEMs5v/EwNwQmIlRmABZmUjkl44wQncNHVrS7F6vT9udwJ4Tvsb
zkiPUHLFoZlMkBQcn4dWpXumV0OqIrISubk08vLriPldHVmByVRp5i6iKjtK
NhdvSC/v2GrzYmbd1bZpUpd4X3xbxzR8PCY6Yp+mqnuQElS6YQlq0U4Cuo88
u9Fmdr2xyIij/xijKqfwApWFBss=
"],
Association["Book" -> 3, "Theorem" -> 28] -> CompressedData["
1:eJy1kNERwzAIQ3mgxgNkgqzUEbJAZ+1GxZzjXHrX/kUfMgYJg7f99dwxs3en
28AKhjsOyOVhEtHiv+vr7EgH4bcO+xOXV3MZInKdXijOuk/pkacoLznz5NFh
ZigyjkaSmypsXSeZyhYMCUN/4vzJpcVjEZmJDzBcA2Q=
"],
Association["Book" -> 3, "Theorem" -> 29] -> CompressedData["
1:eJy1UMENAjEMc9rEORBPFmAlRrgFmJWNiNuKe8ELrDRN5aS2ctsf990APJX+
B7sw081antupAlY1ts+iEd7D6wg+Affw8Qq//tphfGVLHCCQKTuk7Mzsb3sH
BhGDX026uIiFGssxzMWERigftRxYR5agI5rZJgvJqjgVG2nsdqAo/aclaXOm
wAvohAYY
"],
Association["Book" -> 3, "Theorem" -> 30] -> CompressedData["
1:eJy1UNsRgCAMS0qqc7iSI7CAs7qRyEPhw/OL3LUNNH1ct3jskQDO200EkQdY
YqRZgMTg+qkZY+WpweRlPzBMZUPhJc8uWzWoIhKPb5r2U2RgayQZlOmazKT6
CnxPwn4HdjdZXO6exAgX8f4DNA==
"],
Association["Book" -> 3, "Theorem" -> 31] -> CompressedData["
1:eJy1ULsVAjEMsyPLse9WuIaVGOEWYFY2QuFR0EAFKpzETvTJ5bxdTzez+yr/
xF7FMUbNcRyYBvdh+Vk0kxFApLBTAGFgdmZ3J7Zf++PXKaAizSr5gdyge9t6
QYfuglB4LuBcnSCrqqnteiXTDXVed1aUro4QQW9rWNmxoknIXVkllstWwlVh
SQ53/UpkhFFkeMMQI4sMQ8iA7+nTHpPZB0E=
"],
Association["Book" -> 3, "Theorem" -> 32] -> CompressedData["
1:eJy1UEEOwjAMi+0wbeKE4AN8iSfsA7yVH81Zq2oc4LZItRI3cd081/drRUR8
Ck6N24OZvF+xzJjjIiGkfwPoJ45dzqlk5JlWfwSPhUSQwO5yR5sdTgfPgir8
3YFdYTAsqIpkm5ZTmK03BaQ7mmCTsywnL+IrukFfetETvKUNkrQD1A==
"],
Association["Book" -> 3, "Theorem" -> 33] -> CompressedData["
1:eJy9ULkRwzAMw6OcipSpUmYlj+AFPKs3CinqHLtJl0ASxaNICIfXui0rAewZ
fosnKT3u7B0N3Sbob/2cB+cuxZaY999x+TNVDEReESdVR12oLmqUQvlhdOUZ
iyrnNRkcaYwMA5y8HoT1HKSxHPZ9IHsaRdyk3ujGN189A58=
"],
Association["Book" -> 3, "Theorem" -> 34] -> CompressedData["
1:eJy1UMERwjAMsyT74MWLBViJEboAs7IRllt68IBfdRfFseTYyW153BdExNN0
MEjxesH5hIqSENQ/O7YVn66OOaVHDvoDXz0zCRKYKYd72Hyre54mIyeViP2j
19hMiz6RW4/sEOxUO+a1nAtbpgXvFRpwkK7U2lpUFZR4AVXRA6o=
"],
Association["Book" -> 3, "Theorem" -> 35] -> CompressedData["
1:eJy1kMENAjEQA3dt74YfHxqgJUq4Bqj1OsKBk7h7wAssxYo0jmL5utxvS0bE
Ou3fupwBZLEZJWVIH6MliKQdUHeVrwGqJTVLP6+L73RiRnQDhSnSxVzuZZu4
84PGIMYBkbvwE25s+w1eR5GMaWROmj6ewsoZV75VmYJH9Ui2wjj56QMvfgTz
"],
Association["Book" -> 3, "Theorem" -> 36] -> CompressedData["
1:eJy1kMENw1AIQ7ENzRA5ZaWMkAU6azcq/pHaJFJ7ai2EkDDiwbLd1w0R8XD6
u2YCTN4YUxWj6qNTAi2oJ+gEBKCSVEzp12jf74fb7GiMhgEGnTQKvHQoz+pr
URcD33lv7vIimieZAYUCmeoXcOxS700PFXRQmcU47WbHZM8TsVAENw==
"],
Association["Book" -> 3, "Theorem" -> 37] -> CompressedData["
1:eJy9UEEOgzAMs51UgMQn9qU9gQ/srfwIhyIx0LTb5rRWGketm8fyei4EsBb9
HhK9mjBPo6DxSyNYgOCkqJdD8k79x+4VLCsoR3Xo9nrpreMzMom8NfDkLp6K
76yfO8LEaB6Bw7ODmVlvNsQO7UhLhzNnmYMaYwM1bQN5
"],
Association["Book" -> 4, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoB+hr20gCyCELAJZUAnw=
"],
Association["Book" -> 4, "Theorem" -> 2] -> CompressedData["
1:eJy9UEEOgCAMW1uIHP2CX/IJfsC3+iM3IEQPetMmNGN0W9my7esGMzuC/sCM
MiFblmDUmxL92FXlMZW89EuPD7jNlAgSqC4ru9nhdOQZFFBN+afHolsczHiM
G9lnJA9BTzUFjbUhWzt/MuZQD6SoVBstppLhWzoBK08Dgg==
"],
Association["Book" -> 4, "Theorem" -> 3] -> CompressedData["
1:eJy9UEEOwCAIo+D8h1/aE/zA3rofraCJ0WTLLlsjHLAFSqnHXiEip6dfgLwh
i6qC6ZHYQ7AWQemHG74Cd4iYi/dsDD8TuTtclIm3AS/kEyzcojn3TvxgwUQx
kILZRhlfqC/aVwL5
"],
Association["Book" -> 4, "Theorem" -> 4] -> CompressedData["
1:eJy9ULENgDAMix1VYmBm5yVO6APcykfEaSlMTAgrcpo4ldOudd8qzOwQ/QNy
SrPlbcjdCZKRHUJURjhaSf98q3dVMpRjJRFxoZ2zlRsrc/TBPpQv6MyhtQ4e
JKNSIDPAPMIkyB79L2LMWtyYQ6frevqlbidr2wPF
"],
Association["Book" -> 4, "Theorem" -> 5] -> CompressedData["
1:eJy9kMsNAkEMQ5N1vrPUgERLlEAD1EpHOCDECU6Id7AyTqR4crpczxcVkdvI
nzhaCVQ3qc9LI9wMsCC7EzgEHntE78uxfh3Kv3YBSk8sgmGtzu7MZDTqWIl+
tOzlUGskM2Jl0OrEY3SGns6i01OmJ6oquEiVfxVJZjIJKMNtEmabqj1vIZbg
+w1r9/I5UsBKD64pdwD4BpY=
"],
Association["Book" -> 4, "Theorem" -> 6] -> CompressedData["
1:eJy9kMEVAkEIQ2ECgV2rsCVLsAFrtSPD7smDnnzmwLwHA/lwvT9udzez54R/
aZXBfRk/m5IZAQSlS0pIGJJNdjex/5opv1YBBXlWiQdD1r33wFFok5OIwvFy
MhEDvx0bSH00lko4P1Wz1NwMnpOKMavJyF27mm01WIQr6ljkcs8ZG2FZK7He
pFm6kyFk4zud9gK8vwZY
"],
Association["Book" -> 4, "Theorem" -> 7] -> CompressedData["
1:eJy9UNsRgDAIC4EP13AlR3ABZ3Ujgfj60S/PtJe2kAu5jvMyzQZgLfoNUTTA
nxWWoAnsglbkMzw7X0d6N+x5VCzBnYwgK6Q483q3cFRYB5stM5/cIlwVNqG1
NSjCNExb8ryEu5wJK+dbwKEExP5Fnl553QAxzAOc
"],
Association["Book" -> 4, "Theorem" -> 8] -> CompressedData["
1:eJy9UMkNwzAME0klmaMrdYQs0FmzUSXa9a99FSFgQgch0Xqcr+eJiLiabgQB
xPF9abVZmpZBGIgRU9qQ/zb0+//oNm1rQiL70U7tk8spVp2mSkQsnhNWhSZY
60VkUMhaqHBZPsVnZufcoWzIKC9A+kjqK2Vp4w1G6APr
"],
Association["Book" -> 4, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoDNjpb+XQAIyMjGAMZIEwGwOMxQiLJdyxxYbEBgCj
JAKa
"],
Association["Book" -> 4, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoCWTFGBlZpHFKMzIywmhGZhDBwAjmMYDFmRiY6eNK
VDdBnIMWUih8JiYwwtTKCNaOaSAGkxFhJCMTiMvIwMTICvI4E8xuRjS9YIsZ
gaqZgXZDLAJyuBk5ADnDAz4=
"],
Association["Book" -> 4, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoCnQYGRlNccoyMkEcBFTEyMwEBAxMQB6QYgSJQ3hU
BUQYyAhyDhMTWkgxIvNB7sTmOJAizBBmxMJkQjWSEeRXRmawCCgs4GphAlDA
BETAQANiaJAxiDDzAgBbEgNx
"],
Association["Book" -> 4, "Theorem" -> 12] -> CompressedData["
1:eJy9UMkNgDAMi50vH0bgwUIdoQswKxsRA604isQDYfWyY7VuhjylDDObtfwL
AONzkSgmOAPGYLFB+sa+TfPKApAXJ45cOVvhZLq/gMaR5yuhv8JXRb2o3iLs
YIxoWkypdFrv3QIHRwMx
"],
Association["Book" -> 4, "Theorem" -> 13] -> CompressedData["
1:eJzNT8ERgDAII8HryyVcyRG6gLO6kQRa/fnyYY4rJaSEbv3YO8zs1PEjuDtB
MrJDiMoIR5Xk14bvA9MPyrGSDmKi7knlxsq8eZRQW3vyQzN6xUgwtTJqDTID
zCNsfFdTpswqHqzR56Ln6Zd9uwA8hAOp
"],
Association["Book" -> 4, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAAjIyMYAxkgTArA4zFCIsl3LHFhMQGAJkUAo4=
"],
Association["Book" -> 4, "Theorem" -> 15] -> CompressedData["
1:eJy9UNsNhDAMSxOnrZAY4lZiBBa4WdkIu0jwgbgvdFbk5tE2Tj7rd1mLmW2i
vwOPlYhAzQTPyIPS6DR6jYXpbSnxW6iU1iGLAgiIagWoECdy8D3DFEe5wjMz
fuKgKtIYHjrcwi2hDYWXou5sWySEFxOO5GO/ELTQtqzPvc09FewpGAWI
"],
Association["Book" -> 4, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGEWBkgjiIEQiYmYCAgQnIA1KMIHEIj6qACAMZQc5h
YkILKUZkPsid2BwHUoQZwoxYmEyoRjKC/MrIDBYBhQVcLUwACpiACBhoQAwN
MgZeZm4A0RoDBA==
"],
Association["Book" -> 5, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGBgBtZmQEU6OAugAAmjwCfg==
"],
Association["Book" -> 5, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGAjAyMgyU1cMeAACY8gJ9
"],
Association["Book" -> 5, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGBDAxoFsN5TOCAJzPCIKMaEroAhjpax1ORzCg+J6R
EYpgYoxwBtzBAKqrApo=
"],
Association["Book" -> 5, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGCKBbzQQRYQIBCB9MACETIxQw0dF5QEuh9gKdSi5g
ACO88jAWdkfAwgEUXGAOODjgIcIACSqQJFAMpAIoCAD6HgM0
"],
Association["Book" -> 5, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDDACbR9QBwxPAACY4gJ9
"],
Association["Book" -> 5, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDjAxMoAgCDAykukURqhuRjCTEWweI1iAEWomVBIF
MEAxRAuacYxQxsAGDjKAuZEoFwEAzJcCtg==
"],
Association["Book" -> 5, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGEDAyoDmAkRFKARlggiBgAhNAAGYCKTCDCQqQJFEA
AxRDtKAZx4TFGnoDVJ8zMTGCxZjQJcB8RhQeAwD8LwLx
"],
Association["Book" -> 5, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGFDAyMDKCSAoMABGMUFOAFCPEUAhAkkQBDFAM0YJm
3IAHCgaAuZEolwEAxeQCsA==
"],
Association["Book" -> 5, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGOcDtRKAMIyNWFXARRkawCoi6EQIAoP4Chg==
"],
Association["Book" -> 5, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGGjBiZRJSOgqgACNMAJitAn4=
"],
Association["Book" -> 5, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGGjAyM7AwMzICncKMKclEf/dAACMYDQ2AGkgArtoC
kQ==
"],
Association["Book" -> 5, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGHDCCERAzMjNiAKA4AjDT01VgN6G5AEkWLs2IJgLT
ywCVYWSEsWBsFBEoRLcdTsINgRiKrhIYJlAnMkDNAQDfGALi
"],
Association["Book" -> 5, "Theorem" -> 16] -> CompressedData["
1:eJzNj8sNgDAMQ218YA5WYoQuwKxsRJImrVDviBysfJ5k52jX2QjgdvlBaTch
Ni4lgiPkp2klc5YsgLXvUHF1jaGWPSdZYhASQlH5R26m2fIZh2bX+XLiwHxU
rhjwA/bZAw8=
"],
Association["Book" -> 5, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGAWCEuGOQuGaIAwCYwQJ9
"],
Association["Book" -> 5, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGA2ABEcxYXMMIIRgZYexRAA4HRjBAEkAAAKXMAo8=
"],
Association["Book" -> 5, "Theorem" -> 19] -> CompressedData["
1:eJzNj8sNgDAMQ22isAcrdYQuwKxsRL5SJcQV4UPquD68HPMckwAuH38RsRsO
Xbm6tnDsxodSNRa16VZE2Kpff2PtXBJ7gVdUCd2qOyJZz5F3DnaDz7BsQnR6
A+3xAwc=
"],
Association["Book" -> 5, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGB2BixS1FR2fAAQsYDQJAsu8BpmcCjQ==
"],
Association["Book" -> 5, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGCRhETgEBxkHnImIBAJecAn0=
"],
Association["Book" -> 5, "Theorem" -> 22] -> CompressedData["
1:eJzNkFEOgCAIhmEw5zW6UkfwAp21G/XzQ1s110NPfSIiiArL2NahIrKH+g0W
ygMaqTCaFT5JYgUKaGKhocUleENqZsrjOjq6Wc9X8bGvCOU1flpTouDGEtAc
bBStcTdIZWWrIghfnIDzAMxHBKU=
"],
Association["Book" -> 5, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGF2ACATADRDAyAzETIxQw0dMhjIxgAkQBbWaCOAJJ
Fi4NFQQ6E0kcIgQ3iBHJUEZUETDE4TOQIqgUEy41EGVgeyEqANTtAtc=
"],
Association["Book" -> 5, "Theorem" -> 24] -> CompressedData["
1:eJzNULENgDAMi2uHP3iJE/oAt/IRTdIOSMwID5bjWJWbvZ9Hh5ldQf+CB1IU
0UiXOwD5hz3atjUFaKYHyOgiFQvTRjrFTAmZYBldKZSfDmM5ofcS8WGWVA1x
jgEljwFrOS4UifHWDZerBEk=
"],
Association["Book" -> 5, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGEcB0DhMOcdoDFhYGRkYWIAliMjExMUIAXBbEAgtA
hRiZwAxGJLeyMEAVoXkAKoIkyETQOagqGFGYjCjGAwDJtALT
"],
Association["Book" -> 6, "Theorem" -> 1] -> CompressedData["
1:eJzNTkuuAkEIBKuhYXq6x6TNy5vE8bfwQB7BC3hWbyTj5u1cuXi1qAAFVZzv
j9udiei50n/CqW/HWrfLflmGw2We20+h8XeWeScCr/7tvPJZXWUlmqber6NZ
cZEUAFCrBbubw8W9RDWsE1EJfhMwNUGDR+cY3rAiGGEmsHWpASVOVHsEpbSh
DUONktKRWTQsTIuriuYwzixZPPEfwNx3rfdM2TLis8KgFwDKCSk=
"],
Association["Book" -> 6, "Theorem" -> 2] -> CompressedData["
1:eJzNjTsOwjAQRNfO/rJeQ4IV8ZFAQkJQcRmOkAtwVm6EDQUdFQWvmGJmNHOc
77c5AMCjyV+xXQ/jOF1O5/Nyv5umsnHIu5Me1sxoY//rO/+etlgAUirlkFXd
iPCNe1/VrDc0MnMzleYQt4a8a9kJHa1ahumFpuaoEmorOWJCEpFSjxAjxNAx
AxJcQyDupFNa9cxSZ1k4iHKm+KGLMefFMAho1nqOJWJ4AmA7CbY=
"],
Association["Book" -> 6, "Theorem" -> 3] -> CompressedData["
1:eJzNUMkRwkAM8yE7dkiYtEBLlJAGqJWO0JIBXvx4oMfaI40ley/77bqriNzH
81+YIqLOp3Ut1swJYlOhygwI/Dpt/i6pCqCqJpJZlUa0vbAs7L0Jb6+x4NyD
QYS7Z7A9SliTaT/GCoN5IzhgSPozEGDUOFPEZX6qQpfyTPiwHpql6QdcEhs/
zLSTeeqtLg+BNQXR
"],
Association["Book" -> 6, "Theorem" -> 4] -> CompressedData["
1:eJzNjTsOAjEMRPOzHSfZxChaEAUFEohPxVk4wl6As3IjvOnpKHiSRx6PLR+X
13Oxxpj3Kn/G9XZ+lFrKqdaU7mU2+7ZRmEku9Otn8WvirHW9a1N0K6bUdrV2
oQEAxCiqooBQa701dTrhnFWHqGECBsmkkQxAbwlq1YK8huo4ckz6yHtvnPNM
xqGZnAX0zSMirBUQtsHilCGhDsEPLAZOmTmb7WGGIIAu2A996Apf
"],
Association["Book" -> 6, "Theorem" -> 5] -> CompressedData["
1:eJzNjTkOAjEMRbN4SWwcMkzBUiAhUdFRcBGOMBfgrNwIZ3o6Cl7xZX/b35fl
9VxiCOE95N943O5Va722pnqXOZzqxtQNnm/061/fA1OMaZq82PoWMevBbNeL
w4yItXbX7mBns8nMu+GrutoQRC0FC3ZlH7UVIEJCs4KGbQy9q6LC42OCkFOu
HBIGyREotUx+AAAeRg0jNAEhNzGvRILCIlTC8bwH8vgE8QMqcQnz
"],
Association["Book" -> 6, "Theorem" -> 6] -> CompressedData["
1:eJzNjbkNAlEMRP8xtv9prT5arUAQIFIi6IQSaIBa6Qjv5mQETPB8aub8fD2e
3jn3XvF3ut5qr/UyTa3d2+KOVVvvKfG4ya+jvhsG78M8W9PtS1LqB9XdYBZh
BlDKMA4TBqvOqiLrpvRubCusZEbG6IyBaRMLIFBlKNp6tKnkkpMFxRhdCDGL
C+Ra8CRRIzOTBRIRK3m0gsK2pLjJm0WuVYrbnxaQggP8ByvOChE=
"],
Association["Book" -> 6, "Theorem" -> 7] -> CompressedData["
1:eJzNTTFuAzEMsyVRsmX5jByKogWyFOjQ5Dl5Qj6Qt/ZH1WXv1qEERIgiIX7c
H7d7LaV8H/T/cPVw/1xrjMt4KWefM6J3O33pXzf9/pBqpX3PZcuUmsV7xGmZ
tWYGoPeVvBJYNuc+Z6q8NPfkeRDgGTUsz8F8QhRQRBgC8zBTNR9uWcTMhYhV
CkkZVGG8sbAIQOlJcKVwasqq4CeqSrPuauXt/CrYREjqD5fACUM=
"],
Association["Book" -> 6, "Theorem" -> 8] -> CompressedData["
1:eJzNjksKAjEQRDtJdU/+kzAMggjiTtfexCN4Ac/qjexk786Fr6HoD3TV5fl6
PA0RvYf8IbnmfOu9lHve6JTXUqv3sl+XXxt9f2iNsb2PLERBqcdatyYTADE2
1aagSSkaVWRsQkqqU4AcBAEtCRrqhD3gtRdUpHHUKXgtNXLOkbUuLGSFijW8
uNWpG6shM0thgxwRRZfsJkYQfcoh0OG8A4XFwnwAo+QJgg==
"],
Association["Book" -> 6, "Theorem" -> 9] -> CompressedData["
1:eJzNjcEKwjAQRHc7m23SJG21QhAr4qE3v8ZP6A/4rf6Rm4J48+TBNzBsMgNz
XR/3lYnoWe0fWW63vpRj2Z0TxXnWSwFcGMKvd/LXNCUztVaeplNU7Tze9H29
vQGTT3a09UdEzFW2UuyADt4eHmFDI5CgahWThYgQVZ1sSKShhrltSRwtzJBG
2Os+WO5MrbJ6l4U/gDkPaRwdheTr+IFBL1dJCHM=
"],
Association["Book" -> 6, "Theorem" -> 10] -> CompressedData["
1:eJzNTVsKwkAMTJpHs+7W0m2xIAVR6IU8Qi/gWb2RSUH888sPZyCZZAbmuj3u
GwLAM8ZfYl2HeZ6mac5QTotdFhFKNf26Jn93w9bY43guqgejN0oJbQ5yWnbR
xoeZfSrvoa54kMwPo7RDc3xUPeJ0SZlYVUcvYm6gQTeBBW6IosRkMiT3xdkq
qnLH+AEh9v2xVgHrLLorErwAEM8IPw==
"],
Association["Book" -> 6, "Theorem" -> 11] -> CompressedData["
1:eJzNjcEKwjAQRHc7m+2mSdraHoJYKIJXf8ZP8Af8Vv/IbUG8efLgGxg2mYE5
3x+3OxPRc7P/5NrXeqyHNVNaFl0rEOIQf71SvqY5u6m3yjyfkmpneNP3220O
XJbNYrv9iIi7yl5KHdDB/GGIO5qADFWvuDxEgqjq7EMiDTXMbUsS6MIMaYRN
p+h5cLXKaqEIfwBzGfI4BorZtvGJQS/3UAgj
"],
Association["Book" -> 6, "Theorem" -> 12] -> CompressedData["
1:eJzNjVEKwjAQRHc7m03SJG01H0G0iOCJPIIX8KzeyE1B/PPLD9/AsMkMzOX+
uN2ZiJ7d/pSptUPbrZnSetJzA1yc469Hytc0ZzO1Vqn1mFTHgDfT1O9gwBSy
Hb7/iIi5ylZKIzAi2CMgbmgCMlStYrIQCaKq1YZEBhqYvSdxdGWGDMJBa7Tc
mbyyBleEP4C5zHlZHMUc+vieQS++jwf1
"],
Association["Book" -> 6, "Theorem" -> 13] -> CompressedData["
1:eJzNTjtuQzEMk21JFG28jx/SZO6VeoRcoGftjSojc7YO5UBKIgTy8/n99Swi
8rPov6L3iJueMhEP4LrO+2x/naHvrVJkjNSHiLsqNoBxHOc+BjuBSI5Ej50c
JGxd3D35YxEZdtAYvjP4gmOj59tB8L7MVJ/XfPVoUksNz0CJnLTM2oy1taZm
SpN2DQ0okIUWCswiN5ftNgxboPbyC7uGCKo=
"],
Association["Book" -> 6, "Theorem" -> 14] -> CompressedData["
1:eJzNTTkSwkAM8yKfG0LJQDpghgfxhHyAt/IjFDIUNFQUyB75kI/TfL/NTUQe
C/0trpdzP5b0abTt1gwx+q9f5Fe1imR0633s7hV4IyJWDtCiItKWjqqSTV9D
lUAiWARyxUAR7oAzUsQANd7nIy5IU3aZyU6bp/LQxjRTo8ytFtW0fWCfOR1M
3BwKHRvkCRlTBv0=
"],
Association["Book" -> 6, "Theorem" -> 15] -> CompressedData["
1:eJzNTkkOwkAMyxBnmdDhBELqpeJLPKEf4K38CLcSBy6cOGCNPEmcOLmtj/va
ROS50f9iWWouOc7DpslMc/ivN8RXtYpkfFY1yr2HvuG+xUFoaGZlhm0VAGTD
3lRdtWswCe07oihymAb8KWopjP5cxAFpYJWRnNA8QaODIRPRza03OAztA+fM
68V4oikUo6m8AOuyBtY=
"],
Association["Book" -> 6, "Theorem" -> 16] -> CompressedData["
1:eJzNjjEOQkEIRNllYAG/25qvlbW38Qj/Ap7VGwlqY2Nl4SOZEJgwnLfbdWtE
dC/5Yy7jGOSrsxmzWODXAbuv24gUITKb013V84s3EdVbwlkWZq41AZAqeJrK
n1uU+ouFWVm1VGrMC0NVZwb1DurIC9SZAo3rCNI2BoaLijcMCNoHh7DTKpSW
Ct83pgfKqgbU
"],
Association["Book" -> 6, "Theorem" -> 17] -> CompressedData["
1:eJzNjrsNgjEMhJ34kXMeNSAkJFZihH8BZmUj7HQ0VBRc8flkO+fcj+fjKET0
Svyz2hk0Ts4AM7cuv873r1MgoERmc/ow6xBW5RT2j5AFu6BbdlRkcy95dGIq
ybHVV/rWmI01LS9Wi/w4VKtQzYdB6lI4vVSNdWmupl5EI7p86DJxuxqZIM+u
IvQGjjUGsQ==
"],
Association["Book" -> 6, "Theorem" -> 18] -> CompressedData["
1:eJzNjTtuAzEMRClpOPqsREOh4y5B3OU8OYIv4LP6RtZu7y6FH8AHfoDh9Xb/
uwUReex6a/qn/HQbY5TCj9/83/GvA2MI0X01JlJKrfY958XJnEkArfmyL+A0
czNy32xmy2MX0CtR4UY4TgdagII5iYmxH9e0ta3V9SilJDGmmiWqjBg0p5lI
qipWcWhAb+hcS00HgWhl67XK5esM7WBEeALe/AkU
"],
Association["Book" -> 6, "Theorem" -> 19] -> CompressedData["
1:eJzNjc0NQjEMg/vjuGnySh8jIDERI7wFmJWNSOHAjRMHvkiWlVjO5bjfjpxS
eiz5b2bar8beAc4Tf93ev/+e70hr7jZUNwNEsGgtPCyAwX26O9eGZGjnK7Q8
YaGG7YWOaIAqoDFxxACbNo9HtdaUUYFwaUMGK9asuIiwSYarSPmQS5nkeWey
6qiKUZCf5fMHOg==
"],
Association["Book" -> 6, "Theorem" -> 20] -> CompressedData["
1:eJzNjc0NwjAMRu04duzGEWkPSBUSpTN0E0boAszKRri9c+PAk/XkH+nzur+e
OwLA+9C/c2+tVDer82y/zv4emBDTtkXjAKqt1av72FWnSVVEhqGHeyBdl2Vb
llKOjdYaPiViRaVIrypd1pMYo9xVXLzwOamZtXhElAATMgMxXBLmTIqaJTMT
B8pIjxs3IRGmkziaaS0OI1fOQy6U8QM+IAni
"],
Association["Book" -> 6, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLAA6npERQmPKQBmMYBUQdSMEAACfzQKF
"],
Association["Book" -> 6, "Theorem" -> 22] -> CompressedData["
1:eJzNjUsOwjAMRPObdJyW0kBpVQJILLkOR+gFOCs3wumeHQsszdPII4/v6+u5
WmPMu+Lvp9s3u47k9ZJ+Xc2vibPWzbMaFdn3/WNZbkUkJREAImdlKeeCIjnP
OUfUzTCdlGMFkBpBgzIJCsZtQD3Fsqgw1hAMQz7kXh9574x1NgTjo8nV+GTp
GdRoWSSsPw4YCbLZ+hEYU8uOO5MxILQhergPO5oKIw==
"],
Association["Book" -> 6, "Theorem" -> 23] -> CompressedData["
1:eJzNTssRAlEIg0eAx/u46tiALVnCNmCtdiS7Ox69eTDMZCBkAvf1+ViZiF4b
/T9mjAFYP9uvk+PrpjCXOZnZiVrrvQ33HvggIg4OZMWMaLopqprsupuq5deI
HAJtR52b4p6WrGwxoZ7JeVFEiCFAdnQCw8QFEqgVbuZhjOZqUkTKARa5drtd
jBYbkIpRwG+WxAcG
"],
Association["Book" -> 6, "Theorem" -> 24] -> CompressedData["
1:eJzVjTEOAjEMBB3Hdhyfj3CHFIkGiZqWl/CE+wBv5Uc4R01HwxSrlb3avW7P
x5YA4DXkD1juN1Vpvf66+HshpoTuYRSgtd7PzezgHBCFqA7vATubudlcfL/r
rjRy8Yyv69Dpw6p8ijyzcWFyppW1Wu0xRISxmkWAGC4psWTNymsVKdEpzqkM
g4IYqUFGavNhWQpMx4lYyZDTG3gKCIs=
"],
Association["Book" -> 6, "Theorem" -> 25] -> CompressedData["
1:eJzVjdENAjEMQ5OLnbY56G2AhPhjHEa4BZiVjUiL+OWLn3Ol18hO3ev+fOwq
Iq+BI4i83S+l2L97fxSqCpB3iKwrQAKwiFZa61vPOWmpzRoyo32dZCDRuyM6
0mrd8sFcsuFg+qeBbucsDXy+zGPLIgpxVcvRTDkCdxpddK0IVrLUKWOBzQSV
4XSWzd/inwdp
"],
Association["Book" -> 6, "Theorem" -> 26] -> CompressedData["
1:eJzVjbsRwkAQQ+8neW+9cHh8w4xDaqATSnAD1EpH7JmYjIQXKFhppdv+fOwx
hPAa8hfc64TLtf66Vr46KcZk9om01vvWVM8GpxSSIuZqDg2qpnqa7LjLoSAB
M9B9GTof2FrZqQoqJw8QK6Vq7T5USvLVTIaCsMUIZsmCpXJ0eQfi+EFiSp4a
5FSWdm7LFOY2A1I0l/gGOscIZA==
"],
Association["Book" -> 6, "Theorem" -> 27] -> CompressedData["
1:eJzVjcERQjEIRIGwEPK/yegY77ZkCTZgrXYk0bM3L77DMrMsy/X+uN2ZiJ5L
/oNaLY7x89avG2GWutaFqPc5Z+y7hyeqAGqN1EiwzOo+3k5rDWtkRjUvsCOa
I/Jg0eeGCz6+uqac0cxt5iNVya/FjBR0YoYVLRVbmFlWWoCtMCAmkqlFER2H
PkaQb64oaqL8Ar0pB5k=
"],
Association["Book" -> 6, "Theorem" -> 28] -> CompressedData["
1:eJzVTsEJw0AMsyPZd7lQCDS5exc6ROfoCFmgs3aj+lJofn31UxmEkI3ky/a4
byoiz05/gtvVHb8O/RI4DEKqahEZR9IYQM7JU2qtAngzGjLAEIaPX1hbXVdj
bgwrN+ynHeNqC3d/ypV1wRmlFO6VGoPoVYqrIiSg1hfwyHfRKWGyA2rWe+li
tDletNNsLx4lB/o=
"],
Association["Book" -> 6, "Theorem" -> 29] -> CompressedData["
1:eJzVTcERAkEIg0vAY0/H5WEB9mAllnANWKsdyd7N6M+XHwMTmMAk1/VxX1VE
noP+BTd3/Nrzi6GqkDWbSARpLCDi4BGZHcDOSATAWgxvvbGod2MkS4rE9jrQ
0jo3fRmUOKO1xj2yCtMkSnFV1AqojQNnwmbRZcbRPkB15dKFbienWbvwBaQn
Bz0=
"],
Association["Book" -> 6, "Theorem" -> 30] -> CompressedData["
1:eJzVTkkOAkEIhIGCHnpMekm8+yWfMB/wrf5IZmLiyZsXC8JWbLf9cd+ZiJ6H
+Rus0F+vtO8UMwHpa2p1NwNUI4qv65zDXedsmugaqkmJviu9t3qErUFiysip
rmdrNsk2MYBIux1kl5yP8PMgU4oIkRIyWWhhWSzrrAWCQlyLFP2AAcm7ZuSK
S35occULoOAHag==
"],
Association["Book" -> 6, "Theorem" -> 31] -> CompressedData["
1:eJzVj8sNAkEMQ/NzPCOxRdASJWwD1EpHOMuZGxd8iEa286K5n8/H6Wb2mvE/
WvlrIr5HEUa6uyoAiequnFeNgNRMSWaVTKVyCFzpVYpAxSwpwkeCqNqiTSlm
jd1NHcx0C31ymbe1uzYPC24XRl1uGHg0kzrKS2IL2FR/3RIbjPI3vUoFtQ==
"],
Association["Book" -> 6, "Theorem" -> 32] -> CompressedData["
1:eJzVjc0NwjAMRp34s52kaRMFUZUjKzECCzArG+H0zo0LT/KTf2T7/nw9noGI
3lN/RP71Qfs6iSHEffekEYnU2o7er8MsJTMAKQ33cDC0tb01s9kp6+quU8CS
DRljVQxcTtR3Db17YJtDr0ouufoj5kghMkAsNGJQxcaJDSIsziaBa5GirCp8
AkXOZbGFbvWAbLCI8AHuyAhD
"],
Association["Book" -> 6, "Theorem" -> 33] -> CompressedData["
1:eJzljdsNw1AIQ3FsE27UJbpSR8gCmbUbFfLTvy5QI/HyQTzP63UiIt6T/ln1
2x1bEftetcrOJCWO1uqe2WJHVqY8G9ud5Rs6VoPMHvJGB5p+GFNjdrWk+5EQ
ENKxMY4NfjAwN5I1UKNEEl9tQK2jSjGUQIPxAbjoBWY=
"],
Association["Book" -> 7, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGFGBkRHcySIARLAxmMEC5EADVgiIG5oMxAyMDI6aB
GKYPMQAAxXUCrg==
"],
Association["Book" -> 7, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGFmBiwiLAxAQmwRwoFwIgCphQxMB8MGYEQiZUAxmh
GMJhhFjHCBYlAzCAEV55KIMywIggGBkBJVEDRw==
"],
Association["Book" -> 7, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGGGBC5zOBMJhkYGBkZAB6iZGJiREMwGpBDAiJAAxg
zMDECNGJGzAOvRACANOEAr0=
"],
Association["Book" -> 7, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGOGBmBmEwycDAyMgA9BIjMzMjGDCDFIAYEBIBGMCY
gZkJohM3YBx6IQQA4HUCyw==
"],
Association["Book" -> 7, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHGBEB2ARoDhIClMWG2BAplHMBpuBbBedPUc5AADe
BQLH
"],
Association["Book" -> 7, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHmAEOntoupweAACYNwJ9
"],
Association["Book" -> 7, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGIGACo1GAFQAAmVACfg==
"],
Association["Book" -> 7, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGJhi6Lqc1AACV/AJ7
"],
Association["Book" -> 7, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGKAA6nRGr87GLYjVgWAIAmv0CgA==
"],
Association["Book" -> 7, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGKmBhAWJGIGBhAJEMDCDECCGRAAucQAIMUAzhIAGI
GTAOI4QDJUgHDEi24JDHdAIZgBFBMDICABMDAzE=
"],
Association["Book" -> 7, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGASpgYhpoF1AGAJfgAn4=
"],
Association["Book" -> 7, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLmBmJl4UizpqOmUQAQCj6AKJ
"],
Association["Book" -> 7, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLGAFIiYgYGUAkQwMIMQEIZEAK5xAAgxQDOEgAYgZ
MA4ThAMlSAcMSLbgkMd0AhmACUEwMQEAeRAD0Q==
"],
Association["Book" -> 7, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGMmBjZmJkZGNgBAIGBhBiBJPMjFDAzMzMAaJZmRhR
AAMUg0lkAyFmwDhQWShBOmCA2YJbHsqgDDAiCEZGAB46Az0=
"],
Association["Book" -> 7, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGMGBhYMT0AQsLgs0Ik8fiURZMoWEBAKp7ApA=
"],
Association["Book" -> 7, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNGBiYgD6gREIGCAMBkYWFjAfDJhA8iBJJkYUABJk
YYCqw2k4WB2EZmBgJANATMArT8AJxAFGBMHICAAFjgMk
"],
Association["Book" -> 7, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNGBlZmTkYGAEAgYGEGIEk0yMUMDKysoGotmYGVEA
AxSDSWTzIGbAOFBZKEE6YIDZglseyqAMMCIIRkYAIcIDQQ==
"],
Association["Book" -> 7, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNuBgZGJlYAICBgYQYgKTLExQwMnJyQyimTmYUAAD
FDMCIROycUAOIzxQgCywLFiEkQzAAEZ45aEMygAjgmBkBABXpgN8
"],
Association["Book" -> 7, "Theorem" -> 19] -> CompressedData["
1:eJzVUIENgCAMa7c4lC98yRN8wFv9yG2IRr3AEjpWuiYwr9uyEsAe9HOQRHUA
E1BHFJEiZqWYQ1UZlTparA74dtM0kDF5wzxwuKOh6lUkycGOdk5JXkpykyIh
G7nG4nxyXGaX+a9XPTofSO3rCyObm+0zeAAetARy
"],
Association["Book" -> 7, "Theorem" -> 20] -> CompressedData["
1:eJzVjMENgEAIBBduQ64NW7KEa8Ba7UgWNfczMb6cwAAhsIxtHQZgl/5OByJJ
AyRoxggWob2a0xONxhbsdTlpmX4P7npYVXoPKh73V/MNn3I/AMzbBC8=
"],
Association["Book" -> 7, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGAWAHAiDJwMDBysDKyMjKyc4KBuwgSRADQiIAiMvI
ysLOysXJzo5sEgsQwwOFmZkBpBVEgwjSAQMY4ZWHMigDzAiCmRkAJvUEww==
"],
Association["Book" -> 7, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGAWAEAiAJYoBJJkYoYGZmZgPRbHARCGCAYjCJYhID
kgBMFkqQDhhgtuCWhzIo9D+CYGQEAAf3Ayg=
"],
Association["Book" -> 7, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGAWAEAjQBhCCUZgRBGGCAYCwmQfEQBgCyEQKa
"],
Association["Book" -> 7, "Theorem" -> 24] -> CompressedData["
1:eJzdUdsJgDAMvMZaGywW6l//XMkRuoCzupFNteADBH+9hEtyIYGQKS1zUgBW
oT8gxggEwDv0RNx5tpaZPRGpHJmagcUqIBrb4LQex/MiC1BbC61hzB6FvgPF
X/tHcsf1MfmKotHzciVe5oVU3rUBYSQGUA==
"],
Association["Book" -> 7, "Theorem" -> 25] -> CompressedData["
1:eJzdUcENwjAQc+6sJgUKUis+/bESI3QBZmUj4itBpWyAEzm2o1xyym153JcE
4Cn6C8xXYAQuJxzN+jyUwGBmScL8XDQaoKzk8UBO07ZOBozNuKPr6koGVXjD
qiPiLgleI1UIw88x6TdrMxy5bwffH1O7iMx+G0+aHq+Vq3e8AAkOBdU=
"],
Association["Book" -> 7, "Theorem" -> 26] -> CompressedData["
1:eJzdUYkNwyAQM3dWoE9SKVEH6EodIQt01mxUfClRmm5Qg4xtxMGJx/x6zgnA
IvoP3IERuF1xMTvlvgR6M0sS5kPRaICyksczOU37MhkwNuOOrqsrGVThDauO
iIckeI1UIQy3Y9If1mY48tgNvj+mdhGZ/fadND1eK1fveAPt4QW7
"],
Association["Book" -> 7, "Theorem" -> 27] -> CompressedData["
1:eJzdUYkNwyAMPBwrJsJqJTJBVuoILNBZu1FtU6o8G+RAZ99ZGCy29n61BODj
dBtU4KkoRItUzVlVKxEli0rTQ30NwD0ttTCv675HASgPIYJ5tsgcZJCBnofF
Jye4W94hBP+Pef5jL4aK/kccP8amCI+uQyffEq91ZXd8AasvBwk=
"],
Association["Book" -> 7, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGE+DjZuBiYuJk52YHA24mJiZGEIOJmZcdBGGAASTG
zibJycIiKopsABsDAxMzjMPMzMDKCqFBBOmAAYzwykMZ6AA1YoC+AIsxYfqY
EYTA+kEEI9AsAJaGBU8=
"],
Association["Book" -> 7, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGESDPO8MsEACWtgJ8
"],
Association["Book" -> 7, "Theorem" -> 32] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGPBhmgQAAlbECew==
"],
Association["Book" -> 7, "Theorem" -> 33] -> CompressedData["
1:eJzdUdEVwyAIPCCBJ6Y/2SArdQQX6KzdqEJqXpNs0FNP7hTF59Zez0YA3kF/
hQcW5jrNXqu7zyJCfXaS1aMNoA/2opOI2W9+AViHUEXpBnKLBXRgj9Oyi5O8
W3FCCjvSIv5yLKY6l5A4fwwzpcf3B1P0rDiI+h0fU7EGwQ==
"],
Association["Book" -> 7, "Theorem" -> 34] -> CompressedData["
1:eJzdUdsNwjAM9KMOQU6ohJCqfrISI3QBZmUj7CtFrdiAS3L2XeI8lPvyfCxM
RK+kP8MsMg3Wbld3N1XliM568WytOUAx5FxPg2qt++oQYpsohcYxYu+ggG1Y
c1iZlJ0DXheRGUH0b1nmH85JKOx/xPFjRBie/D6Xs+PGSRxnvAHc8Qem
"],
Association["Book" -> 7, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 36] -> CompressedData["
1:eJzdUdsNwjAM9KMOQU6oVIkf/liJEboAs7IR9pVWrdigl+Tsu8R5KM/5/ZqZ
iD5JZ4PIY7B2n9zdVJUjOuvNs7XmAMWQa70MqrXui0OIraIUGseIvYMCtmLJ
YWVSdg54WURmBNG3ssx/nJNQ2P+I48eIMDz5fy1nx42TOM74AsfMB5E=
"],
Association["Book" -> 7, "Theorem" -> 37] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHWBBMBkZoT7E4lEWTKFhAQCgAgKG
"],
Association["Book" -> 7, "Theorem" -> 38] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGM2BkhPoQi0dZ6OsUugEAnAYCgg==
"],
Association["Book" -> 7, "Theorem" -> 39] -> CompressedData["
1:eJzdUYkNwyAM9BMTKluRKnWBrJQRskBn7Ua1L48SdYMecPYdmEfM63tZmYg+
RX+IweL1dHdTVc7orOFo4QDlkEcfB9Xer5UpxA7RGk1TxghQwg5sOaxK2sUB
b4vIjCDiLKt855qEwv533D9GhOHJ71O5Om5cxHnGF434B0I=
"],
Association["Book" -> 8, "Theorem" -> 1] -> CompressedData["
1:eJzdkNENgDAIRA85GtZwJUfoAs7qRgJNmib6558v6bXAHR/d+3l0AXCl/BFv
lriIbPkQqdra6BvibEZvNPc1SEDmp5Dhi1u1JCD1CYuXgYKaOS6m4eMQTOM3
mFJLYukN8sIEnQ==
"],
Association["Book" -> 8, "Theorem" -> 2] -> CompressedData["
1:eJzdkd0NwyAMhI1jOYEDoSp97UNWyghZoLN2o9qmrRp1g36C43z8CMR23Pcj
EdHD5S+5lNJ7uzHz1A2elrrUua5rDcg6o+SrSM7f+woRz++iNVK1USTEAHRg
fqiohWjAJwkdiwhKVkBFEQz/Up+MKs4/c/4Y5hQZ/z40eYM7v2lS6BN4owb0
"], Association["Book" -> 8, "Theorem" -> 3] -> CompressedData["
1:eJzdUVsOgzAMc5K1Ql1BVX9giJ9daUfgApyVGy0JA4G4wazWtd2mD/U9L5+Z
AKxG/4ncTdMrigiNCpJcc33Wcej7qoB27trwEAnhXNYCnHZTCppGxxidFGnH
pj0yUU6J87YIKcFNPMpM/9gm3fn+V1w/hpk84/s7yZrf2Ij0jC9c/AhX
"],
Association["Book" -> 8, "Theorem" -> 4] -> CompressedData["
1:eJzdkesNgzAMhP1oZKOAfyH43ZU6AgswazeqfaAK1A36KbncOS9FeW77a2Mi
epf8KWvE2FSVI2Gd+tTHHtEBZZfB7aHqft2VQdo3OC1LjvMMScxaswLeUCrj
lwr0WERmhHBkO/2pNYmE8+/cP0aEUZPfZ3I1K1fCeccHW9gI9A==
"],
Association["Book" -> 8, "Theorem" -> 5] -> CompressedData["
1:eJzdkd0NgCAMhPuHBFPQFVzJEVjAWd3I0geiQRfwy+USjlxTwlaPvSIAnM3+
Sik6MTMWAzkbRddFNasq5Kw0JxFmkXspAVDoh9QEEKObE0J8Ib2FVnN90y+H
5Z8fQ4Se0fhKbPJ+M7RZF0ikBto=
"],
Association["Book" -> 8, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLVCVYWVmZmZUAAJGZm4hbiEuIVERcXEhIGAAYiY+
XpA8KyuyHl4GBiYuGIeHh4GDA0izsYEJIOCCAQgbLARi8CCJgEmIIgYuLgYw
hw2uDcSGkiBJMA9sPipAjRgmJkawGBOmJxlBCOxiEMEItAMANhYIKw==
"],
Association["Book" -> 8, "Theorem" -> 7] -> CompressedData["
1:eJzdUckNgDAMc1K1QqHwqEB8+LASI7AAs7IRSTgEYgOs1nWcpocyLeu8EIDN
6L8YYwiBJgWFutRFSt8NQ1FAJ7eN5WN8ljQAyxXkjKrSNSUnhVw4tFsm8sNx
PjZBBB6ku8z0yZb0yM9/490YZnKPv38kG/5iI9I7dhYdCAo=
"],
Association["Book" -> 8, "Theorem" -> 8] -> CompressedData["
1:eJzdkdENwyAMRG0jULg4leo/PrtSR8gCnbUb1TZt1agb5AkOn20QiNv+uO9M
RM+QE1NLKTwcLqutBrPrGOaQT7lsUa/1d8dGJPiY3mlZfG0txQF04vHUpp5E
B76Z1NlEUHIDbYpkxm+NYro8/8jxY0Q4c/L/RI6RN9ZwCn0B9uYIDQ==
"],
Association["Book" -> 8, "Theorem" -> 9] -> CompressedData["
1:eJzdkYEJwzAMBOWPlOYrCKQbZKWOkAU6azeqJLchIRv0sB+9/DYIr9vruTUR
eaf8MwCGOcAw+eQ3XxYvJDbu5EOVPF4Ig/FnIjemUS3RDFsn6q5q0aSTe6e0
h4QmYWhqLHr91TwsV++fOX8M0KqH64QtV41g6Yz2AdMKBho=
"],
Association["Book" -> 8, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNeDmZmYCAmYOJhTAAMWMQMiErB7IYYQHCpAFlgWL
MJIBGMAIrzyUQRlgRBCMjAAb3gNB
"],
Association["Book" -> 8, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGN+BmZgICZg4mFMAAxYxAyISsHMhhhAcKkAWWBYsw
kgEYwAivPJRBGWBEEIyMABFtAzY=
"],
Association["Book" -> 8, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGOWBmAgJmDiYUwADFjEDIhKwayGGEBwqQBZYFizCS
ARjACK88lEEZYEQQjIwABwcDKw==
"],
Association["Book" -> 8, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGO2AEAlYmRhTAAMVgEkUxA5IATBZKkA4YYLbglocy
KPQigmBkBADl0gMF
"],
Association["Book" -> 8, "Theorem" -> 14] -> CompressedData["
1:eJzdUdsNgCAMvBZCTAl+gPGfP+dxBBdwVjeS1kc0buCFHHfX8gp1WeeFAGxK
v0edKrlYYpE8DOOYG1By5j5555z3z94EsNwmoevaHIJRg1w4tEUq0iMxPpog
AjPhXqb6ZC2as/3feH8MM1nG38eRDruxErUzdtP4B8U=
"],
Association["Book" -> 8, "Theorem" -> 15] -> CompressedData["
1:eJzdUdsNgCAMvBZCTEE/iPHfT9dxBBdwVjeyrY9o3MALHHdHeYVxWeeFAGxG
/8c4Ucg1V6l9PwxVAe3ctTGEEOOztAVYLlMKmkbHlJwUcuHQHpkoj8T5KIII
3KR7memTbdKd7//G+2OYyTP+vo2s+Y2NSM/YAbFtB58=
"],
Association["Book" -> 8, "Theorem" -> 16] -> CompressedData["
1:eJzlUdsNgCAMvBZCTAl+gPHflRyBBZzVjaT1EYwjeCHH3bW8wlK3tRKAXekH
WMjFEovkaZrn3ICSM4/JO+e87zsTwPKYhGFocwhGDXLj1BapSF1ifDZBBGbC
s0z1xVo0Z/u/8f4YZrKMv08jHXZjJWpnHI/5B3w=
"],
Association["Book" -> 8, "Theorem" -> 17] -> CompressedData["
1:eJzlT0EOgCAMK4MQM9EDId79kk/gA77VH7kNNWr8gQ2UtgwYc12X6gBsSn+A
833uM+dSpikLIJPGIXjvQ7gXDgDxaVJC18kao5GATzRtkYp0S4xbEZhhJl7H
VB+sm+bs/lfDD0fkLKOPn+mwjpWcvLEDbMoHVQ==
"],
Association["Book" -> 8, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGBGBiRAEMEAwUZWBiQlYHDBBGeKCA1TAwwAjSAcQE
vPJQBmWAEUEwMgIA3/IC/w==
"],
Association["Book" -> 8, "Theorem" -> 19] -> CompressedData["
1:eJzlUNsRwCAMCmSSrtQRXKCzdqNCrPbx2d9yJwJBz3Np29oQEbvpH0gmBVNm
hjYvQnyvyWB+ipSq0Sus+kDXFfGVFPfIN5ThPGZ9soflnk/4AFwEHAvJA0M=
"],
Association["Book" -> 8, "Theorem" -> 20] -> CompressedData["
1:eJzlUdsRgCAMC1WQdgA//HMlR2ABZ3UjaXwcnCOYg1ySltexln0rAcDh9BPo
orOaKYE6RXMah2Ga2q4MSHxMSjDzMJMq4oNLM3KRmoR8NSFG0OR3meubvUjH
/Xv0HyMSmMn3WcEHb+wU6hknl4EF8Q==
"],
Association["Book" -> 8, "Theorem" -> 21] -> CompressedData["
1:eJzlkVEOAiEMREuBbBjT7GoAf90fD+QR9gKe1RvZFjVuPIIvZJgZGhLCut1v
WyCih8m/gOvhclx6P9daaW0n7i3FGFP6HmpEvLxDKTRNuufsogDzLIb6oVm0
RAE+jesYIghpgGSBM/xL7dCT379n/zHMwTv+fVWwBXNiSSBPsdYHyw==
"],
Association["Book" -> 8, "Theorem" -> 22] -> CompressedData["
1:eJzlkdENgzAMRC8GH44X6HdXYgQWYNZuVNsBVNQReEpOvrMVJcp729etAfik
PIb+6u7eE8SWbpynaVl+ZwwQPQ0J9wytJFDlIOqhxgiVqldSOoagRBilxUAy
6kOzWa7Ov3P/GJFWmfw/quWqGzMdlV+KKgX1
"],
Association["Book" -> 8, "Theorem" -> 23] -> CompressedData["
1:eJzlkVEKAjEMRNO0ZelIWBdp9Hc9kkfYC3hWb2SSqrh4BB9lOjMNhdJ1u9+2
REQPl//hsC5H1Uvvna564rOWnHMp3yNKxMs7tEbTZHutIQYwz+KYH1rFSjTg
04SOIYKQBUgVBMO/1A8jxf179h/DnKLj3zclX3AnngTyBJCYB6c=
"],
Association["Book" -> 8, "Theorem" -> 24] -> CompressedData["
1:eJzlUcERgDAIo1TCUadwJUfoAs7qRgJV73qOYK4NJORBr1s/9l6I6Az6EWxt
zZqZkVduhqVW1SlBxPIIH3k0a5BDBAPeD1a4KX5fJ3mESEAuBApJjP7mGKaa
V0jMH8Nc0uPvk0qc3BihILgAYJoFtg==
"],
Association["Book" -> 8, "Theorem" -> 25] -> CompressedData["
1:eJzlkdENwyAMRI0BBd2HEyUV/DYrZYQs0Fm7UWyTVI06Qp/QcXdYSIh1f217
IKK3yT8xTa09am30XBZuNcUYU/oeqEQ8X6EUGgbdc3ZRgHEUQ33XLFqiAJ/G
tQ8RhDRAssDp/lQ79OT337l/DHPwjn9fFGzBnFgSyAFz6geY
"],
Association["Book" -> 8, "Theorem" -> 26] -> CompressedData["
1:eJzlUcENhDAMc4Mi8gDJ5dUHn1uJEViAWdmIJgUEYoSzKsd28kjU37otawKw
O/0V5mnKJJEzZRxUu0712R8AscuUgr6vNUbUQVpD1Y3VashC3klwGwIN1dDU
GGj6ZG+Ge68QeH+MSIpMvgclf3TlayejHRTRBwU=
"],
Association["Book" -> 8, "Theorem" -> 27] -> CompressedData["
1:eJzlkYEJwzAMBGXFIjIJvB3wAF2pI2SBztqNKslJacgIPcz7/2UMxo/99dwT
Eb1d/ottq601qrXyumSZppx/xwsRlzP0TvNsu0iIAZSijvmholaiA98mdBwi
KFmAiiIY/lAfRor7r1w/hjlFx/f3JF9wp54U+gHqsQbJ
"],
Association["Book" -> 9, "Theorem" -> 1] -> CompressedData["
1:eJzlkdEJwzAMRM8yIhiOCBzIf6ATZYQs0Fm7USW5LQkZoQ9z1p30IePteO5H
AfAK+TMe3cHau9istVbVc3cGhF/TGqbJ7xzRgFwWC7wequYhG/lLUscQaHBD
U2My6o9GM911heT6MSIlM7k/p8TJjS2c0d5JIweO
"],
Association["Book" -> 9, "Theorem" -> 2] -> CompressedData["
1:eJzlUUEKwCAMixURoWziYfd9aU/YB/bW/Wg2OlD2hAVJk7Rgxf28jtMBuI3+
hlKBrRRZl+C9D2FsLoDoa1JCjLVyJBhUc1YDtTIykYaE3IagCprmtevO1qSb
VyDmjxFxzOT7GmeHGxu5escD94oG+w==
"],
Association["Book" -> 9, "Theorem" -> 3] -> CompressedData["
1:eJzlkdENwyAMRA8DyiE3H8lHfvKVjtQRskBn7Ua1TVM1ygh9QsfdGSEhtv35
2BOAl8vfsa4blvsi81RyzqX8ziZAbkdoDcNge60hBjmO6pjvWtVKNvLbhPZD
oMICtSqD7j/qw0hx/5nzx4ik6OT6mOSL7tSTUt/lNAar
"],
Association["Book" -> 9, "Theorem" -> 4] -> CompressedData["
1:eJzlUdsJgDAMvKYt5iOCgv74I365jyN0AWd1I5P4QHEEj3C9u4SS0qmsSwkA
NqP/YR7RDT21TYoxpvRsNQDJZZhRVXrm7KRgrmsxqD44i4aGO3E+hsACNSxZ
riHTJ1vTnd//xvtjiIJn9H1LsGJTtnYQlh3X9gas
"],
Association["Book" -> 9, "Theorem" -> 5] -> CompressedData["
1:eJzlUUEKgDAMy7oNe6gwQS9exC/5BD/gW/2Rbaei+ARDyZK0jI7N67asAcBu
9ENM6MeBupJijCk9OwUguQwzmkbPnJ0UzG0rBtWVs2houBPnOgQWqGHJcg2Z
Ptma7vz+N94fQxQ8o+9TghWbsrWDsBy2JAaF
"],
Association["Book" -> 9, "Theorem" -> 6] -> CompressedData["
1:eJzlUcENgCAMLAVCHyXBxI8PH67kCCzgrG5kW8RIHMFLc9xdG1LCVo+9OgA4
lX6JeV1wKsF7H8I7LwDI3RBBSnLGaCQgypkVohtHllDxJMZtCIhBDHHkPqT6
Zm2as/tHjB+D6CzD70OcFqnStR0TX6FTBm0=
"],
Association["Book" -> 9, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 8] -> CompressedData["
1:eJzlkdEJgDAMRNO0RXoQ/FE/9MuVHMEFnNWNTFIVxRF8lOvdpRRK53Vb1kBE
u8k/GTqexhRjTOlZj0TcX6EUahrdc3ZRgLYVQ33VLFqiAHfjWg8RhDRAssCp
/lQbevL737w/hjl4x993BFswJ5YEcgDJ6QbG
"],
Association["Book" -> 9, "Theorem" -> 9] -> CompressedData["
1:eJzlkdENgCAMREuBeKQxwT9/XckRXMBZ3ci2qJE4ghfyuDsIgbBs+7oFIjoM
P9XMU00xxpTebSViuUMpNAw65+xQAeMoJvWNWbREAZ7G2TYRhDRAssDV/EVb
9OTn9+o/hjl4x99nBBswZ9cOAjkBaIUGGg==
"],
Association["Book" -> 9, "Theorem" -> 10] -> CompressedData["
1:eJzlkYsNgCAMRMun4UIanMGVHMEFnNWNbIsYiSP4Qo67oyEhrPux7YGITpO/
EpeWU0o5v8umfR0BoFJ0Z3ZRgFrFUN+VRUvjaVz7EEFIA4RlDJm/1Q49+f0z
88fEGLyL31cEWzAnlgRyAVgtBhU=
"],
Association["Book" -> 9, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 12] -> CompressedData["
1:eJzlkesNgCAMhMtDjvvtArqSI7iAs7qRfagJcQQv5KN3bQiEdT+2PYnIafiv
ljqVUusQieT5MaT0rntrDhXAkNbBRg1B4E2cMSSgqAGbDpiivmlNd37+qPFj
ck6e5e8bki34bc0RvABNygXg
"],
Association["Book" -> 9, "Theorem" -> 13] -> CompressedData["
1:eJzlkd0NgCAMhEuhudwMPrmAwziCCzirG9kWNRJH8As5ekdD+Jm3fd2KiBwh
P6a1Wlt7P8IiotNtSAF8NktxAHa87mr0EASeJLU3CShuQPOGoNeXxmK63H9k
/BjVkpl+r1BiIE8bjuAJLwAFrQ==
"],
Association["Book" -> 9, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGMuBkYREVRRZgY2BgYoZxmJkZWFkhNIggHTCAEV55
KAMdoEYMExMjWIwJ0weMIATWDyIYgWYBAGEgA/8=
"],
Association["Book" -> 9, "Theorem" -> 15] -> CompressedData["
1:eJzlj7ENAzEMAyWKpv/xRZoAqbPSj/ALZNZsFMpdikyQs0FLoi3Bz+t1XhkR
75a/ppL8aUqRiT7nHAVwL+vicRdQknZKx9F76wqbGnRYTgrEJnFjLVRdsYkl
ROdmelpmRQJjBCrcKxSOCJFwo17rbX7Bm6f4F+2lbzM/o8cFAA==
"],
Association["Book" -> 9, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGNuDm5kbmsgAxPFCYmRlYWSE0iCAdMIARXnkogzLA
jCCYmQFFogPT
"],
Association["Book" -> 9, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGOODiQuaxADE8UJiZGVhZITSIIB0wgBFeeSiDMsCM
IJiZATr7A8Y=
"],
Association["Book" -> 9, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGOpBE5rAxMDAxwzjMzAysrBAaRJAOGMAIrzyUgQ5Q
I4aJiREsxoTpekYQAusHEYxAswBFMwPd
"],
Association["Book" -> 9, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARJgY2BgYoZxmJkZWFkhNIggHTCAEV55KAMdoEYM
ExMjWIwJ08GMIATWDyIYgWYBADDjA8Q=
"],
Association["Book" -> 9, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQMjI4RkHA7hAQCZkQKA
"],
Association["Book" -> 9, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARQMk8AAAJWpAns=
"],
Association["Book" -> 9, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQwwMzMPtBOoAACbzwKD
"],
Association["Book" -> 9, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQgwMg6XsAAAlz0CfQ==
"],
Association["Book" -> 9, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARgwDpewAACWcwJ8
"],
Association["Book" -> 9, "Theorem" -> 26] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQQMl7AAAJWqAns=
"],
Association["Book" -> 9, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARwwMw+0C6gAAJl9AoA=
"],
Association["Book" -> 9, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQKwDLQDqAAAl/ICfg==
"],
Association["Book" -> 9, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 32] -> CompressedData["
1:eJztkd0JgDAMhNNAOG4Gn7qSI3QBZ3Uj86NCcAU/yvUuCSXQuY59DRE5Q346
uj2OFMBvsxQHYOG+1OhFEHgrqTUkoHgAzQeC8rdGM1O+3+kfozqypt9tRxzk
tpEIXvkBBWg=
"],
Association["Book" -> 9, "Theorem" -> 33] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 34] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARpgHWgHUAYAmJ0Cfw==
"],
Association["Book" -> 9, "Theorem" -> 36] -> CompressedData["
1:eJztUckJwDAM86EM0pU6QhborN2okepPCNkgwghbGMngqz93dzN7SQc7ACyz
TNEA0BoI9ZCUmBXxL8mBQ+1UXyz7lMkSPT8mwqXFeqOzoGs5jYwPQ4QD9Q==
"],
Association["Book" -> 10, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGASZgHMIBAwCWWQJ8
"],
Association["Book" -> 10, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARbANNAOIB8AAJZYAnw=
"],
Association["Book" -> 10, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAVbAzMzNCAYMDIzkAgYwwisPY2EFLEDMxsAANgbE
YWRiYmBiApIwXUA+CAAlWVggKhgZAdrxAzA=
"],
Association["Book" -> 10, "Theorem" -> 6] -> CompressedData["
1:eJztkdEJAzEMQy3bVTjCfXWCrtQRboHO2o0q5ejP0RH6IALJwgnkcbyeByLi
bfnzm3uS+5wdMc0wZHcVAHmpI4xe1OYkh7VuMDOIUIkYOEuZifwmHsopUvPC
+THUaTtgW7uqoiqrmIvQUzxlUCtV960fqYEEyw==
"],
Association["Book" -> 10, "Theorem" -> 7] -> CompressedData["
1:eJztkdENwyAMRO847AYzRVfqCFkgs3aj2CRfkbpBn8QJni2DxHs/PjsBfCv+
/KC5zTkFRIwxvDDrXSIZ4Zml6H3RtjKpMmS1ZcCINEbn1bT0bVTFm/G8+/oY
z9XrRG7wbJcgNcnaAvmUqhr8lWVf805/MgR/
"],
Association["Book" -> 10, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAS7ACAYwmgzAAEZ45WEsrIAFiNnADmFgBHEYmZgY
mJiAJEwXkA92KAMLCwtEBSMjAM7BAx8=
"],
Association["Book" -> 10, "Theorem" -> 9] -> CompressedData["
1:eJztzdEJAjEMBuD0mjSJnq1JFeHgPERwhQPHcIB7cAFndSOrPruB38MfCPnJ
6f643QMAPN/x99PSIW4ARHLuh1L2dZoul93O3UWqu9XG6jjPyzwLvzft0sz6
vngbzJOz13y0atcPlsHVS5m8+GY0bgUXVc3tWYwdhC4QQSTIXUCMGgQTEkUi
JKUQq6EmTEnwK0VRWfEZnPstKnI+rF8zFQ0Q
"],
Association["Book" -> 10, "Theorem" -> 10] -> CompressedData["
1:eJztzdEJAjEMBuC0TdpEewlnEUFFq+IQBafw2adbwFndyJ4+u4EfJIGQn5ym
531yAPCa299vHlEBmFXz3mxdar2ex9HMRIqZlk7LtrVHa5zmTb/sch6sD07V
khU9atHbR+KdSY/XXsNBUw8Yi0h/AiF4cN4RQSBQ7xCDOMaIRIEISciFMqJE
jJHxKwYWXqQLrFIeUDAtN/IGzSoMYg==
"],
Association["Book" -> 10, "Theorem" -> 11] -> CompressedData["
1:eJztkcERwyAMBE8+kDQyjwwdpCWX4AZSazqyRPzKIxVkB25gJQ0PnufrOAXA
u+LPDyIc2GPO6YVZa72THMMzS9FVteWKMqkyutWRA0akMTp1sfRtehVv5ve7
n4/R3K1uIg+oQFgjGxnbAhSpqkFNme3ZwAvbCAVU
"],
Association["Book" -> 10, "Theorem" -> 12] -> CompressedData["
1:eJztkTEOwkAMBNdxyGkV3J4CbsilzWt4Qj7AW/kRdpKKghcw0lnavZFceN5e
z00AvHP8+cXaA8tC0hMzchwjteZnR7/u3B7ZVM853Zk0GBGS0XlItYZyNlN+
RqoBv9ceh7nE6zOJEEUgqlDtVIduByqSrqEMJQxIbP0A6XYJlA==
"],
Association["Book" -> 10, "Theorem" -> 13] -> CompressedData["
1:eJztkcENwkAMBNcYcnbwPU8ByxKKriNKSAPUSkf4kh8PKmAeK3m90j523V7P
jQC8h/z5yRnoq6qGe4SZ6jyLSO+RGonEtVar9fYYTnNPXe4y6DCBhJuE1J3W
MiKejssynnm1RL9bj2EuRz+ISFEIxAzmE/N02gETjayhTEVQQNn6AbnxCTw=
"],
Association["Book" -> 10, "Theorem" -> 14] -> CompressedData["
1:eJztjcENAkEIRWGHAYa/TlbjTS/GmzdbsYRtwFrtSGYasAEfyQt8SLjt79fO
RPQZ+vOL1twdwIrez8dt8wgzpDNDKgZWMXNLP4YiXLpLIE8xTwFtB7fc9Eye
Y+kt7Hq/eH5hZsqqlUgIOSy0skpkXhYp6kLlFNYkKTJhVdGq7rRqSPYQK1/J
xggD
"],
Association["Book" -> 10, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 17] -> CompressedData["
1:eJzt0bERwjAMBVDJcSLZ/iI+cmlScDgcaViEmhGyALOyEXYWYAFeodP9X6hQ
2d+vnYno08bfT895PsVtizpN3o+jmeWsZkkr01EkiJRHS5ZSgKTXuiKdLZtB
SzaFHi4Fdse6ZtygrUTBEoLO9YhzTPUfGomFQMyOHQ2qQ9dJ36tITxK8eOZW
HTp2SAmYSIYB3nuNCF+7kgnv
"],
Association["Book" -> 10, "Theorem" -> 18] -> CompressedData["
1:eJzt0bERgzAMhWHJGOuBbRmcQMGlCOZScNkmI7BAZs1GARbIAvkKNX/xCs3b
+7UxEX2O8/fbMKhf1xbjaG3OXdf1PVKK2CX0Io3I/ETSOM1FNUrZo/eXmFNU
LDlBcbqVkFZdSqcPlSP6e5iAZtg3jGHa/4GWWCgQs2FDDnBVJXUNkZqksWKZ
j3Sq2ATvQ7iSOBettfARX7j8CgM=
"],
Association["Book" -> 10, "Theorem" -> 19] -> CompressedData["
1:eJztjcsRwyAMRBEskgCDnM94JscU4iZSghtIrekowhWkgLzDO2h3Vs/j/Too
hPCZ+vMD+731fjFVEWYA62puc2AyRhujXOeFW3OXism6KBZYU9hZNVNPO3pX
t84QDczCu79IKYVEJBJiDjeimGIl5SaAclbumVQgIOcUUUJ82Ni2GrT4ckWJ
oC+tuAfj
"],
Association["Book" -> 10, "Theorem" -> 20] -> CompressedData["
1:eJztjdERAiEMRAksSYCDMOrcjJ92Yg2WcA1Yqx0ZrgIL8H28j+zO5nG8XweF
ED5Lf37h1nqfpirCDGBOc5sDkzHaGOWyLtyau1Qs5qbYYE1hZ9VMPe3oXd26
QjQwCz/9Q0opJCKREHO4EsUUKyk3AZSzcs+kAgE5p4gS4t3GvtegxZcrSgR9
AYU3B6g=
"],
Association["Book" -> 10, "Theorem" -> 21] -> CompressedData["
1:eJztjbsBwjAMRGX7cpZt5DhQUFBRsg4jZAFmZSPksAAD8IpX3Olz31/PPYjI
e+rPT2xmo6vmTAIYo7u7g55tUraZsDV3qZicu8L7dvhAvT3BTGHQGaOBzHz4
AyBKDIkqoNxCWJhqUlrhnLjSGKhcMpJvpS+IF+tjVGmrX64oEeEDejwHug==
"],
Association["Book" -> 10, "Theorem" -> 22] -> CompressedData["
1:eJztjMsNwjAQRP3bZOP1xqDYKHADJJQzEoGAfaEESkgD1EpHGCqgAJ5G7zAj
zXZ+PmYphHh99Oc3pumeQ2D2nh15n4pTTtmlLnab2NV4K80wnorjsYhogYGR
0hg4U9+vSipqy3I5B75SDITERMPusPfl3xglpJLGCFWJpZIalJWoEQA0gKka
kJqsaREQHXxRNTTOEq6Fqx0ba8q/fQNDDw1h
"],
Association["Book" -> 10, "Theorem" -> 23] -> CompressedData["
1:eJzt0b0NwjAQhuHzX2zn7uw4cSJkUoCUjhEAISRKKkbIAszKRiRI9AzAU7zl
13z7+fmYBQC81vz9aN4M01TXpeQUEYecqB+6IXRbXFnsU6TD6RyY8NgmQiQ7
ZsvdpcTM4cOGrm34di3hzs0YLRPTwaNPy7yUyxsCjAGogIUQSkhw2iqldGWs
QwO6rrRXUikjvzx573ZQO4paas/BvwFdhwt4
"],
Association["Book" -> 10, "Theorem" -> 24] -> CompressedData["
1:eJzt0bsNwkAQRdHZn/czM2uvF1tYKyRInLgEIICEEIkS3AC10hE2EjkFcIIb
vuQd5udjFgDwWvP3q20/jiGU0qaI2KdEXZ/7mHe4stg1NU2nc2TCY06ESLa0
lvN1qDccP2xs24ZvlyHeuSnJMjFNHl1a1qVc3hBgDEAFLIRQQoLTVimlK2Md
GtCh0l5JpYz88uS920NwVGupPUf/Bh/QCxs=
"],
Association["Book" -> 10, "Theorem" -> 25] -> CompressedData["
1:eJztzMsNwjAQBFB/1l5n10s+chy4IAUJBeIeoAdKSAPUSkcYKqAAnkZzmMPM
2/OxaaXU61N/P1v3E1GMEbnvS+3relldGdPQpSH4InU5zeJ4Ou6QmYeQY+Dl
nOTCOacalFYavt9GKTxlCRyFly61bT231ihtNIDSTvVWGzCkg0Wo0HvfeA3o
wBtnDLgvg46JhA6KmihAgBybNxCGCxI=
"],
Association["Book" -> 10, "Theorem" -> 26] -> CompressedData["
1:eJztzD0KwkAQBeCd2Tczm2xi0EIJsbExggcQtLAXA2JhKZha8KzeyHVP4AH8
isf8MLMaX9eRnHPvb/z9zgyJArPpoIiP2+k5GeZda10bynOabA77uorLXSpj
LL2qx+W4aO61ZGaajmOhUiMoPCpD32/Xkr9755jBjr0T5tyCmERIAFE48kTI
4TNiDo2GoqBK0p7EYPwBOT0Kmg==
"],
Association["Book" -> 10, "Theorem" -> 27] -> CompressedData["
1:eJztjDsOwjAQRNf2etefkA0icWzFDVfgFLRAk4IqF6DmmNwII3EBet5II80r
5rg9rpsCgNen/vzA8yDLUiXHGKukEH0Y/I2oI/IuNBN7KUMKUiTNqcN7xRz7
S4mz+3KuLk/jWqcsa8E8c+5kEG7XSiloMQbAQGxDAyrUrnlNzIYYdMcUjDUG
rSVrrUZ0zgYu4IlH1t7tT7s3J0QLZQ==
"],
Association["Book" -> 10, "Theorem" -> 28] -> CompressedData["
1:eJztjDEOwjAMRZ3EsRMX6gKlqUUWrsA12FgYQAy9AGflRgSJC7DzvvSl/4Z/
XJ6XxQHA61N/fmHbm1WdRaTqlCXlId2IVkSZczPSqw1F1HQqU4dLxVn6q0lJ
X86V53H3qHvTu+Fc2DodlNuzcw5aQgAI0LXhAR361Lwn5kAMfsUkIYaAMVKM
0SOmFIUPkIlH9jltTus33R4K+g==
"],
Association["Book" -> 10, "Theorem" -> 29] -> CompressedData["
1:eJztjEEOwjAMBB1iJ6lRgkojFXFAQmYP/Q5nTv0Ab+VHuPAC7sxK3l1b8nV9
3tdARK9t/PmJx7IAUM2AZcdyrzXXmmTbqKqZTWpw23MHI+to2cYPSSYMaK2j
Yp5uDBPoobXij0MI5BIhEhq87KgEZk8hRmYpTLFKKuwlftkOSSQdqUi5SORy
nk9vK4ELLg==
"],
Association["Book" -> 10, "Theorem" -> 30] -> CompressedData["
1:eJztjEEKAjEMRVObNJ3AVKeDgriQCQFrj+MR5gKe1RuZcePave+HD/8nZFmf
jzUAwGuzP7/RWjcbBu6m7CjP45h8aGtEpKlOcjNVFZw7GsuhsU4fEtU+WClz
H+1Y72iNFtmXkv1vCAFcRAAE2cMOKCAm72NEJEaIEonjF1/ERJgqZMxXv+bL
6fwG9UAKzA==
"],
Association["Book" -> 10, "Theorem" -> 31] -> CompressedData["
1:eJztzE0KwjAQBeDEeZPMtPSHpDmAa8GFEkl3uhK69Ai9gOfweN7I2Bu493sw
PHgw+/X5WK0x5v09fz96TcssotOSVRu9aRBhEXiN9+xFxmvufVryfFZKkYpq
GPXSboAYpbRNClqGFKgMOLlu6LA93tVY1E7GWWusYQuSOhAYYDbUeDiuwBsC
aAf2vXGOO3Ysx/7wAWswC6M=
"],
Association["Book" -> 10, "Theorem" -> 32] -> CompressedData["
1:eJztzE0KwjAQBeCJ8yaZaekPSXMA14ILpRJBV9ILeIRewLN6I2Nv4N7vwfDg
wezX13N1RPT+nr9fTctV1aZlNmvsblFVVBEsPeagOt7mPuRlLmfjnLiYxdEu
7QZISUvb5GhlyJHLgJPvhg7b312NQ+1M3jlyJA6sdWAIIELcBHipIBsGeAcJ
PXkvnXjRY3/4AAbnCv4=
"],
Association["Book" -> 10, "Theorem" -> 33] -> CompressedData["
1:eJztzDEKwkAQBdDZP7Mzy67JEQyBHMETiHaCsFhIKklhkyKNhTZ6Ar2bNzKJ
J7D3FX/4fJi6G3LniOg9xd/PmjMQnk22YFaFFCfK4VFnr9ZXOdq9yds1ULzQ
BouDHdLMa7rZMcbFJbSpuKI9+Z0vy8Lmt46cA0AkJBgLAeJ0HMYr7IVgzKai
Kl+kymBWI+95Lyy8Wa4+2S0Pjw==
"],
Association["Book" -> 10, "Theorem" -> 34] -> CompressedData["
1:eJztjDEKwkAQRWdn5u/sZlUQG0mxYOsJPICtQrSQVIH0oofwFp7KGznJDex9
xYf/H/zd+LiMgYg+U/z5nYE51neHCDzRlKKlJEV9dTlZe+9W5vJ0ZG4q98i5
xbXMSFzUfDNL1fpldrm1s/me5tdAITAzkZKyFxLWEF2IqIgpiQkbFDCdIUDY
ZeMGm2k5rPdfIM0NSg==
"],
Association["Book" -> 10, "Theorem" -> 35] -> CompressedData["
1:eJztjTsKwlAQRefd+b3kxUJbSUIQcQGuQxCXkM5KQjoR9+iOnGQJ1p5imMsZ
5g7j4zYmIvos488PADIcJxXRTjbulXvsw2HKrm031RbyegHqHm/JpdXZV5RL
b0/33OdXqULu5e5NU/L6NFFKAIiEBBGIIcnWNhU2JTgjilSjbIHMGMxWU9id
xNF5e/oCY1gMJw==
"],
Association["Book" -> 10, "Theorem" -> 36] -> CompressedData["
1:eJztjEEOwjAMBJ1dO0VKinoliBQCiMdw4wn9AG/tj3Aq8QHOzMFarVdzWd6v
JYjI2s+fX3g2MrXW7rlNtQ61zo/elFrHMc0nj44pjdfzlG/ZNo5Kb1SVHvoz
KQ+llJ0bQ6AEwExAGQCJAlAt+rqjBKOC8BHCF913WYimhk2JDwBsCAk=
"],
Association["Book" -> 10, "Theorem" -> 37] -> CompressedData["
1:eJztjMsNAjEMRP2NkBzB1Su0KAm7N6qhhG2AWukIOyXsmXcY2TOj6cfnfSAA
fFP+nGJjrvuzDxtX9+LeXuksrZnV+xqnmamwcn/cbJhOVuFwRITjyLAKL+5+
iUFEBiRSBWIoRFDijVIRIeIkwhAMpkzEcgwjUMq20g/B8geK
"],
Association["Book" -> 10, "Theorem" -> 38] -> CompressedData["
1:eJztjD0KwkAQhed/s84mlUKIlY1ICntBUtsEYSEXSGflWb2Rmz2CtR+84b2v
mNP6zisCwGc7f37DJOVlnj0fht6GfuevYsb7lDwdb6W6RzZjeU777uFaiWEz
Hk1baUxY2iCX8XrW+pEBiISAGISoTkFCVWRmVQZkrAaZKkgUOgtNRBc1wZJA
X8iACc0=
"],
Association["Book" -> 10, "Theorem" -> 39] -> CompressedData["
1:eJztzD0KAjEQBeDJ/IbE7BHULfYEXkAsrLQJFpJG2H6RLbQXBM/njcyuN7D2
K97weDBtf829A4D3FH8/6rJ5s7WPYaLkX20WtWGVgz27vN8ipgcWb2G0U5yJ
xpudQ1jcfYlpxHKRgzRNsvmhA+cQEYCBsRZAZKd1qJdJGNCITFmVv0CVkEgN
ROjIxLRbbj4qtg5k
"],
Association["Book" -> 10, "Theorem" -> 40] -> CompressedData["
1:eJztjMsJAkEQRHu6u7bno4J4EYVZPBuAEXhdGD3IXjcAxSQMw5zMyNkJwbPv
UFD1oA7T4zI5IvrM8edXCjrgiZiSpuQV+VWCt929rKx/l+HMHHseEcIe19SQ
bpHDzcxnG5ehyq0NVnff/hw5x8xESsq1kLC6rgoRFTElMWGDAqYNAoSrjNVg
My+n9fELecMMNQ==
"],
Association["Book" -> 10, "Theorem" -> 41] -> CompressedData["
1:eJztkbsNwlAMRf29yXs2iD6iQMo+SAxAkQUYgCmomICB2AgnDT0150i2LF3d
xqfldlmYiN7r+PMzgGNGDCtuyHz2Ecf50YfM1/UsjOTwNk64tw1X9MrD06L5
nmPS1jLDvp1aP1Fikk0mI6nFLOA6hMzLQktSVTGVYHPdCZvEwT8kUgim
"],
Association["Book" -> 10, "Theorem" -> 42] -> CompressedData["
1:eJztzLsRwjAQBND77J0kJBOBx0NGwGdogMQ0QODA44AUN0CtdARWCcS8YOd2
g9vPr3FmInov8fe76f4sw6ZrvWvjanSU860vueyu3zPnpO6Kod82j2xVCO5A
Tm4NokPRBJyOl4PVb0okAiFRgkitYGEzNsAMxMq8LKxSsUhce4yJi5mDLcD0
A4B8CVM=
"],
Association["Book" -> 10, "Theorem" -> 43] -> CompressedData["
1:eJztjM0JwlAQhPdndt/G99BTIOTmQSQHC1DBDgQxkALSQGq1I5PXgle/wzAz
MHOcl/fMRPTZ5M8PvKYytn3nfRd5NOThfis599fVltyom2J6tIdntkpKbsCu
cSsIh6IknIfLyeqZEolASJQgUiNY2IzXkRmIlXlrWKXCIrH3iOBi5mBLSPIF
U9kJBw==
"],
Association["Book" -> 10, "Theorem" -> 44] -> CompressedData["
1:eJztjD0KwkAUhN//Zn272oiEWFn5dwUhhQhpVPAIuYBn9UYm7wq2fjDDzBSz
G9+vEQHgM9ufX7iX56ZrrWsX/jDx4/WyKr7tp1g8sxnLrV/XwTXIaV48m1Zp
TFhqktP+fND4YgAiISAGIYoqSKiKzKzKgIyxIFOARGlpqcnooiY4KdEXIJwI
pw==
"],
Association["Book" -> 10, "Theorem" -> 45] -> CompressedData["
1:eJztjLsNwkAQRPczu3f23eEMZJmEBCNRABIENIAlRAEEboBa6QhzLZDygqcZ
jTS7+fWYmYjeX/35idW0Hvow9LG9OdLhci45bU9LTKlVd8X9uumexSohuAOp
cSuIDkUOGMfj3uqVEolASJRMpFawsBkbYA5iZUaVVlgkdh6bhrMtO1tAkA/7
yAh8
"],
Association["Book" -> 10, "Theorem" -> 46] -> CompressedData["
1:eJztkb0NwlAMhP3/sF9iFNHQIMQy1IgmQnRZgEGYjo0waRiAlu+su6uu8Wl5
XBcEgNfH/vyGRe9eJ5Z9drPDcx4143Y5E/bEsObHdpcVtRjYW4tJ3WOLsTff
ZKZ957h+woBAqxAUqIKQjBCEkIVriFegClUfUJQnYqFxp2/JTAf8
"],
Association["Book" -> 10, "Theorem" -> 47] -> CompressedData["
1:eJztjL0NwkAUg9+P/e6SC6FCitJRJRITQINoqGhghCzArGxEcivQ8hWWbck+
Lu/XoiLy2eTPjwzjEOOQ2ydR5utl35XxvNpSGg86HrdDfy+spBQE2ibYIQcc
u4R5Ok2sRy5iBhNzgVmNUFNS1xEJUVfdGnWrqFnuI+esHRlQJtC/vAEH+A==
"],
Association["Book" -> 10, "Theorem" -> 48] -> CompressedData["
1:eJztjMkNwjAURP/u5cvBOLngCAEtceeSBqg1HZGEErjyNHoaaaR5LO/nggCw
7vrzK6VoKWYleY+neq9zq9F7vyhOGX1or9swhy/WsnkMU1S3cRuvllMbGx8/
tIUY96JEIJsRDESAVZgUISixsIjxATCnIO4ZI4mJauAzfQBCLgcZ
"],
Association["Book" -> 10, "Theorem" -> 49] -> CompressedData["
1:eJztzDsOwjAQBND9jWPZOMnaSkE6TsBdOEL6CHFUboSTggvQ8qTZYkba2/Z8
bExE7+P8/WyfX3vMV8Bzq6350gzuc9QCxbrc61r9FGKBASg9uJjCI/I0jehP
RJiEyIRMaSDhs2DtGGY2GDFUcA5faQwpFc4hWN+CFP4AsxwHvg==
"],
Association["Book" -> 10, "Theorem" -> 50] -> CompressedData["
1:eJztzM0NwjAMBWD/PTdNCYqbQ3tlBFZhhN4RYlQ2IuTAAlz5JPvwnuXL8bgd
TESvz/r7Xb0/07IBMUdtLbYwRNSkBYq9Xdd9jcFTgQEofXAyRSTM/RL9hwiT
EJmQKU0kPALWjmFmkxFDBaP4ymfPufDibr1zKfwGcnEHSQ==
"],
Association["Book" -> 10, "Theorem" -> 51] -> CompressedData["
1:eJztzMENAkEIBVBmgQF2BcwYY2J0E+1iE6uwhG3AWu3IUVvw6Dt8Dj+fy/q4
rwUAnu/4+4FlUW2Zoe4RsXHPfkTmlGx+jha3D9FjWq/mjPRTSB+kmln0F4gD
lKEwAzLEUIhQilIlZmQmVi6439FUqdZKXxXVdJQrbHl0EpLpYC/avQkb
"],
Association["Book" -> 10, "Theorem" -> 52] -> CompressedData["
1:eJztzDsOwjAQBND9jWPZOGFtpUg6TsBdOEJ6xFm5EY4LTkDJk2aLGWlvx+tx
MBG9z/P3C8+YN8Bzq6352gzu16gFin291736EGKBASg9uJjCI/KyzOgfRJiE
yIRMaSLhUbB2DDObjBgqGMNXmkNKhXMI1rcghT8w+AbQ
"],
Association["Book" -> 10, "Theorem" -> 53] -> CompressedData["
1:eJztzLsRwkAMBFD99nw+I8byBXZKCbRCCW6AWukIcQEVEPJmpGBXo9v5fJxM
RK/P+vuJuuxAzLH2HnsYItaqDsXR79uxxVCqwwB4Di6miIo5L5EPRJiEyIRM
aSLhEbAmhplNRgwVjOKrXUtrzkspll0R5zfxiQZb
"],
Association["Book" -> 10, "Theorem" -> 54] -> CompressedData["
1:eJzty9sNwlAMA9DEzkPlplBGQEJMwCSM0AWYlY3I7Qx8ciJFlqPc9vdrVxH5
zPX3G8vqrMd1W7NyxlGLuRvrPNaqPDy9McMd9Hm8OO9jnKL/ARGq0AUUaE8X
IFpHeCc1gtqgB1G1RERoqgVAM+cXmxEFXQ==
"],
Association["Book" -> 10, "Theorem" -> 55] -> CompressedData["
1:eJzti70NAmEMQxM7Px9cGqhPSAgQYh1GuAWYlY3IXcEElLziyZbs8/J6Lioi
71V/fsSerNP9UVV57VjTFGRw3I41KjYuRjq/BMs4Z+bouypFAbYpAYh3Jdwj
iO3WhkGh2ruVDnHIXVDDzAFzOj6t+QWb
"],
Association["Book" -> 10, "Theorem" -> 56] -> CompressedData["
1:eJztizEOwlAMQ5PYye9XfjuxMbEg1IEdCXVjZeAIvQBn5Ua0/wyMPMmWbcmn
9f1aVUQ+u/35FcE235eW7XjbYmZFBPhcDtMjvVPLvmQNHzkEwbHwMl/P3v8Q
MaOJQWjWK9XUXQG4QxTaF4V11KxMUYaqSQ/qJscXRCYHFw==
"],
Association["Book" -> 10, "Theorem" -> 57] -> CompressedData["
1:eJztyz0KwkAQBeDZN39h180Zoh7BCwgWNmIhEkQIQqoIoqClp/RGrvEKln7F
Gx6Pmfa3XR+I6PWJv5+Zt2o+NG3062y/XgL5jq7yePE2jdTS0w8xTh7VMeUz
upNutK6zj++BQgBAJCQohQAJVoZyhVUIzuwmZvJFZgxmc1LlrbDwqlm8AT2b
DLY=
"],
Association["Book" -> 10, "Theorem" -> 58] -> CompressedData["
1:eJztizsKwlAURO838178gFgYMAhuwNIdWIrogyDYpbG0dpnuyJu3BktPMTBz
mP34uo1MRJ8p/vyOkhI2z7JE/75eTiJtLw/PufMyq2gz3+UBSFvcFzlkhzNi
T/XNxCwiREYmUUjFuAmhaqowUqjAzR1WIXeVkG0YX0/LcXX4AmLbCjM=
"],
Association["Book" -> 10, "Theorem" -> 59] -> CompressedData["
1:eJztkbsRwlAMBHX62e9JMM49BHZBBBRA4AZogD6gLTpCOKEBQnZndHPJJVq2
22UDEb0+588P6aOf1mcfMh/XM8MTYW2c/d52TLx7DG6p0eyImKW1zNDvgtRP
hEC8C1LiCoAdVZjUykJKEhFW4YCaHBjKMdkbf2gHcA==
"],
Association["Book" -> 10, "Theorem" -> 60] -> CompressedData["
1:eJztjcENwlAMQxPbSX5FYAcG6oURugCzshFBPbAAR56lyJal+H48H4eb2etz
/vyS7lBtHVHrFkqJ3RmXOlmp2FiVKmaGxnLva+v7QDCjxTiM6DLAAXAKFxA4
s4/MfdaUZQFupJRLb1TtBOA=
"],
Association["Book" -> 10, "Theorem" -> 61] -> CompressedData["
1:eJzti8sNAkEMQxPHk8zOT3tdceJMKSAhUcI2QK10xLASHXDkHSw9yz7vz8eu
IvL6xJ+fcl97H1ePXls2D+Ppto2tlYPsHoll8VRZPRlH4qWN6sfVRABC1ITA
VAAKIZEsaNMjKWcF6pdcIi9ZK9znzBl4A+hqBj8=
"],
Association["Book" -> 10, "Theorem" -> 62] -> CompressedData["
1:eJzti7ENwlAMRO3z2U6+f9KjVPTsQYnECFmAWdmID4gNKPOKk57u7rw/7ruK
yPMdB/9l6X29RfaqySKN2/W0bL19iUhnzeHFCjcuzktfKz5PEwEIURMCQwEo
hAQtacPTR69jpD+yZU6zNkQQHkx7Ab5LBeo=
"],
Association["Book" -> 10, "Theorem" -> 63] -> CompressedData["
1:eJztkbENAlEMQxM7CbkjX+gKBkBiEiZA1EiI66ioGZON+FxzC1DyLNmF5cqH
+XmZVUTeX/vzY4737ZC72/mkGqmVQ3vldVwgMlkRnl7pvXxgjNbK1zX7JxQV
LFJxQQ8C0RuD0FbEjDB6qDknmKH2mw9aMgdV
"],
Association["Book" -> 10, "Theorem" -> 64] -> CompressedData["
1:eJztkbsNAkEMRO3xZ/HeYXQiQWRUQ45IEETXALXSEWYTGiDkWRq/xE7mtD4v
KxPR6xN/fs1taxmP6xk8JYe3OLa7Dsz7LNFaXyyi7zgOHpvM9O+xVCdCTBjD
ZIRaYDiYFCwq9UgGVILymdVkgSimvb8BAo8GeA==
"],
Association["Book" -> 10, "Theorem" -> 65] -> CompressedData["
1:eJztkbERwkAMBHU6Sfb79Qy5IxoicE7iBiiAKiiNjhBOaICQ3RndXHCRLvt9
2yEir8/583OWKfN5uyoiMbzNazzagTOWGFN42mh+wljZW2a375b1EwpEDyEm
WgFooIqKeVmwFJJq1A5zDoVpP/sbCOkGgw==
"],
Association["Book" -> 10, "Theorem" -> 66] -> CompressedData["
1:eJzti9kNwkAQQ+fwjCeLBBs6oIzkkxIoIQ1QKx2x2Rr45Ek+JMuP4/06VEQ+
p/35PVfWunYa09hv/dLvmFQyiwATLI69Jdv+3DBfJuLmepbwIQlTKQHU4T5C
YxQEkDERs6jIJbRZpCUKi38BfN0FlQ==
"],
Association["Book" -> 10, "Theorem" -> 67] -> CompressedData["
1:eJzty7ENwlAMBFD7fLbzv/NJjVJRMwg9I2QBZmUjkkiMQMcrTjqd7ra9npuK
yPuIvx+IHHNNFmlcH9dlHe3UIzJYLbxY4cbhvM+X4nkyEYAQNSGwVwAKIUFz
2t6DcFMz16/smVPTjji2YNoHfhMFZg==
"],
Association["Book" -> 10, "Theorem" -> 68] -> CompressedData["
1:eJztizsKwlAUROfN/RmuZgU24hYsLbQTgoWmsk1hFQi4U3fkS1yDnaeYYTjM
bpjuQwHwnuPPL9h35yO5frGPaJ5xbRbMcvRbZo6rPmf50Iu17SaWT0EpJAGF
sg6QWryK2iqmYIiEq7t+gbtQxANm0qmonLaHDx9UClk=
"],
Association["Book" -> 10, "Theorem" -> 69] -> CompressedData["
1:eJzti7ENwlAMRM9nO84PpIjSICEFUTMAE9BGAgqUNgswKxvh/B3oeMVJd093
Xt+PVQB8tvjzE+7zjexOXLyUoz93FW32U3lFtFMsfUl5iDlyb+tFIEISMBiz
QGnSpFA11TBoKMPNPawCd2XKLo2P23IdLl93QAhW
"],
Association["Book" -> 10, "Theorem" -> 70] -> CompressedData["
1:eJztkbERwlAMQy3LNjj+4ehTsRAFA1BkAQbIlGyEk4YJ6HjvzjoVqnxbX48V
IvLez5/f8LwrYqA8z0tseeCMKeoUPqzSL6iFmWOUfWfsn1Ageggx0Q5AA11U
zNuGrZBUoxbMOStM6+ofrWsFwA==
"],
Association["Book" -> 10, "Theorem" -> 71] -> CompressedData["
1:eJztkb0NwmAMRH3nv3yOAKUNFSulT5MFmJWNcGiYgI73JJ+uuMqP47kdEJHX
ef78iA2IKyoy19zjgzHmKDO/eA2/oe6sHGOK70r7JyoQtmeakAKAgS4U87bR
VjpoqglzXUjjvPgbaeQFKw==
"],
Association["Book" -> 10, "Theorem" -> 72] -> CompressedData["
1:eJztkbsNgEAMQxM75PgcSIiGlpUY4RZgVjbigpCYgI5XxEqsuPFWjr2oiJwx
fr5CtZl0pHcLVz5Y5pDcso8Mc2HvKSV7n1g7gUQxuJWCKmqgapggaEQIpAai
Lo04OMetndoLEo8ERQ==
"],
Association["Book" -> 10, "Theorem" -> 73] -> CompressedData["
1:eJztyssNwjAQBNBd7ydeJiiCC0KEGFwSJaQBaqWj2FADt7zDjDSa5/p+rUxE
nx67v6kTKurS8/51m4EFjzKhoPQZM67NqZ1VhYRlOFByOjKrK0vOPoi4Wbgb
u6Y2NsL8qxTjJeJM5gYV9RjzBiIVB3o=
"],
Association["Book" -> 10, "Theorem" -> 74] -> CompressedData["
1:eJztzLERAkEMQ1GJb3tvbyAmZuiIEq4BaqUj1iRUQMYL7MCWbsfzcVjSq8ff
78CdCijmRw6YZEISfWT05rJ+IxBm7DqVznZUiG3rSC4V6cQZ/sKe+3XVqlti
RYzeIFQElQ==
"],
Association["Book" -> 10, "Theorem" -> 75] -> CompressedData["
1:eJztyksKwkAQBNDq/ySKE8E4UZmFR/AqrgR3WQs5qzdy1DO48xU0VdDnebnO
BOD5Pn8/VLWkfJv6/foj4l69lPFxGqdhOWgpflzlIXftlYjQIgIIUhsMJuXW
iNVM1MCdWy8s4vzlbmrhFaFp5xq2vWxeH+YHqg==
"],
Association["Book" -> 10, "Theorem" -> 76] -> CompressedData["
1:eJztzL0JAkEUBOB58/6OXfU6ECzCEswPMZQFrwExNTSyPTvybnsw8wsGBoY5
zPfzLAA+a/z9EltmfcSldB71lddSNs+h1e2b7eZTjONu6FuBCEnAYFwKlCax
ntBU3cBUzfCI8A5mStVImPtkSzvtj1+uewmX
"],
Association["Book" -> 10, "Theorem" -> 77] -> CompressedData["
1:eJztjLERwkAQAyX27t/+gZiYwA25BDdArXTEPQkVOPMGuhnppNfx3g9L+ky5
OBVaQGf9kR0GmZCUvc2kLo96jECYPnRrutvRQizLrGTRIp04w3+w1/GsWc2V
qIrRFw9/BHA=
"],
Association["Book" -> 10, "Theorem" -> 78] -> CompressedData["
1:eJztyrENwlAQA1Cfz/f/KfyIgirFL+ioGYURsgBCYgwahmAgNiJJxQJ0vMKS
ZR/n62U2AO81/n4rapviXjfhrZdnluz52A2dr0m3HMdWtqfBjCQgiLZWyrQM
pMJDYIr1C9yd7hqw7Hu5/Hw4fQAdqgfL
"],
Association["Book" -> 10, "Theorem" -> 79] -> CompressedData["
1:eJztyrENwkAQRNGd2dm9O8uAnJGSgERAD27BkhtwA9RKRxwISiDjBSON9E/b
fdlgZo/X/P3YfJzWffnIcA0tY1RNucaiy/V2znfoZqRodAuyX1BwREBeQv3X
hIge4asdsraKHSPVS4U/AXfNBX4=
"],
Association["Book" -> 10, "Theorem" -> 80] -> CompressedData["
1:eJztyrERhDAMBEDpdJLsMQwZCUNA/tV8CTTwtX5HGPdAxgY3c9Id5+97qoj8
73g9bV+3pQ4lI4Othje2cOMc/MzLxLEzEYAQNQmgVwPUhYTzJv2JQL/SBjUr
U9ZStQ+C9GTaBTe/BNw=
"],
Association["Book" -> 10, "Theorem" -> 81] -> CompressedData["
1:eJztisENwzAMAyWRsuT4UbhIH0H66UoZIQtk1m5UJ52hvx6IAwHytR/briLy
PvXn5zxvy3Thec+sLXuJyp5a18w2P2ZeNxsx6FncTDisEkIKSIAqWRQOd3wZ
UwSzTQqzwnCi2wc/TwT4
"],
Association["Book" -> 10, "Theorem" -> 82] -> CompressedData["
1:eJztkcENwzAUQr8Bo9StfWoGyEoZIR3As3aj2rlkgtz6kEDi/xvb0fcjRcR3
2p/7eXzKCbG8WG0/c11c0TqKW6u+Xjk2YaTA0MwcQCQSeVw0OlEST8ImxOxE
4Q0JbS0/UkIFKA==
"],
Association["Book" -> 10, "Theorem" -> 83] -> CompressedData["
1:eJztysENg0AQQ9EZ2zOzi4iSFjiRQ6qhBBqgVjqCbBE55R2+ZMnLfmy7m9n5
zd8PPGKoyqCmnjGrpaS5tL4/a44TzQDBQCvgnoScHuFShWTekkGQgcGB9sre
mz9RKUaqcAEjiATP
"],
Association["Book" -> 10, "Theorem" -> 84] -> CompressedData["
1:eJztkcENwzAMAylSchHbMdAB8uhKGcELZNZsVLUokA3y6h1EfvjTax77NADn
J/7cQf0SKrX0CO/Rmg+um2odY9U1VP5EMDD9NWH01OCEJ1JeigjRFYsVatCd
7fl4Awl+BFs=
"],
Association["Book" -> 10, "Theorem" -> 85] -> CompressedData["
1:eJztissNAjEMRP1L4tgB1iINcOCAhDhQCiVsAYtSKh0RJGrgxNPMm8uc1udj
RQB4ffTnJ4xtjE3rJVr04y169OtSY8bcbT8PRDyLIkAZGiEzF1ROLMI5laQJ
uZlkmgjRd+piqnfw4gdJYruzvwE7oggP
"],
Association["Book" -> 10, "Theorem" -> 86] -> CompressedData["
1:eJztibsNwkAQRPd7n90DvPI1QECAhAgohRJcgJFLdUccEjUQ8TTzJpjz8nou
CAD7R39+w7pta6nXaNHne/Tot6nGiLnbcfxEPIoiQAkaITNnLKwswkmzFkVu
JokGQvSdOlkpD/DsJ1Gxw8XfDUkHng==
"],
Association["Book" -> 10, "Theorem" -> 87] -> CompressedData["
1:eJztybsVgkAUBND33X37E5bA3MDAhENgJZZAAWirduTDIoi4Z2aSua3v14oA
8N3ndJBt+1h69Nqnvniv85i6x1qrF7+J2IsiQAEqITNHNFYW4aBRTZFrlkCO
6U+I0pjNnlBiGUQlt3v5AeALBzE=
"],
Association["Book" -> 10, "Theorem" -> 88] -> CompressedData["
1:eJzticsNQjEMBP1NHDvAs0gDHDggIQ6UQgmvABCl0hFBogZOjHZnD3tYH7cV
AeD10Z9f8bxbO2XPsb/kyHFeWs54hG/nS8SzKAJUoBMyc0VjZREuWtUUubsU
mgjRd9riZleIGjtR8c0x3rMTBr8=
"],
Association["Book" -> 10, "Theorem" -> 89] -> CompressedData["
1:eJzticsNAjEMRP1NHDuwa5EGOHBAQhwohRK2AKiVjggSNXDiaebNYY7b874h
ALw++vMzHtbO2XMcrjlyXNaWMx7h+3kS8SyKABXohMxc0VhZhItWNUXuLoUm
QvSdtrrZDaLGIiq+O8Ubhg0GTg==
"],
Association["Book" -> 10, "Theorem" -> 90] -> CompressedData["
1:eJztybsRAkEMA1Dbsne9P7i94HICAhKGgEoo4RqgVjrCUAQRbyQlOu3Px85E
9PrM3+94ucw+13mLbtelzIiP0Q/xiSDKqiSJujCAzA6DKpJlc2P0qkkC5EtF
ylLd79RyO6ppHef2BlvFBeU=
"],
Association["Book" -> 10, "Theorem" -> 91] -> CompressedData["
1:eJzty7ENgEAMQ9HEdoKuoWADVmIEFmBWNsJXsQEVX7noSdHt53WcGRH3XH8f
Vt2SX1OLzK21jjHKJyCCGawADSSQJpzZE0lQ+eY/VZCUZXmahQfbqAOx
"],
Association["Book" -> 10, "Theorem" -> 92] -> CompressedData["
1:eJzt0bEVwjAMBFCdopPtF9tKXgpqRoIRskBmZSNEwQpU/OKau+7u5/U8ISKv
T/z90i3GPI4W+6x14+yPEaUUzwbINxSkwKQpNIFGZYaz0sV8ccsdFF/dGH0I
1cdiVtdoby3RBP0=
"],
Association["Book" -> 10, "Theorem" -> 93] -> CompressedData["
1:eJztidEJwkAQRGd3du7MfQSSEySiQtB0kEosIQ1Yqx15AWvwyzcw8Gbm7fXc
DMB7rz8/5d5NdVzmYeof1zhfdOvqWEs7zAwtJEDkJo6w8EPbPSSG4CWr0En/
QiqUU0UKnVJkHdfhA0+yBZw=
"],
Association["Book" -> 10, "Theorem" -> 94] -> CompressedData["
1:eJzticENglAQBd++fbufgERKwC4sghMXThqCBXigAzu0I78U4ck5TDKZy/ac
NwPw/urPbyn3tj29mlvX71wfmnMYzs1xDGYkAUGsAacs6yDlHgKLe8nIzDiA
5HTPAkUsqjWN1w/QgQeO
"],
Association["Book" -> 10, "Theorem" -> 95] -> CompressedData["
1:eJztkcERwkAMAyXbseMcd56QCmiDMighDVArHXFQBC92Rnrs6Kfb+XycBPD6
1J8fM65Hq2PYVjku915mVlOLEPOPCDBQIIUK99VVwyNmELnkIpQ5/aLktree
HW7WVW1tI98cLgTq
"],
Association["Book" -> 10, "Theorem" -> 96] -> CompressedData["
1:eJztib0RQGAQRPf2FjcMApHgC2RynShBA2Z0ojQd+YlUIPKCndn3hmWdFwNw
3PPzNZFHir0qE/deWzRNnT/eYEYSEES7L2W6AqnMM4EhFi/g7nRXiau3cvnU
jSd2rAYl
"],
Association["Book" -> 10, "Theorem" -> 97] -> CompressedData["
1:eJzt0bsNhDAQBNDZD2t7MUYkZCCRkiFRxwVXAg1crXSEjyKIeMFIM+ksx+97
EIDzH6/HfaZh74a5t5JLXtvOSx2Z6xsEM8CQiUiotiaKiFbBFdqwBRZmlRuL
pBBT2uDqRVktj34BQEMFcg==
"],
Association["Book" -> 10, "Theorem" -> 98] -> CompressedData["
1:eJzt0bsRgDAMA1D5E4eEkDuYAApaCkZhhCzArGyEYQgqXqE7q1DjpZ1HIwDX
E7/vzdNexqVaGeqw5ZKqd8z+DYIZYChEJORX6EREXcwKDWyRhVnlxSIpdimt
yJqrsvpgfwMkowUU
"],
Association["Book" -> 10, "Theorem" -> 99] -> CompressedData["
1:eJztiMsJgEAUA/O+uyr4AWEVvViCrViCVw/WakeuWIQXJxAmWfZz2wnA9dTP
B0xpaI9RU/Kpatom5ouIkCMCCGIeDCblbMRqJmrgwq0UFnF+cTe14DOCxt41
WLfWNyyyBUU=
"],
Association["Book" -> 10, "Theorem" -> 100] -> CompressedData["
1:eJzticENg0AQA71e7x5SROgAiSYogT9JAxHwJ62moxw0wYd5WPLMsOyvxQD8
jrm5gubzaL/cVr2z6555OoMZSUAQ7biUqQbS3cPB4l4yMjNOUHVNaqCIWZRP
/fgHb6sGbA==
"],
Association["Book" -> 10, "Theorem" -> 101] -> CompressedData["
1:eJzt0bsRgCAQhOG9BxwwB86YGxgY2Y0l0IC12pFoEyZ+wR9sums/j04Arie/
T9S2VGtefS+epzEwjzcIIQARTkRChKQmIjqkotDIwViYVV4sYilb2lC0NCWN
Pucb/ZwEpQ==
"],
Association["Book" -> 10, "Theorem" -> 102] -> CompressedData["
1:eJztyakNgAAUA9D+thzhCAKFQODQjMIILEDCHCzHRhyGETA80aTtsKzzEgCO
O37fKIuee+ctr+sqfZZABEnAMOOudPg6SFuJwdzM0hckUXIBJ2osa2rHEytC
BUQ=
"],
Association["Book" -> 10, "Theorem" -> 103] -> CompressedData["
1:eJztiMENgDAMAx3qNE2KhJBYgBHgwx6MwALMykYUluDDWTrpPB/nfgiA69HP
RwzBMXyMdVuspYigTRUgokWHLJne/pTIXIg0VbPCUowv8kiz9XCtpkavHjcI
pgTG
"],
Association["Book" -> 10, "Theorem" -> 104] -> CompressedData["
1:eJzth90NQEAYBPf72btDEImQS7woQStK0IBadeREEV7MJpuZ9Tj3QwBcz/18
RfZpjrnp+i6VEhGUmQGGVEKh4lpM1ElzQqvA2tQs6AtJZwwL6GkMHjls7Q3m
8wR2
"],
Association["Book" -> 10, "Theorem" -> 105] -> CompressedData["
1:eJztyrsNgFAMQ1HHcQIVr6ZkBRagp0LUiOItwKxsxGcJGk5h6Uoe6rFWA3A+
8/sM901LltK1bxrMSAKCeAdIWT4/yj0ENu5NRmbGC5LTPVsoYtZdUz9eGe0F
Yg==
"],
Association["Book" -> 10, "Theorem" -> 106] -> CompressedData["
1:eJztzLsVgDAUAlAQXn5Ha2tXcoQs4KxuZFI5go234NDA0a+zE8A94/cdKcuS
ttFtQVRuWBJW0slQKZGlGJKDIYb5ElnbXmtgvnhMKDzJDgO3
"],
Association["Book" -> 10, "Theorem" -> 107] -> CompressedData["
1:eJztiTEOQFAUBPftLn6EKFRKndpRHMEFxFHdyP8qN9CYYpLJzPux7QHgKvr5
kMln6vuufiIQQRIwzChJh/MgXakymMzmBSRRcov8B8tax+UG7K8Ejw==
"],
Association["Book" -> 10, "Theorem" -> 108] -> CompressedData["
1:eJztkcENgDAMAx07CqBW4tUBWIkRugCzshFpP4zAh7NkW/766NfZDcA97OdL
uEWtJd5B+Ylg4JSNlkFxocEJDXy6ECFmX03BRjn3Vh62vwOD
"],
Association["Book" -> 10, "Theorem" -> 109] -> CompressedData["
1:eJzt0bERgDAMA0DLsZyQM2QGVmKELMCsbIQpmIGGL3Qq1Gmf5zEhItcTv09t
o9bqWYB8Q0EKTBaFJtCozHA2upgXt9xB8QrjiBCqRzFrfe03xTADzA==
"],
Association["Book" -> 10, "Theorem" -> 110] -> CompressedData["
1:eJztyUENgDAUA9D+tmPAEoIFbghACRJmAK04gnFBAhfeoWnTpR57DQBni9+3
cilj97RABEnAMKNNOnwfpK1ksDdz94IkSh7gpMmytnm9ALv/A+s=
"],
Association["Book" -> 10, "Theorem" -> 111] -> CompressedData["
1:eJzticsNgCAAQ/sDPOAQruQILOCsbiScHMGLfUmTvh7jOgcB3Kv+fJy+9/Ku
CDCW0MSskCjJ82CsZnkJTkCWtKQi9mbHpeUBsrIDSQ==
"],
Association["Book" -> 10, "Theorem" -> 112] -> CompressedData["
1:eJztkbsNgEAMQ53Yl/tswUosgHQFLbOyEYGGEWh4ki3brZd5rNMAnLf9fM22
t7cwP3FEyqFUh2cUWWQIFYpS5YOREdFGt+GqnrsGL+kkBCg=
"],
Association["Book" -> 10, "Theorem" -> 113] -> CompressedData["
1:eJztkbERgDAMA2VLMQ5MwUoUDJAFmJWNMDSMQMPfve57rePYhgE47/n5nD3f
Zn3iiNKhssMrRTYZQo2ilHwwMiJy7ra4wqVJnRfHfwO5
"],
Association["Book" -> 10, "Theorem" -> 114] -> CompressedData["
1:eJztkcENgDAMA53YDWm3YCVG6ALMykakfBiBDyfZOvnrfZ7HNADXqp/vyVdZ
nzii4lClw0tFNhlCjaK08cHIiMjRbbjS1z78Bq2IA2I=
"],
Association["Book" -> 10, "Theorem" -> 115] -> CompressedData["
1:eJztxLsNgDAMBUA/+yV2goACKRIlKzFCFmBWNuIzBQVX3NaPvUNEzqffN5iZ
GOAummQB1LQi8uBk5BR5TAinE7c3wKjrPLVWJcpAVhYlLsVrBAM=
"],
Association["Book" -> 11, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAAjHh4pAEAlWgCfA==
"],
Association["Book" -> 11, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWABwNhgBMcII/Z4ISK2gEoAlk8CgQ==
"],
Association["Book" -> 11, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSABjAyQ6GBkhPDIBACWJAJ/
"],
Association["Book" -> 11, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAB4swM7MzMjIwMbIwMLMwsbCxsDExAHhcrK1QB
E7oOYPQxMbMwMaFEIwCtXQLu
"],
Association["Book" -> 11, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWABrAzsTExAmp2BgYWZlY2FjYEJGEFcrKxQeSZ0
DUBZJmYWJiaUaAQApooC1Q==
"],
Association["Book" -> 11, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweABXNycjIwMLCwMjDysjEyMDBwsjIxMbGzMQMDA
xMzBzMjAzIQEGIEARAJ1MoIRSBoAscwDHw==
"],
Association["Book" -> 11, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweABwPhgBAIQixHGRUgR1A1WDACXZwKI
"],
Association["Book" -> 11, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSACLMzs7AxsjAyMPKxMQMDMxM7MzsTECARAgpkR
KIECGBgYQbJAjRAmSCUAqt4C9w==
"],
Association["Book" -> 11, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWACwkwsDMxsDIx8rIzMjAyCPCxMzGxsbKysrEws
rEJAcTYWJACMPkYQgFAMDExMLIyMALxeA2o=
"],
Association["Book" -> 11, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaACzIwMzKwMTJysTMxMDBJ8DExMrKzsbGxsDKxs
/OwMDOysSAConJGRiREUi0xAJlAzCyMjALhRA2A=
"],
Association["Book" -> 11, "Theorem" -> 11] -> CompressedData["
1:eJztyrERgDAMQ1HJlo251NzRshIjZIHMykaEhhkoeMVvpKOPsxPA9eT3LTuw
IIJ0muXWjKzMrEhWeM3h5aS0SoKb23w3Cje4wgNz
"],
Association["Book" -> 11, "Theorem" -> 12] -> CompressedData["
1:eJztxLERgEAIBEDuOGB4A2NDW7KEb8Ba7cgxsgUDN9h9nseEmV1Pv89piwAc
ydwWAl1VIwod3sGXA1JLMqeTOVa53beyA4c=
"],
Association["Book" -> 11, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAD4FhhIlc3AJWSAn0=
"],
Association["Book" -> 11, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaADjAzMTKysTCwMTMAI4mRhgQozoatjBioFARRB
AJ5ZAq4=
"],
Association["Book" -> 11, "Theorem" -> 15] -> CompressedData["
1:eJzt0UEBgDAMBMFcrrkkMrCEhBpAK45KX1jgwTzWwB7zOifM7N75fRATcGB0
6XlUkrI1KrxaL7gzSIZxc2XQFrRUA30=
"],
Association["Book" -> 11, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAEFEQMAJUdAns=
"],
Association["Book" -> 11, "Theorem" -> 17] -> CompressedData["
1:eJztxLENgDAMBEC//P6YwiiwAStlhCzArGyEqFiBgivumOeYMLPr6fdFQMjp
GdsitVCoCU0s4uVA1dp7WFY6yR1uN7dCA7A=
"],
Association["Book" -> 11, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAErIzMjIwczEyMzGxsoGhiBAkxMqDHGBMjIxMT
iAaqAAIgCwCe+wK6
"],
Association["Book" -> 11, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAFoPhhZGRE4mEHTEhsAJXhAoE=
"],
Association["Book" -> 11, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAFPLyMzIyMjCzMzOBoYmRghCJkwMTEwsQEFARi
JrAuZgCgwgLO
"],
Association["Book" -> 11, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAFLIyswAhiYWNjYGQEMhiZGRiZGEBsGACymZjZ
mJhAoiAJsCYAng4CxA==
"],
Association["Book" -> 11, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAFjEzACGJmYoJxIQgFMDGxMDExwuRAAACZiAKk
"],
Association["Book" -> 11, "Theorem" -> 23] -> CompressedData["
1:eJztkUERwDAQAoGDTGzUUiTEQLXWUS8u+ugOs4/9cu17bQJ4jn4+jfsjVUQF
slUjI07PYRXUlVCL5UnxBaKhAwU=
"],
Association["Book" -> 11, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAG4kxMTKysXJycnAwcnDxcDAwcLEgAqICRkYkR
FItMQCYDAwszIyMAr2EDNw==
"],
Association["Book" -> 11, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAGXJwsTEx8vLy87Fy8rHzMjLwcrAjAxMjIwcbB
wcHCwMzCzMzMxMbBwsIIALdrA6I=
"],
Association["Book" -> 11, "Theorem" -> 26] -> CompressedData["
1:eJztxDERgEAQA8AkFzJcjwEsIeENoBVHzFdYoPgt9hz3NQjgmS2/dojsJHuC
3qqjT5F220bJktMyXqrtAz8=
"],
Association["Book" -> 11, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAGzExMnOzsbGy87AycLGy8HCzMLCzMcMDOzcHO
ycrAxsHHDFQmyMzKCACt8AOH
"],
Association["Book" -> 11, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAH7OxQBhO6DDD6GJmYGVFjEQCYTwKT
"],
Association["Book" -> 11, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAHctBoYmFkRI0wII+ZlYWZmYkBLMMIEmAAAJzw
Aro=
"],
Association["Book" -> 11, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVABLAyMqBEG5DGzsjAzMwElGEFckDQAlzoCmg==
"],
Association["Book" -> 11, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAH8hJi7EISDGYsjLI8HEDAxgEGTMzMLMwsLMzM
DExMLExMjCy8rCyMAMMhA/c=
"],
Association["Book" -> 11, "Theorem" -> 32] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAABpqsnAaM3EzMHILcCMDExsbMxMLMzMTAxARi
sHKysTIBAMKeA/4=
"],
Association["Book" -> 11, "Theorem" -> 33] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAA+mxcnozcTMwcQjw8PNxc3GDAxMbGyszCwsLE
wMzEzMTCwgrkMwEAwGMD9g==
"],
Association["Book" -> 11, "Theorem" -> 34] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAAbNyKjCxMbCzigpyCAmIcYMDEyc7CzMLCysLA
ysTCBGSwsrMxAwCzxwOu
"],
Association["Book" -> 11, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAAnKwMrMyMrCyMCMDMyMjKxMLKyszAxMjMxMrI
xsHIzAAAnUEC4g==
"],
Association["Book" -> 11, "Theorem" -> 36] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAB7AwsrMxc7EwQwAwigAJAwMLKwMnMw8zMxsLO
zMIIAJ/iAww=
"],
Association["Book" -> 11, "Theorem" -> 37] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVABjNxMzBxCPDw83FzcYMDExsbKzMLCwsTAzMTM
xMLCCuQzAQCrCANu
"],
Association["Book" -> 11, "Theorem" -> 38] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZABTAyMTCxIgImBgZGRiREYi4wMIJKBiYWJCQCb
ewLE
"],
Association["Book" -> 11, "Theorem" -> 39] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdABLIzyXGwIwMTIyMLMwsLMzMDExMLExMjCy8rC
CACkXgMr
"],
Association["Book" -> 12, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRACeuxs3BzcnFwcHGwcHBzM7KwsbKxsbGwMfOzc
rGxcHNxM7IwArGMDlg==
"],
Association["Book" -> 12, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVACzCyiQqLCIjwcXBwcHGzcnEwsDMzMTAwsjFxM
zGzszExMjACqjgNr
"],
Association["Book" -> 12, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZACvBwcHOxQzMTIyMzCwszMysDMxsbExMgiwMrK
CACiaQMq
"],
Association["Book" -> 12, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAC2hraSnJKSvJKikpMQgLMzEzMrKwMzMwsrKxM
7BycXKwAw5oEdg==
"],
Association["Book" -> 12, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRADqdk+Hs622rbW1ozK0iABJkYGFhYmZgZmJmYW
ViYA5WkFng==
"],
Association["Book" -> 12, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVADWvKKvq56rs5OjLzCID4TIwMLMxMLAzMTMzMb
IwDKGgSx
"],
Association["Book" -> 12, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZADAZ4udlp2NjaMKjIgLhMjAwsLEzMDMxMzCysT
AM28BNk=
"],
Association["Book" -> 12, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAD9sYmpiZmRozGWiAeEyMDCwsTEwMzEzMrKzMA
wbQEcw==
"],
Association["Book" -> 12, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAEsvIy8oryjPz8IA4TEwMLM5BgZmJmZWMCAKmh
A3Q=
"],
Association["Book" -> 12, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAEcTZx0dGM/AIgNhMTAyMLCyMDMxMzCzMjAMBa
BGY=
"],
Association["Book" -> 12, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAEVuWZGYx8/CAmExMDIyszIwMzEzMLMyMAuy4E
OA==
"],
Association["Book" -> 12, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAE8gryjHx8IBYTEwMjKzMDAzMTMysTMwCgVwMU
"],
Association["Book" -> 12, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAFaWmMfPwgBhMTAyMrMyMDMxMzCzMjAKnrA4I=
"],
Association["Book" -> 12, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAFeYx8/CCaiYmBkZWZgYGZiZmFmREAoWkDIw==
"],
Association["Book" -> 12, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAFjHz8IIqJiYGRlZmRgZmJmYWZEQCX/QK2
"],
Association["Book" -> 12, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAFjIwgxMDIwMTMxMTEwATkMgAAlasCjg==
"],
Association["Book" -> 12, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAGBUDMyMjIwMrCxMDAxMLGwcQCAJ4lAxI=
"],
Association["Book" -> 12, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAHjIyMDKwsTAwMTCxsHEwsAJXVAqI=
"],
Association["Book" -> 13, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAGnGw6GqwMrKyczCysrNyMzAwAnDoDFQ==
"],
Association["Book" -> 13, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAGbJycTIysLEzMTIzMbIzMDACXOgKz
"],
Association["Book" -> 13, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAHnJysDMwszMwsjCxsjMwMAJb7ArE=
"],
Association["Book" -> 13, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAHeqwMbKyczCysrLyMzAwAmRQC4w==
"],
Association["Book" -> 13, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAHrAxsLJzMLKysXIzMDACWegKx
"],
Association["Book" -> 13, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTAAHCycoszMLGzCdgIAl3MDFQ==
"],
Association["Book" -> 13, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXACjAwAlOQCew==
"],
Association["Book" -> 13, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXAAnOz8LCwsbOwsrACWdQK7
"],
Association["Book" -> 13, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbAAcuycwixsrCwsAJcgAtI=
"],
Association["Book" -> 13, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfAAbBx8rBxsLKwAlfYCsg==
"],
Association["Book" -> 13, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTABTCzMTLncTgCWvgM/
"],
Association["Book" -> 13, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXABPNxsLCzMAJWQAqI=
"],
Association["Book" -> 13, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbABzBxcLGwAlT0CmQ==
"],
Association["Book" -> 13, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfABHCzsDACVHAKN
"],
Association["Book" -> 13, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTACLKwMAJT4AoM=
"],
Association["Book" -> 13, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXAC3EEAlUoC1w==
"],
Association["Book" -> 13, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbACGgCVCgKi
"],
Association["Book" -> 13, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"]],
SelectWithContents->True,
Selectable->False], "}"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"dataA", "=",
RowBox[{
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "[", "\"\<Book\>\"", "]"}],
"\[Rule]", " ",
RowBox[{"N", "[",
RowBox[{"Mean", "[",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "]"}], "]"}]}], "&"}], "/@",
"res"}]}], ",", "vals", ",", "acc", ",", "xval"}], "}"}], ",",
"\[IndentingNewLine]",
RowBox[{
RowBox[{"vals", "=",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}]}], ";",
RowBox[{"acc", "=",
RowBox[{"Association", "[",
RowBox[{"MapIndexed", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"First", "[", "#2", "]"}], "\[Rule]", " ", "#1"}],
"&"}], ",",
RowBox[{"Accumulate", "[",
RowBox[{"Values", "[",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}], "]"}], "]"}]}],
"]"}], "]"}]}], ";", "\[IndentingNewLine]",
RowBox[{"xval", "=",
RowBox[{"Association", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "-",
RowBox[{
RowBox[{"vals", "[",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}], "/", "2"}]}],
")"}]}], "&"}], "/@",
RowBox[{"Normal", "[", "acc", "]"}]}], "]"}]}], ";",
RowBox[{"Show", "[",
RowBox[{"{",
RowBox[{
RowBox[{"ListLinePlot", "[",
RowBox[{
RowBox[{"Values", "[", "dataA", "]"}], ",",
RowBox[{"Axes", "\[Rule]",
RowBox[{"{",
RowBox[{"False", ",", "True"}], "}"}]}], ",",
RowBox[{"Filling", "\[Rule]", "Axis"}], ",",
RowBox[{"Frame", "\[Rule]", " ", "True"}], ",",
RowBox[{"FrameLabel", "\[Rule]",
RowBox[{"{",
RowBox[{
"\"\<theorems by book\>\"", ",",
"\"\<average shortening\>\""}], "}"}]}], ",",
RowBox[{"FrameTicks", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"True", ",", "False"}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], ",",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"{",
RowBox[{"0", ",", "0"}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Normal", "[", "xval", "]"}]}], ",", "False"}],
"}"}]}], "}"}]}], ",",
RowBox[{"ColorFunctionScaling", "\[Rule]", "False"}], ",",
RowBox[{"ColorFunction", "\[Rule]", " ",
RowBox[{"Function", "[",
RowBox[{
RowBox[{"{",
RowBox[{"x", ",", "y"}], "}"}], ",",
RowBox[{"Piecewise", "[",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "6", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "6", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "10", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "10", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "13", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "13", "]"}]}]}], "}"}]}], "}"}],
"]"}]}], "]"}]}]}], " ", "]"}], ",",
RowBox[{"Graphics", "[",
RowBox[{"{",
RowBox[{
RowBox[{"GrayLevel", "[", "0.5", "]"}], ",",
RowBox[{"Line", "[",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"#", ",",
RowBox[{"-", "5"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{"#", ",", "10"}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Values", "[", "acc", "]"}]}], "]"}]}], "}"}],
"]"}]}], "}"}], "]"}]}]}], "]"}]], "Input"]
}, Open ]]
|
The rather unimpressive best result—an average shortening of 7.2—is achieved with 10.33 (which says that it’s possible to come up with numbers x and y such that ![]() and
and ![]() are irrational, while x y and x + y are rational).
are irrational, while x y and x + y are rational).
The maximum shortenings are more impressive—with 10.41 and 10.78 achieving the maximum shortening of 165

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"res", "=",
RowBox[{"{",
InterpretationBox[
DynamicModuleBox[{Typeset`open = False},
TemplateBox[{"Expression", "SequenceIcon",
GridBox[{{
RowBox[{
TagBox["\"Head: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["Sequence", "IconizedItem"]}]}, {
RowBox[{
TagBox["\"Length: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["465", "IconizedItem"]}]}, {
RowBox[{
TagBox["\"Byte count: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["5397840", "IconizedItem"]}]}},
GridBoxAlignment -> {"Columns" -> {{Left}}},
DefaultBaseStyle -> "Column",
GridBoxItemSize -> {
"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}],
Dynamic[Typeset`open]},
"IconizedObject"]],
Sequence[
Association["Book" -> 1, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 1, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIYWBgYmRnBLBoBFihNSztGNkAOWQCuDgKK
"],
Association["Book" -> 1, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKAgIWNhYWRbMDAQEABO5SG2cGAC2A1HdUq6gL8BoLt
I+w9agCI5xlgPibVSuTYAwDLWQPN
"],
Association["Book" -> 1, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKAgJERyhgFQx8AAJpGAn0=
"],
Association["Book" -> 1, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJAgJ2Tg5kJCBmZGJABEyoXC4ApwKuSHUozI+sYBfgB
M7mKAf41Ar4=
"],
Association["Book" -> 1, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLAgJWFgXaAHUoz4lU1CsgHyCELALB1Aow=
"],
Association["Book" -> 1, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIggJuVBQiZWRjhQoyMjCwsYAoqhFCMACwwmgVZFKgD
AiGAHVkxMxZTRgEDOKAZIGENxqwMMBY8SrBFAKYMAC5tAuc=
"],
Association["Book" -> 1, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKggJ0VBNmYmBihgImJiY0NTEGF4DJIgBWIGRiANCuy
KFAHBEIAO5JiRhZGJEvRABYLGFEEceokE+A3EGwfI3ZnURkALQKGMwM4rBmY
gJ5mAgcaKATh4Y81AjBlAC8MBBg=
"],
Association["Book" -> 1, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJggIOLjZOdgxEuxMjIyMEBpqBCyIphgAVGsyCLAnVA
IAQwQWlWEMGGxZRRwAAOaAZIWIMxFwOMBY8SbBEAAUxIbABHwQL7
"],
Association["Book" -> 1, "Theorem" -> 10] -> CompressedData["
1:eJydUUESgCAIXJjk0C/6Uk/wA721H4WIpJN1aB1hZhEWcMvHngnAWUxAVlkS
MzmYOSVzTkWkg+gF1EvPakY9kYj6uKgMmiMmAoTevaf+w3dB06NnW7VT7xdT
vo0Dum0bJBirHYPpnmG7BivJ0lYe+59+gEfgjWi9CwMwA+M=
"],
Association["Book" -> 1, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIQgJWXm4cRLsTIyMjDA6agQqiKIYAFRrMgiwJ1QCAE
MMHMR9YxCtAAKJwhYQ3GfAwwFjxKsEUABDAhsQFG6wL+
"],
Association["Book" -> 1, "Theorem" -> 12] -> CompressedData["
1:eJydUMERwzAIkxDpHlmpI2SBzNqNGsBpyKXNo7qz8XFCMpqX9bkQwCuuhkku
WYCkJPcsYgAC2BETj5wj3D8iW18MJnZ1GzU5wm+c1FtFmZE3s3/hXvDwq3Wb
f61f/8NI4yJWzSTiiOybfTy21PNkRLQp6BZh2p6f4YqRUeu8AY+BA1g=
"],
Association["Book" -> 1, "Theorem" -> 13] -> CompressedData["
1:eJy9kNENgCAMRHstfsIOruQILuCsbmSvoBKNfhlfCD2a0oOO8zLNEJGVW08u
Ztows5wVlAg8yJUEJhVpFxHMr0FFW5HGAgbqdOtxgg5hoxqrDvErvd+79xcP
88m3LxrtCifIk8//yeVIaJfcAMoOA2g=
"],
Association["Book" -> 1, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJQAB8zIxMUMDMz8vAwMTACAUQOQzEQsIBlmRhZWODK
gICZiZGJAQQhAEazgnVgMWUUAAEwvBkggQjGfKDwA7PgAYstAiCACYkNAFr6
AxM=
"],
Association["Book" -> 1, "Theorem" -> 15] -> CompressedData["
1:eJydUMENgCAM7NHCkx1cyRFYwFndyFJAUYMhHklTyvVabknbmkBEew53BJaK
EBCjgNk5GBxI+agodGHmHKUk9S149sin8Go/vOaQ98wTTfbSL1dq9XHrP8wJ
4rGPlSa0MumThz5Rv4ltkhmp1ov9XP0fTUDbxHXFAxB0A6o=
"],
Association["Book" -> 1, "Theorem" -> 16] -> CompressedData["
1:eJydUdsNwyAMvGKcWBBF+ckAXakjZIHO2o3qAyTSJs1HT8jY3Pkhc9+ej+0G
4EXzhWWacs5mNq+zqgldIWBA2IPqUVUBixodQBViTTFJQmolXSk8bkD6J2QH
D0Kot7Ssy9y/EC7Z3o+T0PbE4pctBLIMD8XqYxGir+ysPR0zRdkmFm+t0WSE
OmHD0FTxMGD7kY/HN8qGBSc=
"],
Association["Book" -> 1, "Theorem" -> 17] -> CompressedData["
1:eJytUMkNAjEMHF/JWvBgP/xpiRK2AWqlI+yEVWDJk4mUxNbYY89te9w3AvDM
6wj3pSxmdlovZsJn9yIJcgJ9IsmVRAAjU+ZIaPAYWCvHQX13jIwCEicZE8kd
WZ1IOURDin+8UdmqIvgzZvsPDD2iXIsGva/fXEhXOMOfZj3ZiBiWzeTzU4rA
muQ1nGA1VqSnrrrPcxSQPsJ32xf6SwRy
"],
Association["Book" -> 1, "Theorem" -> 18] -> CompressedData["
1:eJydUcENwzAIvMOBGsmVukJX6ghZoLN2oxocKZbS5NGTjMEcB8LP9f1aCeAT
5oBH8+bu93YTMbFaTQKoAGcEt5g74IVULcAgoqmqKHQT7C9Mi3TOIRN6QI47
zkhfFf+Dy2mmfjFJ2L0w/dwCIxvhQWw8JhH7yn61D8eMKEnpG+2CLjUV6rKc
TcvtRzAv5gvPEARC
"],
Association["Book" -> 1, "Theorem" -> 19] -> CompressedData["
1:eJydkNkNAyEMRD02GBYtRaSllLANpNZ0FB9SQs6PPCEzAh8Mp+NyPkBEVw/v
zDHHGHNvzE20dxUHHeAVGNJaIxoFULUgUqsAe9UqFRUJxxKQawsfhzqyYL2Y
bafUMUy+Vv4J/7yNefZa9+0vSMtpKXT8Avstp8dn8jAS8fiyNeEubJAqKGzS
FmLIFhm9lNfGS322peXwBoEJBTQ=
"],
Association["Book" -> 1, "Theorem" -> 20] -> CompressedData["
1:eJydUUESwjAIhAViGzvV8Qd+ySf0A77VH7nQquOMenAnISQQyG7Oy/WyqIjc
0nzA8XTofT/tgB6tNY+ENTMv1GJm4GRApJvqPDcIz+DAFGN4IMBaqMFDq9Ke
u2+IyFZrO9BJT1YfLBD+/ep/sJ/RpJbPTd7kb052G5J9WYrAJXL7im5wTzUq
EatyqLRnsj8uJbFhUKGOZjKahGrHKEqZ29qHUEuF359fn2FSVYQaQ+5i6QZJ
"],
Association["Book" -> 1, "Theorem" -> 21] -> CompressedData["
1:eJydUcERwjAMcyQrpL2DHViJEboAs7IRttsCD8oDXezYia2zkutyvy3NzB7p
vuE89z4mAZfh7l0JOumF2kgibJBmXa3N84BJUU1OPEU1iKBCLQdUzJ7ZEaJd
q0lIrthtjQFQftz6H/jzVjlyjJu6Q39K2pHqy6dKUpm+bzd4qPY6JtaXQ5W9
in1vSmG901oyWgRi65Rtb84dMH6OHHF9Bq1YDBHYEw8WBhY=
"],
Association["Book" -> 1, "Theorem" -> 22] -> CompressedData["
1:eJydUdsVQiEMa5u0esXjnwO4kiO4gLO6kaHXx4/6YQ6EQgqFcLpczxc3s9uk
jziOMfabiMO2qljVTGajB5JQU2S2wH0MwICITeY+h9alRYSkyZq6ubtyvha1
qqy1V0HBjGyNAbDy684/wZ+qiptBWZw3ERNPzNc3ywQNNadv9QG9GdnL7dO0
pNNeyfnclF0Nlu6kLbSCL7Ezl80VwRVOSPY3wr0/g9anOCh/7/RtByU=
"],
Association["Book" -> 1, "Theorem" -> 23] -> CompressedData["
1:eJydUclxAzEMoygAXI3XfqSDtJQS3EBqTUcGd51HZuI8Ag2hg5AgUe/3z4/7
iIivpt9xu62FzLcdQK5GoQw9oySBQpERO0Zer8TgzLxIS7s2Oj3n9CFplmaG
hwjkS9O1tlWOBuxY7uMc+xpc28ud/4T+zNo8Alapb2IWvtGvP1hw84NF9grJ
Th/kejkgT3TUrqo1rW9uQfetLRtVzeAYrqcYa46dlxg+FnPyxCCSzB84PyQO
vwQT4wEkUQik
"],
Association["Book" -> 1, "Theorem" -> 24] -> CompressedData["
1:eJydUcERwjAMs2TXoRwHb56sxAgswKxshBQ4eJUHSuo4ZzWSk8vtfr0hIh4O
Gziva5H7rirujJrI+iBJVi1LxGkHjtEEATS59r7HkgsToGiAQ4USKmxqtiAB
L822dFdoC039WmPb7n+o31WX5TbtSZeRaucNda+YAjSycqby6GYx78EkfWod
k5NvTsKcyai5cyKhMSAlFaM1gUMdXUa9ZOcpjvwCfgA/ULxc+eB4AhvDBf8=
"],
Association["Book" -> 1, "Theorem" -> 25] -> CompressedData["
1:eJydUdERQjEIIxDwPe88XcGVHMEFnNWNDFQ/9cO0TenBEaDX++N2h5k9m75h
3+l+LJK+NWQwGZk5BhnuLivNLhv8cCiHAyj3vY5VGekBuMLEIpqMEH2VLCHI
vsqrpYumJ7SVg/Wj3L/A3952q9romjSMUDtvqHtxCNAKxpirz74mKFMH0V1P
6IoJzEAmYF6dTkLbBinJaaUNnPLcbnDJThasUX6A+QB9kK2qRvwF+p8F9Q==
"],
Association["Book" -> 1, "Theorem" -> 26] -> CompressedData["
1:eJydUNsNwyAMPJuXSYUyQ1fqCFmgs3ajcJAqSEn56EkYPw6f8XN7vzYB8KH5
iTWHEDWXkpRAAWQEOSnmDJgL3nsHdCJW86YGOxrVjNBWAsRNFHVADUT6zdPL
s3H/wfT/gx4noT0fNr9tQVhleGnWk42Ic2V38nSWRRGb5IPSdYMJWgslhO88
N+Nf2+6XQgQ8
"],
Association["Book" -> 1, "Theorem" -> 27] -> CompressedData["
1:eJydUVEOwyAIfaC0xCzZfnaAXqlH6AV21t1oPuxil3V+7EURAXmAy/ZYNwHw
pPiNq9mkF3dTAg7IEQyZkxngyXLOqfkVuJdctKDseapFuGoAJA0I9YB6qbni
5G7uYbl/YNx/52MllP1h6DEFoVfkJFkzRiD6yM7oqbgrLChvpM6uM1Q43PfI
vtqX/Uc+jC9qmgQa
"],
Association["Book" -> 1, "Theorem" -> 28] -> CompressedData["
1:eJydUcERwzAIkwBfcsldM0NX6ghZoLN2oyKc9vypH9XDxkggbN/P5+MkgJeW
CVozP/ZtCcE2wki7wKpdoN3RogoySydvgfBg5Ik9K4Ku2Cd+chFkB+tmuWe3
aj+t/Qs2Zy9ac4QB5ECxiEwRdb2RHeoNJSxpVwwyG4N1DTRXdEDP5xnLZW/t
17TJ8vMTX7wBXgIEJA==
"],
Association["Book" -> 1, "Theorem" -> 29] -> CompressedData["
1:eJyVUEESwkAIS4BevfgCv+QT+oG+1R+VgDqd1daanYElwEL2Ni/3mQAeMke4
kuHuVnCCGyhAyOQtojhVyjn7NJJy2Ump4P7Q7H55Q8/IiIYn/2vdv3HuwdIw
Up9FX/rGCQPzjkqmdJboScGl5RP5/3vbWu9G2Ca9ArkiA3o=
"],
Association["Book" -> 1, "Theorem" -> 30] -> CompressedData["
1:eJy1UNsJgEAMS9rerzu4kiPcAs7qRvaBoIjn16VwzYWUlqx93zoBHPEMQZqK
MKHpfo6Y6+kq4t4wq7IqRUjMUticqw12lj373UVc+t+58zB/tSeETBotPkuw
KM/06wZ5EccJSdkDHQ==
"],
Association["Book" -> 1, "Theorem" -> 31] -> CompressedData["
1:eJyVUdtxAzAIA0s8TH/y0wG6UkfIAp01GwWc3PUr6VU2nM/CCPDX9ef7qiJy
G/cen2stflQvW2Z7527LHAsPYwEiQV17h2tf8FLl3AwQaUDvBTDTKFCl8LVo
1S4Pr4FVtUSFRBV6Ax7xZ7n/RL5lj960F5kVZt69PJHTGqzRDZoNeViSQx+H
vdtgnCH4AwFEx5+xDIk4sVNH55I+tihcyjTcBT3QHntnZXRmQkn9xVLN6K84
D0F1V8gdy+EINQ==
"],
Association["Book" -> 1, "Theorem" -> 32] -> CompressedData["
1:eJyVkLtxAzEMRPFbLInjXKDMoVtyCWrAtaojgedx4MDW+PEDAliCHLzfPz/u
KiKPvb0gwrGOqpWBPJhrTo4mswMIbI2LGuAhYWZvt5sp9JSSNckdIm0to5iq
CX9/tGrOZM5qoopkUVjlPd3B8/V3/wf/zu60bztGEUj4N+Q+o/Ee6ORXNrpd
21yiMXo52oHnBbKvtn5HtsA9L+2Q3WhIO4QYpFL9NHF2wW50g64crhH6A/Lo
v8j1ngbU5QmkvQgQ
"],
Association["Book" -> 1, "Theorem" -> 33] -> CompressedData["
1:eJyVUcERwjAMkxwTcr22O7ASI3QBZmUjLAe43HEUqkcSW1LsOJftdt0I4K7l
F9apuWALYaRbB9N7hvaCk6c2shLMDhlSqmw3WNG57NSUSVA5qIT8EQaRt/sf
7R6C7bNPWn24AeRAMYlIUbz2j4fJb0hhSrtikNl4aK2g5lyXmIR5iZKK1lq/
dRtX8fUTbzwATsQEIg==
"],
Association["Book" -> 1, "Theorem" -> 34] -> CompressedData["
1:eJyVUVsOwjAMS+xMG/3iD/HJlTjCLsBZuRF2i8bEBw9PnRLHkt30st6ua0bE
3b+vOLbJ4AlJYOYAkMKMqgjGVF0qFgUcGCzCHcRioOiaHzztYtgubaE61KZa
gfVL3H/Az1OP0/mVgZnjyh0KlyZE6fNN99NNpJNdmGMF2euXYCtk1BpjtiSa
NqFtFcLdeVmeefAe0Nn6S+zJB+pEBOc=
"],
Association["Book" -> 1, "Theorem" -> 35] -> CompressedData["
1:eJydUMENAjEMix0Tjr5gBFZihFuAWdmIJNyjAnFIpFLT1HZt9brebyvM7FHb
7xqhXDzDAvAIkiJae6Rk5nZQM70hntzcHTUxb7mV19l3jCQ1MbtSBZQ+R1M/
v6v9q7iPbnDlEKtPEBrIKxRe/eMzK7WsiU19MSaa5hxjuEVbjkQoT8tyuSzL
t7SJgvFm/ARWigQ1
"],
Association["Book" -> 1, "Theorem" -> 36] -> CompressedData["
1:eJyNUdsNAjEMs/No+YDPG4CVGOEWYFY2Is6dkPgA1ZWSNk6bOL3vz8dOAC+Z
BcSlVl4NbubuEWFBEsSsCGDIqDQyih3uWZRXghVOVxetQ47fRedMF2aBocfC
4ZHI1PPua+2uI/6yXY/y1ZJLBxu6GCUbkgWjtMkqu1keEisI8W3tHEbtj9H1
tj2pQpkTPiR0AmOEDVKDvG3bp1t+z65O9R8q03XZo30DroYEyA==
"],
Association["Book" -> 1, "Theorem" -> 37] -> CompressedData["
1:eJyNkM1tRCEMhP03NhghlHfey7aUEraB1JqOYoiinBK9DzECj6UxPF8f7y8m
os8td7geb4/Rsl8j11qZubL38OYm24awmLGziUi6CwdP6tQcQJVKWxMnYQbh
79A5R/fwPgsboyJGUIypc6oqYt4c9zb5rxtRokStZc4AHPpD5j7Xu6C1UOa3
a2bbPqJr1VbUBeoHhGqr/l3ZDapxevccVn8pyhlkoMlsLsTp6DiE7SiG8S/K
3NvVO+iEMpyVvgAy2Ain
"],
Association["Book" -> 1, "Theorem" -> 38] -> CompressedData["
1:eJyNkFtOBSEMhnsvBU5HdJ5N3JJLOBtwre7IcozxxZj5gKYtPxT6dv94vyMA
fG5ziafX9dxy5uw558js6R7SXGjvKiGJoJMQUWiFjgMcTJiNmZjVjAyYSOH7
yJ+cZ84WMc/C1jqOvgL6WrIOZvYYV597lf8vjCijAHNmnt0snH8YY/tecA0P
d/OdEakvs8pD1Hst9gqc2wOLnTHbbdHtcrCoalYhqcYQYzMQhRdErmZiVw+z
UqiJstYU/IURbyNvN4US7OoNGb4Av5UJbQ==
"],
Association["Book" -> 1, "Theorem" -> 39] -> CompressedData["
1:eJyNkMltQzEMRLkvWmxAp1zTkktwA641HYVSEOQU4z9BA4lDYCh9Pl+PJwLA
15ZrrI8eLe+9jbXGGGtkuoUJbVMJSQQNhYiaGaHjgIAwVa1SaQQJEKKC/B96
mz3NLWchfUd0B++T52Rm9XF53Iu0t657CVdXcXNVU/5ljH2udynX0jJ/XBHZ
9hFeqzZrXZTtoM4c1b8ru4HZT++eQ+ovidEbiMFEFCPACE09uOwoVME/GDHj
nqlwQlENGb4B98UIkA==
"],
Association["Book" -> 1, "Theorem" -> 40] -> CompressedData["
1:eJyNkFtSBCEMRRNuHqQ7Q4szNf9uySXMBlyrOzL4KH8sqw+QIg8I3JfH2+uD
ieh9mZM8PfeRmVuOkXPmdA/pLm3ltHETYW/SWgst13knJxPAgAaoWVNCK/N1
5E/ut5E9Im+FzetxbDNomxPzAOCxn3/uOf6/MKKMEh3HGPfNLBw/ZK69F6jh
4W6+IiL1Zah8F9WCl+Pon1gAG8yWLLqSCIiqjmokJUwDWycxujKjxORuHmZV
oSYKrSn8C5gve14uSlWwuncGfQCQ2glc
"],
Association["Book" -> 1, "Theorem" -> 41] -> CompressedData["
1:eJyVUNttBDEIBIaHDetd6TpISynhGkit6Sh4pShfiS5jgTAzYPDb8+P9yUT0
ud2rOEbl46jruirzzMwRM1Q2ZcKiyiEqIukuHLxo0nAzB8TMxhAniFiLf33i
XDU9fK6GHkdmVFDUwloALNY/xn0J9Scb0Q5EY1Sd0asYvlG1497L0MeabOuM
qm76djjPNlhfDH7DAhit35ktAOLW7jm0/1LAGaRGi1ldiNNtdu8uHepdxKb8
AzDnfGQa7W7G7gz6AsRHCHQ=
"],
Association["Book" -> 1, "Theorem" -> 42] -> CompressedData["
1:eJyVUUtOxTAMdPwZf1qVlsJjzZU4wrsAZ+VGON2wAj0mkjXyWDOJ837//LgP
Ivqa5WHg7TXTMzOqfFFdNJJltIepiBlDwMxmRgOjKAmi6qqsagZW0iY9/GvC
7aWiA+LczxPPx3HUllTbk2wlIpH1n+s+gvhTzeziRMuy77eKSJ/PlImI5uIN
6ePpjqsDYPZxDbU4VcwaF5Ai1bwN5BIlBW2ydxDzoMEEEBudNKR3SdbWqhG9
PxgHxHX8oJe/Vq4raOb2J8QQ+gYKUwj+
"],
Association["Book" -> 1, "Theorem" -> 43] -> CompressedData["
1:eJyVUMkRwkAMk2UxO2wHPGmJEtIAtdJRLIdHGIZM0GN9SD7W9+X5WALAy895
BDJiZNKIrh2UgMRFrTAl8ppIJVtYWW5Q2s+DmZI2ZQEe4foKoW5P/bXuCfCY
fdPeQ7TdUdFEpcK87dfHXE+0sKWbYifj3pkz65zuNOsSda0a6eg2xq9tq1XU
QT8Hr/f/A/0=
"],
Association["Book" -> 1, "Theorem" -> 44] -> CompressedData["
1:eJyVUMltBDEMk3VbtmceqSAtpYRtILWmo1D7yWsRLA0I1GHq+Hx8fz0GEf20
eQMfERYRWuWlepkny4CGqYgZ63BmVlUaPiYlGYtMd1hTcELKyPWl/lk1s2ru
s3fsfc5aRau2niNQqvneuP/j9SiNKpggWuu+z8qc0WtKQxVccIsQvKgIj464
e8f9WdTcn05IPuETa4CLJGJIwsPHuNFo4JLClElstGjIYCab27qPNxhSYfwH
Yb4qrsup+6Iwh9AvVKcIfg==
"],
Association["Book" -> 1, "Theorem" -> 45] -> CompressedData["
1:eJyVUclRBDAM8yHLTgaKoCVK2AaolY5QwoMXMKuZXPKtvD0+3h9uZp9newYc
FgkKwAJfAhFmQGZVwivcu8qjo53Ow0fEsTJgupZl/Jq+W24JtoC918Jqm9Ui
qg79ZLv/An9ab706J9kz03XHTBzUWQJKnNpjHeYKg+J1ITWLHilnXvRKNGYS
ozh8i6gkVCE/n5FWZQ5r98irLKQeXvcmdwCOqR+osuLXokE2eEpk/wJVLAeC
"],
Association["Book" -> 1, "Theorem" -> 46] -> CompressedData["
1:eJyVjzFyAzEIRUEfEMLs2I3XjRtfKUfwBXLW3CiwkxlXScavQIgPQv/x/Px4
MhF9dXiL87rd73m57Ju76zKMroJ4iLARxhhuxqwcNMlN1YChKu7DaJRA8vvS
TF/T54qMsFPhy8hWaqYq1OPd7/5H/qmaUXujiG3LtlJefsjs3ArYcZh6V0Sk
5SPgugM7rC6GeaATCJQXaDeUPo/erRbVJIERk4ZSMosJIaxHtDBRVrAKvwDz
Oj3WUupXpEYY9A2bpQiD
"],
Association["Book" -> 1, "Theorem" -> 47] -> CompressedData["
1:eJydUEFOBDEMS+PESaphpFmJEye+xBP2A7yVH5EWceCwSGC1bqs4VuPX+/vb
fYjIx6K/4WVW5ZyV59MxL4KjPaBDzez5dANmhKqrDwz61xMAaRC6Q+APzau8
nJFM0m/XdcVJibM8szs9H3f+E/PXKtlk6+yBgwziG5ncQ7ET2Me+Ap3CKm9C
VW/04K2JDRa2fvESrLW06x+qJmqdmCikbHiYuqm2p3ZwB30oOufxA0fWcbgs
tzkyBuQTW+EIDw==
"],
Association["Book" -> 1, "Theorem" -> 48] -> CompressedData["
1:eJytUFFKBUEMa9OknXXfzkPwAl7JI7wLeFZvZGcFeQoKgvmYmZBpGvJ8e325
uZm9reOPEFkkcx6Xy2NBgBkCHhFPk61uY8DlBFGK2DIRgSrRAv2b+NlbKUYw
mal5XI+YZZpqV6lGO/wztl/VqpVpxRpjZUh+oor3aKbz0S2c1714En2gvmk9
ufjoRe40LNZ1mtK7PwSjywuktFGOBOhfsIv7TluLH3yUh70DiBMHQA==
"],
Association["Book" -> 2, "Theorem" -> 1] -> CompressedData["
1:eJydkFFuhCEIhMGBEZRs/mQf+twr9Qh7gZ61N6qaJn3qJt0vEZUBdXx/fH48
VES+dvgv9/u83a6KCA+i7RREm5lS0FobEaquJSkjSAKNtDFaSFuC+N+XVkX2
6DlqDM5FJIVZXuUOj3rhuU+ZT1VStjfJrCq6by8/zLnX3PZ4JnrfGTPb8gm4
rjXAtSH6wTuQWF7gpwDop3YbW50CxVzf5FKq1k0wTosvaK4OddNfoJrjLdNl
n2JqVMg3M/MIKA==
"],
Association["Book" -> 2, "Theorem" -> 2] -> CompressedData["
1:eJydUEFOBDEMS+rETTqdQdobIw7wJZ6wH+Ct/Ih0hMSJlcCHtI1jpfbb/eP9
riLyucqf8XrcbudTRHgQbXUg2syUgtZakKquKZSgO4HmbhHNpBUh+H3pPiN7
9BxzDG5z2yIpzOlzusMj//PdR9gesqQsbzLnvu/LSnn5xnGsOwvgddD76pjZ
oq+C5xM4wXoQ/YJ3IFFe4Gug+H7N7rWolJUN+pBGmapGE1TIJfECzdWhbvoD
qOZ4yaxQS20lUcgXPpMIVQ==
"],
Association["Book" -> 2, "Theorem" -> 3] -> CompressedData["
1:eJydkEtOBDEMRO2UXbG7kx5pdrTYcCWOMBfgrNwIp4XEipHgLZxP2XHKb4+P
94eKyOcKf+e4389bRHgQbV1AtJkpBa21IFVdUyhBdwLN3SKaSStB8HvTOSJ7
9NzGtnEf+x5JYQ4fwx0e+a/vPmF/qpKyvMkYc85lpbx8cxxrzwK8FnpfN2a2
5Cvg5QROsA5Ev/AOJMoLfCWU3q/cWY2qsmaDvkmjDFWjCWrIVeIFzdWhbvoD
VHN7zayh1itWJQr5AgqqCDQ=
"],
Association["Book" -> 2, "Theorem" -> 4] -> CompressedData["
1:eJydUEGOAjEMSxynmc4gjtznSzyBD/DW/dE6u4DEAQ7jVlGVOE7q/Xa/3tzM
fjocAJljzlyD/lBwAekB4LRtYljq1CA7xUSVyhDJ4/PQHBtFj8qqYGQgaciB
TIkQeWzdz7h8rZIKMBujSgsAE0/su96cAifXVXdZO8OhL8udfkZvnViUWfjf
tsgNvkRUlD3is6wtDHPl0hAmARsaHoTam9s+/vX6G+LMCDib4BHS+AWRrQZv
"], Association["Book" -> 2, "Theorem" -> 5] -> CompressedData["
1:eJydkEtuwzAMREkOf4plu45WBbJpj9Qj5AI9a29Uyll0lS7yAI0wGlEffty/
v+5MRD9TXuFzvEd0j4BMK8Siyk4QkTBjNk4ycgUWMwHUXXTGU54ee+zrkq0t
676usb1t26UHZb/a9TCDt3zxuU+5/JtGlCjR7TbGkUV9DQ96j9IoEOcUnnNF
VU89N41RA1EmkCfeqiFwBxw6Q7RZoqMuqgICw5PEaWdWK5fuoWqFq7GpmPIf
YN56tclITWGiwaBfdowIww==
"],
Association["Book" -> 2, "Theorem" -> 6] -> CompressedData["
1:eJydkEtyAzEIRIFuQPL8MtbGXvpKOYIvkLPmRmFmkaychV+VkLpaCNDj+fX5
VBH5PsJbjHvmGpmwQ5mokRoCM0t3VdcmLkGgZxrACKM4SQFfvrpvy9R6n5Zt
WXL9WNfLnNLmq193d0Rv77b7isu/bmaF6vZ2G2NvES1rkBqpmOc6IwvkueXp
lk38XhqjFrJEop1EByZEAAEeJvqRwlGFKkGgiCYWsqnSS1XVJL0IujrNqX9A
dZ3rm1zohBtTIT9Hnwif
"],
Association["Book" -> 2, "Theorem" -> 7] -> CompressedData["
1:eJydUEFyAzEIAwtk8NrJsdcmT8oT8oG+tT8q3ulMT+khOmBjIbC4Pb8eTxWR
7x3ewzUiPIm2E4g2M6WgtRakqmsKJehOoLlbRIO0IgSvh64Z2aPnmGPwmMcR
SWFOn9MdHvn2d1/g+JclZXuTOdda20p5+cXlsu8sgOdB7/vFzDZ9BnzegTtY
CZEnvAOJ8gLfNcX3s3bVoFLWbtCHNMpUNZqgllwSL9BcHeqmf4Bqjo9qK7uL
lUQhP6JhCA8=
"],
Association["Book" -> 2, "Theorem" -> 8] -> CompressedData["
1:eJydkEFuAzEIRYEPfFtNPJ7FKOteKUfIBXLW3qh4qqqbtos8y19YHwzi/fG8
P1REPpa8CDmYHbZiEzV3DYGZMUI1tElIOtDcDfBM82Uv+fPPOWZPss/rnHHd
9q1tXdq2Y9+AINvr4/7O5V+39xIXud2OY7bMRnwzxopZoA47+eW6+6ln0px1
wXoQ7aQWhjdkAglfJvoq8aMaVYFAlV0sZagaTLUx6R5FemgkwvWHSh+XMUZI
VEs3p0I+AekaCFo=
"],
Association["Book" -> 2, "Theorem" -> 9] -> CompressedData["
1:eJylUMkRwkAMsyXLJNABP1qihDRArXSEzDAMD+ABStZeK/Gl03Y5bxkR1zG/
4lh7ISNdY6y9OPy6mC4/TIksElRI0ekwkvxYktzBheAMQipnIKodwijUH+O+
hb5+BWam8QDLpj3EeHg439kGm5LjQw+jWZmUr7wP7SQzzbpj5azxgtlz/nx0
s56FAIOJbEe0GtZ3OvqYnPcJy16Ly8Jau7f1TcYNy9kFaA==
"],
Association["Book" -> 2, "Theorem" -> 10] -> CompressedData["
1:eJylUNERQjEIgwRo6xau5AhvAWd1I0PP8/xQPzTtQZsCDZyP6+VwM7u1+Rm5
im6uGm3li02vmfDQomeS2mBappXrbE5+rEguqBCUQYxR0wcspq4QAvGP3Heo
r69Aa2oPMGRKItqjxYkrgcVMZK7NRLespnXkFq0kMcXYmNFtvEBloyMfv8Et
YKDR4aUbNQ3rmbHEiuz9hMZepygFKp7pqaHbHbzDBW8=
"],
Association["Book" -> 2, "Theorem" -> 11] -> CompressedData["
1:eJylUUtORDEMS+I4aSseaPROwJXmCHOBOSs3wn07JGABXliqm4/rvj+e94eb
2cemv+P1ZcUAzCIjq2pmJVDdHgx4eiHidhwRgWSGFQkL/jiQOTQJbHbzOM4b
3pb1IYUA58C/7H6D/vV2re3JbM4x5KircDkRdBDrzYWStsg5t6Kyi6+iXa/7
3twX5lLrpTe4ZSx1k0OL3PUb4aR5WoYrNXckYu+gMqFBaad/wTnqPNuo2Dpq
qPUTT5gHcw==
"],
Association["Book" -> 2, "Theorem" -> 12] -> CompressedData["
1:eJylUdsNAjEMS2yne7ASI9wCzMpG2D0kkBD84L7TxE3cy3G7Hl1V90x/YLGN
Ku6VizFK6pYbW0OOBNLWmiZQ7fENgJJRC+bwASXm5L3pzflfup+Yn7dMPcg6
g1S4p41JkRSSpKtyPy32lLj2lpGFDdlPz7AXw1bMirRD5sxj/8aSZfCrSLif
tmId4RTt7P7O4CtobXEcND0mrAcqpwSq
"],
Association["Book" -> 2, "Theorem" -> 13] -> CompressedData["
1:eJylUcENAzEIAxtIKt0SXakj3AKd9TaqyfVTVe3nrASsQIgh9/352N3MjjZX
AGemmQfluWVlRM4JBMjiTHK7TXHUyDACsMTPchEIlZIFxqjmMDDEqmIGL8r9
wv+CaKW5ZKGVQY20pgX0FkTadbiPV/ydtHohuosz5+zujDEX7aWr6zWXHqVo
nBbuClmX1B+xMreRGrZO/QOBHlMnYnhNp70AIrAFww==
"],
Association["Book" -> 2, "Theorem" -> 14] -> CompressedData["
1:eJylUMsNQjEMy99Nt2AlRmABZmUjnAcICQkuWGqSNq5j5XS5ni8qIrcJf8EO
BRU1M01TNa1MMbfUECAr2SnYAu/kmLh9VQNWWHg0uh1oeLdUoyiElch/7X5i
/exyuEhM3ns8FOKFtaYGEYiqrmKfL3nEeBC7eWJewA+DUVjkPxk9OVlsDrLZ
iwq3Jy5QVeduI9wzfe+ducXTfcUbNhY2jUk6Z2ukhd4BqdwHNw==
"],
Association["Book" -> 3, "Theorem" -> 1] -> CompressedData["
1:eJylUNsRgCAMa9J+eG7hSo7AAs7qRvYB6nmePwYoj5YQsrRtbRCRPcI/JIPK
PAGonXqnUCGDnWeZL+yDTB3Ugm/ImmNU+rfcB/iZHe8BoSTidTHXjMkbXaqn
szR/il4ULxAZE+XRcKqMQddhxk6bDppq3VUblr2pLdr7yQF9XQOY
"],
Association["Book" -> 3, "Theorem" -> 2] -> CompressedData["
1:eJylUNERglAMa9o8BJnClRyBBZzVjUxbuFM/+CEfvaMJL2ke2+u5wczeOS5i
vplx9rGuC+w+jRFkcNBDEC8LlwI+lZx24ukC/BfWOyCJ63H/DM9ZbwmZQXKi
k1SWnsrWiYO50fG55y5CssShUScA0bNIBML7MKnVloQGHZ0K1mcaH4+F+Xd9
3pVpXX75I+wDM5MEaQ==
"],
Association["Book" -> 3, "Theorem" -> 3] -> CompressedData["
1:eJy1UMENAjEMs+P0uAFYgJUY4RZgVjYicY+TTkLigYjaqErs2M1te9w3Anh2
+jWuQF6kdR2AUoI0Rg4sWjQRATAkixFfNN/tONdIxif436NUw8qdy0SwA3Y0
vU3HZa8b7h8gdjd4fNoIzuzypHh+L0imyMxEmpE1zY+6Om9v36+1sR+8AJNx
A44=
"],
Association["Book" -> 3, "Theorem" -> 4] -> CompressedData["
1:eJy1UMENwkAMs+Nc2zVYiRG6ALOyEYmPVqqExAeiu+gUx7Evt/1x3wng2ekH
kau0bQNQSpDGyIFFiyYcAEOyGPFF84DjWiMZn9r/HqUaVu5cJoIdsKPpbTou
ew0YP5vYaPD8tDs4s8uT4vm9IJkiMxNpRtY0P+rqur1jI62N98ELdBwDeQ==
"], Association["Book" -> 3, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 3, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 3, "Theorem" -> 7] -> CompressedData["
1:eJytUMkNwzAMo6RKcR55dYKu1BGyQGbtRiXloEAf7SsEJOuyTPOxH8/dALzk
rsBqXlUIN7NgWqOWjARTGFh1QAYE/PeaEDL7YOKuHdmx2rlcRPeDP1z0XtJR
ItL3SFoonhc9Tr4QO3Lsj7OulfOrzZpdb9/QberhetlUnur0/BjGKa0vdszu
tZlwm0VO8pSeXyARdzuFbrwBClUEVA==
"],
Association["Book" -> 3, "Theorem" -> 8] -> CompressedData["
1:eJytUNsNwkAMs53rlTVYiRG6ALOyEXHuWvUDEEL4pCS6OA/nut1vGwE8bP6C
iN4vZEukiVhDrbcmgGLZaAtyHKH3XWhMFxVz//XPp9Lf8IV+WZxXkWVQmtug
VnWL0URRi1b+IBVR3DlwooT5KtMnW0OmkMkc40Bc8p0GJSdcC74Axml9aTwB
pdQDwg==
"],
Association["Book" -> 3, "Theorem" -> 9] -> CompressedData["
1:eJy9UNsNgDAI5E4/XMOVHKELOKsbyQGNNTHxx0gaKMf71rZvDWZ2SH0jC+DN
KE1pGTJjMnBwkjO/zOxh3jFU+e9CzY4lYos8DuEnXBu7hy6ZgwQjsa7CIOwV
xZN/LJkLJudqfo2LjEf2MDw7ARBVAyI=
"],
Association["Book" -> 3, "Theorem" -> 10] -> CompressedData["
1:eJytUMERwzAIkwSLZKWMkAU6azcKWHbau17zin0GWzIg2I7XfhDAu81DKzMA
1YUSE1lOMlWOtREgmfxftGgO87XgY/Y5ubPgPUt/iWghbSe2tFifFSsaUUTj
ccVzPFZXPZGA7SBrNqKT1diwOsaY08zdBAzqR7HTgp/IEzliA1s=
"],
Association["Book" -> 3, "Theorem" -> 11] -> CompressedData["
1:eJytUEESwkAIg5Cs4/gBr37JJ/QDvrU/MlAPXvTUbJsuDIWQx/Z6bhkRe9NZ
uN8QqwCSWtdVoug05hGqpkod/QJZcxoHk07SPdGN60S5g/8NyaNkrRZi9nbl
F/2pgws+1lxUZyh1XlPUqjlB4bON7wsabqsAwf9WD5IicoY6ZOTKi6eTmTkl
3r7d+Jbs+/hkUxsB2t03n0AFSQ==
"],
Association["Book" -> 3, "Theorem" -> 12] -> CompressedData["
1:eJytUNEVwkAIgxDOp1u4kiN0AWd1IxPOD3/0q7k2PXgUQu7H83FkRLxMp+GG
WAWQ7HVd1Wwqi3kaVVPUjn6BrDnGZlJJqifcuM6Ua/xvSO6StSxErO1KL/yp
zQUdaS62M+x2vqfIqjlB4bON7gs9bKuAhv4tD+qOyBmqkJErL5pOZuaUaHu7
8S1Z9/FJphoByt03ePkFMA==
"],
Association["Book" -> 3, "Theorem" -> 13] -> CompressedData["
1:eJytUMERgCAMaxKOPVzJEVzAWd1I2oinH1+WIy2UljTLtq8bIuJI+NHQNaw1
jQVRzP4IRiig+kyf9cMKHhbezv5LN7l90/ETKYkkXneTi/mZMWs+KgeE7nrU
YU7FksJYyaEN4Wat4VYgfWd3TMuYMd/6cPrnPCdT2wN9
"],
Association["Book" -> 3, "Theorem" -> 14] -> CompressedData["
1:eJytUMERwjAMsyXbKceLBwOwEiN0AWZlI5QQjvYBr+qhc07SxdZtfdxXN7Nn
pwNxZWWRRDAQABO8nBeQnqwwAm6Jn/lQSvGRjVahBwwMTVGUeuy6ZvyrAm8L
hOikQzTFHD7ghnfIJHInkRvzEKc2f4PpSnNaJ3k5GjNU5sL0sYh/ke6B1ntR
b2h+aoq+AJ39BTE=
"],
Association["Book" -> 3, "Theorem" -> 15] -> CompressedData["
1:eJytUNsRgDAIS4BT13AlR+gCzupGQqmeH/auH80Hj5LQHHs5j0IAV4SZUDOj
QyAUz0pZt0U0OlPECDb+KVuI7Dsx2+6wh9dLRYfRFfOjZHY/uhj73dRjUhh1
0uSRa1uU8Gc0O3FYmN8INyjsAyk=
"],
Association["Book" -> 3, "Theorem" -> 16] -> CompressedData["
1:eJytkLERhTAMQ2UrR5GKFViJEViAWf9GX7JTUFHhS8zFxNZTjus+rwDwc/o0
9jmZSYayvqpIIoGZ3NMX5lu3eyJXhEInpLNPGvk17vvA0tNmm6Epmiuar3kX
MYtR1lXnulQOGPF0pbehc/3UquES2rZ+rIRNQ3UWwxijtQKl9gB0h8cTpefG
wB/gTQQu
"],
Association["Book" -> 3, "Theorem" -> 17] -> CompressedData["
1:eJytUEESAjEIIwGdXhyPnv2ST9gP+FZ/ZCDreNLT0k7aAg2B+/Z8bIiIV8Ox
drmCZKFwYiaCSRBY57pVx1fk78+QETaOw6v0LBEdLvc/4dSjZdky1VupwRY4
KL05ofh42AcH4eaNkxRfz0yGMbldqAou5u10XUpjHDIGmDuTBa5OYOwjSnHp
+gbVdAQS
"],
Association["Book" -> 3, "Theorem" -> 18] -> CompressedData["
1:eJytUMERwzAIQxL99pl/V8oIWaCzdqMKcNNX+4rskzHGQsfjeO4HIuJVdDE2
SBSEpJIBxwQzdWc9Z/D3XxjEoMswS75aFZfb/S/Y/Ti2BjZRRlgmh+1X/RSf
DOtgM+z55C6Kb4ZN0bXVKBPTbPaUO0hplGuYay4Lt2VyRiRrOXwDqMED5g==
"],
Association["Book" -> 3, "Theorem" -> 19] -> CompressedData["
1:eJytUMsVwzAMEoj03BW6UkfIAp21G1USTnrLKdgPf8A21mv/vHdExLfpbiCT
grAxlSgCCW35ZKuKvDhaIIxxw021VJZye9ZrtWU6llFfo0R2SHPlzZHi2GEP
HEZlPnlM8d/hUIy3H5Lgx9xtr4kyfTMDXHVZeKyQLlHZulo/nKgD4w==
"],
Association["Book" -> 3, "Theorem" -> 20] -> CompressedData["
1:eJytT8kNAjEM9DmOIyHYD39aooRtgFrpCHsBIR7wWsenZuJMLuvtujIR3Tvt
bueTsPFCB5rhbiLiQ+aUQcIs5L8fzczhwKialgkgQcjUclXDsrfU+IsClbRr
RMLMXd8W0b2XaR2Hd7RGs4btRapQr8E36kZXaHM2RjTSXeuo/VQDjMQowXoU
KnJ9G5+VXP5lKGV15QmasdIDpmQGpA==
"],
Association["Book" -> 3, "Theorem" -> 21] -> CompressedData["
1:eJytUDESwzAIA0uAr70M2bv0S3lCPtC39kcVuQxd2ik6DLaMjU7P/bXtbmbv
TtfjYUZbfPV1ZnKMkdOXhdPg7pa/h0YECVA1JgUQpmNGpID71Urj7y2gVIqS
HiiQWdVKJAgtSEgcBVHN8FBacTZpJZTPHjRTSTZfnRQs/a9B7jQM733ICbeb
KPkh/9hPCWc528MvMEo+ySTZ5hke9gFq8AaS
"],
Association["Book" -> 3, "Theorem" -> 22] -> CompressedData["
1:eJy1UNsNAkEI5DHccIm5DzuwJUu4BqzVjhwuGr/0SyfswDKwS7jst+vuZnYf
+gtg7Sc/ryQigotvG9oUu3V87KoqIBPytUJIpOnKKpJL8tdj1lc1U9Rm1P+V
siS7OdBFnALzcFmcDI5Ju55FOpTyqslDJTD5HpKhu2cOd1iGs2asKrfFwrUP
7Q/TinS0wnjDJekBqFGrqmDF4g9bKQa7
"],
Association["Book" -> 3, "Theorem" -> 23] -> CompressedData["
1:eJy1UNsNgDAI5GiNJPy4gis5QhdwVjeyUE3rI/1S0vIoBwed07okENFm6g/R
qKykR8REsBOyj9Ap40ZyABRrt6S/nrO/f+WzSUzXQvdhBpYFXpqVRwc6FHcE
WkeEaXDKyaij8EicExLOL3usjzLCte0OVh0Dbw==
"],
Association["Book" -> 3, "Theorem" -> 24] -> CompressedData["
1:eJy1ULENwzAMI0ULGTt06dqXckIeyK35KLJQ24WBdGoImBJoi5L83vZ1I4Cj
0i0oLz7xAEEzGoMhCpLJdVnFQNIUwwBWs3+P+duw9eMXgFglpWnergzfvB3c
9vkoGJTHnfFHNVtqaXF66oqGacv+vEFtNsSvqigidAJ/wQOf
"],
Association["Book" -> 3, "Theorem" -> 25] -> CompressedData["
1:eJy1UNsNwkAMy8MehJUYoQswazfCDqJUquhX69NZed3FyWN5PZeMiNV0D5o6
qExUiRvoThuJ/01JUIU08CGEDEW6W97VKnGedboty1LgEb7Y23YPEcOquT0Y
TMSlU73lPVjVXFITB6MgCrUtC4EXU9D2kD9on7Mn5PyYYHa8AW+eBWc=
"],
Association["Book" -> 3, "Theorem" -> 26] -> CompressedData["
1:eJy1UEEOgzAMsxMHrrvwgH1pT+ADe+t+RJpRKiFtJ7BUp3Ib1+lzfb9WAvg0
ugm24AGCZjTSDU6HZD7pZw8TRaeaBrDmdXXI//OTI1ZHDmZf6ZT3UIZvnQ7u
8+wKBtWKYP5R282tVcEo3fPBsuVxvcN7NmiSQlmhDWSRA5U=
"],
Association["Book" -> 3, "Theorem" -> 27] -> CompressedData["
1:eJy1UMsNQjEMs5v/EwNwQmIlRmABZmUjkl44wQncNHVrS7F6vT9udwJ4Tvsb
zkiPUHLFoZlMkBQcn4dWpXumV0OqIrISubk08vLriPldHVmByVRp5i6iKjtK
NhdvSC/v2GrzYmbd1bZpUpd4X3xbxzR8PCY6Yp+mqnuQElS6YQlq0U4Cuo88
u9Fmdr2xyIij/xijKqfwApWFBss=
"],
Association["Book" -> 3, "Theorem" -> 28] -> CompressedData["
1:eJy1kNERwzAIQ3mgxgNkgqzUEbJAZ+1GxZzjXHrX/kUfMgYJg7f99dwxs3en
28AKhjsOyOVhEtHiv+vr7EgH4bcO+xOXV3MZInKdXijOuk/pkacoLznz5NFh
ZigyjkaSmypsXSeZyhYMCUN/4vzJpcVjEZmJDzBcA2Q=
"],
Association["Book" -> 3, "Theorem" -> 29] -> CompressedData["
1:eJy1UMENAjEMc9rEORBPFmAlRrgFmJWNiNuKe8ELrDRN5aS2ctsf990APJX+
B7sw081antupAlY1ts+iEd7D6wg+Affw8Qq//tphfGVLHCCQKTuk7Mzsb3sH
BhGDX026uIiFGssxzMWERigftRxYR5agI5rZJgvJqjgVG2nsdqAo/aclaXOm
wAvohAYY
"],
Association["Book" -> 3, "Theorem" -> 30] -> CompressedData["
1:eJy1UNsRgCAMS0qqc7iSI7CAs7qRyEPhw/OL3LUNNH1ct3jskQDO200EkQdY
YqRZgMTg+qkZY+WpweRlPzBMZUPhJc8uWzWoIhKPb5r2U2RgayQZlOmazKT6
CnxPwn4HdjdZXO6exAgX8f4DNA==
"],
Association["Book" -> 3, "Theorem" -> 31] -> CompressedData["
1:eJy1ULsVAjEMsyPLse9WuIaVGOEWYFY2QuFR0EAFKpzETvTJ5bxdTzez+yr/
xF7FMUbNcRyYBvdh+Vk0kxFApLBTAGFgdmZ3J7Zf++PXKaAizSr5gdyge9t6
QYfuglB4LuBcnSCrqqnteiXTDXVed1aUro4QQW9rWNmxoknIXVkllstWwlVh
SQ53/UpkhFFkeMMQI4sMQ8iA7+nTHpPZB0E=
"],
Association["Book" -> 3, "Theorem" -> 32] -> CompressedData["
1:eJy1UEEOwjAMi+0wbeKE4AN8iSfsA7yVH81Zq2oc4LZItRI3cd081/drRUR8
Ck6N24OZvF+xzJjjIiGkfwPoJ45dzqlk5JlWfwSPhUSQwO5yR5sdTgfPgir8
3YFdYTAsqIpkm5ZTmK03BaQ7mmCTsywnL+IrukFfetETvKUNkrQD1A==
"],
Association["Book" -> 3, "Theorem" -> 33] -> CompressedData["
1:eJy9ULkRwzAMw6OcipSpUmYlj+AFPKs3CinqHLtJl0ASxaNICIfXui0rAewZ
fosnKT3u7B0N3Sbob/2cB+cuxZaY999x+TNVDEReESdVR12oLmqUQvlhdOUZ
iyrnNRkcaYwMA5y8HoT1HKSxHPZ9IHsaRdyk3ujGN189A58=
"],
Association["Book" -> 3, "Theorem" -> 34] -> CompressedData["
1:eJy1UMERwjAMsyT74MWLBViJEboAs7IRllt68IBfdRfFseTYyW153BdExNN0
MEjxesH5hIqSENQ/O7YVn66OOaVHDvoDXz0zCRKYKYd72Hyre54mIyeViP2j
19hMiz6RW4/sEOxUO+a1nAtbpgXvFRpwkK7U2lpUFZR4AVXRA6o=
"],
Association["Book" -> 3, "Theorem" -> 35] -> CompressedData["
1:eJy1kMENAjEQA3dt74YfHxqgJUq4Bqj1OsKBk7h7wAssxYo0jmL5utxvS0bE
Ou3fupwBZLEZJWVIH6MliKQdUHeVrwGqJTVLP6+L73RiRnQDhSnSxVzuZZu4
84PGIMYBkbvwE25s+w1eR5GMaWROmj6ewsoZV75VmYJH9Ui2wjj56QMvfgTz
"],
Association["Book" -> 3, "Theorem" -> 36] -> CompressedData["
1:eJy1kMENw1AIQ7ENzRA5ZaWMkAU6azcq/pHaJFJ7ai2EkDDiwbLd1w0R8XD6
u2YCTN4YUxWj6qNTAi2oJ+gEBKCSVEzp12jf74fb7GiMhgEGnTQKvHQoz+pr
URcD33lv7vIimieZAYUCmeoXcOxS700PFXRQmcU47WbHZM8TsVAENw==
"],
Association["Book" -> 3, "Theorem" -> 37] -> CompressedData["
1:eJy9UEEOgzAMs51UgMQn9qU9gQ/srfwIhyIx0LTb5rRWGketm8fyei4EsBb9
HhK9mjBPo6DxSyNYgOCkqJdD8k79x+4VLCsoR3Xo9nrpreMzMom8NfDkLp6K
76yfO8LEaB6Bw7ODmVlvNsQO7UhLhzNnmYMaYwM1bQN5
"],
Association["Book" -> 4, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoB+hr20gCyCELAJZUAnw=
"],
Association["Book" -> 4, "Theorem" -> 2] -> CompressedData["
1:eJy9UEEOgCAMW1uIHP2CX/IJfsC3+iM3IEQPetMmNGN0W9my7esGMzuC/sCM
MiFblmDUmxL92FXlMZW89EuPD7jNlAgSqC4ru9nhdOQZFFBN+afHolsczHiM
G9lnJA9BTzUFjbUhWzt/MuZQD6SoVBstppLhWzoBK08Dgg==
"],
Association["Book" -> 4, "Theorem" -> 3] -> CompressedData["
1:eJy9UEEOwCAIo+D8h1/aE/zA3rofraCJ0WTLLlsjHLAFSqnHXiEip6dfgLwh
i6qC6ZHYQ7AWQemHG74Cd4iYi/dsDD8TuTtclIm3AS/kEyzcojn3TvxgwUQx
kILZRhlfqC/aVwL5
"],
Association["Book" -> 4, "Theorem" -> 4] -> CompressedData["
1:eJy9ULENgDAMix1VYmBm5yVO6APcykfEaSlMTAgrcpo4ldOudd8qzOwQ/QNy
SrPlbcjdCZKRHUJURjhaSf98q3dVMpRjJRFxoZ2zlRsrc/TBPpQv6MyhtQ4e
JKNSIDPAPMIkyB79L2LMWtyYQ6frevqlbidr2wPF
"],
Association["Book" -> 4, "Theorem" -> 5] -> CompressedData["
1:eJy9kMsNAkEMQ5N1vrPUgERLlEAD1EpHOCDECU6Id7AyTqR4crpczxcVkdvI
nzhaCVQ3qc9LI9wMsCC7EzgEHntE78uxfh3Kv3YBSk8sgmGtzu7MZDTqWIl+
tOzlUGskM2Jl0OrEY3SGns6i01OmJ6oquEiVfxVJZjIJKMNtEmabqj1vIZbg
+w1r9/I5UsBKD64pdwD4BpY=
"],
Association["Book" -> 4, "Theorem" -> 6] -> CompressedData["
1:eJy9kMEVAkEIQ2ECgV2rsCVLsAFrtSPD7smDnnzmwLwHA/lwvT9udzez54R/
aZXBfRk/m5IZAQSlS0pIGJJNdjex/5opv1YBBXlWiQdD1r33wFFok5OIwvFy
MhEDvx0bSH00lko4P1Wz1NwMnpOKMavJyF27mm01WIQr6ljkcs8ZG2FZK7He
pFm6kyFk4zud9gK8vwZY
"],
Association["Book" -> 4, "Theorem" -> 7] -> CompressedData["
1:eJy9UNsRgDAIC4EP13AlR3ABZ3Ujgfj60S/PtJe2kAu5jvMyzQZgLfoNUTTA
nxWWoAnsglbkMzw7X0d6N+x5VCzBnYwgK6Q483q3cFRYB5stM5/cIlwVNqG1
NSjCNExb8ryEu5wJK+dbwKEExP5Fnl553QAxzAOc
"],
Association["Book" -> 4, "Theorem" -> 8] -> CompressedData["
1:eJy9UMkNwzAME0klmaMrdYQs0FmzUSXa9a99FSFgQgch0Xqcr+eJiLiabgQB
xPF9abVZmpZBGIgRU9qQ/zb0+//oNm1rQiL70U7tk8spVp2mSkQsnhNWhSZY
60VkUMhaqHBZPsVnZufcoWzIKC9A+kjqK2Vp4w1G6APr
"],
Association["Book" -> 4, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoDNjpb+XQAIyMjGAMZIEwGwOMxQiLJdyxxYbEBgCj
JAKa
"],
Association["Book" -> 4, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoCWTFGBlZpHFKMzIywmhGZhDBwAjmMYDFmRiY6eNK
VDdBnIMWUih8JiYwwtTKCNaOaSAGkxFhJCMTiMvIwMTICvI4E8xuRjS9YIsZ
gaqZgXZDLAJyuBk5ADnDAz4=
"],
Association["Book" -> 4, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoCnQYGRlNccoyMkEcBFTEyMwEBAxMQB6QYgSJQ3hU
BUQYyAhyDhMTWkgxIvNB7sTmOJAizBBmxMJkQjWSEeRXRmawCCgs4GphAlDA
BETAQANiaJAxiDDzAgBbEgNx
"],
Association["Book" -> 4, "Theorem" -> 12] -> CompressedData["
1:eJy9UMkNgDAMi50vH0bgwUIdoQswKxsRA604isQDYfWyY7VuhjylDDObtfwL
AONzkSgmOAPGYLFB+sa+TfPKApAXJ45cOVvhZLq/gMaR5yuhv8JXRb2o3iLs
YIxoWkypdFrv3QIHRwMx
"],
Association["Book" -> 4, "Theorem" -> 13] -> CompressedData["
1:eJzNT8ERgDAII8HryyVcyRG6gLO6kQRa/fnyYY4rJaSEbv3YO8zs1PEjuDtB
MrJDiMoIR5Xk14bvA9MPyrGSDmKi7knlxsq8eZRQW3vyQzN6xUgwtTJqDTID
zCNsfFdTpswqHqzR56Ln6Zd9uwA8hAOp
"],
Association["Book" -> 4, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAAjIyMYAxkgTArA4zFCIsl3LHFhMQGAJkUAo4=
"],
Association["Book" -> 4, "Theorem" -> 15] -> CompressedData["
1:eJy9UNsNhDAMSxOnrZAY4lZiBBa4WdkIu0jwgbgvdFbk5tE2Tj7rd1mLmW2i
vwOPlYhAzQTPyIPS6DR6jYXpbSnxW6iU1iGLAgiIagWoECdy8D3DFEe5wjMz
fuKgKtIYHjrcwi2hDYWXou5sWySEFxOO5GO/ELTQtqzPvc09FewpGAWI
"],
Association["Book" -> 4, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGEWBkgjiIEQiYmYCAgQnIA1KMIHEIj6qACAMZQc5h
YkILKUZkPsid2BwHUoQZwoxYmEyoRjKC/MrIDBYBhQVcLUwACpiACBhoQAwN
MgZeZm4A0RoDBA==
"],
Association["Book" -> 5, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGBgBtZmQEU6OAugAAmjwCfg==
"],
Association["Book" -> 5, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGAjAyMgyU1cMeAACY8gJ9
"],
Association["Book" -> 5, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGBDAxoFsN5TOCAJzPCIKMaEroAhjpax1ORzCg+J6R
EYpgYoxwBtzBAKqrApo=
"],
Association["Book" -> 5, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGCKBbzQQRYQIBCB9MACETIxQw0dF5QEuh9gKdSi5g
ACO88jAWdkfAwgEUXGAOODjgIcIACSqQJFAMpAIoCAD6HgM0
"],
Association["Book" -> 5, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDDACbR9QBwxPAACY4gJ9
"],
Association["Book" -> 5, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDjAxMoAgCDAykukURqhuRjCTEWweI1iAEWomVBIF
MEAxRAuacYxQxsAGDjKAuZEoFwEAzJcCtg==
"],
Association["Book" -> 5, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGEDAyoDmAkRFKARlggiBgAhNAAGYCKTCDCQqQJFEA
AxRDtKAZx4TFGnoDVJ8zMTGCxZjQJcB8RhQeAwD8LwLx
"],
Association["Book" -> 5, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGFDAyMDKCSAoMABGMUFOAFCPEUAhAkkQBDFAM0YJm
3IAHCgaAuZEolwEAxeQCsA==
"],
Association["Book" -> 5, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGOcDtRKAMIyNWFXARRkawCoi6EQIAoP4Chg==
"],
Association["Book" -> 5, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGGjBiZRJSOgqgACNMAJitAn4=
"],
Association["Book" -> 5, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGGjAyM7AwMzICncKMKclEf/dAACMYDQ2AGkgArtoC
kQ==
"],
Association["Book" -> 5, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGHDCCERAzMjNiAKA4AjDT01VgN6G5AEkWLs2IJgLT
ywCVYWSEsWBsFBEoRLcdTsINgRiKrhIYJlAnMkDNAQDfGALi
"],
Association["Book" -> 5, "Theorem" -> 16] -> CompressedData["
1:eJzNj8sNgDAMQ218YA5WYoQuwKxsRJImrVDviBysfJ5k52jX2QjgdvlBaTch
Ni4lgiPkp2klc5YsgLXvUHF1jaGWPSdZYhASQlH5R26m2fIZh2bX+XLiwHxU
rhjwA/bZAw8=
"],
Association["Book" -> 5, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGAWCEuGOQuGaIAwCYwQJ9
"],
Association["Book" -> 5, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGA2ABEcxYXMMIIRgZYexRAA4HRjBAEkAAAKXMAo8=
"],
Association["Book" -> 5, "Theorem" -> 19] -> CompressedData["
1:eJzNj8sNgDAMQ22isAcrdYQuwKxsRL5SJcQV4UPquD68HPMckwAuH38RsRsO
Xbm6tnDsxodSNRa16VZE2Kpff2PtXBJ7gVdUCd2qOyJZz5F3DnaDz7BsQnR6
A+3xAwc=
"],
Association["Book" -> 5, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGB2BixS1FR2fAAQsYDQJAsu8BpmcCjQ==
"],
Association["Book" -> 5, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGCRhETgEBxkHnImIBAJecAn0=
"],
Association["Book" -> 5, "Theorem" -> 22] -> CompressedData["
1:eJzNkFEOgCAIhmEw5zW6UkfwAp21G/XzQ1s110NPfSIiiArL2NahIrKH+g0W
ygMaqTCaFT5JYgUKaGKhocUleENqZsrjOjq6Wc9X8bGvCOU1flpTouDGEtAc
bBStcTdIZWWrIghfnIDzAMxHBKU=
"],
Association["Book" -> 5, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGF2ACATADRDAyAzETIxQw0dMhjIxgAkQBbWaCOAJJ
Fi4NFQQ6E0kcIgQ3iBHJUEZUETDE4TOQIqgUEy41EGVgeyEqANTtAtc=
"],
Association["Book" -> 5, "Theorem" -> 24] -> CompressedData["
1:eJzNULENgDAMi2uHP3iJE/oAt/IRTdIOSMwID5bjWJWbvZ9Hh5ldQf+CB1IU
0UiXOwD5hz3atjUFaKYHyOgiFQvTRjrFTAmZYBldKZSfDmM5ofcS8WGWVA1x
jgEljwFrOS4UifHWDZerBEk=
"],
Association["Book" -> 5, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGEcB0DhMOcdoDFhYGRkYWIAliMjExMUIAXBbEAgtA
hRiZwAxGJLeyMEAVoXkAKoIkyETQOagqGFGYjCjGAwDJtALT
"],
Association["Book" -> 6, "Theorem" -> 1] -> CompressedData["
1:eJzNTkuuAkEIBKuhYXq6x6TNy5vE8bfwQB7BC3hWbyTj5u1cuXi1qAAFVZzv
j9udiei50n/CqW/HWrfLflmGw2We20+h8XeWeScCr/7tvPJZXWUlmqber6NZ
cZEUAFCrBbubw8W9RDWsE1EJfhMwNUGDR+cY3rAiGGEmsHWpASVOVHsEpbSh
DUONktKRWTQsTIuriuYwzixZPPEfwNx3rfdM2TLis8KgFwDKCSk=
"],
Association["Book" -> 6, "Theorem" -> 2] -> CompressedData["
1:eJzNjTsOwjAQRNfO/rJeQ4IV8ZFAQkJQcRmOkAtwVm6EDQUdFQWvmGJmNHOc
77c5AMCjyV+xXQ/jOF1O5/Nyv5umsnHIu5Me1sxoY//rO/+etlgAUirlkFXd
iPCNe1/VrDc0MnMzleYQt4a8a9kJHa1ahumFpuaoEmorOWJCEpFSjxAjxNAx
AxJcQyDupFNa9cxSZ1k4iHKm+KGLMefFMAho1nqOJWJ4AmA7CbY=
"],
Association["Book" -> 6, "Theorem" -> 3] -> CompressedData["
1:eJzNUMkRwkAM8yE7dkiYtEBLlJAGqJWO0JIBXvx4oMfaI40ley/77bqriNzH
81+YIqLOp3Ut1swJYlOhygwI/Dpt/i6pCqCqJpJZlUa0vbAs7L0Jb6+x4NyD
QYS7Z7A9SliTaT/GCoN5IzhgSPozEGDUOFPEZX6qQpfyTPiwHpql6QdcEhs/
zLSTeeqtLg+BNQXR
"],
Association["Book" -> 6, "Theorem" -> 4] -> CompressedData["
1:eJzNjTsOAjEMRPOzHSfZxChaEAUFEohPxVk4wl6As3IjvOnpKHiSRx6PLR+X
13Oxxpj3Kn/G9XZ+lFrKqdaU7mU2+7ZRmEku9Otn8WvirHW9a1N0K6bUdrV2
oQEAxCiqooBQa701dTrhnFWHqGECBsmkkQxAbwlq1YK8huo4ckz6yHtvnPNM
xqGZnAX0zSMirBUQtsHilCGhDsEPLAZOmTmb7WGGIIAu2A996Apf
"],
Association["Book" -> 6, "Theorem" -> 5] -> CompressedData["
1:eJzNjTkOAjEMRbN4SWwcMkzBUiAhUdFRcBGOMBfgrNwIZ3o6Cl7xZX/b35fl
9VxiCOE95N943O5Va722pnqXOZzqxtQNnm/061/fA1OMaZq82PoWMevBbNeL
w4yItXbX7mBns8nMu+GrutoQRC0FC3ZlH7UVIEJCs4KGbQy9q6LC42OCkFOu
HBIGyREotUx+AAAeRg0jNAEhNzGvRILCIlTC8bwH8vgE8QMqcQnz
"],
Association["Book" -> 6, "Theorem" -> 6] -> CompressedData["
1:eJzNjbkNAlEMRP8xtv9prT5arUAQIFIi6IQSaIBa6Qjv5mQETPB8aub8fD2e
3jn3XvF3ut5qr/UyTa3d2+KOVVvvKfG4ya+jvhsG78M8W9PtS1LqB9XdYBZh
BlDKMA4TBqvOqiLrpvRubCusZEbG6IyBaRMLIFBlKNp6tKnkkpMFxRhdCDGL
C+Ra8CRRIzOTBRIRK3m0gsK2pLjJm0WuVYrbnxaQggP8ByvOChE=
"],
Association["Book" -> 6, "Theorem" -> 7] -> CompressedData["
1:eJzNTTFuAzEMsyVRsmX5jByKogWyFOjQ5Dl5Qj6Qt/ZH1WXv1qEERIgiIX7c
H7d7LaV8H/T/cPVw/1xrjMt4KWefM6J3O33pXzf9/pBqpX3PZcuUmsV7xGmZ
tWYGoPeVvBJYNuc+Z6q8NPfkeRDgGTUsz8F8QhRQRBgC8zBTNR9uWcTMhYhV
CkkZVGG8sbAIQOlJcKVwasqq4CeqSrPuauXt/CrYREjqD5fACUM=
"],
Association["Book" -> 6, "Theorem" -> 8] -> CompressedData["
1:eJzNjksKAjEQRDtJdU/+kzAMggjiTtfexCN4Ac/qjexk786Fr6HoD3TV5fl6
PA0RvYf8IbnmfOu9lHve6JTXUqv3sl+XXxt9f2iNsb2PLERBqcdatyYTADE2
1aagSSkaVWRsQkqqU4AcBAEtCRrqhD3gtRdUpHHUKXgtNXLOkbUuLGSFijW8
uNWpG6shM0thgxwRRZfsJkYQfcoh0OG8A4XFwnwAo+QJgg==
"],
Association["Book" -> 6, "Theorem" -> 9] -> CompressedData["
1:eJzNjcEKwjAQRHc7m23SJG21QhAr4qE3v8ZP6A/4rf6Rm4J48+TBNzBsMgNz
XR/3lYnoWe0fWW63vpRj2Z0TxXnWSwFcGMKvd/LXNCUztVaeplNU7Tze9H29
vQGTT3a09UdEzFW2UuyADt4eHmFDI5CgahWThYgQVZ1sSKShhrltSRwtzJBG
2Os+WO5MrbJ6l4U/gDkPaRwdheTr+IFBL1dJCHM=
"],
Association["Book" -> 6, "Theorem" -> 10] -> CompressedData["
1:eJzNTVsKwkAMTJpHs+7W0m2xIAVR6IU8Qi/gWb2RSUH888sPZyCZZAbmuj3u
GwLAM8ZfYl2HeZ6mac5QTotdFhFKNf26Jn93w9bY43guqgejN0oJbQ5yWnbR
xoeZfSrvoa54kMwPo7RDc3xUPeJ0SZlYVUcvYm6gQTeBBW6IosRkMiT3xdkq
qnLH+AEh9v2xVgHrLLorErwAEM8IPw==
"],
Association["Book" -> 6, "Theorem" -> 11] -> CompressedData["
1:eJzNjcEKwjAQRHc7m+2mSdraHoJYKIJXf8ZP8Af8Vv/IbUG8efLgGxg2mYE5
3x+3OxPRc7P/5NrXeqyHNVNaFl0rEOIQf71SvqY5u6m3yjyfkmpneNP3220O
XJbNYrv9iIi7yl5KHdDB/GGIO5qADFWvuDxEgqjq7EMiDTXMbUsS6MIMaYRN
p+h5cLXKaqEIfwBzGfI4BorZtvGJQS/3UAgj
"],
Association["Book" -> 6, "Theorem" -> 12] -> CompressedData["
1:eJzNjVEKwjAQRHc7m03SJG01H0G0iOCJPIIX8KzeyE1B/PPLD9/AsMkMzOX+
uN2ZiJ7d/pSptUPbrZnSetJzA1yc469Hytc0ZzO1Vqn1mFTHgDfT1O9gwBSy
Hb7/iIi5ylZKIzAi2CMgbmgCMlStYrIQCaKq1YZEBhqYvSdxdGWGDMJBa7Tc
mbyyBleEP4C5zHlZHMUc+vieQS++jwf1
"],
Association["Book" -> 6, "Theorem" -> 13] -> CompressedData["
1:eJzNTjtuQzEMk21JFG28jx/SZO6VeoRcoGftjSojc7YO5UBKIgTy8/n99Swi
8rPov6L3iJueMhEP4LrO+2x/naHvrVJkjNSHiLsqNoBxHOc+BjuBSI5Ej50c
JGxd3D35YxEZdtAYvjP4gmOj59tB8L7MVJ/XfPVoUksNz0CJnLTM2oy1taZm
SpN2DQ0okIUWCswiN5ftNgxboPbyC7uGCKo=
"],
Association["Book" -> 6, "Theorem" -> 14] -> CompressedData["
1:eJzNTTkSwkAM8yKfG0LJQDpghgfxhHyAt/IjFDIUNFQUyB75kI/TfL/NTUQe
C/0trpdzP5b0abTt1gwx+q9f5Fe1imR0633s7hV4IyJWDtCiItKWjqqSTV9D
lUAiWARyxUAR7oAzUsQANd7nIy5IU3aZyU6bp/LQxjRTo8ytFtW0fWCfOR1M
3BwKHRvkCRlTBv0=
"],
Association["Book" -> 6, "Theorem" -> 15] -> CompressedData["
1:eJzNTkkOwkAMyxBnmdDhBELqpeJLPKEf4K38CLcSBy6cOGCNPEmcOLmtj/va
ROS50f9iWWouOc7DpslMc/ivN8RXtYpkfFY1yr2HvuG+xUFoaGZlhm0VAGTD
3lRdtWswCe07oihymAb8KWopjP5cxAFpYJWRnNA8QaODIRPRza03OAztA+fM
68V4oikUo6m8AOuyBtY=
"],
Association["Book" -> 6, "Theorem" -> 16] -> CompressedData["
1:eJzNjjEOQkEIRNllYAG/25qvlbW38Qj/Ap7VGwlqY2Nl4SOZEJgwnLfbdWtE
dC/5Yy7jGOSrsxmzWODXAbuv24gUITKb013V84s3EdVbwlkWZq41AZAqeJrK
n1uU+ouFWVm1VGrMC0NVZwb1DurIC9SZAo3rCNI2BoaLijcMCNoHh7DTKpSW
Ct83pgfKqgbU
"],
Association["Book" -> 6, "Theorem" -> 17] -> CompressedData["
1:eJzNjrsNgjEMhJ34kXMeNSAkJFZihH8BZmUj7HQ0VBRc8flkO+fcj+fjKET0
Svyz2hk0Ts4AM7cuv873r1MgoERmc/ow6xBW5RT2j5AFu6BbdlRkcy95dGIq
ybHVV/rWmI01LS9Wi/w4VKtQzYdB6lI4vVSNdWmupl5EI7p86DJxuxqZIM+u
IvQGjjUGsQ==
"],
Association["Book" -> 6, "Theorem" -> 18] -> CompressedData["
1:eJzNjTtuAzEMRClpOPqsREOh4y5B3OU8OYIv4LP6RtZu7y6FH8AHfoDh9Xb/
uwUReex6a/qn/HQbY5TCj9/83/GvA2MI0X01JlJKrfY958XJnEkArfmyL+A0
czNy32xmy2MX0CtR4UY4TgdagII5iYmxH9e0ta3V9SilJDGmmiWqjBg0p5lI
qipWcWhAb+hcS00HgWhl67XK5esM7WBEeALe/AkU
"],
Association["Book" -> 6, "Theorem" -> 19] -> CompressedData["
1:eJzNjc0NQjEMg/vjuGnySh8jIDERI7wFmJWNSOHAjRMHvkiWlVjO5bjfjpxS
eiz5b2bar8beAc4Tf93ev/+e70hr7jZUNwNEsGgtPCyAwX26O9eGZGjnK7Q8
YaGG7YWOaIAqoDFxxACbNo9HtdaUUYFwaUMGK9asuIiwSYarSPmQS5nkeWey
6qiKUZCf5fMHOg==
"],
Association["Book" -> 6, "Theorem" -> 20] -> CompressedData["
1:eJzNjc0NwjAMRu04duzGEWkPSBUSpTN0E0boAszKRri9c+PAk/XkH+nzur+e
OwLA+9C/c2+tVDer82y/zv4emBDTtkXjAKqt1av72FWnSVVEhqGHeyBdl2Vb
llKOjdYaPiViRaVIrypd1pMYo9xVXLzwOamZtXhElAATMgMxXBLmTIqaJTMT
B8pIjxs3IRGmkziaaS0OI1fOQy6U8QM+IAni
"],
Association["Book" -> 6, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLAA6npERQmPKQBmMYBUQdSMEAACfzQKF
"],
Association["Book" -> 6, "Theorem" -> 22] -> CompressedData["
1:eJzNjUsOwjAMRPObdJyW0kBpVQJILLkOR+gFOCs3wumeHQsszdPII4/v6+u5
WmPMu+Lvp9s3u47k9ZJ+Xc2vibPWzbMaFdn3/WNZbkUkJREAImdlKeeCIjnP
OUfUzTCdlGMFkBpBgzIJCsZtQD3Fsqgw1hAMQz7kXh9574x1NgTjo8nV+GTp
GdRoWSSsPw4YCbLZ+hEYU8uOO5MxILQhergPO5oKIw==
"],
Association["Book" -> 6, "Theorem" -> 23] -> CompressedData["
1:eJzNTssRAlEIg0eAx/u46tiALVnCNmCtdiS7Ox69eTDMZCBkAvf1+ViZiF4b
/T9mjAFYP9uvk+PrpjCXOZnZiVrrvQ33HvggIg4OZMWMaLopqprsupuq5deI
HAJtR52b4p6WrGwxoZ7JeVFEiCFAdnQCw8QFEqgVbuZhjOZqUkTKARa5drtd
jBYbkIpRwG+WxAcG
"],
Association["Book" -> 6, "Theorem" -> 24] -> CompressedData["
1:eJzVjTEOAjEMBB3Hdhyfj3CHFIkGiZqWl/CE+wBv5Uc4R01HwxSrlb3avW7P
x5YA4DXkD1juN1Vpvf66+HshpoTuYRSgtd7PzezgHBCFqA7vATubudlcfL/r
rjRy8Yyv69Dpw6p8ijyzcWFyppW1Wu0xRISxmkWAGC4psWTNymsVKdEpzqkM
g4IYqUFGavNhWQpMx4lYyZDTG3gKCIs=
"],
Association["Book" -> 6, "Theorem" -> 25] -> CompressedData["
1:eJzVjdENAjEMQ5OLnbY56G2AhPhjHEa4BZiVjUiL+OWLn3Ol18hO3ev+fOwq
Iq+BI4i83S+l2L97fxSqCpB3iKwrQAKwiFZa61vPOWmpzRoyo32dZCDRuyM6
0mrd8sFcsuFg+qeBbucsDXy+zGPLIgpxVcvRTDkCdxpddK0IVrLUKWOBzQSV
4XSWzd/inwdp
"],
Association["Book" -> 6, "Theorem" -> 26] -> CompressedData["
1:eJzVjbsRwkAQQ+8neW+9cHh8w4xDaqATSnAD1EpH7JmYjIQXKFhppdv+fOwx
hPAa8hfc64TLtf66Vr46KcZk9om01vvWVM8GpxSSIuZqDg2qpnqa7LjLoSAB
M9B9GTof2FrZqQoqJw8QK6Vq7T5USvLVTIaCsMUIZsmCpXJ0eQfi+EFiSp4a
5FSWdm7LFOY2A1I0l/gGOscIZA==
"],
Association["Book" -> 6, "Theorem" -> 27] -> CompressedData["
1:eJzVjcERQjEIRIGwEPK/yegY77ZkCTZgrXYk0bM3L77DMrMsy/X+uN2ZiJ5L
/oNaLY7x89avG2GWutaFqPc5Z+y7hyeqAGqN1EiwzOo+3k5rDWtkRjUvsCOa
I/Jg0eeGCz6+uqac0cxt5iNVya/FjBR0YoYVLRVbmFlWWoCtMCAmkqlFER2H
PkaQb64oaqL8Ar0pB5k=
"],
Association["Book" -> 6, "Theorem" -> 28] -> CompressedData["
1:eJzVTsEJw0AMsyPZd7lQCDS5exc6ROfoCFmgs3aj+lJofn31UxmEkI3ky/a4
byoiz05/gtvVHb8O/RI4DEKqahEZR9IYQM7JU2qtAngzGjLAEIaPX1hbXVdj
bgwrN+ynHeNqC3d/ypV1wRmlFO6VGoPoVYqrIiSg1hfwyHfRKWGyA2rWe+li
tDletNNsLx4lB/o=
"],
Association["Book" -> 6, "Theorem" -> 29] -> CompressedData["
1:eJzVTcERAkEIg0vAY0/H5WEB9mAllnANWKsdyd7N6M+XHwMTmMAk1/VxX1VE
noP+BTd3/Nrzi6GqkDWbSARpLCDi4BGZHcDOSATAWgxvvbGod2MkS4rE9jrQ
0jo3fRmUOKO1xj2yCtMkSnFV1AqojQNnwmbRZcbRPkB15dKFbienWbvwBaQn
Bz0=
"],
Association["Book" -> 6, "Theorem" -> 30] -> CompressedData["
1:eJzVTkkOAkEIhIGCHnpMekm8+yWfMB/wrf5IZmLiyZsXC8JWbLf9cd+ZiJ6H
+Rus0F+vtO8UMwHpa2p1NwNUI4qv65zDXedsmugaqkmJviu9t3qErUFiysip
rmdrNsk2MYBIux1kl5yP8PMgU4oIkRIyWWhhWSzrrAWCQlyLFP2AAcm7ZuSK
S35occULoOAHag==
"],
Association["Book" -> 6, "Theorem" -> 31] -> CompressedData["
1:eJzVj8sNAkEMQ/NzPCOxRdASJWwD1EpHOMuZGxd8iEa286K5n8/H6Wb2mvE/
WvlrIr5HEUa6uyoAiequnFeNgNRMSWaVTKVyCFzpVYpAxSwpwkeCqNqiTSlm
jd1NHcx0C31ymbe1uzYPC24XRl1uGHg0kzrKS2IL2FR/3RIbjPI3vUoFtQ==
"],
Association["Book" -> 6, "Theorem" -> 32] -> CompressedData["
1:eJzVjc0NwjAMRp34s52kaRMFUZUjKzECCzArG+H0zo0LT/KTf2T7/nw9noGI
3lN/RP71Qfs6iSHEffekEYnU2o7er8MsJTMAKQ33cDC0tb01s9kp6+quU8CS
DRljVQxcTtR3Db17YJtDr0ouufoj5kghMkAsNGJQxcaJDSIsziaBa5GirCp8
AkXOZbGFbvWAbLCI8AHuyAhD
"],
Association["Book" -> 6, "Theorem" -> 33] -> CompressedData["
1:eJzljdsNw1AIQ3FsE27UJbpSR8gCmbUbFfLTvy5QI/HyQTzP63UiIt6T/ln1
2x1bEftetcrOJCWO1uqe2WJHVqY8G9ud5Rs6VoPMHvJGB5p+GFNjdrWk+5EQ
ENKxMY4NfjAwN5I1UKNEEl9tQK2jSjGUQIPxAbjoBWY=
"],
Association["Book" -> 7, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGFGBkRHcySIARLAxmMEC5EADVgiIG5oMxAyMDI6aB
GKYPMQAAxXUCrg==
"],
Association["Book" -> 7, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGFmBiwiLAxAQmwRwoFwIgCphQxMB8MGYEQiZUAxmh
GMJhhFjHCBYlAzCAEV55KIMywIggGBkBJVEDRw==
"],
Association["Book" -> 7, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGGGBC5zOBMJhkYGBkZAB6iZGJiREMwGpBDAiJAAxg
zMDECNGJGzAOvRACANOEAr0=
"],
Association["Book" -> 7, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGOGBmBmEwycDAyMgA9BIjMzMjGDCDFIAYEBIBGMCY
gZkJohM3YBx6IQQA4HUCyw==
"],
Association["Book" -> 7, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHGBEB2ARoDhIClMWG2BAplHMBpuBbBedPUc5AADe
BQLH
"],
Association["Book" -> 7, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHmAEOntoupweAACYNwJ9
"],
Association["Book" -> 7, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGIGACo1GAFQAAmVACfg==
"],
Association["Book" -> 7, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGJhi6Lqc1AACV/AJ7
"],
Association["Book" -> 7, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGKAA6nRGr87GLYjVgWAIAmv0CgA==
"],
Association["Book" -> 7, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGKmBhAWJGIGBhAJEMDCDECCGRAAucQAIMUAzhIAGI
GTAOI4QDJUgHDEi24JDHdAIZgBFBMDICABMDAzE=
"],
Association["Book" -> 7, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGASpgYhpoF1AGAJfgAn4=
"],
Association["Book" -> 7, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLmBmJl4UizpqOmUQAQCj6AKJ
"],
Association["Book" -> 7, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLGAFIiYgYGUAkQwMIMQEIZEAK5xAAgxQDOEgAYgZ
MA4ThAMlSAcMSLbgkMd0AhmACUEwMQEAeRAD0Q==
"],
Association["Book" -> 7, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGMmBjZmJkZGNgBAIGBhBiBJPMjFDAzMzMAaJZmRhR
AAMUg0lkAyFmwDhQWShBOmCA2YJbHsqgDDAiCEZGAB46Az0=
"],
Association["Book" -> 7, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGMGBhYMT0AQsLgs0Ik8fiURZMoWEBAKp7ApA=
"],
Association["Book" -> 7, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNGBiYgD6gREIGCAMBkYWFjAfDJhA8iBJJkYUABJk
YYCqw2k4WB2EZmBgJANATMArT8AJxAFGBMHICAAFjgMk
"],
Association["Book" -> 7, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNGBlZmTkYGAEAgYGEGIEk0yMUMDKysoGotmYGVEA
AxSDSWTzIGbAOFBZKEE6YIDZglseyqAMMCIIRkYAIcIDQQ==
"],
Association["Book" -> 7, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNuBgZGJlYAICBgYQYgKTLExQwMnJyQyimTmYUAAD
FDMCIROycUAOIzxQgCywLFiEkQzAAEZ45aEMygAjgmBkBABXpgN8
"],
Association["Book" -> 7, "Theorem" -> 19] -> CompressedData["
1:eJzVUIENgCAMa7c4lC98yRN8wFv9yG2IRr3AEjpWuiYwr9uyEsAe9HOQRHUA
E1BHFJEiZqWYQ1UZlTparA74dtM0kDF5wzxwuKOh6lUkycGOdk5JXkpykyIh
G7nG4nxyXGaX+a9XPTofSO3rCyObm+0zeAAetARy
"],
Association["Book" -> 7, "Theorem" -> 20] -> CompressedData["
1:eJzVjMENgEAIBBduQ64NW7KEa8Ba7UgWNfczMb6cwAAhsIxtHQZgl/5OByJJ
AyRoxggWob2a0xONxhbsdTlpmX4P7npYVXoPKh73V/MNn3I/AMzbBC8=
"],
Association["Book" -> 7, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGAWAHAiDJwMDBysDKyMjKyc4KBuwgSRADQiIAiMvI
ysLOysXJzo5sEgsQwwOFmZkBpBVEgwjSAQMY4ZWHMigDzAiCmRkAJvUEww==
"],
Association["Book" -> 7, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGAWAEAiAJYoBJJkYoYGZmZgPRbHARCGCAYjCJYhID
kgBMFkqQDhhgtuCWhzIo9D+CYGQEAAf3Ayg=
"],
Association["Book" -> 7, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGAWAEAjQBhCCUZgRBGGCAYCwmQfEQBgCyEQKa
"],
Association["Book" -> 7, "Theorem" -> 24] -> CompressedData["
1:eJzdUdsJgDAMvMZaGywW6l//XMkRuoCzupFNteADBH+9hEtyIYGQKS1zUgBW
oT8gxggEwDv0RNx5tpaZPRGpHJmagcUqIBrb4LQex/MiC1BbC61hzB6FvgPF
X/tHcsf1MfmKotHzciVe5oVU3rUBYSQGUA==
"],
Association["Book" -> 7, "Theorem" -> 25] -> CompressedData["
1:eJzdUcENwjAQc+6sJgUKUis+/bESI3QBZmUj4itBpWyAEzm2o1xyym153JcE
4Cn6C8xXYAQuJxzN+jyUwGBmScL8XDQaoKzk8UBO07ZOBozNuKPr6koGVXjD
qiPiLgleI1UIw88x6TdrMxy5bwffH1O7iMx+G0+aHq+Vq3e8AAkOBdU=
"],
Association["Book" -> 7, "Theorem" -> 26] -> CompressedData["
1:eJzdUYkNwyAQM3dWoE9SKVEH6EodIQt01mxUfClRmm5Qg4xtxMGJx/x6zgnA
IvoP3IERuF1xMTvlvgR6M0sS5kPRaICyksczOU37MhkwNuOOrqsrGVThDauO
iIckeI1UIQy3Y9If1mY48tgNvj+mdhGZ/fadND1eK1fveAPt4QW7
"],
Association["Book" -> 7, "Theorem" -> 27] -> CompressedData["
1:eJzdUYkNwyAMPBwrJsJqJTJBVuoILNBZu1FtU6o8G+RAZ99ZGCy29n61BODj
dBtU4KkoRItUzVlVKxEli0rTQ30NwD0ttTCv675HASgPIYJ5tsgcZJCBnofF
Jye4W94hBP+Pef5jL4aK/kccP8amCI+uQyffEq91ZXd8AasvBwk=
"],
Association["Book" -> 7, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGE+DjZuBiYuJk52YHA24mJiZGEIOJmZcdBGGAASTG
zibJycIiKopsABsDAxMzjMPMzMDKCqFBBOmAAYzwykMZ6AA1YoC+AIsxYfqY
EYTA+kEEI9AsAJaGBU8=
"],
Association["Book" -> 7, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGESDPO8MsEACWtgJ8
"],
Association["Book" -> 7, "Theorem" -> 32] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGPBhmgQAAlbECew==
"],
Association["Book" -> 7, "Theorem" -> 33] -> CompressedData["
1:eJzdUdEVwyAIPCCBJ6Y/2SArdQQX6KzdqEJqXpNs0FNP7hTF59Zez0YA3kF/
hQcW5jrNXqu7zyJCfXaS1aMNoA/2opOI2W9+AViHUEXpBnKLBXRgj9Oyi5O8
W3FCCjvSIv5yLKY6l5A4fwwzpcf3B1P0rDiI+h0fU7EGwQ==
"],
Association["Book" -> 7, "Theorem" -> 34] -> CompressedData["
1:eJzdUdsNwjAM9KMOQU6ohJCqfrISI3QBZmUj7CtFrdiAS3L2XeI8lPvyfCxM
RK+kP8MsMg3Wbld3N1XliM568WytOUAx5FxPg2qt++oQYpsohcYxYu+ggG1Y
c1iZlJ0DXheRGUH0b1nmH85JKOx/xPFjRBie/D6Xs+PGSRxnvAHc8Qem
"],
Association["Book" -> 7, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 36] -> CompressedData["
1:eJzdUdsNwjAM9KMOQU6oVIkf/liJEboAs7IR9pVWrdigl+Tsu8R5KM/5/ZqZ
iD5JZ4PIY7B2n9zdVJUjOuvNs7XmAMWQa70MqrXui0OIraIUGseIvYMCtmLJ
YWVSdg54WURmBNG3ssx/nJNQ2P+I48eIMDz5fy1nx42TOM74AsfMB5E=
"],
Association["Book" -> 7, "Theorem" -> 37] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHWBBMBkZoT7E4lEWTKFhAQCgAgKG
"],
Association["Book" -> 7, "Theorem" -> 38] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGM2BkhPoQi0dZ6OsUugEAnAYCgg==
"],
Association["Book" -> 7, "Theorem" -> 39] -> CompressedData["
1:eJzdUYkNwyAM9BMTKluRKnWBrJQRskBn7Ua1L48SdYMecPYdmEfM63tZmYg+
RX+IweL1dHdTVc7orOFo4QDlkEcfB9Xer5UpxA7RGk1TxghQwg5sOaxK2sUB
b4vIjCDiLKt855qEwv533D9GhOHJ71O5Om5cxHnGF434B0I=
"],
Association["Book" -> 8, "Theorem" -> 1] -> CompressedData["
1:eJzdkNENgDAIRA85GtZwJUfoAs7qRgJNmib6558v6bXAHR/d+3l0AXCl/BFv
lriIbPkQqdra6BvibEZvNPc1SEDmp5Dhi1u1JCD1CYuXgYKaOS6m4eMQTOM3
mFJLYukN8sIEnQ==
"],
Association["Book" -> 8, "Theorem" -> 2] -> CompressedData["
1:eJzdkd0NwyAMhI1jOYEDoSp97UNWyghZoLN2o9qmrRp1g36C43z8CMR23Pcj
EdHD5S+5lNJ7uzHz1A2elrrUua5rDcg6o+SrSM7f+woRz++iNVK1USTEAHRg
fqiohWjAJwkdiwhKVkBFEQz/Up+MKs4/c/4Y5hQZ/z40eYM7v2lS6BN4owb0
"], Association["Book" -> 8, "Theorem" -> 3] -> CompressedData["
1:eJzdUVsOgzAMc5K1Ql1BVX9giJ9daUfgApyVGy0JA4G4wazWtd2mD/U9L5+Z
AKxG/4ncTdMrigiNCpJcc33Wcej7qoB27trwEAnhXNYCnHZTCppGxxidFGnH
pj0yUU6J87YIKcFNPMpM/9gm3fn+V1w/hpk84/s7yZrf2Ij0jC9c/AhX
"],
Association["Book" -> 8, "Theorem" -> 4] -> CompressedData["
1:eJzdkesNgzAMhP1oZKOAfyH43ZU6AgswazeqfaAK1A36KbncOS9FeW77a2Mi
epf8KWvE2FSVI2Gd+tTHHtEBZZfB7aHqft2VQdo3OC1LjvMMScxaswLeUCrj
lwr0WERmhHBkO/2pNYmE8+/cP0aEUZPfZ3I1K1fCeccHW9gI9A==
"],
Association["Book" -> 8, "Theorem" -> 5] -> CompressedData["
1:eJzdkd0NgCAMhPuHBFPQFVzJEVjAWd3I0geiQRfwy+USjlxTwlaPvSIAnM3+
Sik6MTMWAzkbRddFNasq5Kw0JxFmkXspAVDoh9QEEKObE0J8Ib2FVnN90y+H
5Z8fQ4Se0fhKbPJ+M7RZF0ikBto=
"],
Association["Book" -> 8, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLVCVYWVmZmZUAAJGZm4hbiEuIVERcXEhIGAAYiY+
XpA8KyuyHl4GBiYuGIeHh4GDA0izsYEJIOCCAQgbLARi8CCJgEmIIgYuLgYw
hw2uDcSGkiBJMA9sPipAjRgmJkawGBOmJxlBCOxiEMEItAMANhYIKw==
"],
Association["Book" -> 8, "Theorem" -> 7] -> CompressedData["
1:eJzdUckNgDAMc1K1QqHwqEB8+LASI7AAs7IRSTgEYgOs1nWcpocyLeu8EIDN
6L8YYwiBJgWFutRFSt8NQ1FAJ7eN5WN8ljQAyxXkjKrSNSUnhVw4tFsm8sNx
PjZBBB6ku8z0yZb0yM9/490YZnKPv38kG/5iI9I7dhYdCAo=
"],
Association["Book" -> 8, "Theorem" -> 8] -> CompressedData["
1:eJzdkdENwyAMRG0jULg4leo/PrtSR8gCnbUb1TZt1agb5AkOn20QiNv+uO9M
RM+QE1NLKTwcLqutBrPrGOaQT7lsUa/1d8dGJPiY3mlZfG0txQF04vHUpp5E
B76Z1NlEUHIDbYpkxm+NYro8/8jxY0Q4c/L/RI6RN9ZwCn0B9uYIDQ==
"],
Association["Book" -> 8, "Theorem" -> 9] -> CompressedData["
1:eJzdkYEJwzAMBOWPlOYrCKQbZKWOkAU6azeqJLchIRv0sB+9/DYIr9vruTUR
eaf8MwCGOcAw+eQ3XxYvJDbu5EOVPF4Ig/FnIjemUS3RDFsn6q5q0aSTe6e0
h4QmYWhqLHr91TwsV++fOX8M0KqH64QtV41g6Yz2AdMKBho=
"],
Association["Book" -> 8, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNeDmZmYCAmYOJhTAAMWMQMiErB7IYYQHCpAFlgWL
MJIBGMAIrzyUQRlgRBCMjAAb3gNB
"],
Association["Book" -> 8, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGN+BmZgICZg4mFMAAxYxAyISsHMhhhAcKkAWWBYsw
kgEYwAivPJRBGWBEEIyMABFtAzY=
"],
Association["Book" -> 8, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGOWBmAgJmDiYUwADFjEDIhKwayGGEBwqQBZYFizCS
ARjACK88lEEZYEQQjIwABwcDKw==
"],
Association["Book" -> 8, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGO2AEAlYmRhTAAMVgEkUxA5IATBZKkA4YYLbglocy
KPQigmBkBADl0gMF
"],
Association["Book" -> 8, "Theorem" -> 14] -> CompressedData["
1:eJzdUdsNgCAMvBZCTAl+gPGfP+dxBBdwVjeS1kc0buCFHHfX8gp1WeeFAGxK
v0edKrlYYpE8DOOYG1By5j5555z3z94EsNwmoevaHIJRg1w4tEUq0iMxPpog
AjPhXqb6ZC2as/3feH8MM1nG38eRDruxErUzdtP4B8U=
"],
Association["Book" -> 8, "Theorem" -> 15] -> CompressedData["
1:eJzdUdsNgCAMvBZCTEE/iPHfT9dxBBdwVjeyrY9o3MALHHdHeYVxWeeFAGxG
/8c4Ucg1V6l9PwxVAe3ctTGEEOOztAVYLlMKmkbHlJwUcuHQHpkoj8T5KIII
3KR7memTbdKd7//G+2OYyTP+vo2s+Y2NSM/YAbFtB58=
"],
Association["Book" -> 8, "Theorem" -> 16] -> CompressedData["
1:eJzlUdsNgCAMvBZCTAl+gPHflRyBBZzVjaT1EYwjeCHH3bW8wlK3tRKAXekH
WMjFEovkaZrn3ICSM4/JO+e87zsTwPKYhGFocwhGDXLj1BapSF1ifDZBBGbC
s0z1xVo0Z/u/8f4YZrKMv08jHXZjJWpnHI/5B3w=
"],
Association["Book" -> 8, "Theorem" -> 17] -> CompressedData["
1:eJzlT0EOgCAMK4MQM9EDId79kk/gA77VH7kNNWr8gQ2UtgwYc12X6gBsSn+A
833uM+dSpikLIJPGIXjvQ7gXDgDxaVJC18kao5GATzRtkYp0S4xbEZhhJl7H
VB+sm+bs/lfDD0fkLKOPn+mwjpWcvLEDbMoHVQ==
"],
Association["Book" -> 8, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGBGBiRAEMEAwUZWBiQlYHDBBGeKCA1TAwwAjSAcQE
vPJQBmWAEUEwMgIA3/IC/w==
"],
Association["Book" -> 8, "Theorem" -> 19] -> CompressedData["
1:eJzlUNsRwCAMCmSSrtQRXKCzdqNCrPbx2d9yJwJBz3Np29oQEbvpH0gmBVNm
hjYvQnyvyWB+ipSq0Sus+kDXFfGVFPfIN5ThPGZ9soflnk/4AFwEHAvJA0M=
"],
Association["Book" -> 8, "Theorem" -> 20] -> CompressedData["
1:eJzlUdsRgCAMC1WQdgA//HMlR2ABZ3UjaXwcnCOYg1ySltexln0rAcDh9BPo
orOaKYE6RXMah2Ga2q4MSHxMSjDzMJMq4oNLM3KRmoR8NSFG0OR3meubvUjH
/Xv0HyMSmMn3WcEHb+wU6hknl4EF8Q==
"],
Association["Book" -> 8, "Theorem" -> 21] -> CompressedData["
1:eJzlkVEOAiEMREuBbBjT7GoAf90fD+QR9gKe1RvZFjVuPIIvZJgZGhLCut1v
WyCih8m/gOvhclx6P9daaW0n7i3FGFP6HmpEvLxDKTRNuufsogDzLIb6oVm0
RAE+jesYIghpgGSBM/xL7dCT379n/zHMwTv+fVWwBXNiSSBPsdYHyw==
"],
Association["Book" -> 8, "Theorem" -> 22] -> CompressedData["
1:eJzlkdENgzAMRC8GH44X6HdXYgQWYNZuVNsBVNQReEpOvrMVJcp729etAfik
PIb+6u7eE8SWbpynaVl+ZwwQPQ0J9wytJFDlIOqhxgiVqldSOoagRBilxUAy
6kOzWa7Ov3P/GJFWmfw/quWqGzMdlV+KKgX1
"],
Association["Book" -> 8, "Theorem" -> 23] -> CompressedData["
1:eJzlkVEKAjEMRNO0ZelIWBdp9Hc9kkfYC3hWb2SSqrh4BB9lOjMNhdJ1u9+2
REQPl//hsC5H1Uvvna564rOWnHMp3yNKxMs7tEbTZHutIQYwz+KYH1rFSjTg
04SOIYKQBUgVBMO/1A8jxf179h/DnKLj3zclX3AnngTyBJCYB6c=
"],
Association["Book" -> 8, "Theorem" -> 24] -> CompressedData["
1:eJzlUcERgDAIo1TCUadwJUfoAs7qRgJV73qOYK4NJORBr1s/9l6I6Az6EWxt
zZqZkVduhqVW1SlBxPIIH3k0a5BDBAPeD1a4KX5fJ3mESEAuBApJjP7mGKaa
V0jMH8Nc0uPvk0qc3BihILgAYJoFtg==
"],
Association["Book" -> 8, "Theorem" -> 25] -> CompressedData["
1:eJzlkdENwyAMRI0BBd2HEyUV/DYrZYQs0Fm7UWyTVI06Qp/QcXdYSIh1f217
IKK3yT8xTa09am30XBZuNcUYU/oeqEQ8X6EUGgbdc3ZRgHEUQ33XLFqiAJ/G
tQ8RhDRAssDp/lQ79OT337l/DHPwjn9fFGzBnFgSyAFz6geY
"],
Association["Book" -> 8, "Theorem" -> 26] -> CompressedData["
1:eJzlUcENhDAMc4Mi8gDJ5dUHn1uJEViAWdmIJgUEYoSzKsd28kjU37otawKw
O/0V5mnKJJEzZRxUu0712R8AscuUgr6vNUbUQVpD1Y3VashC3klwGwIN1dDU
GGj6ZG+Ge68QeH+MSIpMvgclf3TlayejHRTRBwU=
"],
Association["Book" -> 8, "Theorem" -> 27] -> CompressedData["
1:eJzlkYEJwzAMBGXFIjIJvB3wAF2pI2SBztqNKslJacgIPcz7/2UMxo/99dwT
Eb1d/ottq601qrXyumSZppx/xwsRlzP0TvNsu0iIAZSijvmholaiA98mdBwi
KFmAiiIY/lAfRor7r1w/hjlFx/f3JF9wp54U+gHqsQbJ
"],
Association["Book" -> 9, "Theorem" -> 1] -> CompressedData["
1:eJzlkdEJwzAMRM8yIhiOCBzIf6ATZYQs0Fm7USW5LQkZoQ9z1p30IePteO5H
AfAK+TMe3cHau9istVbVc3cGhF/TGqbJ7xzRgFwWC7wequYhG/lLUscQaHBD
U2My6o9GM911heT6MSIlM7k/p8TJjS2c0d5JIweO
"],
Association["Book" -> 9, "Theorem" -> 2] -> CompressedData["
1:eJzlUUEKwCAMixURoWziYfd9aU/YB/bW/Wg2OlD2hAVJk7Rgxf28jtMBuI3+
hlKBrRRZl+C9D2FsLoDoa1JCjLVyJBhUc1YDtTIykYaE3IagCprmtevO1qSb
VyDmjxFxzOT7GmeHGxu5escD94oG+w==
"],
Association["Book" -> 9, "Theorem" -> 3] -> CompressedData["
1:eJzlkdENwyAMRA8DyiE3H8lHfvKVjtQRskBn7Ua1TVM1ygh9QsfdGSEhtv35
2BOAl8vfsa4blvsi81RyzqX8ziZAbkdoDcNge60hBjmO6pjvWtVKNvLbhPZD
oMICtSqD7j/qw0hx/5nzx4ik6OT6mOSL7tSTUt/lNAar
"],
Association["Book" -> 9, "Theorem" -> 4] -> CompressedData["
1:eJzlUdsJgDAMvKYt5iOCgv74I365jyN0AWd1I5P4QHEEj3C9u4SS0qmsSwkA
NqP/YR7RDT21TYoxpvRsNQDJZZhRVXrm7KRgrmsxqD44i4aGO3E+hsACNSxZ
riHTJ1vTnd//xvtjiIJn9H1LsGJTtnYQlh3X9gas
"],
Association["Book" -> 9, "Theorem" -> 5] -> CompressedData["
1:eJzlUUEKgDAMy7oNe6gwQS9exC/5BD/gW/2Rbaei+ARDyZK0jI7N67asAcBu
9ENM6MeBupJijCk9OwUguQwzmkbPnJ0UzG0rBtWVs2houBPnOgQWqGHJcg2Z
Ptma7vz+N94fQxQ8o+9TghWbsrWDsBy2JAaF
"],
Association["Book" -> 9, "Theorem" -> 6] -> CompressedData["
1:eJzlUcENgCAMLAVCHyXBxI8PH67kCCzgrG5kW8RIHMFLc9xdG1LCVo+9OgA4
lX6JeV1wKsF7H8I7LwDI3RBBSnLGaCQgypkVohtHllDxJMZtCIhBDHHkPqT6
Zm2as/tHjB+D6CzD70OcFqnStR0TX6FTBm0=
"],
Association["Book" -> 9, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 8] -> CompressedData["
1:eJzlkdEJgDAMRNO0RXoQ/FE/9MuVHMEFnNWNTFIVxRF8lOvdpRRK53Vb1kBE
u8k/GTqexhRjTOlZj0TcX6EUahrdc3ZRgLYVQ33VLFqiAHfjWg8RhDRAssCp
/lQbevL737w/hjl4x993BFswJ5YEcgDJ6QbG
"],
Association["Book" -> 9, "Theorem" -> 9] -> CompressedData["
1:eJzlkdENgCAMREuBeKQxwT9/XckRXMBZ3ci2qJE4ghfyuDsIgbBs+7oFIjoM
P9XMU00xxpTebSViuUMpNAw65+xQAeMoJvWNWbREAZ7G2TYRhDRAssDV/EVb
9OTn9+o/hjl4x99nBBswZ9cOAjkBaIUGGg==
"],
Association["Book" -> 9, "Theorem" -> 10] -> CompressedData["
1:eJzlkYsNgCAMRMun4UIanMGVHMEFnNWNbIsYiSP4Qo67oyEhrPux7YGITpO/
EpeWU0o5v8umfR0BoFJ0Z3ZRgFrFUN+VRUvjaVz7EEFIA4RlDJm/1Q49+f0z
88fEGLyL31cEWzAnlgRyAVgtBhU=
"],
Association["Book" -> 9, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 12] -> CompressedData["
1:eJzlkesNgCAMhMtDjvvtArqSI7iAs7qRfagJcQQv5KN3bQiEdT+2PYnIafiv
ljqVUusQieT5MaT0rntrDhXAkNbBRg1B4E2cMSSgqAGbDpiivmlNd37+qPFj
ck6e5e8bki34bc0RvABNygXg
"],
Association["Book" -> 9, "Theorem" -> 13] -> CompressedData["
1:eJzlkd0NgCAMhEuhudwMPrmAwziCCzirG9kWNRJH8As5ekdD+Jm3fd2KiBwh
P6a1Wlt7P8IiotNtSAF8NktxAHa87mr0EASeJLU3CShuQPOGoNeXxmK63H9k
/BjVkpl+r1BiIE8bjuAJLwAFrQ==
"],
Association["Book" -> 9, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGMuBkYREVRRZgY2BgYoZxmJkZWFkhNIggHTCAEV55
KAMdoEYMExMjWIwJ0weMIATWDyIYgWYBAGEgA/8=
"],
Association["Book" -> 9, "Theorem" -> 15] -> CompressedData["
1:eJzlj7ENAzEMAyWKpv/xRZoAqbPSj/ALZNZsFMpdikyQs0FLoi3Bz+t1XhkR
75a/ppL8aUqRiT7nHAVwL+vicRdQknZKx9F76wqbGnRYTgrEJnFjLVRdsYkl
ROdmelpmRQJjBCrcKxSOCJFwo17rbX7Bm6f4F+2lbzM/o8cFAA==
"],
Association["Book" -> 9, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGNuDm5kbmsgAxPFCYmRlYWSE0iCAdMIARXnkogzLA
jCCYmQFFogPT
"],
Association["Book" -> 9, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGOODiQuaxADE8UJiZGVhZITSIIB0wgBFeeSiDMsCM
IJiZATr7A8Y=
"],
Association["Book" -> 9, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGOpBE5rAxMDAxwzjMzAysrBAaRJAOGMAIrzyUgQ5Q
I4aJiREsxoTpekYQAusHEYxAswBFMwPd
"],
Association["Book" -> 9, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARJgY2BgYoZxmJkZWFkhNIggHTCAEV55KAMdoEYM
ExMjWIwJ08GMIATWDyIYgWYBADDjA8Q=
"],
Association["Book" -> 9, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQMjI4RkHA7hAQCZkQKA
"],
Association["Book" -> 9, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARQMk8AAAJWpAns=
"],
Association["Book" -> 9, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQwwMzMPtBOoAACbzwKD
"],
Association["Book" -> 9, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQgwMg6XsAAAlz0CfQ==
"],
Association["Book" -> 9, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARgwDpewAACWcwJ8
"],
Association["Book" -> 9, "Theorem" -> 26] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQQMl7AAAJWqAns=
"],
Association["Book" -> 9, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARwwMw+0C6gAAJl9AoA=
"],
Association["Book" -> 9, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQKwDLQDqAAAl/ICfg==
"],
Association["Book" -> 9, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 32] -> CompressedData["
1:eJztkd0JgDAMhNNAOG4Gn7qSI3QBZ3Uj86NCcAU/yvUuCSXQuY59DRE5Q346
uj2OFMBvsxQHYOG+1OhFEHgrqTUkoHgAzQeC8rdGM1O+3+kfozqypt9tRxzk
tpEIXvkBBWg=
"],
Association["Book" -> 9, "Theorem" -> 33] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 34] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARpgHWgHUAYAmJ0Cfw==
"],
Association["Book" -> 9, "Theorem" -> 36] -> CompressedData["
1:eJztUckJwDAM86EM0pU6QhborN2okepPCNkgwghbGMngqz93dzN7SQc7ACyz
TNEA0BoI9ZCUmBXxL8mBQ+1UXyz7lMkSPT8mwqXFeqOzoGs5jYwPQ4QD9Q==
"],
Association["Book" -> 10, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGASZgHMIBAwCWWQJ8
"],
Association["Book" -> 10, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARbANNAOIB8AAJZYAnw=
"],
Association["Book" -> 10, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAVbAzMzNCAYMDIzkAgYwwisPY2EFLEDMxsAANgbE
YWRiYmBiApIwXUA+CAAlWVggKhgZAdrxAzA=
"],
Association["Book" -> 10, "Theorem" -> 6] -> CompressedData["
1:eJztkdEJAzEMQy3bVTjCfXWCrtQRboHO2o0q5ejP0RH6IALJwgnkcbyeByLi
bfnzm3uS+5wdMc0wZHcVAHmpI4xe1OYkh7VuMDOIUIkYOEuZifwmHsopUvPC
+THUaTtgW7uqoiqrmIvQUzxlUCtV960fqYEEyw==
"],
Association["Book" -> 10, "Theorem" -> 7] -> CompressedData["
1:eJztkdENwyAMRO847AYzRVfqCFkgs3aj2CRfkbpBn8QJni2DxHs/PjsBfCv+
/KC5zTkFRIwxvDDrXSIZ4Zml6H3RtjKpMmS1ZcCINEbn1bT0bVTFm/G8+/oY
z9XrRG7wbJcgNcnaAvmUqhr8lWVf805/MgR/
"],
Association["Book" -> 10, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAS7ACAYwmgzAAEZ45WEsrIAFiNnADmFgBHEYmZgY
mJiAJEwXkA92KAMLCwtEBSMjAM7BAx8=
"],
Association["Book" -> 10, "Theorem" -> 9] -> CompressedData["
1:eJztzdEJAjEMBuD0mjSJnq1JFeHgPERwhQPHcIB7cAFndSOrPruB38MfCPnJ
6f643QMAPN/x99PSIW4ARHLuh1L2dZoul93O3UWqu9XG6jjPyzwLvzft0sz6
vngbzJOz13y0atcPlsHVS5m8+GY0bgUXVc3tWYwdhC4QQSTIXUCMGgQTEkUi
JKUQq6EmTEnwK0VRWfEZnPstKnI+rF8zFQ0Q
"],
Association["Book" -> 10, "Theorem" -> 10] -> CompressedData["
1:eJztzdEJAjEMBuC0TdpEewlnEUFFq+IQBafw2adbwFndyJ4+u4EfJIGQn5ym
531yAPCa299vHlEBmFXz3mxdar2ex9HMRIqZlk7LtrVHa5zmTb/sch6sD07V
khU9atHbR+KdSY/XXsNBUw8Yi0h/AiF4cN4RQSBQ7xCDOMaIRIEISciFMqJE
jJHxKwYWXqQLrFIeUDAtN/IGzSoMYg==
"],
Association["Book" -> 10, "Theorem" -> 11] -> CompressedData["
1:eJztkcERwyAMBE8+kDQyjwwdpCWX4AZSazqyRPzKIxVkB25gJQ0PnufrOAXA
u+LPDyIc2GPO6YVZa72THMMzS9FVteWKMqkyutWRA0akMTp1sfRtehVv5ve7
n4/R3K1uIg+oQFgjGxnbAhSpqkFNme3ZwAvbCAVU
"],
Association["Book" -> 10, "Theorem" -> 12] -> CompressedData["
1:eJztkTEOwkAMBNdxyGkV3J4CbsilzWt4Qj7AW/kRdpKKghcw0lnavZFceN5e
z00AvHP8+cXaA8tC0hMzchwjteZnR7/u3B7ZVM853Zk0GBGS0XlItYZyNlN+
RqoBv9ceh7nE6zOJEEUgqlDtVIduByqSrqEMJQxIbP0A6XYJlA==
"],
Association["Book" -> 10, "Theorem" -> 13] -> CompressedData["
1:eJztkcENwkAMBNcYcnbwPU8ByxKKriNKSAPUSkf4kh8PKmAeK3m90j523V7P
jQC8h/z5yRnoq6qGe4SZ6jyLSO+RGonEtVar9fYYTnNPXe4y6DCBhJuE1J3W
MiKejssynnm1RL9bj2EuRz+ISFEIxAzmE/N02gETjayhTEVQQNn6AbnxCTw=
"],
Association["Book" -> 10, "Theorem" -> 14] -> CompressedData["
1:eJztjcENAkEIRWGHAYa/TlbjTS/GmzdbsYRtwFrtSGYasAEfyQt8SLjt79fO
RPQZ+vOL1twdwIrez8dt8wgzpDNDKgZWMXNLP4YiXLpLIE8xTwFtB7fc9Eye
Y+kt7Hq/eH5hZsqqlUgIOSy0skpkXhYp6kLlFNYkKTJhVdGq7rRqSPYQK1/J
xggD
"],
Association["Book" -> 10, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 17] -> CompressedData["
1:eJzt0bERwjAMBVDJcSLZ/iI+cmlScDgcaViEmhGyALOyEXYWYAFeodP9X6hQ
2d+vnYno08bfT895PsVtizpN3o+jmeWsZkkr01EkiJRHS5ZSgKTXuiKdLZtB
SzaFHi4Fdse6ZtygrUTBEoLO9YhzTPUfGomFQMyOHQ2qQ9dJ36tITxK8eOZW
HTp2SAmYSIYB3nuNCF+7kgnv
"],
Association["Book" -> 10, "Theorem" -> 18] -> CompressedData["
1:eJzt0bERgzAMhWHJGOuBbRmcQMGlCOZScNkmI7BAZs1GARbIAvkKNX/xCs3b
+7UxEX2O8/fbMKhf1xbjaG3OXdf1PVKK2CX0Io3I/ETSOM1FNUrZo/eXmFNU
LDlBcbqVkFZdSqcPlSP6e5iAZtg3jGHa/4GWWCgQs2FDDnBVJXUNkZqksWKZ
j3Sq2ATvQ7iSOBettfARX7j8CgM=
"],
Association["Book" -> 10, "Theorem" -> 19] -> CompressedData["
1:eJztjcsRwyAMRBEskgCDnM94JscU4iZSghtIrekowhWkgLzDO2h3Vs/j/Too
hPCZ+vMD+731fjFVEWYA62puc2AyRhujXOeFW3OXism6KBZYU9hZNVNPO3pX
t84QDczCu79IKYVEJBJiDjeimGIl5SaAclbumVQgIOcUUUJ82Ni2GrT4ckWJ
oC+tuAfj
"],
Association["Book" -> 10, "Theorem" -> 20] -> CompressedData["
1:eJztjdERAiEMRAksSYCDMOrcjJ92Yg2WcA1Yqx0ZrgIL8H28j+zO5nG8XweF
ED5Lf37h1nqfpirCDGBOc5sDkzHaGOWyLtyau1Qs5qbYYE1hZ9VMPe3oXd26
QjQwCz/9Q0opJCKREHO4EsUUKyk3AZSzcs+kAgE5p4gS4t3GvtegxZcrSgR9
AYU3B6g=
"],
Association["Book" -> 10, "Theorem" -> 21] -> CompressedData["
1:eJztjbsBwjAMRGX7cpZt5DhQUFBRsg4jZAFmZSPksAAD8IpX3Olz31/PPYjI
e+rPT2xmo6vmTAIYo7u7g55tUraZsDV3qZicu8L7dvhAvT3BTGHQGaOBzHz4
AyBKDIkqoNxCWJhqUlrhnLjSGKhcMpJvpS+IF+tjVGmrX64oEeEDejwHug==
"],
Association["Book" -> 10, "Theorem" -> 22] -> CompressedData["
1:eJztjMsNwjAQRP3bZOP1xqDYKHADJJQzEoGAfaEESkgD1EpHGCqgAJ5G7zAj
zXZ+PmYphHh99Oc3pumeQ2D2nh15n4pTTtmlLnab2NV4K80wnorjsYhogYGR
0hg4U9+vSipqy3I5B75SDITERMPusPfl3xglpJLGCFWJpZIalJWoEQA0gKka
kJqsaREQHXxRNTTOEq6Fqx0ba8q/fQNDDw1h
"],
Association["Book" -> 10, "Theorem" -> 23] -> CompressedData["
1:eJzt0b0NwjAQhuHzX2zn7uw4cSJkUoCUjhEAISRKKkbIAszKRiRI9AzAU7zl
13z7+fmYBQC81vz9aN4M01TXpeQUEYecqB+6IXRbXFnsU6TD6RyY8NgmQiQ7
ZsvdpcTM4cOGrm34di3hzs0YLRPTwaNPy7yUyxsCjAGogIUQSkhw2iqldGWs
QwO6rrRXUikjvzx573ZQO4paas/BvwFdhwt4
"],
Association["Book" -> 10, "Theorem" -> 24] -> CompressedData["
1:eJzt0bsNwkAQRdHZn/czM2uvF1tYKyRInLgEIICEEIkS3AC10hE2EjkFcIIb
vuQd5udjFgDwWvP3q20/jiGU0qaI2KdEXZ/7mHe4stg1NU2nc2TCY06ESLa0
lvN1qDccP2xs24ZvlyHeuSnJMjFNHl1a1qVc3hBgDEAFLIRQQoLTVimlK2Md
GtCh0l5JpYz88uS920NwVGupPUf/Bh/QCxs=
"],
Association["Book" -> 10, "Theorem" -> 25] -> CompressedData["
1:eJztzMsNwjAQBFB/1l5n10s+chy4IAUJBeIeoAdKSAPUSkcYKqAAnkZzmMPM
2/OxaaXU61N/P1v3E1GMEbnvS+3relldGdPQpSH4InU5zeJ4Ou6QmYeQY+Dl
nOTCOacalFYavt9GKTxlCRyFly61bT231ihtNIDSTvVWGzCkg0Wo0HvfeA3o
wBtnDLgvg46JhA6KmihAgBybNxCGCxI=
"],
Association["Book" -> 10, "Theorem" -> 26] -> CompressedData["
1:eJztzD0KwkAQBeCd2Tczm2xi0EIJsbExggcQtLAXA2JhKZha8KzeyHVP4AH8
isf8MLMaX9eRnHPvb/z9zgyJArPpoIiP2+k5GeZda10bynOabA77uorLXSpj
LL2qx+W4aO61ZGaajmOhUiMoPCpD32/Xkr9755jBjr0T5tyCmERIAFE48kTI
4TNiDo2GoqBK0p7EYPwBOT0Kmg==
"],
Association["Book" -> 10, "Theorem" -> 27] -> CompressedData["
1:eJztjDsOwjAQRNf2etefkA0icWzFDVfgFLRAk4IqF6DmmNwII3EBet5II80r
5rg9rpsCgNen/vzA8yDLUiXHGKukEH0Y/I2oI/IuNBN7KUMKUiTNqcN7xRz7
S4mz+3KuLk/jWqcsa8E8c+5kEG7XSiloMQbAQGxDAyrUrnlNzIYYdMcUjDUG
rSVrrUZ0zgYu4IlH1t7tT7s3J0QLZQ==
"],
Association["Book" -> 10, "Theorem" -> 28] -> CompressedData["
1:eJztjDEOwjAMRZ3EsRMX6gKlqUUWrsA12FgYQAy9AGflRgSJC7DzvvSl/4Z/
XJ6XxQHA61N/fmHbm1WdRaTqlCXlId2IVkSZczPSqw1F1HQqU4dLxVn6q0lJ
X86V53H3qHvTu+Fc2DodlNuzcw5aQgAI0LXhAR361Lwn5kAMfsUkIYaAMVKM
0SOmFIUPkIlH9jltTus33R4K+g==
"],
Association["Book" -> 10, "Theorem" -> 29] -> CompressedData["
1:eJztjEEOwjAMBB1iJ6lRgkojFXFAQmYP/Q5nTv0Ab+VHuPAC7sxK3l1b8nV9
3tdARK9t/PmJx7IAUM2AZcdyrzXXmmTbqKqZTWpw23MHI+to2cYPSSYMaK2j
Yp5uDBPoobXij0MI5BIhEhq87KgEZk8hRmYpTLFKKuwlftkOSSQdqUi5SORy
nk9vK4ELLg==
"],
Association["Book" -> 10, "Theorem" -> 30] -> CompressedData["
1:eJztjEEKAjEMRVObNJ3AVKeDgriQCQFrj+MR5gKe1RuZcePave+HD/8nZFmf
jzUAwGuzP7/RWjcbBu6m7CjP45h8aGtEpKlOcjNVFZw7GsuhsU4fEtU+WClz
H+1Y72iNFtmXkv1vCAFcRAAE2cMOKCAm72NEJEaIEonjF1/ERJgqZMxXv+bL
6fwG9UAKzA==
"],
Association["Book" -> 10, "Theorem" -> 31] -> CompressedData["
1:eJztzE0KwjAQBeDEeZPMtPSHpDmAa8GFEkl3uhK69Ai9gOfweN7I2Bu493sw
PHgw+/X5WK0x5v09fz96TcssotOSVRu9aRBhEXiN9+xFxmvufVryfFZKkYpq
GPXSboAYpbRNClqGFKgMOLlu6LA93tVY1E7GWWusYQuSOhAYYDbUeDiuwBsC
aAf2vXGOO3Ysx/7wAWswC6M=
"],
Association["Book" -> 10, "Theorem" -> 32] -> CompressedData["
1:eJztzE0KwjAQBeCJ8yaZaekPSXMA14ILpRJBV9ILeIRewLN6I2Nv4N7vwfDg
wezX13N1RPT+nr9fTctV1aZlNmvsblFVVBEsPeagOt7mPuRlLmfjnLiYxdEu
7QZISUvb5GhlyJHLgJPvhg7b312NQ+1M3jlyJA6sdWAIIELcBHipIBsGeAcJ
PXkvnXjRY3/4AAbnCv4=
"],
Association["Book" -> 10, "Theorem" -> 33] -> CompressedData["
1:eJztzDEKwkAQBdDZP7Mzy67JEQyBHMETiHaCsFhIKklhkyKNhTZ6Ar2bNzKJ
J7D3FX/4fJi6G3LniOg9xd/PmjMQnk22YFaFFCfK4VFnr9ZXOdq9yds1ULzQ
BouDHdLMa7rZMcbFJbSpuKI9+Z0vy8Lmt46cA0AkJBgLAeJ0HMYr7IVgzKai
Kl+kymBWI+95Lyy8Wa4+2S0Pjw==
"],
Association["Book" -> 10, "Theorem" -> 34] -> CompressedData["
1:eJztjDEKwkAQRWdn5u/sZlUQG0mxYOsJPICtQrSQVIH0oofwFp7KGznJDex9
xYf/H/zd+LiMgYg+U/z5nYE51neHCDzRlKKlJEV9dTlZe+9W5vJ0ZG4q98i5
xbXMSFzUfDNL1fpldrm1s/me5tdAITAzkZKyFxLWEF2IqIgpiQkbFDCdIUDY
ZeMGm2k5rPdfIM0NSg==
"],
Association["Book" -> 10, "Theorem" -> 35] -> CompressedData["
1:eJztjTsKwlAQRefd+b3kxUJbSUIQcQGuQxCXkM5KQjoR9+iOnGQJ1p5imMsZ
5g7j4zYmIvos488PADIcJxXRTjbulXvsw2HKrm031RbyegHqHm/JpdXZV5RL
b0/33OdXqULu5e5NU/L6NFFKAIiEBBGIIcnWNhU2JTgjilSjbIHMGMxWU9id
xNF5e/oCY1gMJw==
"],
Association["Book" -> 10, "Theorem" -> 36] -> CompressedData["
1:eJztjEEOwjAMBJ1dO0VKinoliBQCiMdw4wn9AG/tj3Aq8QHOzMFarVdzWd6v
JYjI2s+fX3g2MrXW7rlNtQ61zo/elFrHMc0nj44pjdfzlG/ZNo5Kb1SVHvoz
KQ+llJ0bQ6AEwExAGQCJAlAt+rqjBKOC8BHCF913WYimhk2JDwBsCAk=
"],
Association["Book" -> 10, "Theorem" -> 37] -> CompressedData["
1:eJztjMsNAjEMRP2NkBzB1Su0KAm7N6qhhG2AWukIOyXsmXcY2TOj6cfnfSAA
fFP+nGJjrvuzDxtX9+LeXuksrZnV+xqnmamwcn/cbJhOVuFwRITjyLAKL+5+
iUFEBiRSBWIoRFDijVIRIeIkwhAMpkzEcgwjUMq20g/B8geK
"],
Association["Book" -> 10, "Theorem" -> 38] -> CompressedData["
1:eJztjD0KwkAQhed/s84mlUKIlY1ICntBUtsEYSEXSGflWb2Rmz2CtR+84b2v
mNP6zisCwGc7f37DJOVlnj0fht6GfuevYsb7lDwdb6W6RzZjeU777uFaiWEz
Hk1baUxY2iCX8XrW+pEBiISAGISoTkFCVWRmVQZkrAaZKkgUOgtNRBc1wZJA
X8iACc0=
"],
Association["Book" -> 10, "Theorem" -> 39] -> CompressedData["
1:eJztzD0KAjEQBeDJ/IbE7BHULfYEXkAsrLQJFpJG2H6RLbQXBM/njcyuN7D2
K97weDBtf829A4D3FH8/6rJ5s7WPYaLkX20WtWGVgz27vN8ipgcWb2G0U5yJ
xpudQ1jcfYlpxHKRgzRNsvmhA+cQEYCBsRZAZKd1qJdJGNCITFmVv0CVkEgN
ROjIxLRbbj4qtg5k
"],
Association["Book" -> 10, "Theorem" -> 40] -> CompressedData["
1:eJztjMsJAkEQRHu6u7bno4J4EYVZPBuAEXhdGD3IXjcAxSQMw5zMyNkJwbPv
UFD1oA7T4zI5IvrM8edXCjrgiZiSpuQV+VWCt929rKx/l+HMHHseEcIe19SQ
bpHDzcxnG5ehyq0NVnff/hw5x8xESsq1kLC6rgoRFTElMWGDAqYNAoSrjNVg
My+n9fELecMMNQ==
"],
Association["Book" -> 10, "Theorem" -> 41] -> CompressedData["
1:eJztkbsNwlAMRf29yXs2iD6iQMo+SAxAkQUYgCmomICB2AgnDT0150i2LF3d
xqfldlmYiN7r+PMzgGNGDCtuyHz2Ecf50YfM1/UsjOTwNk64tw1X9MrD06L5
nmPS1jLDvp1aP1Fikk0mI6nFLOA6hMzLQktSVTGVYHPdCZvEwT8kUgim
"],
Association["Book" -> 10, "Theorem" -> 42] -> CompressedData["
1:eJztzLsRwjAQBND77J0kJBOBx0NGwGdogMQ0QODA44AUN0CtdARWCcS8YOd2
g9vPr3FmInov8fe76f4sw6ZrvWvjanSU860vueyu3zPnpO6Kod82j2xVCO5A
Tm4NokPRBJyOl4PVb0okAiFRgkitYGEzNsAMxMq8LKxSsUhce4yJi5mDLcD0
A4B8CVM=
"],
Association["Book" -> 10, "Theorem" -> 43] -> CompressedData["
1:eJztjM0JwlAQhPdndt/G99BTIOTmQSQHC1DBDgQxkALSQGq1I5PXgle/wzAz
MHOcl/fMRPTZ5M8PvKYytn3nfRd5NOThfis599fVltyom2J6tIdntkpKbsCu
cSsIh6IknIfLyeqZEolASJQgUiNY2IzXkRmIlXlrWKXCIrH3iOBi5mBLSPIF
U9kJBw==
"],
Association["Book" -> 10, "Theorem" -> 44] -> CompressedData["
1:eJztjD0KwkAUhN//Zn272oiEWFn5dwUhhQhpVPAIuYBn9UYm7wq2fjDDzBSz
G9+vEQHgM9ufX7iX56ZrrWsX/jDx4/WyKr7tp1g8sxnLrV/XwTXIaV48m1Zp
TFhqktP+fND4YgAiISAGIYoqSKiKzKzKgIyxIFOARGlpqcnooiY4KdEXIJwI
pw==
"],
Association["Book" -> 10, "Theorem" -> 45] -> CompressedData["
1:eJztjLsNwkAQRPczu3f23eEMZJmEBCNRABIENIAlRAEEboBa6QhzLZDygqcZ
jTS7+fWYmYjeX/35idW0Hvow9LG9OdLhci45bU9LTKlVd8X9uumexSohuAOp
cSuIDkUOGMfj3uqVEolASJRMpFawsBkbYA5iZUaVVlgkdh6bhrMtO1tAkA/7
yAh8
"],
Association["Book" -> 10, "Theorem" -> 46] -> CompressedData["
1:eJztkb0NwlAMhP3/sF9iFNHQIMQy1IgmQnRZgEGYjo0waRiAlu+su6uu8Wl5
XBcEgNfH/vyGRe9eJ5Z9drPDcx4143Y5E/bEsObHdpcVtRjYW4tJ3WOLsTff
ZKZ957h+woBAqxAUqIKQjBCEkIVriFegClUfUJQnYqFxp2/JTAf8
"],
Association["Book" -> 10, "Theorem" -> 47] -> CompressedData["
1:eJztjL0NwkAUg9+P/e6SC6FCitJRJRITQINoqGhghCzArGxEcivQ8hWWbck+
Lu/XoiLy2eTPjwzjEOOQ2ydR5utl35XxvNpSGg86HrdDfy+spBQE2ibYIQcc
u4R5Ok2sRy5iBhNzgVmNUFNS1xEJUVfdGnWrqFnuI+esHRlQJtC/vAEH+A==
"],
Association["Book" -> 10, "Theorem" -> 48] -> CompressedData["
1:eJztjMkNwjAURP/u5cvBOLngCAEtceeSBqg1HZGEErjyNHoaaaR5LO/nggCw
7vrzK6VoKWYleY+neq9zq9F7vyhOGX1or9swhy/WsnkMU1S3cRuvllMbGx8/
tIUY96JEIJsRDESAVZgUISixsIjxATCnIO4ZI4mJauAzfQBCLgcZ
"],
Association["Book" -> 10, "Theorem" -> 49] -> CompressedData["
1:eJztzDsOwjAQBND9jWPZOMnaSkE6TsBdOEL6CHFUboSTggvQ8qTZYkba2/Z8
bExE7+P8/WyfX3vMV8Bzq6350gzuc9QCxbrc61r9FGKBASg9uJjCI/I0jehP
RJiEyIRMaSDhs2DtGGY2GDFUcA5faQwpFc4hWN+CFP4AsxwHvg==
"],
Association["Book" -> 10, "Theorem" -> 50] -> CompressedData["
1:eJztzM0NwjAMBWD/PTdNCYqbQ3tlBFZhhN4RYlQ2IuTAAlz5JPvwnuXL8bgd
TESvz/r7Xb0/07IBMUdtLbYwRNSkBYq9Xdd9jcFTgQEofXAyRSTM/RL9hwiT
EJmQKU0kPALWjmFmkxFDBaP4ymfPufDibr1zKfwGcnEHSQ==
"],
Association["Book" -> 10, "Theorem" -> 51] -> CompressedData["
1:eJztzMENAkEIBVBmgQF2BcwYY2J0E+1iE6uwhG3AWu3IUVvw6Dt8Dj+fy/q4
rwUAnu/4+4FlUW2Zoe4RsXHPfkTmlGx+jha3D9FjWq/mjPRTSB+kmln0F4gD
lKEwAzLEUIhQilIlZmQmVi6439FUqdZKXxXVdJQrbHl0EpLpYC/avQkb
"],
Association["Book" -> 10, "Theorem" -> 52] -> CompressedData["
1:eJztzDsOwjAQBND9jWPZOGFtpUg6TsBdOEJ6xFm5EY4LTkDJk2aLGWlvx+tx
MBG9z/P3C8+YN8Bzq6352gzu16gFin291736EGKBASg9uJjCI/KyzOgfRJiE
yIRMaSLhUbB2DDObjBgqGMNXmkNKhXMI1rcghT8w+AbQ
"],
Association["Book" -> 10, "Theorem" -> 53] -> CompressedData["
1:eJztzLsRwkAMBFD99nw+I8byBXZKCbRCCW6AWukIcQEVEPJmpGBXo9v5fJxM
RK/P+vuJuuxAzLH2HnsYItaqDsXR79uxxVCqwwB4Di6miIo5L5EPRJiEyIRM
aSLhEbAmhplNRgwVjOKrXUtrzkspll0R5zfxiQZb
"],
Association["Book" -> 10, "Theorem" -> 54] -> CompressedData["
1:eJzty9sNwlAMA9DEzkPlplBGQEJMwCSM0AWYlY3I7Qx8ciJFlqPc9vdrVxH5
zPX3G8vqrMd1W7NyxlGLuRvrPNaqPDy9McMd9Hm8OO9jnKL/ARGq0AUUaE8X
IFpHeCc1gtqgB1G1RERoqgVAM+cXmxEFXQ==
"],
Association["Book" -> 10, "Theorem" -> 55] -> CompressedData["
1:eJzti70NAmEMQxM7Px9cGqhPSAgQYh1GuAWYlY3IXcEElLziyZbs8/J6Lioi
71V/fsSerNP9UVV57VjTFGRw3I41KjYuRjq/BMs4Z+bouypFAbYpAYh3Jdwj
iO3WhkGh2ruVDnHIXVDDzAFzOj6t+QWb
"],
Association["Book" -> 10, "Theorem" -> 56] -> CompressedData["
1:eJztizEOwlAMQ5PYye9XfjuxMbEg1IEdCXVjZeAIvQBn5Ua0/wyMPMmWbcmn
9f1aVUQ+u/35FcE235eW7XjbYmZFBPhcDtMjvVPLvmQNHzkEwbHwMl/P3v8Q
MaOJQWjWK9XUXQG4QxTaF4V11KxMUYaqSQ/qJscXRCYHFw==
"],
Association["Book" -> 10, "Theorem" -> 57] -> CompressedData["
1:eJztyz0KwkAQBeDZN39h180Zoh7BCwgWNmIhEkQIQqoIoqClp/RGrvEKln7F
Gx6Pmfa3XR+I6PWJv5+Zt2o+NG3062y/XgL5jq7yePE2jdTS0w8xTh7VMeUz
upNutK6zj++BQgBAJCQohQAJVoZyhVUIzuwmZvJFZgxmc1LlrbDwqlm8AT2b
DLY=
"],
Association["Book" -> 10, "Theorem" -> 58] -> CompressedData["
1:eJztizsKwlAURO838178gFgYMAhuwNIdWIrogyDYpbG0dpnuyJu3BktPMTBz
mP34uo1MRJ8p/vyOkhI2z7JE/75eTiJtLw/PufMyq2gz3+UBSFvcFzlkhzNi
T/XNxCwiREYmUUjFuAmhaqowUqjAzR1WIXeVkG0YX0/LcXX4AmLbCjM=
"],
Association["Book" -> 10, "Theorem" -> 59] -> CompressedData["
1:eJztkbsRwlAMBHX62e9JMM49BHZBBBRA4AZogD6gLTpCOKEBQnZndHPJJVq2
22UDEb0+588P6aOf1mcfMh/XM8MTYW2c/d52TLx7DG6p0eyImKW1zNDvgtRP
hEC8C1LiCoAdVZjUykJKEhFW4YCaHBjKMdkbf2gHcA==
"],
Association["Book" -> 10, "Theorem" -> 60] -> CompressedData["
1:eJztjcENwlAMQxPbSX5FYAcG6oURugCzshFBPbAAR56lyJal+H48H4eb2etz
/vyS7lBtHVHrFkqJ3RmXOlmp2FiVKmaGxnLva+v7QDCjxTiM6DLAAXAKFxA4
s4/MfdaUZQFupJRLb1TtBOA=
"],
Association["Book" -> 10, "Theorem" -> 61] -> CompressedData["
1:eJzti8sNAkEMQxPHk8zOT3tdceJMKSAhUcI2QK10xLASHXDkHSw9yz7vz8eu
IvL6xJ+fcl97H1ePXls2D+Ppto2tlYPsHoll8VRZPRlH4qWN6sfVRABC1ITA
VAAKIZEsaNMjKWcF6pdcIi9ZK9znzBl4A+hqBj8=
"],
Association["Book" -> 10, "Theorem" -> 62] -> CompressedData["
1:eJzti7ENwlAMRO3z2U6+f9KjVPTsQYnECFmAWdmID4gNKPOKk57u7rw/7ruK
yPMdB/9l6X29RfaqySKN2/W0bL19iUhnzeHFCjcuzktfKz5PEwEIURMCQwEo
hAQtacPTR69jpD+yZU6zNkQQHkx7Ab5LBeo=
"],
Association["Book" -> 10, "Theorem" -> 63] -> CompressedData["
1:eJztkbENAlEMQxM7CbkjX+gKBkBiEiZA1EiI66ioGZON+FxzC1DyLNmF5cqH
+XmZVUTeX/vzY4737ZC72/mkGqmVQ3vldVwgMlkRnl7pvXxgjNbK1zX7JxQV
LFJxQQ8C0RuD0FbEjDB6qDknmKH2mw9aMgdV
"],
Association["Book" -> 10, "Theorem" -> 64] -> CompressedData["
1:eJztkbsNAkEMRO3xZ/HeYXQiQWRUQ45IEETXALXSEWYTGiDkWRq/xE7mtD4v
KxPR6xN/fs1taxmP6xk8JYe3OLa7Dsz7LNFaXyyi7zgOHpvM9O+xVCdCTBjD
ZIRaYDiYFCwq9UgGVILymdVkgSimvb8BAo8GeA==
"],
Association["Book" -> 10, "Theorem" -> 65] -> CompressedData["
1:eJztkbERwkAMBHU6Sfb79Qy5IxoicE7iBiiAKiiNjhBOaICQ3RndXHCRLvt9
2yEir8/583OWKfN5uyoiMbzNazzagTOWGFN42mh+wljZW2a375b1EwpEDyEm
WgFooIqKeVmwFJJq1A5zDoVpP/sbCOkGgw==
"],
Association["Book" -> 10, "Theorem" -> 66] -> CompressedData["
1:eJzti9kNwkAQQ+fwjCeLBBs6oIzkkxIoIQ1QKx2x2Rr45Ek+JMuP4/06VEQ+
p/35PVfWunYa09hv/dLvmFQyiwATLI69Jdv+3DBfJuLmepbwIQlTKQHU4T5C
YxQEkDERs6jIJbRZpCUKi38BfN0FlQ==
"],
Association["Book" -> 10, "Theorem" -> 67] -> CompressedData["
1:eJzty7ENwlAMBFD7fLbzv/NJjVJRMwg9I2QBZmUjkkiMQMcrTjqd7ra9npuK
yPuIvx+IHHNNFmlcH9dlHe3UIzJYLbxY4cbhvM+X4nkyEYAQNSGwVwAKIUFz
2t6DcFMz16/smVPTjji2YNoHfhMFZg==
"],
Association["Book" -> 10, "Theorem" -> 68] -> CompressedData["
1:eJztizsKwlAUROfN/RmuZgU24hYsLbQTgoWmsk1hFQi4U3fkS1yDnaeYYTjM
bpjuQwHwnuPPL9h35yO5frGPaJ5xbRbMcvRbZo6rPmf50Iu17SaWT0EpJAGF
sg6QWryK2iqmYIiEq7t+gbtQxANm0qmonLaHDx9UClk=
"],
Association["Book" -> 10, "Theorem" -> 69] -> CompressedData["
1:eJzti7ENwlAMRM9nO84PpIjSICEFUTMAE9BGAgqUNgswKxvh/B3oeMVJd093
Xt+PVQB8tvjzE+7zjexOXLyUoz93FW32U3lFtFMsfUl5iDlyb+tFIEISMBiz
QGnSpFA11TBoKMPNPawCd2XKLo2P23IdLl93QAhW
"],
Association["Book" -> 10, "Theorem" -> 70] -> CompressedData["
1:eJztkbERwlAMQy3LNjj+4ehTsRAFA1BkAQbIlGyEk4YJ6HjvzjoVqnxbX48V
IvLez5/f8LwrYqA8z0tseeCMKeoUPqzSL6iFmWOUfWfsn1Ageggx0Q5AA11U
zNuGrZBUoxbMOStM6+ofrWsFwA==
"],
Association["Book" -> 10, "Theorem" -> 71] -> CompressedData["
1:eJztkb0NwmAMRH3nv3yOAKUNFSulT5MFmJWNcGiYgI73JJ+uuMqP47kdEJHX
ef78iA2IKyoy19zjgzHmKDO/eA2/oe6sHGOK70r7JyoQtmeakAKAgS4U87bR
VjpoqglzXUjjvPgbaeQFKw==
"],
Association["Book" -> 10, "Theorem" -> 72] -> CompressedData["
1:eJztkbsNgEAMQxM75PgcSIiGlpUY4RZgVjbigpCYgI5XxEqsuPFWjr2oiJwx
fr5CtZl0pHcLVz5Y5pDcso8Mc2HvKSV7n1g7gUQxuJWCKmqgapggaEQIpAai
Lo04OMetndoLEo8ERQ==
"],
Association["Book" -> 10, "Theorem" -> 73] -> CompressedData["
1:eJztyssNwjAQBNBd7ydeJiiCC0KEGFwSJaQBaqWj2FADt7zDjDSa5/p+rUxE
nx67v6kTKurS8/51m4EFjzKhoPQZM67NqZ1VhYRlOFByOjKrK0vOPoi4Wbgb
u6Y2NsL8qxTjJeJM5gYV9RjzBiIVB3o=
"],
Association["Book" -> 10, "Theorem" -> 74] -> CompressedData["
1:eJztzLERAkEMQ1GJb3tvbyAmZuiIEq4BaqUj1iRUQMYL7MCWbsfzcVjSq8ff
78CdCijmRw6YZEISfWT05rJ+IxBm7DqVznZUiG3rSC4V6cQZ/sKe+3XVqlti
RYzeIFQElQ==
"],
Association["Book" -> 10, "Theorem" -> 75] -> CompressedData["
1:eJztyksKwkAQBNDq/ySKE8E4UZmFR/AqrgR3WQs5qzdy1DO48xU0VdDnebnO
BOD5Pn8/VLWkfJv6/foj4l69lPFxGqdhOWgpflzlIXftlYjQIgIIUhsMJuXW
iNVM1MCdWy8s4vzlbmrhFaFp5xq2vWxeH+YHqg==
"],
Association["Book" -> 10, "Theorem" -> 76] -> CompressedData["
1:eJztzL0JAkEUBOB58/6OXfU6ECzCEswPMZQFrwExNTSyPTvybnsw8wsGBoY5
zPfzLAA+a/z9EltmfcSldB71lddSNs+h1e2b7eZTjONu6FuBCEnAYFwKlCax
ntBU3cBUzfCI8A5mStVImPtkSzvtj1+uewmX
"],
Association["Book" -> 10, "Theorem" -> 77] -> CompressedData["
1:eJztjLERwkAQAyX27t/+gZiYwA25BDdArXTEPQkVOPMGuhnppNfx3g9L+ky5
OBVaQGf9kR0GmZCUvc2kLo96jECYPnRrutvRQizLrGTRIp04w3+w1/GsWc2V
qIrRFw9/BHA=
"],
Association["Book" -> 10, "Theorem" -> 78] -> CompressedData["
1:eJztyrENwlAQA1Cfz/f/KfyIgirFL+ioGYURsgBCYgwahmAgNiJJxQJ0vMKS
ZR/n62U2AO81/n4rapviXjfhrZdnluz52A2dr0m3HMdWtqfBjCQgiLZWyrQM
pMJDYIr1C9yd7hqw7Hu5/Hw4fQAdqgfL
"],
Association["Book" -> 10, "Theorem" -> 79] -> CompressedData["
1:eJztyrENwkAQRNGd2dm9O8uAnJGSgERAD27BkhtwA9RKRxwISiDjBSON9E/b
fdlgZo/X/P3YfJzWffnIcA0tY1RNucaiy/V2znfoZqRodAuyX1BwREBeQv3X
hIge4asdsraKHSPVS4U/AXfNBX4=
"],
Association["Book" -> 10, "Theorem" -> 80] -> CompressedData["
1:eJztyrERhDAMBEDpdJLsMQwZCUNA/tV8CTTwtX5HGPdAxgY3c9Id5+97qoj8
73g9bV+3pQ4lI4Othje2cOMc/MzLxLEzEYAQNQmgVwPUhYTzJv2JQL/SBjUr
U9ZStQ+C9GTaBTe/BNw=
"],
Association["Book" -> 10, "Theorem" -> 81] -> CompressedData["
1:eJztisENwzAMAyWRsuT4UbhIH0H66UoZIQtk1m5UJ52hvx6IAwHytR/briLy
PvXn5zxvy3Thec+sLXuJyp5a18w2P2ZeNxsx6FncTDisEkIKSIAqWRQOd3wZ
UwSzTQqzwnCi2wc/TwT4
"],
Association["Book" -> 10, "Theorem" -> 82] -> CompressedData["
1:eJztkcENwzAUQr8Bo9StfWoGyEoZIR3As3aj2rlkgtz6kEDi/xvb0fcjRcR3
2p/7eXzKCbG8WG0/c11c0TqKW6u+Xjk2YaTA0MwcQCQSeVw0OlEST8ImxOxE
4Q0JbS0/UkIFKA==
"],
Association["Book" -> 10, "Theorem" -> 83] -> CompressedData["
1:eJztysENg0AQQ9EZ2zOzi4iSFjiRQ6qhBBqgVjqCbBE55R2+ZMnLfmy7m9n5
zd8PPGKoyqCmnjGrpaS5tL4/a44TzQDBQCvgnoScHuFShWTekkGQgcGB9sre
mz9RKUaqcAEjiATP
"],
Association["Book" -> 10, "Theorem" -> 84] -> CompressedData["
1:eJztkcENwzAMAylSchHbMdAB8uhKGcELZNZsVLUokA3y6h1EfvjTax77NADn
J/7cQf0SKrX0CO/Rmg+um2odY9U1VP5EMDD9NWH01OCEJ1JeigjRFYsVatCd
7fl4Awl+BFs=
"],
Association["Book" -> 10, "Theorem" -> 85] -> CompressedData["
1:eJztissNAjEMRP1L4tgB1iINcOCAhDhQCiVsAYtSKh0RJGrgxNPMm8uc1udj
RQB4ffTnJ4xtjE3rJVr04y169OtSY8bcbT8PRDyLIkAZGiEzF1ROLMI5laQJ
uZlkmgjRd+piqnfw4gdJYruzvwE7oggP
"],
Association["Book" -> 10, "Theorem" -> 86] -> CompressedData["
1:eJztibsNwkAQRPd7n90DvPI1QECAhAgohRJcgJFLdUccEjUQ8TTzJpjz8nou
CAD7R39+w7pta6nXaNHne/Tot6nGiLnbcfxEPIoiQAkaITNnLKwswkmzFkVu
JokGQvSdOlkpD/DsJ1Gxw8XfDUkHng==
"],
Association["Book" -> 10, "Theorem" -> 87] -> CompressedData["
1:eJztybsVgkAUBND33X37E5bA3MDAhENgJZZAAWirduTDIoi4Z2aSua3v14oA
8N3ndJBt+1h69Nqnvniv85i6x1qrF7+J2IsiQAEqITNHNFYW4aBRTZFrlkCO
6U+I0pjNnlBiGUQlt3v5AeALBzE=
"],
Association["Book" -> 10, "Theorem" -> 88] -> CompressedData["
1:eJzticsNQjEMBP1NHDvAs0gDHDggIQ6UQgmvABCl0hFBogZOjHZnD3tYH7cV
AeD10Z9f8bxbO2XPsb/kyHFeWs54hG/nS8SzKAJUoBMyc0VjZREuWtUUubsU
mgjRd9riZleIGjtR8c0x3rMTBr8=
"],
Association["Book" -> 10, "Theorem" -> 89] -> CompressedData["
1:eJzticsNAjEMRP1NHDuwa5EGOHBAQhwohRK2AKiVjggSNXDiaebNYY7b874h
ALw++vMzHtbO2XMcrjlyXNaWMx7h+3kS8SyKABXohMxc0VhZhItWNUXuLoUm
QvSdtrrZDaLGIiq+O8Ubhg0GTg==
"],
Association["Book" -> 10, "Theorem" -> 90] -> CompressedData["
1:eJztybsRAkEMA1Dbsne9P7i94HICAhKGgEoo4RqgVjrCUAQRbyQlOu3Px85E
9PrM3+94ucw+13mLbtelzIiP0Q/xiSDKqiSJujCAzA6DKpJlc2P0qkkC5EtF
ylLd79RyO6ppHef2BlvFBeU=
"],
Association["Book" -> 10, "Theorem" -> 91] -> CompressedData["
1:eJzty7ENgEAMQ9HEdoKuoWADVmIEFmBWNsJXsQEVX7noSdHt53WcGRH3XH8f
Vt2SX1OLzK21jjHKJyCCGawADSSQJpzZE0lQ+eY/VZCUZXmahQfbqAOx
"],
Association["Book" -> 10, "Theorem" -> 92] -> CompressedData["
1:eJzt0bEVwjAMBFCdopPtF9tKXgpqRoIRskBmZSNEwQpU/OKau+7u5/U8ISKv
T/z90i3GPI4W+6x14+yPEaUUzwbINxSkwKQpNIFGZYaz0sV8ccsdFF/dGH0I
1cdiVtdoby3RBP0=
"],
Association["Book" -> 10, "Theorem" -> 93] -> CompressedData["
1:eJztidEJwkAQRGd3du7MfQSSEySiQtB0kEosIQ1Yqx15AWvwyzcw8Gbm7fXc
DMB7rz8/5d5NdVzmYeof1zhfdOvqWEs7zAwtJEDkJo6w8EPbPSSG4CWr0En/
QiqUU0UKnVJkHdfhA0+yBZw=
"],
Association["Book" -> 10, "Theorem" -> 94] -> CompressedData["
1:eJzticENglAQBd++fbufgERKwC4sghMXThqCBXigAzu0I78U4ck5TDKZy/ac
NwPw/urPbyn3tj29mlvX71wfmnMYzs1xDGYkAUGsAacs6yDlHgKLe8nIzDiA
5HTPAkUsqjWN1w/QgQeO
"],
Association["Book" -> 10, "Theorem" -> 95] -> CompressedData["
1:eJztkcERwkAMAyXbseMcd56QCmiDMighDVArHXFQBC92Rnrs6Kfb+XycBPD6
1J8fM65Hq2PYVjku915mVlOLEPOPCDBQIIUK99VVwyNmELnkIpQ5/aLktree
HW7WVW1tI98cLgTq
"],
Association["Book" -> 10, "Theorem" -> 96] -> CompressedData["
1:eJztib0RQGAQRPf2FjcMApHgC2RynShBA2Z0ojQd+YlUIPKCndn3hmWdFwNw
3PPzNZFHir0qE/deWzRNnT/eYEYSEES7L2W6AqnMM4EhFi/g7nRXiau3cvnU
jSd2rAYl
"],
Association["Book" -> 10, "Theorem" -> 97] -> CompressedData["
1:eJzt0bsNhDAQBNDZD2t7MUYkZCCRkiFRxwVXAg1crXSEjyKIeMFIM+ksx+97
EIDzH6/HfaZh74a5t5JLXtvOSx2Z6xsEM8CQiUiotiaKiFbBFdqwBRZmlRuL
pBBT2uDqRVktj34BQEMFcg==
"],
Association["Book" -> 10, "Theorem" -> 98] -> CompressedData["
1:eJzt0bsRgDAMA1D5E4eEkDuYAApaCkZhhCzArGyEYQgqXqE7q1DjpZ1HIwDX
E7/vzdNexqVaGeqw5ZKqd8z+DYIZYChEJORX6EREXcwKDWyRhVnlxSIpdimt
yJqrsvpgfwMkowUU
"],
Association["Book" -> 10, "Theorem" -> 99] -> CompressedData["
1:eJztiMsJgEAUA/O+uyr4AWEVvViCrViCVw/WakeuWIQXJxAmWfZz2wnA9dTP
B0xpaI9RU/Kpatom5ouIkCMCCGIeDCblbMRqJmrgwq0UFnF+cTe14DOCxt41
WLfWNyyyBUU=
"],
Association["Book" -> 10, "Theorem" -> 100] -> CompressedData["
1:eJzticENg0AQA71e7x5SROgAiSYogT9JAxHwJ62moxw0wYd5WPLMsOyvxQD8
jrm5gubzaL/cVr2z6555OoMZSUAQ7biUqQbS3cPB4l4yMjNOUHVNaqCIWZRP
/fgHb6sGbA==
"],
Association["Book" -> 10, "Theorem" -> 101] -> CompressedData["
1:eJzt0bsRgCAQhOG9BxwwB86YGxgY2Y0l0IC12pFoEyZ+wR9sums/j04Arie/
T9S2VGtefS+epzEwjzcIIQARTkRChKQmIjqkotDIwViYVV4sYilb2lC0NCWN
Pucb/ZwEpQ==
"],
Association["Book" -> 10, "Theorem" -> 102] -> CompressedData["
1:eJztyakNgAAUA9D+thzhCAKFQODQjMIILEDCHCzHRhyGETA80aTtsKzzEgCO
O37fKIuee+ctr+sqfZZABEnAMOOudPg6SFuJwdzM0hckUXIBJ2osa2rHEytC
BUQ=
"],
Association["Book" -> 10, "Theorem" -> 103] -> CompressedData["
1:eJztiMENgDAMAx3qNE2KhJBYgBHgwx6MwALMykYUluDDWTrpPB/nfgiA69HP
RwzBMXyMdVuspYigTRUgokWHLJne/pTIXIg0VbPCUowv8kiz9XCtpkavHjcI
pgTG
"],
Association["Book" -> 10, "Theorem" -> 104] -> CompressedData["
1:eJzth90NQEAYBPf72btDEImQS7woQStK0IBadeREEV7MJpuZ9Tj3QwBcz/18
RfZpjrnp+i6VEhGUmQGGVEKh4lpM1ElzQqvA2tQs6AtJZwwL6GkMHjls7Q3m
8wR2
"],
Association["Book" -> 10, "Theorem" -> 105] -> CompressedData["
1:eJztyrsNgFAMQ1HHcQIVr6ZkBRagp0LUiOItwKxsxGcJGk5h6Uoe6rFWA3A+
8/sM901LltK1bxrMSAKCeAdIWT4/yj0ENu5NRmbGC5LTPVsoYtZdUz9eGe0F
Yg==
"],
Association["Book" -> 10, "Theorem" -> 106] -> CompressedData["
1:eJztzLsVgDAUAlAQXn5Ha2tXcoQs4KxuZFI5go234NDA0a+zE8A94/cdKcuS
ttFtQVRuWBJW0slQKZGlGJKDIYb5ElnbXmtgvnhMKDzJDgO3
"],
Association["Book" -> 10, "Theorem" -> 107] -> CompressedData["
1:eJztiTEOQFAUBPftLn6EKFRKndpRHMEFxFHdyP8qN9CYYpLJzPux7QHgKvr5
kMln6vuufiIQQRIwzChJh/MgXakymMzmBSRRcov8B8tax+UG7K8Ejw==
"],
Association["Book" -> 10, "Theorem" -> 108] -> CompressedData["
1:eJztkcENgDAMAx07CqBW4tUBWIkRugCzshFpP4zAh7NkW/766NfZDcA97OdL
uEWtJd5B+Ylg4JSNlkFxocEJDXy6ECFmX03BRjn3Vh62vwOD
"],
Association["Book" -> 10, "Theorem" -> 109] -> CompressedData["
1:eJzt0bERgDAMA0DLsZyQM2QGVmKELMCsbIQpmIGGL3Qq1Gmf5zEhItcTv09t
o9bqWYB8Q0EKTBaFJtCozHA2upgXt9xB8QrjiBCqRzFrfe03xTADzA==
"],
Association["Book" -> 10, "Theorem" -> 110] -> CompressedData["
1:eJztyUENgDAUA9D+tmPAEoIFbghACRJmAK04gnFBAhfeoWnTpR57DQBni9+3
cilj97RABEnAMKNNOnwfpK1ksDdz94IkSh7gpMmytnm9ALv/A+s=
"],
Association["Book" -> 10, "Theorem" -> 111] -> CompressedData["
1:eJzticsNgCAAQ/sDPOAQruQILOCsbiScHMGLfUmTvh7jOgcB3Kv+fJy+9/Ku
CDCW0MSskCjJ82CsZnkJTkCWtKQi9mbHpeUBsrIDSQ==
"],
Association["Book" -> 10, "Theorem" -> 112] -> CompressedData["
1:eJztkbsNgEAMQ53Yl/tswUosgHQFLbOyEYGGEWh4ki3brZd5rNMAnLf9fM22
t7cwP3FEyqFUh2cUWWQIFYpS5YOREdFGt+GqnrsGL+kkBCg=
"],
Association["Book" -> 10, "Theorem" -> 113] -> CompressedData["
1:eJztkbERgDAMA2VLMQ5MwUoUDJAFmJWNMDSMQMPfve57rePYhgE47/n5nD3f
Zn3iiNKhssMrRTYZQo2ilHwwMiJy7ra4wqVJnRfHfwO5
"],
Association["Book" -> 10, "Theorem" -> 114] -> CompressedData["
1:eJztkcENgDAMA53YDWm3YCVG6ALMykakfBiBDyfZOvnrfZ7HNADXqp/vyVdZ
nzii4lClw0tFNhlCjaK08cHIiMjRbbjS1z78Bq2IA2I=
"],
Association["Book" -> 10, "Theorem" -> 115] -> CompressedData["
1:eJztxLsNgDAMBUA/+yV2goACKRIlKzFCFmBWNuIzBQVX3NaPvUNEzqffN5iZ
GOAummQB1LQi8uBk5BR5TAinE7c3wKjrPLVWJcpAVhYlLsVrBAM=
"],
Association["Book" -> 11, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAAjHh4pAEAlWgCfA==
"],
Association["Book" -> 11, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWABwNhgBMcII/Z4ISK2gEoAlk8CgQ==
"],
Association["Book" -> 11, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSABjAyQ6GBkhPDIBACWJAJ/
"],
Association["Book" -> 11, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAB4swM7MzMjIwMbIwMLMwsbCxsDExAHhcrK1QB
E7oOYPQxMbMwMaFEIwCtXQLu
"],
Association["Book" -> 11, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWABrAzsTExAmp2BgYWZlY2FjYEJGEFcrKxQeSZ0
DUBZJmYWJiaUaAQApooC1Q==
"],
Association["Book" -> 11, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweABXNycjIwMLCwMjDysjEyMDBwsjIxMbGzMQMDA
xMzBzMjAzIQEGIEARAJ1MoIRSBoAscwDHw==
"],
Association["Book" -> 11, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweABwPhgBAIQixHGRUgR1A1WDACXZwKI
"],
Association["Book" -> 11, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSACLMzs7AxsjAyMPKxMQMDMxM7MzsTECARAgpkR
KIECGBgYQbJAjRAmSCUAqt4C9w==
"],
Association["Book" -> 11, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWACwkwsDMxsDIx8rIzMjAyCPCxMzGxsbKysrEws
rEJAcTYWJACMPkYQgFAMDExMLIyMALxeA2o=
"],
Association["Book" -> 11, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaACzIwMzKwMTJysTMxMDBJ8DExMrKzsbGxsDKxs
/OwMDOysSAConJGRiREUi0xAJlAzCyMjALhRA2A=
"],
Association["Book" -> 11, "Theorem" -> 11] -> CompressedData["
1:eJztyrERgDAMQ1HJlo251NzRshIjZIHMykaEhhkoeMVvpKOPsxPA9eT3LTuw
IIJ0muXWjKzMrEhWeM3h5aS0SoKb23w3Cje4wgNz
"],
Association["Book" -> 11, "Theorem" -> 12] -> CompressedData["
1:eJztxLERgEAIBEDuOGB4A2NDW7KEb8Ba7cgxsgUDN9h9nseEmV1Pv89piwAc
ydwWAl1VIwod3sGXA1JLMqeTOVa53beyA4c=
"],
Association["Book" -> 11, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAD4FhhIlc3AJWSAn0=
"],
Association["Book" -> 11, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaADjAzMTKysTCwMTMAI4mRhgQozoatjBioFARRB
AJ5ZAq4=
"],
Association["Book" -> 11, "Theorem" -> 15] -> CompressedData["
1:eJzt0UEBgDAMBMFcrrkkMrCEhBpAK45KX1jgwTzWwB7zOifM7N75fRATcGB0
6XlUkrI1KrxaL7gzSIZxc2XQFrRUA30=
"],
Association["Book" -> 11, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAEFEQMAJUdAns=
"],
Association["Book" -> 11, "Theorem" -> 17] -> CompressedData["
1:eJztxLENgDAMBEC//P6YwiiwAStlhCzArGyEqFiBgivumOeYMLPr6fdFQMjp
GdsitVCoCU0s4uVA1dp7WFY6yR1uN7dCA7A=
"],
Association["Book" -> 11, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAErIzMjIwczEyMzGxsoGhiBAkxMqDHGBMjIxMT
iAaqAAIgCwCe+wK6
"],
Association["Book" -> 11, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAFoPhhZGRE4mEHTEhsAJXhAoE=
"],
Association["Book" -> 11, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAFPLyMzIyMjCzMzOBoYmRghCJkwMTEwsQEFARi
JrAuZgCgwgLO
"],
Association["Book" -> 11, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAFLIyswAhiYWNjYGQEMhiZGRiZGEBsGACymZjZ
mJhAoiAJsCYAng4CxA==
"],
Association["Book" -> 11, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAFjEzACGJmYoJxIQgFMDGxMDExwuRAAACZiAKk
"],
Association["Book" -> 11, "Theorem" -> 23] -> CompressedData["
1:eJztkUERwDAQAoGDTGzUUiTEQLXWUS8u+ugOs4/9cu17bQJ4jn4+jfsjVUQF
slUjI07PYRXUlVCL5UnxBaKhAwU=
"],
Association["Book" -> 11, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAG4kxMTKysXJycnAwcnDxcDAwcLEgAqICRkYkR
FItMQCYDAwszIyMAr2EDNw==
"],
Association["Book" -> 11, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAGXJwsTEx8vLy87Fy8rHzMjLwcrAjAxMjIwcbB
wcHCwMzCzMzMxMbBwsIIALdrA6I=
"],
Association["Book" -> 11, "Theorem" -> 26] -> CompressedData["
1:eJztxDERgEAQA8AkFzJcjwEsIeENoBVHzFdYoPgt9hz3NQjgmS2/dojsJHuC
3qqjT5F220bJktMyXqrtAz8=
"],
Association["Book" -> 11, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAGzExMnOzsbGy87AycLGy8HCzMLCzMcMDOzcHO
ycrAxsHHDFQmyMzKCACt8AOH
"],
Association["Book" -> 11, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAH7OxQBhO6DDD6GJmYGVFjEQCYTwKT
"],
Association["Book" -> 11, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAHctBoYmFkRI0wII+ZlYWZmYkBLMMIEmAAAJzw
Aro=
"],
Association["Book" -> 11, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVABLAyMqBEG5DGzsjAzMwElGEFckDQAlzoCmg==
"],
Association["Book" -> 11, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAH8hJi7EISDGYsjLI8HEDAxgEGTMzMLMwsLMzM
DExMLExMjCy8rCyMAMMhA/c=
"],
Association["Book" -> 11, "Theorem" -> 32] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAABpqsnAaM3EzMHILcCMDExsbMxMLMzMTAxARi
sHKysTIBAMKeA/4=
"],
Association["Book" -> 11, "Theorem" -> 33] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAA+mxcnozcTMwcQjw8PNxc3GDAxMbGyszCwsLE
wMzEzMTCwgrkMwEAwGMD9g==
"],
Association["Book" -> 11, "Theorem" -> 34] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAAbNyKjCxMbCzigpyCAmIcYMDEyc7CzMLCysLA
ysTCBGSwsrMxAwCzxwOu
"],
Association["Book" -> 11, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAAnKwMrMyMrCyMCMDMyMjKxMLKyszAxMjMxMrI
xsHIzAAAnUEC4g==
"],
Association["Book" -> 11, "Theorem" -> 36] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAB7AwsrMxc7EwQwAwigAJAwMLKwMnMw8zMxsLO
zMIIAJ/iAww=
"],
Association["Book" -> 11, "Theorem" -> 37] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVABjNxMzBxCPDw83FzcYMDExsbKzMLCwsTAzMTM
xMLCCuQzAQCrCANu
"],
Association["Book" -> 11, "Theorem" -> 38] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZABTAyMTCxIgImBgZGRiREYi4wMIJKBiYWJCQCb
ewLE
"],
Association["Book" -> 11, "Theorem" -> 39] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdABLIzyXGwIwMTIyMLMwsLMzMDExMLExMjCy8rC
CACkXgMr
"],
Association["Book" -> 12, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRACeuxs3BzcnFwcHGwcHBzM7KwsbKxsbGwMfOzc
rGxcHNxM7IwArGMDlg==
"],
Association["Book" -> 12, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVACzCyiQqLCIjwcXBwcHGzcnEwsDMzMTAwsjFxM
zGzszExMjACqjgNr
"],
Association["Book" -> 12, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZACvBwcHOxQzMTIyMzCwszMysDMxsbExMgiwMrK
CACiaQMq
"],
Association["Book" -> 12, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAC2hraSnJKSvJKikpMQgLMzEzMrKwMzMwsrKxM
7BycXKwAw5oEdg==
"],
Association["Book" -> 12, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRADqdk+Hs622rbW1ozK0iABJkYGFhYmZgZmJmYW
ViYA5WkFng==
"],
Association["Book" -> 12, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVADWvKKvq56rs5OjLzCID4TIwMLMxMLAzMTMzMb
IwDKGgSx
"],
Association["Book" -> 12, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZADAZ4udlp2NjaMKjIgLhMjAwsLEzMDMxMzCysT
AM28BNk=
"],
Association["Book" -> 12, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAD9sYmpiZmRozGWiAeEyMDCwsTEwMzEzMrKzMA
wbQEcw==
"],
Association["Book" -> 12, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAEsvIy8oryjPz8IA4TEwMLM5BgZmJmZWMCAKmh
A3Q=
"],
Association["Book" -> 12, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAEcTZx0dGM/AIgNhMTAyMLCyMDMxMzCzMjAMBa
BGY=
"],
Association["Book" -> 12, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAEVuWZGYx8/CAmExMDIyszIwMzEzMLMyMAuy4E
OA==
"],
Association["Book" -> 12, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAE8gryjHx8IBYTEwMjKzMDAzMTMysTMwCgVwMU
"],
Association["Book" -> 12, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAFaWmMfPwgBhMTAyMrMyMDMxMzCzMjAKnrA4I=
"],
Association["Book" -> 12, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAFeYx8/CCaiYmBkZWZgYGZiZmFmREAoWkDIw==
"],
Association["Book" -> 12, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAFjHz8IIqJiYGRlZmRgZmJmYWZEQCX/QK2
"],
Association["Book" -> 12, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAFjIwgxMDIwMTMxMTEwATkMgAAlasCjg==
"],
Association["Book" -> 12, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAGBUDMyMjIwMrCxMDAxMLGwcQCAJ4lAxI=
"],
Association["Book" -> 12, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAHjIyMDKwsTAwMTCxsHEwsAJXVAqI=
"],
Association["Book" -> 13, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAGnGw6GqwMrKyczCysrNyMzAwAnDoDFQ==
"],
Association["Book" -> 13, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAGbJycTIysLEzMTIzMbIzMDACXOgKz
"],
Association["Book" -> 13, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAHnJysDMwszMwsjCxsjMwMAJb7ArE=
"],
Association["Book" -> 13, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAHeqwMbKyczCysrLyMzAwAmRQC4w==
"],
Association["Book" -> 13, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAHrAxsLJzMLKysXIzMDACWegKx
"],
Association["Book" -> 13, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTAAHCycoszMLGzCdgIAl3MDFQ==
"],
Association["Book" -> 13, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXACjAwAlOQCew==
"],
Association["Book" -> 13, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXAAnOz8LCwsbOwsrACWdQK7
"],
Association["Book" -> 13, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbAAcuycwixsrCwsAJcgAtI=
"],
Association["Book" -> 13, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfAAbBx8rBxsLKwAlfYCsg==
"],
Association["Book" -> 13, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTABTCzMTLncTgCWvgM/
"],
Association["Book" -> 13, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXABPNxsLCzMAJWQAqI=
"],
Association["Book" -> 13, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbABzBxcLGwAlT0CmQ==
"],
Association["Book" -> 13, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfABHCzsDACVHAKN
"],
Association["Book" -> 13, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTACLKwMAJT4AoM=
"],
Association["Book" -> 13, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXAC3EEAlUoC1w==
"],
Association["Book" -> 13, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbACGgCVCgKi
"],
Association["Book" -> 13, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"]],
SelectWithContents->True,
Selectable->False], "}"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"dataA", "=",
RowBox[{
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "[", "\"\<Book\>\"", "]"}],
"\[Rule]",
RowBox[{"Max", "[",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "]"}]}], "&"}], "/@",
"res"}]}], ",", "vals", ",", "acc", ",", "xval"}], "}"}], ",",
RowBox[{
RowBox[{"vals", "=",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"acc", "=",
RowBox[{"Association", "[",
RowBox[{"MapIndexed", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"First", "[", "#2", "]"}], "\[Rule]", "#1"}], "&"}],
",",
RowBox[{"Accumulate", "[",
RowBox[{"Values", "[",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}], "]"}], "]"}]}],
"]"}], "]"}]}], ";", "\[IndentingNewLine]",
RowBox[{"xval", "=",
RowBox[{"Association", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "-",
RowBox[{
RowBox[{"vals", "[",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}], "/", "2"}]}],
")"}]}], "&"}], "/@",
RowBox[{"Normal", "[", "acc", "]"}]}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"Show", "[",
RowBox[{"{",
RowBox[{
RowBox[{"ListLinePlot", "[",
RowBox[{
RowBox[{"Values", "[", "dataA", "]"}], ",",
RowBox[{"Axes", "\[Rule]",
RowBox[{"{",
RowBox[{"False", ",", "True"}], "}"}]}], ",",
RowBox[{"Filling", "\[Rule]", "Axis"}], ",",
RowBox[{"Frame", "\[Rule]", "True"}], ",",
RowBox[{"FrameLabel", "\[Rule]",
RowBox[{"{",
RowBox[{
"\"\<theorems by book\>\"", ",",
"\"\<maximum shortening\>\""}], "}"}]}], ",",
RowBox[{"FrameTicks", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"True", ",", "False"}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], ",",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"{",
RowBox[{"0", ",", "0"}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Normal", "[", "xval", "]"}]}], ",", "False"}],
"}"}]}], "}"}]}], ",",
RowBox[{"ColorFunctionScaling", "\[Rule]", "False"}], ",",
RowBox[{"ColorFunction", "\[Rule]",
RowBox[{"Function", "[",
RowBox[{
RowBox[{"{",
RowBox[{"x", ",", "y"}], "}"}], ",",
RowBox[{"Piecewise", "[",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "6", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "6", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "10", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "10", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "13", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "13", "]"}]}]}], "}"}]}], "}"}],
"]"}]}], "]"}]}]}], "]"}], ",",
RowBox[{"Graphics", "[",
RowBox[{"{",
RowBox[{
RowBox[{"GrayLevel", "[", "0.5", "]"}], ",",
RowBox[{"Line", "[",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"#", ",",
RowBox[{"-", "5"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{"#", ",", "200"}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Values", "[", "acc", "]"}]}], "]"}]}], "}"}],
"]"}]}], "}"}], "]"}]}]}], "]"}]], "Input"]
}, Open ]]
|
although this shortening is very concentrated around “nearby theorems”:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"res", "=",
RowBox[{"{",
InterpretationBox[
DynamicModuleBox[{Typeset`open = False},
TemplateBox[{"Expression", "SequenceIcon",
GridBox[{{
RowBox[{
TagBox["\"Head: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["Sequence", "IconizedItem"]}]}, {
RowBox[{
TagBox["\"Length: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["465", "IconizedItem"]}]}, {
RowBox[{
TagBox["\"Byte count: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["5397840", "IconizedItem"]}]}},
GridBoxAlignment -> {"Columns" -> {{Left}}},
DefaultBaseStyle -> "Column",
GridBoxItemSize -> {
"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}],
Dynamic[Typeset`open]},
"IconizedObject"]],
Sequence[
Association["Book" -> 1, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 1, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIYWBgYmRnBLBoBFihNSztGNkAOWQCuDgKK
"],
Association["Book" -> 1, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKAgIWNhYWRbMDAQEABO5SG2cGAC2A1HdUq6gL8BoLt
I+w9agCI5xlgPibVSuTYAwDLWQPN
"],
Association["Book" -> 1, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKAgJERyhgFQx8AAJpGAn0=
"],
Association["Book" -> 1, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJAgJ2Tg5kJCBmZGJABEyoXC4ApwKuSHUozI+sYBfgB
M7mKAf41Ar4=
"],
Association["Book" -> 1, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLAgJWFgXaAHUoz4lU1CsgHyCELALB1Aow=
"],
Association["Book" -> 1, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIggJuVBQiZWRjhQoyMjCwsYAoqhFCMACwwmgVZFKgD
AiGAHVkxMxZTRgEDOKAZIGENxqwMMBY8SrBFAKYMAC5tAuc=
"],
Association["Book" -> 1, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKggJ0VBNmYmBihgImJiY0NTEGF4DJIgBWIGRiANCuy
KFAHBEIAO5JiRhZGJEvRABYLGFEEceokE+A3EGwfI3ZnURkALQKGMwM4rBmY
gJ5mAgcaKATh4Y81AjBlAC8MBBg=
"],
Association["Book" -> 1, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJggIOLjZOdgxEuxMjIyMEBpqBCyIphgAVGsyCLAnVA
IAQwQWlWEMGGxZRRwAAOaAZIWIMxFwOMBY8SbBEAAUxIbABHwQL7
"],
Association["Book" -> 1, "Theorem" -> 10] -> CompressedData["
1:eJydUUESgCAIXJjk0C/6Uk/wA721H4WIpJN1aB1hZhEWcMvHngnAWUxAVlkS
MzmYOSVzTkWkg+gF1EvPakY9kYj6uKgMmiMmAoTevaf+w3dB06NnW7VT7xdT
vo0Dum0bJBirHYPpnmG7BivJ0lYe+59+gEfgjWi9CwMwA+M=
"],
Association["Book" -> 1, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIQgJWXm4cRLsTIyMjDA6agQqiKIYAFRrMgiwJ1QCAE
MMHMR9YxCtAAKJwhYQ3GfAwwFjxKsEUABDAhsQFG6wL+
"],
Association["Book" -> 1, "Theorem" -> 12] -> CompressedData["
1:eJydUMERwzAIkxDpHlmpI2SBzNqNGsBpyKXNo7qz8XFCMpqX9bkQwCuuhkku
WYCkJPcsYgAC2BETj5wj3D8iW18MJnZ1GzU5wm+c1FtFmZE3s3/hXvDwq3Wb
f61f/8NI4yJWzSTiiOybfTy21PNkRLQp6BZh2p6f4YqRUeu8AY+BA1g=
"],
Association["Book" -> 1, "Theorem" -> 13] -> CompressedData["
1:eJy9kNENgCAMRHstfsIOruQILuCsbmSvoBKNfhlfCD2a0oOO8zLNEJGVW08u
Ztows5wVlAg8yJUEJhVpFxHMr0FFW5HGAgbqdOtxgg5hoxqrDvErvd+79xcP
88m3LxrtCifIk8//yeVIaJfcAMoOA2g=
"],
Association["Book" -> 1, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJQAB8zIxMUMDMz8vAwMTACAUQOQzEQsIBlmRhZWODK
gICZiZGJAQQhAEazgnVgMWUUAAEwvBkggQjGfKDwA7PgAYstAiCACYkNAFr6
AxM=
"],
Association["Book" -> 1, "Theorem" -> 15] -> CompressedData["
1:eJydUMENgCAM7NHCkx1cyRFYwFndyFJAUYMhHklTyvVabknbmkBEew53BJaK
EBCjgNk5GBxI+agodGHmHKUk9S149sin8Go/vOaQ98wTTfbSL1dq9XHrP8wJ
4rGPlSa0MumThz5Rv4ltkhmp1ov9XP0fTUDbxHXFAxB0A6o=
"],
Association["Book" -> 1, "Theorem" -> 16] -> CompressedData["
1:eJydUdsNwyAMvGKcWBBF+ckAXakjZIHO2o3qAyTSJs1HT8jY3Pkhc9+ej+0G
4EXzhWWacs5mNq+zqgldIWBA2IPqUVUBixodQBViTTFJQmolXSk8bkD6J2QH
D0Kot7Ssy9y/EC7Z3o+T0PbE4pctBLIMD8XqYxGir+ysPR0zRdkmFm+t0WSE
OmHD0FTxMGD7kY/HN8qGBSc=
"],
Association["Book" -> 1, "Theorem" -> 17] -> CompressedData["
1:eJytUMkNAjEMHF/JWvBgP/xpiRK2AWqlI+yEVWDJk4mUxNbYY89te9w3AvDM
6wj3pSxmdlovZsJn9yIJcgJ9IsmVRAAjU+ZIaPAYWCvHQX13jIwCEicZE8kd
WZ1IOURDin+8UdmqIvgzZvsPDD2iXIsGva/fXEhXOMOfZj3ZiBiWzeTzU4rA
muQ1nGA1VqSnrrrPcxSQPsJ32xf6SwRy
"],
Association["Book" -> 1, "Theorem" -> 18] -> CompressedData["
1:eJydUcENwzAIvMOBGsmVukJX6ghZoLN2oxocKZbS5NGTjMEcB8LP9f1aCeAT
5oBH8+bu93YTMbFaTQKoAGcEt5g74IVULcAgoqmqKHQT7C9Mi3TOIRN6QI47
zkhfFf+Dy2mmfjFJ2L0w/dwCIxvhQWw8JhH7yn61D8eMKEnpG+2CLjUV6rKc
TcvtRzAv5gvPEARC
"],
Association["Book" -> 1, "Theorem" -> 19] -> CompressedData["
1:eJydkNkNAyEMRD02GBYtRaSllLANpNZ0FB9SQs6PPCEzAh8Mp+NyPkBEVw/v
zDHHGHNvzE20dxUHHeAVGNJaIxoFULUgUqsAe9UqFRUJxxKQawsfhzqyYL2Y
bafUMUy+Vv4J/7yNefZa9+0vSMtpKXT8Avstp8dn8jAS8fiyNeEubJAqKGzS
FmLIFhm9lNfGS322peXwBoEJBTQ=
"],
Association["Book" -> 1, "Theorem" -> 20] -> CompressedData["
1:eJydUUESwjAIhAViGzvV8Qd+ySf0A77VH7nQquOMenAnISQQyG7Oy/WyqIjc
0nzA8XTofT/tgB6tNY+ENTMv1GJm4GRApJvqPDcIz+DAFGN4IMBaqMFDq9Ke
u2+IyFZrO9BJT1YfLBD+/ep/sJ/RpJbPTd7kb052G5J9WYrAJXL7im5wTzUq
EatyqLRnsj8uJbFhUKGOZjKahGrHKEqZ29qHUEuF359fn2FSVYQaQ+5i6QZJ
"],
Association["Book" -> 1, "Theorem" -> 21] -> CompressedData["
1:eJydUcERwjAMcyQrpL2DHViJEboAs7IRttsCD8oDXezYia2zkutyvy3NzB7p
vuE89z4mAZfh7l0JOumF2kgibJBmXa3N84BJUU1OPEU1iKBCLQdUzJ7ZEaJd
q0lIrthtjQFQftz6H/jzVjlyjJu6Q39K2pHqy6dKUpm+bzd4qPY6JtaXQ5W9
in1vSmG901oyWgRi65Rtb84dMH6OHHF9Bq1YDBHYEw8WBhY=
"],
Association["Book" -> 1, "Theorem" -> 22] -> CompressedData["
1:eJydUdsVQiEMa5u0esXjnwO4kiO4gLO6kaHXx4/6YQ6EQgqFcLpczxc3s9uk
jziOMfabiMO2qljVTGajB5JQU2S2wH0MwICITeY+h9alRYSkyZq6ubtyvha1
qqy1V0HBjGyNAbDy684/wZ+qiptBWZw3ERNPzNc3ywQNNadv9QG9GdnL7dO0
pNNeyfnclF0Nlu6kLbSCL7Ezl80VwRVOSPY3wr0/g9anOCh/7/RtByU=
"],
Association["Book" -> 1, "Theorem" -> 23] -> CompressedData["
1:eJydUclxAzEMoygAXI3XfqSDtJQS3EBqTUcGd51HZuI8Ag2hg5AgUe/3z4/7
iIivpt9xu62FzLcdQK5GoQw9oySBQpERO0Zer8TgzLxIS7s2Oj3n9CFplmaG
hwjkS9O1tlWOBuxY7uMc+xpc28ud/4T+zNo8Alapb2IWvtGvP1hw84NF9grJ
Th/kejkgT3TUrqo1rW9uQfetLRtVzeAYrqcYa46dlxg+FnPyxCCSzB84PyQO
vwQT4wEkUQik
"],
Association["Book" -> 1, "Theorem" -> 24] -> CompressedData["
1:eJydUcERwjAMs2TXoRwHb56sxAgswKxshBQ4eJUHSuo4ZzWSk8vtfr0hIh4O
Gziva5H7rirujJrI+iBJVi1LxGkHjtEEATS59r7HkgsToGiAQ4USKmxqtiAB
L822dFdoC039WmPb7n+o31WX5TbtSZeRaucNda+YAjSycqby6GYx78EkfWod
k5NvTsKcyai5cyKhMSAlFaM1gUMdXUa9ZOcpjvwCfgA/ULxc+eB4AhvDBf8=
"],
Association["Book" -> 1, "Theorem" -> 25] -> CompressedData["
1:eJydUdERQjEIIxDwPe88XcGVHMEFnNWNDFQ/9cO0TenBEaDX++N2h5k9m75h
3+l+LJK+NWQwGZk5BhnuLivNLhv8cCiHAyj3vY5VGekBuMLEIpqMEH2VLCHI
vsqrpYumJ7SVg/Wj3L/A3952q9romjSMUDtvqHtxCNAKxpirz74mKFMH0V1P
6IoJzEAmYF6dTkLbBinJaaUNnPLcbnDJThasUX6A+QB9kK2qRvwF+p8F9Q==
"],
Association["Book" -> 1, "Theorem" -> 26] -> CompressedData["
1:eJydUNsNwyAMPJuXSYUyQ1fqCFmgs3ajcJAqSEn56EkYPw6f8XN7vzYB8KH5
iTWHEDWXkpRAAWQEOSnmDJgL3nsHdCJW86YGOxrVjNBWAsRNFHVADUT6zdPL
s3H/wfT/gx4noT0fNr9tQVhleGnWk42Ic2V38nSWRRGb5IPSdYMJWgslhO88
N+Nf2+6XQgQ8
"],
Association["Book" -> 1, "Theorem" -> 27] -> CompressedData["
1:eJydUVEOwyAIfaC0xCzZfnaAXqlH6AV21t1oPuxil3V+7EURAXmAy/ZYNwHw
pPiNq9mkF3dTAg7IEQyZkxngyXLOqfkVuJdctKDseapFuGoAJA0I9YB6qbni
5G7uYbl/YNx/52MllP1h6DEFoVfkJFkzRiD6yM7oqbgrLChvpM6uM1Q43PfI
vtqX/Uc+jC9qmgQa
"],
Association["Book" -> 1, "Theorem" -> 28] -> CompressedData["
1:eJydUcERwzAIkwBfcsldM0NX6ghZoLN2oyKc9vypH9XDxkggbN/P5+MkgJeW
CVozP/ZtCcE2wki7wKpdoN3RogoySydvgfBg5Ik9K4Ku2Cd+chFkB+tmuWe3
aj+t/Qs2Zy9ac4QB5ECxiEwRdb2RHeoNJSxpVwwyG4N1DTRXdEDP5xnLZW/t
17TJ8vMTX7wBXgIEJA==
"],
Association["Book" -> 1, "Theorem" -> 29] -> CompressedData["
1:eJyVUEESwkAIS4BevfgCv+QT+oG+1R+VgDqd1daanYElwEL2Ni/3mQAeMke4
kuHuVnCCGyhAyOQtojhVyjn7NJJy2Ump4P7Q7H55Q8/IiIYn/2vdv3HuwdIw
Up9FX/rGCQPzjkqmdJboScGl5RP5/3vbWu9G2Ca9ArkiA3o=
"],
Association["Book" -> 1, "Theorem" -> 30] -> CompressedData["
1:eJy1UNsJgEAMS9rerzu4kiPcAs7qRvaBoIjn16VwzYWUlqx93zoBHPEMQZqK
MKHpfo6Y6+kq4t4wq7IqRUjMUticqw12lj373UVc+t+58zB/tSeETBotPkuw
KM/06wZ5EccJSdkDHQ==
"],
Association["Book" -> 1, "Theorem" -> 31] -> CompressedData["
1:eJyVUdtxAzAIA0s8TH/y0wG6UkfIAp01GwWc3PUr6VU2nM/CCPDX9ef7qiJy
G/cen2stflQvW2Z7527LHAsPYwEiQV17h2tf8FLl3AwQaUDvBTDTKFCl8LVo
1S4Pr4FVtUSFRBV6Ax7xZ7n/RL5lj960F5kVZt69PJHTGqzRDZoNeViSQx+H
vdtgnCH4AwFEx5+xDIk4sVNH55I+tihcyjTcBT3QHntnZXRmQkn9xVLN6K84
D0F1V8gdy+EINQ==
"],
Association["Book" -> 1, "Theorem" -> 32] -> CompressedData["
1:eJyVkLtxAzEMRPFbLInjXKDMoVtyCWrAtaojgedx4MDW+PEDAliCHLzfPz/u
KiKPvb0gwrGOqpWBPJhrTo4mswMIbI2LGuAhYWZvt5sp9JSSNckdIm0to5iq
CX9/tGrOZM5qoopkUVjlPd3B8/V3/wf/zu60bztGEUj4N+Q+o/Ee6ORXNrpd
21yiMXo52oHnBbKvtn5HtsA9L+2Q3WhIO4QYpFL9NHF2wW50g64crhH6A/Lo
v8j1ngbU5QmkvQgQ
"],
Association["Book" -> 1, "Theorem" -> 33] -> CompressedData["
1:eJyVUcERwjAMkxwTcr22O7ASI3QBZmUjLAe43HEUqkcSW1LsOJftdt0I4K7l
F9apuWALYaRbB9N7hvaCk6c2shLMDhlSqmw3WNG57NSUSVA5qIT8EQaRt/sf
7R6C7bNPWn24AeRAMYlIUbz2j4fJb0hhSrtikNl4aK2g5lyXmIR5iZKK1lq/
dRtX8fUTbzwATsQEIg==
"],
Association["Book" -> 1, "Theorem" -> 34] -> CompressedData["
1:eJyVUVsOwjAMS+xMG/3iD/HJlTjCLsBZuRF2i8bEBw9PnRLHkt30st6ua0bE
3b+vOLbJ4AlJYOYAkMKMqgjGVF0qFgUcGCzCHcRioOiaHzztYtgubaE61KZa
gfVL3H/Az1OP0/mVgZnjyh0KlyZE6fNN99NNpJNdmGMF2euXYCtk1BpjtiSa
NqFtFcLdeVmeefAe0Nn6S+zJB+pEBOc=
"],
Association["Book" -> 1, "Theorem" -> 35] -> CompressedData["
1:eJydUMENAjEMix0Tjr5gBFZihFuAWdmIJNyjAnFIpFLT1HZt9brebyvM7FHb
7xqhXDzDAvAIkiJae6Rk5nZQM70hntzcHTUxb7mV19l3jCQ1MbtSBZQ+R1M/
v6v9q7iPbnDlEKtPEBrIKxRe/eMzK7WsiU19MSaa5hxjuEVbjkQoT8tyuSzL
t7SJgvFm/ARWigQ1
"],
Association["Book" -> 1, "Theorem" -> 36] -> CompressedData["
1:eJyNUdsNAjEMs/No+YDPG4CVGOEWYFY2Is6dkPgA1ZWSNk6bOL3vz8dOAC+Z
BcSlVl4NbubuEWFBEsSsCGDIqDQyih3uWZRXghVOVxetQ47fRedMF2aBocfC
4ZHI1PPua+2uI/6yXY/y1ZJLBxu6GCUbkgWjtMkqu1keEisI8W3tHEbtj9H1
tj2pQpkTPiR0AmOEDVKDvG3bp1t+z65O9R8q03XZo30DroYEyA==
"],
Association["Book" -> 1, "Theorem" -> 37] -> CompressedData["
1:eJyNkM1tRCEMhP03NhghlHfey7aUEraB1JqOYoiinBK9DzECj6UxPF8f7y8m
os8td7geb4/Rsl8j11qZubL38OYm24awmLGziUi6CwdP6tQcQJVKWxMnYQbh
79A5R/fwPgsboyJGUIypc6oqYt4c9zb5rxtRokStZc4AHPpD5j7Xu6C1UOa3
a2bbPqJr1VbUBeoHhGqr/l3ZDapxevccVn8pyhlkoMlsLsTp6DiE7SiG8S/K
3NvVO+iEMpyVvgAy2Ain
"],
Association["Book" -> 1, "Theorem" -> 38] -> CompressedData["
1:eJyNkFtOBSEMhnsvBU5HdJ5N3JJLOBtwre7IcozxxZj5gKYtPxT6dv94vyMA
fG5ziafX9dxy5uw558js6R7SXGjvKiGJoJMQUWiFjgMcTJiNmZjVjAyYSOH7
yJ+cZ84WMc/C1jqOvgL6WrIOZvYYV597lf8vjCijAHNmnt0snH8YY/tecA0P
d/OdEakvs8pD1Hst9gqc2wOLnTHbbdHtcrCoalYhqcYQYzMQhRdErmZiVw+z
UqiJstYU/IURbyNvN4US7OoNGb4Av5UJbQ==
"],
Association["Book" -> 1, "Theorem" -> 39] -> CompressedData["
1:eJyNkMltQzEMRLkvWmxAp1zTkktwA641HYVSEOQU4z9BA4lDYCh9Pl+PJwLA
15ZrrI8eLe+9jbXGGGtkuoUJbVMJSQQNhYiaGaHjgIAwVa1SaQQJEKKC/B96
mz3NLWchfUd0B++T52Rm9XF53Iu0t657CVdXcXNVU/5ljH2udynX0jJ/XBHZ
9hFeqzZrXZTtoM4c1b8ru4HZT++eQ+ovidEbiMFEFCPACE09uOwoVME/GDHj
nqlwQlENGb4B98UIkA==
"],
Association["Book" -> 1, "Theorem" -> 40] -> CompressedData["
1:eJyNkFtSBCEMRRNuHqQ7Q4szNf9uySXMBlyrOzL4KH8sqw+QIg8I3JfH2+uD
ieh9mZM8PfeRmVuOkXPmdA/pLm3ltHETYW/SWgst13knJxPAgAaoWVNCK/N1
5E/ut5E9Im+FzetxbDNomxPzAOCxn3/uOf6/MKKMEh3HGPfNLBw/ZK69F6jh
4W6+IiL1Zah8F9WCl+Pon1gAG8yWLLqSCIiqjmokJUwDWycxujKjxORuHmZV
oSYKrSn8C5gve14uSlWwuncGfQCQ2glc
"],
Association["Book" -> 1, "Theorem" -> 41] -> CompressedData["
1:eJyVUNttBDEIBIaHDetd6TpISynhGkit6Sh4pShfiS5jgTAzYPDb8+P9yUT0
ud2rOEbl46jruirzzMwRM1Q2ZcKiyiEqIukuHLxo0nAzB8TMxhAniFiLf33i
XDU9fK6GHkdmVFDUwloALNY/xn0J9Scb0Q5EY1Sd0asYvlG1497L0MeabOuM
qm76djjPNlhfDH7DAhit35ktAOLW7jm0/1LAGaRGi1ldiNNtdu8uHepdxKb8
AzDnfGQa7W7G7gz6AsRHCHQ=
"],
Association["Book" -> 1, "Theorem" -> 42] -> CompressedData["
1:eJyVUUtOxTAMdPwZf1qVlsJjzZU4wrsAZ+VGON2wAj0mkjXyWDOJ837//LgP
Ivqa5WHg7TXTMzOqfFFdNJJltIepiBlDwMxmRgOjKAmi6qqsagZW0iY9/GvC
7aWiA+LczxPPx3HUllTbk2wlIpH1n+s+gvhTzeziRMuy77eKSJ/PlImI5uIN
6ePpjqsDYPZxDbU4VcwaF5Ai1bwN5BIlBW2ydxDzoMEEEBudNKR3SdbWqhG9
PxgHxHX8oJe/Vq4raOb2J8QQ+gYKUwj+
"],
Association["Book" -> 1, "Theorem" -> 43] -> CompressedData["
1:eJyVUMkRwkAMk2UxO2wHPGmJEtIAtdJRLIdHGIZM0GN9SD7W9+X5WALAy895
BDJiZNKIrh2UgMRFrTAl8ppIJVtYWW5Q2s+DmZI2ZQEe4foKoW5P/bXuCfCY
fdPeQ7TdUdFEpcK87dfHXE+0sKWbYifj3pkz65zuNOsSda0a6eg2xq9tq1XU
QT8Hr/f/A/0=
"],
Association["Book" -> 1, "Theorem" -> 44] -> CompressedData["
1:eJyVUMltBDEMk3VbtmceqSAtpYRtILWmo1D7yWsRLA0I1GHq+Hx8fz0GEf20
eQMfERYRWuWlepkny4CGqYgZ63BmVlUaPiYlGYtMd1hTcELKyPWl/lk1s2ru
s3fsfc5aRau2niNQqvneuP/j9SiNKpggWuu+z8qc0WtKQxVccIsQvKgIj464
e8f9WdTcn05IPuETa4CLJGJIwsPHuNFo4JLClElstGjIYCab27qPNxhSYfwH
Yb4qrsup+6Iwh9AvVKcIfg==
"],
Association["Book" -> 1, "Theorem" -> 45] -> CompressedData["
1:eJyVUclRBDAM8yHLTgaKoCVK2AaolY5QwoMXMKuZXPKtvD0+3h9uZp9newYc
FgkKwAJfAhFmQGZVwivcu8qjo53Ow0fEsTJgupZl/Jq+W24JtoC918Jqm9Ui
qg79ZLv/An9ab706J9kz03XHTBzUWQJKnNpjHeYKg+J1ITWLHilnXvRKNGYS
ozh8i6gkVCE/n5FWZQ5r98irLKQeXvcmdwCOqR+osuLXokE2eEpk/wJVLAeC
"],
Association["Book" -> 1, "Theorem" -> 46] -> CompressedData["
1:eJyVjzFyAzEIRUEfEMLs2I3XjRtfKUfwBXLW3CiwkxlXScavQIgPQv/x/Px4
MhF9dXiL87rd73m57Ju76zKMroJ4iLARxhhuxqwcNMlN1YChKu7DaJRA8vvS
TF/T54qMsFPhy8hWaqYq1OPd7/5H/qmaUXujiG3LtlJefsjs3ArYcZh6V0Sk
5SPgugM7rC6GeaATCJQXaDeUPo/erRbVJIERk4ZSMosJIaxHtDBRVrAKvwDz
Oj3WUupXpEYY9A2bpQiD
"],
Association["Book" -> 1, "Theorem" -> 47] -> CompressedData["
1:eJydUEFOBDEMS+PESaphpFmJEye+xBP2A7yVH5EWceCwSGC1bqs4VuPX+/vb
fYjIx6K/4WVW5ZyV59MxL4KjPaBDzez5dANmhKqrDwz61xMAaRC6Q+APzau8
nJFM0m/XdcVJibM8szs9H3f+E/PXKtlk6+yBgwziG5ncQ7ET2Me+Ap3CKm9C
VW/04K2JDRa2fvESrLW06x+qJmqdmCikbHiYuqm2p3ZwB30oOufxA0fWcbgs
tzkyBuQTW+EIDw==
"],
Association["Book" -> 1, "Theorem" -> 48] -> CompressedData["
1:eJytUFFKBUEMa9OknXXfzkPwAl7JI7wLeFZvZGcFeQoKgvmYmZBpGvJ8e325
uZm9reOPEFkkcx6Xy2NBgBkCHhFPk61uY8DlBFGK2DIRgSrRAv2b+NlbKUYw
mal5XI+YZZpqV6lGO/wztl/VqpVpxRpjZUh+oor3aKbz0S2c1714En2gvmk9
ufjoRe40LNZ1mtK7PwSjywuktFGOBOhfsIv7TluLH3yUh70DiBMHQA==
"],
Association["Book" -> 2, "Theorem" -> 1] -> CompressedData["
1:eJydkFFuhCEIhMGBEZRs/mQf+twr9Qh7gZ61N6qaJn3qJt0vEZUBdXx/fH48
VES+dvgv9/u83a6KCA+i7RREm5lS0FobEaquJSkjSAKNtDFaSFuC+N+XVkX2
6DlqDM5FJIVZXuUOj3rhuU+ZT1VStjfJrCq6by8/zLnX3PZ4JnrfGTPb8gm4
rjXAtSH6wTuQWF7gpwDop3YbW50CxVzf5FKq1k0wTosvaK4OddNfoJrjLdNl
n2JqVMg3M/MIKA==
"],
Association["Book" -> 2, "Theorem" -> 2] -> CompressedData["
1:eJydUEFOBDEMS+rETTqdQdobIw7wJZ6wH+Ct/Ih0hMSJlcCHtI1jpfbb/eP9
riLyucqf8XrcbudTRHgQbXUg2syUgtZakKquKZSgO4HmbhHNpBUh+H3pPiN7
9BxzDG5z2yIpzOlzusMj//PdR9gesqQsbzLnvu/LSnn5xnGsOwvgddD76pjZ
oq+C5xM4wXoQ/YJ3IFFe4Gug+H7N7rWolJUN+pBGmapGE1TIJfECzdWhbvoD
qOZ4yaxQS20lUcgXPpMIVQ==
"],
Association["Book" -> 2, "Theorem" -> 3] -> CompressedData["
1:eJydkEtOBDEMRO2UXbG7kx5pdrTYcCWOMBfgrNwIp4XEipHgLZxP2XHKb4+P
94eKyOcKf+e4389bRHgQbV1AtJkpBa21IFVdUyhBdwLN3SKaSStB8HvTOSJ7
9NzGtnEf+x5JYQ4fwx0e+a/vPmF/qpKyvMkYc85lpbx8cxxrzwK8FnpfN2a2
5Cvg5QROsA5Ev/AOJMoLfCWU3q/cWY2qsmaDvkmjDFWjCWrIVeIFzdWhbvoD
VHN7zayh1itWJQr5AgqqCDQ=
"],
Association["Book" -> 2, "Theorem" -> 4] -> CompressedData["
1:eJydUEGOAjEMSxynmc4gjtznSzyBD/DW/dE6u4DEAQ7jVlGVOE7q/Xa/3tzM
fjocAJljzlyD/lBwAekB4LRtYljq1CA7xUSVyhDJ4/PQHBtFj8qqYGQgaciB
TIkQeWzdz7h8rZIKMBujSgsAE0/su96cAifXVXdZO8OhL8udfkZvnViUWfjf
tsgNvkRUlD3is6wtDHPl0hAmARsaHoTam9s+/vX6G+LMCDib4BHS+AWRrQZv
"], Association["Book" -> 2, "Theorem" -> 5] -> CompressedData["
1:eJydkEtuwzAMREkOf4plu45WBbJpj9Qj5AI9a29Uyll0lS7yAI0wGlEffty/
v+5MRD9TXuFzvEd0j4BMK8Siyk4QkTBjNk4ycgUWMwHUXXTGU54ee+zrkq0t
676usb1t26UHZb/a9TCDt3zxuU+5/JtGlCjR7TbGkUV9DQ96j9IoEOcUnnNF
VU89N41RA1EmkCfeqiFwBxw6Q7RZoqMuqgICw5PEaWdWK5fuoWqFq7GpmPIf
YN56tclITWGiwaBfdowIww==
"],
Association["Book" -> 2, "Theorem" -> 6] -> CompressedData["
1:eJydkEtyAzEIRIFuQPL8MtbGXvpKOYIvkLPmRmFmkaychV+VkLpaCNDj+fX5
VBH5PsJbjHvmGpmwQ5mokRoCM0t3VdcmLkGgZxrACKM4SQFfvrpvy9R6n5Zt
WXL9WNfLnNLmq193d0Rv77b7isu/bmaF6vZ2G2NvES1rkBqpmOc6IwvkueXp
lk38XhqjFrJEop1EByZEAAEeJvqRwlGFKkGgiCYWsqnSS1XVJL0IujrNqX9A
dZ3rm1zohBtTIT9Hnwif
"],
Association["Book" -> 2, "Theorem" -> 7] -> CompressedData["
1:eJydUEFyAzEIAwtk8NrJsdcmT8oT8oG+tT8q3ulMT+khOmBjIbC4Pb8eTxWR
7x3ewzUiPIm2E4g2M6WgtRakqmsKJehOoLlbRIO0IgSvh64Z2aPnmGPwmMcR
SWFOn9MdHvn2d1/g+JclZXuTOdda20p5+cXlsu8sgOdB7/vFzDZ9BnzegTtY
CZEnvAOJ8gLfNcX3s3bVoFLWbtCHNMpUNZqgllwSL9BcHeqmf4Bqjo9qK7uL
lUQhP6JhCA8=
"],
Association["Book" -> 2, "Theorem" -> 8] -> CompressedData["
1:eJydkEFuAzEIRYEPfFtNPJ7FKOteKUfIBXLW3qh4qqqbtos8y19YHwzi/fG8
P1REPpa8CDmYHbZiEzV3DYGZMUI1tElIOtDcDfBM82Uv+fPPOWZPss/rnHHd
9q1tXdq2Y9+AINvr4/7O5V+39xIXud2OY7bMRnwzxopZoA47+eW6+6ln0px1
wXoQ7aQWhjdkAglfJvoq8aMaVYFAlV0sZagaTLUx6R5FemgkwvWHSh+XMUZI
VEs3p0I+AekaCFo=
"],
Association["Book" -> 2, "Theorem" -> 9] -> CompressedData["
1:eJylUMkRwkAMsyXLJNABP1qihDRArXSEzDAMD+ABStZeK/Gl03Y5bxkR1zG/
4lh7ISNdY6y9OPy6mC4/TIksElRI0ekwkvxYktzBheAMQipnIKodwijUH+O+
hb5+BWam8QDLpj3EeHg439kGm5LjQw+jWZmUr7wP7SQzzbpj5azxgtlz/nx0
s56FAIOJbEe0GtZ3OvqYnPcJy16Ly8Jau7f1TcYNy9kFaA==
"],
Association["Book" -> 2, "Theorem" -> 10] -> CompressedData["
1:eJylUNERQjEIgwRo6xau5AhvAWd1I0PP8/xQPzTtQZsCDZyP6+VwM7u1+Rm5
im6uGm3li02vmfDQomeS2mBappXrbE5+rEguqBCUQYxR0wcspq4QAvGP3Heo
r69Aa2oPMGRKItqjxYkrgcVMZK7NRLespnXkFq0kMcXYmNFtvEBloyMfv8Et
YKDR4aUbNQ3rmbHEiuz9hMZepygFKp7pqaHbHbzDBW8=
"],
Association["Book" -> 2, "Theorem" -> 11] -> CompressedData["
1:eJylUUtORDEMS+I4aSseaPROwJXmCHOBOSs3wn07JGABXliqm4/rvj+e94eb
2cemv+P1ZcUAzCIjq2pmJVDdHgx4eiHidhwRgWSGFQkL/jiQOTQJbHbzOM4b
3pb1IYUA58C/7H6D/vV2re3JbM4x5KircDkRdBDrzYWStsg5t6Kyi6+iXa/7
3twX5lLrpTe4ZSx1k0OL3PUb4aR5WoYrNXckYu+gMqFBaad/wTnqPNuo2Dpq
qPUTT5gHcw==
"],
Association["Book" -> 2, "Theorem" -> 12] -> CompressedData["
1:eJylUdsNAjEMS2yne7ASI9wCzMpG2D0kkBD84L7TxE3cy3G7Hl1V90x/YLGN
Ku6VizFK6pYbW0OOBNLWmiZQ7fENgJJRC+bwASXm5L3pzflfup+Yn7dMPcg6
g1S4p41JkRSSpKtyPy32lLj2lpGFDdlPz7AXw1bMirRD5sxj/8aSZfCrSLif
tmId4RTt7P7O4CtobXEcND0mrAcqpwSq
"],
Association["Book" -> 2, "Theorem" -> 13] -> CompressedData["
1:eJylUcENAzEIAxtIKt0SXakj3AKd9TaqyfVTVe3nrASsQIgh9/352N3MjjZX
AGemmQfluWVlRM4JBMjiTHK7TXHUyDACsMTPchEIlZIFxqjmMDDEqmIGL8r9
wv+CaKW5ZKGVQY20pgX0FkTadbiPV/ydtHohuosz5+zujDEX7aWr6zWXHqVo
nBbuClmX1B+xMreRGrZO/QOBHlMnYnhNp70AIrAFww==
"],
Association["Book" -> 2, "Theorem" -> 14] -> CompressedData["
1:eJylUMsNQjEMy99Nt2AlRmABZmUjnAcICQkuWGqSNq5j5XS5ni8qIrcJf8EO
BRU1M01TNa1MMbfUECAr2SnYAu/kmLh9VQNWWHg0uh1oeLdUoyiElch/7X5i
/exyuEhM3ns8FOKFtaYGEYiqrmKfL3nEeBC7eWJewA+DUVjkPxk9OVlsDrLZ
iwq3Jy5QVeduI9wzfe+ducXTfcUbNhY2jUk6Z2ukhd4BqdwHNw==
"],
Association["Book" -> 3, "Theorem" -> 1] -> CompressedData["
1:eJylUNsRgCAMa9J+eG7hSo7AAs7qRvYB6nmePwYoj5YQsrRtbRCRPcI/JIPK
PAGonXqnUCGDnWeZL+yDTB3Ugm/ImmNU+rfcB/iZHe8BoSTidTHXjMkbXaqn
szR/il4ULxAZE+XRcKqMQddhxk6bDppq3VUblr2pLdr7yQF9XQOY
"],
Association["Book" -> 3, "Theorem" -> 2] -> CompressedData["
1:eJylUNERglAMa9o8BJnClRyBBZzVjUxbuFM/+CEfvaMJL2ke2+u5wczeOS5i
vplx9rGuC+w+jRFkcNBDEC8LlwI+lZx24ukC/BfWOyCJ63H/DM9ZbwmZQXKi
k1SWnsrWiYO50fG55y5CssShUScA0bNIBML7MKnVloQGHZ0K1mcaH4+F+Xd9
3pVpXX75I+wDM5MEaQ==
"],
Association["Book" -> 3, "Theorem" -> 3] -> CompressedData["
1:eJy1UMENAjEMs+P0uAFYgJUY4RZgVjYicY+TTkLigYjaqErs2M1te9w3Anh2
+jWuQF6kdR2AUoI0Rg4sWjQRATAkixFfNN/tONdIxif436NUw8qdy0SwA3Y0
vU3HZa8b7h8gdjd4fNoIzuzypHh+L0imyMxEmpE1zY+6Om9v36+1sR+8AJNx
A44=
"],
Association["Book" -> 3, "Theorem" -> 4] -> CompressedData["
1:eJy1UMENwkAMs+Nc2zVYiRG6ALOyEYmPVqqExAeiu+gUx7Evt/1x3wng2ekH
kau0bQNQSpDGyIFFiyYcAEOyGPFF84DjWiMZn9r/HqUaVu5cJoIdsKPpbTou
ew0YP5vYaPD8tDs4s8uT4vm9IJkiMxNpRtY0P+rqur1jI62N98ELdBwDeQ==
"], Association["Book" -> 3, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 3, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 3, "Theorem" -> 7] -> CompressedData["
1:eJytUMkNwzAMo6RKcR55dYKu1BGyQGbtRiXloEAf7SsEJOuyTPOxH8/dALzk
rsBqXlUIN7NgWqOWjARTGFh1QAYE/PeaEDL7YOKuHdmx2rlcRPeDP1z0XtJR
ItL3SFoonhc9Tr4QO3Lsj7OulfOrzZpdb9/QberhetlUnur0/BjGKa0vdszu
tZlwm0VO8pSeXyARdzuFbrwBClUEVA==
"],
Association["Book" -> 3, "Theorem" -> 8] -> CompressedData["
1:eJytUNsNwkAMs53rlTVYiRG6ALOyEXHuWvUDEEL4pCS6OA/nut1vGwE8bP6C
iN4vZEukiVhDrbcmgGLZaAtyHKH3XWhMFxVz//XPp9Lf8IV+WZxXkWVQmtug
VnWL0URRi1b+IBVR3DlwooT5KtMnW0OmkMkc40Bc8p0GJSdcC74Axml9aTwB
pdQDwg==
"],
Association["Book" -> 3, "Theorem" -> 9] -> CompressedData["
1:eJy9UNsNgDAI5E4/XMOVHKELOKsbyQGNNTHxx0gaKMf71rZvDWZ2SH0jC+DN
KE1pGTJjMnBwkjO/zOxh3jFU+e9CzY4lYos8DuEnXBu7hy6ZgwQjsa7CIOwV
xZN/LJkLJudqfo2LjEf2MDw7ARBVAyI=
"],
Association["Book" -> 3, "Theorem" -> 10] -> CompressedData["
1:eJytUMERwzAIkwSLZKWMkAU6azcKWHbau17zin0GWzIg2I7XfhDAu81DKzMA
1YUSE1lOMlWOtREgmfxftGgO87XgY/Y5ubPgPUt/iWghbSe2tFifFSsaUUTj
ccVzPFZXPZGA7SBrNqKT1diwOsaY08zdBAzqR7HTgp/IEzliA1s=
"],
Association["Book" -> 3, "Theorem" -> 11] -> CompressedData["
1:eJytUEESwkAIg5Cs4/gBr37JJ/QDvrU/MlAPXvTUbJsuDIWQx/Z6bhkRe9NZ
uN8QqwCSWtdVoug05hGqpkod/QJZcxoHk07SPdGN60S5g/8NyaNkrRZi9nbl
F/2pgws+1lxUZyh1XlPUqjlB4bON7wsabqsAwf9WD5IicoY6ZOTKi6eTmTkl
3r7d+Jbs+/hkUxsB2t03n0AFSQ==
"],
Association["Book" -> 3, "Theorem" -> 12] -> CompressedData["
1:eJytUNEVwkAIgxDOp1u4kiN0AWd1IxPOD3/0q7k2PXgUQu7H83FkRLxMp+GG
WAWQ7HVd1Wwqi3kaVVPUjn6BrDnGZlJJqifcuM6Ua/xvSO6StSxErO1KL/yp
zQUdaS62M+x2vqfIqjlB4bON7gs9bKuAhv4tD+qOyBmqkJErL5pOZuaUaHu7
8S1Z9/FJphoByt03ePkFMA==
"],
Association["Book" -> 3, "Theorem" -> 13] -> CompressedData["
1:eJytUMERgCAMaxKOPVzJEVzAWd1I2oinH1+WIy2UljTLtq8bIuJI+NHQNaw1
jQVRzP4IRiig+kyf9cMKHhbezv5LN7l90/ETKYkkXneTi/mZMWs+KgeE7nrU
YU7FksJYyaEN4Wat4VYgfWd3TMuYMd/6cPrnPCdT2wN9
"],
Association["Book" -> 3, "Theorem" -> 14] -> CompressedData["
1:eJytUMERwjAMsyXbKceLBwOwEiN0AWZlI5QQjvYBr+qhc07SxdZtfdxXN7Nn
pwNxZWWRRDAQABO8nBeQnqwwAm6Jn/lQSvGRjVahBwwMTVGUeuy6ZvyrAm8L
hOikQzTFHD7ghnfIJHInkRvzEKc2f4PpSnNaJ3k5GjNU5sL0sYh/ke6B1ntR
b2h+aoq+AJ39BTE=
"],
Association["Book" -> 3, "Theorem" -> 15] -> CompressedData["
1:eJytUNsRgDAIS4BT13AlR+gCzupGQqmeH/auH80Hj5LQHHs5j0IAV4SZUDOj
QyAUz0pZt0U0OlPECDb+KVuI7Dsx2+6wh9dLRYfRFfOjZHY/uhj73dRjUhh1
0uSRa1uU8Gc0O3FYmN8INyjsAyk=
"],
Association["Book" -> 3, "Theorem" -> 16] -> CompressedData["
1:eJytkLERhTAMQ2UrR5GKFViJEViAWf9GX7JTUFHhS8zFxNZTjus+rwDwc/o0
9jmZSYayvqpIIoGZ3NMX5lu3eyJXhEInpLNPGvk17vvA0tNmm6Epmiuar3kX
MYtR1lXnulQOGPF0pbehc/3UquES2rZ+rIRNQ3UWwxijtQKl9gB0h8cTpefG
wB/gTQQu
"],
Association["Book" -> 3, "Theorem" -> 17] -> CompressedData["
1:eJytUEESAjEIIwGdXhyPnv2ST9gP+FZ/ZCDreNLT0k7aAg2B+/Z8bIiIV8Ox
drmCZKFwYiaCSRBY57pVx1fk78+QETaOw6v0LBEdLvc/4dSjZdky1VupwRY4
KL05ofh42AcH4eaNkxRfz0yGMbldqAou5u10XUpjHDIGmDuTBa5OYOwjSnHp
+gbVdAQS
"],
Association["Book" -> 3, "Theorem" -> 18] -> CompressedData["
1:eJytUMERwzAIQxL99pl/V8oIWaCzdqMKcNNX+4rskzHGQsfjeO4HIuJVdDE2
SBSEpJIBxwQzdWc9Z/D3XxjEoMswS75aFZfb/S/Y/Ti2BjZRRlgmh+1X/RSf
DOtgM+z55C6Kb4ZN0bXVKBPTbPaUO0hplGuYay4Lt2VyRiRrOXwDqMED5g==
"],
Association["Book" -> 3, "Theorem" -> 19] -> CompressedData["
1:eJytUMsVwzAMEoj03BW6UkfIAp21G1USTnrLKdgPf8A21mv/vHdExLfpbiCT
grAxlSgCCW35ZKuKvDhaIIxxw021VJZye9ZrtWU6llFfo0R2SHPlzZHi2GEP
HEZlPnlM8d/hUIy3H5Lgx9xtr4kyfTMDXHVZeKyQLlHZulo/nKgD4w==
"],
Association["Book" -> 3, "Theorem" -> 20] -> CompressedData["
1:eJytT8kNAjEM9DmOIyHYD39aooRtgFrpCHsBIR7wWsenZuJMLuvtujIR3Tvt
bueTsPFCB5rhbiLiQ+aUQcIs5L8fzczhwKialgkgQcjUclXDsrfU+IsClbRr
RMLMXd8W0b2XaR2Hd7RGs4btRapQr8E36kZXaHM2RjTSXeuo/VQDjMQowXoU
KnJ9G5+VXP5lKGV15QmasdIDpmQGpA==
"],
Association["Book" -> 3, "Theorem" -> 21] -> CompressedData["
1:eJytUDESwzAIA0uAr70M2bv0S3lCPtC39kcVuQxd2ik6DLaMjU7P/bXtbmbv
TtfjYUZbfPV1ZnKMkdOXhdPg7pa/h0YECVA1JgUQpmNGpID71Urj7y2gVIqS
HiiQWdVKJAgtSEgcBVHN8FBacTZpJZTPHjRTSTZfnRQs/a9B7jQM733ICbeb
KPkh/9hPCWc528MvMEo+ySTZ5hke9gFq8AaS
"],
Association["Book" -> 3, "Theorem" -> 22] -> CompressedData["
1:eJy1UNsNAkEI5DHccIm5DzuwJUu4BqzVjhwuGr/0SyfswDKwS7jst+vuZnYf
+gtg7Sc/ryQigotvG9oUu3V87KoqIBPytUJIpOnKKpJL8tdj1lc1U9Rm1P+V
siS7OdBFnALzcFmcDI5Ju55FOpTyqslDJTD5HpKhu2cOd1iGs2asKrfFwrUP
7Q/TinS0wnjDJekBqFGrqmDF4g9bKQa7
"],
Association["Book" -> 3, "Theorem" -> 23] -> CompressedData["
1:eJy1UNsNgDAI5GiNJPy4gis5QhdwVjeyUE3rI/1S0vIoBwed07okENFm6g/R
qKykR8REsBOyj9Ap40ZyABRrt6S/nrO/f+WzSUzXQvdhBpYFXpqVRwc6FHcE
WkeEaXDKyaij8EicExLOL3usjzLCte0OVh0Dbw==
"],
Association["Book" -> 3, "Theorem" -> 24] -> CompressedData["
1:eJy1ULENwzAMI0ULGTt06dqXckIeyK35KLJQ24WBdGoImBJoi5L83vZ1I4Cj
0i0oLz7xAEEzGoMhCpLJdVnFQNIUwwBWs3+P+duw9eMXgFglpWnergzfvB3c
9vkoGJTHnfFHNVtqaXF66oqGacv+vEFtNsSvqigidAJ/wQOf
"],
Association["Book" -> 3, "Theorem" -> 25] -> CompressedData["
1:eJy1UNsNwkAMy8MehJUYoQswazfCDqJUquhX69NZed3FyWN5PZeMiNV0D5o6
qExUiRvoThuJ/01JUIU08CGEDEW6W97VKnGedboty1LgEb7Y23YPEcOquT0Y
TMSlU73lPVjVXFITB6MgCrUtC4EXU9D2kD9on7Mn5PyYYHa8AW+eBWc=
"],
Association["Book" -> 3, "Theorem" -> 26] -> CompressedData["
1:eJy1UEEOgzAMsxMHrrvwgH1pT+ADe+t+RJpRKiFtJ7BUp3Ib1+lzfb9WAvg0
ugm24AGCZjTSDU6HZD7pZw8TRaeaBrDmdXXI//OTI1ZHDmZf6ZT3UIZvnQ7u
8+wKBtWKYP5R282tVcEo3fPBsuVxvcN7NmiSQlmhDWSRA5U=
"],
Association["Book" -> 3, "Theorem" -> 27] -> CompressedData["
1:eJy1UMsNQjEMs5v/EwNwQmIlRmABZmUjkl44wQncNHVrS7F6vT9udwJ4Tvsb
zkiPUHLFoZlMkBQcn4dWpXumV0OqIrISubk08vLriPldHVmByVRp5i6iKjtK
NhdvSC/v2GrzYmbd1bZpUpd4X3xbxzR8PCY6Yp+mqnuQElS6YQlq0U4Cuo88
u9Fmdr2xyIij/xijKqfwApWFBss=
"],
Association["Book" -> 3, "Theorem" -> 28] -> CompressedData["
1:eJy1kNERwzAIQ3mgxgNkgqzUEbJAZ+1GxZzjXHrX/kUfMgYJg7f99dwxs3en
28AKhjsOyOVhEtHiv+vr7EgH4bcO+xOXV3MZInKdXijOuk/pkacoLznz5NFh
ZigyjkaSmypsXSeZyhYMCUN/4vzJpcVjEZmJDzBcA2Q=
"],
Association["Book" -> 3, "Theorem" -> 29] -> CompressedData["
1:eJy1UMENAjEMc9rEORBPFmAlRrgFmJWNiNuKe8ELrDRN5aS2ctsf990APJX+
B7sw081antupAlY1ts+iEd7D6wg+Affw8Qq//tphfGVLHCCQKTuk7Mzsb3sH
BhGDX026uIiFGssxzMWERigftRxYR5agI5rZJgvJqjgVG2nsdqAo/aclaXOm
wAvohAYY
"],
Association["Book" -> 3, "Theorem" -> 30] -> CompressedData["
1:eJy1UNsRgCAMS0qqc7iSI7CAs7qRyEPhw/OL3LUNNH1ct3jskQDO200EkQdY
YqRZgMTg+qkZY+WpweRlPzBMZUPhJc8uWzWoIhKPb5r2U2RgayQZlOmazKT6
CnxPwn4HdjdZXO6exAgX8f4DNA==
"],
Association["Book" -> 3, "Theorem" -> 31] -> CompressedData["
1:eJy1ULsVAjEMsyPLse9WuIaVGOEWYFY2QuFR0EAFKpzETvTJ5bxdTzez+yr/
xF7FMUbNcRyYBvdh+Vk0kxFApLBTAGFgdmZ3J7Zf++PXKaAizSr5gdyge9t6
QYfuglB4LuBcnSCrqqnteiXTDXVed1aUro4QQW9rWNmxoknIXVkllstWwlVh
SQ53/UpkhFFkeMMQI4sMQ8iA7+nTHpPZB0E=
"],
Association["Book" -> 3, "Theorem" -> 32] -> CompressedData["
1:eJy1UEEOwjAMi+0wbeKE4AN8iSfsA7yVH81Zq2oc4LZItRI3cd081/drRUR8
Ck6N24OZvF+xzJjjIiGkfwPoJ45dzqlk5JlWfwSPhUSQwO5yR5sdTgfPgir8
3YFdYTAsqIpkm5ZTmK03BaQ7mmCTsywnL+IrukFfetETvKUNkrQD1A==
"],
Association["Book" -> 3, "Theorem" -> 33] -> CompressedData["
1:eJy9ULkRwzAMw6OcipSpUmYlj+AFPKs3CinqHLtJl0ASxaNICIfXui0rAewZ
fosnKT3u7B0N3Sbob/2cB+cuxZaY999x+TNVDEReESdVR12oLmqUQvlhdOUZ
iyrnNRkcaYwMA5y8HoT1HKSxHPZ9IHsaRdyk3ujGN189A58=
"],
Association["Book" -> 3, "Theorem" -> 34] -> CompressedData["
1:eJy1UMERwjAMsyT74MWLBViJEboAs7IRllt68IBfdRfFseTYyW153BdExNN0
MEjxesH5hIqSENQ/O7YVn66OOaVHDvoDXz0zCRKYKYd72Hyre54mIyeViP2j
19hMiz6RW4/sEOxUO+a1nAtbpgXvFRpwkK7U2lpUFZR4AVXRA6o=
"],
Association["Book" -> 3, "Theorem" -> 35] -> CompressedData["
1:eJy1kMENAjEQA3dt74YfHxqgJUq4Bqj1OsKBk7h7wAssxYo0jmL5utxvS0bE
Ou3fupwBZLEZJWVIH6MliKQdUHeVrwGqJTVLP6+L73RiRnQDhSnSxVzuZZu4
84PGIMYBkbvwE25s+w1eR5GMaWROmj6ewsoZV75VmYJH9Ui2wjj56QMvfgTz
"],
Association["Book" -> 3, "Theorem" -> 36] -> CompressedData["
1:eJy1kMENw1AIQ7ENzRA5ZaWMkAU6azcq/pHaJFJ7ai2EkDDiwbLd1w0R8XD6
u2YCTN4YUxWj6qNTAi2oJ+gEBKCSVEzp12jf74fb7GiMhgEGnTQKvHQoz+pr
URcD33lv7vIimieZAYUCmeoXcOxS700PFXRQmcU47WbHZM8TsVAENw==
"],
Association["Book" -> 3, "Theorem" -> 37] -> CompressedData["
1:eJy9UEEOgzAMs51UgMQn9qU9gQ/srfwIhyIx0LTb5rRWGketm8fyei4EsBb9
HhK9mjBPo6DxSyNYgOCkqJdD8k79x+4VLCsoR3Xo9nrpreMzMom8NfDkLp6K
76yfO8LEaB6Bw7ODmVlvNsQO7UhLhzNnmYMaYwM1bQN5
"],
Association["Book" -> 4, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoB+hr20gCyCELAJZUAnw=
"],
Association["Book" -> 4, "Theorem" -> 2] -> CompressedData["
1:eJy9UEEOgCAMW1uIHP2CX/IJfsC3+iM3IEQPetMmNGN0W9my7esGMzuC/sCM
MiFblmDUmxL92FXlMZW89EuPD7jNlAgSqC4ru9nhdOQZFFBN+afHolsczHiM
G9lnJA9BTzUFjbUhWzt/MuZQD6SoVBstppLhWzoBK08Dgg==
"],
Association["Book" -> 4, "Theorem" -> 3] -> CompressedData["
1:eJy9UEEOwCAIo+D8h1/aE/zA3rofraCJ0WTLLlsjHLAFSqnHXiEip6dfgLwh
i6qC6ZHYQ7AWQemHG74Cd4iYi/dsDD8TuTtclIm3AS/kEyzcojn3TvxgwUQx
kILZRhlfqC/aVwL5
"],
Association["Book" -> 4, "Theorem" -> 4] -> CompressedData["
1:eJy9ULENgDAMix1VYmBm5yVO6APcykfEaSlMTAgrcpo4ldOudd8qzOwQ/QNy
SrPlbcjdCZKRHUJURjhaSf98q3dVMpRjJRFxoZ2zlRsrc/TBPpQv6MyhtQ4e
JKNSIDPAPMIkyB79L2LMWtyYQ6frevqlbidr2wPF
"],
Association["Book" -> 4, "Theorem" -> 5] -> CompressedData["
1:eJy9kMsNAkEMQ5N1vrPUgERLlEAD1EpHOCDECU6Id7AyTqR4crpczxcVkdvI
nzhaCVQ3qc9LI9wMsCC7EzgEHntE78uxfh3Kv3YBSk8sgmGtzu7MZDTqWIl+
tOzlUGskM2Jl0OrEY3SGns6i01OmJ6oquEiVfxVJZjIJKMNtEmabqj1vIZbg
+w1r9/I5UsBKD64pdwD4BpY=
"],
Association["Book" -> 4, "Theorem" -> 6] -> CompressedData["
1:eJy9kMEVAkEIQ2ECgV2rsCVLsAFrtSPD7smDnnzmwLwHA/lwvT9udzez54R/
aZXBfRk/m5IZAQSlS0pIGJJNdjex/5opv1YBBXlWiQdD1r33wFFok5OIwvFy
MhEDvx0bSH00lko4P1Wz1NwMnpOKMavJyF27mm01WIQr6ljkcs8ZG2FZK7He
pFm6kyFk4zud9gK8vwZY
"],
Association["Book" -> 4, "Theorem" -> 7] -> CompressedData["
1:eJy9UNsRgDAIC4EP13AlR3ABZ3Ujgfj60S/PtJe2kAu5jvMyzQZgLfoNUTTA
nxWWoAnsglbkMzw7X0d6N+x5VCzBnYwgK6Q483q3cFRYB5stM5/cIlwVNqG1
NSjCNExb8ryEu5wJK+dbwKEExP5Fnl553QAxzAOc
"],
Association["Book" -> 4, "Theorem" -> 8] -> CompressedData["
1:eJy9UMkNwzAME0klmaMrdYQs0FmzUSXa9a99FSFgQgch0Xqcr+eJiLiabgQB
xPF9abVZmpZBGIgRU9qQ/zb0+//oNm1rQiL70U7tk8spVp2mSkQsnhNWhSZY
60VkUMhaqHBZPsVnZufcoWzIKC9A+kjqK2Vp4w1G6APr
"],
Association["Book" -> 4, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoDNjpb+XQAIyMjGAMZIEwGwOMxQiLJdyxxYbEBgCj
JAKa
"],
Association["Book" -> 4, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoCWTFGBlZpHFKMzIywmhGZhDBwAjmMYDFmRiY6eNK
VDdBnIMWUih8JiYwwtTKCNaOaSAGkxFhJCMTiMvIwMTICvI4E8xuRjS9YIsZ
gaqZgXZDLAJyuBk5ADnDAz4=
"],
Association["Book" -> 4, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoCnQYGRlNccoyMkEcBFTEyMwEBAxMQB6QYgSJQ3hU
BUQYyAhyDhMTWkgxIvNB7sTmOJAizBBmxMJkQjWSEeRXRmawCCgs4GphAlDA
BETAQANiaJAxiDDzAgBbEgNx
"],
Association["Book" -> 4, "Theorem" -> 12] -> CompressedData["
1:eJy9UMkNgDAMi50vH0bgwUIdoQswKxsRA604isQDYfWyY7VuhjylDDObtfwL
AONzkSgmOAPGYLFB+sa+TfPKApAXJ45cOVvhZLq/gMaR5yuhv8JXRb2o3iLs
YIxoWkypdFrv3QIHRwMx
"],
Association["Book" -> 4, "Theorem" -> 13] -> CompressedData["
1:eJzNT8ERgDAII8HryyVcyRG6gLO6kQRa/fnyYY4rJaSEbv3YO8zs1PEjuDtB
MrJDiMoIR5Xk14bvA9MPyrGSDmKi7knlxsq8eZRQW3vyQzN6xUgwtTJqDTID
zCNsfFdTpswqHqzR56Ln6Zd9uwA8hAOp
"],
Association["Book" -> 4, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAAjIyMYAxkgTArA4zFCIsl3LHFhMQGAJkUAo4=
"],
Association["Book" -> 4, "Theorem" -> 15] -> CompressedData["
1:eJy9UNsNhDAMSxOnrZAY4lZiBBa4WdkIu0jwgbgvdFbk5tE2Tj7rd1mLmW2i
vwOPlYhAzQTPyIPS6DR6jYXpbSnxW6iU1iGLAgiIagWoECdy8D3DFEe5wjMz
fuKgKtIYHjrcwi2hDYWXou5sWySEFxOO5GO/ELTQtqzPvc09FewpGAWI
"],
Association["Book" -> 4, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGEWBkgjiIEQiYmYCAgQnIA1KMIHEIj6qACAMZQc5h
YkILKUZkPsid2BwHUoQZwoxYmEyoRjKC/MrIDBYBhQVcLUwACpiACBhoQAwN
MgZeZm4A0RoDBA==
"],
Association["Book" -> 5, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGBgBtZmQEU6OAugAAmjwCfg==
"],
Association["Book" -> 5, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGAjAyMgyU1cMeAACY8gJ9
"],
Association["Book" -> 5, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGBDAxoFsN5TOCAJzPCIKMaEroAhjpax1ORzCg+J6R
EYpgYoxwBtzBAKqrApo=
"],
Association["Book" -> 5, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGCKBbzQQRYQIBCB9MACETIxQw0dF5QEuh9gKdSi5g
ACO88jAWdkfAwgEUXGAOODjgIcIACSqQJFAMpAIoCAD6HgM0
"],
Association["Book" -> 5, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDDACbR9QBwxPAACY4gJ9
"],
Association["Book" -> 5, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDjAxMoAgCDAykukURqhuRjCTEWweI1iAEWomVBIF
MEAxRAuacYxQxsAGDjKAuZEoFwEAzJcCtg==
"],
Association["Book" -> 5, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGEDAyoDmAkRFKARlggiBgAhNAAGYCKTCDCQqQJFEA
AxRDtKAZx4TFGnoDVJ8zMTGCxZjQJcB8RhQeAwD8LwLx
"],
Association["Book" -> 5, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGFDAyMDKCSAoMABGMUFOAFCPEUAhAkkQBDFAM0YJm
3IAHCgaAuZEolwEAxeQCsA==
"],
Association["Book" -> 5, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGOcDtRKAMIyNWFXARRkawCoi6EQIAoP4Chg==
"],
Association["Book" -> 5, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGGjBiZRJSOgqgACNMAJitAn4=
"],
Association["Book" -> 5, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGGjAyM7AwMzICncKMKclEf/dAACMYDQ2AGkgArtoC
kQ==
"],
Association["Book" -> 5, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGHDCCERAzMjNiAKA4AjDT01VgN6G5AEkWLs2IJgLT
ywCVYWSEsWBsFBEoRLcdTsINgRiKrhIYJlAnMkDNAQDfGALi
"],
Association["Book" -> 5, "Theorem" -> 16] -> CompressedData["
1:eJzNj8sNgDAMQ218YA5WYoQuwKxsRJImrVDviBysfJ5k52jX2QjgdvlBaTch
Ni4lgiPkp2klc5YsgLXvUHF1jaGWPSdZYhASQlH5R26m2fIZh2bX+XLiwHxU
rhjwA/bZAw8=
"],
Association["Book" -> 5, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGAWCEuGOQuGaIAwCYwQJ9
"],
Association["Book" -> 5, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGA2ABEcxYXMMIIRgZYexRAA4HRjBAEkAAAKXMAo8=
"],
Association["Book" -> 5, "Theorem" -> 19] -> CompressedData["
1:eJzNj8sNgDAMQ22isAcrdYQuwKxsRL5SJcQV4UPquD68HPMckwAuH38RsRsO
Xbm6tnDsxodSNRa16VZE2Kpff2PtXBJ7gVdUCd2qOyJZz5F3DnaDz7BsQnR6
A+3xAwc=
"],
Association["Book" -> 5, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGB2BixS1FR2fAAQsYDQJAsu8BpmcCjQ==
"],
Association["Book" -> 5, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGCRhETgEBxkHnImIBAJecAn0=
"],
Association["Book" -> 5, "Theorem" -> 22] -> CompressedData["
1:eJzNkFEOgCAIhmEw5zW6UkfwAp21G/XzQ1s110NPfSIiiArL2NahIrKH+g0W
ygMaqTCaFT5JYgUKaGKhocUleENqZsrjOjq6Wc9X8bGvCOU1flpTouDGEtAc
bBStcTdIZWWrIghfnIDzAMxHBKU=
"],
Association["Book" -> 5, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGF2ACATADRDAyAzETIxQw0dMhjIxgAkQBbWaCOAJJ
Fi4NFQQ6E0kcIgQ3iBHJUEZUETDE4TOQIqgUEy41EGVgeyEqANTtAtc=
"],
Association["Book" -> 5, "Theorem" -> 24] -> CompressedData["
1:eJzNULENgDAMi2uHP3iJE/oAt/IRTdIOSMwID5bjWJWbvZ9Hh5ldQf+CB1IU
0UiXOwD5hz3atjUFaKYHyOgiFQvTRjrFTAmZYBldKZSfDmM5ofcS8WGWVA1x
jgEljwFrOS4UifHWDZerBEk=
"],
Association["Book" -> 5, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGEcB0DhMOcdoDFhYGRkYWIAliMjExMUIAXBbEAgtA
hRiZwAxGJLeyMEAVoXkAKoIkyETQOagqGFGYjCjGAwDJtALT
"],
Association["Book" -> 6, "Theorem" -> 1] -> CompressedData["
1:eJzNTkuuAkEIBKuhYXq6x6TNy5vE8bfwQB7BC3hWbyTj5u1cuXi1qAAFVZzv
j9udiei50n/CqW/HWrfLflmGw2We20+h8XeWeScCr/7tvPJZXWUlmqber6NZ
cZEUAFCrBbubw8W9RDWsE1EJfhMwNUGDR+cY3rAiGGEmsHWpASVOVHsEpbSh
DUONktKRWTQsTIuriuYwzixZPPEfwNx3rfdM2TLis8KgFwDKCSk=
"],
Association["Book" -> 6, "Theorem" -> 2] -> CompressedData["
1:eJzNjTsOwjAQRNfO/rJeQ4IV8ZFAQkJQcRmOkAtwVm6EDQUdFQWvmGJmNHOc
77c5AMCjyV+xXQ/jOF1O5/Nyv5umsnHIu5Me1sxoY//rO/+etlgAUirlkFXd
iPCNe1/VrDc0MnMzleYQt4a8a9kJHa1ahumFpuaoEmorOWJCEpFSjxAjxNAx
AxJcQyDupFNa9cxSZ1k4iHKm+KGLMefFMAho1nqOJWJ4AmA7CbY=
"],
Association["Book" -> 6, "Theorem" -> 3] -> CompressedData["
1:eJzNUMkRwkAM8yE7dkiYtEBLlJAGqJWO0JIBXvx4oMfaI40ley/77bqriNzH
81+YIqLOp3Ut1swJYlOhygwI/Dpt/i6pCqCqJpJZlUa0vbAs7L0Jb6+x4NyD
QYS7Z7A9SliTaT/GCoN5IzhgSPozEGDUOFPEZX6qQpfyTPiwHpql6QdcEhs/
zLSTeeqtLg+BNQXR
"],
Association["Book" -> 6, "Theorem" -> 4] -> CompressedData["
1:eJzNjTsOAjEMRPOzHSfZxChaEAUFEohPxVk4wl6As3IjvOnpKHiSRx6PLR+X
13Oxxpj3Kn/G9XZ+lFrKqdaU7mU2+7ZRmEku9Otn8WvirHW9a1N0K6bUdrV2
oQEAxCiqooBQa701dTrhnFWHqGECBsmkkQxAbwlq1YK8huo4ckz6yHtvnPNM
xqGZnAX0zSMirBUQtsHilCGhDsEPLAZOmTmb7WGGIIAu2A996Apf
"],
Association["Book" -> 6, "Theorem" -> 5] -> CompressedData["
1:eJzNjTkOAjEMRbN4SWwcMkzBUiAhUdFRcBGOMBfgrNwIZ3o6Cl7xZX/b35fl
9VxiCOE95N943O5Va722pnqXOZzqxtQNnm/061/fA1OMaZq82PoWMevBbNeL
w4yItXbX7mBns8nMu+GrutoQRC0FC3ZlH7UVIEJCs4KGbQy9q6LC42OCkFOu
HBIGyREotUx+AAAeRg0jNAEhNzGvRILCIlTC8bwH8vgE8QMqcQnz
"],
Association["Book" -> 6, "Theorem" -> 6] -> CompressedData["
1:eJzNjbkNAlEMRP8xtv9prT5arUAQIFIi6IQSaIBa6Qjv5mQETPB8aub8fD2e
3jn3XvF3ut5qr/UyTa3d2+KOVVvvKfG4ya+jvhsG78M8W9PtS1LqB9XdYBZh
BlDKMA4TBqvOqiLrpvRubCusZEbG6IyBaRMLIFBlKNp6tKnkkpMFxRhdCDGL
C+Ra8CRRIzOTBRIRK3m0gsK2pLjJm0WuVYrbnxaQggP8ByvOChE=
"],
Association["Book" -> 6, "Theorem" -> 7] -> CompressedData["
1:eJzNTTFuAzEMsyVRsmX5jByKogWyFOjQ5Dl5Qj6Qt/ZH1WXv1qEERIgiIX7c
H7d7LaV8H/T/cPVw/1xrjMt4KWefM6J3O33pXzf9/pBqpX3PZcuUmsV7xGmZ
tWYGoPeVvBJYNuc+Z6q8NPfkeRDgGTUsz8F8QhRQRBgC8zBTNR9uWcTMhYhV
CkkZVGG8sbAIQOlJcKVwasqq4CeqSrPuauXt/CrYREjqD5fACUM=
"],
Association["Book" -> 6, "Theorem" -> 8] -> CompressedData["
1:eJzNjksKAjEQRDtJdU/+kzAMggjiTtfexCN4Ac/qjexk786Fr6HoD3TV5fl6
PA0RvYf8IbnmfOu9lHve6JTXUqv3sl+XXxt9f2iNsb2PLERBqcdatyYTADE2
1aagSSkaVWRsQkqqU4AcBAEtCRrqhD3gtRdUpHHUKXgtNXLOkbUuLGSFijW8
uNWpG6shM0thgxwRRZfsJkYQfcoh0OG8A4XFwnwAo+QJgg==
"],
Association["Book" -> 6, "Theorem" -> 9] -> CompressedData["
1:eJzNjcEKwjAQRHc7m23SJG21QhAr4qE3v8ZP6A/4rf6Rm4J48+TBNzBsMgNz
XR/3lYnoWe0fWW63vpRj2Z0TxXnWSwFcGMKvd/LXNCUztVaeplNU7Tze9H29
vQGTT3a09UdEzFW2UuyADt4eHmFDI5CgahWThYgQVZ1sSKShhrltSRwtzJBG
2Os+WO5MrbJ6l4U/gDkPaRwdheTr+IFBL1dJCHM=
"],
Association["Book" -> 6, "Theorem" -> 10] -> CompressedData["
1:eJzNTVsKwkAMTJpHs+7W0m2xIAVR6IU8Qi/gWb2RSUH888sPZyCZZAbmuj3u
GwLAM8ZfYl2HeZ6mac5QTotdFhFKNf26Jn93w9bY43guqgejN0oJbQ5yWnbR
xoeZfSrvoa54kMwPo7RDc3xUPeJ0SZlYVUcvYm6gQTeBBW6IosRkMiT3xdkq
qnLH+AEh9v2xVgHrLLorErwAEM8IPw==
"],
Association["Book" -> 6, "Theorem" -> 11] -> CompressedData["
1:eJzNjcEKwjAQRHc7m+2mSdraHoJYKIJXf8ZP8Af8Vv/IbUG8efLgGxg2mYE5
3x+3OxPRc7P/5NrXeqyHNVNaFl0rEOIQf71SvqY5u6m3yjyfkmpneNP3220O
XJbNYrv9iIi7yl5KHdDB/GGIO5qADFWvuDxEgqjq7EMiDTXMbUsS6MIMaYRN
p+h5cLXKaqEIfwBzGfI4BorZtvGJQS/3UAgj
"],
Association["Book" -> 6, "Theorem" -> 12] -> CompressedData["
1:eJzNjVEKwjAQRHc7m03SJG01H0G0iOCJPIIX8KzeyE1B/PPLD9/AsMkMzOX+
uN2ZiJ7d/pSptUPbrZnSetJzA1yc469Hytc0ZzO1Vqn1mFTHgDfT1O9gwBSy
Hb7/iIi5ylZKIzAi2CMgbmgCMlStYrIQCaKq1YZEBhqYvSdxdGWGDMJBa7Tc
mbyyBleEP4C5zHlZHMUc+vieQS++jwf1
"],
Association["Book" -> 6, "Theorem" -> 13] -> CompressedData["
1:eJzNTjtuQzEMk21JFG28jx/SZO6VeoRcoGftjSojc7YO5UBKIgTy8/n99Swi
8rPov6L3iJueMhEP4LrO+2x/naHvrVJkjNSHiLsqNoBxHOc+BjuBSI5Ej50c
JGxd3D35YxEZdtAYvjP4gmOj59tB8L7MVJ/XfPVoUksNz0CJnLTM2oy1taZm
SpN2DQ0okIUWCswiN5ftNgxboPbyC7uGCKo=
"],
Association["Book" -> 6, "Theorem" -> 14] -> CompressedData["
1:eJzNTTkSwkAM8yKfG0LJQDpghgfxhHyAt/IjFDIUNFQUyB75kI/TfL/NTUQe
C/0trpdzP5b0abTt1gwx+q9f5Fe1imR0633s7hV4IyJWDtCiItKWjqqSTV9D
lUAiWARyxUAR7oAzUsQANd7nIy5IU3aZyU6bp/LQxjRTo8ytFtW0fWCfOR1M
3BwKHRvkCRlTBv0=
"],
Association["Book" -> 6, "Theorem" -> 15] -> CompressedData["
1:eJzNTkkOwkAMyxBnmdDhBELqpeJLPKEf4K38CLcSBy6cOGCNPEmcOLmtj/va
ROS50f9iWWouOc7DpslMc/ivN8RXtYpkfFY1yr2HvuG+xUFoaGZlhm0VAGTD
3lRdtWswCe07oihymAb8KWopjP5cxAFpYJWRnNA8QaODIRPRza03OAztA+fM
68V4oikUo6m8AOuyBtY=
"],
Association["Book" -> 6, "Theorem" -> 16] -> CompressedData["
1:eJzNjjEOQkEIRNllYAG/25qvlbW38Qj/Ap7VGwlqY2Nl4SOZEJgwnLfbdWtE
dC/5Yy7jGOSrsxmzWODXAbuv24gUITKb013V84s3EdVbwlkWZq41AZAqeJrK
n1uU+ouFWVm1VGrMC0NVZwb1DurIC9SZAo3rCNI2BoaLijcMCNoHh7DTKpSW
Ct83pgfKqgbU
"],
Association["Book" -> 6, "Theorem" -> 17] -> CompressedData["
1:eJzNjrsNgjEMhJ34kXMeNSAkJFZihH8BZmUj7HQ0VBRc8flkO+fcj+fjKET0
Svyz2hk0Ts4AM7cuv873r1MgoERmc/ow6xBW5RT2j5AFu6BbdlRkcy95dGIq
ybHVV/rWmI01LS9Wi/w4VKtQzYdB6lI4vVSNdWmupl5EI7p86DJxuxqZIM+u
IvQGjjUGsQ==
"],
Association["Book" -> 6, "Theorem" -> 18] -> CompressedData["
1:eJzNjTtuAzEMRClpOPqsREOh4y5B3OU8OYIv4LP6RtZu7y6FH8AHfoDh9Xb/
uwUReex6a/qn/HQbY5TCj9/83/GvA2MI0X01JlJKrfY958XJnEkArfmyL+A0
czNy32xmy2MX0CtR4UY4TgdagII5iYmxH9e0ta3V9SilJDGmmiWqjBg0p5lI
qipWcWhAb+hcS00HgWhl67XK5esM7WBEeALe/AkU
"],
Association["Book" -> 6, "Theorem" -> 19] -> CompressedData["
1:eJzNjc0NQjEMg/vjuGnySh8jIDERI7wFmJWNSOHAjRMHvkiWlVjO5bjfjpxS
eiz5b2bar8beAc4Tf93ev/+e70hr7jZUNwNEsGgtPCyAwX26O9eGZGjnK7Q8
YaGG7YWOaIAqoDFxxACbNo9HtdaUUYFwaUMGK9asuIiwSYarSPmQS5nkeWey
6qiKUZCf5fMHOg==
"],
Association["Book" -> 6, "Theorem" -> 20] -> CompressedData["
1:eJzNjc0NwjAMRu04duzGEWkPSBUSpTN0E0boAszKRri9c+PAk/XkH+nzur+e
OwLA+9C/c2+tVDer82y/zv4emBDTtkXjAKqt1av72FWnSVVEhqGHeyBdl2Vb
llKOjdYaPiViRaVIrypd1pMYo9xVXLzwOamZtXhElAATMgMxXBLmTIqaJTMT
B8pIjxs3IRGmkziaaS0OI1fOQy6U8QM+IAni
"],
Association["Book" -> 6, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLAA6npERQmPKQBmMYBUQdSMEAACfzQKF
"],
Association["Book" -> 6, "Theorem" -> 22] -> CompressedData["
1:eJzNjUsOwjAMRPObdJyW0kBpVQJILLkOR+gFOCs3wumeHQsszdPII4/v6+u5
WmPMu+Lvp9s3u47k9ZJ+Xc2vibPWzbMaFdn3/WNZbkUkJREAImdlKeeCIjnP
OUfUzTCdlGMFkBpBgzIJCsZtQD3Fsqgw1hAMQz7kXh9574x1NgTjo8nV+GTp
GdRoWSSsPw4YCbLZ+hEYU8uOO5MxILQhergPO5oKIw==
"],
Association["Book" -> 6, "Theorem" -> 23] -> CompressedData["
1:eJzNTssRAlEIg0eAx/u46tiALVnCNmCtdiS7Ox69eTDMZCBkAvf1+ViZiF4b
/T9mjAFYP9uvk+PrpjCXOZnZiVrrvQ33HvggIg4OZMWMaLopqprsupuq5deI
HAJtR52b4p6WrGwxoZ7JeVFEiCFAdnQCw8QFEqgVbuZhjOZqUkTKARa5drtd
jBYbkIpRwG+WxAcG
"],
Association["Book" -> 6, "Theorem" -> 24] -> CompressedData["
1:eJzVjTEOAjEMBB3Hdhyfj3CHFIkGiZqWl/CE+wBv5Uc4R01HwxSrlb3avW7P
x5YA4DXkD1juN1Vpvf66+HshpoTuYRSgtd7PzezgHBCFqA7vATubudlcfL/r
rjRy8Yyv69Dpw6p8ijyzcWFyppW1Wu0xRISxmkWAGC4psWTNymsVKdEpzqkM
g4IYqUFGavNhWQpMx4lYyZDTG3gKCIs=
"],
Association["Book" -> 6, "Theorem" -> 25] -> CompressedData["
1:eJzVjdENAjEMQ5OLnbY56G2AhPhjHEa4BZiVjUiL+OWLn3Ol18hO3ev+fOwq
Iq+BI4i83S+l2L97fxSqCpB3iKwrQAKwiFZa61vPOWmpzRoyo32dZCDRuyM6
0mrd8sFcsuFg+qeBbucsDXy+zGPLIgpxVcvRTDkCdxpddK0IVrLUKWOBzQSV
4XSWzd/inwdp
"],
Association["Book" -> 6, "Theorem" -> 26] -> CompressedData["
1:eJzVjbsRwkAQQ+8neW+9cHh8w4xDaqATSnAD1EpH7JmYjIQXKFhppdv+fOwx
hPAa8hfc64TLtf66Vr46KcZk9om01vvWVM8GpxSSIuZqDg2qpnqa7LjLoSAB
M9B9GTof2FrZqQoqJw8QK6Vq7T5USvLVTIaCsMUIZsmCpXJ0eQfi+EFiSp4a
5FSWdm7LFOY2A1I0l/gGOscIZA==
"],
Association["Book" -> 6, "Theorem" -> 27] -> CompressedData["
1:eJzVjcERQjEIRIGwEPK/yegY77ZkCTZgrXYk0bM3L77DMrMsy/X+uN2ZiJ5L
/oNaLY7x89avG2GWutaFqPc5Z+y7hyeqAGqN1EiwzOo+3k5rDWtkRjUvsCOa
I/Jg0eeGCz6+uqac0cxt5iNVya/FjBR0YoYVLRVbmFlWWoCtMCAmkqlFER2H
PkaQb64oaqL8Ar0pB5k=
"],
Association["Book" -> 6, "Theorem" -> 28] -> CompressedData["
1:eJzVTsEJw0AMsyPZd7lQCDS5exc6ROfoCFmgs3aj+lJofn31UxmEkI3ky/a4
byoiz05/gtvVHb8O/RI4DEKqahEZR9IYQM7JU2qtAngzGjLAEIaPX1hbXVdj
bgwrN+ynHeNqC3d/ypV1wRmlFO6VGoPoVYqrIiSg1hfwyHfRKWGyA2rWe+li
tDletNNsLx4lB/o=
"],
Association["Book" -> 6, "Theorem" -> 29] -> CompressedData["
1:eJzVTcERAkEIg0vAY0/H5WEB9mAllnANWKsdyd7N6M+XHwMTmMAk1/VxX1VE
noP+BTd3/Nrzi6GqkDWbSARpLCDi4BGZHcDOSATAWgxvvbGod2MkS4rE9jrQ
0jo3fRmUOKO1xj2yCtMkSnFV1AqojQNnwmbRZcbRPkB15dKFbienWbvwBaQn
Bz0=
"],
Association["Book" -> 6, "Theorem" -> 30] -> CompressedData["
1:eJzVTkkOAkEIhIGCHnpMekm8+yWfMB/wrf5IZmLiyZsXC8JWbLf9cd+ZiJ6H
+Rus0F+vtO8UMwHpa2p1NwNUI4qv65zDXedsmugaqkmJviu9t3qErUFiysip
rmdrNsk2MYBIux1kl5yP8PMgU4oIkRIyWWhhWSzrrAWCQlyLFP2AAcm7ZuSK
S35occULoOAHag==
"],
Association["Book" -> 6, "Theorem" -> 31] -> CompressedData["
1:eJzVj8sNAkEMQ/NzPCOxRdASJWwD1EpHOMuZGxd8iEa286K5n8/H6Wb2mvE/
WvlrIr5HEUa6uyoAiequnFeNgNRMSWaVTKVyCFzpVYpAxSwpwkeCqNqiTSlm
jd1NHcx0C31ymbe1uzYPC24XRl1uGHg0kzrKS2IL2FR/3RIbjPI3vUoFtQ==
"],
Association["Book" -> 6, "Theorem" -> 32] -> CompressedData["
1:eJzVjc0NwjAMRp34s52kaRMFUZUjKzECCzArG+H0zo0LT/KTf2T7/nw9noGI
3lN/RP71Qfs6iSHEffekEYnU2o7er8MsJTMAKQ33cDC0tb01s9kp6+quU8CS
DRljVQxcTtR3Db17YJtDr0ouufoj5kghMkAsNGJQxcaJDSIsziaBa5GirCp8
AkXOZbGFbvWAbLCI8AHuyAhD
"],
Association["Book" -> 6, "Theorem" -> 33] -> CompressedData["
1:eJzljdsNw1AIQ3FsE27UJbpSR8gCmbUbFfLTvy5QI/HyQTzP63UiIt6T/ln1
2x1bEftetcrOJCWO1uqe2WJHVqY8G9ud5Rs6VoPMHvJGB5p+GFNjdrWk+5EQ
ENKxMY4NfjAwN5I1UKNEEl9tQK2jSjGUQIPxAbjoBWY=
"],
Association["Book" -> 7, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGFGBkRHcySIARLAxmMEC5EADVgiIG5oMxAyMDI6aB
GKYPMQAAxXUCrg==
"],
Association["Book" -> 7, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGFmBiwiLAxAQmwRwoFwIgCphQxMB8MGYEQiZUAxmh
GMJhhFjHCBYlAzCAEV55KIMywIggGBkBJVEDRw==
"],
Association["Book" -> 7, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGGGBC5zOBMJhkYGBkZAB6iZGJiREMwGpBDAiJAAxg
zMDECNGJGzAOvRACANOEAr0=
"],
Association["Book" -> 7, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGOGBmBmEwycDAyMgA9BIjMzMjGDCDFIAYEBIBGMCY
gZkJohM3YBx6IQQA4HUCyw==
"],
Association["Book" -> 7, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHGBEB2ARoDhIClMWG2BAplHMBpuBbBedPUc5AADe
BQLH
"],
Association["Book" -> 7, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHmAEOntoupweAACYNwJ9
"],
Association["Book" -> 7, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGIGACo1GAFQAAmVACfg==
"],
Association["Book" -> 7, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGJhi6Lqc1AACV/AJ7
"],
Association["Book" -> 7, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGKAA6nRGr87GLYjVgWAIAmv0CgA==
"],
Association["Book" -> 7, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGKmBhAWJGIGBhAJEMDCDECCGRAAucQAIMUAzhIAGI
GTAOI4QDJUgHDEi24JDHdAIZgBFBMDICABMDAzE=
"],
Association["Book" -> 7, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGASpgYhpoF1AGAJfgAn4=
"],
Association["Book" -> 7, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLmBmJl4UizpqOmUQAQCj6AKJ
"],
Association["Book" -> 7, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLGAFIiYgYGUAkQwMIMQEIZEAK5xAAgxQDOEgAYgZ
MA4ThAMlSAcMSLbgkMd0AhmACUEwMQEAeRAD0Q==
"],
Association["Book" -> 7, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGMmBjZmJkZGNgBAIGBhBiBJPMjFDAzMzMAaJZmRhR
AAMUg0lkAyFmwDhQWShBOmCA2YJbHsqgDDAiCEZGAB46Az0=
"],
Association["Book" -> 7, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGMGBhYMT0AQsLgs0Ik8fiURZMoWEBAKp7ApA=
"],
Association["Book" -> 7, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNGBiYgD6gREIGCAMBkYWFjAfDJhA8iBJJkYUABJk
YYCqw2k4WB2EZmBgJANATMArT8AJxAFGBMHICAAFjgMk
"],
Association["Book" -> 7, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNGBlZmTkYGAEAgYGEGIEk0yMUMDKysoGotmYGVEA
AxSDSWTzIGbAOFBZKEE6YIDZglseyqAMMCIIRkYAIcIDQQ==
"],
Association["Book" -> 7, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNuBgZGJlYAICBgYQYgKTLExQwMnJyQyimTmYUAAD
FDMCIROycUAOIzxQgCywLFiEkQzAAEZ45aEMygAjgmBkBABXpgN8
"],
Association["Book" -> 7, "Theorem" -> 19] -> CompressedData["
1:eJzVUIENgCAMa7c4lC98yRN8wFv9yG2IRr3AEjpWuiYwr9uyEsAe9HOQRHUA
E1BHFJEiZqWYQ1UZlTparA74dtM0kDF5wzxwuKOh6lUkycGOdk5JXkpykyIh
G7nG4nxyXGaX+a9XPTofSO3rCyObm+0zeAAetARy
"],
Association["Book" -> 7, "Theorem" -> 20] -> CompressedData["
1:eJzVjMENgEAIBBduQ64NW7KEa8Ba7UgWNfczMb6cwAAhsIxtHQZgl/5OByJJ
AyRoxggWob2a0xONxhbsdTlpmX4P7npYVXoPKh73V/MNn3I/AMzbBC8=
"],
Association["Book" -> 7, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGAWAHAiDJwMDBysDKyMjKyc4KBuwgSRADQiIAiMvI
ysLOysXJzo5sEgsQwwOFmZkBpBVEgwjSAQMY4ZWHMigDzAiCmRkAJvUEww==
"],
Association["Book" -> 7, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGAWAEAiAJYoBJJkYoYGZmZgPRbHARCGCAYjCJYhID
kgBMFkqQDhhgtuCWhzIo9D+CYGQEAAf3Ayg=
"],
Association["Book" -> 7, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGAWAEAjQBhCCUZgRBGGCAYCwmQfEQBgCyEQKa
"],
Association["Book" -> 7, "Theorem" -> 24] -> CompressedData["
1:eJzdUdsJgDAMvMZaGywW6l//XMkRuoCzupFNteADBH+9hEtyIYGQKS1zUgBW
oT8gxggEwDv0RNx5tpaZPRGpHJmagcUqIBrb4LQex/MiC1BbC61hzB6FvgPF
X/tHcsf1MfmKotHzciVe5oVU3rUBYSQGUA==
"],
Association["Book" -> 7, "Theorem" -> 25] -> CompressedData["
1:eJzdUcENwjAQc+6sJgUKUis+/bESI3QBZmUj4itBpWyAEzm2o1xyym153JcE
4Cn6C8xXYAQuJxzN+jyUwGBmScL8XDQaoKzk8UBO07ZOBozNuKPr6koGVXjD
qiPiLgleI1UIw88x6TdrMxy5bwffH1O7iMx+G0+aHq+Vq3e8AAkOBdU=
"],
Association["Book" -> 7, "Theorem" -> 26] -> CompressedData["
1:eJzdUYkNwyAQM3dWoE9SKVEH6EodIQt01mxUfClRmm5Qg4xtxMGJx/x6zgnA
IvoP3IERuF1xMTvlvgR6M0sS5kPRaICyksczOU37MhkwNuOOrqsrGVThDauO
iIckeI1UIQy3Y9If1mY48tgNvj+mdhGZ/fadND1eK1fveAPt4QW7
"],
Association["Book" -> 7, "Theorem" -> 27] -> CompressedData["
1:eJzdUYkNwyAMPBwrJsJqJTJBVuoILNBZu1FtU6o8G+RAZ99ZGCy29n61BODj
dBtU4KkoRItUzVlVKxEli0rTQ30NwD0ttTCv675HASgPIYJ5tsgcZJCBnofF
Jye4W94hBP+Pef5jL4aK/kccP8amCI+uQyffEq91ZXd8AasvBwk=
"],
Association["Book" -> 7, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGE+DjZuBiYuJk52YHA24mJiZGEIOJmZcdBGGAASTG
zibJycIiKopsABsDAxMzjMPMzMDKCqFBBOmAAYzwykMZ6AA1YoC+AIsxYfqY
EYTA+kEEI9AsAJaGBU8=
"],
Association["Book" -> 7, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGESDPO8MsEACWtgJ8
"],
Association["Book" -> 7, "Theorem" -> 32] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGPBhmgQAAlbECew==
"],
Association["Book" -> 7, "Theorem" -> 33] -> CompressedData["
1:eJzdUdEVwyAIPCCBJ6Y/2SArdQQX6KzdqEJqXpNs0FNP7hTF59Zez0YA3kF/
hQcW5jrNXqu7zyJCfXaS1aMNoA/2opOI2W9+AViHUEXpBnKLBXRgj9Oyi5O8
W3FCCjvSIv5yLKY6l5A4fwwzpcf3B1P0rDiI+h0fU7EGwQ==
"],
Association["Book" -> 7, "Theorem" -> 34] -> CompressedData["
1:eJzdUdsNwjAM9KMOQU6ohJCqfrISI3QBZmUj7CtFrdiAS3L2XeI8lPvyfCxM
RK+kP8MsMg3Wbld3N1XliM568WytOUAx5FxPg2qt++oQYpsohcYxYu+ggG1Y
c1iZlJ0DXheRGUH0b1nmH85JKOx/xPFjRBie/D6Xs+PGSRxnvAHc8Qem
"],
Association["Book" -> 7, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 36] -> CompressedData["
1:eJzdUdsNwjAM9KMOQU6oVIkf/liJEboAs7IR9pVWrdigl+Tsu8R5KM/5/ZqZ
iD5JZ4PIY7B2n9zdVJUjOuvNs7XmAMWQa70MqrXui0OIraIUGseIvYMCtmLJ
YWVSdg54WURmBNG3ssx/nJNQ2P+I48eIMDz5fy1nx42TOM74AsfMB5E=
"],
Association["Book" -> 7, "Theorem" -> 37] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHWBBMBkZoT7E4lEWTKFhAQCgAgKG
"],
Association["Book" -> 7, "Theorem" -> 38] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGM2BkhPoQi0dZ6OsUugEAnAYCgg==
"],
Association["Book" -> 7, "Theorem" -> 39] -> CompressedData["
1:eJzdUYkNwyAM9BMTKluRKnWBrJQRskBn7Ua1L48SdYMecPYdmEfM63tZmYg+
RX+IweL1dHdTVc7orOFo4QDlkEcfB9Xer5UpxA7RGk1TxghQwg5sOaxK2sUB
b4vIjCDiLKt855qEwv533D9GhOHJ71O5Om5cxHnGF434B0I=
"],
Association["Book" -> 8, "Theorem" -> 1] -> CompressedData["
1:eJzdkNENgDAIRA85GtZwJUfoAs7qRgJNmib6558v6bXAHR/d+3l0AXCl/BFv
lriIbPkQqdra6BvibEZvNPc1SEDmp5Dhi1u1JCD1CYuXgYKaOS6m4eMQTOM3
mFJLYukN8sIEnQ==
"],
Association["Book" -> 8, "Theorem" -> 2] -> CompressedData["
1:eJzdkd0NwyAMhI1jOYEDoSp97UNWyghZoLN2o9qmrRp1g36C43z8CMR23Pcj
EdHD5S+5lNJ7uzHz1A2elrrUua5rDcg6o+SrSM7f+woRz++iNVK1USTEAHRg
fqiohWjAJwkdiwhKVkBFEQz/Up+MKs4/c/4Y5hQZ/z40eYM7v2lS6BN4owb0
"], Association["Book" -> 8, "Theorem" -> 3] -> CompressedData["
1:eJzdUVsOgzAMc5K1Ql1BVX9giJ9daUfgApyVGy0JA4G4wazWtd2mD/U9L5+Z
AKxG/4ncTdMrigiNCpJcc33Wcej7qoB27trwEAnhXNYCnHZTCppGxxidFGnH
pj0yUU6J87YIKcFNPMpM/9gm3fn+V1w/hpk84/s7yZrf2Ij0jC9c/AhX
"],
Association["Book" -> 8, "Theorem" -> 4] -> CompressedData["
1:eJzdkesNgzAMhP1oZKOAfyH43ZU6AgswazeqfaAK1A36KbncOS9FeW77a2Mi
epf8KWvE2FSVI2Gd+tTHHtEBZZfB7aHqft2VQdo3OC1LjvMMScxaswLeUCrj
lwr0WERmhHBkO/2pNYmE8+/cP0aEUZPfZ3I1K1fCeccHW9gI9A==
"],
Association["Book" -> 8, "Theorem" -> 5] -> CompressedData["
1:eJzdkd0NgCAMhPuHBFPQFVzJEVjAWd3I0geiQRfwy+USjlxTwlaPvSIAnM3+
Sik6MTMWAzkbRddFNasq5Kw0JxFmkXspAVDoh9QEEKObE0J8Ib2FVnN90y+H
5Z8fQ4Se0fhKbPJ+M7RZF0ikBto=
"],
Association["Book" -> 8, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLVCVYWVmZmZUAAJGZm4hbiEuIVERcXEhIGAAYiY+
XpA8KyuyHl4GBiYuGIeHh4GDA0izsYEJIOCCAQgbLARi8CCJgEmIIgYuLgYw
hw2uDcSGkiBJMA9sPipAjRgmJkawGBOmJxlBCOxiEMEItAMANhYIKw==
"],
Association["Book" -> 8, "Theorem" -> 7] -> CompressedData["
1:eJzdUckNgDAMc1K1QqHwqEB8+LASI7AAs7IRSTgEYgOs1nWcpocyLeu8EIDN
6L8YYwiBJgWFutRFSt8NQ1FAJ7eN5WN8ljQAyxXkjKrSNSUnhVw4tFsm8sNx
PjZBBB6ku8z0yZb0yM9/490YZnKPv38kG/5iI9I7dhYdCAo=
"],
Association["Book" -> 8, "Theorem" -> 8] -> CompressedData["
1:eJzdkdENwyAMRG0jULg4leo/PrtSR8gCnbUb1TZt1agb5AkOn20QiNv+uO9M
RM+QE1NLKTwcLqutBrPrGOaQT7lsUa/1d8dGJPiY3mlZfG0txQF04vHUpp5E
B76Z1NlEUHIDbYpkxm+NYro8/8jxY0Q4c/L/RI6RN9ZwCn0B9uYIDQ==
"],
Association["Book" -> 8, "Theorem" -> 9] -> CompressedData["
1:eJzdkYEJwzAMBOWPlOYrCKQbZKWOkAU6azeqJLchIRv0sB+9/DYIr9vruTUR
eaf8MwCGOcAw+eQ3XxYvJDbu5EOVPF4Ig/FnIjemUS3RDFsn6q5q0aSTe6e0
h4QmYWhqLHr91TwsV++fOX8M0KqH64QtV41g6Yz2AdMKBho=
"],
Association["Book" -> 8, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNeDmZmYCAmYOJhTAAMWMQMiErB7IYYQHCpAFlgWL
MJIBGMAIrzyUQRlgRBCMjAAb3gNB
"],
Association["Book" -> 8, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGN+BmZgICZg4mFMAAxYxAyISsHMhhhAcKkAWWBYsw
kgEYwAivPJRBGWBEEIyMABFtAzY=
"],
Association["Book" -> 8, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGOWBmAgJmDiYUwADFjEDIhKwayGGEBwqQBZYFizCS
ARjACK88lEEZYEQQjIwABwcDKw==
"],
Association["Book" -> 8, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGO2AEAlYmRhTAAMVgEkUxA5IATBZKkA4YYLbglocy
KPQigmBkBADl0gMF
"],
Association["Book" -> 8, "Theorem" -> 14] -> CompressedData["
1:eJzdUdsNgCAMvBZCTAl+gPGfP+dxBBdwVjeS1kc0buCFHHfX8gp1WeeFAGxK
v0edKrlYYpE8DOOYG1By5j5555z3z94EsNwmoevaHIJRg1w4tEUq0iMxPpog
AjPhXqb6ZC2as/3feH8MM1nG38eRDruxErUzdtP4B8U=
"],
Association["Book" -> 8, "Theorem" -> 15] -> CompressedData["
1:eJzdUdsNgCAMvBZCTEE/iPHfT9dxBBdwVjeyrY9o3MALHHdHeYVxWeeFAGxG
/8c4Ucg1V6l9PwxVAe3ctTGEEOOztAVYLlMKmkbHlJwUcuHQHpkoj8T5KIII
3KR7memTbdKd7//G+2OYyTP+vo2s+Y2NSM/YAbFtB58=
"],
Association["Book" -> 8, "Theorem" -> 16] -> CompressedData["
1:eJzlUdsNgCAMvBZCTAl+gPHflRyBBZzVjaT1EYwjeCHH3bW8wlK3tRKAXekH
WMjFEovkaZrn3ICSM4/JO+e87zsTwPKYhGFocwhGDXLj1BapSF1ifDZBBGbC
s0z1xVo0Z/u/8f4YZrKMv08jHXZjJWpnHI/5B3w=
"],
Association["Book" -> 8, "Theorem" -> 17] -> CompressedData["
1:eJzlT0EOgCAMK4MQM9EDId79kk/gA77VH7kNNWr8gQ2UtgwYc12X6gBsSn+A
833uM+dSpikLIJPGIXjvQ7gXDgDxaVJC18kao5GATzRtkYp0S4xbEZhhJl7H
VB+sm+bs/lfDD0fkLKOPn+mwjpWcvLEDbMoHVQ==
"],
Association["Book" -> 8, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGBGBiRAEMEAwUZWBiQlYHDBBGeKCA1TAwwAjSAcQE
vPJQBmWAEUEwMgIA3/IC/w==
"],
Association["Book" -> 8, "Theorem" -> 19] -> CompressedData["
1:eJzlUNsRwCAMCmSSrtQRXKCzdqNCrPbx2d9yJwJBz3Np29oQEbvpH0gmBVNm
hjYvQnyvyWB+ipSq0Sus+kDXFfGVFPfIN5ThPGZ9soflnk/4AFwEHAvJA0M=
"],
Association["Book" -> 8, "Theorem" -> 20] -> CompressedData["
1:eJzlUdsRgCAMC1WQdgA//HMlR2ABZ3UjaXwcnCOYg1ySltexln0rAcDh9BPo
orOaKYE6RXMah2Ga2q4MSHxMSjDzMJMq4oNLM3KRmoR8NSFG0OR3meubvUjH
/Xv0HyMSmMn3WcEHb+wU6hknl4EF8Q==
"],
Association["Book" -> 8, "Theorem" -> 21] -> CompressedData["
1:eJzlkVEOAiEMREuBbBjT7GoAf90fD+QR9gKe1RvZFjVuPIIvZJgZGhLCut1v
WyCih8m/gOvhclx6P9daaW0n7i3FGFP6HmpEvLxDKTRNuufsogDzLIb6oVm0
RAE+jesYIghpgGSBM/xL7dCT379n/zHMwTv+fVWwBXNiSSBPsdYHyw==
"],
Association["Book" -> 8, "Theorem" -> 22] -> CompressedData["
1:eJzlkdENgzAMRC8GH44X6HdXYgQWYNZuVNsBVNQReEpOvrMVJcp729etAfik
PIb+6u7eE8SWbpynaVl+ZwwQPQ0J9wytJFDlIOqhxgiVqldSOoagRBilxUAy
6kOzWa7Ov3P/GJFWmfw/quWqGzMdlV+KKgX1
"],
Association["Book" -> 8, "Theorem" -> 23] -> CompressedData["
1:eJzlkVEKAjEMRNO0ZelIWBdp9Hc9kkfYC3hWb2SSqrh4BB9lOjMNhdJ1u9+2
REQPl//hsC5H1Uvvna564rOWnHMp3yNKxMs7tEbTZHutIQYwz+KYH1rFSjTg
04SOIYKQBUgVBMO/1A8jxf179h/DnKLj3zclX3AnngTyBJCYB6c=
"],
Association["Book" -> 8, "Theorem" -> 24] -> CompressedData["
1:eJzlUcERgDAIo1TCUadwJUfoAs7qRgJV73qOYK4NJORBr1s/9l6I6Az6EWxt
zZqZkVduhqVW1SlBxPIIH3k0a5BDBAPeD1a4KX5fJ3mESEAuBApJjP7mGKaa
V0jMH8Nc0uPvk0qc3BihILgAYJoFtg==
"],
Association["Book" -> 8, "Theorem" -> 25] -> CompressedData["
1:eJzlkdENwyAMRI0BBd2HEyUV/DYrZYQs0Fm7UWyTVI06Qp/QcXdYSIh1f217
IKK3yT8xTa09am30XBZuNcUYU/oeqEQ8X6EUGgbdc3ZRgHEUQ33XLFqiAJ/G
tQ8RhDRAssDp/lQ79OT337l/DHPwjn9fFGzBnFgSyAFz6geY
"],
Association["Book" -> 8, "Theorem" -> 26] -> CompressedData["
1:eJzlUcENhDAMc4Mi8gDJ5dUHn1uJEViAWdmIJgUEYoSzKsd28kjU37otawKw
O/0V5mnKJJEzZRxUu0712R8AscuUgr6vNUbUQVpD1Y3VashC3klwGwIN1dDU
GGj6ZG+Ge68QeH+MSIpMvgclf3TlayejHRTRBwU=
"],
Association["Book" -> 8, "Theorem" -> 27] -> CompressedData["
1:eJzlkYEJwzAMBGXFIjIJvB3wAF2pI2SBztqNKslJacgIPcz7/2UMxo/99dwT
Eb1d/ottq601qrXyumSZppx/xwsRlzP0TvNsu0iIAZSijvmholaiA98mdBwi
KFmAiiIY/lAfRor7r1w/hjlFx/f3JF9wp54U+gHqsQbJ
"],
Association["Book" -> 9, "Theorem" -> 1] -> CompressedData["
1:eJzlkdEJwzAMRM8yIhiOCBzIf6ATZYQs0Fm7USW5LQkZoQ9z1p30IePteO5H
AfAK+TMe3cHau9istVbVc3cGhF/TGqbJ7xzRgFwWC7wequYhG/lLUscQaHBD
U2My6o9GM911heT6MSIlM7k/p8TJjS2c0d5JIweO
"],
Association["Book" -> 9, "Theorem" -> 2] -> CompressedData["
1:eJzlUUEKwCAMixURoWziYfd9aU/YB/bW/Wg2OlD2hAVJk7Rgxf28jtMBuI3+
hlKBrRRZl+C9D2FsLoDoa1JCjLVyJBhUc1YDtTIykYaE3IagCprmtevO1qSb
VyDmjxFxzOT7GmeHGxu5escD94oG+w==
"],
Association["Book" -> 9, "Theorem" -> 3] -> CompressedData["
1:eJzlkdENwyAMRA8DyiE3H8lHfvKVjtQRskBn7Ua1TVM1ygh9QsfdGSEhtv35
2BOAl8vfsa4blvsi81RyzqX8ziZAbkdoDcNge60hBjmO6pjvWtVKNvLbhPZD
oMICtSqD7j/qw0hx/5nzx4ik6OT6mOSL7tSTUt/lNAar
"],
Association["Book" -> 9, "Theorem" -> 4] -> CompressedData["
1:eJzlUdsJgDAMvKYt5iOCgv74I365jyN0AWd1I5P4QHEEj3C9u4SS0qmsSwkA
NqP/YR7RDT21TYoxpvRsNQDJZZhRVXrm7KRgrmsxqD44i4aGO3E+hsACNSxZ
riHTJ1vTnd//xvtjiIJn9H1LsGJTtnYQlh3X9gas
"],
Association["Book" -> 9, "Theorem" -> 5] -> CompressedData["
1:eJzlUUEKgDAMy7oNe6gwQS9exC/5BD/gW/2Rbaei+ARDyZK0jI7N67asAcBu
9ENM6MeBupJijCk9OwUguQwzmkbPnJ0UzG0rBtWVs2houBPnOgQWqGHJcg2Z
Ptma7vz+N94fQxQ8o+9TghWbsrWDsBy2JAaF
"],
Association["Book" -> 9, "Theorem" -> 6] -> CompressedData["
1:eJzlUcENgCAMLAVCHyXBxI8PH67kCCzgrG5kW8RIHMFLc9xdG1LCVo+9OgA4
lX6JeV1wKsF7H8I7LwDI3RBBSnLGaCQgypkVohtHllDxJMZtCIhBDHHkPqT6
Zm2as/tHjB+D6CzD70OcFqnStR0TX6FTBm0=
"],
Association["Book" -> 9, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 8] -> CompressedData["
1:eJzlkdEJgDAMRNO0RXoQ/FE/9MuVHMEFnNWNTFIVxRF8lOvdpRRK53Vb1kBE
u8k/GTqexhRjTOlZj0TcX6EUahrdc3ZRgLYVQ33VLFqiAHfjWg8RhDRAssCp
/lQbevL737w/hjl4x993BFswJ5YEcgDJ6QbG
"],
Association["Book" -> 9, "Theorem" -> 9] -> CompressedData["
1:eJzlkdENgCAMREuBeKQxwT9/XckRXMBZ3ci2qJE4ghfyuDsIgbBs+7oFIjoM
P9XMU00xxpTebSViuUMpNAw65+xQAeMoJvWNWbREAZ7G2TYRhDRAssDV/EVb
9OTn9+o/hjl4x99nBBswZ9cOAjkBaIUGGg==
"],
Association["Book" -> 9, "Theorem" -> 10] -> CompressedData["
1:eJzlkYsNgCAMRMun4UIanMGVHMEFnNWNbIsYiSP4Qo67oyEhrPux7YGITpO/
EpeWU0o5v8umfR0BoFJ0Z3ZRgFrFUN+VRUvjaVz7EEFIA4RlDJm/1Q49+f0z
88fEGLyL31cEWzAnlgRyAVgtBhU=
"],
Association["Book" -> 9, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 12] -> CompressedData["
1:eJzlkesNgCAMhMtDjvvtArqSI7iAs7qRfagJcQQv5KN3bQiEdT+2PYnIafiv
ljqVUusQieT5MaT0rntrDhXAkNbBRg1B4E2cMSSgqAGbDpiivmlNd37+qPFj
ck6e5e8bki34bc0RvABNygXg
"],
Association["Book" -> 9, "Theorem" -> 13] -> CompressedData["
1:eJzlkd0NgCAMhEuhudwMPrmAwziCCzirG9kWNRJH8As5ekdD+Jm3fd2KiBwh
P6a1Wlt7P8IiotNtSAF8NktxAHa87mr0EASeJLU3CShuQPOGoNeXxmK63H9k
/BjVkpl+r1BiIE8bjuAJLwAFrQ==
"],
Association["Book" -> 9, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGMuBkYREVRRZgY2BgYoZxmJkZWFkhNIggHTCAEV55
KAMdoEYMExMjWIwJ0weMIATWDyIYgWYBAGEgA/8=
"],
Association["Book" -> 9, "Theorem" -> 15] -> CompressedData["
1:eJzlj7ENAzEMAyWKpv/xRZoAqbPSj/ALZNZsFMpdikyQs0FLoi3Bz+t1XhkR
75a/ppL8aUqRiT7nHAVwL+vicRdQknZKx9F76wqbGnRYTgrEJnFjLVRdsYkl
ROdmelpmRQJjBCrcKxSOCJFwo17rbX7Bm6f4F+2lbzM/o8cFAA==
"],
Association["Book" -> 9, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGNuDm5kbmsgAxPFCYmRlYWSE0iCAdMIARXnkogzLA
jCCYmQFFogPT
"],
Association["Book" -> 9, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGOODiQuaxADE8UJiZGVhZITSIIB0wgBFeeSiDMsCM
IJiZATr7A8Y=
"],
Association["Book" -> 9, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGOpBE5rAxMDAxwzjMzAysrBAaRJAOGMAIrzyUgQ5Q
I4aJiREsxoTpekYQAusHEYxAswBFMwPd
"],
Association["Book" -> 9, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARJgY2BgYoZxmJkZWFkhNIggHTCAEV55KAMdoEYM
ExMjWIwJ08GMIATWDyIYgWYBADDjA8Q=
"],
Association["Book" -> 9, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQMjI4RkHA7hAQCZkQKA
"],
Association["Book" -> 9, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARQMk8AAAJWpAns=
"],
Association["Book" -> 9, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQwwMzMPtBOoAACbzwKD
"],
Association["Book" -> 9, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQgwMg6XsAAAlz0CfQ==
"],
Association["Book" -> 9, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARgwDpewAACWcwJ8
"],
Association["Book" -> 9, "Theorem" -> 26] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQQMl7AAAJWqAns=
"],
Association["Book" -> 9, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARwwMw+0C6gAAJl9AoA=
"],
Association["Book" -> 9, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQKwDLQDqAAAl/ICfg==
"],
Association["Book" -> 9, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 32] -> CompressedData["
1:eJztkd0JgDAMhNNAOG4Gn7qSI3QBZ3Uj86NCcAU/yvUuCSXQuY59DRE5Q346
uj2OFMBvsxQHYOG+1OhFEHgrqTUkoHgAzQeC8rdGM1O+3+kfozqypt9tRxzk
tpEIXvkBBWg=
"],
Association["Book" -> 9, "Theorem" -> 33] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 34] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARpgHWgHUAYAmJ0Cfw==
"],
Association["Book" -> 9, "Theorem" -> 36] -> CompressedData["
1:eJztUckJwDAM86EM0pU6QhborN2okepPCNkgwghbGMngqz93dzN7SQc7ACyz
TNEA0BoI9ZCUmBXxL8mBQ+1UXyz7lMkSPT8mwqXFeqOzoGs5jYwPQ4QD9Q==
"],
Association["Book" -> 10, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGASZgHMIBAwCWWQJ8
"],
Association["Book" -> 10, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARbANNAOIB8AAJZYAnw=
"],
Association["Book" -> 10, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAVbAzMzNCAYMDIzkAgYwwisPY2EFLEDMxsAANgbE
YWRiYmBiApIwXUA+CAAlWVggKhgZAdrxAzA=
"],
Association["Book" -> 10, "Theorem" -> 6] -> CompressedData["
1:eJztkdEJAzEMQy3bVTjCfXWCrtQRboHO2o0q5ejP0RH6IALJwgnkcbyeByLi
bfnzm3uS+5wdMc0wZHcVAHmpI4xe1OYkh7VuMDOIUIkYOEuZifwmHsopUvPC
+THUaTtgW7uqoiqrmIvQUzxlUCtV960fqYEEyw==
"],
Association["Book" -> 10, "Theorem" -> 7] -> CompressedData["
1:eJztkdENwyAMRO847AYzRVfqCFkgs3aj2CRfkbpBn8QJni2DxHs/PjsBfCv+
/KC5zTkFRIwxvDDrXSIZ4Zml6H3RtjKpMmS1ZcCINEbn1bT0bVTFm/G8+/oY
z9XrRG7wbJcgNcnaAvmUqhr8lWVf805/MgR/
"],
Association["Book" -> 10, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAS7ACAYwmgzAAEZ45WEsrIAFiNnADmFgBHEYmZgY
mJiAJEwXkA92KAMLCwtEBSMjAM7BAx8=
"],
Association["Book" -> 10, "Theorem" -> 9] -> CompressedData["
1:eJztzdEJAjEMBuD0mjSJnq1JFeHgPERwhQPHcIB7cAFndSOrPruB38MfCPnJ
6f643QMAPN/x99PSIW4ARHLuh1L2dZoul93O3UWqu9XG6jjPyzwLvzft0sz6
vngbzJOz13y0atcPlsHVS5m8+GY0bgUXVc3tWYwdhC4QQSTIXUCMGgQTEkUi
JKUQq6EmTEnwK0VRWfEZnPstKnI+rF8zFQ0Q
"],
Association["Book" -> 10, "Theorem" -> 10] -> CompressedData["
1:eJztzdEJAjEMBuC0TdpEewlnEUFFq+IQBafw2adbwFndyJ4+u4EfJIGQn5ym
531yAPCa299vHlEBmFXz3mxdar2ex9HMRIqZlk7LtrVHa5zmTb/sch6sD07V
khU9atHbR+KdSY/XXsNBUw8Yi0h/AiF4cN4RQSBQ7xCDOMaIRIEISciFMqJE
jJHxKwYWXqQLrFIeUDAtN/IGzSoMYg==
"],
Association["Book" -> 10, "Theorem" -> 11] -> CompressedData["
1:eJztkcERwyAMBE8+kDQyjwwdpCWX4AZSazqyRPzKIxVkB25gJQ0PnufrOAXA
u+LPDyIc2GPO6YVZa72THMMzS9FVteWKMqkyutWRA0akMTp1sfRtehVv5ve7
n4/R3K1uIg+oQFgjGxnbAhSpqkFNme3ZwAvbCAVU
"],
Association["Book" -> 10, "Theorem" -> 12] -> CompressedData["
1:eJztkTEOwkAMBNdxyGkV3J4CbsilzWt4Qj7AW/kRdpKKghcw0lnavZFceN5e
z00AvHP8+cXaA8tC0hMzchwjteZnR7/u3B7ZVM853Zk0GBGS0XlItYZyNlN+
RqoBv9ceh7nE6zOJEEUgqlDtVIduByqSrqEMJQxIbP0A6XYJlA==
"],
Association["Book" -> 10, "Theorem" -> 13] -> CompressedData["
1:eJztkcENwkAMBNcYcnbwPU8ByxKKriNKSAPUSkf4kh8PKmAeK3m90j523V7P
jQC8h/z5yRnoq6qGe4SZ6jyLSO+RGonEtVar9fYYTnNPXe4y6DCBhJuE1J3W
MiKejssynnm1RL9bj2EuRz+ISFEIxAzmE/N02gETjayhTEVQQNn6AbnxCTw=
"],
Association["Book" -> 10, "Theorem" -> 14] -> CompressedData["
1:eJztjcENAkEIRWGHAYa/TlbjTS/GmzdbsYRtwFrtSGYasAEfyQt8SLjt79fO
RPQZ+vOL1twdwIrez8dt8wgzpDNDKgZWMXNLP4YiXLpLIE8xTwFtB7fc9Eye
Y+kt7Hq/eH5hZsqqlUgIOSy0skpkXhYp6kLlFNYkKTJhVdGq7rRqSPYQK1/J
xggD
"],
Association["Book" -> 10, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 17] -> CompressedData["
1:eJzt0bERwjAMBVDJcSLZ/iI+cmlScDgcaViEmhGyALOyEXYWYAFeodP9X6hQ
2d+vnYno08bfT895PsVtizpN3o+jmeWsZkkr01EkiJRHS5ZSgKTXuiKdLZtB
SzaFHi4Fdse6ZtygrUTBEoLO9YhzTPUfGomFQMyOHQ2qQ9dJ36tITxK8eOZW
HTp2SAmYSIYB3nuNCF+7kgnv
"],
Association["Book" -> 10, "Theorem" -> 18] -> CompressedData["
1:eJzt0bERgzAMhWHJGOuBbRmcQMGlCOZScNkmI7BAZs1GARbIAvkKNX/xCs3b
+7UxEX2O8/fbMKhf1xbjaG3OXdf1PVKK2CX0Io3I/ETSOM1FNUrZo/eXmFNU
LDlBcbqVkFZdSqcPlSP6e5iAZtg3jGHa/4GWWCgQs2FDDnBVJXUNkZqksWKZ
j3Sq2ATvQ7iSOBettfARX7j8CgM=
"],
Association["Book" -> 10, "Theorem" -> 19] -> CompressedData["
1:eJztjcsRwyAMRBEskgCDnM94JscU4iZSghtIrekowhWkgLzDO2h3Vs/j/Too
hPCZ+vMD+731fjFVEWYA62puc2AyRhujXOeFW3OXism6KBZYU9hZNVNPO3pX
t84QDczCu79IKYVEJBJiDjeimGIl5SaAclbumVQgIOcUUUJ82Ni2GrT4ckWJ
oC+tuAfj
"],
Association["Book" -> 10, "Theorem" -> 20] -> CompressedData["
1:eJztjdERAiEMRAksSYCDMOrcjJ92Yg2WcA1Yqx0ZrgIL8H28j+zO5nG8XweF
ED5Lf37h1nqfpirCDGBOc5sDkzHaGOWyLtyau1Qs5qbYYE1hZ9VMPe3oXd26
QjQwCz/9Q0opJCKREHO4EsUUKyk3AZSzcs+kAgE5p4gS4t3GvtegxZcrSgR9
AYU3B6g=
"],
Association["Book" -> 10, "Theorem" -> 21] -> CompressedData["
1:eJztjbsBwjAMRGX7cpZt5DhQUFBRsg4jZAFmZSPksAAD8IpX3Olz31/PPYjI
e+rPT2xmo6vmTAIYo7u7g55tUraZsDV3qZicu8L7dvhAvT3BTGHQGaOBzHz4
AyBKDIkqoNxCWJhqUlrhnLjSGKhcMpJvpS+IF+tjVGmrX64oEeEDejwHug==
"],
Association["Book" -> 10, "Theorem" -> 22] -> CompressedData["
1:eJztjMsNwjAQRP3bZOP1xqDYKHADJJQzEoGAfaEESkgD1EpHGCqgAJ5G7zAj
zXZ+PmYphHh99Oc3pumeQ2D2nh15n4pTTtmlLnab2NV4K80wnorjsYhogYGR
0hg4U9+vSipqy3I5B75SDITERMPusPfl3xglpJLGCFWJpZIalJWoEQA0gKka
kJqsaREQHXxRNTTOEq6Fqx0ba8q/fQNDDw1h
"],
Association["Book" -> 10, "Theorem" -> 23] -> CompressedData["
1:eJzt0b0NwjAQhuHzX2zn7uw4cSJkUoCUjhEAISRKKkbIAszKRiRI9AzAU7zl
13z7+fmYBQC81vz9aN4M01TXpeQUEYecqB+6IXRbXFnsU6TD6RyY8NgmQiQ7
ZsvdpcTM4cOGrm34di3hzs0YLRPTwaNPy7yUyxsCjAGogIUQSkhw2iqldGWs
QwO6rrRXUikjvzx573ZQO4paas/BvwFdhwt4
"],
Association["Book" -> 10, "Theorem" -> 24] -> CompressedData["
1:eJzt0bsNwkAQRdHZn/czM2uvF1tYKyRInLgEIICEEIkS3AC10hE2EjkFcIIb
vuQd5udjFgDwWvP3q20/jiGU0qaI2KdEXZ/7mHe4stg1NU2nc2TCY06ESLa0
lvN1qDccP2xs24ZvlyHeuSnJMjFNHl1a1qVc3hBgDEAFLIRQQoLTVimlK2Md
GtCh0l5JpYz88uS920NwVGupPUf/Bh/QCxs=
"],
Association["Book" -> 10, "Theorem" -> 25] -> CompressedData["
1:eJztzMsNwjAQBFB/1l5n10s+chy4IAUJBeIeoAdKSAPUSkcYKqAAnkZzmMPM
2/OxaaXU61N/P1v3E1GMEbnvS+3relldGdPQpSH4InU5zeJ4Ou6QmYeQY+Dl
nOTCOacalFYavt9GKTxlCRyFly61bT231ihtNIDSTvVWGzCkg0Wo0HvfeA3o
wBtnDLgvg46JhA6KmihAgBybNxCGCxI=
"],
Association["Book" -> 10, "Theorem" -> 26] -> CompressedData["
1:eJztzD0KwkAQBeCd2Tczm2xi0EIJsbExggcQtLAXA2JhKZha8KzeyHVP4AH8
isf8MLMaX9eRnHPvb/z9zgyJArPpoIiP2+k5GeZda10bynOabA77uorLXSpj
LL2qx+W4aO61ZGaajmOhUiMoPCpD32/Xkr9755jBjr0T5tyCmERIAFE48kTI
4TNiDo2GoqBK0p7EYPwBOT0Kmg==
"],
Association["Book" -> 10, "Theorem" -> 27] -> CompressedData["
1:eJztjDsOwjAQRNf2etefkA0icWzFDVfgFLRAk4IqF6DmmNwII3EBet5II80r
5rg9rpsCgNen/vzA8yDLUiXHGKukEH0Y/I2oI/IuNBN7KUMKUiTNqcN7xRz7
S4mz+3KuLk/jWqcsa8E8c+5kEG7XSiloMQbAQGxDAyrUrnlNzIYYdMcUjDUG
rSVrrUZ0zgYu4IlH1t7tT7s3J0QLZQ==
"],
Association["Book" -> 10, "Theorem" -> 28] -> CompressedData["
1:eJztjDEOwjAMRZ3EsRMX6gKlqUUWrsA12FgYQAy9AGflRgSJC7DzvvSl/4Z/
XJ6XxQHA61N/fmHbm1WdRaTqlCXlId2IVkSZczPSqw1F1HQqU4dLxVn6q0lJ
X86V53H3qHvTu+Fc2DodlNuzcw5aQgAI0LXhAR361Lwn5kAMfsUkIYaAMVKM
0SOmFIUPkIlH9jltTus33R4K+g==
"],
Association["Book" -> 10, "Theorem" -> 29] -> CompressedData["
1:eJztjEEOwjAMBB1iJ6lRgkojFXFAQmYP/Q5nTv0Ab+VHuPAC7sxK3l1b8nV9
3tdARK9t/PmJx7IAUM2AZcdyrzXXmmTbqKqZTWpw23MHI+to2cYPSSYMaK2j
Yp5uDBPoobXij0MI5BIhEhq87KgEZk8hRmYpTLFKKuwlftkOSSQdqUi5SORy
nk9vK4ELLg==
"],
Association["Book" -> 10, "Theorem" -> 30] -> CompressedData["
1:eJztjEEKAjEMRVObNJ3AVKeDgriQCQFrj+MR5gKe1RuZcePave+HD/8nZFmf
jzUAwGuzP7/RWjcbBu6m7CjP45h8aGtEpKlOcjNVFZw7GsuhsU4fEtU+WClz
H+1Y72iNFtmXkv1vCAFcRAAE2cMOKCAm72NEJEaIEonjF1/ERJgqZMxXv+bL
6fwG9UAKzA==
"],
Association["Book" -> 10, "Theorem" -> 31] -> CompressedData["
1:eJztzE0KwjAQBeDEeZPMtPSHpDmAa8GFEkl3uhK69Ai9gOfweN7I2Bu493sw
PHgw+/X5WK0x5v09fz96TcssotOSVRu9aRBhEXiN9+xFxmvufVryfFZKkYpq
GPXSboAYpbRNClqGFKgMOLlu6LA93tVY1E7GWWusYQuSOhAYYDbUeDiuwBsC
aAf2vXGOO3Ysx/7wAWswC6M=
"],
Association["Book" -> 10, "Theorem" -> 32] -> CompressedData["
1:eJztzE0KwjAQBeCJ8yaZaekPSXMA14ILpRJBV9ILeIRewLN6I2Nv4N7vwfDg
wezX13N1RPT+nr9fTctV1aZlNmvsblFVVBEsPeagOt7mPuRlLmfjnLiYxdEu
7QZISUvb5GhlyJHLgJPvhg7b312NQ+1M3jlyJA6sdWAIIELcBHipIBsGeAcJ
PXkvnXjRY3/4AAbnCv4=
"],
Association["Book" -> 10, "Theorem" -> 33] -> CompressedData["
1:eJztzDEKwkAQBdDZP7Mzy67JEQyBHMETiHaCsFhIKklhkyKNhTZ6Ar2bNzKJ
J7D3FX/4fJi6G3LniOg9xd/PmjMQnk22YFaFFCfK4VFnr9ZXOdq9yds1ULzQ
BouDHdLMa7rZMcbFJbSpuKI9+Z0vy8Lmt46cA0AkJBgLAeJ0HMYr7IVgzKai
Kl+kymBWI+95Lyy8Wa4+2S0Pjw==
"],
Association["Book" -> 10, "Theorem" -> 34] -> CompressedData["
1:eJztjDEKwkAQRWdn5u/sZlUQG0mxYOsJPICtQrSQVIH0oofwFp7KGznJDex9
xYf/H/zd+LiMgYg+U/z5nYE51neHCDzRlKKlJEV9dTlZe+9W5vJ0ZG4q98i5
xbXMSFzUfDNL1fpldrm1s/me5tdAITAzkZKyFxLWEF2IqIgpiQkbFDCdIUDY
ZeMGm2k5rPdfIM0NSg==
"],
Association["Book" -> 10, "Theorem" -> 35] -> CompressedData["
1:eJztjTsKwlAQRefd+b3kxUJbSUIQcQGuQxCXkM5KQjoR9+iOnGQJ1p5imMsZ
5g7j4zYmIvos488PADIcJxXRTjbulXvsw2HKrm031RbyegHqHm/JpdXZV5RL
b0/33OdXqULu5e5NU/L6NFFKAIiEBBGIIcnWNhU2JTgjilSjbIHMGMxWU9id
xNF5e/oCY1gMJw==
"],
Association["Book" -> 10, "Theorem" -> 36] -> CompressedData["
1:eJztjEEOwjAMBJ1dO0VKinoliBQCiMdw4wn9AG/tj3Aq8QHOzMFarVdzWd6v
JYjI2s+fX3g2MrXW7rlNtQ61zo/elFrHMc0nj44pjdfzlG/ZNo5Kb1SVHvoz
KQ+llJ0bQ6AEwExAGQCJAlAt+rqjBKOC8BHCF913WYimhk2JDwBsCAk=
"],
Association["Book" -> 10, "Theorem" -> 37] -> CompressedData["
1:eJztjMsNAjEMRP2NkBzB1Su0KAm7N6qhhG2AWukIOyXsmXcY2TOj6cfnfSAA
fFP+nGJjrvuzDxtX9+LeXuksrZnV+xqnmamwcn/cbJhOVuFwRITjyLAKL+5+
iUFEBiRSBWIoRFDijVIRIeIkwhAMpkzEcgwjUMq20g/B8geK
"],
Association["Book" -> 10, "Theorem" -> 38] -> CompressedData["
1:eJztjD0KwkAQhed/s84mlUKIlY1ICntBUtsEYSEXSGflWb2Rmz2CtR+84b2v
mNP6zisCwGc7f37DJOVlnj0fht6GfuevYsb7lDwdb6W6RzZjeU777uFaiWEz
Hk1baUxY2iCX8XrW+pEBiISAGISoTkFCVWRmVQZkrAaZKkgUOgtNRBc1wZJA
X8iACc0=
"],
Association["Book" -> 10, "Theorem" -> 39] -> CompressedData["
1:eJztzD0KAjEQBeDJ/IbE7BHULfYEXkAsrLQJFpJG2H6RLbQXBM/njcyuN7D2
K97weDBtf829A4D3FH8/6rJ5s7WPYaLkX20WtWGVgz27vN8ipgcWb2G0U5yJ
xpudQ1jcfYlpxHKRgzRNsvmhA+cQEYCBsRZAZKd1qJdJGNCITFmVv0CVkEgN
ROjIxLRbbj4qtg5k
"],
Association["Book" -> 10, "Theorem" -> 40] -> CompressedData["
1:eJztjMsJAkEQRHu6u7bno4J4EYVZPBuAEXhdGD3IXjcAxSQMw5zMyNkJwbPv
UFD1oA7T4zI5IvrM8edXCjrgiZiSpuQV+VWCt929rKx/l+HMHHseEcIe19SQ
bpHDzcxnG5ehyq0NVnff/hw5x8xESsq1kLC6rgoRFTElMWGDAqYNAoSrjNVg
My+n9fELecMMNQ==
"],
Association["Book" -> 10, "Theorem" -> 41] -> CompressedData["
1:eJztkbsNwlAMRf29yXs2iD6iQMo+SAxAkQUYgCmomICB2AgnDT0150i2LF3d
xqfldlmYiN7r+PMzgGNGDCtuyHz2Ecf50YfM1/UsjOTwNk64tw1X9MrD06L5
nmPS1jLDvp1aP1Fikk0mI6nFLOA6hMzLQktSVTGVYHPdCZvEwT8kUgim
"],
Association["Book" -> 10, "Theorem" -> 42] -> CompressedData["
1:eJztzLsRwjAQBND77J0kJBOBx0NGwGdogMQ0QODA44AUN0CtdARWCcS8YOd2
g9vPr3FmInov8fe76f4sw6ZrvWvjanSU860vueyu3zPnpO6Kod82j2xVCO5A
Tm4NokPRBJyOl4PVb0okAiFRgkitYGEzNsAMxMq8LKxSsUhce4yJi5mDLcD0
A4B8CVM=
"],
Association["Book" -> 10, "Theorem" -> 43] -> CompressedData["
1:eJztjM0JwlAQhPdndt/G99BTIOTmQSQHC1DBDgQxkALSQGq1I5PXgle/wzAz
MHOcl/fMRPTZ5M8PvKYytn3nfRd5NOThfis599fVltyom2J6tIdntkpKbsCu
cSsIh6IknIfLyeqZEolASJQgUiNY2IzXkRmIlXlrWKXCIrH3iOBi5mBLSPIF
U9kJBw==
"],
Association["Book" -> 10, "Theorem" -> 44] -> CompressedData["
1:eJztjD0KwkAUhN//Zn272oiEWFn5dwUhhQhpVPAIuYBn9UYm7wq2fjDDzBSz
G9+vEQHgM9ufX7iX56ZrrWsX/jDx4/WyKr7tp1g8sxnLrV/XwTXIaV48m1Zp
TFhqktP+fND4YgAiISAGIYoqSKiKzKzKgIyxIFOARGlpqcnooiY4KdEXIJwI
pw==
"],
Association["Book" -> 10, "Theorem" -> 45] -> CompressedData["
1:eJztjLsNwkAQRPczu3f23eEMZJmEBCNRABIENIAlRAEEboBa6QhzLZDygqcZ
jTS7+fWYmYjeX/35idW0Hvow9LG9OdLhci45bU9LTKlVd8X9uumexSohuAOp
cSuIDkUOGMfj3uqVEolASJRMpFawsBkbYA5iZUaVVlgkdh6bhrMtO1tAkA/7
yAh8
"],
Association["Book" -> 10, "Theorem" -> 46] -> CompressedData["
1:eJztkb0NwlAMhP3/sF9iFNHQIMQy1IgmQnRZgEGYjo0waRiAlu+su6uu8Wl5
XBcEgNfH/vyGRe9eJ5Z9drPDcx4143Y5E/bEsObHdpcVtRjYW4tJ3WOLsTff
ZKZ957h+woBAqxAUqIKQjBCEkIVriFegClUfUJQnYqFxp2/JTAf8
"],
Association["Book" -> 10, "Theorem" -> 47] -> CompressedData["
1:eJztjL0NwkAUg9+P/e6SC6FCitJRJRITQINoqGhghCzArGxEcivQ8hWWbck+
Lu/XoiLy2eTPjwzjEOOQ2ydR5utl35XxvNpSGg86HrdDfy+spBQE2ibYIQcc
u4R5Ok2sRy5iBhNzgVmNUFNS1xEJUVfdGnWrqFnuI+esHRlQJtC/vAEH+A==
"],
Association["Book" -> 10, "Theorem" -> 48] -> CompressedData["
1:eJztjMkNwjAURP/u5cvBOLngCAEtceeSBqg1HZGEErjyNHoaaaR5LO/nggCw
7vrzK6VoKWYleY+neq9zq9F7vyhOGX1or9swhy/WsnkMU1S3cRuvllMbGx8/
tIUY96JEIJsRDESAVZgUISixsIjxATCnIO4ZI4mJauAzfQBCLgcZ
"],
Association["Book" -> 10, "Theorem" -> 49] -> CompressedData["
1:eJztzDsOwjAQBND9jWPZOMnaSkE6TsBdOEL6CHFUboSTggvQ8qTZYkba2/Z8
bExE7+P8/WyfX3vMV8Bzq6350gzuc9QCxbrc61r9FGKBASg9uJjCI/I0jehP
RJiEyIRMaSDhs2DtGGY2GDFUcA5faQwpFc4hWN+CFP4AsxwHvg==
"],
Association["Book" -> 10, "Theorem" -> 50] -> CompressedData["
1:eJztzM0NwjAMBWD/PTdNCYqbQ3tlBFZhhN4RYlQ2IuTAAlz5JPvwnuXL8bgd
TESvz/r7Xb0/07IBMUdtLbYwRNSkBYq9Xdd9jcFTgQEofXAyRSTM/RL9hwiT
EJmQKU0kPALWjmFmkxFDBaP4ymfPufDibr1zKfwGcnEHSQ==
"],
Association["Book" -> 10, "Theorem" -> 51] -> CompressedData["
1:eJztzMENAkEIBVBmgQF2BcwYY2J0E+1iE6uwhG3AWu3IUVvw6Dt8Dj+fy/q4
rwUAnu/4+4FlUW2Zoe4RsXHPfkTmlGx+jha3D9FjWq/mjPRTSB+kmln0F4gD
lKEwAzLEUIhQilIlZmQmVi6439FUqdZKXxXVdJQrbHl0EpLpYC/avQkb
"],
Association["Book" -> 10, "Theorem" -> 52] -> CompressedData["
1:eJztzDsOwjAQBND9jWPZOGFtpUg6TsBdOEJ6xFm5EY4LTkDJk2aLGWlvx+tx
MBG9z/P3C8+YN8Bzq6352gzu16gFin291736EGKBASg9uJjCI/KyzOgfRJiE
yIRMaSLhUbB2DDObjBgqGMNXmkNKhXMI1rcghT8w+AbQ
"],
Association["Book" -> 10, "Theorem" -> 53] -> CompressedData["
1:eJztzLsRwkAMBFD99nw+I8byBXZKCbRCCW6AWukIcQEVEPJmpGBXo9v5fJxM
RK/P+vuJuuxAzLH2HnsYItaqDsXR79uxxVCqwwB4Di6miIo5L5EPRJiEyIRM
aSLhEbAmhplNRgwVjOKrXUtrzkspll0R5zfxiQZb
"],
Association["Book" -> 10, "Theorem" -> 54] -> CompressedData["
1:eJzty9sNwlAMA9DEzkPlplBGQEJMwCSM0AWYlY3I7Qx8ciJFlqPc9vdrVxH5
zPX3G8vqrMd1W7NyxlGLuRvrPNaqPDy9McMd9Hm8OO9jnKL/ARGq0AUUaE8X
IFpHeCc1gtqgB1G1RERoqgVAM+cXmxEFXQ==
"],
Association["Book" -> 10, "Theorem" -> 55] -> CompressedData["
1:eJzti70NAmEMQxM7Px9cGqhPSAgQYh1GuAWYlY3IXcEElLziyZbs8/J6Lioi
71V/fsSerNP9UVV57VjTFGRw3I41KjYuRjq/BMs4Z+bouypFAbYpAYh3Jdwj
iO3WhkGh2ruVDnHIXVDDzAFzOj6t+QWb
"],
Association["Book" -> 10, "Theorem" -> 56] -> CompressedData["
1:eJztizEOwlAMQ5PYye9XfjuxMbEg1IEdCXVjZeAIvQBn5Ua0/wyMPMmWbcmn
9f1aVUQ+u/35FcE235eW7XjbYmZFBPhcDtMjvVPLvmQNHzkEwbHwMl/P3v8Q
MaOJQWjWK9XUXQG4QxTaF4V11KxMUYaqSQ/qJscXRCYHFw==
"],
Association["Book" -> 10, "Theorem" -> 57] -> CompressedData["
1:eJztyz0KwkAQBeDZN39h180Zoh7BCwgWNmIhEkQIQqoIoqClp/RGrvEKln7F
Gx6Pmfa3XR+I6PWJv5+Zt2o+NG3062y/XgL5jq7yePE2jdTS0w8xTh7VMeUz
upNutK6zj++BQgBAJCQohQAJVoZyhVUIzuwmZvJFZgxmc1LlrbDwqlm8AT2b
DLY=
"],
Association["Book" -> 10, "Theorem" -> 58] -> CompressedData["
1:eJztizsKwlAURO838178gFgYMAhuwNIdWIrogyDYpbG0dpnuyJu3BktPMTBz
mP34uo1MRJ8p/vyOkhI2z7JE/75eTiJtLw/PufMyq2gz3+UBSFvcFzlkhzNi
T/XNxCwiREYmUUjFuAmhaqowUqjAzR1WIXeVkG0YX0/LcXX4AmLbCjM=
"],
Association["Book" -> 10, "Theorem" -> 59] -> CompressedData["
1:eJztkbsRwlAMBHX62e9JMM49BHZBBBRA4AZogD6gLTpCOKEBQnZndHPJJVq2
22UDEb0+588P6aOf1mcfMh/XM8MTYW2c/d52TLx7DG6p0eyImKW1zNDvgtRP
hEC8C1LiCoAdVZjUykJKEhFW4YCaHBjKMdkbf2gHcA==
"],
Association["Book" -> 10, "Theorem" -> 60] -> CompressedData["
1:eJztjcENwlAMQxPbSX5FYAcG6oURugCzshFBPbAAR56lyJal+H48H4eb2etz
/vyS7lBtHVHrFkqJ3RmXOlmp2FiVKmaGxnLva+v7QDCjxTiM6DLAAXAKFxA4
s4/MfdaUZQFupJRLb1TtBOA=
"],
Association["Book" -> 10, "Theorem" -> 61] -> CompressedData["
1:eJzti8sNAkEMQxPHk8zOT3tdceJMKSAhUcI2QK10xLASHXDkHSw9yz7vz8eu
IvL6xJ+fcl97H1ePXls2D+Ppto2tlYPsHoll8VRZPRlH4qWN6sfVRABC1ITA
VAAKIZEsaNMjKWcF6pdcIi9ZK9znzBl4A+hqBj8=
"],
Association["Book" -> 10, "Theorem" -> 62] -> CompressedData["
1:eJzti7ENwlAMRO3z2U6+f9KjVPTsQYnECFmAWdmID4gNKPOKk57u7rw/7ruK
yPMdB/9l6X29RfaqySKN2/W0bL19iUhnzeHFCjcuzktfKz5PEwEIURMCQwEo
hAQtacPTR69jpD+yZU6zNkQQHkx7Ab5LBeo=
"],
Association["Book" -> 10, "Theorem" -> 63] -> CompressedData["
1:eJztkbENAlEMQxM7CbkjX+gKBkBiEiZA1EiI66ioGZON+FxzC1DyLNmF5cqH
+XmZVUTeX/vzY4737ZC72/mkGqmVQ3vldVwgMlkRnl7pvXxgjNbK1zX7JxQV
LFJxQQ8C0RuD0FbEjDB6qDknmKH2mw9aMgdV
"],
Association["Book" -> 10, "Theorem" -> 64] -> CompressedData["
1:eJztkbsNAkEMRO3xZ/HeYXQiQWRUQ45IEETXALXSEWYTGiDkWRq/xE7mtD4v
KxPR6xN/fs1taxmP6xk8JYe3OLa7Dsz7LNFaXyyi7zgOHpvM9O+xVCdCTBjD
ZIRaYDiYFCwq9UgGVILymdVkgSimvb8BAo8GeA==
"],
Association["Book" -> 10, "Theorem" -> 65] -> CompressedData["
1:eJztkbERwkAMBHU6Sfb79Qy5IxoicE7iBiiAKiiNjhBOaICQ3RndXHCRLvt9
2yEir8/583OWKfN5uyoiMbzNazzagTOWGFN42mh+wljZW2a375b1EwpEDyEm
WgFooIqKeVmwFJJq1A5zDoVpP/sbCOkGgw==
"],
Association["Book" -> 10, "Theorem" -> 66] -> CompressedData["
1:eJzti9kNwkAQQ+fwjCeLBBs6oIzkkxIoIQ1QKx2x2Rr45Ek+JMuP4/06VEQ+
p/35PVfWunYa09hv/dLvmFQyiwATLI69Jdv+3DBfJuLmepbwIQlTKQHU4T5C
YxQEkDERs6jIJbRZpCUKi38BfN0FlQ==
"],
Association["Book" -> 10, "Theorem" -> 67] -> CompressedData["
1:eJzty7ENwlAMBFD7fLbzv/NJjVJRMwg9I2QBZmUjkkiMQMcrTjqd7ra9npuK
yPuIvx+IHHNNFmlcH9dlHe3UIzJYLbxY4cbhvM+X4nkyEYAQNSGwVwAKIUFz
2t6DcFMz16/smVPTjji2YNoHfhMFZg==
"],
Association["Book" -> 10, "Theorem" -> 68] -> CompressedData["
1:eJztizsKwlAUROfN/RmuZgU24hYsLbQTgoWmsk1hFQi4U3fkS1yDnaeYYTjM
bpjuQwHwnuPPL9h35yO5frGPaJ5xbRbMcvRbZo6rPmf50Iu17SaWT0EpJAGF
sg6QWryK2iqmYIiEq7t+gbtQxANm0qmonLaHDx9UClk=
"],
Association["Book" -> 10, "Theorem" -> 69] -> CompressedData["
1:eJzti7ENwlAMRM9nO84PpIjSICEFUTMAE9BGAgqUNgswKxvh/B3oeMVJd093
Xt+PVQB8tvjzE+7zjexOXLyUoz93FW32U3lFtFMsfUl5iDlyb+tFIEISMBiz
QGnSpFA11TBoKMPNPawCd2XKLo2P23IdLl93QAhW
"],
Association["Book" -> 10, "Theorem" -> 70] -> CompressedData["
1:eJztkbERwlAMQy3LNjj+4ehTsRAFA1BkAQbIlGyEk4YJ6HjvzjoVqnxbX48V
IvLez5/f8LwrYqA8z0tseeCMKeoUPqzSL6iFmWOUfWfsn1Ageggx0Q5AA11U
zNuGrZBUoxbMOStM6+ofrWsFwA==
"],
Association["Book" -> 10, "Theorem" -> 71] -> CompressedData["
1:eJztkb0NwmAMRH3nv3yOAKUNFSulT5MFmJWNcGiYgI73JJ+uuMqP47kdEJHX
ef78iA2IKyoy19zjgzHmKDO/eA2/oe6sHGOK70r7JyoQtmeakAKAgS4U87bR
VjpoqglzXUjjvPgbaeQFKw==
"],
Association["Book" -> 10, "Theorem" -> 72] -> CompressedData["
1:eJztkbsNgEAMQxM75PgcSIiGlpUY4RZgVjbigpCYgI5XxEqsuPFWjr2oiJwx
fr5CtZl0pHcLVz5Y5pDcso8Mc2HvKSV7n1g7gUQxuJWCKmqgapggaEQIpAai
Lo04OMetndoLEo8ERQ==
"],
Association["Book" -> 10, "Theorem" -> 73] -> CompressedData["
1:eJztyssNwjAQBNBd7ydeJiiCC0KEGFwSJaQBaqWj2FADt7zDjDSa5/p+rUxE
nx67v6kTKurS8/51m4EFjzKhoPQZM67NqZ1VhYRlOFByOjKrK0vOPoi4Wbgb
u6Y2NsL8qxTjJeJM5gYV9RjzBiIVB3o=
"],
Association["Book" -> 10, "Theorem" -> 74] -> CompressedData["
1:eJztzLERAkEMQ1GJb3tvbyAmZuiIEq4BaqUj1iRUQMYL7MCWbsfzcVjSq8ff
78CdCijmRw6YZEISfWT05rJ+IxBm7DqVznZUiG3rSC4V6cQZ/sKe+3XVqlti
RYzeIFQElQ==
"],
Association["Book" -> 10, "Theorem" -> 75] -> CompressedData["
1:eJztyksKwkAQBNDq/ySKE8E4UZmFR/AqrgR3WQs5qzdy1DO48xU0VdDnebnO
BOD5Pn8/VLWkfJv6/foj4l69lPFxGqdhOWgpflzlIXftlYjQIgIIUhsMJuXW
iNVM1MCdWy8s4vzlbmrhFaFp5xq2vWxeH+YHqg==
"],
Association["Book" -> 10, "Theorem" -> 76] -> CompressedData["
1:eJztzL0JAkEUBOB58/6OXfU6ECzCEswPMZQFrwExNTSyPTvybnsw8wsGBoY5
zPfzLAA+a/z9EltmfcSldB71lddSNs+h1e2b7eZTjONu6FuBCEnAYFwKlCax
ntBU3cBUzfCI8A5mStVImPtkSzvtj1+uewmX
"],
Association["Book" -> 10, "Theorem" -> 77] -> CompressedData["
1:eJztjLERwkAQAyX27t/+gZiYwA25BDdArXTEPQkVOPMGuhnppNfx3g9L+ky5
OBVaQGf9kR0GmZCUvc2kLo96jECYPnRrutvRQizLrGTRIp04w3+w1/GsWc2V
qIrRFw9/BHA=
"],
Association["Book" -> 10, "Theorem" -> 78] -> CompressedData["
1:eJztyrENwlAQA1Cfz/f/KfyIgirFL+ioGYURsgBCYgwahmAgNiJJxQJ0vMKS
ZR/n62U2AO81/n4rapviXjfhrZdnluz52A2dr0m3HMdWtqfBjCQgiLZWyrQM
pMJDYIr1C9yd7hqw7Hu5/Hw4fQAdqgfL
"],
Association["Book" -> 10, "Theorem" -> 79] -> CompressedData["
1:eJztyrENwkAQRNGd2dm9O8uAnJGSgERAD27BkhtwA9RKRxwISiDjBSON9E/b
fdlgZo/X/P3YfJzWffnIcA0tY1RNucaiy/V2znfoZqRodAuyX1BwREBeQv3X
hIge4asdsraKHSPVS4U/AXfNBX4=
"],
Association["Book" -> 10, "Theorem" -> 80] -> CompressedData["
1:eJztyrERhDAMBEDpdJLsMQwZCUNA/tV8CTTwtX5HGPdAxgY3c9Id5+97qoj8
73g9bV+3pQ4lI4Othje2cOMc/MzLxLEzEYAQNQmgVwPUhYTzJv2JQL/SBjUr
U9ZStQ+C9GTaBTe/BNw=
"],
Association["Book" -> 10, "Theorem" -> 81] -> CompressedData["
1:eJztisENwzAMAyWRsuT4UbhIH0H66UoZIQtk1m5UJ52hvx6IAwHytR/briLy
PvXn5zxvy3Thec+sLXuJyp5a18w2P2ZeNxsx6FncTDisEkIKSIAqWRQOd3wZ
UwSzTQqzwnCi2wc/TwT4
"],
Association["Book" -> 10, "Theorem" -> 82] -> CompressedData["
1:eJztkcENwzAUQr8Bo9StfWoGyEoZIR3As3aj2rlkgtz6kEDi/xvb0fcjRcR3
2p/7eXzKCbG8WG0/c11c0TqKW6u+Xjk2YaTA0MwcQCQSeVw0OlEST8ImxOxE
4Q0JbS0/UkIFKA==
"],
Association["Book" -> 10, "Theorem" -> 83] -> CompressedData["
1:eJztysENg0AQQ9EZ2zOzi4iSFjiRQ6qhBBqgVjqCbBE55R2+ZMnLfmy7m9n5
zd8PPGKoyqCmnjGrpaS5tL4/a44TzQDBQCvgnoScHuFShWTekkGQgcGB9sre
mz9RKUaqcAEjiATP
"],
Association["Book" -> 10, "Theorem" -> 84] -> CompressedData["
1:eJztkcENwzAMAylSchHbMdAB8uhKGcELZNZsVLUokA3y6h1EfvjTax77NADn
J/7cQf0SKrX0CO/Rmg+um2odY9U1VP5EMDD9NWH01OCEJ1JeigjRFYsVatCd
7fl4Awl+BFs=
"],
Association["Book" -> 10, "Theorem" -> 85] -> CompressedData["
1:eJztissNAjEMRP1L4tgB1iINcOCAhDhQCiVsAYtSKh0RJGrgxNPMm8uc1udj
RQB4ffTnJ4xtjE3rJVr04y169OtSY8bcbT8PRDyLIkAZGiEzF1ROLMI5laQJ
uZlkmgjRd+piqnfw4gdJYruzvwE7oggP
"],
Association["Book" -> 10, "Theorem" -> 86] -> CompressedData["
1:eJztibsNwkAQRPd7n90DvPI1QECAhAgohRJcgJFLdUccEjUQ8TTzJpjz8nou
CAD7R39+w7pta6nXaNHne/Tot6nGiLnbcfxEPIoiQAkaITNnLKwswkmzFkVu
JokGQvSdOlkpD/DsJ1Gxw8XfDUkHng==
"],
Association["Book" -> 10, "Theorem" -> 87] -> CompressedData["
1:eJztybsVgkAUBND33X37E5bA3MDAhENgJZZAAWirduTDIoi4Z2aSua3v14oA
8N3ndJBt+1h69Nqnvniv85i6x1qrF7+J2IsiQAEqITNHNFYW4aBRTZFrlkCO
6U+I0pjNnlBiGUQlt3v5AeALBzE=
"],
Association["Book" -> 10, "Theorem" -> 88] -> CompressedData["
1:eJzticsNQjEMBP1NHDvAs0gDHDggIQ6UQgmvABCl0hFBogZOjHZnD3tYH7cV
AeD10Z9f8bxbO2XPsb/kyHFeWs54hG/nS8SzKAJUoBMyc0VjZREuWtUUubsU
mgjRd9riZleIGjtR8c0x3rMTBr8=
"],
Association["Book" -> 10, "Theorem" -> 89] -> CompressedData["
1:eJzticsNAjEMRP1NHDuwa5EGOHBAQhwohRK2AKiVjggSNXDiaebNYY7b874h
ALw++vMzHtbO2XMcrjlyXNaWMx7h+3kS8SyKABXohMxc0VhZhItWNUXuLoUm
QvSdtrrZDaLGIiq+O8Ubhg0GTg==
"],
Association["Book" -> 10, "Theorem" -> 90] -> CompressedData["
1:eJztybsRAkEMA1Dbsne9P7i94HICAhKGgEoo4RqgVjrCUAQRbyQlOu3Px85E
9PrM3+94ucw+13mLbtelzIiP0Q/xiSDKqiSJujCAzA6DKpJlc2P0qkkC5EtF
ylLd79RyO6ppHef2BlvFBeU=
"],
Association["Book" -> 10, "Theorem" -> 91] -> CompressedData["
1:eJzty7ENgEAMQ9HEdoKuoWADVmIEFmBWNsJXsQEVX7noSdHt53WcGRH3XH8f
Vt2SX1OLzK21jjHKJyCCGawADSSQJpzZE0lQ+eY/VZCUZXmahQfbqAOx
"],
Association["Book" -> 10, "Theorem" -> 92] -> CompressedData["
1:eJzt0bEVwjAMBFCdopPtF9tKXgpqRoIRskBmZSNEwQpU/OKau+7u5/U8ISKv
T/z90i3GPI4W+6x14+yPEaUUzwbINxSkwKQpNIFGZYaz0sV8ccsdFF/dGH0I
1cdiVtdoby3RBP0=
"],
Association["Book" -> 10, "Theorem" -> 93] -> CompressedData["
1:eJztidEJwkAQRGd3du7MfQSSEySiQtB0kEosIQ1Yqx15AWvwyzcw8Gbm7fXc
DMB7rz8/5d5NdVzmYeof1zhfdOvqWEs7zAwtJEDkJo6w8EPbPSSG4CWr0En/
QiqUU0UKnVJkHdfhA0+yBZw=
"],
Association["Book" -> 10, "Theorem" -> 94] -> CompressedData["
1:eJzticENglAQBd++fbufgERKwC4sghMXThqCBXigAzu0I78U4ck5TDKZy/ac
NwPw/urPbyn3tj29mlvX71wfmnMYzs1xDGYkAUGsAacs6yDlHgKLe8nIzDiA
5HTPAkUsqjWN1w/QgQeO
"],
Association["Book" -> 10, "Theorem" -> 95] -> CompressedData["
1:eJztkcERwkAMAyXbseMcd56QCmiDMighDVArHXFQBC92Rnrs6Kfb+XycBPD6
1J8fM65Hq2PYVjku915mVlOLEPOPCDBQIIUK99VVwyNmELnkIpQ5/aLktree
HW7WVW1tI98cLgTq
"],
Association["Book" -> 10, "Theorem" -> 96] -> CompressedData["
1:eJztib0RQGAQRPf2FjcMApHgC2RynShBA2Z0ojQd+YlUIPKCndn3hmWdFwNw
3PPzNZFHir0qE/deWzRNnT/eYEYSEES7L2W6AqnMM4EhFi/g7nRXiau3cvnU
jSd2rAYl
"],
Association["Book" -> 10, "Theorem" -> 97] -> CompressedData["
1:eJzt0bsNhDAQBNDZD2t7MUYkZCCRkiFRxwVXAg1crXSEjyKIeMFIM+ksx+97
EIDzH6/HfaZh74a5t5JLXtvOSx2Z6xsEM8CQiUiotiaKiFbBFdqwBRZmlRuL
pBBT2uDqRVktj34BQEMFcg==
"],
Association["Book" -> 10, "Theorem" -> 98] -> CompressedData["
1:eJzt0bsRgDAMA1D5E4eEkDuYAApaCkZhhCzArGyEYQgqXqE7q1DjpZ1HIwDX
E7/vzdNexqVaGeqw5ZKqd8z+DYIZYChEJORX6EREXcwKDWyRhVnlxSIpdimt
yJqrsvpgfwMkowUU
"],
Association["Book" -> 10, "Theorem" -> 99] -> CompressedData["
1:eJztiMsJgEAUA/O+uyr4AWEVvViCrViCVw/WakeuWIQXJxAmWfZz2wnA9dTP
B0xpaI9RU/Kpatom5ouIkCMCCGIeDCblbMRqJmrgwq0UFnF+cTe14DOCxt41
WLfWNyyyBUU=
"],
Association["Book" -> 10, "Theorem" -> 100] -> CompressedData["
1:eJzticENg0AQA71e7x5SROgAiSYogT9JAxHwJ62moxw0wYd5WPLMsOyvxQD8
jrm5gubzaL/cVr2z6555OoMZSUAQ7biUqQbS3cPB4l4yMjNOUHVNaqCIWZRP
/fgHb6sGbA==
"],
Association["Book" -> 10, "Theorem" -> 101] -> CompressedData["
1:eJzt0bsRgCAQhOG9BxwwB86YGxgY2Y0l0IC12pFoEyZ+wR9sums/j04Arie/
T9S2VGtefS+epzEwjzcIIQARTkRChKQmIjqkotDIwViYVV4sYilb2lC0NCWN
Pucb/ZwEpQ==
"],
Association["Book" -> 10, "Theorem" -> 102] -> CompressedData["
1:eJztyakNgAAUA9D+thzhCAKFQODQjMIILEDCHCzHRhyGETA80aTtsKzzEgCO
O37fKIuee+ctr+sqfZZABEnAMOOudPg6SFuJwdzM0hckUXIBJ2osa2rHEytC
BUQ=
"],
Association["Book" -> 10, "Theorem" -> 103] -> CompressedData["
1:eJztiMENgDAMAx3qNE2KhJBYgBHgwx6MwALMykYUluDDWTrpPB/nfgiA69HP
RwzBMXyMdVuspYigTRUgokWHLJne/pTIXIg0VbPCUowv8kiz9XCtpkavHjcI
pgTG
"],
Association["Book" -> 10, "Theorem" -> 104] -> CompressedData["
1:eJzth90NQEAYBPf72btDEImQS7woQStK0IBadeREEV7MJpuZ9Tj3QwBcz/18
RfZpjrnp+i6VEhGUmQGGVEKh4lpM1ElzQqvA2tQs6AtJZwwL6GkMHjls7Q3m
8wR2
"],
Association["Book" -> 10, "Theorem" -> 105] -> CompressedData["
1:eJztyrsNgFAMQ1HHcQIVr6ZkBRagp0LUiOItwKxsxGcJGk5h6Uoe6rFWA3A+
8/sM901LltK1bxrMSAKCeAdIWT4/yj0ENu5NRmbGC5LTPVsoYtZdUz9eGe0F
Yg==
"],
Association["Book" -> 10, "Theorem" -> 106] -> CompressedData["
1:eJztzLsVgDAUAlAQXn5Ha2tXcoQs4KxuZFI5go234NDA0a+zE8A94/cdKcuS
ttFtQVRuWBJW0slQKZGlGJKDIYb5ElnbXmtgvnhMKDzJDgO3
"],
Association["Book" -> 10, "Theorem" -> 107] -> CompressedData["
1:eJztiTEOQFAUBPftLn6EKFRKndpRHMEFxFHdyP8qN9CYYpLJzPux7QHgKvr5
kMln6vuufiIQQRIwzChJh/MgXakymMzmBSRRcov8B8tax+UG7K8Ejw==
"],
Association["Book" -> 10, "Theorem" -> 108] -> CompressedData["
1:eJztkcENgDAMAx07CqBW4tUBWIkRugCzshFpP4zAh7NkW/766NfZDcA97OdL
uEWtJd5B+Ylg4JSNlkFxocEJDXy6ECFmX03BRjn3Vh62vwOD
"],
Association["Book" -> 10, "Theorem" -> 109] -> CompressedData["
1:eJzt0bERgDAMA0DLsZyQM2QGVmKELMCsbIQpmIGGL3Qq1Gmf5zEhItcTv09t
o9bqWYB8Q0EKTBaFJtCozHA2upgXt9xB8QrjiBCqRzFrfe03xTADzA==
"],
Association["Book" -> 10, "Theorem" -> 110] -> CompressedData["
1:eJztyUENgDAUA9D+tmPAEoIFbghACRJmAK04gnFBAhfeoWnTpR57DQBni9+3
cilj97RABEnAMKNNOnwfpK1ksDdz94IkSh7gpMmytnm9ALv/A+s=
"],
Association["Book" -> 10, "Theorem" -> 111] -> CompressedData["
1:eJzticsNgCAAQ/sDPOAQruQILOCsbiScHMGLfUmTvh7jOgcB3Kv+fJy+9/Ku
CDCW0MSskCjJ82CsZnkJTkCWtKQi9mbHpeUBsrIDSQ==
"],
Association["Book" -> 10, "Theorem" -> 112] -> CompressedData["
1:eJztkbsNgEAMQ53Yl/tswUosgHQFLbOyEYGGEWh4ki3brZd5rNMAnLf9fM22
t7cwP3FEyqFUh2cUWWQIFYpS5YOREdFGt+GqnrsGL+kkBCg=
"],
Association["Book" -> 10, "Theorem" -> 113] -> CompressedData["
1:eJztkbERgDAMA2VLMQ5MwUoUDJAFmJWNMDSMQMPfve57rePYhgE47/n5nD3f
Zn3iiNKhssMrRTYZQo2ilHwwMiJy7ra4wqVJnRfHfwO5
"],
Association["Book" -> 10, "Theorem" -> 114] -> CompressedData["
1:eJztkcENgDAMA53YDWm3YCVG6ALMykakfBiBDyfZOvnrfZ7HNADXqp/vyVdZ
nzii4lClw0tFNhlCjaK08cHIiMjRbbjS1z78Bq2IA2I=
"],
Association["Book" -> 10, "Theorem" -> 115] -> CompressedData["
1:eJztxLsNgDAMBUA/+yV2goACKRIlKzFCFmBWNuIzBQVX3NaPvUNEzqffN5iZ
GOAummQB1LQi8uBk5BR5TAinE7c3wKjrPLVWJcpAVhYlLsVrBAM=
"],
Association["Book" -> 11, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAAjHh4pAEAlWgCfA==
"],
Association["Book" -> 11, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWABwNhgBMcII/Z4ISK2gEoAlk8CgQ==
"],
Association["Book" -> 11, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSABjAyQ6GBkhPDIBACWJAJ/
"],
Association["Book" -> 11, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAB4swM7MzMjIwMbIwMLMwsbCxsDExAHhcrK1QB
E7oOYPQxMbMwMaFEIwCtXQLu
"],
Association["Book" -> 11, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWABrAzsTExAmp2BgYWZlY2FjYEJGEFcrKxQeSZ0
DUBZJmYWJiaUaAQApooC1Q==
"],
Association["Book" -> 11, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweABXNycjIwMLCwMjDysjEyMDBwsjIxMbGzMQMDA
xMzBzMjAzIQEGIEARAJ1MoIRSBoAscwDHw==
"],
Association["Book" -> 11, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweABwPhgBAIQixHGRUgR1A1WDACXZwKI
"],
Association["Book" -> 11, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSACLMzs7AxsjAyMPKxMQMDMxM7MzsTECARAgpkR
KIECGBgYQbJAjRAmSCUAqt4C9w==
"],
Association["Book" -> 11, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWACwkwsDMxsDIx8rIzMjAyCPCxMzGxsbKysrEws
rEJAcTYWJACMPkYQgFAMDExMLIyMALxeA2o=
"],
Association["Book" -> 11, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaACzIwMzKwMTJysTMxMDBJ8DExMrKzsbGxsDKxs
/OwMDOysSAConJGRiREUi0xAJlAzCyMjALhRA2A=
"],
Association["Book" -> 11, "Theorem" -> 11] -> CompressedData["
1:eJztyrERgDAMQ1HJlo251NzRshIjZIHMykaEhhkoeMVvpKOPsxPA9eT3LTuw
IIJ0muXWjKzMrEhWeM3h5aS0SoKb23w3Cje4wgNz
"],
Association["Book" -> 11, "Theorem" -> 12] -> CompressedData["
1:eJztxLERgEAIBEDuOGB4A2NDW7KEb8Ba7cgxsgUDN9h9nseEmV1Pv89piwAc
ydwWAl1VIwod3sGXA1JLMqeTOVa53beyA4c=
"],
Association["Book" -> 11, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAD4FhhIlc3AJWSAn0=
"],
Association["Book" -> 11, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaADjAzMTKysTCwMTMAI4mRhgQozoatjBioFARRB
AJ5ZAq4=
"],
Association["Book" -> 11, "Theorem" -> 15] -> CompressedData["
1:eJzt0UEBgDAMBMFcrrkkMrCEhBpAK45KX1jgwTzWwB7zOifM7N75fRATcGB0
6XlUkrI1KrxaL7gzSIZxc2XQFrRUA30=
"],
Association["Book" -> 11, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAEFEQMAJUdAns=
"],
Association["Book" -> 11, "Theorem" -> 17] -> CompressedData["
1:eJztxLENgDAMBEC//P6YwiiwAStlhCzArGyEqFiBgivumOeYMLPr6fdFQMjp
GdsitVCoCU0s4uVA1dp7WFY6yR1uN7dCA7A=
"],
Association["Book" -> 11, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAErIzMjIwczEyMzGxsoGhiBAkxMqDHGBMjIxMT
iAaqAAIgCwCe+wK6
"],
Association["Book" -> 11, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAFoPhhZGRE4mEHTEhsAJXhAoE=
"],
Association["Book" -> 11, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAFPLyMzIyMjCzMzOBoYmRghCJkwMTEwsQEFARi
JrAuZgCgwgLO
"],
Association["Book" -> 11, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAFLIyswAhiYWNjYGQEMhiZGRiZGEBsGACymZjZ
mJhAoiAJsCYAng4CxA==
"],
Association["Book" -> 11, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAFjEzACGJmYoJxIQgFMDGxMDExwuRAAACZiAKk
"],
Association["Book" -> 11, "Theorem" -> 23] -> CompressedData["
1:eJztkUERwDAQAoGDTGzUUiTEQLXWUS8u+ugOs4/9cu17bQJ4jn4+jfsjVUQF
slUjI07PYRXUlVCL5UnxBaKhAwU=
"],
Association["Book" -> 11, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAG4kxMTKysXJycnAwcnDxcDAwcLEgAqICRkYkR
FItMQCYDAwszIyMAr2EDNw==
"],
Association["Book" -> 11, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAGXJwsTEx8vLy87Fy8rHzMjLwcrAjAxMjIwcbB
wcHCwMzCzMzMxMbBwsIIALdrA6I=
"],
Association["Book" -> 11, "Theorem" -> 26] -> CompressedData["
1:eJztxDERgEAQA8AkFzJcjwEsIeENoBVHzFdYoPgt9hz3NQjgmS2/dojsJHuC
3qqjT5F220bJktMyXqrtAz8=
"],
Association["Book" -> 11, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAGzExMnOzsbGy87AycLGy8HCzMLCzMcMDOzcHO
ycrAxsHHDFQmyMzKCACt8AOH
"],
Association["Book" -> 11, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAH7OxQBhO6DDD6GJmYGVFjEQCYTwKT
"],
Association["Book" -> 11, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAHctBoYmFkRI0wII+ZlYWZmYkBLMMIEmAAAJzw
Aro=
"],
Association["Book" -> 11, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVABLAyMqBEG5DGzsjAzMwElGEFckDQAlzoCmg==
"],
Association["Book" -> 11, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAH8hJi7EISDGYsjLI8HEDAxgEGTMzMLMwsLMzM
DExMLExMjCy8rCyMAMMhA/c=
"],
Association["Book" -> 11, "Theorem" -> 32] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAABpqsnAaM3EzMHILcCMDExsbMxMLMzMTAxARi
sHKysTIBAMKeA/4=
"],
Association["Book" -> 11, "Theorem" -> 33] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAA+mxcnozcTMwcQjw8PNxc3GDAxMbGyszCwsLE
wMzEzMTCwgrkMwEAwGMD9g==
"],
Association["Book" -> 11, "Theorem" -> 34] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAAbNyKjCxMbCzigpyCAmIcYMDEyc7CzMLCysLA
ysTCBGSwsrMxAwCzxwOu
"],
Association["Book" -> 11, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAAnKwMrMyMrCyMCMDMyMjKxMLKyszAxMjMxMrI
xsHIzAAAnUEC4g==
"],
Association["Book" -> 11, "Theorem" -> 36] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAB7AwsrMxc7EwQwAwigAJAwMLKwMnMw8zMxsLO
zMIIAJ/iAww=
"],
Association["Book" -> 11, "Theorem" -> 37] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVABjNxMzBxCPDw83FzcYMDExsbKzMLCwsTAzMTM
xMLCCuQzAQCrCANu
"],
Association["Book" -> 11, "Theorem" -> 38] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZABTAyMTCxIgImBgZGRiREYi4wMIJKBiYWJCQCb
ewLE
"],
Association["Book" -> 11, "Theorem" -> 39] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdABLIzyXGwIwMTIyMLMwsLMzMDExMLExMjCy8rC
CACkXgMr
"],
Association["Book" -> 12, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRACeuxs3BzcnFwcHGwcHBzM7KwsbKxsbGwMfOzc
rGxcHNxM7IwArGMDlg==
"],
Association["Book" -> 12, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVACzCyiQqLCIjwcXBwcHGzcnEwsDMzMTAwsjFxM
zGzszExMjACqjgNr
"],
Association["Book" -> 12, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZACvBwcHOxQzMTIyMzCwszMysDMxsbExMgiwMrK
CACiaQMq
"],
Association["Book" -> 12, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAC2hraSnJKSvJKikpMQgLMzEzMrKwMzMwsrKxM
7BycXKwAw5oEdg==
"],
Association["Book" -> 12, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRADqdk+Hs622rbW1ozK0iABJkYGFhYmZgZmJmYW
ViYA5WkFng==
"],
Association["Book" -> 12, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVADWvKKvq56rs5OjLzCID4TIwMLMxMLAzMTMzMb
IwDKGgSx
"],
Association["Book" -> 12, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZADAZ4udlp2NjaMKjIgLhMjAwsLEzMDMxMzCysT
AM28BNk=
"],
Association["Book" -> 12, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAD9sYmpiZmRozGWiAeEyMDCwsTEwMzEzMrKzMA
wbQEcw==
"],
Association["Book" -> 12, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAEsvIy8oryjPz8IA4TEwMLM5BgZmJmZWMCAKmh
A3Q=
"],
Association["Book" -> 12, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAEcTZx0dGM/AIgNhMTAyMLCyMDMxMzCzMjAMBa
BGY=
"],
Association["Book" -> 12, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAEVuWZGYx8/CAmExMDIyszIwMzEzMLMyMAuy4E
OA==
"],
Association["Book" -> 12, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAE8gryjHx8IBYTEwMjKzMDAzMTMysTMwCgVwMU
"],
Association["Book" -> 12, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAFaWmMfPwgBhMTAyMrMyMDMxMzCzMjAKnrA4I=
"],
Association["Book" -> 12, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAFeYx8/CCaiYmBkZWZgYGZiZmFmREAoWkDIw==
"],
Association["Book" -> 12, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAFjHz8IIqJiYGRlZmRgZmJmYWZEQCX/QK2
"],
Association["Book" -> 12, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAFjIwgxMDIwMTMxMTEwATkMgAAlasCjg==
"],
Association["Book" -> 12, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAGBUDMyMjIwMrCxMDAxMLGwcQCAJ4lAxI=
"],
Association["Book" -> 12, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAHjIyMDKwsTAwMTCxsHEwsAJXVAqI=
"],
Association["Book" -> 13, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAGnGw6GqwMrKyczCysrNyMzAwAnDoDFQ==
"],
Association["Book" -> 13, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAGbJycTIysLEzMTIzMbIzMDACXOgKz
"],
Association["Book" -> 13, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAHnJysDMwszMwsjCxsjMwMAJb7ArE=
"],
Association["Book" -> 13, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAHeqwMbKyczCysrLyMzAwAmRQC4w==
"],
Association["Book" -> 13, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAHrAxsLJzMLKysXIzMDACWegKx
"],
Association["Book" -> 13, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTAAHCycoszMLGzCdgIAl3MDFQ==
"],
Association["Book" -> 13, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXACjAwAlOQCew==
"],
Association["Book" -> 13, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXAAnOz8LCwsbOwsrACWdQK7
"],
Association["Book" -> 13, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbAAcuycwixsrCwsAJcgAtI=
"],
Association["Book" -> 13, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfAAbBx8rBxsLKwAlfYCsg==
"],
Association["Book" -> 13, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTABTCzMTLncTgCWvgM/
"],
Association["Book" -> 13, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXABPNxsLCzMAJWQAqI=
"],
Association["Book" -> 13, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbABzBxcLGwAlT0CmQ==
"],
Association["Book" -> 13, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfABHCzsDACVHAKN
"],
Association["Book" -> 13, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTACLKwMAJT4AoM=
"],
Association["Book" -> 13, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXAC3EEAlUoC1w==
"],
Association["Book" -> 13, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbACGgCVCgKi
"],
Association["Book" -> 13, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"]],
SelectWithContents->True,
Selectable->False], "}"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"ListLinePlot", "[",
RowBox[{
RowBox[{
RowBox[{"Values", "[", "res", "]"}], "[",
RowBox[{"[",
RowBox[{"{",
RowBox[{"316", ",", "353"}], "}"}], "]"}], "]"}], ",",
RowBox[{"PlotRange", "\[Rule]", "All"}], ",",
RowBox[{"PlotStyle", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "10", "]"}], ",",
RowBox[{"GrayLevel", "[", "0.85", "]"}]}], "}"}]}], ",",
RowBox[{"Frame", "\[Rule]", "True"}], ",",
RowBox[{"PlotLegends", "\[Rule]",
RowBox[{"{",
RowBox[{"10.41", ",", "10.78"}], "}"}]}]}], "]"}]], "Input"]
}, Open ]]
|
By the way, adding a superaxiom can not only decrease the number of intermediate theorems used in a proof, it can also decrease the “depth” of the proof, i.e. the longest path needed to reach an axiom (or superaxiom). Here is the average depth reduction achieved by adding each possible theorem as a superaxiom:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"(*",
RowBox[{
RowBox[{"proofDepth", "[", "g_", "]"}], ":=", "\n",
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{"pp", ",", "newpp", ",", "len"}], "}"}], ",", "\n",
"\t",
RowBox[{"Max", "[", "\n", "\t\t",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"v", ",", "\n", "\t\t\t",
RowBox[{
RowBox[{"newpp", " ", "=", " ",
RowBox[{"pp", " ", "=", " ",
RowBox[{"FindPath", "[",
RowBox[{"g", ",",
RowBox[{
RowBox[{"VertexList", "[", "g", "]"}], "[",
RowBox[{"[", "1", "]"}], "]"}], ",", "v"}], "]"}]}]}],
";", "\n", "\t\t\t",
RowBox[{"len", " ", "=", " ",
RowBox[{"Length", "[",
RowBox[{
RowBox[{"Replace", "[",
RowBox[{"pp", ",",
RowBox[{
RowBox[{"{", "}"}], "\[Rule]",
RowBox[{"{",
RowBox[{"{", "}"}], "}"}]}]}], "]"}], "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}]}], ";",
"\[IndentingNewLine]", "\t\t\t",
RowBox[{"While", "[",
RowBox[{
RowBox[{"newpp", "=!=",
RowBox[{"{", "}"}]}], ",", "\[IndentingNewLine]",
"\t\t\t\t",
RowBox[{
RowBox[{"pp", " ", "=", " ", "newpp"}], ";",
"\[IndentingNewLine]", "\t\t\t\t",
RowBox[{"newpp", " ", "=", " ",
RowBox[{"FindPath", "[",
RowBox[{"g", ",",
RowBox[{
RowBox[{"VertexList", "[", "g", "]"}], "[",
RowBox[{"[", "1", "]"}], "]"}], ",", "v", ",",
RowBox[{"{",
RowBox[{"++", "len"}], "}"}]}], "]"}]}]}]}],
"\[IndentingNewLine]", "\t\t\t", "]"}], ";", "\n",
"\t\t\t",
RowBox[{"Length", "[",
RowBox[{
RowBox[{"Replace", "[",
RowBox[{"pp", ",",
RowBox[{
RowBox[{"{", "}"}], "\[Rule]",
RowBox[{"{",
RowBox[{"{", "}"}], "}"}]}]}], "]"}], "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}]}]}], "\n", "\t\t",
"]"}], "/@",
RowBox[{"Rest", "[",
RowBox[{"VertexList", "[", "g", "]"}], "]"}]}], "\n", "\t",
"]"}]}], "\n", "]"}]}], "*)"}]], "Input"],
Cell[BoxData[
RowBox[{"(*",
RowBox[{
RowBox[{"resDepth", "=",
RowBox[{
RowBox[{
"ResourceFunction", "[", "\"\<ParallelMapMonitored\>\"", "]"}],
"[",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"t", ",",
RowBox[{"t", "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"(",
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"Order", "[",
RowBox[{"#", ",", "t"}], "]"}], "\[NotEqual]",
RowBox[{"-", "1"}]}], ",", "0", ",",
RowBox[{"With", "[",
RowBox[{
RowBox[{"{",
RowBox[{"g", "=",
RowBox[{"Subgraph", "[",
RowBox[{"euc", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{"euc", ",", "#"}], "]"}]}], "]"}]}],
"}"}], ",",
RowBox[{"Catch", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"proofDepth", "[", "g", "]"}], "-",
RowBox[{"If", "[",
RowBox[{
RowBox[{"!",
RowBox[{"GraphQ", "[", "#", "]"}]}], ",",
RowBox[{"Throw", "[", "0", "]"}], ",",
RowBox[{"proofDepth", "[", "#", "]"}]}], "]"}]}],
"&"}], "[",
RowBox[{"PruneSubgraph", "[",
RowBox[{"g", ",",
RowBox[{"Subgraph", "[",
RowBox[{"euc", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{"euc", ",", "t"}], "]"}]}], "]"}]}],
"]"}], "]"}], "]"}]}], "]"}]}], "]"}], ")"}],
"&"}], "/@",
RowBox[{"Complement", "[",
RowBox[{
RowBox[{"VertexList", "[", "euc", "]"}], ",", "axioms"}],
"]"}]}], ")"}]}]}], "]"}], ",",
RowBox[{"Complement", "[",
RowBox[{
RowBox[{"VertexList", "[", "euc", "]"}], ",", "axioms"}],
"]"}]}], "]"}]}], ";"}], "*)"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"resDepth", "=",
InterpretationBox[
DynamicModuleBox[{Typeset`open = False},
TemplateBox[{"List", "ListIcon",
GridBox[{{
RowBox[{
TagBox["\"Head: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["List", "IconizedItem"]}]}, {
RowBox[{
TagBox["\"Length: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["465", "IconizedItem"]}]}, {
RowBox[{
TagBox["\"Byte count: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["5397840", "IconizedItem"]}]}},
GridBoxAlignment -> {"Columns" -> {{Left}}}, DefaultBaseStyle ->
"Column",
GridBoxItemSize -> {
"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}],
Dynamic[Typeset`open]},
"IconizedObject"]],
{Association["Book" -> 1, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 1, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIYmBiYgICBdoAJjR4F1AbIIQsArJwCig==
"],
Association["Book" -> 1, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKAgImJiRkGgCxWZlZWKBNIgCShGESAaRQA1s/EDJOA
6mNGqGRGpphBGnAADKNBpqNaRV2A30CwfUzYnUVlAPE8OCJAJAO2cMYB4JED
BQACnQUe
"],
Association["Book" -> 1, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 1, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJAgJkFGbCysAIBC7GAgQFTDEU3M5okAy6A1XSidJIJ
8BsItg+r96gOIJ5ngPmYEisB1kMHXg==
"],
Association["Book" -> 1, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLAgBkEmKAEKzMrK4IPBMxQDCLANApgYABLwSRA+qAQ
JoJMMYM04AAYRoNMR7WKugC/gWD7mLA7i8oA4nkGcPgwgBmY4YwDoCsEAPhf
BRc=
"],
Association["Book" -> 1, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIggJV8QFAzM5RmgWvAAbCajmoVdQF+A8H2EfYeNQDE
8wwwH5NqJQsSGwDHtwiE
"],
Association["Book" -> 1, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKggJVsQFAvM5RmgWvAAbCajmoVdQF+A8H2EfYeNQDE
8wwwH5NqJQsSGwC+xQh/
"],
Association["Book" -> 1, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJggA0MWJEBOzsrO6oAK5oASD0DA5BmR9aEpooJSrNA
aQZcgBULQBHEqZNMgN9AsH2s2J1FZQDxPAPMx6RYyY7GBwDfHQiW
"],
Association["Book" -> 1, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLggJWdFQHYoRy4GDuUQFbEysoGFADqZGVjR9XJDoZQ
wARXCwEMuAArFoAiiFMnmQC/gWD7WLE7i8oA4nkQZgeRpFjJjsYHAN7VCJk=
"], Association["Book" -> 1, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIQgJWdnZ0NGaBxsQBWIGZgANKseBQxQWkWqA4GXACb
ZhRBnDrJBPgNBNvHhtVZWPxLjAhOAPE8A8zHDCRpRlUMAKIqCZo=
"],
Association["Book" -> 1, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKQACsIsLGxsbKxsrOzgXnsrFDADiXgAhDFQAzSx4YQ
ZmcHK0RSx8SKChhwAVYsgIEonWQC/AaC7WPF7iwqA4jnGWA+JsVKdjQ+AMpC
CIs=
"],
Association["Book" -> 1, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKQAQcHGzJA42IBrEDMwACkWfEoYoLSLFAdDLgANs0o
gjh1kgnwGwi2jw27s7AHBdkA4nkGmI8ZSDQOWTEAlYQJlQ==
"],
Association["Book" -> 1, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJQAAcbMmBnZ0MFrBgAKMjAAJIAy4IUQNggLkw5E1SC
BSLLim4pHKBYBTWUAcaGWEVdgNspEOdAlED8iel3pFDAJ0kMANvGygBhs4EQ
Kyy4sQY7HgAABbcIwA==
"],
Association["Book" -> 1, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJQARsy4OBgIwBYgRikiZUVjyImKM0C1YFhKVbLoQBF
EKdOMgF+A8H2sWF1Fhb/EiOCE0A8zwDzMQNJmlEVAwB3oQmC
"],
Association["Book" -> 1, "Theorem" -> 16] -> CompressedData["
1:eJydUIkNgCAMrAY4yhau5Ags4KxuZAuYoDwxXkKvvV5TYIvHHhciOjW8wOzZ
KzhkngLiJhIGV+6Q6VbWkhoN1vt2aUFvw0McTv6Em3bTPjnONbeytpU+KEOQ
fjwIgOQsj0Ya1lIpm7RCd9xU+QVhTQvA
"],
Association["Book" -> 1, "Theorem" -> 17] -> CompressedData["
1:eJytUNsNhDAMCyfy6hasdCOwwM16G2GnCJUD8XWWGiWNHbdZ1s97nUTky/CL
jAwiW0P0zF4icw/V2KEFB08k3MFjEzXyElLQSS91g9Zn5IZzY9oRpQaV8x1q
5ELXsmPxZ9hjt/zwWjM+TEeYncpz8yBxI5fbgXs0A0ZYoDT+ElH6LuvTGdcZ
w6jqzsPoDSMYCb0=
"],
Association["Book" -> 1, "Theorem" -> 18] -> CompressedData["
1:eJytUNkNwlAMC6ip7bcFKzFCF2BWNmqOorai4gtLOZxEseTH8nouNzN7Z/rC
UGOIVATRnBlUZzYQUzMJqPFgHYzYC0Lf8q5upwi4dCVa0AHcxOzTF/kz5p/b
0mNczZsRO9xPNJfnSR0djLrEviw1N+RfE0zuaULJAA4gSzDH1ZOJ7U+WFaJN
C+U=
"],
Association["Book" -> 1, "Theorem" -> 19] -> CompressedData["
1:eJytkd0NwkAMgwNq6tidgpUYoQswKxuRpKC24sQT30PO+VEs5W7r475ezOxZ
4ZtlUUIxQooIlE6lqjDJGBtg0EwCpCXHsyQyR0Mgttm4sqWmDHByaFroQFvn
ax/dyZ+Zf3bbL3Jqfh9ix/2UVvNc6aHDoYbszTQi3VB7jTC51xe0DeAA6snM
MVoytehjxwvdpQwX
"],
Association["Book" -> 1, "Theorem" -> 20] -> CompressedData["
1:eJydkesNwjAMhA2qe2e7DMFKjNAFmJWNuKRCbaXAD74ojl/JRcl9fT7Wi5m9
mhmwNCKDXIokUn4ms2VCyHIDwVD/DcisLV1VyWJBo/fyGoFSZlIIjxiLijwg
NWqmfXyZ+rrzT+afVYmbUV0ztxvsuJ/CVjxnetPhoYbsRQlFuKGdawFL9/YF
XQZwAG1R5BgdMnWnPzbf/bgMMg==
"],
Association["Book" -> 1, "Theorem" -> 21] -> CompressedData["
1:eJydUUEOwyAM86bSOAmf2Jf2hH5gb92P5lBNbaV2hxmITBwIMo/l9VxuAN4V
ztAF0sjezYzhGmERTrqgyBXmNMDdJCYZSvUUSaZpjFrepWd6Ttpac79oCsQO
1NQKfLlCXp78E/NPVc0Bqmrm+oINrR22JR4zo2hn1Ck2sRrJyTKbEInyqcut
8Qut8lqt6Nkl0yDDbH4A0T8MGw==
"],
Association["Book" -> 1, "Theorem" -> 22] -> CompressedData["
1:eJydUcENwjAMNAj3znY6BCsxAgswKxtxSYXaSi0PLopjnx1f5Nyfr8fzYmbv
bg4xtxYZ5FwkkfIzmZ0JQZYLEAyz1oDMWuiqShYLWqOW1wiUmJtCeMSZqOUG
UqN22teXqdObf2L6mZW4GVU1cXnBCvdd2JN7ZhRtBnWINSmhCDf0vhawdG/6
giEDOIB+KHIcNbkNZwybH9XuDBs=
"],
Association["Book" -> 1, "Theorem" -> 23] -> CompressedData["
1:eJydUUEOwjAMC2iZnWQ8gi/xhH2At/Ij3A60Tdo44Epp4rhx1d7n52O+mNmr
hWNMU2SQtyKJVJ7JbEwIivwgGU0MZNZCV1WyWNDqWl4jUGIGlfCIU9PcQG6a
nmnfXKFOT/6J8WdX5maUauRygxXuu7I190wXbR/qCGtTRhFuaHMtYOk+6Qu6
DeAA2qbKcTRk6El/bL4BwpQMEA==
"],
Association["Book" -> 1, "Theorem" -> 24] -> CompressedData["
1:eJydUMENwkAMC4jUTtKqM7ASI7AAs7IRviuoVGp54NPlEseKo7veH7f7ycye
LRxgjgxyLJJI5ZnMxoSgyDeCIe0EZNZCV1WyWNDpWp4jUGIuKuERh575BblR
N+2TK9Txuv9h+NmVuRmlGrhssMJ9U7bmlumi74/aw9qUUYQb2lwLWLrP4xTd
BnAA7VHl2Bty6Un/bL4AttMMDQ==
"],
Association["Book" -> 1, "Theorem" -> 25] -> CompressedData["
1:eJydUO0Ng1AIpI14B2icoSt1BBforN2oPGyjJuqP3svj4yAc4TG/nvNNRN7N
nMHcyCFIwjN2pzfGEmn5hdFEphFwj4WOCGcwkK96eTdDJNNlCjU7lfQNUo35
XX5xmrhY9y/0l9UUF2F29Vw2WKG6S1txz1TT9lBHWIspZKaCNlcM4qrTMFrJ
AAqgucwUR0O6CurY/ACc/Av+
"],
Association["Book" -> 1, "Theorem" -> 26] -> CompressedData["
1:eJytUMENAyEMy1Vnh7DFrdQRboHO2o3qEJ3Eo5z6qAUmIUYOOc7X89zM7J20
RI/WmrekgTwArQm6DbOsRGSxpP16U6IHnJntiqm9dPQJGGbudsUj+TPWrVQ7
JamP4ga3xV8go95pTjosoAAaPahxaZYsEfnNNmmf8g9Dowkc
"],
Association["Book" -> 1, "Theorem" -> 27] -> CompressedData["
1:eJytUMENgDAIRFMKuIUrOUIXcFY3kqM2qSY1PrwUCjnoQdeyb2UiogNuDFNV
gVXgZvbTwWkjAmOmzCj3eIlGsat2ZsloTx5nt6GgdOAQE6EWR/IzxqPUcWpJ
LHrf+4FX8gtcyMx3xVNk7NL4y6B0LC3NpS4/ATroCRA=
"],
Association["Book" -> 1, "Theorem" -> 28] -> CompressedData["
1:eJyVkQsOAiEMRKvZ6Uy5hVfyCHsBz+qNbGE1YOImvkBTwvQHt/1x3y9m9ixz
gkS1CHUYpCZAEoQidelHpNFQtCMgd3GVvO42ujvgJ/VGQE/fU4jG7gOV/rzd
//ndSkGmQaq8WsFMzTHBvr7x7FqrbhXqfarB8p2tlSStZTkdQ4fWHGvZ8RXb
5wy8AMq5CaQ=
"],
Association["Book" -> 1, "Theorem" -> 29] -> CompressedData["
1:eJytUMERgDAIi57pwy26kiN0AWd1IyuFU6H2ZR5cCFxSmsu+lQnAcZUR1uRA
3kxQGaC6Dm2HtjOTIi4Uws+4V5IawXiL+hdjQ8mjPYtP+JY9yAVR7dDUjoec
XCvsQxmjnVWYnoasCIk=
"],
Association["Book" -> 1, "Theorem" -> 30] -> CompressedData["
1:eJytUEEOgCAMq8byD7/kE/iAb/VHQmHRbIR4sIel25qWsefzyAuAq5YpkgP5
MKGwqhLpS9PQNCup4UYRfkpjN4LxFvUv5obKoz2Lb/iWI+iCOB3Q1I6HTi4V
9qGM0c4qbG91pAh/
"],
Association["Book" -> 1, "Theorem" -> 31] -> CompressedData["
1:eJyVUIENwzAIY1NTDCRH9KWd0Ad26z6ayVa1lbpOdQJyDAHEND8f801EXunO
0aAKNx5XdwOMoMcXBhWpVRkMwKm0IAk0DY1Ijns4qcXAr1rCfjbzDcBLc1k4
Xfs77kWMp1E2FwGzRnwmWFHK7pnBvdKTtos6whrMRtykctkQEtdSa+W2qLJQ
6rSS9KjI0IewPuMbTTcL2Q==
"],
Association["Book" -> 1, "Theorem" -> 32] -> CompressedData["
1:eJyVUIkNwkAMC6hX5xPpCqzECF2AWdmIJEhAhaDCp7PyyXnO6/WyHojoVrQD
ZRbTeqxqZp4/DS03SQaI3IGOZTEvEYAhcEKakcFjOCLEpqzAcP3aq6W12xgX
pSZp2ymsuuyP+x/m36vXpJxVsz5We2GMjVvJbaSLcmr7iL7hmaxGIiCIMBNA
JsPdy8vzCxJaxFx/I1HH4qlFpIe8A/tfDH0=
"],
Association["Book" -> 1, "Theorem" -> 33] -> CompressedData["
1:eJyVkYsNwzAIRGmV445s0ZU6QhborN0o4HxkV4raPlkIojMHzmN5PZebmb0r
fCNCDQapDpAEoTCrPKI+qDSc9wuqgryTXslEdwf80kpNvtmgtRCNLQeyvX4Y
9y+uRynIDEiV1yjoqT062M4nnlNr1I1CHVUtlu9sc0kyWtppXzo09hhtt18x
nTWwAoCTCXg=
"],
Association["Book" -> 1, "Theorem" -> 34] -> CompressedData["
1:eJyVkIENwjAMBA3q+53QJViJEboAs7IRfqugFCkCTlHkJPbn7et2v20nM3to
+8qlheBKxgBIgohmprg1XSRB9soP7pxJ18NCdwd8+pOqSkLyu4axYiDl4xe7
/zC3IsjckFkuKxhRHwOs9Ymn6zjmHRPjdVJjvTfrnoOyDgtX/1Wx5mQnSL9m
tbxtAE9x0Ql3
"],
Association["Book" -> 1, "Theorem" -> 35] -> CompressedData["
1:eJyVkQEOwjAIRdHs84HsEl7JI+wCntUb2V/n0mkW9aWh0MAH0styuy4nM7vL
fCdDcCZjACRBRJrJz9RDI8jq+cGVM+m6J7o74IeNVNUlJL9qGLsPNPn4adw/
OB5FkM2gZblGwYj2GGA/73ibOvZ5+8R4RVqsKq3UygoWrv17xVz1Kb21fX7F
tMXAA16uCW4=
"],
Association["Book" -> 1, "Theorem" -> 36] -> CompressedData["
1:eJyNkGsOAjEIhNEszCzZS3glj7AX8KzeSIYf2ppo+rWQQimP3s7H/byY2VNq
ATZJcMCBkp27GQi4k7J0hYK9misQ8m6ICPf4V6cfdPpORFRynd1Vb63ddX63
IoBSXlHdvY9ojgH0/iaqa85xs+dtabDMtNTsRrcqB4kTeRyfKjP96fqrbQh4
AV+gCXg=
"],
Association["Book" -> 1, "Theorem" -> 37] -> CompressedData["
1:eJyNkIkNwjAMRQ1q4uPbpiuwEiN0AWZlI5yKq0igfsuJnh3Fx3m5XpYDEd3G
sUcxl7kj3fMhB9xVWJTIjdnMBqucIpjBOSwiABzDNVMwwUwb7HeZ9TlQd6i7
GRwEDy1UBXJnu7vV/2ZtdFrj9V7DmX6q9w1WUpp+q6dqbiIi5W/MJ9lazci4
Z5AIBTevdTYeWweP6blIhMtfqv8sslqbBkFRAbkDa0kNMA==
"],
Association["Book" -> 1, "Theorem" -> 38] -> CompressedData["
1:eJyNkI0NwkAIhdG0BzwO4gqu5AhdwFndyHdNtNZE0+9yJA8If9flfltOIvIY
5hB5yeo9agMOlJuai3SoAujdzY15qqHF1wn9ZwZ6t5gC8Dnws0tVxmDU92Gi
QqLSM92d/qPjHqX9jWJMyvVa4xLwT1rbSQZt9m9audfOY8a/yXoprN0g0FYp
PGnpzNv5rMmrh44cpTJT/jeshyyONq1qbWBPVHYNIg==
"],
Association["Book" -> 1, "Theorem" -> 39] -> CompressedData["
1:eJyNkIsNwjAMRA1q4s/ZpiuwEiN0AWZlI5yKX5FAPcmJnh3FPp+X62U5ENFt
HPsUc7gj3fMhB9xVWJTIjdnMBqucIpjBycEZEQCO4ZopmGCmDfa7yfocqDvU
3QwOgocWqgK5e9yd6n+rNiYte72XOdNP9b7BKkrTb/VUzU1GpOKN+SRbuxkZ
9wwSoeDmtc7GY+vg4Z6LRLjipfrPImu0aRAUlZA7OWYNEg==
"],
Association["Book" -> 1, "Theorem" -> 40] -> CompressedData["
1:eJyNkIsJAkEMRFe53WTy68GWLOEasFY7cvZATwXlHiQwScjvst6u66m1dp/u
IFkRXjsGs4KKorUwETOLgEJZJ+JSkhKE8TMTEeqLm6HDfs6oSp/M/pjOy5tX
IhMA48fXPcb4m7W5Kc8bg0cY3hnjQzKpHd+MAuojokrbZT2VbdOsmYzKxpeW
dP4OXZJfd5k1QqUqtBfsZ1lcbdnUNkAfH/ANAg==
"],
Association["Book" -> 1, "Theorem" -> 41] -> CompressedData["
1:eJyVkIkNwjAMRQ1q4uPbZoauxAhdgFnZCKfiKhKo/MiJnm3Fx7xczsuBiK7j
2qtwR7rnXQ64q7AokRuzmQ1WOUUwg3OciABwDNdMwQQzbbDvJdZ0oN5QdzM4
CB5aqArkH+3uUv8ZtdFpjdd7DWf6rt43WEFp+qmeqrnxiJS9MB9kazUj455B
IhTcvNbZeGwdPKbnIhEue6r+s8hqbRoERTnkBgqrDPY=
"],
Association["Book" -> 1, "Theorem" -> 42] -> CompressedData["
1:eJyVUNsRwyAMo72AHzj2DFmpI2SBztqNKsM17U97qeBEjAQO2vb7bb+UUh5J
p2HhH7Bu5taIBYoyqaq7sLCbEXVyWskmrpZm7gu+exX72iGAPJCrjiIMbUMw
RdDvn989g/ZTVQXhea3pAZloLRklxgTXIbwMw+QqnvrhYlZENHckRVTj1Oim
Ran5WkhKUEUOUmlF0J1gAVWETMRvCHOEI6tlXCg96QlnJw11
"],
Association["Book" -> 1, "Theorem" -> 43] -> CompressedData["
1:eJyVkIENwjAMBA3q+52IJViJEboAs3Yj/C6gFClSOUWRk9ift+/r87FezGzT
dh4yBkASRDQzxa3pIgmy613BzpV0PSx0d8CnH6iqJCT/1jBWDKR8/GX3BHMr
e7+5IbNcVjCiPgZY6xdP13HMOybG56TGem/WPQdlHRau/qvilpOdIP2a1fK1
AbwA7fsJKA==
"],
Association["Book" -> 1, "Theorem" -> 44] -> CompressedData["
1:eJyVUNkNQkEIRONbjuHQEmzJEmzAWu1I9nl9qXGyGRaGDITj+XI6b4joOukP
HBLIzJgPnokYLErkJmxmgIpKAMzgYGc00n07IwS7GRbgo39lRTWyesr8VDhF
lNZeVaPiv3V/Y3xVzZp62zHsBb2jS81r4SHIsmpmT+qmMA1dex5dItYnelZa
7GyVepAqyHhkECslL+6uC0e6GbdZ8sycWd5QkZqHsh18uqEN9QYv6Q1p
"],
Association["Book" -> 1, "Theorem" -> 45] -> CompressedData["
1:eJyVUO2NQzEIS6tLwA4QdYRb6UboAjdrNyq8fkj90VbPURDBxkn4Pf//nQ+t
tUuFPQj3iCDpAN3sNKhojVQh4Q5VNTPRqSG5PAEc3Rih/MlG9sm39svTM1Ft
XAlza2VRLnCLnc/9ivGRZb009xh8Ajf0XtlWuBO6VUA+AjA8Z4JNc1epEvqs
JJmnjcqLRKRJzTGz5tJLpeS0VNTvBZ1zUvQFa8ZaOdnUTJQWV9uRDQ4=
"],
Association["Book" -> 1, "Theorem" -> 46] -> CompressedData["
1:eJyVUNsRAjEIROcSHoHkLMGWLOEasFY7csmN+qXO7SQwLBsCXLf7bTsR0SPN
Ibit69ojRpi6e6uqCtYrW0JFJcYo3Ni584gIsOcI7V3a0qAozb5WT7niAXxk
eYee1EIRAuZH2/2H+jOboxFurTlaHn0BVDY0+ZkxKTNru91FQ3VMZk4FiChW
9FaMd4SPkCbj2oNEKLjkDgpHLoFTw4hMmOUDFbG44IMlo2wF7gmYOwzA
"],
Association["Book" -> 1, "Theorem" -> 47] -> CompressedData["
1:eJyVUMENwzAIpFUcOMA4HaErdYQs0Fm7UbETReqjrXK2DgwnfPZ9fT7WCxG9
Op3DLdyrmVvUWBafIUzkOrMqWhOBtB5MgoObD/HVjWsVnUyVi+vX4Tkj12Bo
JDRAiF5DQttpu38w/+wCnVI1D0/D1o5Seq66O84tZfO48SZywEdlvCqR/wPB
ofDjlBeVAuI+gFhIUcws2yrOnGU0RmEVZvlANa8VU08N5hneeCUMkQ==
"],
Association["Book" -> 1, "Theorem" -> 48] -> CompressedData["
1:eJyVkAEOwjAIRatZB/9Dy67glTzCLuBZvZFMl7iZuGQvgaT0U365zY/7fCml
PJd0kk4aQE7Rp/ARKqU4RyExhUIREaqmXbo0d29mV4dEkIORUjv/vo0N1hN0
lIxlYPain7d7zHh4C2SyVI0fS/y6qxU/6KayCit3PYtIM3J5q4jL6U0OqlWK
AO5FNEdXs/y2Ol0kywhBldy26I4GtsYBzJ3DPCsvQC0MXQ==
"],
Association["Book" -> 2, "Theorem" -> 1] -> CompressedData["
1:eJydUO0NQjEIRGPLx+uVGVzJEd4CzupGHjXqL0300kLgrhQ479fLfhCRW5lf
kTmBifAxxtbdXWSMrlFwc0Nm002hqQmA2SPgmbadNiraiI+lS+58QI8qP6gX
DzhDIvBHu1/Rv7I1mvD2XqPV8SeYqoZWfjFhbbHxsA/RdJ8rs6YizJwreinm
K+JHpCW0A2Im0FY7aIpagpZGGYWp2htuFkh+cKqoWqG7A1wEDJc=
"],
Association["Book" -> 2, "Theorem" -> 2] -> CompressedData["
1:eJydUNsNwzAIpFVsHgZbGaErdYQs0Fm7UQ9HTb8aqT3ZILgzBm7b475diOiZ
5mesPWKEqbu3qqpE7pUtoaISYxRu7Nx5RASy1wjtXdrSoCjNvlZOueIBfGR5
h57UQhEC5v+0e4Z6yuZohFtrjpZH30AqG5r5yZiUydpud9FQHTMzpwJEFCs6
FOOI8BFoMq49SISCS+6gcOQSODWMyIRZPlARixUfLBllK3AvQdIMiw==
"],
Association["Book" -> 2, "Theorem" -> 3] -> CompressedData["
1:eJydUNsNwzAIpFVsHgZbGaErdYQs0Fm7UQ9HTb8aqT3ZILgzBm7b475diOiZ
5nf0iBGm7t6qqhK5V7aEikqMUbixc+cREcheI7R3aUuDojT7WjjligfwkeUd
elILRQiY/9XuCeopm6MRbq05Wh59A6lsaOYnY1Ima7vdRUN1zMycChBRrOhQ
jCPCR6DJuPYgEQouuYPCkUvg1DAiE2b5QEUsVnywZJStwL0AJkMMeg==
"],
Association["Book" -> 2, "Theorem" -> 4] -> CompressedData["
1:eJydkN0VwjAIhdEjBW6gdgVXcoQu4Kxu5E20+lQf+p2T8Bsg3NbHfT2JyLNf
B6haCoFEmKuKIFWj4+RaZdp01tIi9J4LVuWhDTBL7NbNrNZJEplAyyZt6CyD
Nh8bd5/pbxR90mDWBNIniA2dht3dGAKuI4r3PZKmJWIZnu2hO8+3CIMfazSK
EOd6StwlTbleNeXf2c3MGDJ1V/Mf1FEzG1y6xUG6eAHLbQwW
"],
Association["Book" -> 2, "Theorem" -> 5] -> CompressedData["
1:eJydUMsRQjEIRMcEdgOoJdiSJdiAtdqRJG/Ukx7cSUhg+V9u9+ttJyKPKf7B
OU9EhI8OQMS9K8lBGMwzmw51TU0vkHsPuNs4DBIN/Jo2IohKFPOzxULARB6r
Duh/tvsV/Sc7R5O6vVdPmAcvlGk2tOyLobXFcpObUwK5LGuqghlqRW+PfGtV
qGih9gwxSGir9aJpuI+h5eJaGk3VPoBZRmbisLRCPU/9vQxq
"],
Association["Book" -> 2, "Theorem" -> 6] -> CompressedData["
1:eJydUMsRQjEIRMcEdgNoC7ZkCa8Ba7UjSd6oJz24k5DA8r9u99t2EJHHFH8h
L0SEjw5AxL0ryUEYzDObDnVNTS+QRw+42zgNEg38mjUiiEoU87PHQsBEnqsO
6P+2+w39JztHk7q9V0+YBy+UaTa07IuhtcVyl7tTArksa6qCGWpFb498a1Wo
aKH2DDFIaKv1omm4j6Hl4loaTdU+gFlGZuK0tEI9T+JhDFk=
"],
Association["Book" -> 2, "Theorem" -> 7] -> CompressedData["
1:eJydUNsNwzAIpFVsHgZHHiErdYQs0Fm7UQ9XTb/Sj5xsENwZA9v+fOw3Inql
uYYwdfdWVZXIvbIlVFRiXQs3du68RgSy9wjtXdrSoCjNzotCrngAH1neoSe1
UISA+eV2T1D/sjka4daao+XRL5DKhmZ+MiZlsvaxU1SG6piZORUgoljRoRhH
hI9Ak3HtQSIUXHIHhSOXwKlhRCbM8oOKWAx8sGSUrcC9Ac+YDEg=
"],
Association["Book" -> 2, "Theorem" -> 8] -> CompressedData["
1:eJydkNERAyEIREnmFBYRa7iWUsI1kFrTUcBLLj9JPu6NI4I7yrJu99t2IaJH
bidR9G6tAiAyq6wJBGLuhRsbO7sFqlfrMJO2tFAU6M833R2J9zj0AKYEGxgj
qgo73+536n+L2WnYqzWt5cKbKGVHsz6DSpm3uu+7KNz4rLw0KoIY0aHwI5u/
KSlX7yQg5xKjQ+EccuOQGEemwiwfIJKjciwzCyI8Ab/yDEg=
"],
Association["Book" -> 2, "Theorem" -> 9] -> CompressedData["
1:eJylkNkNQkEIRUcjywXGrQNbsgQbsFY78o7rM1E/9CQQGLaB3eG4P8xaa6eh
fmWbtQoTs9bKRADtXUVks1yGpa11pb16D2DegzGBVKZa5ceWmcg7KJJMpvAV
QOT6j+++Rb9GI6jALOVw7jFh7DuBQZcX95IUD/OGO+W17GqNQZBm7hxKN53H
KoEHyl3NrCg6TH8i7hVRhcVozTNR+xlsMQvF
"],
Association["Book" -> 2, "Theorem" -> 10] -> CompressedData["
1:eJylUNtxwzAMU3ohRfBhuyN0pYzgBTprNwqk1P5q8tHgjpJIggBPX/v3bb+0
1n7G8W9UrNml99Z4CaDLoiLyuSzeo2+6amVVAR/lWiUQd9ee/lQxwuMAOFpR
0RhgCnhs76z7F/Rl18emIEtp7mMDHBCZOTEPwmbll/cgjsrsn4NmjFNklG2q
YBhBWjejKdDCJCOFKdKM/lg7RPkk5QT76Z6J65DmN5Frd2oJC98=
"],
Association["Book" -> 2, "Theorem" -> 11] -> CompressedData["
1:eJylkNENAjEMQwu6traTa2AEVmIEFmBWNqLt3Q8S8AH+qBrnyYlyud2vt0NK
6TGe33WKtRiQklTgrgiAiIgKQ6uthrtHa0c3rCu09BLZ/GMgKQ6JEntOMCwp
uPm2tr/WfaPytSuNnTpVNDaa4qacx28aewPT4UZsWGli42R2ChCxOxzNXk2+
D8qZqZKuVNEvkWWdqYIDA4rKDBcqXhR2jtCiHuy0caonsrsMRw==
"],
Association["Book" -> 2, "Theorem" -> 12] -> CompressedData["
1:eJylUNkRQjEIREeO5Yg12JIl2IC12pEkz+PD0R93JgGWhRBOl+v5siOi27z+
QLmYKtEIZgCZzMI1hmloyVFGVjW/r+AqNg531vSv/TIdWI0y20QATo7ECuH1
37ifkJ9Zn5P2EfEXsIF5eovwZdwWg02xyaQctZiHxs0chmdVJzta+n5IFeSi
WWRGOffYW9X1cVbtjaowjNXeYDPE6PLDjBIxzR0cLAun
"],
Association["Book" -> 2, "Theorem" -> 13] -> CompressedData["
1:eJylUNsNAkEIRHO7MAPr5kqwJUu4BqzVjmT34iXG6I8ECDATXtftfttOIvIY
7h/xaoBIsKo7ejfCWu80t6Zde0Rc3M+RaSMXJ600fm1HwJPjwAxSsztA7ob2
57ofUn+i4zRJq5U5fiheUsqIOesTycMmyt3vpBVY9+0nNUn5LsPBWI9sTlMZ
fSlqI3Bz1EKLOp6MrlDLBmpvAo8EF4NZZJyVJ0YHC8Y=
"],
Association["Book" -> 2, "Theorem" -> 14] -> CompressedData["
1:eJylkNENAjEMQwuiTeyk1xlYiRFYgFnZCPc4TkIIfnhVozSO0sjn6+1yPZRS
7jP8RYNZKUAz0sdo7p4Z1cIWndEFcOyJZfE4kUQNfp0WkZhkZGII9CzRgxJS
Yfy77sf6P1XOTXVb4w6e1DqztbAJvlZAvoJM6UTH2rN1uRO+VyTqtUr6yOSk
mSuvVsKqMuhSlsxxaajMoPkbo8smnkI9iZz2PQBQHwwQ
"],
Association["Book" -> 3, "Theorem" -> 1] -> CompressedData["
1:eJytj9ENgDAIRE/Tg67hSo7QBZzVjSwQk/pRYqIvKb2mwMHWjr0tAE4L3yAF
UNYqQlLtDNBZqdK1lq4tbdrsUWrV/cat/fEz81FinEihmzMh/XyDuxG2skXE
7tE7t3bvMoxxAX9CB/M=
"],
Association["Book" -> 3, "Theorem" -> 2] -> CompressedData["
1:eJylUAkOAkEIQ7NsKfMKv+QT9gO+1R9ZWLMeiZq4ZCBDBwrT03I5Lwczu1bY
aRFmZMQYCoxkZioLIpGslzgq6sapUie/cL1YEcUz+LnzT5t/fs3k81ybyHPb
xD17wQazTyPrzvdCHyVE93ZpPvrXirFlGgRQDg0FLOClGFwsgBcu1wjHu0hF
MrU6LXbcAC5BCps=
"],
Association["Book" -> 3, "Theorem" -> 3] -> CompressedData["
1:eJytUNsRwyAMc3uxLcgUWSkjZIHOmo0qTEPhes1PojM+Y/khWLbXuj1EZC/u
KmYRICElqAJekPEJNPBUj+vEmEX6d5SOiP4heYPcAXbKxj4es6KEx3txITCS
HlbZ+mZvNQfl7T+8tX/nORflDElcpUJT40+hcmbD0h8NdFNHvwGSFwgu
"],
Association["Book" -> 3, "Theorem" -> 4] -> CompressedData["
1:eJytUNsRwyAMc3vYFmyRlTpCFuis3ajCNDwul35FZ3zG8kOw7e/X/hCRT3U3
AMjIGaqAVxT8Ag081eOaGLNIL+foiuhfkvfIHbC/bOzjMatKeHwWFwIj6WGN
bW/2XnNQ3v/De/uY51xUCiRzlQpNjT+FxpktS08a6NJEfwGA5wgj
"],
Association["Book" -> 3, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 3, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 3, "Theorem" -> 7] -> CompressedData["
1:eJytUEEOwkAIRFM6M4uNb/BLPqEf8K3+SNhGaxPrqbO7LDBkINzmx30+mdmz
zBGYAClIkYyIxmAgj1SZs4TIzJAhXNqVaV9g3nzN3n6aOGjcD8a/bDY3Y1aN
XCZY4b4Ji9xmepGWjexiJbOR5IbSNcGa+/UyqbcBHEB9GTl+iQzd6cvmCzM9
CoU=
"],
Association["Book" -> 3, "Theorem" -> 8] -> CompressedData["
1:eJytUNsNwzAIdKpgOKiH6EodIQt01m7Ug0TpQ0o/qp4NEsfjEJfldl2m1to9
3V8AA8IIWIyhFhbKB4DciakI8zlDcRxOsXe4072Sx50/on/NUpyOVT03ofm+
iYjXgkV6/WLWnbdC4UWiGK9Sf/avFbFHpYamqhRVbaYyzgEVTuldkqdRQvTz
SDlkruvUse0BDiAKjw==
"],
Association["Book" -> 3, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKoA9hZQQBEsiMBsCArE1iMlZ0FJMvGyorbEGStIN1A
mgHGBnOoDHA7BeIciBKwz6B+wQ7wShIDwLaxgkIRTDJA/A4xG7/VYLtZkJwB
AEV2B84=
"],
Association["Book" -> 3, "Theorem" -> 10] -> CompressedData["
1:eJytUMERgCAMqx5t5nAlR2ABZ3UjaRAsd+qLHHCQtE3plo89LyJy+jEJALQA
6heDATejupJVJH+Y6mcNHcH8gZzXboX9qvQr28w78R/E5tggSXBVtU2hxTQJ
fR7o6U890A3CUKmfjmbR9G1IKcgXGukHyA==
"],
Association["Book" -> 3, "Theorem" -> 11] -> CompressedData["
1:eJytUNsNAjEMK+jSxDE3BCsxwi3ArGyEm0PHQzo+EGkbKa4TWzkv18tyaK3d
RvpXzAwFgmTGHHQdAMKOIMjApBIG7I6I98hUegX3O3+M/vVX4kpi9eFELzcn
ZlkGC8y6hayeH0TTRlhIFjWf/SuDWyUhwBvMJOreJACcquxm5u7hPkTNP5c0
hky1nVp23AHqgwpr
"],
Association["Book" -> 3, "Theorem" -> 12] -> CompressedData["
1:eJytUNsNAjEMK+hSxwkMwUqMcAswKxvh5tDxkI4PdGkbKa4TW7nMt+t8aK3d
R9ot0hX0zAw/e0KHpLAjk5nOSSWN3JzgnxGh9A5ud/4Z/eevxJXE6sOJXqxO
zKIMFhh1C1k8P4mmjWQhUdR49S+MXCsJkWg0kyjQJECequxmBsCBIWr4XtIY
MtV2atn+ANabCl4=
"],
Association["Book" -> 3, "Theorem" -> 13] -> CompressedData["
1:eJytUIENwzAIS6cSMOSJvbQT+kBv3UcztOqqSdukaU5AimXA4bqst2Vqrd0z
/Q9GwGIMs7BQHgDkLghEGGY+IcDHBie4M53J95U/on/5Tyaqejph+OFExMtg
kV63mM3zLpTIRVRtSf1ZvynieHGQKhjKoarNVCIGVNild0mewRGir0vKJnNt
p5ZtD8T+Clw=
"],
Association["Book" -> 3, "Theorem" -> 14] -> CompressedData["
1:eJytT8ERwzAIo73YgGScrtCVOkIW6KzdqNiXR9q79hXdgY0sEL5vz8d2EZHX
SCfiZjBEBCyMTgTJHrzSdV3RFgJaOn72w7MJoCca80hCMuctK3Oeu65I/fua
5iLpWevcZMaOUvwLdmB2Ye3u/VNkGQ7soj6qiemmYqWSovlpLWGRmWi1aipW
dVVztQNyHr2TWIAxmi3JN3M2Czg=
"],
Association["Book" -> 3, "Theorem" -> 15] -> CompressedData["
1:eJytkMsNAjEMRA3axOPMRFsDLVHCNkCtdITNR4IDe9p3GI0cx7/LdrtuJzO7
lxwJBkByYIJQkK1N6uzuGeQi0pv497ukUagMkhQDBCl9IA4e1/r+NijJrJ4z
4YtA76Uv/6aVj0+kpE/kIXZ4PkZtnI3ySDbcs+lwU2vqa8ARqpyI1SPLj4z8
IqYsUXWClfsAAUAKsQ==
"],
Association["Book" -> 3, "Theorem" -> 16] -> CompressedData["
1:eJytUNsNw0AIo1UINkzRlTpCFuis3ajmUlW5j+YrPunAvIx4bK/ndjOzd3+X
opIpoJChRxLAnR0sLqLp5N/uPABfa7uvMU0uxnqaHXpQ1ToWOsJ9op2cI6Oo
oEOc4JdsIdIt3KuMYSmBAJsywiMCMpLwmEforlptaXc/Nj7HiQpO
"],
Association["Book" -> 3, "Theorem" -> 17] -> CompressedData["
1:eJytT9sNwkAMS1HT2LljCFZihC7ArGxELK5VBYKvWkqsvJ3b+rivk5k95c5F
71lAR7KYZBIXUV45F8OTP4c1KeQGJGyLlD9b7fK3CkhTdS3jfBn1A+COTxwy
OTINaF99em807UU9RrqFe6ZFWIYjQIUR4WUoqhMeh0XUrlbiZq18K8MLvtgK
Tg==
"],
Association["Book" -> 3, "Theorem" -> 18] -> CompressedData["
1:eJytkMsRwzAIRInHmF2SJtKSS3ADrjUdhY8m9sU5GY1AINh50nvb1+0hIp90
N9vLw1DLnSSAKYL7k3OmSl7O5mRaS7SOoM5dvxt2+XsLpIuupXnQFGmq/uMc
gFUZpN2YlWbv1/gxj1PbeBhpwtB1MRNXhaFSM9PYiBCCaocG2AiOubL6bHwB
qMwKUQ==
"],
Association["Book" -> 3, "Theorem" -> 19] -> CompressedData["
1:eJytUMERwzAIo70QJHWKrtQRskBnzUYVl6Tn9pFX5MMyYIPwc3m/lltErL1d
DRnwopmkiHuTHpzMSPHsKRo64DpxeB2/Wut8mgVak2/Ne3sbewYgE/8YItoj
+h5/sE05JnswMqMypagKVaLAdqsqbTC5RdZQiMdXTV1yU4YPk6IKLg==
"],
Association["Book" -> 3, "Theorem" -> 20] -> CompressedData["
1:eJytUMENAjEMC+h6cZxTwwqsxAi3ALOyEUkf6CoEr7NUt4nd1Op9fz72i4i8
ik5HhKpraNdbRJC8xqYR5ouT2jb+vOmejkTujiI6heMMgIyzo65/VVZSpGut
UDiitaksce4MU6b2r+4BH7EeMlNRM0BUxa31vlUFpJBgEVBrGlGfhWUMsRHy
DQpXCqk=
"],
Association["Book" -> 3, "Theorem" -> 21] -> CompressedData["
1:eJytUMENwzAIpFUwcLbjKBt0pY6QBTprNyrYUao+0ldOMmC4E2c/ttdzuxHR
O8L1WFmqzNJkba0BuLealsXylIHEBadC52oAUYygpL3u/flqp+nvVDWCs9Lw
o8NFgBmHz91g7+xOB5GLaumd8Rp89YNRjpsvEjESM1/KQjCutZiJqojEyZFd
JfoDwD9Vp14asqcP5QgKow==
"],
Association["Book" -> 3, "Theorem" -> 22] -> CompressedData["
1:eJy1UMERwjAMC1wd2UraABuwEiN0AWZlI+ykV44HvEB3sR1bOiu5rvfbekgp
PSL8AYIZCxourTWSxzbn09nKVMgslR91ztUAoxhBk/a695dfG81fp6oRnJWH
Hx0uAiLcfW4Ge2dzOohSVWvvjNfwpR+Mut98EWAJZr5UkGgyz9UMqgDilMiu
gr6B9E/VqZfG4ukJy5UKkg==
"],
Association["Book" -> 3, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJoATg4ONg52DnZWcGAiZWdjR3IZwGy2YAYpzZ2JMAK
REDMzgBjgzlUBridAnEORAkr2HJWPACvJDEAaBEnJysDyMusDBAGMATBUhy4
rWaHESxIfADUoweN
"],
Association["Book" -> 3, "Theorem" -> 24] -> CompressedData["
1:eJy1j9ENgzAMRN0qlxdol2AlRmABZmUjnASpQSJ80Yt08UUX+zwt67y8zGzL
9BekD19GJIHeIkKKwWUU6v5SA47bak3RT8e8b1jm8YtV1wFdgU59NtFwa/VB
wyArizqbvyc/WcZeM2UDJVFoWu6v3QeD
"],
Association["Book" -> 3, "Theorem" -> 25] -> CompressedData["
1:eJy1kOsNAjEMgwsisd3rDcFKjHALMCsb4RYhFRD84j4pkds8lfN2vWyHUsqt
u33AmmuqSqKOVZBQwy9YfS3izGK4sNgGItu/t8yfUbI7ZyVfESPGQjPTT33I
0EfSe58nHgREwdCAR0drbcQzIuGz2ZJKTPXWC+UznXrmODZ5BxG9Cc0=
"],
Association["Book" -> 3, "Theorem" -> 26] -> CompressedData["
1:eJy1j9ENgCAMRKvheGpcwpUcwQWc1Y0saCIm4pceydEjR3udlnVeGjPbEv0E
RgYkgVoRoYvBZRSq/lEBztuOmqy/DvneMM/jinWsA3oClfpuouDS6oP6XpYX
dTZ/7/wkGWvNlAzkRKFouQOTxwdw
"],
Association["Book" -> 3, "Theorem" -> 27] -> CompressedData["
1:eJy1jt0NwjAMhA1q6v+kK7ASI3QBZu1GvVQgyAM8lU9KnPPZsW/r475eiGjr
17/ghRsIs2sLbU18cjMt1b62RIR3EEMTeDp5hkKqui9n7zj/dK1vqqiaDegn
pQwSpoyZo8ix9JARwXlLfyk7pjHhIwxlobDSaoVr+hwcrKX3swykeaZO/YnS
QNgB/y4LBQ==
"],
Association["Book" -> 3, "Theorem" -> 28] -> CompressedData["
1:eJy1T0EOgCAMm4aukPgJv+QT/IBv9UeOYeJMxJOWpKykbN28bss6iMhe6Tdw
IgASI6hk1mRSQXR/IIDnLa2m668jvjf0ebxitXVIPIGd+m5i4Gi1QaVAfFFj
sfdsp0rtNUM10BOl0PIAesQHXw==
"],
Association["Book" -> 3, "Theorem" -> 29] -> CompressedData["
1:eJy1UNsRwjAMC1zdWGqMe2zASozQBZiVjbDTB1/wBbqcHVvKRfZtedyXUynl
meF/qFd3b+TZje7ahomkOD8+CBoJ5sUCMBQYsfXnXzscv7JAhlCN6ScPdohw
97ky1N7ZnK5CMcQA2WGXhkgBxaGwo+rDx6xUsoiW3JNdUEM31ZqSViFBo+ob
ULWWaxqyik9apBfEngrq
"],
Association["Book" -> 3, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJoCNjZWYGAnYmdnY0dCFiAHDYgxqmeFQuAC7Lj00km
wG8g2D5WLM5ixyBh4uwwEXZ0PTgBKGRAFnFysjJA2OxgT3MAISgA2ZCtRTWW
A2YTC8J2VgBT/Ac6
"],
Association["Book" -> 3, "Theorem" -> 31] -> CompressedData["
1:eJy1TkEOwjAMK2hdXCedKo0P8CWesA/wVn5Emk7bCU4QVW7jOK7v2/OxXVJK
rw7/rNYayWtbuN6ok3qTF36U+5jwips0A5EQ706j/Trf/HUKdHDVPPJgpOiV
M4+ce8C8Rw8cogrUYBhSnvtDUY/OPxKRJO7L1I9kMytZWJwXVS2iIoTI6YHi
m1bddgqTQifwBm4ZCmE=
"],
Association["Book" -> 3, "Theorem" -> 32] -> CompressedData["
1:eJy1UMENwkAMO1BziZ0WCW6CrtQRugCzshHJqRUCAS+IIivxWefI83pd1kMp
5Zbw17qc6X5sJ7RmPjhpMvKj2t5Ukoymm02/Pq9+fQ3zgFDV55MAiCT2ZWc7
A7MdQoRNhIdqmzt2PcBIJYxUtWhuRRDWQk6AElKrujs02qj6GlB+N0REGMGc
7xsACgM=
"],
Association["Book" -> 3, "Theorem" -> 33] -> CompressedData["
1:eJy1UEESwkAIQ6csCRx66PgAv+QT+gHf6o8EnGoverKZncxCssByXe+39SQi
j6Jjsbj7+TJzWSKmcKeGfzVjj3zocAiKwQww/3u68VMFitI1PjMVk1Qt7gD+
0rZMMwuD3oETfFfoe3OJm5KNVE2M+U9RCqhWBsuFpSsSFtaF9yuqk0vFlJNl
M49MPgEdYQoZ
"],
Association["Book" -> 3, "Theorem" -> 34] -> CompressedData["
1:eJy1kEsOwjAQQwfUfOwpYlFxAK7EEXoBzsqN8ExTdQUr8OJpPlbi5L4+H+vJ
zF6BP4vu59vVl8V9ctKL87OX7CHuhWRbm5PLr8PVr1tdLshVj2BBALUGs+kj
ahmTJEJ1JmY1RMf+nK1OxnJs4ktKgTWAFI29NBnQCM3gUvOWB/dDcTNdmJRM
tqzfHi4KKA==
"],
Association["Book" -> 3, "Theorem" -> 35] -> CompressedData["
1:eJy1UNEVAjEIQ9+1EOBaV3AlR7gFnNWNTK3P80e/NB80QAppz9v1sh1E5DbC
v3Fqx4D27rlkppY1P0oB+ABPxAhkMnkEk/i1t/q1y+Ui3FkrpjNMa0QpeGHW
rOzJU1Wbo2G/RJE5bE4aZTZtNh7bVKzUCFE+mv9kK2N4qioVXaFqrvYGzgu0
CF84kjQ6hXcr4Apv
"],
Association["Book" -> 3, "Theorem" -> 36] -> CompressedData["
1:eJy1UMERAjEIROc4YCGXGmzJEq4Ba7UjYZLx7qMvZSYhwMIuue2P+34homdd
f7d+bZDeYUtECG/xEWkn8+lpvN2tW/u1tPVrNcmJPFFrCQGQZ6piPpSOnPIR
TBQ7Svq7KUEK0zGp0lnUuWWxMYloBEmQCTdtUAmECFeHQVi3E+/8JrhjgUPd
PGfbCxdpCmY=
"],
Association["Book" -> 3, "Theorem" -> 37] -> CompressedData["
1:eJy1UMENAjEMC+jaxE5yzMBKjHALMCsbkZYTug+8wGqjuHadqtftfttOIvIY
5f84JyzTsUSEtYiPxnDHgPveFKQoBvUL8tcv61/VGl5FRDtJ1Jp7one88Tqz
diC7aSXWw6UyGWGYacNaog2drEGqKlStniGuzWkwrZLZOIej2doO+Rif5FnK
YqQlvLLxBBVkCnM=
"],
Association["Book" -> 4, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoAJjAgBlGElCHClAEqe4wAs6GKMHmLCoDiOcZwOHD
AGYwE6sVXSEAiRUENQ==
"],
Association["Book" -> 4, "Theorem" -> 2] -> CompressedData["
1:eJy9UMERwjAMM3dNLNnleHQCVmKELsCsbIRcLtAPvLj6odiKbCu5rvfbejKz
R8ERccllyZwyIlvGV1lEoCJGorBXqU7g/G9f/eetlguk6js/CpK9F27FYFsx
BAZINIMzNw0/zXgzutTJepwWtUbzqgy0QHME6UFxnpkCinLfGSlT9S+YlGpa
1OgnytcJ5A==
"],
Association["Book" -> 4, "Theorem" -> 3] -> CompressedData["
1:eJy9TsERAjEIxJkjwEKKsCVLuAauVjsSkouOD3057jBLgCXsdT9u+4WI7kV/
gffusTng7PioAqAFzMcgyqxnv//aVvs6zeNJqWrlp0IXsrV8zgmUocvzKWyh
GqODIcVrfyriWeUhZiMRAUiFIOweJgwTqxgQqIi+fwJP2qoy65bpAalGCco=
"], Association["Book" -> 4, "Theorem" -> 4] -> CompressedData["
1:eJy9kNENhEAIRDERdoa1CVuyBBu4Wq+jA9fE1Q/9MfcS2CFAhuy8fpZ1EJFv
pv/gTo4kJyVvhg64v9J0rNYoXsYebo4U15ptB/WYncpoQnnFfOt0ABHntSbS
iCauWqs4UsDALMOr5EyhFqBE9LS/GlM2A/wAsz8J2Q==
"],
Association["Book" -> 4, "Theorem" -> 5] -> CompressedData["
1:eJy9kFEKwkAMRCM0zWQSUOgJvJJH6AU8qzcywVaKRb+kD7KbnQyb7F7n+20+
icijl4OYmEOQ0DO/elig4AoIWU+lX/491PizCvRM5Rpf7Tu8qE0Vn2wULkoA
sfP18xbTu9hfYmZiqplCF1ol6WoZpVtEuFUGdGz7JCOTQ19JZ4/2BJYaCbs=
"], Association["Book" -> 4, "Theorem" -> 6] -> CompressedData["
1:eJy9UMENwkAMC1LT+JwIsQIrMUIXYFY2wlFLhUDwQljKXc72w+fzcr0sBzO7
9fEvjJySpB/50SKZEPgACFtfo4XTrzPNX1WgM8k1r7l6hqDLHa94YrgxCeSb
r7+3mXaxK4kIC/cq1WAMLTU8KsVHZo7QBvTsUJJiVnHqetRRR7sDeNcJpQ==
"], Association["Book" -> 4, "Theorem" -> 7] -> CompressedData["
1:eJy9T9EJAlEMq3C9JnlTuJIj3ALO6kY2+E4ORb/EQN+jbUiT83a9bKeIuPn5
G7iQRIofGZJgaAeE2DvPf21p/boF7KlZ6zzfRWcAMvGKw0RzMoDxxnO8SXou
HYzMqEwpqkKVKNBtVWUX+usTWQchWmu0ucWSD2e4A0fuCU0=
"],
Association["Book" -> 4, "Theorem" -> 8] -> CompressedData["
1:eJy9UEEOwjAMC9La2M4Eb+BLPGEf4K38iKTbEEKCE5qluoltNVGvy/22nMzs
UXQcppDYzvoaiDcogsy7RFaddPn3Rv2nq9o0T++kNnBFa1UNYTMwFEo7Zahc
aucKQcRLScputDkIoLl7DnVaeHOFvAkz4KVzJX4iv0ZTvoyZIRBPvjMKHw==
"], Association["Book" -> 4, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoCFghgJA8CkARpLqDCDgXogSbs6gMIJ5ngPmYEisB
tpEGmQ==
"],
Association["Book" -> 4, "Theorem" -> 10] -> CompressedData["
1:eJy9UNsRwjAMM3fEsRxzwAhdiRG6ALN2o8ptmusPfHHow4li+RFN8/s1X0Rk
yfBPPB9a4/4x7d6QcAIdQopO49f76NcshzNQpcc+Yy1VDOxvVk6ki8IRpyKK
zGGHakvaXrV9XqXSnps4xLVwppYSXtnIzKJannkdYD+0tOzKNtbQ6BRWfsAJ
1A==
"],
Association["Book" -> 4, "Theorem" -> 11] -> CompressedData["
1:eJy9UEEOAjEIxEQYGLtejA/wSz5hP+Bb/ZGUrs1e9GScNJTMlIFyWx/39SAi
zx7+iqsrLx/VCMZEG5dMwqP9ehz7qmbzDPnK5gRvmGXuA1HHtZiNLFHZPzTy
zcD3Jl0cBb0RaQLDeRG6hClJqC4NEQrgFICmJ2KHrGRf2bF8WSt7AUzhCY0=
"], Association["Book" -> 4, "Theorem" -> 12] -> CompressedData["
1:eJy9UEsSQiEMqzP2kwjuPIBX8gjvAp7VG9nC02GjK8csaEloCFy3+207iMij
lv8ilJePIkAsaA3o0l/bQPt1GvuqkpUpTxlmsnhHM8s+JrIyiw5mJ4eorLHZ
70+I1aTEOYBxm4mbn7swBKYkXbU3B9TdT+Gu6enrD+UkK9hx+LIV9wRCGQmI
"], Association["Book" -> 4, "Theorem" -> 13] -> CompressedData["
1:eJy9kNENgCAMRGtiyx1M4UqO4ALO6ka24AeY6JfxJYVrruQalm1ft0lEjjh+
RslHL3fwuqVpksWbj7FXt+b5tmZ1oR6zoXUTyjuWq9MBeI3PmqhpJlm1FMkI
AQOj9awUM4magOTV0/5qDtkCcAJCjQmK
"],
Association["Book" -> 4, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoDVhZ8UhhAhRBqruFsEtZsTuLygDieQaYj0mxkh2I
WZD4AJP6BoE=
"],
Association["Book" -> 4, "Theorem" -> 15] -> CompressedData["
1:eJy9UMENAjEMCxJpazdlB1ZihFvgZmUjnCtFfOCFsCpHsaMm8nXbb9vJzO5J
fwc+O8CgoIpIImjqul4Hefn1KeWrS4pCUyVPmcCEO5/aMtqhgFykoXTBxTnU
iPZSROqOVotqhbGWMcxDSXhE0F15lOJzUVV1vKFlNOyd566vA8GG9gBIiQnf
"], Association["Book" -> 4, "Theorem" -> 16] -> CompressedData["
1:eJzNUNsRAjEIxBlhWZKzB1uyhGvAWu1ISM7M/fnjhzsZwiywPO7787FfRORV
5o9ABhf6/GQRzv7rhvZlnDKZZWuCD8zS9wmO5zqYgxxBjVpo+oeAn0UqOAuq
UYQJDLdNwoWmkYTq1kEqgNYATU3whKyMOtl16EYr7g32BwlO
"],
Association["Book" -> 5, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGBgBtZmQEU6OAugAAmjwCfg==
"],
Association["Book" -> 5, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGAjAyMgyU1cMeAACY8gJ9
"],
Association["Book" -> 5, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGBDAxDJjVwx0AAJjxAn0=
"],
Association["Book" -> 5, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGCAyg1cMbAACWOwJ7
"],
Association["Book" -> 5, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDDACbWcEk4MQgN02JAEAnPQCgQ==
"],
Association["Book" -> 5, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDjAxMDAyMA6sG3ABJjAaigAAnmQCgw==
"],
Association["Book" -> 5, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGFDAyMA64G7ACRjAaigAAmkcCfw==
"],
Association["Book" -> 5, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGFDAyMDGCSEbGAXcKKmACo6EIAKI0AoY=
"],
Association["Book" -> 5, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGORgCThxcAACWEwJ7
"],
Association["Book" -> 5, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGGDAOAjdgAYxgNBQBAJj0An4=
"],
Association["Book" -> 5, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGGjAyMjAzAgGQNdBOQQJMYDQUAQCkugKI
"],
Association["Book" -> 5, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGATbACEZDEQAAllMCfA==
"],
Association["Book" -> 5, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGAWBiYWJiYGJkHmh3IAEmRkYmBoZBEj4kAQCuhgKR
"], Association["Book" -> 5, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGATbACEZDEQAAllMCfA==
"],
Association["Book" -> 5, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGAwC6g5GJcbC4BgSArmECu2vIAQChmwKH
"],
Association["Book" -> 5, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGCWBkYmAdaDcgASYgAJID7QwyAACmRQKM
"],
Association["Book" -> 5, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGB2AC4sHjGrBbBpNzSAAAmi0Cfw==
"],
Association["Book" -> 5, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDxhMrmECo6EIAJkKAn8=
"],
Association["Book" -> 5, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGATbAAkZDEQAAmqYCgg==
"],
Association["Book" -> 5, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDWBkGmgXIAMmkGsGlYuIBACc/wKD
"],
Association["Book" -> 5, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGATbAysjIysAwFMMHAJ48Aoc=
"],
Association["Book" -> 5, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGATbAxMzMBCQH2hlkAACdfwKG
"],
Association["Book" -> 6, "Theorem" -> 1] -> CompressedData["
1:eJzNkMENQjEMQ4NEm8RNmzACKzHCX4BZ2Yi0fD43Thx4B1exrUTqdbvfthMR
Pab8ExE2iaRFuFsYWTjcAZiNX9+rX1NgSrYqDvRFWqnL2AMpKwPekqUBHbo6
e0sEKoeTYU4rWtdA4Do6idKFS++mhfuw1jiXpRQGmOWDiriP/JzzXJidls8T
yZsKeQ==
"],
Association["Book" -> 6, "Theorem" -> 2] -> CompressedData["
1:eJzNkNENwjAMRI1EEvsSx2qZgJUYoQswKxtxCaX88cUHT8pF9p1sydftfttO
IvIY8lesMbiQtpBYQvhaBICI/ut1+asLUCpTGQf2gi3qbOyGpukBb2Gow7rN
zJ5ShenRoclqWnMbBCV3FzVZS3Jvlor3VmvhMAorL0U/mCqPwuOcx0BmnN8T
+hcKqg==
"],
Association["Book" -> 6, "Theorem" -> 3] -> CompressedData["
1:eJzNTsERAjEIxBkTYInhzrMBW7KEa8Ba7UiIZvz58uHOsEl2gc11v9/2AxE9
kv4Lnris29Z8WdxPRtYd7qoK779Oq19dIEijq2JAs14IKX/0FhNShgdMiqYO
7WNojolAZSppxmssyCBlYua4s9CZizUrXIBmcTJbVBEpLB/U2OfdHUeYqKll
zhOtgAov
"],
Association["Book" -> 6, "Theorem" -> 4] -> CompressedData["
1:eJzNj90NwjAMhA2N2/gvUbIBKzFCF2BWNuIaSh+Q+sYDJ+Uk332yldv6uK8X
Inpu9mdqvfcKlQiz7o1aq16rubcevz42nzZpmpLqlchBzXpI3kIEH8FeZB6d
6sdE2FVcBrNTOavkI0GJaVS4KGKkyxJwpy4c4cKMf6sylm0sl8LyJTW8FOZi
YLH3Bcq3CoU=
"],
Association["Book" -> 6, "Theorem" -> 5] -> CompressedData["
1:eJzNTdsNAjEMC1zbS9yEqMANwEqMcAswKxuR3gOJD/74wIqsyLbs2/y4zwci
enb6N0yXCYHmTfVaGzW4udeKdrZfb5WvThqGBByJNFIFUKyQFSEFL8JmcF48
YCeRLFtI9hQzhN9Kz/DaEovxEMYxfkhcNlPJBRrLhZmtci7uRT4RLRFIPWz1
1Htfo68KWw==
"],
Association["Book" -> 6, "Theorem" -> 6] -> CompressedData["
1:eJzNjsENwjAMRQ1NXPvbIYoKA7ASI3QBZmUjnFRF6oEbB56ip+T/KM59fT7W
ExG9uv6O5Yag1eZ+tUYN1WvtyVJ+PYq/NmmaktmZyOMWA44N3YgoPIIuAySP
Dtilmnur2B2IQOWThOI0qpioaoR5jj00Vi7FNTM8JrOIFJPMtbIewfhaKu5a
7NKffAOKlApL
"],
Association["Book" -> 6, "Theorem" -> 7] -> CompressedData["
1:eJzNjskNAjEMRY00SbwyiYACaIkSpgFqpSO+M4gbtznwlThenmPft+djOxHR
K83/6aZQ78P9aoOGrlBEjEscPan+rCw4ZnBWUFXVsZKZquxCChaxSS4Lh8us
TeKDFbyakOwUIFbh9JGfBtEsYVBrTFzQQ01IW0mqVXPHNGYO4VZ7z8RX7LkW
7hJnlzDPL99+wgpW
"],
Association["Book" -> 6, "Theorem" -> 8] -> CompressedData["
1:eJzNjcsNwkAMRA2Jszv+yCyiAVqihDRArXSEdxOQOHDjwDuM5JmR57reb+uB
iB5d/hBN2qmZXaJR07CI7pz910PL12SeplnkSGTZWkRMNrCRVuow9qDyyERe
ArAJDKOzt2oV1LeTYV4jykVASUrxVJCC3Q3MarnMpfuFOYLxiUhvzG4G1+h/
n2gaCjQ=
"],
Association["Book" -> 6, "Theorem" -> 9] -> CompressedData["
1:eJzNkMsNAjEMRI1E4m9i7aYCWqKEbYBa6YghLMuNEwdGykieebKlXLbbdTsR
0f1p/6gxRixQLkl4kamqmf3Xd+rX1gzmoKod0pcQwWewF1JmZ/Y2QN2062R2
SsRUjgQlplnNa0bGtTcSpZVLRGjh1sOdsQyGqTHLRyqCT8m0s7mpqzeAD2pQ
Cjg=
"],
Association["Book" -> 6, "Theorem" -> 10] -> CompressedData["
1:eJzNjcsNAjEMRI1E4l8cK7sV0BIlbAPUSkcMYVlunDjwJI/kmZF92W7X7URE
96f8JesaA+RIwrRMVc3sv35Tv6ZmEEer2oG+gAWdxh5ImZnZW1Dqpl1nZ2+J
mMrhIMQ2o/nNyLj2IFFauEQ0LRy9uTOOQbAFs3xQkZF9DDubm7p6oPgAVOIK
Lg==
"],
Association["Book" -> 6, "Theorem" -> 11] -> CompressedData["
1:eJzNkNENAjEMQ4NEm8RpGx1iAVZihFuAWdkIU47jjy8+sFRLsZ8SqZf1dl0P
InJ/2n/q3BYqlxS+lunumePXV+rXFqAFqYpd/hIj+gy2wsrsgLcRGvDhk9ko
M7jtCUtOs5rXINA6upjLSUtrzYv20SKUy2icuqp95Gb8lEwcEfDw6AQfPLUK
Ew==
"],
Association["Book" -> 6, "Theorem" -> 12] -> CompressedData["
1:eJzNkNENAjEMQ4NE28RJG91twEqMcAswKxthynH88cUHlmop9lMi9bLdrttJ
RO5P+1PFQuWSwheZZpY5fn2kfm0BmpOqOGQvMaLPYC+0zA54G6EBGzaZnVKF
6ZGw5DSreQ2CVkcXNVlbiQgrrY9wb1xG49Rb049MlZ+SiTMc5uad4AMkLQn/
"], Association["Book" -> 6, "Theorem" -> 13] -> CompressedData["
1:eJzNjcsNAjEMRI2E1/EnjqWtgJYoYRugVjpiCMuKEycOzGEizxvHl+123U5E
dH/av2qMiFWLSsfI7N2r/Nc3lq/UDJZoLXZIX0IEn8EOGk9m9jZVdlPX2dlb
rZm2IwHENBEOMQsJc+/ESi6MbgjGEGER6Y63ivVDWA6zTDv3DE0fgX8f+DEJ
wQ==
"],
Association["Book" -> 6, "Theorem" -> 14] -> CompressedData["
1:eJzNTcENAjEMy0m0idOoQtcJWIkRbgFmZaNzenASH148cFWrsV3ntj3u2yIi
z6S/xVjXuIbwIgIg9V+vqF9ddxKYqn4CB0pJ5shzwKaCdyBRu6Onf6bMHPZS
kCan+YuLVFU0O8VMAqW1Bmc+3CmjK4ryqfaB4X0Mv8xCNBZiB9YCCaE=
"],
Association["Book" -> 6, "Theorem" -> 15] -> CompressedData["
1:eJzNjdENwjAMRI1EYp9jpZANWIkRugCzshHnFCrxwxcffVFOse9i39bHfT2J
yDPluIwRlxBeRACU/u8N9afrTgFT1XewUUoqS54Nmx18AkldHEv6e8rMYe8O
0mQ1f3GRqormTDGTQGmtwZkPd7bRFUX5VPvi6n0MP8+BaJ3yAr/oCY0=
"],
Association["Book" -> 6, "Theorem" -> 16] -> CompressedData["
1:eJzNjksOAkEIRDGRhio6nUnGC8yVPMJcwLN6I+lPTNy4cmEtCFS9AMf5uJ8X
EXn28se6cQvhRpAAItqvD5SvKZkFSRW+hSnV3g1jBT6c+SkmVhrRMJhFuRO+
HPQwp8HnIVWIAZViLoRGRMZEdU8bzaBWaeYf2mvbd177wkDkQrwAnbAJdA==
"], Association["Book" -> 6, "Theorem" -> 17] -> CompressedData["
1:eJzNTsENAjEMCxJpY6eqTuoErHQj3ALMykYkbT98ePHAj0ixLduP63leNxF5
5fln8KD4QZAA6P3X+eV7O+MgXMXduYAF1bkoiS3YZNZSLFvpRMf0bJcZYZtB
ivElPIpUITUDpJoQGp0hE80saPQKrY212gdG62PwnoEOj0C8AYYuCWE=
"],
Association["Book" -> 6, "Theorem" -> 18] -> CompressedData["
1:eJzNjdENwjAMRA1NXPtiE4UNWKkjdIHOykY4KUXio398cIqekruL/Vi3Zb0Q
0bPjr1UaNVSrFUC7+6/H82mSpikBVyKLFgOGXborrOAw3oHkkQEHVHNPFQd7
SaDycQLxGlFsVC2EeY47NE52N81cLDaziHiRzLWyfiv+RiO5mXq59ZEvs9sJ
nQ==
"],
Association["Book" -> 6, "Theorem" -> 19] -> CompressedData["
1:eJzNkMsNAjEMRB2JxJ7Jb5cOaIkStgFqpSOc7ILEgdsemINlzxvZkm/b474F
EXmO8t/q0tdaagXYezt7e/qNQhDS/1M9lcjMXdgV4+imcQCbDsh3AVIjGmbm
SJkR9nEc+jSRH1RVUaBQzOSKmHN2TBbSbTRF1FpV7UsL2rrwMhZm5O7BF5Vy
CXw=
"],
Association["Book" -> 6, "Theorem" -> 20] -> CompressedData["
1:eJzNTcENwkAMC/TSJE7KcUIMwEqM0AWYlY3IXVV48eOBpViJbTm39XFfD0T0
7PTvaO7V41Tr5Xr+dff81SnTVIAjUc3UDMAxYBuY+zaETYcOxYCdMtRdw849
pDB9K0l5DSs/iggJc4BUKIQdbiyIUBVVXUxZWhOPDzQC5gGUxcNyPCtfoeQJ
ng==
"],
Association["Book" -> 6, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 6, "Theorem" -> 22] -> CompressedData["
1:eJzNTckRwkAMMySO5WPJMqmAlighDVArHeF1mOHFjwd6yLakkW/7476fiOg5
6O9hcQlvbd22/uvq5aszT9Psfia6ZmqxgruZHmAeW96u5ZihFK3EO8Y5bYT0
SGUIphh76kV5lZUfRYQke40gFMKe3SwWAQiApmDpXTw+wKAUbG4R2jzyj74A
jHEJlQ==
"],
Association["Book" -> 6, "Theorem" -> 23] -> CompressedData["
1:eJzNjd0NAjEMg4N0bWKnP+KYgJUY4RZgVjYiLcdJPPDGA1Zlpf6s5Lrdb9tJ
RB7D/l+11Eqi9/brzfkrWeKRMXi0Mg/hpZTGNIMd2ExAvg3IjWiYnb1lRtiR
BIzfRHFIVUWBQjGTFcndA5OFjBhNkbRWVftQZ7ucuRSMk97DnmCGCVM=
"],
Association["Book" -> 6, "Theorem" -> 24] -> CompressedData["
1:eJzVUMERwjAMMzSJLTtOr3ddgJUYoQswKxvhpAVe/fFBDzmydMqdb9vjvl2I
6NnpD1DXFcA8t18Xl1MnTVNSvRIZERcz0x3YUUp/jcVhSB6e6psi1BQNI3Ok
RBTy2YQZqsv4hGKQcmlOAlo4u1dk9lbNOMqcu3Jm+QIicZRl0dQLAbOgF229
CXE=
"],
Association["Book" -> 6, "Theorem" -> 25] -> CompressedData["
1:eJzVjcEVwkAIRNHIAgOb+IwN2JIlpAFrtSPZTaInb16cA2+Y+Q9uy+O+HIjo
2cY/CDZf56jnX98t36thIOBIFEkVd8cqW8XcXA+2QntiwD4Ssg2ynVKF6Ttp
jHbA8yGzkDC7kxhdhGtUzxVRCosIXDKr7PGRRYzmGHGKCRZp8+4LU7IJTg==
"], Association["Book" -> 6, "Theorem" -> 26] -> CompressedData["
1:eJzVTcERwjAMMzSJLcdx6B0LsBIjdAFmZSOcttAXPz7oIVuWTr4tj/tyIqLn
oL/AFUDv/uva8tVJ05RUz0SViIuZ6QZsKGVs62E3JK+e6psi5ArHmtlTIgr5
XMIMNaTFxxikXLyRgC6cWzNkbm61cpQ1HqoxywGIzN37rElNYag1gi9KfAla
"], Association["Book" -> 6, "Theorem" -> 27] -> CompressedData["
1:eJzVkMEVwyAMQ90GsC1smKErdYQskFmzUQ1J21NvvUQHg6z/xHs81u253oho
H+MaUqD39u/W8jNJy5KAO1ENqpgZDumhUsZtLs5A8syA9wioQZtO5qREoPLZ
RBhuWIsX4yBwaU6i1Dm7m2b2ZrVylBkP58zylYrEp/SOBBuV6gG+ADQPCT8=
"], Association["Book" -> 6, "Theorem" -> 28] -> CompressedData["
1:eJzVjUEOwkAMAwMl2Th1BEJq73yJJ/QDvJUfsbtt4cSNC5ZiRfYouS2P+3IQ
kWezP9E8kZdfH7Xv1TBIxFGElTKSsQqrVNvWg63wniBitwphg7BT7gF/J43x
DtQnoqptIsQgV9Nk9jc001JKRCmaqSM/AisDZJx4Bphju/sCKeAJIA==
"],
Association["Book" -> 6, "Theorem" -> 29] -> CompressedData["
1:eJzVjbsRAkEMQw2H12tZe8cQkNMSJVwD1EpHeO8DERkJCjQe6Y11mx/3+SAi
z27/oit5/vXP8r0aBgGOIkyqkMQqX6XaryXYirokDuyWkG+Q71St8PpOOlMX
IEdE1cRUI8RcLqaNLWcCLEXNDLDMmgY/cnL0wIgTJ3iLiPz7AhRJCRs=
"],
Association["Book" -> 6, "Theorem" -> 30] -> CompressedData["
1:eJzVTcsNwlAMC5T0JY4jKjZgJUboAszKRuS9Fjhx44KlRPFH8XW939aDiDz6
+huQy69fzt+taRLgWK2VmsnEBt+g2q8h7IYNxYHXqlDAw0dmT5nB7a2UWazT
KpHWWh93UZdL00yyU5pp6UBzJTX4gZGByMTpTDgjqs2fAB4JFA==
"],
Association["Book" -> 6, "Theorem" -> 31] -> CompressedData["
1:eJzVTsENwkAMC1JzOTtBJ9igKzFCF2DWbtSkpfDixwcrZ8V2lNy8PB/LRUTW
ov/BGL/e2L4mUxaZTb7W3J0HcEC1ut14BX13QJ6UQ5WCJ9dQJ/rbSUpV0vMQ
YGKqQUGXu6nT6wwjg8QVpoabeXzQI/JfwzkBKTxq5QbvWQj7
"],
Association["Book" -> 6, "Theorem" -> 32] -> CompressedData["
1:eJzVjcENAjEMBA2XnL1rR0oLtEQJ1wC10hGOT4gXPz6MIitxVrO343E/LiLy
XOOPmL8W7l9/2rY18lqd+07S6xAnva8b14InVhuQ75GhIAKVgRdmhCE98BUK
5KsE2aiqoumlmMrQnnF0ZYSZmlnAus6pHh8sVkOQbfjA8EgrXuyaCQw=
"],
Association["Book" -> 6, "Theorem" -> 33] -> CompressedData["
1:eJzlTdsNgCAQOxOBewDO4EqOwALO6kYWotH7cQGb3KPXQte2b20ioqO3PyN+
qqpoAldUQN4IwVGI7C/DZCLmLsyoh9rNdKQlwkcITUxZw1IrVJUrOCcJ/X1i
h6JWisx9hTVjnLAjCHo=
"],
Association["Book" -> 7, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGFGBkHHJOpjcAAJhIAn0=
"],
Association["Book" -> 7, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGFmBiGmgXDHYAAJloAn4=
"],
Association["Book" -> 7, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGGGAaaAcMdgAAlyQCfA==
"],
Association["Book" -> 7, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHGBEB2ARoDhIClMWG2BAplHMBpuBbBedPUc5AADe
BQLH
"],
Association["Book" -> 7, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHmBkZGACIiYGIGZkBNKMQAAUBsuASSTAxIgFMCBh
lDAAcpgYUa0aagAA3vACyA==
"],
Association["Book" -> 7, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGIGACo1GAFQAAmVACfg==
"],
Association["Book" -> 7, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGJhi6Lqc1AACV/AJ7
"],
Association["Book" -> 7, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGJGBiYGRiYoRiBkYgYGAAIUYwGxkwoQuAFSPTyOYC
OUzIAoxDL4QA4bYCyw==
"],
Association["Book" -> 7, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGKmBhAWImIGBhYAQCBgYmBiCDgZEBzIUAkCyIZmFi
RAEMEMwE1YkAIGOQBRiHXggBAO5yAtg=
"],
Association["Book" -> 7, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLmBiIl4UizpqOmUQAQCe5gKE
"],
Association["Book" -> 7, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLGABIiYgYGFgBAIGBiYGIIOBkQHMhQCQLIhmYWJE
AQwQzATViQAgY5AFGIdeCAEA6hIC1A==
"],
Association["Book" -> 7, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGMmBlAgJWBkYgYGBgYgAyGBgZwFwIAMqygWhWJkYU
wADBTAxMTIwoYQAyBlmAceiFEADsTALX
"],
Association["Book" -> 7, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGMGDGKohVlEjNwwAAAKCmAoY=
"],
Association["Book" -> 7, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGG2BmJlIdbZ0xYAAAnWcCgw==
"],
Association["Book" -> 7, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNGACAjYGRiAAshmADAZGBjAXAoCyrCCalYkRBTBA
MBNQPyNKGICMQRZgHHohBADnBgLS
"],
Association["Book" -> 7, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNmBhYmJjYAECIJOBgZkZiICAhQVMMbOxsbGCaFYo
HwYgqphZGJiYgBwkAOQwIQugyg4JAABadQNP
"],
Association["Book" -> 7, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGOGBiYmJgAQIGBiBiZgYiZmZGFhZmGGACC7AyowAG
CMUCppFNA3KYwAKMYMSAKjskAABE6gM6
"],
Association["Book" -> 7, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGOmBmYmAGAiADiFgYWJiYWIBcFhDBzAQEIJqRkRkF
gHSAlEF1IhnGwMDEhMRnYaGzbygHADl2Ay4=
"],
Association["Book" -> 7, "Theorem" -> 21] -> CompressedData["
1:eJzVy9ENACEIA9DSFPdwJUdwgZv1Njrqj94IvhBCQ9rnM2YAeL2uR6gAHkGk
MrVkoY8I/bjhB1pzc6tAnlm4zQdqfQNk
"],
Association["Book" -> 7, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGAWAEAgYGJhCDgRHChQAmJiZWEM3KxIgCGCCYiYGJ
iRElDEDGMKKYTGevUA4A2CACxA==
"],
Association["Book" -> 7, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 24] -> CompressedData["
1:eJzdj8EVgDAIQ1NaknYMV3KELuCsbtTCybsH3/MDCeHGMa9zFgB3yB8YYwAC
SLBWuuR7JJLp1aio3pUgbuFmWx7sYB5LyUZrn/zzhgXesgPj
"],
Association["Book" -> 7, "Theorem" -> 25] -> CompressedData["
1:eJzdj9EJgEAMQ3NtmuoYruQIt4CzutFdBcF/PwRfQ1tCKHTrx94bgLPaL1gX
IAEJclcEp8iQVJNuYtUNyiMTZpnPO8S0ammXZu6Td94wAIljA4U=
"],
Association["Book" -> 7, "Theorem" -> 26] -> CompressedData["
1:eJzdj+EJgFAIhO/pebZGKzXCW6BZ2ygNgv73I+jzUDkOwXXu2xwAjm7/YAES
kCB3RbBEhqSedBO7btAemTDLfJ4hyuplXKrcJ9+84QSAAAN8
"],
Association["Book" -> 7, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGDWBnYGBjY2BjZmZjZWdnBWJ2djY2NjDNzMTGDoIc
HOxgwAASA9FMTEAC1QwmVhCDEYwYWFgGxCuUAADCiQPI
"],
Association["Book" -> 7, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGE2BjY2BjZmZjZWUBIhYWVjY2NhDNwszExgKCMMAA
EmNh4WRgYmJnRzaAhQEoBGIwghFQ3YD4gxIAAHIpA28=
"],
Association["Book" -> 7, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGESDPO8MsEACWtgJ8
"],
Association["Book" -> 7, "Theorem" -> 32] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGPBhmgQAAlbECew==
"],
Association["Book" -> 7, "Theorem" -> 33] -> CompressedData["
1:eJzdyYENgDAMA7Aky7a+wUucsAe4lY/oJiHBCWC1UaNu49gHAZwzfiUQpYTk
1myLZO2JDIe7b8gtdoWV5SGLNA+uwfv7CRdjZQNf
"],
Association["Book" -> 7, "Theorem" -> 34] -> CompressedData["
1:eJzdj7ENgFAQQuEO9N8YruQILuCsbqRfY2JvYeILoYBQMC3rvBDA1u1nVGZF
usp2kvRwQDY3j75BL6WEIuK5FnAFPAXpkxNv2AFslwNp
"],
Association["Book" -> 7, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 36] -> CompressedData["
1:eJzdj8ENgDAUQuF/0HYMV3KELuCsblSrMfHuwcQXwgHCgaVtayOAfdjfyKyR
rtV2kvR0QBYXz77BKKWEIuI5FnAFPAXpkw9v6GOOA2A=
"],
Association["Book" -> 7, "Theorem" -> 37] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHWCmqrIhBwCaZwKA
"],
Association["Book" -> 7, "Theorem" -> 38] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGKmAeaAfQCAAAl2oCfQ==
"],
Association["Book" -> 7, "Theorem" -> 39] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGIWBiZeXkZGVlZWFkZGQFAUZGDlYOVnZWGGAAYmYW
FmYGFiYmJmSdLEDNYAFGMGJgYRkQD1ACAFPWA1A=
"],
Association["Book" -> 8, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGI2BlAQNWIGADMRgZWVAAAxAzQ2kWZI1ADhMTMp+F
YagBADvWAzY=
"],
Association["Book" -> 8, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGJeBkY+Pk5ORmAwIOIGBmYmVnZWdhB7HZgYABiJnZ
2VkYWIAAWR87AwMTK4jBCARAClV2SAAAnxIDpQ==
"],
Association["Book" -> 8, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGJ2Bj5+Hh4mFkZGTlAQJGRhYOFg5WDi4ODk4OIGAA
YmZ2diYGFhYmJmRt7AwMTOwgBlAnKHBYWAbE9ZQAAKLzA6o=
"],
Association["Book" -> 8, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGKeBkY2NjYmRkZAXSbIyMHKwcrOxANisYMAAxMwsL
MwMLExMTsi4WBgaIACMYMbCwDIjjKQEARbsDQg==
"],
Association["Book" -> 8, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGK2BjY2VmZGRkZQMCRkZ2NiAEsllZgYgVLMnCwsTA
wsKIEgYsDAxMTCAGUCdIgoVlQNxOCQAAQCsDPQ==
"],
Association["Book" -> 8, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLeDjYWNkZGTlBQJGRhYOEOTi4ODkAAIGIGZmZ2dh
YAECZD3sDAxM7CAGUCcocFBlhwQAAJCEA5g=
"],
Association["Book" -> 8, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGL+BhY2RkZOUFAkZGFg4Q5OLg4OQAAgYgZmZnZ2Fg
AQJkLewMDEzsIAZQJyhwUGWHBAAAgwIDig==
"],
Association["Book" -> 8, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGMWBjZGRk5QUCRkYWLiDk5ODg4uEAAgYgi5mdnYWB
BQiQdbAzMDCxgxhAnaDAQZUdEgAAf3kDhw==
"],
Association["Book" -> 8, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGM2ADAg4gYGZiZWdlZ2EHsdmBgAGImdnZWRhYgABZ
AzsDAxMriMEIBEAKVXZIAABl+QNq
"],
Association["Book" -> 8, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNWBnZ2UGAlYWZhTAAKFYGJiYgBwkAOQwMSHzmRmG
GgAAA+IC+Q==
"],
Association["Book" -> 8, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGN2BnZQYCVhZmFMAAoVgYmJiAHCQA5DAxIfOZGYYa
AAD9LgLy
"],
Association["Book" -> 8, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGOWBlBgJWFmYUwAChWBiYmIAcJADkMDEh85kZhhoA
APaQAus=
"],
Association["Book" -> 8, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGO2AEAlYmRhTAAMFMDExACRTFDAxMjCia6exaygEA
urYCpg==
"],
Association["Book" -> 8, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGPeAV4GVkZOEAQS4ODk4OIGAAYmYgYmBhYWJCVsvB
wMDEDmIwAgGQYmEZECdTAgBfIQNk
"],
Association["Book" -> 8, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGP+AXYGRk4QBBLi4OTg4gYABiZnZ2ZgYWFiYmZKXs
DAxM7CAGIxAAKRaWAXExJQAAVC0DWA==
"],
Association["Book" -> 8, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAOBlZGThAEEuDg5ODiBgAGJmIGJgYWFiQlbJwcDA
xA5iMAIBkGJhGRAHUwIARB4DRw==
"],
Association["Book" -> 8, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAmBkZOEAQS4uDk4OIGAAYmZ2dmYGFhYmJmSF7AwM
TOwQHYygwGFhGRD3UgIAN2sDOQ==
"],
Association["Book" -> 8, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGBGBiRAEMEMzEwASUQFbHCFKKzB96IQQAsmACnQ==
"], Association["Book" -> 8, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGBmBGAVAuCwMTE5CDrIwBKISijc7upBwAAN5lAtE=
"], Association["Book" -> 8, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGCGDhYuFkgQEGIGZmYWFiYGFiRAkDFgYGJiYQgxGM
gOoGxLGUAAD1qgLs
"],
Association["Book" -> 8, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGCmDhY+Hm5ODh4eLk5GTg5eJk5uFhZmBhYWJCVsTD
wMDEBWIwAgFIE8uAuJUSAABP2QNX
"],
Association["Book" -> 8, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGDGDhZIEBBiBmZmFhYmBhYkQJAxYGBiYmEIMRjIDq
BsSplAAA6PYC3g==
"],
Association["Book" -> 8, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGDmDh5uTg4eHi5ORk4OXiZObhYWZgYWFiQlbCw8DA
xAViMAIBSAvLgLiUEgAAP5cDRQ==
"],
Association["Book" -> 8, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGEGBhZYEABiBmZmFhYmBhYkQJAxYGBiYmEIMRjIDq
BsShlAAA3igC0g==
"],
Association["Book" -> 8, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGEuDg4OHh5OLiYuDj5GLm5WVmYGFhYkJWwMvAwMQD
YjACAZBiYRkQd1ICADfGAz0=
"],
Association["Book" -> 8, "Theorem" -> 26] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGFODg4OAEYgZOTg5mTk4mBhYWJiZkeU4GBiZ2EIMR
CIAUC8uAOJMSAAAQHQMO
"],
Association["Book" -> 8, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGFuDk5AACBiBm5uBgYmBhYUQJAw4GBiZ2EIORESzB
wjIgrqQEAAAEIgMA
"],
Association["Book" -> 9, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGGODjAAIGTg4OZi4uFgYWIECW5WJgYOIEMRiBAEih
yg4JAAAOWwMN
"],
Association["Book" -> 9, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGGuAAAgZODg5mTk4WBhYgQJbkZGBg4gQxGIEASKHK
DgkAAP+OAvw=
"],
Association["Book" -> 9, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGHODh4Wbg4uVh5uZmYmBhYUQJA24GBiYOEIORESzB
wjIgTqQEAAAIPQMG
"],
Association["Book" -> 9, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGHhDgY+Dj4WHm5WViYGFhRAkDXgYGJh4Qg5ERLMHC
MiAupAQAAA5GAw4=
"],
Association["Book" -> 9, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGIOBj4OPhYeblZWJgYWFECQNeBgYmHhCDkREswcIy
IA6kBAAAAGYC/g==
"],
Association["Book" -> 9, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGJODi4WHm4GBiYGFhRAkDDgYGJg4Qg5ERLMHCMiDO
owQAAOGpAtk=
"],
Association["Book" -> 9, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGJuDiZObjZ2ZgYWFiQhbmZ2Bg4gUxGIEASLGwDIjr
KAEA60YC5g==
"],
Association["Book" -> 9, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGKOBh5uJiYmBhYUQJAy4GBiZ2EIORESzBwjIgjqME
AADTBALI
"],
Association["Book" -> 9, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGKmDmZWdiYGFhRAkDdgYGJnYQg5ERLMHCMiBuowQA
AMaSArk=
"],
Association["Book" -> 9, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGLhBgZmBhYWJCEWJgYOIDMRiBAEixsAyIyygBAM8v
AsU=
"],
Association["Book" -> 9, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGMGBmYGFhYkIOBCEGBiY+EIMRCIAUC8vAuIwCAADE
JAK4
"],
Association["Book" -> 9, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGNGBiYmdH5rOAhEAMRjBiYGEZEGdRAgCwogKe
"],
Association["Book" -> 9, "Theorem" -> 15] -> CompressedData["
1:eJzlkIENwzAIBEllAjzEO3SljJAFOms3CthKInWFnjDPA5Ylv4/PfixE9K30
1zAvv3/wuit3as2IkLibWZ3JKsMn2fSh65j6zHOrV1TnvogRF/1yyNdSSEVi
I1UKYQRYOCzMWERyJKzKog9ZY+uAtXIwlJzbDAij
"],
Association["Book" -> 9, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGNmBjYUHmAjlMTMh8FoahBgCr8AKY
"],
Association["Book" -> 9, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGOGBhQeExMDAx4ZQdEgAApwQCkg==
"],
Association["Book" -> 9, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGOuBE5rAwMDAxgRiMYMTAwjIgbqIEAACpQQKV
"],
Association["Book" -> 9, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARJgYWBgYgIxGMGIgYVlgB1EOgAAofECjA==
"],
Association["Book" -> 9, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQMjI4RkHA7hAQCZkQKA
"],
Association["Book" -> 9, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARQMk8AAAJWpAns=
"],
Association["Book" -> 9, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQwwMTENtBOoAACZgAKA
"],
Association["Book" -> 9, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQgwMg6XsAAAlz0CfQ==
"],
Association["Book" -> 9, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARgwDpewAACWcwJ8
"],
Association["Book" -> 9, "Theorem" -> 26] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQQMl7AAAJWqAns=
"],
Association["Book" -> 9, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARwwMQ20C6gAAJf0An4=
"],
Association["Book" -> 9, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQIwD7QDqAAAly4CfQ==
"],
Association["Book" -> 9, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 32] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGASpg4gORjEAApFhYBtg1pAMAqUoClg==
"],
Association["Book" -> 9, "Theorem" -> 33] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 34] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARpgRmIzMQ2YM8gFAJnpAoE=
"],
Association["Book" -> 9, "Theorem" -> 36] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGATbACARAioVloB1CMgAAnVgChg==
"],
Association["Book" -> 10, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGASZgHMIBAwCWWQJ8
"],
Association["Book" -> 10, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARbANNAOIB8AAJZYAnw=
"],
Association["Book" -> 10, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQ7ANtAOIA8AAJksAoA=
"],
Association["Book" -> 10, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAXbAzsLAwDrQjiADAACgSgKK
"],
Association["Book" -> 10, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQ7AwsDAOtBuIAMAAJtCAoM=
"],
Association["Book" -> 10, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 9] -> CompressedData["
1:eJztjcENAjEMBH0Ske1dx748EG9aooRrgFrpiASQeNEB81jJs1r5etxvxyYi
jxV/fnI+bVuJmAEITqrG2PfMVOXMpXLKulS5LwO+fS4UlZhHJbNeuFfGx3CV
6WtCzGeqKtpaQEwltBH0pogwUzPrbk3HUMYXi4AzUKeewc4gOp5sEQo6
"],
Association["Book" -> 10, "Theorem" -> 10] -> CompressedData["
1:eJztjssNAlEIRZlkXvhcHszbuLclS5gGrNWOBDVxZQeexU04QOB63m/nRkSP
jj+/2bctiUTM4Cgy1zqOiGBGZasomZdM1TaGt5/RQ5ZhVWQg8oVqhn8Muhna
K7C6xczEY7iRMDkPGHSwuYuwiEyVwWsx/Iu4m8It9xmOWT/a1Cdc2goj
"],
Association["Book" -> 10, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAT7AM9AOIBkAAJ06AoY=
"],
Association["Book" -> 10, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 14] -> CompressedData["
1:eJztjesNAkEIhDGRGxjYvcQObMkSrgFrtSPZXR8/bcAvYQLDBK7H/XacROQx
5M8vto0MrvKF6ug4DC5sOk6+pUJBD5+ZV8qMbh+nljXNVX0BIFDNFIVcoK1l
KrKnGcysuwH7jsgvPrV3nls0j+rq7hOxRAjb
"],
Association["Book" -> 10, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 17] -> CompressedData["
1:eJztjdsNAkEIRdnEXeZygdiCLVnCNmCtdiTDRP20AU8Iz5NwOx/3cxOR50x/
fnJ1D5Ag3rjPnuwlaRXRV668pASyN2y1JAMCH6Putsx6YmZiemSIQkJ3d8eu
UZ+oU9GabKiOLxgjIzNx6amo8gLS+wjR
"],
Association["Book" -> 10, "Theorem" -> 18] -> CompressedData["
1:eJztjdsNAkEIRdnEXeZygR5syRK2ga3VjmSYqJ824AnheRLu5/U4NxF5zvTn
N+4BEsQb99mTvSStIvrKlZeUQPaGrZZkQOBj1N2WWT/MTEyPDFFI6O7u2DXq
E3UqWpMN1fEFY2RkJm49FVVeyCsIwQ==
"],
Association["Book" -> 10, "Theorem" -> 19] -> CompressedData["
1:eJztjcsNAzEIRIkUGwZjLGsrSEspYRvYWrej4I+UawrIOyAz84Rf5/U+H0R0
j/HnB46mCyxyHq8Z7ELS7JaxtOwKx3S2JaKQnWCUsQ2O+CJSUs5eSUCNk5kh
cXUrhUOpHJsps3yBSG/euz7nQZQa4wOv0Qi0
"],
Association["Book" -> 10, "Theorem" -> 20] -> CompressedData["
1:eJztjcsNAzEIRIkUGwZjLEvbQFpKCdvA1rodBX+kXFNA3gGZmSf8Oq/3+SCi
e4w/v9B0gUXO4zWDXUia3TKWll3hmM62RBSyE4wytsERP0RKytkrCahxMjMk
rm6lcCiVYzNlli8Q6c171+c8iFJjfACjbAii
"],
Association["Book" -> 10, "Theorem" -> 21] -> CompressedData["
1:eJztjesNgDAIhDGx5VFLdQRXcoQu4KxuJLQ+/jqAH8klx11grftWBwA4XH4+
IR3uxOhq1qZDoQV3oZVUWD1/WkTCdG3YQ3PO3B+AYNQMxLBgyHnigFmnlNAq
JgFFEOmFiUrRUmRsBzm5nJV3CIE=
"],
Association["Book" -> 10, "Theorem" -> 22] -> CompressedData["
1:eJztjO0JgjEQgytY7jN922sXcCVHeBdwVjfyioJ/HcAHLhxJyO183M9LKeW5
5c9vRMzVmjs2ZjN1zbmwGnAALNvpEaljfEoNhhUNC29YsoyZTmDsEII+xrDc
F6FCtaoWogKqaiqV1D0DZoZwpd7J/Au7K/KOK1p+5iqQF2ieClw=
"],
Association["Book" -> 10, "Theorem" -> 23] -> CompressedData["
1:eJztjLsNAkEMRBcJy5/12LvcBaS0RAnXALXSEV4ISCmAJ2uCNyPfjsf9OLXW
niv+/Mh1zAgzLMxm5Swwwr1OdZmxbZVx+YwQa7QHJvyNapTbyuyYq4RizMys
98zcmMisEbfOJGZKbO4iLCKuQpzJ3b+IOyIgeUaH9aoU+gJJdAoi
"],
Association["Book" -> 10, "Theorem" -> 24] -> CompressedData["
1:eJztjMsNAjEMRIOE5U88drK7DdASJWwD1EpHOHDgSgE8WXN4M/LtfNzPS2vt
ueLPr4wZYYaF2aycBUa416kuM/a9MrbPCLFGR2DC36hGub3MgblKKMbMzPrO
zI2JzBpx60xipsTmLsIi4irEmdz9i7gjApJXdFivSqEvOcwKCg==
"],
Association["Book" -> 10, "Theorem" -> 25] -> CompressedData["
1:eJztjN0NAkEIhNdEwj97CxVcS5ZwDVirHcn64qsFOCFfyMDMeT0f122M8dr4
62dVhKqIi6tWsypLsr0elu1kZnMdDe+ncPXK8Op9iyXcOhaevvZxR9Za1uXM
OBDAbACORCAVBrQwIiQiYwKcE9W+4g/jmPeuElUTdn4DLR4KAQ==
"],
Association["Book" -> 10, "Theorem" -> 26] -> CompressedData["
1:eJztjMsNAjEMRINE5PFnrIQlKzjSEiVsA9RKR2S1F44UwDvY1huNH9vruZ1K
Ke99/PkdMxy4D4C3Me5cM9MyVXfTloXkpc+TnB6JsSRXHjUNw3Q0EL6HDLTe
+3X+FtECkWCBFmq1MJUaGu5VVSla5674QoCWvXU/U81dPYz2Afe/CWA=
"],
Association["Book" -> 10, "Theorem" -> 27] -> CompressedData["
1:eJztjTEOwlAMQz8SX2nyEzulrcTKlThCL8BZuREpCzN73xAlsWU/9tdzv7TW
3sc4+YN7OEDFGFkzk6nc5gMz1icQVCKhQJk2DmSsTHw9s9pCq4CVYB5iXcEl
rKJFpEnvZq1ru0mPcO9i7tOkBVRFq2L4jxLrrKYrHLWHD+oHP4EKRg==
"],
Association["Book" -> 10, "Theorem" -> 28] -> CompressedData["
1:eJztjUESAkEIA8cqp1gYSNjV8e6XfMJ+wLf6I1kvnr3bhxSQFLnvz8d+aq29
DvnzC+ERVIyRpZlM5VwPzFiXQLlEQoEK3TiQMZn4ZFa1Kw3gJJiHWVvwElaf
RaRJ72ata9ukR7h3Mfdl0QKqolUx/EuZtVbTGY6awwf1DTDxCjE=
"],
Association["Book" -> 10, "Theorem" -> 29] -> CompressedData["
1:eJztjLERAkEMA80MHvtsWf9D8DktUcI3QK10hI8LiMnZQMHK1v18Ps6LiLxm
/PmJY99JqmZnNswgi4wxTeXynGhX3X9yEREMog24dMyXjB42MzFVQNTkZloF
qIFwN3fncLNts8SXAQTQu9e+7aIYFW/gBQly
"],
Association["Book" -> 10, "Theorem" -> 30] -> CompressedData["
1:eJztjLENAlEMQ4NE5FziWCc2YCVGuAWYlY3I5wpqel7h4jnx/Xg+jouZvVb8
+Y19l+RekzWoUmopsUzX6bXwqab/5ElmKsUx1KlzvVTOLgCDO2kOu8G7SQfF
CESEtgAkFL9sZCZn9zq3U7Sy8w3QtglW
"],
Association["Book" -> 10, "Theorem" -> 31] -> CompressedData["
1:eJztjDEOQjEMQ4tEiJrGTtWRjStxhH8BzsqNcGFgZucpciLHye143I9Ta+25
5c+PXFmMmNIpatZaquglBwXp2OMnFOrk5Hqzna4QCQ5qqUJVpd6aeXMzoGlY
bshMczAvFxfsW+gjv0Qm+tD9mQNaAIF4ARq0CfI=
"],
Association["Book" -> 10, "Theorem" -> 32] -> CompressedData["
1:eJztjMENQjEMQ4tEftQ0dqpuwEqM8BdgVjbChQNn7jxFTuQ4uZ2P+3lprT23
/PkVFiOmdIqatZYqeslBQTr2+AmFOjm53mynK0SCg1qqUFWpr2be3AxoGpYb
MtMczONwwb6FPvJLZKIP3V85oAUQiBcKjgnY
"],
Association["Book" -> 10, "Theorem" -> 33] -> CompressedData["
1:eJztjEsOwjAMRI2EXcefpkosUthxJY7QC3BWboSzYt09bzHyaJ78PN6v4wIA
nxl/TtOHSH30qEmGe7gL1qFhbiPCbPSIntJdYnMfNYUJs+9l3ruHzfHGKW9W
8ikiAhKVAqjQFnSzmlWMiJhZlBcyI7Uf2bWUdV2vIhqa9Na+MjQKMQ==
"],
Association["Book" -> 10, "Theorem" -> 34] -> CompressedData["
1:eJztzLENQkEMA9BDIrnLJXEC5EsIKlZihL8As7IRHxpqel5hybLk2/q4r7vW
2vMdf79biBLXyrQ8WwAGDElcygNxLou81nKiqZiVoZGFjzEAKaQGyt5jjHJP
t+2TiBoxizTSduzkZrHVaczcexftwu6s9sVmQ8Qc+zknVHQeEC8N1AnN
"],
Association["Book" -> 10, "Theorem" -> 35] -> CompressedData["
1:eJztzTEOwkAMBMBDwo59Xm9OBHFp+RJPyAd4Kz/ikoaeOlOs5LVkP7f3a7uU
Uj57nP4gAi4dw4I5855pDkZnm/e+jeiL1GBd0YLoeXAjfeVo2op9SXskGnCc
lCKq7kWi3CZJYB5jhaqaWQ2bNFMDPwqEO5nXOl6FRzTyC+x2CZw=
"],
Association["Book" -> 10, "Theorem" -> 36] -> CompressedData["
1:eJztjNENw0AIQ4lUZMxx1SkbdKWMkAU6azcKXNXmP995EjYGya/9ve2LiHxK
bq6wNpItYZvWvNcl96kl7IMc8/LNpHsO/4xfimxMEwOii5kE1MMVGgxSAeQL
aqawk9y9P7P0UcnpZQdL/AfT
"],
Association["Book" -> 10, "Theorem" -> 37] -> CompressedData["
1:eJztjNENw0AIQ4lUZMxx0a2QlTpCFsis3ahwUZv/fOdJ2Bgkb/vx3hcR+ZQ8
3KKRbAnbtOa9LrlPLeE6yDEvZybdc/hn/FJkYZoYEF3MJKAertBgkAogX1Az
hV3k7n3N0lclp5d9AUGeB8I=
"],
Association["Book" -> 10, "Theorem" -> 38] -> CompressedData["
1:eJztjEsOwjAMRINE5PFnHKWlgS1X4gi9AGflRqSsWLPmLcajN5Lv+/Oxn0op
ryP+/AbAcR2DW2ZaptptmmVdSS59VnJ6JLY1OYgPGobpaCD8GBlYeu+X+U9E
C0SCBVpCq4Wp1NBwr6pK0TpvxRcCtOyt+Zlq7uphtDev8wjp
"],
Association["Book" -> 10, "Theorem" -> 39] -> CompressedData["
1:eJztzE0OwkAIBeAxEcrwMzQz1LbuvJJH6AU8qzeSrty79lsQXnjhcbyex6WU
8j7H349GeBruZmHG4HcJNV1HqO4jYjD7zststnoWTkS21SWXzRY9jzfK8qw1
3wFAAcRaC0jpE5iqZ2RFRCJioQlVUfQrs9TaWrsyS0gavX8A9vYJ0Q==
"],
Association["Book" -> 10, "Theorem" -> 40] -> CompressedData["
1:eJztzMEJQkEMBNAVTHazSSZRI3wED7ZkCb8Ba7Ujv168e/YdBoaBua2P+7pr
rT3f8feryrRcLAADhiQu5YFYyiKvdT7RVMzK0MjCxxiAFFIDZe8xRrmn2/ZG
RI2YRRppO3Zys9jqNGbuvYt2YXdW+2KzIWKO/ZwTKjoPiBfaFwl3
"],
Association["Book" -> 10, "Theorem" -> 41] -> CompressedData["
1:eJztzEEOQjEIBFBMpC0w0GoT3XwXXskj/At4Vm8kdeXatS+EZCCZ+/587Aci
eq319zOkie4+3ZvAsMXoMTcMxe0ym2poYFjg2j9EPCwir3ru6xkCx4BlGTMT
l6JKLCTMrTFW5FpzqlktrGD5ksHllJVHiJpJNI94A6VYCNQ=
"],
Association["Book" -> 10, "Theorem" -> 42] -> CompressedData["
1:eJztjDEOwkAQAw+J09m7602OJCBKvsQT8gHeyo84qKipmcK2bMm3/XHfD6WU
51v+/M62XnXJTMskN0Dzskg69RGl0SOxLamz8IFhGJ0Mgr9HBebe+zq+WmNB
a6EClmC1MLYaDPdKUo11eMUXDZiyT92PornTw2QvjvAIsQ==
"],
Association["Book" -> 10, "Theorem" -> 43] -> CompressedData["
1:eJztjMsNwkAQQxeJ1Xg+nmSzJIgjLVFCGqBWOmLDiTtX3sG2bMn3/fnYT6WU
1yF/fmC98ZqZlqm2AZx7J7m0EcnRI7H25EZ80DCMjgbCj5GBubV2GVciWiAS
LNASWi1MpYaGe1VVitbhFV8IMGWbmp+p5q4eRnsDhG4Inw==
"],
Association["Book" -> 10, "Theorem" -> 44] -> CompressedData["
1:eJztjLsNwzAQQxUgwvE+PEGWod4rZQQvkFmzUeRU6dPmFSRBAjzO5+O8lVJe
l/z5hcmZmZapNgFuY5Dc+ork6pHYR3ISHzQMq6OB8GtkYOu97+tJRAtEggVa
QquFqdTQcK+qStG6vOILAVr21vxONXf1MNobdzMIhw==
"],
Association["Book" -> 10, "Theorem" -> 45] -> CompressedData["
1:eJztjDsOAjEQQ4NEFHtmPErYT8+VOMJegLNyI7JU9LS8wrZsyffj+TgupZTX
KX9+QntmWia5AerLIuk2ZpRmj8S2pHbhA8MwOxkEP0cF+hhjnUetsaC1UAGL
WC2MrQbDvZJUY51e8UUDeo4+/CqaOz1M9gZo2ghx
"],
Association["Book" -> 10, "Theorem" -> 46] -> CompressedData["
1:eJztjDsOwkAMRI2EN/7OJspSpeJKHCEX4KzcCC8VPS2vGM/TSL6fz8d5IaLX
jD+/sXVgB0TD15HoOEZ0P8ZtFwuYlWAd9kHU4HWjAnOEWuaao/4wM3FrZsRB
yizCPpWXpbq4SWML1i9KUrdMv4aau7ok8AZvTwhm
"],
Association["Book" -> 10, "Theorem" -> 47] -> CompressedData["
1:eJztjLsNAkEQQxeJ1Xg+nrth4XJaooRrgFrpiD0iclJeYFu25Pv+fOyn1trr
kD8/kpmWqbYBXMcgeakZydkjcRvJjfigYZgdDYQfIwNrVV3njYg2iAQbtIV2
C1PpoeHeVZWifXrHFwIsWUv5mWru6mG0N1XQCE0=
"],
Association["Book" -> 10, "Theorem" -> 48] -> CompressedData["
1:eJztzLsVwkAMRFFxDkIafRevG6AlSnAD1EpH2BBQACk3eMEEc9se9+1ERM8j
f79ap6/TrKGVlY2uoVpVZg7DyLVHfSAcQFbsux3pQPaS2F+YhUQkghi0gOEs
wuGsynhjNmPB10V15HXOPDci3SKt/AVPiAhK
"],
Association["Book" -> 10, "Theorem" -> 49] -> CompressedData["
1:eJztjDsOAkEMQ4PEaOL8Fle7LVfiCHsBzsqNyFDR0/IiWbEc534+H+dFRF5L
/vzMzmOHE6iNrCpSUQtHgbwVa/sAN/SYt+oK+6IrjH4CqNgYkWKQnCMs0BZh
NtDMdr3qF1M1nEG7JjQdHp72BmMTCGE=
"],
Association["Book" -> 10, "Theorem" -> 50] -> CompressedData["
1:eJztjDsOAkEMQ4PEaOL8FlfQciWOsBfYs+6NyFDR0/IiWbEc57kfr/0iIueS
P7/D+wNOoDayqkhFLRwF8las7QPc0GPeqivsi64w+gegYmNEikFyjrBAW4TZ
QDPb9apfTNVwBu2a0HR4eNobVmcISg==
"],
Association["Book" -> 10, "Theorem" -> 51] -> CompressedData["
1:eJztjMENw1AIQ6lUBNh8UEboSh0hC3TWbJTQSxbose9g2Zbs1/557w8ROUb+
/IDuCFYVOEqumoAuXKGL1V8i7oZjK2ZCXBdmJqaaEDdJU4Khhkx3c/cVrrZt
xrzxTAQT/VyVXExixQlAMwhT
"],
Association["Book" -> 10, "Theorem" -> 52] -> CompressedData["
1:eJztjMsNAkEMQ4PEaOL8Fp/2TEuUsA1srdsRGU4UwJEXyYrlOM/jfB03EbmW
/PkFO5xAbWRVkYpaOArko1jbB7ihx7xVV9gXXWH0B0DFxogUg+QcYYG2CLOB
ZrbrVb+YquEM2j2h6fDwtDdAFAgh
"],
Association["Book" -> 10, "Theorem" -> 53] -> CompressedData["
1:eJztjN0NwkAMg4PU08X5az0CKzFCF2BWNiLXpw7AI18kK5bjPM/363yIyGfJ
n58AJ1A7WVWkohaOAnkUa7+AG3rMW3WFfdEVxnoAFRsjUgySc4QF2iLMBprZ
rle9MVXDGbQtoenw8LQvM64ICg==
"],
Association["Book" -> 10, "Theorem" -> 54] -> CompressedData["
1:eJztjNENw0AIQ4mUOzAGRboNslJGyAKdtRsV+pMF+llLfhgkfN6v695E5N34
6zdiAmA2j0Yt4QhklsGvFvvi7iDQsWa9JOtf1QRmkVJh2QjGgBVVp6p6eTqm
2qNhdnis8J3WlaxWfAD28Qdw
"],
Association["Book" -> 10, "Theorem" -> 55] -> CompressedData["
1:eJztjNsNAlEIRDGRwAxzNxorsCVL2Aas1Y6E9cMG/PQkHCbhcd+fj/1kZq/R
nx9RaDTmEaGN2CARag+riAI5xgzx2bz1eTfLCC3LtBWeooeLqvKIQJcTHvml
87W58EzMy+PZG+hNB1o=
"],
Association["Book" -> 10, "Theorem" -> 56] -> CompressedData["
1:eJzti8ENAjEQA4NEtPbuOlEuXAG0RAnXALXSETleFMCTediWLd+P5+O4lFJe
p/z5FYC2OSVtY0WpNUfDPpt24QPTsTo5hDhHJbYxxm29zVhglipgSVZPp9Vk
RlSSMtblFV8Y0NvoPa6iRzDS5W8VSQfV
"],
Association["Book" -> 10, "Theorem" -> 57] -> CompressedData["
1:eJzty80NwjAMBWAjYde/SdUktBxZiRG6ALOyES6XLsCR7/DkJ9uP/fXcLwDw
PuLvZ2x4+NqHH9Gbar3rmCPW2uOLOTYZOWwx/FjeOI9nl3xGREAiEUCDZcJw
r1nViYiZ1XgidzI/ZTeRUspV1bql1pYPXs0Iwg==
"],
Association["Book" -> 10, "Theorem" -> 58] -> CompressedData["
1:eJzty7sNAkEMBFAjYe/6b2BXuuQCWqKEa4Ba6Yg7Ehog5AUjjUZz356P7QQA
ryP+fmd6RizTMtY5byhaMiq1asRH75E8orRi2DFGH+7ltn8REZCIGVDh2tDN
cq9iRNRaY21M7qT2RWad2TzOIpLKKpfIN0YBCG4=
"],
Association["Book" -> 10, "Theorem" -> 59] -> CompressedData["
1:eJztjEsKAjEQRFuwkvQnlYwDIgyz8EoeYS7gWb2RiSsP4NJH0/Cq6bofz8dx
EpHXXH9+CHvjukW32K9rMaMxujNu7YNqpZMjtUubR2rU6OHjFYAgJTOBigKl
IKYi5zHZPSdYQL8YUnUZledQc1eWSr4BHxMH3w==
"],
Association["Book" -> 10, "Theorem" -> 60] -> CompressedData["
1:eJzti8sNwzAMQ1VbMS1RsVCgC3SljpAFMms2qt1b7z32geCBn+dxvo6biFzL
/vySTJKZALlzOAZGBpPjg8PBWS23VRJ4zJzzWSsEpQBSuwBba96KAqGqZgad
8q7bN2H3CNN9rq2xe/gbyk8Gvg==
"],
Association["Book" -> 10, "Theorem" -> 61] -> CompressedData["
1:eJzti8sNAjEQQweJ0Xg+TjawFEBLlLANUCsdkXCiAI68gy092ffj+ThOIvJa
8een7CTbFeDqQMO4NW6MD6jAdFw+V7Cwjd73eVR1gVlR4HJxnVs3La9MdXea
q1YqvjCg9zFGnumR6ZnBeAPzKgeZ
"],
Association["Book" -> 10, "Theorem" -> 62] -> CompressedData["
1:eJzti8sNAjEQQweJUTwfJ5rVijstbQnbwNZKRyScKIAj72BLT/bzvI7zJiKv
FX9+C8n+ALja0VF7Z9E/IB3TcflYwcRWY+zzp2qC1pICk810bq1pWkaombGZ
aobiiwaMUVVxp3mERTj9DesnB4o=
"],
Association["Book" -> 10, "Theorem" -> 63] -> CompressedData["
1:eJzti8sNAjEQQwcJJxlPJh9tVoIjLVHCNkCtdETCiQL2yJNl6cny43g9j4uI
vFf9OZmx51J9jC3RSbbq97bzS1LSyOqdLGu8KXNu2eYNgCAEUqCiQEqwpYhx
JprFAHPoD1Ncuxe7mnIzLanX/gHuxQeG
"],
Association["Book" -> 10, "Theorem" -> 64] -> CompressedData["
1:eJzti8sRwkAMQ5cZtLHlT5JhOXKgJUpIA9RKR3g5UQBH3kHWG43vx/NxnFpr
rxl/fs3w1W7jehF6kiXrNvhBlGl1vSLnmMqILUZ9AWjonWzwpoAIbCqWpboY
pYMO/aIkdI+wsyvN1CQy3+QvB18=
"],
Association["Book" -> 10, "Theorem" -> 65] -> CompressedData["
1:eJztjMENAjEMBI3EJrG98eVAunvxoCVKuAaolY5weFEAT0aWpVnLez+ej+Mk
Iq+5/vwcDuNtuzazsODw4L58UO3hEZnaZZnHUHYOej4BEJRiJlBRoDVwKmrN
qe61wAj9IqXrmpVnqrlrtB7xBuoJB3U=
"],
Association["Book" -> 10, "Theorem" -> 66] -> CompressedData["
1:eJzti9ENwkAMQw+JXG0nOeh1gq7ECF2AWdmIlC8G4JMn2bJkez+ej+PSWnud
9uf33IHMHEMYFcIz9cFTENxL8LP0QM5t8/qYsS2k1CpMGt1AiAZ0krHQutjx
RVUj17nqGrV05k2hN73vBxc=
"],
Association["Book" -> 10, "Theorem" -> 67] -> CompressedData["
1:eJzty8sNAkEMA9AgEcXOZ6JhK6AlStgGqJWOmOFEA9x4Bx8s+34+H+dFRF47
/n4AqGU4BvoY1eUfSMfqavexoxKzu8e6qFJgliWg3KhrS9NkRijJMqpmKL4Y
0D3njGsREYzw8jfBYQcv
"],
Association["Book" -> 10, "Theorem" -> 68] -> CompressedData["
1:eJzti8sNwkAMRI2EHX/Gmyi7C+FIS5SQBqiVjthwoQJuvMNonkZz35+P/URE
ryP+/ILaWnWfb96XzCtaflDNzfooW3Yc40UbsMDGg5mJRcyIg9aJE5iHOkRE
VT10EkACX4aHWSnl7B4tLKIu6xsCYwgD
"],
Association["Book" -> 10, "Theorem" -> 69] -> CompressedData["
1:eJzty8sNwkAMBFAjYXv934BTQFqihDRArXREwoUKuPEOI41Gs+3Px34BgNcZ
fz/R6x3VUnuW1ez8GCNTOqdVtp9jjY6Y4ccBEQGJRAANbozhXkdVJyJmFmOh
CDL/Ivch4pFXVU0T0yXrDeP4B6Y=
"],
Association["Book" -> 10, "Theorem" -> 70] -> CompressedData["
1:eJztjMsNwkAMRB2J2V1/dhJAIue0lBLSALXSEV5OaSA3nixLb2zNdrz3YxKR
z1h/ruH1bGY0xuKMdf6h2ulkpvaYx5EaPZbw/AcgKMVMoKJAa4ihqDWnutcC
C+iJlK73rLyFmruydfILxDIHJg==
"],
Association["Book" -> 10, "Theorem" -> 71] -> CompressedData["
1:eJztytENwjAMBFAjcUl85zitWgZgJUboAszKRqSIFfjj6XzSSb4fz8dxMbPX
WX8/sjVyJ5euEbfx4S6Jk5KDG5nOiCX2+Q7AUAppcHOgNcQ5UetMlWoBA/7F
eXN0X3vqGk7Js/XMN7RLBwI=
"],
Association["Book" -> 10, "Theorem" -> 72] -> CompressedData["
1:eJztzNENwjAMBFBzTmPnYiVB6gKs1BG6QGdlIww/TMAfTyd/nE5+nNdx3kTk
+T5/v2LG3cg1Jtf8cGc0zskYHFzGnkXacw1AoOomqFKx1YquaoZSMsWtKEg0
fiGC7c7eyzALb77l1xePgAZn
"],
Association["Book" -> 10, "Theorem" -> 73] -> CompressedData["
1:eJztjLENgEAMA4MEJPZjpB+BlRiBBZiVjUhomICOKxydYnk7zv0YzOyq+PmM
DnS0BrTMggSEolXkn48pyySNPq+yCJNPkjC5loX06ngawz1eEEH1HB3LmGN5
bpDmBpg=
"],
Association["Book" -> 10, "Theorem" -> 74] -> CompressedData["
1:eJztjdsJgFAMQyt4bRKsoBu4kiPcBZzVjWw/xAn881AKeUD2fh59MLOr3s93
kBslUvkLgMxjOazwUdnN2OTTEgZYeIsINo95lrw6nkpwxwsBxZoDY6kcSQM3
gOAGcQ==
"],
Association["Book" -> 10, "Theorem" -> 75] -> CompressedData["
1:eJztyssNwmAMA+AgEaXJn9iF8hBHVmKELsCsbETKhQm48R2sWM59fT7WnYi8
tvj7IQ6wzvOM5cPjwgB4JXi4bWOguNSpX81MTDVC1OVoWpWpFpnT5A3u5qSP
/OqxKwp7DPRdOehv23YHxA==
"],
Association["Book" -> 10, "Theorem" -> 76] -> CompressedData["
1:eJztyssNwkAMBFAjYcef8W60WHzEiZYoIQ1QKx2RcEkF3HiH0Yw0j+X1XA5E
9N7i75e85sxLr/xSzZtt/ZqFfvc6awEzbH0yM7GIGXHQmDiBvk6HiKiqh06S
KYGdAGHWWju6R4VFnMb4AMOHB38=
"],
Association["Book" -> 10, "Theorem" -> 77] -> CompressedData["
1:eJztjdEJgEAMQyt4Ng1WECdwJUe4BZzVjUx/dAL/fJRA0kD2fh59MLOr5OdT
goygtAAidFGJ2B6not5Gn5Y0wNJbZkbznGfSq+NyhDteAmCuGhjLaUQBbnES
Bk4=
"],
Association["Book" -> 10, "Theorem" -> 78] -> CompressedData["
1:eJztyrENAkEMRFEjYZ+9M7ZXBJAcAS1RwjVArXTEQUIFZLzgSyPNbXvct4OI
PN/5+6050bzkR3h3rNXoXoke1/JzcjL2n6qKmkWIQk6LJtn7HDQzdx/wxTIN
/DISEVV1xEAjgNn1Aq/+B0M=
"],
Association["Book" -> 10, "Theorem" -> 79] -> CompressedData["
1:eJztyrENQkEMg+EgEcVO4tM7QKJmJUZ4CzArG3GIhgXo+ArrL3zbH/f9YGbP
9/z92HnoKnx0IjGUEGoF1NjmnJd1i6AhomWgiZ6dDG92lZNU0H0lvgQwx9xO
dRSzipWpfAGEdAau
"],
Association["Book" -> 10, "Theorem" -> 80] -> CompressedData["
1:eJztissNwlAQAxeJ1dr7yctDSJxpKSWkgdRKR2w40QA3RvYcLD/3Y9svIvI6
9efXLPUo/4B0OJbqIk5VYp1j3PulSoFZloByo/aXpsmMUJJlVI2evzBgHXPO
uBYZ0fHyN3+DBqE=
"],
Association["Book" -> 10, "Theorem" -> 81] -> CompressedData["
1:eJztzMsRg0AMA1AzE2HLa2OyVJCWKIEGqJWO+FxSQW55B40OGn22fd0GETnu
+Pu5mqs/GEUyMzjRi84KZi3ZrhGgoqoRAkon2GCKcJiBD9xV+TWazfleer6u
u2we6VM7AYiXBro=
"],
Association["Book" -> 10, "Theorem" -> 82] -> CompressedData["
1:eJztytENgzAQA9BDqpOc75JwAvW/KzECCzArGzX0iwX465NlyZI/+7Htk4ic
V/09b1n5U5Szkb0G2WoPvpXus6/jA0CQEilQUaAU+DWR80g2ywl06M0YVaM2
e7lyMW0lenwBdLAGhQ==
"],
Association["Book" -> 10, "Theorem" -> 83] -> CompressedData["
1:eJztyrENAgEMQ9EgEcV2ErgcLMBKjHALMCsbcYiGCah4xZcL37bHfTuY2fOd
vx9ofJQgnFpopHBBF5aZue6XCBoiqg20la4Sw4uV6SQ76L5PfAlgOc+seWwq
kym1XmnUBnQ=
"],
Association["Book" -> 10, "Theorem" -> 84] -> CompressedData["
1:eJztjNEJwzAQQ69Q2dadfe5Bf/vRlTpCFsis2aiXkBnylSchEAh9l/W3PERk
2+PmCuYBOdzCXU3nVI9PsI/+6u9cABCUoiqgEGgNY6+oNV3NaoF2UFMnyD9G
Xj6dakZvw+MPeDsGig==
"],
Association["Book" -> 10, "Theorem" -> 85] -> CompressedData["
1:eJztyrsNhEAMBFAjnfHfi0XAprRECTRArXTEEl0HF92TZjTB7Od1nBMA3G/9
/UTfet9ElvSsWrKy3pmSbVjHAZGAEFWBCJTQ2ARJ1eeZmNmFkVoj8y8eiVCt
T1iYmYeGPJLKBvk=
"],
Association["Book" -> 10, "Theorem" -> 86] -> CompressedData["
1:eJztycsNwkAQA9BBYuL5b0Y5JFdaooQ0QK10xOZEB5x4ki1Lfpyv53kjovdV
f7+xH8euulZU91pdfc3SGtM2f2YQmM0IIAO7uDLMYlkgIqHCGAMeXzKTadb3
9HT3SEv9AIjyBuE=
"],
Association["Book" -> 10, "Theorem" -> 87] -> CompressedData["
1:eJztycsNwkAQA9BBYuL5b0a57JWWKCENUCsdsTnRASeeZMuSH+fred6I6H3V
34/MOVX3iureq6uvWVpjOdbNDAKzGQFkYBdXhllsG0QkVBhjwONLVjLN+p6e
7h5pqR9//wbL
"],
Association["Book" -> 10, "Theorem" -> 88] -> CompressedData["
1:eJztycsNwkAQA9BBYuL5b0Y5wDUtpYQ0QK10xOZEB5x4ki1L3s/Xcd6I6H3V
3688H6prRXWv1dXXLK0xbfNlBoHZjAAysIsrwyyWBSISKowx4PElM5lmfU9P
d4+01A918gay
"],
Association["Book" -> 10, "Theorem" -> 89] -> CompressedData["
1:eJztybsNw0AMA1AZsEz9z0KK1FkpI3iBzJqNfK6yQSo/gAQBvo7P+1iI6HvV
7W+eqntFde/V1dcsrTE95skMArMZAWRgF1eGWWwbRCRUGGPA40dmMs16TU93
j7TUE2xiBpo=
"],
Association["Book" -> 10, "Theorem" -> 90] -> CompressedData["
1:eJztycsNg0AQA9BByuD5LyMqSEspgQZSazpiOdEBpzzJliW/j+/nWIjod9Xf
c1S3iureqquvWVpj2ufHDAKzGQFkYBdXhlmsK0QkVBhjwOMmM5lm/UpPd4+0
1BNjTwaD
"],
Association["Book" -> 10, "Theorem" -> 91] -> CompressedData["
1:eJztycENgDAMA8Ag0caOkx8LsBIjsACzshGFDxvw4iRblrzux7ZPZnbe9ftQ
KTJuCsaYrFBVaVzuMAJZ9oyWykYk0727e4z0YHe8GrAwl4xZBEWJ5AU/kwXi
"],
Association["Book" -> 10, "Theorem" -> 92] -> CompressedData["
1:eJztjLENgDAMBI1EZF/iJAImYCVGYAFmZSOckgWouOKK/9fv53Wck4jcQz9f
4hR6dxptiI0SEE1KKgruoiYrKZcM6u5mRuRKslpN7cXCsm51LjnGjEMeRYEG
EA==
"],
Association["Book" -> 10, "Theorem" -> 93] -> CompressedData["
1:eJzti8sJgEAMBSMYssnmp9iALVnCNmCtdmQ82YEn5zDwGN4+zmNMAHA9+vmU
lIzY0rPUs5YtuVgFIgJCFAFkWAnNVJFEtTUunJk4gru+VKzp5rN3V61HD74B
YqoGog==
"],
Association["Book" -> 10, "Theorem" -> 94] -> CompressedData["
1:eJztyMsNg0AMhGFHwsaP8YI2G4S40VJK2AZSazoCTukgJ77DL83s/fPuDyL6
Xrn9l7XMXLNh2rwt+gJm2PkzM7GIGXFQHTmB6ZwOEVFVDx0lUwI/AoRZKWVw
jxYW8az1AFdSBnk=
"],
Association["Book" -> 10, "Theorem" -> 95] -> CompressedData["
1:eJztytENgDAIBFBMrPQoUKsTuJIjdAFndSPplxv45UvuEsgd/Tr7RET3qN/H
YKaoiNqBhhI83iJCwosbMWjjpKpIbK6lMAKPy5jzCzm31Vu1WSBjY5EHPxAG
Ag==
"],
Association["Book" -> 10, "Theorem" -> 96] -> CompressedData["
1:eJztyLENg1AMhGFHio397p6NKNJEFKzECG8BZs1GQJUNUuUrfuluG8c+HiLy
ufP3a1nIehPV1vRX58y4XlUVNYsQhSyTdrKu2Whm7t7gk/Vu4JeRiMjMJxoK
AcyVJ0g6BkI=
"],
Association["Book" -> 10, "Theorem" -> 97] -> CompressedData["
1:eJztycERgzAQQ9FlJjvatSXbARqgJUqgAWqlI8gpHeSUd/gHaTvO/ZjM7Prk
7+eWpkW9aZaK5nfv6zMCMLiT5rAKj1LSQTICEcEMxxio/EpS5Gj9papSnyuV
N0YXBkE=
"],
Association["Book" -> 10, "Theorem" -> 98] -> CompressedData["
1:eJztycERg0AMQ1FnJh7Zu9LikDRAS5RAA6k1HQVOdMCJd/gHadm+6/Yws9+R
2/WG3pqGZqlpflV99g2AwZ00h3V4tJYOkhGICGY4qtB5SlJkjemprtb3K5V/
P8sGMA==
"],
Association["Book" -> 10, "Theorem" -> 99] -> CompressedData["
1:eJztybsRgEAIBFCckeHg+JyfxNCWLOEasFY7EiNLMPEFO+yy9/PoAwBcT/w+
0DymLWoLcYvF1pyICAhRBJBhJjRTRRLVUjg5M3EEV33lM6ubj149b9MafANC
pAZK
"],
Association["Book" -> 10, "Theorem" -> 100] -> CompressedData["
1:eJztyLsNhEAMhGEjYePHeA8tCwEZLVECDVArHcFFV8IlfMEvzWzHuR8dEV3f
vP4hZ+Tqy6INGGHPw8zEImbEQXXgBD7PdIiIqnroIJkS+BEgzEopvXu0sIip
1hs11QYd
"],
Association["Book" -> 10, "Theorem" -> 101] -> CompressedData["
1:eJztycENgDAMA8AgEdlJmxIQC7ASI7AAs7IR5cUIfDhZftjbce7HICLXU79P
xNxiibDIOXPtAwCBqrsopEDpbgr3SoJkNSoyUeqLPa2xTmOU8NIvC7sBLKsF
7Q==
"],
Association["Book" -> 10, "Theorem" -> 102] -> CompressedData["
1:eJztx7ENgEAMBEEjYWP/3fsRARkBLVECDVArHQERJZAwwUq77se2dyJyPvl9
g2hlSZ8rR8b9qipqFiEKmQatZLu30MzcvcAHq9XAl5GIyMweBQ0BjC0vJgwF
4g==
"],
Association["Book" -> 10, "Theorem" -> 103] -> CompressedData["
1:eJztx8ENgDAMQ9EgETltnFSCCViJEboAs7IRhQsjcOEdvuytH3ufROS88/sI
3cNrxLoudVwAAlVSFLJAI0gFk2YwsywGtAbnqzzNzNmd1ccqUS4j6gXn
"],
Association["Book" -> 10, "Theorem" -> 104] -> CompressedData["
1:eJztybsNgEAMA9AgEfmSy0cCFmAlRrgFmJWNCBUj0PAKy5b3cR5jIqLrid9X
skdqeK6+1QJAYFYlFlrA7mYMNWtNSohAMqXbq86a4TFHj+puPeUGI9IF8Q==
"],
Association["Book" -> 10, "Theorem" -> 105] -> CompressedData["
1:eJztx7sNgDAMRVEjYePPS0AhomclRsgCzMpGhIoRaDjFle7ezqMNRHQ9+X3G
66YVmGF9mJlYxIw4qEycgNTXISKq6qGTpCSBlwBhlnMe3aOGRaxLuQEXSwXB
"],
Association["Book" -> 10, "Theorem" -> 106] -> CompressedData["
1:eJztissJgEAQQ0dwzQdHsARbsoRtwFrtyJ2TJXjxHUJeyNGvs08RcVf8fIdE
FR7ddhjLlkFGomWmGnJdbdQHw0yALyKdu625zPIY+AAF5gU4
"],
Association["Book" -> 10, "Theorem" -> 107] -> CompressedData["
1:eJztx7ENgDAMRFEjYcfO2Q6ioGclRsgCzMpGhIoRaHjF193ez6NPRHQ9+X0o
dQtf3MZkZmIRM2LQWjjc27jVRURVK7RIhMBf4g6zzJxR0WDA0vIGDE8FlQ==
"],
Association["Book" -> 10, "Theorem" -> 108] -> CompressedData["
1:eJzth8ENgDAMA4OEm8ZNKypYgJUYoQswKxuRTsEH62z5znFfYxGRZ86fL2N0
3/yIB0CQEikwMSBn+FSoBlqKJtBhxoCcDanWa+Pqxr1Yy33rL/ssBUM=
"],
Association["Book" -> 10, "Theorem" -> 109] -> CompressedData["
1:eJztytEJgDAMBNAIhtylqdA6QVdyhC7grG5k/HQCf3xw4Tgy5nnMRUSu5/w+
xZKYRdXEyAgxSKd6cdIiAgBzNypqheGlsfW9rsXzmdwyN/7wBUc=
"],
Association["Book" -> 10, "Theorem" -> 110] -> CompressedData["
1:eJztx8ERgDAIRFGcEQJZwEw6sCVLSAPWakfGkyV48R3+zu7jPMZCRNeT37fC
m9tcZiYWMSMG9cLhvs1bXURUtUKLRAj8Je4wy8wVFQkDWvYb/ioFaw==
"],
Association["Book" -> 10, "Theorem" -> 111] -> CompressedData["
1:eJztxcENgDAMQ9HQpjFOokqMwEqM0AWYlY0AcWICLjx92evYtzGJyHHP72O9
97iuVghKAaTOAjQzt6JgqipJ6FN7Sy6Z1LDmtAhPPwHe7QSG
"],
Association["Book" -> 10, "Theorem" -> 112] -> CompressedData["
1:eJztxcENgCAQRNE1cRzYARINMV5tyRJowFrtSDxagRff4f+9nUcbzOx68vva
uuVegEbA3SBbgBgxgZ5AUpJToZ/hLae5Vo05Bk9eipJu9Y4FLg==
"],
Association["Book" -> 10, "Theorem" -> 113] -> CompressedData["
1:eJztxbENgDAQBMFH4jj/n40EskRMS5TgBqiVjjAhFZAwwe7ezqMNZnY9+X1u
Kz0AjUCEQbYC7pjAyCApKajUz/RW8lKrxuIpss+zsm7uhwUW
"],
Association["Book" -> 10, "Theorem" -> 114] -> CompressedData["
1:eJztxckNgDAQQ9FBwjizRQKlAVqihDRArXREOFIBF5707b2fR59E5Hrm970c
ARQCZgKXDVDFAlqApLsbvYxnectYW/M5tVhorRZ2A+eYBP0=
"],
Association["Book" -> 10, "Theorem" -> 115] -> CompressedData["
1:eJztysENgDAMQ9EgUZw4SauOwEqM0AWYlY0oJ1bgwDt8yZL3cR5jEZHrye8b
SAqx1RQ1aSgRYQVZwx1mlpgrCOjLVHurvXOlcX48Z27wIgUV
"],
Association["Book" -> 11, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAAjHh4pAEAlWgCfA==
"],
Association["Book" -> 11, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweADlMQLAJUeAns=
"],
Association["Book" -> 11, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaABjEgk2QAAlWYCfA==
"],
Association["Book" -> 11, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAB3BwM7Bxs7KwMnKwMHGysHBwcrECKlZOTE0iC
AAeUhgMgnwMEWFkgfHYQAQDQOwQW
"],
Association["Book" -> 11, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWABHAzsHGzsrAycrAwcbGwcHBysbGysrJycnEAS
BNigNBwA+RwgwMoC4bODCADMswQI
"],
Association["Book" -> 11, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAB3BxAwMDBysDBycbOwcrKwcbOzsnJycbKysoO
4bEiAxCPA6iMnQWiAiwNAM7LBBU=
"],
Association["Book" -> 11, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSADFEYKAJUhAns=
"],
Association["Book" -> 11, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSACbGwcHAxcrAwcHGwcrBysrKzs7FycnKwgBpgA
k3AA4nEAVbGzsIF5YGkAyekEAA==
"],
Association["Book" -> 11, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWACvOysDKwcDKzcbOwcrOy8nKysXGxsHKysrOzs
rNwcIBIVAIU4OFhZgBJs7BBZAMu1BBE=
"],
Association["Book" -> 11, "Theorem" -> 10] -> CompressedData["
1:eJztycENQFAYBOFfYnZXiB60pITXgFp1xIuTDhx8h7nM1o69DVV19vw+xRQu
Zjl4nUBSAJslvW8hCeM95Odex8gEAg==
"],
Association["Book" -> 11, "Theorem" -> 11] -> CompressedData["
1:eJztx8EJgEAMRNEIhsxMgtiCLVnCNrC12pHxZAsefIcP/xjzHIuZXU9+37Kb
wyTPFD22ikZS0QdF4EWglFVaKUCsLm7XfgSY
"],
Association["Book" -> 11, "Theorem" -> 12] -> CompressedData["
1:eJztx7ENgEAMBEEjYfnu7OBboCVK+AaolY4wES0Q/AQr7TGvc25mdr9Z/sZh
kmeKHqOikVT0QRH4EChllXYKEKuLB9PiBIo=
"],
Association["Book" -> 11, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 11, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaADrAwcrGwc7BysrKzs7JwcIBorYAdisCwLgs8K
AL5vA8k=
"],
Association["Book" -> 11, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAEnNysXBxcnFxcXBysrKwgGsTkBAJuTjTABcQs
HFxAxZzcQCUcANIZBIg=
"],
Association["Book" -> 11, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 11, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAE7Ky8vDycrOy8fDzc3OycnJxAAsjjZWfnQABO
Dg5+fj5+fi4WLk4ukBpeIAEA07sEow==
"],
Association["Book" -> 11, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAEbOwcrOycHOzsXGxs7KysrOzsrJxAGsSEAyAH
qIiDg52FjZ2dDayGlRUAvbED1w==
"],
Association["Book" -> 11, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAEbGxsrCAAo4kFALVAA5g=
"],
Association["Book" -> 11, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAFPHycrKwcHBzs7Kzs7OwgCshjZedAA1xAzAJi
cHJygigAwwgEJA==
"],
Association["Book" -> 11, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAFvJycHEDAyckOBFwggoMDhJEBNxcPNzcHC4jJ
xcnFBaQAxMoEPQ==
"],
Association["Book" -> 11, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAFnKysHBwc7Oys7OzsIArIY2XnQAOcQMwCZnCC
mBwAvXAECQ==
"],
Association["Book" -> 11, "Theorem" -> 23] -> CompressedData["
1:eJzth8sNgFAQAtfE/bE0YUuW8BqwVjsSu/DgECZwrOtcm5ndr36+i0dNuEdm
dqcHGBQzqlJAoUnsRXZr6T7DVgRa
"],
Association["Book" -> 11, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAGnKysPGxsHKysrBzsrLwcrOzsrKiAg5WDg4OV
hZWdg40dSABFALXIA7U=
"],
Association["Book" -> 11, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAG3Jw8bGw8nJycPFyc3DwgxIECQEI8HCycXEBp
IBMoAgDDUwRJ
"],
Association["Book" -> 11, "Theorem" -> 26] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAGPOxAwMnJycXOycoOJNk5EICTg4OHi5uHh4uF
i5uDk5uThwsoCAC9FgQk
"],
Association["Book" -> 11, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAGPOzs7JycnHzsnKzsQJIDCXBycPDw8PEIcrFw
83JxcnPy8gEVAgC97wQ9
"],
Association["Book" -> 11, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAHnJysOAAHEIEAKwuEzw4iAK2LA4A=
"],
Association["Book" -> 11, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAH/KwQwM6KBoACHCDAyoKkAACtLwN+
"],
Association["Book" -> 11, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAHrBDAzooGgAIcIMDKgqQAAKp9A28=
"],
Association["Book" -> 11, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAH3NzcPFzcrEJcvLzcHCiAEwS4WLg4uTm5ubh5
gBwAuoUEGw==
"],
Association["Book" -> 11, "Theorem" -> 32] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAAQrzcHEJsXBxc3LzcCMABRJzcHBxcLJxcPJwg
EU4uTgC88gQ5
"],
Association["Book" -> 11, "Theorem" -> 33] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAAvNyc4my8HJzcfDwIwMHNzcfFzcHBwcLDxcXJ
zcPNzcnFCQC85QRC
"],
Association["Book" -> 11, "Theorem" -> 34] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAA3JxCbBwcnNx8PAjAwc3NwcXNwcfBwsPNxcnN
w83NycUJALk5BCw=
"],
Association["Book" -> 11, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAAHNysnBzcnMiAg4ODk5sXyGDh4OAGyvHwcHBy
AACxagPj
"],
Association["Book" -> 11, "Theorem" -> 36] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRABnBzsnNxc3EiAg5ubk5uPn5OThYeTj5OTm5eT
k4sTALQTBAs=
"],
Association["Book" -> 11, "Theorem" -> 37] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVABbLwcnNx8PAjAwc3Nx8XNwcHBwsPFxcnNw83N
ycUJALQXBAo=
"],
Association["Book" -> 11, "Theorem" -> 38] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZABbKzsrOyogBUoxMrKwsrBygrmsbICAKZqA14=
"],
Association["Book" -> 11, "Theorem" -> 39] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdABXLy83BwogBMEuFi4OLk5ubm4eYAcAKx5A8I=
"], Association["Book" -> 12, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRACwuw8SICDh4eLl4+Pi4uFl4+Xk4+bl4eTixMA
sgMEDg==
"],
Association["Book" -> 12, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAC7DxIgIuHh5OLi5+fi4WHm4eDj5sXyOUEAK8q
A/U=
"],
Association["Book" -> 12, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZACvFwIwAEiOIGYhZuTn5Obm5uPg4MDAKrpA8M=
"], Association["Book" -> 12, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdACgoKCAgIC/AL8/PwcfHxcnFx8XBwsPJxcnNzc
3LxACgCwzwQA
"],
Association["Book" -> 12, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRADEpISIuLiouJi4hzCwlzcvHxcHCycQMDNy83N
ycUJALbaBEA=
"],
Association["Book" -> 12, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVADoqJCoqIiQMghJMTFzcvHxcHCCQTcvNzcnFyc
ALG3BBI=
"],
Association["Book" -> 12, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZADEiKioiJAyCEszMXNy8fFwcIJBNy83NycXJwA
r/cEBA==
"],
Association["Book" -> 12, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdADIiAgKsIhLs7FzcvHxcHCCQTcQMDJxQkArYMD
7w==
"],
Association["Book" -> 12, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAEIuKC4hLiHIJCXNy8fFycLJxAwM3Lzc3JxQkA
q2cD3A==
"],
Association["Book" -> 12, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAEkqKSkpIcfEJc3Lx8XBwsnEDADQScXJwAqgED
zQ==
"],
Association["Book" -> 12, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAEorKyshx8/FzcvHxcHCycQMANBJxcnACoUgO9
"],
Association["Book" -> 12, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAEIsLCHCIiXNy8fFxcLJxAwA0EnFycAKScA5g=
"],
Association["Book" -> 12, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAFsrIcfPxc3Lx8XBwsnEDADQScXJwAo40Diw==
"],
Association["Book" -> 12, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAFshx8/FzcvHxcHCycQMANBJxcnACg8gNu
"],
Association["Book" -> 12, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAFHHz8XNy8fFwcLJxAwA0EnFycAJ50A1E=
"],
Association["Book" -> 12, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAFHBxc3FxAwMLFxcHBCQQcHBwAnE0DKw==
"],
Association["Book" -> 12, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAGUpycXDw8XCy83BycPNzcQB4nAJ1vA0Y=
"],
Association["Book" -> 12, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAGnJxcPDxcLLzcHJw83NxAHicAm4EDLA==
"],
Association["Book" -> 13, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAG3IJiwlwsvNxcnJyc3PxAAgCccAM/
"],
Association["Book" -> 13, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAGgvz8XCxcnFyc3EAIBACa1QMg
"],
Association["Book" -> 13, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAHXFycLBxAwMXJxQmkAJjbAvk=
"],
Association["Book" -> 13, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAHwlwsvNxcnJyc3PxAAgCZWwMN
"],
Association["Book" -> 13, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAHXCy83FycnJzc/EACAJhRAvo=
"],
Association["Book" -> 13, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAHLLzcvNzc3Dw8XLycAJgYAvw=
"],
Association["Book" -> 13, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTAArAgAAJYsArE=
"],
Association["Book" -> 13, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXAAHKycnGxcvJxcnACWqALS
"],
Association["Book" -> 13, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbAA/Jz8PNzcnFycAJb9At8=
"],
Association["Book" -> 13, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfAAnNy83LycXJwAlmgCzw==
"],
Association["Book" -> 13, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTABPGwcnMJ8QgCWDQLQ
"],
Association["Book" -> 13, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXABXHxcnFycAJXEArg=
"],
Association["Book" -> 13, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbAB3LycXJwAlYUCrg==
"],
Association["Book" -> 13, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfAB3BycHACVQAKe
"],
Association["Book" -> 13, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTACnJycAJUYApU=
"],
Association["Book" -> 13, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXACfGIAlRQCng==
"],
Association["Book" -> 13, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbAC/ACU8QKJ
"],
Association["Book" -> 13, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"]},
SelectWithContents->True,
Selectable->False]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"dataA", "=",
RowBox[{
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "[", "\"\<Book\>\"", "]"}],
"\[Rule]", " ",
RowBox[{"N", "[",
RowBox[{"Mean", "[",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "]"}], "]"}]}], "&"}], "/@",
"resDepth"}]}], ",", "vals", ",", "acc", ",", "xval"}], "}"}],
",", "\[IndentingNewLine]",
RowBox[{
RowBox[{"vals", "=",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}]}], ";",
RowBox[{"acc", "=",
RowBox[{"Association", "[",
RowBox[{"MapIndexed", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"First", "[", "#2", "]"}], "\[Rule]", " ", "#1"}],
"&"}], ",",
RowBox[{"Accumulate", "[",
RowBox[{"Values", "[",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}], "]"}], "]"}]}],
"]"}], "]"}]}], ";", "\[IndentingNewLine]",
RowBox[{"xval", "=",
RowBox[{"Association", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "-",
RowBox[{
RowBox[{"vals", "[",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}], "/", "2"}]}],
")"}]}], "&"}], "/@",
RowBox[{"Normal", "[", "acc", "]"}]}], "]"}]}], ";",
RowBox[{"Show", "[",
RowBox[{"{",
RowBox[{
RowBox[{"ListLinePlot", "[",
RowBox[{
RowBox[{"Values", "[", "dataA", "]"}], ",",
RowBox[{"Axes", "\[Rule]",
RowBox[{"{",
RowBox[{"False", ",", "True"}], "}"}]}], ",",
RowBox[{"Filling", "\[Rule]", "Axis"}], ",",
RowBox[{"Frame", "\[Rule]", " ", "True"}], ",",
RowBox[{"FrameLabel", "\[Rule]",
RowBox[{"{",
RowBox[{
"\"\<theorems by book\>\"", ",",
"\"\<average depth reduction\>\""}], "}"}]}], ",",
RowBox[{"FrameTicks", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"True", ",", "False"}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], ",",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"{",
RowBox[{"0", ",", "0"}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Normal", "[", "xval", "]"}]}], ",", "False"}],
"}"}]}], "}"}]}], ",",
RowBox[{"ColorFunctionScaling", "\[Rule]", "False"}], ",",
RowBox[{"ColorFunction", "\[Rule]", " ",
RowBox[{"Function", "[",
RowBox[{
RowBox[{"{",
RowBox[{"x", ",", "y"}], "}"}], ",",
RowBox[{"Piecewise", "[",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "6", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "6", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "10", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "10", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "13", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "13", "]"}]}]}], "}"}]}], "}"}],
"]"}]}], "]"}]}]}], " ", "]"}], ",",
RowBox[{"Graphics", "[",
RowBox[{"{",
RowBox[{
RowBox[{"GrayLevel", "[", "0.5", "]"}], ",",
RowBox[{"Line", "[",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"#", ",",
RowBox[{"-", "5"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{"#", ",", "10"}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Values", "[", "acc", "]"}]}], "]"}]}], "}"}],
"]"}]}], "}"}], "]"}]}]}], "]"}]], "Input"]
}, Open ]]
|
(The peak in Book 9 is 9.15, which reduces the depth of many subsequent theorems by 10 steps, though—in a possible goof—is not actually used by Euclid in the proofs of any of them.)
Here is the maximum depth reduction achieved by adding each possible theorem:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"resDepth", "=",
InterpretationBox[
DynamicModuleBox[{Typeset`open = False},
TemplateBox[{"List", "ListIcon",
GridBox[{{
RowBox[{
TagBox["\"Head: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["List", "IconizedItem"]}]}, {
RowBox[{
TagBox["\"Length: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["465", "IconizedItem"]}]}, {
RowBox[{
TagBox["\"Byte count: \"", "IconizedLabel"],
"\[InvisibleSpace]",
TagBox["5397840", "IconizedItem"]}]}},
GridBoxAlignment -> {"Columns" -> {{Left}}}, DefaultBaseStyle ->
"Column",
GridBoxItemSize -> {
"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}],
Dynamic[Typeset`open]},
"IconizedObject"]],
{Association["Book" -> 1, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 1, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIYmBiYgICBdoAJjR4F1AbIIQsArJwCig==
"],
Association["Book" -> 1, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKAgImJiRkGgCxWZlZWKBNIgCShGESAaRQA1s/EDJOA
6mNGqGRGpphBGnAADKNBpqNaRV2A30CwfUzYnUVlAPE8OCJAJAO2cMYB4JED
BQACnQUe
"],
Association["Book" -> 1, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 1, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJAgJkFGbCysAIBC7GAgQFTDEU3M5okAy6A1XSidJIJ
8BsItg+r96gOIJ5ngPmYEisB1kMHXg==
"],
Association["Book" -> 1, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLAgBkEmKAEKzMrK4IPBMxQDCLANApgYABLwSRA+qAQ
JoJMMYM04AAYRoNMR7WKugC/gWD7mLA7i8oA4nkGcPgwgBmY4YwDoCsEAPhf
BRc=
"],
Association["Book" -> 1, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIggJV8QFAzM5RmgWvAAbCajmoVdQF+A8H2EfYeNQDE
8wwwH5NqJQsSGwDHtwiE
"],
Association["Book" -> 1, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKggJVsQFAvM5RmgWvAAbCajmoVdQF+A8H2EfYeNQDE
8wwwH5NqJQsSGwC+xQh/
"],
Association["Book" -> 1, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJggA0MWJEBOzsrO6oAK5oASD0DA5BmR9aEpooJSrNA
aQZcgBULQBHEqZNMgN9AsH2s2J1FZQDxPAPMx6RYyY7GBwDfHQiW
"],
Association["Book" -> 1, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLggJWdFQHYoRy4GDuUQFbEysoGFADqZGVjR9XJDoZQ
wARXCwEMuAArFoAiiFMnmQC/gWD7WLE7i8oA4nkQZgeRpFjJjsYHAN7VCJk=
"], Association["Book" -> 1, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIQgJWdnZ0NGaBxsQBWIGZgANKseBQxQWkWqA4GXACb
ZhRBnDrJBPgNBNvHhtVZWPxLjAhOAPE8A8zHDCRpRlUMAKIqCZo=
"],
Association["Book" -> 1, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKQACsIsLGxsbKxsrOzgXnsrFDADiXgAhDFQAzSx4YQ
ZmcHK0RSx8SKChhwAVYsgIEonWQC/AaC7WPF7iwqA4jnGWA+JsVKdjQ+AMpC
CIs=
"],
Association["Book" -> 1, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKQAQcHGzJA42IBrEDMwACkWfEoYoLSLFAdDLgANs0o
gjh1kgnwGwi2jw27s7AHBdkA4nkGmI8ZSDQOWTEAlYQJlQ==
"],
Association["Book" -> 1, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJQAAcbMmBnZ0MFrBgAKMjAAJIAy4IUQNggLkw5E1SC
BSLLim4pHKBYBTWUAcaGWEVdgNspEOdAlED8iel3pFDAJ0kMANvGygBhs4EQ
Kyy4sQY7HgAABbcIwA==
"],
Association["Book" -> 1, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJQARsy4OBgIwBYgRikiZUVjyImKM0C1YFhKVbLoQBF
EKdOMgF+A8H2sWF1Fhb/EiOCE0A8zwDzMQNJmlEVAwB3oQmC
"],
Association["Book" -> 1, "Theorem" -> 16] -> CompressedData["
1:eJydUIkNgCAMrAY4yhau5Ags4KxuZAuYoDwxXkKvvV5TYIvHHhciOjW8wOzZ
KzhkngLiJhIGV+6Q6VbWkhoN1vt2aUFvw0McTv6Em3bTPjnONbeytpU+KEOQ
fjwIgOQsj0Ya1lIpm7RCd9xU+QVhTQvA
"],
Association["Book" -> 1, "Theorem" -> 17] -> CompressedData["
1:eJytUNsNhDAMCyfy6hasdCOwwM16G2GnCJUD8XWWGiWNHbdZ1s97nUTky/CL
jAwiW0P0zF4icw/V2KEFB08k3MFjEzXyElLQSS91g9Zn5IZzY9oRpQaV8x1q
5ELXsmPxZ9hjt/zwWjM+TEeYncpz8yBxI5fbgXs0A0ZYoDT+ElH6LuvTGdcZ
w6jqzsPoDSMYCb0=
"],
Association["Book" -> 1, "Theorem" -> 18] -> CompressedData["
1:eJytUNkNwlAMC6ip7bcFKzFCF2BWNmqOorai4gtLOZxEseTH8nouNzN7Z/rC
UGOIVATRnBlUZzYQUzMJqPFgHYzYC0Lf8q5upwi4dCVa0AHcxOzTF/kz5p/b
0mNczZsRO9xPNJfnSR0djLrEviw1N+RfE0zuaULJAA4gSzDH1ZOJ7U+WFaJN
C+U=
"],
Association["Book" -> 1, "Theorem" -> 19] -> CompressedData["
1:eJytkd0NwkAMgwNq6tidgpUYoQswKxuRpKC24sQT30PO+VEs5W7r475ezOxZ
4ZtlUUIxQooIlE6lqjDJGBtg0EwCpCXHsyQyR0Mgttm4sqWmDHByaFroQFvn
ax/dyZ+Zf3bbL3Jqfh9ix/2UVvNc6aHDoYbszTQi3VB7jTC51xe0DeAA6snM
MVoytehjxwvdpQwX
"],
Association["Book" -> 1, "Theorem" -> 20] -> CompressedData["
1:eJydkesNwjAMhA2qe2e7DMFKjNAFmJWNuKRCbaXAD74ojl/JRcl9fT7Wi5m9
mhmwNCKDXIokUn4ms2VCyHIDwVD/DcisLV1VyWJBo/fyGoFSZlIIjxiLijwg
NWqmfXyZ+rrzT+afVYmbUV0ztxvsuJ/CVjxnetPhoYbsRQlFuKGdawFL9/YF
XQZwAG1R5BgdMnWnPzbf/bgMMg==
"],
Association["Book" -> 1, "Theorem" -> 21] -> CompressedData["
1:eJydUUEOwyAM86bSOAmf2Jf2hH5gb92P5lBNbaV2hxmITBwIMo/l9VxuAN4V
ztAF0sjezYzhGmERTrqgyBXmNMDdJCYZSvUUSaZpjFrepWd6Ttpac79oCsQO
1NQKfLlCXp78E/NPVc0Bqmrm+oINrR22JR4zo2hn1Ck2sRrJyTKbEInyqcut
8Qut8lqt6Nkl0yDDbH4A0T8MGw==
"],
Association["Book" -> 1, "Theorem" -> 22] -> CompressedData["
1:eJydUcENwjAMNAj3znY6BCsxAgswKxtxSYXaSi0PLopjnx1f5Nyfr8fzYmbv
bg4xtxYZ5FwkkfIzmZ0JQZYLEAyz1oDMWuiqShYLWqOW1wiUmJtCeMSZqOUG
UqN22teXqdObf2L6mZW4GVU1cXnBCvdd2JN7ZhRtBnWINSmhCDf0vhawdG/6
giEDOIB+KHIcNbkNZwybH9XuDBs=
"],
Association["Book" -> 1, "Theorem" -> 23] -> CompressedData["
1:eJydUUEOwjAMC2iZnWQ8gi/xhH2At/Ij3A60Tdo44Epp4rhx1d7n52O+mNmr
hWNMU2SQtyKJVJ7JbEwIivwgGU0MZNZCV1WyWNDqWl4jUGIGlfCIU9PcQG6a
nmnfXKFOT/6J8WdX5maUauRygxXuu7I190wXbR/qCGtTRhFuaHMtYOk+6Qu6
DeAA2qbKcTRk6El/bL4BwpQMEA==
"],
Association["Book" -> 1, "Theorem" -> 24] -> CompressedData["
1:eJydUMENwkAMC4jUTtKqM7ASI7AAs7IRviuoVGp54NPlEseKo7veH7f7ycye
LRxgjgxyLJJI5ZnMxoSgyDeCIe0EZNZCV1WyWNDpWp4jUGIuKuERh575BblR
N+2TK9Txuv9h+NmVuRmlGrhssMJ9U7bmlumi74/aw9qUUYQb2lwLWLrP4xTd
BnAA7VHl2Bty6Un/bL4AttMMDQ==
"],
Association["Book" -> 1, "Theorem" -> 25] -> CompressedData["
1:eJydUO0Ng1AIpI14B2icoSt1BBforN2oPGyjJuqP3svj4yAc4TG/nvNNRN7N
nMHcyCFIwjN2pzfGEmn5hdFEphFwj4WOCGcwkK96eTdDJNNlCjU7lfQNUo35
XX5xmrhY9y/0l9UUF2F29Vw2WKG6S1txz1TT9lBHWIspZKaCNlcM4qrTMFrJ
AAqgucwUR0O6CurY/ACc/Av+
"],
Association["Book" -> 1, "Theorem" -> 26] -> CompressedData["
1:eJytUMENAyEMy1Vnh7DFrdQRboHO2o3qEJ3Eo5z6qAUmIUYOOc7X89zM7J20
RI/WmrekgTwArQm6DbOsRGSxpP16U6IHnJntiqm9dPQJGGbudsUj+TPWrVQ7
JamP4ga3xV8go95pTjosoAAaPahxaZYsEfnNNmmf8g9Dowkc
"],
Association["Book" -> 1, "Theorem" -> 27] -> CompressedData["
1:eJytUMENgDAIRFMKuIUrOUIXcFY3kqM2qSY1PrwUCjnoQdeyb2UiogNuDFNV
gVXgZvbTwWkjAmOmzCj3eIlGsat2ZsloTx5nt6GgdOAQE6EWR/IzxqPUcWpJ
LHrf+4FX8gtcyMx3xVNk7NL4y6B0LC3NpS4/ATroCRA=
"],
Association["Book" -> 1, "Theorem" -> 28] -> CompressedData["
1:eJyVkQsOAiEMRKvZ6Uy5hVfyCHsBz+qNbGE1YOImvkBTwvQHt/1x3y9m9ixz
gkS1CHUYpCZAEoQidelHpNFQtCMgd3GVvO42ujvgJ/VGQE/fU4jG7gOV/rzd
//ndSkGmQaq8WsFMzTHBvr7x7FqrbhXqfarB8p2tlSStZTkdQ4fWHGvZ8RXb
5wy8AMq5CaQ=
"],
Association["Book" -> 1, "Theorem" -> 29] -> CompressedData["
1:eJytUMERgDAIi57pwy26kiN0AWd1IyuFU6H2ZR5cCFxSmsu+lQnAcZUR1uRA
3kxQGaC6Dm2HtjOTIi4Uws+4V5IawXiL+hdjQ8mjPYtP+JY9yAVR7dDUjoec
XCvsQxmjnVWYnoasCIk=
"],
Association["Book" -> 1, "Theorem" -> 30] -> CompressedData["
1:eJytUEEOgCAMq8byD7/kE/iAb/VHQmHRbIR4sIel25qWsefzyAuAq5YpkgP5
MKGwqhLpS9PQNCup4UYRfkpjN4LxFvUv5obKoz2Lb/iWI+iCOB3Q1I6HTi4V
9qGM0c4qbG91pAh/
"],
Association["Book" -> 1, "Theorem" -> 31] -> CompressedData["
1:eJyVUIENwzAIY1NTDCRH9KWd0Ad26z6ayVa1lbpOdQJyDAHEND8f801EXunO
0aAKNx5XdwOMoMcXBhWpVRkMwKm0IAk0DY1Ijns4qcXAr1rCfjbzDcBLc1k4
Xfs77kWMp1E2FwGzRnwmWFHK7pnBvdKTtos6whrMRtykctkQEtdSa+W2qLJQ
6rSS9KjI0IewPuMbTTcL2Q==
"],
Association["Book" -> 1, "Theorem" -> 32] -> CompressedData["
1:eJyVUIkNwkAMC6hX5xPpCqzECF2AWdmIJEhAhaDCp7PyyXnO6/WyHojoVrQD
ZRbTeqxqZp4/DS03SQaI3IGOZTEvEYAhcEKakcFjOCLEpqzAcP3aq6W12xgX
pSZp2ymsuuyP+x/m36vXpJxVsz5We2GMjVvJbaSLcmr7iL7hmaxGIiCIMBNA
JsPdy8vzCxJaxFx/I1HH4qlFpIe8A/tfDH0=
"],
Association["Book" -> 1, "Theorem" -> 33] -> CompressedData["
1:eJyVkYsNwzAIRGmV445s0ZU6QhborN0o4HxkV4raPlkIojMHzmN5PZebmb0r
fCNCDQapDpAEoTCrPKI+qDSc9wuqgryTXslEdwf80kpNvtmgtRCNLQeyvX4Y
9y+uRynIDEiV1yjoqT062M4nnlNr1I1CHVUtlu9sc0kyWtppXzo09hhtt18x
nTWwAoCTCXg=
"],
Association["Book" -> 1, "Theorem" -> 34] -> CompressedData["
1:eJyVkIENwjAMBA3q+53QJViJEboAs7IRfqugFCkCTlHkJPbn7et2v20nM3to
+8qlheBKxgBIgohmprg1XSRB9soP7pxJ18NCdwd8+pOqSkLyu4axYiDl4xe7
/zC3IsjckFkuKxhRHwOs9Ymn6zjmHRPjdVJjvTfrnoOyDgtX/1Wx5mQnSL9m
tbxtAE9x0Ql3
"],
Association["Book" -> 1, "Theorem" -> 35] -> CompressedData["
1:eJyVkQEOwjAIRdHs84HsEl7JI+wCntUb2V/n0mkW9aWh0MAH0styuy4nM7vL
fCdDcCZjACRBRJrJz9RDI8jq+cGVM+m6J7o74IeNVNUlJL9qGLsPNPn4adw/
OB5FkM2gZblGwYj2GGA/73ibOvZ5+8R4RVqsKq3UygoWrv17xVz1Kb21fX7F
tMXAA16uCW4=
"],
Association["Book" -> 1, "Theorem" -> 36] -> CompressedData["
1:eJyNkGsOAjEIhNEszCzZS3glj7AX8KzeSIYf2ppo+rWQQimP3s7H/byY2VNq
ATZJcMCBkp27GQi4k7J0hYK9misQ8m6ICPf4V6cfdPpORFRynd1Vb63ddX63
IoBSXlHdvY9ojgH0/iaqa85xs+dtabDMtNTsRrcqB4kTeRyfKjP96fqrbQh4
AV+gCXg=
"],
Association["Book" -> 1, "Theorem" -> 37] -> CompressedData["
1:eJyNkIkNwjAMRQ1q4uPbpiuwEiN0AWZlI5yKq0igfsuJnh3Fx3m5XpYDEd3G
sUcxl7kj3fMhB9xVWJTIjdnMBqucIpjBOSwiABzDNVMwwUwb7HeZ9TlQd6i7
GRwEDy1UBXJnu7vV/2ZtdFrj9V7DmX6q9w1WUpp+q6dqbiIi5W/MJ9lazci4
Z5AIBTevdTYeWweP6blIhMtfqv8sslqbBkFRAbkDa0kNMA==
"],
Association["Book" -> 1, "Theorem" -> 38] -> CompressedData["
1:eJyNkI0NwkAIhdG0BzwO4gqu5AhdwFndyHdNtNZE0+9yJA8If9flfltOIvIY
5hB5yeo9agMOlJuai3SoAujdzY15qqHF1wn9ZwZ6t5gC8Dnws0tVxmDU92Gi
QqLSM92d/qPjHqX9jWJMyvVa4xLwT1rbSQZt9m9audfOY8a/yXoprN0g0FYp
PGnpzNv5rMmrh44cpTJT/jeshyyONq1qbWBPVHYNIg==
"],
Association["Book" -> 1, "Theorem" -> 39] -> CompressedData["
1:eJyNkIsNwjAMRA1q4s/ZpiuwEiN0AWZlI5yKX5FAPcmJnh3FPp+X62U5ENFt
HPsUc7gj3fMhB9xVWJTIjdnMBqucIpjBycEZEQCO4ZopmGCmDfa7yfocqDvU
3QwOgocWqgK5e9yd6n+rNiYte72XOdNP9b7BKkrTb/VUzU1GpOKN+SRbuxkZ
9wwSoeDmtc7GY+vg4Z6LRLjipfrPImu0aRAUlZA7OWYNEg==
"],
Association["Book" -> 1, "Theorem" -> 40] -> CompressedData["
1:eJyNkIsJAkEMRFe53WTy68GWLOEasFY7cvZATwXlHiQwScjvst6u66m1dp/u
IFkRXjsGs4KKorUwETOLgEJZJ+JSkhKE8TMTEeqLm6HDfs6oSp/M/pjOy5tX
IhMA48fXPcb4m7W5Kc8bg0cY3hnjQzKpHd+MAuojokrbZT2VbdOsmYzKxpeW
dP4OXZJfd5k1QqUqtBfsZ1lcbdnUNkAfH/ANAg==
"],
Association["Book" -> 1, "Theorem" -> 41] -> CompressedData["
1:eJyVkIkNwjAMRQ1q4uPbZoauxAhdgFnZCKfiKhKo/MiJnm3Fx7xczsuBiK7j
2qtwR7rnXQ64q7AokRuzmQ1WOUUwg3OciABwDNdMwQQzbbDvJdZ0oN5QdzM4
CB5aqArkH+3uUv8ZtdFpjdd7DWf6rt43WEFp+qmeqrnxiJS9MB9kazUj455B
IhTcvNbZeGwdPKbnIhEue6r+s8hqbRoERTnkBgqrDPY=
"],
Association["Book" -> 1, "Theorem" -> 42] -> CompressedData["
1:eJyVUNsRwyAMo72AHzj2DFmpI2SBztqNKsM17U97qeBEjAQO2vb7bb+UUh5J
p2HhH7Bu5taIBYoyqaq7sLCbEXVyWskmrpZm7gu+exX72iGAPJCrjiIMbUMw
RdDvn989g/ZTVQXhea3pAZloLRklxgTXIbwMw+QqnvrhYlZENHckRVTj1Oim
Ran5WkhKUEUOUmlF0J1gAVWETMRvCHOEI6tlXCg96QlnJw11
"],
Association["Book" -> 1, "Theorem" -> 43] -> CompressedData["
1:eJyVkIENwjAMBA3q+52IJViJEboAs3Yj/C6gFClSOUWRk9ift+/r87FezGzT
dh4yBkASRDQzxa3pIgmy613BzpV0PSx0d8CnH6iqJCT/1jBWDKR8/GX3BHMr
e7+5IbNcVjCiPgZY6xdP13HMOybG56TGem/WPQdlHRau/qvilpOdIP2a1fK1
AbwA7fsJKA==
"],
Association["Book" -> 1, "Theorem" -> 44] -> CompressedData["
1:eJyVUNkNQkEIRONbjuHQEmzJEmzAWu1I9nl9qXGyGRaGDITj+XI6b4joOukP
HBLIzJgPnokYLErkJmxmgIpKAMzgYGc00n07IwS7GRbgo39lRTWyesr8VDhF
lNZeVaPiv3V/Y3xVzZp62zHsBb2jS81r4SHIsmpmT+qmMA1dex5dItYnelZa
7GyVepAqyHhkECslL+6uC0e6GbdZ8sycWd5QkZqHsh18uqEN9QYv6Q1p
"],
Association["Book" -> 1, "Theorem" -> 45] -> CompressedData["
1:eJyVUO2NQzEIS6tLwA4QdYRb6UboAjdrNyq8fkj90VbPURDBxkn4Pf//nQ+t
tUuFPQj3iCDpAN3sNKhojVQh4Q5VNTPRqSG5PAEc3Rih/MlG9sm39svTM1Ft
XAlza2VRLnCLnc/9ivGRZb009xh8Ajf0XtlWuBO6VUA+AjA8Z4JNc1epEvqs
JJmnjcqLRKRJzTGz5tJLpeS0VNTvBZ1zUvQFa8ZaOdnUTJQWV9uRDQ4=
"],
Association["Book" -> 1, "Theorem" -> 46] -> CompressedData["
1:eJyVUNsRAjEIROcSHoHkLMGWLOEasFY7csmN+qXO7SQwLBsCXLf7bTsR0SPN
Ibit69ojRpi6e6uqCtYrW0JFJcYo3Ni584gIsOcI7V3a0qAozb5WT7niAXxk
eYee1EIRAuZH2/2H+jOboxFurTlaHn0BVDY0+ZkxKTNru91FQ3VMZk4FiChW
9FaMd4SPkCbj2oNEKLjkDgpHLoFTw4hMmOUDFbG44IMlo2wF7gmYOwzA
"],
Association["Book" -> 1, "Theorem" -> 47] -> CompressedData["
1:eJyVUMENwzAIpFUcOMA4HaErdYQs0Fm7UbETReqjrXK2DgwnfPZ9fT7WCxG9
Op3DLdyrmVvUWBafIUzkOrMqWhOBtB5MgoObD/HVjWsVnUyVi+vX4Tkj12Bo
JDRAiF5DQttpu38w/+wCnVI1D0/D1o5Seq66O84tZfO48SZywEdlvCqR/wPB
ofDjlBeVAuI+gFhIUcws2yrOnGU0RmEVZvlANa8VU08N5hneeCUMkQ==
"],
Association["Book" -> 1, "Theorem" -> 48] -> CompressedData["
1:eJyVkAEOwjAIRatZB/9Dy67glTzCLuBZvZFMl7iZuGQvgaT0U365zY/7fCml
PJd0kk4aQE7Rp/ARKqU4RyExhUIREaqmXbo0d29mV4dEkIORUjv/vo0N1hN0
lIxlYPain7d7zHh4C2SyVI0fS/y6qxU/6KayCit3PYtIM3J5q4jL6U0OqlWK
AO5FNEdXs/y2Ol0kywhBldy26I4GtsYBzJ3DPCsvQC0MXQ==
"],
Association["Book" -> 2, "Theorem" -> 1] -> CompressedData["
1:eJydUO0NQjEIRGPLx+uVGVzJEd4CzupGHjXqL0300kLgrhQ479fLfhCRW5lf
kTmBifAxxtbdXWSMrlFwc0Nm002hqQmA2SPgmbadNiraiI+lS+58QI8qP6gX
DzhDIvBHu1/Rv7I1mvD2XqPV8SeYqoZWfjFhbbHxsA/RdJ8rs6YizJwreinm
K+JHpCW0A2Im0FY7aIpagpZGGYWp2htuFkh+cKqoWqG7A1wEDJc=
"],
Association["Book" -> 2, "Theorem" -> 2] -> CompressedData["
1:eJydUNsNwzAIpFVsHgZbGaErdYQs0Fm7UQ9HTb8aqT3ZILgzBm7b475diOiZ
5mesPWKEqbu3qqpE7pUtoaISYxRu7Nx5RASy1wjtXdrSoCjNvlZOueIBfGR5
h57UQhEC5v+0e4Z6yuZohFtrjpZH30AqG5r5yZiUydpud9FQHTMzpwJEFCs6
FOOI8BFoMq49SISCS+6gcOQSODWMyIRZPlARixUfLBllK3AvQdIMiw==
"],
Association["Book" -> 2, "Theorem" -> 3] -> CompressedData["
1:eJydUNsNwzAIpFVsHgZbGaErdYQs0Fm7UQ9HTb8aqT3ZILgzBm7b475diOiZ
5nf0iBGm7t6qqhK5V7aEikqMUbixc+cREcheI7R3aUuDojT7WjjligfwkeUd
elILRQiY/9XuCeopm6MRbq05Wh59A6lsaOYnY1Ima7vdRUN1zMycChBRrOhQ
jCPCR6DJuPYgEQouuYPCkUvg1DAiE2b5QEUsVnywZJStwL0AJkMMeg==
"],
Association["Book" -> 2, "Theorem" -> 4] -> CompressedData["
1:eJydkN0VwjAIhdEjBW6gdgVXcoQu4Kxu5E20+lQf+p2T8Bsg3NbHfT2JyLNf
B6haCoFEmKuKIFWj4+RaZdp01tIi9J4LVuWhDTBL7NbNrNZJEplAyyZt6CyD
Nh8bd5/pbxR90mDWBNIniA2dht3dGAKuI4r3PZKmJWIZnu2hO8+3CIMfazSK
EOd6StwlTbleNeXf2c3MGDJ1V/Mf1FEzG1y6xUG6eAHLbQwW
"],
Association["Book" -> 2, "Theorem" -> 5] -> CompressedData["
1:eJydUMsRQjEIRMcEdgOoJdiSJdiAtdqRJG/Ukx7cSUhg+V9u9+ttJyKPKf7B
OU9EhI8OQMS9K8lBGMwzmw51TU0vkHsPuNs4DBIN/Jo2IohKFPOzxULARB6r
Duh/tvsV/Sc7R5O6vVdPmAcvlGk2tOyLobXFcpObUwK5LGuqghlqRW+PfGtV
qGih9gwxSGir9aJpuI+h5eJaGk3VPoBZRmbisLRCPU/9vQxq
"],
Association["Book" -> 2, "Theorem" -> 6] -> CompressedData["
1:eJydUMsRQjEIRMcEdgNoC7ZkCa8Ba7UjSd6oJz24k5DA8r9u99t2EJHHFH8h
L0SEjw5AxL0ryUEYzDObDnVNTS+QRw+42zgNEg38mjUiiEoU87PHQsBEnqsO
6P+2+w39JztHk7q9V0+YBy+UaTa07IuhtcVyl7tTArksa6qCGWpFb498a1Wo
aKH2DDFIaKv1omm4j6Hl4loaTdU+gFlGZuK0tEI9T+JhDFk=
"],
Association["Book" -> 2, "Theorem" -> 7] -> CompressedData["
1:eJydUNsNwzAIpFVsHgZHHiErdYQs0Fm7UQ9XTb/Sj5xsENwZA9v+fOw3Inql
uYYwdfdWVZXIvbIlVFRiXQs3du68RgSy9wjtXdrSoCjNzotCrngAH1neoSe1
UISA+eV2T1D/sjka4daao+XRL5DKhmZ+MiZlsvaxU1SG6piZORUgoljRoRhH
hI9Ak3HtQSIUXHIHhSOXwKlhRCbM8oOKWAx8sGSUrcC9Ac+YDEg=
"],
Association["Book" -> 2, "Theorem" -> 8] -> CompressedData["
1:eJydkNERAyEIREnmFBYRa7iWUsI1kFrTUcBLLj9JPu6NI4I7yrJu99t2IaJH
bidR9G6tAiAyq6wJBGLuhRsbO7sFqlfrMJO2tFAU6M833R2J9zj0AKYEGxgj
qgo73+536n+L2WnYqzWt5cKbKGVHsz6DSpm3uu+7KNz4rLw0KoIY0aHwI5u/
KSlX7yQg5xKjQ+EccuOQGEemwiwfIJKjciwzCyI8Ab/yDEg=
"],
Association["Book" -> 2, "Theorem" -> 9] -> CompressedData["
1:eJylkNkNQkEIRUcjywXGrQNbsgQbsFY78o7rM1E/9CQQGLaB3eG4P8xaa6eh
fmWbtQoTs9bKRADtXUVks1yGpa11pb16D2DegzGBVKZa5ceWmcg7KJJMpvAV
QOT6j+++Rb9GI6jALOVw7jFh7DuBQZcX95IUD/OGO+W17GqNQZBm7hxKN53H
KoEHyl3NrCg6TH8i7hVRhcVozTNR+xlsMQvF
"],
Association["Book" -> 2, "Theorem" -> 10] -> CompressedData["
1:eJylUNtxwzAMU3ohRfBhuyN0pYzgBTprNwqk1P5q8tHgjpJIggBPX/v3bb+0
1n7G8W9UrNml99Z4CaDLoiLyuSzeo2+6amVVAR/lWiUQd9ee/lQxwuMAOFpR
0RhgCnhs76z7F/Rl18emIEtp7mMDHBCZOTEPwmbll/cgjsrsn4NmjFNklG2q
YBhBWjejKdDCJCOFKdKM/lg7RPkk5QT76Z6J65DmN5Frd2oJC98=
"],
Association["Book" -> 2, "Theorem" -> 11] -> CompressedData["
1:eJylkNENAjEMQwu6traTa2AEVmIEFmBWNqLt3Q8S8AH+qBrnyYlyud2vt0NK
6TGe33WKtRiQklTgrgiAiIgKQ6uthrtHa0c3rCu09BLZ/GMgKQ6JEntOMCwp
uPm2tr/WfaPytSuNnTpVNDaa4qacx28aewPT4UZsWGli42R2ChCxOxzNXk2+
D8qZqZKuVNEvkWWdqYIDA4rKDBcqXhR2jtCiHuy0caonsrsMRw==
"],
Association["Book" -> 2, "Theorem" -> 12] -> CompressedData["
1:eJylUNkRQjEIREeO5Yg12JIl2IC12pEkz+PD0R93JgGWhRBOl+v5siOi27z+
QLmYKtEIZgCZzMI1hmloyVFGVjW/r+AqNg531vSv/TIdWI0y20QATo7ECuH1
37ifkJ9Zn5P2EfEXsIF5eovwZdwWg02xyaQctZiHxs0chmdVJzta+n5IFeSi
WWRGOffYW9X1cVbtjaowjNXeYDPE6PLDjBIxzR0cLAun
"],
Association["Book" -> 2, "Theorem" -> 13] -> CompressedData["
1:eJylUNsNAkEIRHO7MAPr5kqwJUu4BqzVjmT34iXG6I8ECDATXtftfttOIvIY
7h/xaoBIsKo7ejfCWu80t6Zde0Rc3M+RaSMXJ600fm1HwJPjwAxSsztA7ob2
57ofUn+i4zRJq5U5fiheUsqIOesTycMmyt3vpBVY9+0nNUn5LsPBWI9sTlMZ
fSlqI3Bz1EKLOp6MrlDLBmpvAo8EF4NZZJyVJ0YHC8Y=
"],
Association["Book" -> 2, "Theorem" -> 14] -> CompressedData["
1:eJylkNENAjEMQwuiTeyk1xlYiRFYgFnZCPc4TkIIfnhVozSO0sjn6+1yPZRS
7jP8RYNZKUAz0sdo7p4Z1cIWndEFcOyJZfE4kUQNfp0WkZhkZGII9CzRgxJS
Yfy77sf6P1XOTXVb4w6e1DqztbAJvlZAvoJM6UTH2rN1uRO+VyTqtUr6yOSk
mSuvVsKqMuhSlsxxaajMoPkbo8smnkI9iZz2PQBQHwwQ
"],
Association["Book" -> 3, "Theorem" -> 1] -> CompressedData["
1:eJytj9ENgDAIRE/Tg67hSo7QBZzVjSwQk/pRYqIvKb2mwMHWjr0tAE4L3yAF
UNYqQlLtDNBZqdK1lq4tbdrsUWrV/cat/fEz81FinEihmzMh/XyDuxG2skXE
7tE7t3bvMoxxAX9CB/M=
"],
Association["Book" -> 3, "Theorem" -> 2] -> CompressedData["
1:eJylUAkOAkEIQ7NsKfMKv+QT9gO+1R9ZWLMeiZq4ZCBDBwrT03I5Lwczu1bY
aRFmZMQYCoxkZioLIpGslzgq6sapUie/cL1YEcUz+LnzT5t/fs3k81ybyHPb
xD17wQazTyPrzvdCHyVE93ZpPvrXirFlGgRQDg0FLOClGFwsgBcu1wjHu0hF
MrU6LXbcAC5BCps=
"],
Association["Book" -> 3, "Theorem" -> 3] -> CompressedData["
1:eJytUNsRwyAMc3uxLcgUWSkjZIHOmo0qTEPhes1PojM+Y/khWLbXuj1EZC/u
KmYRICElqAJekPEJNPBUj+vEmEX6d5SOiP4heYPcAXbKxj4es6KEx3txITCS
HlbZ+mZvNQfl7T+8tX/nORflDElcpUJT40+hcmbD0h8NdFNHvwGSFwgu
"],
Association["Book" -> 3, "Theorem" -> 4] -> CompressedData["
1:eJytUNsRwyAMc3vYFmyRlTpCFuis3ajCNDwul35FZ3zG8kOw7e/X/hCRT3U3
AMjIGaqAVxT8Ag081eOaGLNIL+foiuhfkvfIHbC/bOzjMatKeHwWFwIj6WGN
bW/2XnNQ3v/De/uY51xUCiRzlQpNjT+FxpktS08a6NJEfwGA5wgj
"],
Association["Book" -> 3, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 3, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 3, "Theorem" -> 7] -> CompressedData["
1:eJytUEEOwkAIRFM6M4uNb/BLPqEf8K3+SNhGaxPrqbO7LDBkINzmx30+mdmz
zBGYAClIkYyIxmAgj1SZs4TIzJAhXNqVaV9g3nzN3n6aOGjcD8a/bDY3Y1aN
XCZY4b4Ji9xmepGWjexiJbOR5IbSNcGa+/UyqbcBHEB9GTl+iQzd6cvmCzM9
CoU=
"],
Association["Book" -> 3, "Theorem" -> 8] -> CompressedData["
1:eJytUNsNwzAIdKpgOKiH6EodIQt01m7Ug0TpQ0o/qp4NEsfjEJfldl2m1to9
3V8AA8IIWIyhFhbKB4DciakI8zlDcRxOsXe4072Sx50/on/NUpyOVT03ofm+
iYjXgkV6/WLWnbdC4UWiGK9Sf/avFbFHpYamqhRVbaYyzgEVTuldkqdRQvTz
SDlkruvUse0BDiAKjw==
"],
Association["Book" -> 3, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKoA9hZQQBEsiMBsCArE1iMlZ0FJMvGyorbEGStIN1A
mgHGBnOoDHA7BeIciBKwz6B+wQ7wShIDwLaxgkIRTDJA/A4xG7/VYLtZkJwB
AEV2B84=
"],
Association["Book" -> 3, "Theorem" -> 10] -> CompressedData["
1:eJytUMERgCAMqx5t5nAlR2ABZ3UjaRAsd+qLHHCQtE3plo89LyJy+jEJALQA
6heDATejupJVJH+Y6mcNHcH8gZzXboX9qvQr28w78R/E5tggSXBVtU2hxTQJ
fR7o6U890A3CUKmfjmbR9G1IKcgXGukHyA==
"],
Association["Book" -> 3, "Theorem" -> 11] -> CompressedData["
1:eJytUNsNAjEMK+jSxDE3BCsxwi3ArGyEm0PHQzo+EGkbKa4TWzkv18tyaK3d
RvpXzAwFgmTGHHQdAMKOIMjApBIG7I6I98hUegX3O3+M/vVX4kpi9eFELzcn
ZlkGC8y6hayeH0TTRlhIFjWf/SuDWyUhwBvMJOreJACcquxm5u7hPkTNP5c0
hky1nVp23AHqgwpr
"],
Association["Book" -> 3, "Theorem" -> 12] -> CompressedData["
1:eJytUNsNAjEMK+hSxwkMwUqMcAswKxvh5tDxkI4PdGkbKa4TW7nMt+t8aK3d
R9ot0hX0zAw/e0KHpLAjk5nOSSWN3JzgnxGh9A5ud/4Z/eevxJXE6sOJXqxO
zKIMFhh1C1k8P4mmjWQhUdR49S+MXCsJkWg0kyjQJECequxmBsCBIWr4XtIY
MtV2atn+ANabCl4=
"],
Association["Book" -> 3, "Theorem" -> 13] -> CompressedData["
1:eJytUIENwzAIS6cSMOSJvbQT+kBv3UcztOqqSdukaU5AimXA4bqst2Vqrd0z
/Q9GwGIMs7BQHgDkLghEGGY+IcDHBie4M53J95U/on/5Tyaqejph+OFExMtg
kV63mM3zLpTIRVRtSf1ZvynieHGQKhjKoarNVCIGVNild0mewRGir0vKJnNt
p5ZtD8T+Clw=
"],
Association["Book" -> 3, "Theorem" -> 14] -> CompressedData["
1:eJytT8ERwzAIo73YgGScrtCVOkIW6KzdqNiXR9q79hXdgY0sEL5vz8d2EZHX
SCfiZjBEBCyMTgTJHrzSdV3RFgJaOn72w7MJoCca80hCMuctK3Oeu65I/fua
5iLpWevcZMaOUvwLdmB2Ye3u/VNkGQ7soj6qiemmYqWSovlpLWGRmWi1aipW
dVVztQNyHr2TWIAxmi3JN3M2Czg=
"],
Association["Book" -> 3, "Theorem" -> 15] -> CompressedData["
1:eJytkMsNAjEMRA3axOPMRFsDLVHCNkCtdITNR4IDe9p3GI0cx7/LdrtuJzO7
lxwJBkByYIJQkK1N6uzuGeQi0pv497ukUagMkhQDBCl9IA4e1/r+NijJrJ4z
4YtA76Uv/6aVj0+kpE/kIXZ4PkZtnI3ySDbcs+lwU2vqa8ARqpyI1SPLj4z8
IqYsUXWClfsAAUAKsQ==
"],
Association["Book" -> 3, "Theorem" -> 16] -> CompressedData["
1:eJytUNsNw0AIo1UINkzRlTpCFuis3ajmUlW5j+YrPunAvIx4bK/ndjOzd3+X
opIpoJChRxLAnR0sLqLp5N/uPABfa7uvMU0uxnqaHXpQ1ToWOsJ9op2cI6Oo
oEOc4JdsIdIt3KuMYSmBAJsywiMCMpLwmEforlptaXc/Nj7HiQpO
"],
Association["Book" -> 3, "Theorem" -> 17] -> CompressedData["
1:eJytT9sNwkAMS1HT2LljCFZihC7ArGxELK5VBYKvWkqsvJ3b+rivk5k95c5F
71lAR7KYZBIXUV45F8OTP4c1KeQGJGyLlD9b7fK3CkhTdS3jfBn1A+COTxwy
OTINaF99em807UU9RrqFe6ZFWIYjQIUR4WUoqhMeh0XUrlbiZq18K8MLvtgK
Tg==
"],
Association["Book" -> 3, "Theorem" -> 18] -> CompressedData["
1:eJytkMsRwzAIRInHmF2SJtKSS3ADrjUdhY8m9sU5GY1AINh50nvb1+0hIp90
N9vLw1DLnSSAKYL7k3OmSl7O5mRaS7SOoM5dvxt2+XsLpIuupXnQFGmq/uMc
gFUZpN2YlWbv1/gxj1PbeBhpwtB1MRNXhaFSM9PYiBCCaocG2AiOubL6bHwB
qMwKUQ==
"],
Association["Book" -> 3, "Theorem" -> 19] -> CompressedData["
1:eJytUMERwzAIo70QJHWKrtQRskBnzUYVl6Tn9pFX5MMyYIPwc3m/lltErL1d
DRnwopmkiHuTHpzMSPHsKRo64DpxeB2/Wut8mgVak2/Ne3sbewYgE/8YItoj
+h5/sE05JnswMqMypagKVaLAdqsqbTC5RdZQiMdXTV1yU4YPk6IKLg==
"],
Association["Book" -> 3, "Theorem" -> 20] -> CompressedData["
1:eJytUMENAjEMC+h6cZxTwwqsxAi3ALOyEUkf6CoEr7NUt4nd1Op9fz72i4i8
ik5HhKpraNdbRJC8xqYR5ouT2jb+vOmejkTujiI6heMMgIyzo65/VVZSpGut
UDiitaksce4MU6b2r+4BH7EeMlNRM0BUxa31vlUFpJBgEVBrGlGfhWUMsRHy
DQpXCqk=
"],
Association["Book" -> 3, "Theorem" -> 21] -> CompressedData["
1:eJytUMENwzAIpFUwcLbjKBt0pY6QBTprNyrYUao+0ldOMmC4E2c/ttdzuxHR
O8L1WFmqzNJkba0BuLealsXylIHEBadC52oAUYygpL3u/flqp+nvVDWCs9Lw
o8NFgBmHz91g7+xOB5GLaumd8Rp89YNRjpsvEjESM1/KQjCutZiJqojEyZFd
JfoDwD9Vp14asqcP5QgKow==
"],
Association["Book" -> 3, "Theorem" -> 22] -> CompressedData["
1:eJy1UMERwjAMC1wd2UraABuwEiN0AWZlI+ykV44HvEB3sR1bOiu5rvfbekgp
PSL8AYIZCxourTWSxzbn09nKVMgslR91ztUAoxhBk/a695dfG81fp6oRnJWH
Hx0uAiLcfW4Ge2dzOohSVWvvjNfwpR+Mut98EWAJZr5UkGgyz9UMqgDilMiu
gr6B9E/VqZfG4ukJy5UKkg==
"],
Association["Book" -> 3, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJoATg4ONg52DnZWcGAiZWdjR3IZwGy2YAYpzZ2JMAK
REDMzgBjgzlUBridAnEORAkr2HJWPACvJDEAaBEnJysDyMusDBAGMATBUhy4
rWaHESxIfADUoweN
"],
Association["Book" -> 3, "Theorem" -> 24] -> CompressedData["
1:eJy1j9ENgzAMRN0qlxdol2AlRmABZmUjnASpQSJ80Yt08UUX+zwt67y8zGzL
9BekD19GJIHeIkKKwWUU6v5SA47bak3RT8e8b1jm8YtV1wFdgU59NtFwa/VB
wyArizqbvyc/WcZeM2UDJVFoWu6v3QeD
"],
Association["Book" -> 3, "Theorem" -> 25] -> CompressedData["
1:eJy1kOsNAjEMgwsisd3rDcFKjHALMCsb4RYhFRD84j4pkds8lfN2vWyHUsqt
u33AmmuqSqKOVZBQwy9YfS3izGK4sNgGItu/t8yfUbI7ZyVfESPGQjPTT33I
0EfSe58nHgREwdCAR0drbcQzIuGz2ZJKTPXWC+UznXrmODZ5BxG9Cc0=
"],
Association["Book" -> 3, "Theorem" -> 26] -> CompressedData["
1:eJy1j9ENgCAMRKvheGpcwpUcwQWc1Y0saCIm4pceydEjR3udlnVeGjPbEv0E
RgYkgVoRoYvBZRSq/lEBztuOmqy/DvneMM/jinWsA3oClfpuouDS6oP6XpYX
dTZ/7/wkGWvNlAzkRKFouQOTxwdw
"],
Association["Book" -> 3, "Theorem" -> 27] -> CompressedData["
1:eJy1jt0NwjAMhA1q6v+kK7ASI3QBZu1GvVQgyAM8lU9KnPPZsW/r475eiGjr
17/ghRsIs2sLbU18cjMt1b62RIR3EEMTeDp5hkKqui9n7zj/dK1vqqiaDegn
pQwSpoyZo8ix9JARwXlLfyk7pjHhIwxlobDSaoVr+hwcrKX3swykeaZO/YnS
QNgB/y4LBQ==
"],
Association["Book" -> 3, "Theorem" -> 28] -> CompressedData["
1:eJy1T0EOgCAMm4aukPgJv+QT/IBv9UeOYeJMxJOWpKykbN28bss6iMhe6Tdw
IgASI6hk1mRSQXR/IIDnLa2m668jvjf0ebxitXVIPIGd+m5i4Gi1QaVAfFFj
sfdsp0rtNUM10BOl0PIAesQHXw==
"],
Association["Book" -> 3, "Theorem" -> 29] -> CompressedData["
1:eJy1UNsRwjAMC1zdWGqMe2zASozQBZiVjbDTB1/wBbqcHVvKRfZtedyXUynl
meF/qFd3b+TZje7ahomkOD8+CBoJ5sUCMBQYsfXnXzscv7JAhlCN6ScPdohw
97ky1N7ZnK5CMcQA2WGXhkgBxaGwo+rDx6xUsoiW3JNdUEM31ZqSViFBo+ob
ULWWaxqyik9apBfEngrq
"],
Association["Book" -> 3, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJoCNjZWYGAnYmdnY0dCFiAHDYgxqmeFQuAC7Lj00km
wG8g2D5WLM5ixyBh4uwwEXZ0PTgBKGRAFnFysjJA2OxgT3MAISgA2ZCtRTWW
A2YTC8J2VgBT/Ac6
"],
Association["Book" -> 3, "Theorem" -> 31] -> CompressedData["
1:eJy1TkEOwjAMK2hdXCedKo0P8CWesA/wVn5Emk7bCU4QVW7jOK7v2/OxXVJK
rw7/rNYayWtbuN6ok3qTF36U+5jwips0A5EQ706j/Trf/HUKdHDVPPJgpOiV
M4+ce8C8Rw8cogrUYBhSnvtDUY/OPxKRJO7L1I9kMytZWJwXVS2iIoTI6YHi
m1bddgqTQifwBm4ZCmE=
"],
Association["Book" -> 3, "Theorem" -> 32] -> CompressedData["
1:eJy1UMENwkAMO1BziZ0WCW6CrtQRugCzshHJqRUCAS+IIivxWefI83pd1kMp
5Zbw17qc6X5sJ7RmPjhpMvKj2t5Ukoymm02/Pq9+fQ3zgFDV55MAiCT2ZWc7
A7MdQoRNhIdqmzt2PcBIJYxUtWhuRRDWQk6AElKrujs02qj6GlB+N0REGMGc
7xsACgM=
"],
Association["Book" -> 3, "Theorem" -> 33] -> CompressedData["
1:eJy1UEESwkAIQ6csCRx66PgAv+QT+gHf6o8EnGoverKZncxCssByXe+39SQi
j6Jjsbj7+TJzWSKmcKeGfzVjj3zocAiKwQww/3u68VMFitI1PjMVk1Qt7gD+
0rZMMwuD3oETfFfoe3OJm5KNVE2M+U9RCqhWBsuFpSsSFtaF9yuqk0vFlJNl
M49MPgEdYQoZ
"],
Association["Book" -> 3, "Theorem" -> 34] -> CompressedData["
1:eJy1kEsOwjAQQwfUfOwpYlFxAK7EEXoBzsqN8ExTdQUr8OJpPlbi5L4+H+vJ
zF6BP4vu59vVl8V9ctKL87OX7CHuhWRbm5PLr8PVr1tdLshVj2BBALUGs+kj
ahmTJEJ1JmY1RMf+nK1OxnJs4ktKgTWAFI29NBnQCM3gUvOWB/dDcTNdmJRM
tqzfHi4KKA==
"],
Association["Book" -> 3, "Theorem" -> 35] -> CompressedData["
1:eJy1UNEVAjEIQ9+1EOBaV3AlR7gFnNWNTK3P80e/NB80QAppz9v1sh1E5DbC
v3Fqx4D27rlkppY1P0oB+ABPxAhkMnkEk/i1t/q1y+Ui3FkrpjNMa0QpeGHW
rOzJU1Wbo2G/RJE5bE4aZTZtNh7bVKzUCFE+mv9kK2N4qioVXaFqrvYGzgu0
CF84kjQ6hXcr4Apv
"],
Association["Book" -> 3, "Theorem" -> 36] -> CompressedData["
1:eJy1UMERAjEIROc4YCGXGmzJEq4Ba7UjYZLx7qMvZSYhwMIuue2P+34homdd
f7d+bZDeYUtECG/xEWkn8+lpvN2tW/u1tPVrNcmJPFFrCQGQZ6piPpSOnPIR
TBQ7Svq7KUEK0zGp0lnUuWWxMYloBEmQCTdtUAmECFeHQVi3E+/8JrhjgUPd
PGfbCxdpCmY=
"],
Association["Book" -> 3, "Theorem" -> 37] -> CompressedData["
1:eJy1UMENAjEMC+jaxE5yzMBKjHALMCsbkZYTug+8wGqjuHadqtftfttOIvIY
5f84JyzTsUSEtYiPxnDHgPveFKQoBvUL8tcv61/VGl5FRDtJ1Jp7one88Tqz
diC7aSXWw6UyGWGYacNaog2drEGqKlStniGuzWkwrZLZOIej2doO+Rif5FnK
YqQlvLLxBBVkCnM=
"],
Association["Book" -> 4, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoAJjAgBlGElCHClAEqe4wAs6GKMHmLCoDiOcZwOHD
AGYwE6sVXSEAiRUENQ==
"],
Association["Book" -> 4, "Theorem" -> 2] -> CompressedData["
1:eJy9UMERwjAMM3dNLNnleHQCVmKELsCsbIRcLtAPvLj6odiKbCu5rvfbejKz
R8ERccllyZwyIlvGV1lEoCJGorBXqU7g/G9f/eetlguk6js/CpK9F27FYFsx
BAZINIMzNw0/zXgzutTJepwWtUbzqgy0QHME6UFxnpkCinLfGSlT9S+YlGpa
1OgnytcJ5A==
"],
Association["Book" -> 4, "Theorem" -> 3] -> CompressedData["
1:eJy9TsERAjEIxJkjwEKKsCVLuAauVjsSkouOD3057jBLgCXsdT9u+4WI7kV/
gffusTng7PioAqAFzMcgyqxnv//aVvs6zeNJqWrlp0IXsrV8zgmUocvzKWyh
GqODIcVrfyriWeUhZiMRAUiFIOweJgwTqxgQqIi+fwJP2qoy65bpAalGCco=
"], Association["Book" -> 4, "Theorem" -> 4] -> CompressedData["
1:eJy9kNENhEAIRDERdoa1CVuyBBu4Wq+jA9fE1Q/9MfcS2CFAhuy8fpZ1EJFv
pv/gTo4kJyVvhg64v9J0rNYoXsYebo4U15ptB/WYncpoQnnFfOt0ABHntSbS
iCauWqs4UsDALMOr5EyhFqBE9LS/GlM2A/wAsz8J2Q==
"],
Association["Book" -> 4, "Theorem" -> 5] -> CompressedData["
1:eJy9kFEKwkAMRCM0zWQSUOgJvJJH6AU8qzcywVaKRb+kD7KbnQyb7F7n+20+
icijl4OYmEOQ0DO/elig4AoIWU+lX/491PizCvRM5Rpf7Tu8qE0Vn2wULkoA
sfP18xbTu9hfYmZiqplCF1ol6WoZpVtEuFUGdGz7JCOTQ19JZ4/2BJYaCbs=
"], Association["Book" -> 4, "Theorem" -> 6] -> CompressedData["
1:eJy9UMENwkAMC1LT+JwIsQIrMUIXYFY2wlFLhUDwQljKXc72w+fzcr0sBzO7
9fEvjJySpB/50SKZEPgACFtfo4XTrzPNX1WgM8k1r7l6hqDLHa94YrgxCeSb
r7+3mXaxK4kIC/cq1WAMLTU8KsVHZo7QBvTsUJJiVnHqetRRR7sDeNcJpQ==
"], Association["Book" -> 4, "Theorem" -> 7] -> CompressedData["
1:eJy9T9EJAlEMq3C9JnlTuJIj3ALO6kY2+E4ORb/EQN+jbUiT83a9bKeIuPn5
G7iQRIofGZJgaAeE2DvPf21p/boF7KlZ6zzfRWcAMvGKw0RzMoDxxnO8SXou
HYzMqEwpqkKVKNBtVWUX+usTWQchWmu0ucWSD2e4A0fuCU0=
"],
Association["Book" -> 4, "Theorem" -> 8] -> CompressedData["
1:eJy9UEEOwjAMC9La2M4Eb+BLPGEf4K38iKTbEEKCE5qluoltNVGvy/22nMzs
UXQcppDYzvoaiDcogsy7RFaddPn3Rv2nq9o0T++kNnBFa1UNYTMwFEo7Zahc
aucKQcRLScputDkIoLl7DnVaeHOFvAkz4KVzJX4iv0ZTvoyZIRBPvjMKHw==
"], Association["Book" -> 4, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoCFghgJA8CkARpLqDCDgXogSbs6gMIJ5ngPmYEisB
tpEGmQ==
"],
Association["Book" -> 4, "Theorem" -> 10] -> CompressedData["
1:eJy9UNsRwjAMM3fEsRxzwAhdiRG6ALN2o8ptmusPfHHow4li+RFN8/s1X0Rk
yfBPPB9a4/4x7d6QcAIdQopO49f76NcshzNQpcc+Yy1VDOxvVk6ki8IRpyKK
zGGHakvaXrV9XqXSnps4xLVwppYSXtnIzKJannkdYD+0tOzKNtbQ6BRWfsAJ
1A==
"],
Association["Book" -> 4, "Theorem" -> 11] -> CompressedData["
1:eJy9UEEOAjEIxEQYGLtejA/wSz5hP+Bb/ZGUrs1e9GScNJTMlIFyWx/39SAi
zx7+iqsrLx/VCMZEG5dMwqP9ehz7qmbzDPnK5gRvmGXuA1HHtZiNLFHZPzTy
zcD3Jl0cBb0RaQLDeRG6hClJqC4NEQrgFICmJ2KHrGRf2bF8WSt7AUzhCY0=
"], Association["Book" -> 4, "Theorem" -> 12] -> CompressedData["
1:eJy9UEsSQiEMqzP2kwjuPIBX8gjvAp7VG9nC02GjK8csaEloCFy3+207iMij
lv8ilJePIkAsaA3o0l/bQPt1GvuqkpUpTxlmsnhHM8s+JrIyiw5mJ4eorLHZ
70+I1aTEOYBxm4mbn7swBKYkXbU3B9TdT+Gu6enrD+UkK9hx+LIV9wRCGQmI
"], Association["Book" -> 4, "Theorem" -> 13] -> CompressedData["
1:eJy9kNENgCAMRGtiyx1M4UqO4ALO6ka24AeY6JfxJYVrruQalm1ft0lEjjh+
RslHL3fwuqVpksWbj7FXt+b5tmZ1oR6zoXUTyjuWq9MBeI3PmqhpJlm1FMkI
AQOj9awUM4magOTV0/5qDtkCcAJCjQmK
"],
Association["Book" -> 4, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCLoDVhZ8UhhAhRBqruFsEtZsTuLygDieQaYj0mxkh2I
WZD4AJP6BoE=
"],
Association["Book" -> 4, "Theorem" -> 15] -> CompressedData["
1:eJy9UMENAjEMCxJpazdlB1ZihFvgZmUjnCtFfOCFsCpHsaMm8nXbb9vJzO5J
fwc+O8CgoIpIImjqul4Hefn1KeWrS4pCUyVPmcCEO5/aMtqhgFykoXTBxTnU
iPZSROqOVotqhbGWMcxDSXhE0F15lOJzUVV1vKFlNOyd566vA8GG9gBIiQnf
"], Association["Book" -> 4, "Theorem" -> 16] -> CompressedData["
1:eJzNUNsRAjEIxBlhWZKzB1uyhGvAWu1ISM7M/fnjhzsZwiywPO7787FfRORV
5o9ABhf6/GQRzv7rhvZlnDKZZWuCD8zS9wmO5zqYgxxBjVpo+oeAn0UqOAuq
UYQJDLdNwoWmkYTq1kEqgNYATU3whKyMOtl16EYr7g32BwlO
"],
Association["Book" -> 5, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGBgBtZmQEU6OAugAAmjwCfg==
"],
Association["Book" -> 5, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGAjAyMgyU1cMeAACY8gJ9
"],
Association["Book" -> 5, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGBDAxDJjVwx0AAJjxAn0=
"],
Association["Book" -> 5, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGCAyg1cMbAACWOwJ7
"],
Association["Book" -> 5, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDDACbWcEk4MQgN02JAEAnPQCgQ==
"],
Association["Book" -> 5, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDjAxMDAyMA6sG3ABJjAaigAAnmQCgw==
"],
Association["Book" -> 5, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGFDAyMA64G7ACRjAaigAAmkcCfw==
"],
Association["Book" -> 5, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGFDAyMDGCSEbGAXcKKmACo6EIAKI0AoY=
"],
Association["Book" -> 5, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGORgCThxcAACWEwJ7
"],
Association["Book" -> 5, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGGDAOAjdgAYxgNBQBAJj0An4=
"],
Association["Book" -> 5, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 5, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGGjAyMjAzAgGQNdBOQQJMYDQUAQCkugKI
"],
Association["Book" -> 5, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGATbACEZDEQAAllMCfA==
"],
Association["Book" -> 5, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGAWBiYWJiYGJkHmh3IAEmRkYmBoZBEj4kAQCuhgKR
"], Association["Book" -> 5, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGATbACEZDEQAAllMCfA==
"],
Association["Book" -> 5, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGAwC6g5GJcbC4BgSArmECu2vIAQChmwKH
"],
Association["Book" -> 5, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGCWBkYmAdaDcgASYgAJID7QwyAACmRQKM
"],
Association["Book" -> 5, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGB2AC4sHjGrBbBpNzSAAAmi0Cfw==
"],
Association["Book" -> 5, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDxhMrmECo6EIAJkKAn8=
"],
Association["Book" -> 5, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGATbAAkZDEQAAmqYCgg==
"],
Association["Book" -> 5, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCIGDWBkGmgXIAMmkGsGlYuIBACc/wKD
"],
Association["Book" -> 5, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGATbAysjIysAwFMMHAJ48Aoc=
"],
Association["Book" -> 5, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGATbAxMzMBCQH2hlkAACdfwKG
"],
Association["Book" -> 6, "Theorem" -> 1] -> CompressedData["
1:eJzNkMENQjEMQ4NEm8RNmzACKzHCX4BZ2Yi0fD43Thx4B1exrUTqdbvfthMR
Pab8ExE2iaRFuFsYWTjcAZiNX9+rX1NgSrYqDvRFWqnL2AMpKwPekqUBHbo6
e0sEKoeTYU4rWtdA4Do6idKFS++mhfuw1jiXpRQGmOWDiriP/JzzXJidls8T
yZsKeQ==
"],
Association["Book" -> 6, "Theorem" -> 2] -> CompressedData["
1:eJzNkNENwjAMRI1EEvsSx2qZgJUYoQswKxtxCaX88cUHT8pF9p1sydftfttO
IvIY8lesMbiQtpBYQvhaBICI/ut1+asLUCpTGQf2gi3qbOyGpukBb2Gow7rN
zJ5ShenRoclqWnMbBCV3FzVZS3Jvlor3VmvhMAorL0U/mCqPwuOcx0BmnN8T
+hcKqg==
"],
Association["Book" -> 6, "Theorem" -> 3] -> CompressedData["
1:eJzNTsERAjEIxBkTYInhzrMBW7KEa8Ba7UiIZvz58uHOsEl2gc11v9/2AxE9
kv4Lnris29Z8WdxPRtYd7qoK779Oq19dIEijq2JAs14IKX/0FhNShgdMiqYO
7WNojolAZSppxmssyCBlYua4s9CZizUrXIBmcTJbVBEpLB/U2OfdHUeYqKll
zhOtgAov
"],
Association["Book" -> 6, "Theorem" -> 4] -> CompressedData["
1:eJzNj90NwjAMhA2N2/gvUbIBKzFCF2BWNuIaSh+Q+sYDJ+Uk332yldv6uK8X
Inpu9mdqvfcKlQiz7o1aq16rubcevz42nzZpmpLqlchBzXpI3kIEH8FeZB6d
6sdE2FVcBrNTOavkI0GJaVS4KGKkyxJwpy4c4cKMf6sylm0sl8LyJTW8FOZi
YLH3Bcq3CoU=
"],
Association["Book" -> 6, "Theorem" -> 5] -> CompressedData["
1:eJzNTdsNAjEMC1zbS9yEqMANwEqMcAswKxuR3gOJD/74wIqsyLbs2/y4zwci
enb6N0yXCYHmTfVaGzW4udeKdrZfb5WvThqGBByJNFIFUKyQFSEFL8JmcF48
YCeRLFtI9hQzhN9Kz/DaEovxEMYxfkhcNlPJBRrLhZmtci7uRT4RLRFIPWz1
1Htfo68KWw==
"],
Association["Book" -> 6, "Theorem" -> 6] -> CompressedData["
1:eJzNjsENwjAMRQ1NXPvbIYoKA7ASI3QBZmUjnFRF6oEbB56ip+T/KM59fT7W
ExG9uv6O5Yag1eZ+tUYN1WvtyVJ+PYq/NmmaktmZyOMWA44N3YgoPIIuAySP
Dtilmnur2B2IQOWThOI0qpioaoR5jj00Vi7FNTM8JrOIFJPMtbIewfhaKu5a
7NKffAOKlApL
"],
Association["Book" -> 6, "Theorem" -> 7] -> CompressedData["
1:eJzNjskNAjEMRY00SbwyiYACaIkSpgFqpSO+M4gbtznwlThenmPft+djOxHR
K83/6aZQ78P9aoOGrlBEjEscPan+rCw4ZnBWUFXVsZKZquxCChaxSS4Lh8us
TeKDFbyakOwUIFbh9JGfBtEsYVBrTFzQQ01IW0mqVXPHNGYO4VZ7z8RX7LkW
7hJnlzDPL99+wgpW
"],
Association["Book" -> 6, "Theorem" -> 8] -> CompressedData["
1:eJzNjcsNwkAMRA2Jszv+yCyiAVqihDRArXSEdxOQOHDjwDuM5JmR57reb+uB
iB5d/hBN2qmZXaJR07CI7pz910PL12SeplnkSGTZWkRMNrCRVuow9qDyyERe
ArAJDKOzt2oV1LeTYV4jykVASUrxVJCC3Q3MarnMpfuFOYLxiUhvzG4G1+h/
n2gaCjQ=
"],
Association["Book" -> 6, "Theorem" -> 9] -> CompressedData["
1:eJzNkMsNAjEMRI1E4m9i7aYCWqKEbYBa6YghLMuNEwdGykieebKlXLbbdTsR
0f1p/6gxRixQLkl4kamqmf3Xd+rX1gzmoKod0pcQwWewF1JmZ/Y2QN2062R2
SsRUjgQlplnNa0bGtTcSpZVLRGjh1sOdsQyGqTHLRyqCT8m0s7mpqzeAD2pQ
Cjg=
"],
Association["Book" -> 6, "Theorem" -> 10] -> CompressedData["
1:eJzNjcsNAjEMRI1E4l8cK7sV0BIlbAPUSkcMYVlunDjwJI/kmZF92W7X7URE
96f8JesaA+RIwrRMVc3sv35Tv6ZmEEer2oG+gAWdxh5ImZnZW1Dqpl1nZ2+J
mMrhIMQ2o/nNyLj2IFFauEQ0LRy9uTOOQbAFs3xQkZF9DDubm7p6oPgAVOIK
Lg==
"],
Association["Book" -> 6, "Theorem" -> 11] -> CompressedData["
1:eJzNkNENAjEMQ4NEm8RpGx1iAVZihFuAWdkIU47jjy8+sFRLsZ8SqZf1dl0P
InJ/2n/q3BYqlxS+lunumePXV+rXFqAFqYpd/hIj+gy2wsrsgLcRGvDhk9ko
M7jtCUtOs5rXINA6upjLSUtrzYv20SKUy2icuqp95Gb8lEwcEfDw6AQfPLUK
Ew==
"],
Association["Book" -> 6, "Theorem" -> 12] -> CompressedData["
1:eJzNkNENAjEMQ4NE28RJG91twEqMcAswKxthynH88cUHlmop9lMi9bLdrttJ
RO5P+1PFQuWSwheZZpY5fn2kfm0BmpOqOGQvMaLPYC+0zA54G6EBGzaZnVKF
6ZGw5DSreQ2CVkcXNVlbiQgrrY9wb1xG49Rb049MlZ+SiTMc5uad4AMkLQn/
"], Association["Book" -> 6, "Theorem" -> 13] -> CompressedData["
1:eJzNjcsNAjEMRI2E1/EnjqWtgJYoYRugVjpiCMuKEycOzGEizxvHl+123U5E
dH/av2qMiFWLSsfI7N2r/Nc3lq/UDJZoLXZIX0IEn8EOGk9m9jZVdlPX2dlb
rZm2IwHENBEOMQsJc+/ESi6MbgjGEGER6Y63ivVDWA6zTDv3DE0fgX8f+DEJ
wQ==
"],
Association["Book" -> 6, "Theorem" -> 14] -> CompressedData["
1:eJzNTcENAjEMy0m0idOoQtcJWIkRbgFmZaNzenASH148cFWrsV3ntj3u2yIi
z6S/xVjXuIbwIgIg9V+vqF9ddxKYqn4CB0pJ5shzwKaCdyBRu6Onf6bMHPZS
kCan+YuLVFU0O8VMAqW1Bmc+3CmjK4ryqfaB4X0Mv8xCNBZiB9YCCaE=
"],
Association["Book" -> 6, "Theorem" -> 15] -> CompressedData["
1:eJzNjdENwjAMRI1EYp9jpZANWIkRugCzshHnFCrxwxcffVFOse9i39bHfT2J
yDPluIwRlxBeRACU/u8N9afrTgFT1XewUUoqS54Nmx18AkldHEv6e8rMYe8O
0mQ1f3GRqormTDGTQGmtwZkPd7bRFUX5VPvi6n0MP8+BaJ3yAr/oCY0=
"],
Association["Book" -> 6, "Theorem" -> 16] -> CompressedData["
1:eJzNjksOAkEIRDGRhio6nUnGC8yVPMJcwLN6I+lPTNy4cmEtCFS9AMf5uJ8X
EXn28se6cQvhRpAAItqvD5SvKZkFSRW+hSnV3g1jBT6c+SkmVhrRMJhFuRO+
HPQwp8HnIVWIAZViLoRGRMZEdU8bzaBWaeYf2mvbd177wkDkQrwAnbAJdA==
"], Association["Book" -> 6, "Theorem" -> 17] -> CompressedData["
1:eJzNTsENAjEMCxJpY6eqTuoErHQj3ALMykYkbT98ePHAj0ixLduP63leNxF5
5fln8KD4QZAA6P3X+eV7O+MgXMXduYAF1bkoiS3YZNZSLFvpRMf0bJcZYZtB
ivElPIpUITUDpJoQGp0hE80saPQKrY212gdG62PwnoEOj0C8AYYuCWE=
"],
Association["Book" -> 6, "Theorem" -> 18] -> CompressedData["
1:eJzNjdENwjAMRA1NXPtiE4UNWKkjdIHOykY4KUXio398cIqekruL/Vi3Zb0Q
0bPjr1UaNVSrFUC7+6/H82mSpikBVyKLFgOGXborrOAw3oHkkQEHVHNPFQd7
SaDycQLxGlFsVC2EeY47NE52N81cLDaziHiRzLWyfiv+RiO5mXq59ZEvs9sJ
nQ==
"],
Association["Book" -> 6, "Theorem" -> 19] -> CompressedData["
1:eJzNkMsNAjEMRB2JxJ7Jb5cOaIkStgFqpSOc7ILEgdsemINlzxvZkm/b474F
EXmO8t/q0tdaagXYezt7e/qNQhDS/1M9lcjMXdgV4+imcQCbDsh3AVIjGmbm
SJkR9nEc+jSRH1RVUaBQzOSKmHN2TBbSbTRF1FpV7UsL2rrwMhZm5O7BF5Vy
CXw=
"],
Association["Book" -> 6, "Theorem" -> 20] -> CompressedData["
1:eJzNTcENwkAMC/TSJE7KcUIMwEqM0AWYlY3IXVV48eOBpViJbTm39XFfD0T0
7PTvaO7V41Tr5Xr+dff81SnTVIAjUc3UDMAxYBuY+zaETYcOxYCdMtRdw849
pDB9K0l5DSs/iggJc4BUKIQdbiyIUBVVXUxZWhOPDzQC5gGUxcNyPCtfoeQJ
ng==
"],
Association["Book" -> 6, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 6, "Theorem" -> 22] -> CompressedData["
1:eJzNTckRwkAMMySO5WPJMqmAlighDVArHeF1mOHFjwd6yLakkW/7476fiOg5
6O9hcQlvbd22/uvq5aszT9Psfia6ZmqxgruZHmAeW96u5ZihFK3EO8Y5bYT0
SGUIphh76kV5lZUfRYQke40gFMKe3SwWAQiApmDpXTw+wKAUbG4R2jzyj74A
jHEJlQ==
"],
Association["Book" -> 6, "Theorem" -> 23] -> CompressedData["
1:eJzNjd0NAjEMg4N0bWKnP+KYgJUY4RZgVjYiLcdJPPDGA1Zlpf6s5Lrdb9tJ
RB7D/l+11Eqi9/brzfkrWeKRMXi0Mg/hpZTGNIMd2ExAvg3IjWiYnb1lRtiR
BIzfRHFIVUWBQjGTFcndA5OFjBhNkbRWVftQZ7ucuRSMk97DnmCGCVM=
"],
Association["Book" -> 6, "Theorem" -> 24] -> CompressedData["
1:eJzVUMERwjAMMzSJLTtOr3ddgJUYoQswKxvhpAVe/fFBDzmydMqdb9vjvl2I
6NnpD1DXFcA8t18Xl1MnTVNSvRIZERcz0x3YUUp/jcVhSB6e6psi1BQNI3Ok
RBTy2YQZqsv4hGKQcmlOAlo4u1dk9lbNOMqcu3Jm+QIicZRl0dQLAbOgF229
CXE=
"],
Association["Book" -> 6, "Theorem" -> 25] -> CompressedData["
1:eJzVjcEVwkAIRNHIAgOb+IwN2JIlpAFrtSPZTaInb16cA2+Y+Q9uy+O+HIjo
2cY/CDZf56jnX98t36thIOBIFEkVd8cqW8XcXA+2QntiwD4Ssg2ynVKF6Ttp
jHbA8yGzkDC7kxhdhGtUzxVRCosIXDKr7PGRRYzmGHGKCRZp8+4LU7IJTg==
"], Association["Book" -> 6, "Theorem" -> 26] -> CompressedData["
1:eJzVTcERwjAMMzSJLcdx6B0LsBIjdAFmZSOcttAXPz7oIVuWTr4tj/tyIqLn
oL/AFUDv/uva8tVJ05RUz0SViIuZ6QZsKGVs62E3JK+e6psi5ArHmtlTIgr5
XMIMNaTFxxikXLyRgC6cWzNkbm61cpQ1HqoxywGIzN37rElNYag1gi9KfAla
"], Association["Book" -> 6, "Theorem" -> 27] -> CompressedData["
1:eJzVkMEVwyAMQ90GsC1smKErdYQskFmzUQ1J21NvvUQHg6z/xHs81u253oho
H+MaUqD39u/W8jNJy5KAO1ENqpgZDumhUsZtLs5A8syA9wioQZtO5qREoPLZ
RBhuWIsX4yBwaU6i1Dm7m2b2ZrVylBkP58zylYrEp/SOBBuV6gG+ADQPCT8=
"], Association["Book" -> 6, "Theorem" -> 28] -> CompressedData["
1:eJzVjUEOwkAMAwMl2Th1BEJq73yJJ/QDvJUfsbtt4cSNC5ZiRfYouS2P+3IQ
kWezP9E8kZdfH7Xv1TBIxFGElTKSsQqrVNvWg63wniBitwphg7BT7gF/J43x
DtQnoqptIsQgV9Nk9jc001JKRCmaqSM/AisDZJx4Bphju/sCKeAJIA==
"],
Association["Book" -> 6, "Theorem" -> 29] -> CompressedData["
1:eJzVjbsRAkEMQw2H12tZe8cQkNMSJVwD1EpHeO8DERkJCjQe6Y11mx/3+SAi
z27/oit5/vXP8r0aBgGOIkyqkMQqX6XaryXYirokDuyWkG+Q71St8PpOOlMX
IEdE1cRUI8RcLqaNLWcCLEXNDLDMmgY/cnL0wIgTJ3iLiPz7AhRJCRs=
"],
Association["Book" -> 6, "Theorem" -> 30] -> CompressedData["
1:eJzVTcsNwlAMC5T0JY4jKjZgJUboAszKRuS9Fjhx44KlRPFH8XW939aDiDz6
+huQy69fzt+taRLgWK2VmsnEBt+g2q8h7IYNxYHXqlDAw0dmT5nB7a2UWazT
KpHWWh93UZdL00yyU5pp6UBzJTX4gZGByMTpTDgjqs2fAB4JFA==
"],
Association["Book" -> 6, "Theorem" -> 31] -> CompressedData["
1:eJzVTsENwkAMC1JzOTtBJ9igKzFCF2DWbtSkpfDixwcrZ8V2lNy8PB/LRUTW
ov/BGL/e2L4mUxaZTb7W3J0HcEC1ut14BX13QJ6UQ5WCJ9dQJ/rbSUpV0vMQ
YGKqQUGXu6nT6wwjg8QVpoabeXzQI/JfwzkBKTxq5QbvWQj7
"],
Association["Book" -> 6, "Theorem" -> 32] -> CompressedData["
1:eJzVjcENAjEMBA2XnL1rR0oLtEQJ1wC10hGOT4gXPz6MIitxVrO343E/LiLy
XOOPmL8W7l9/2rY18lqd+07S6xAnva8b14InVhuQ75GhIAKVgRdmhCE98BUK
5KsE2aiqoumlmMrQnnF0ZYSZmlnAus6pHh8sVkOQbfjA8EgrXuyaCQw=
"],
Association["Book" -> 6, "Theorem" -> 33] -> CompressedData["
1:eJzlTdsNgCAQOxOBewDO4EqOwALO6kYWotH7cQGb3KPXQte2b20ioqO3PyN+
qqpoAldUQN4IwVGI7C/DZCLmLsyoh9rNdKQlwkcITUxZw1IrVJUrOCcJ/X1i
h6JWisx9hTVjnLAjCHo=
"],
Association["Book" -> 7, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGFGBkHHJOpjcAAJhIAn0=
"],
Association["Book" -> 7, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGFmBiGmgXDHYAAJloAn4=
"],
Association["Book" -> 7, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGGGAaaAcMdgAAlyQCfA==
"],
Association["Book" -> 7, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHGBEB2ARoDhIClMWG2BAplHMBpuBbBedPUc5AADe
BQLH
"],
Association["Book" -> 7, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHmBkZGACIiYGIGZkBNKMQAAUBsuASSTAxIgFMCBh
lDAAcpgYUa0aagAA3vACyA==
"],
Association["Book" -> 7, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGIGACo1GAFQAAmVACfg==
"],
Association["Book" -> 7, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGJhi6Lqc1AACV/AJ7
"],
Association["Book" -> 7, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGJGBiYGRiYoRiBkYgYGAAIUYwGxkwoQuAFSPTyOYC
OUzIAoxDL4QA4bYCyw==
"],
Association["Book" -> 7, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGKmBhAWImIGBhYAQCBgYmBiCDgZEBzIUAkCyIZmFi
RAEMEMwE1YkAIGOQBRiHXggBAO5yAtg=
"],
Association["Book" -> 7, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLmBiIl4UizpqOmUQAQCe5gKE
"],
Association["Book" -> 7, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLGABIiYgYGFgBAIGBiYGIIOBkQHMhQCQLIhmYWJE
AQwQzATViQAgY5AFGIdeCAEA6hIC1A==
"],
Association["Book" -> 7, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGMmBlAgJWBkYgYGBgYgAyGBgZwFwIAMqygWhWJkYU
wADBTAxMTIwoYQAyBlmAceiFEADsTALX
"],
Association["Book" -> 7, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGMGDGKohVlEjNwwAAAKCmAoY=
"],
Association["Book" -> 7, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGG2BmJlIdbZ0xYAAAnWcCgw==
"],
Association["Book" -> 7, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNGACAjYGRiAAshmADAZGBjAXAoCyrCCalYkRBTBA
MBNQPyNKGICMQRZgHHohBADnBgLS
"],
Association["Book" -> 7, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNmBhYmJjYAECIJOBgZkZiICAhQVMMbOxsbGCaFYo
HwYgqphZGJiYgBwkAOQwIQugyg4JAABadQNP
"],
Association["Book" -> 7, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGOGBiYmJgAQIGBiBiZgYiZmZGFhZmGGACC7AyowAG
CMUCppFNA3KYwAKMYMSAKjskAABE6gM6
"],
Association["Book" -> 7, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGOmBmYmAGAiADiFgYWJiYWIBcFhDBzAQEIJqRkRkF
gHSAlEF1IhnGwMDEhMRnYaGzbygHADl2Ay4=
"],
Association["Book" -> 7, "Theorem" -> 21] -> CompressedData["
1:eJzVy9ENACEIA9DSFPdwJUdwgZv1Njrqj94IvhBCQ9rnM2YAeL2uR6gAHkGk
MrVkoY8I/bjhB1pzc6tAnlm4zQdqfQNk
"],
Association["Book" -> 7, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGAWAEAgYGJhCDgRHChQAmJiZWEM3KxIgCGCCYiYGJ
iRElDEDGMKKYTGevUA4A2CACxA==
"],
Association["Book" -> 7, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 24] -> CompressedData["
1:eJzdj8EVgDAIQ1NaknYMV3KELuCsbtTCybsH3/MDCeHGMa9zFgB3yB8YYwAC
SLBWuuR7JJLp1aio3pUgbuFmWx7sYB5LyUZrn/zzhgXesgPj
"],
Association["Book" -> 7, "Theorem" -> 25] -> CompressedData["
1:eJzdj9EJgEAMQ3NtmuoYruQIt4CzutFdBcF/PwRfQ1tCKHTrx94bgLPaL1gX
IAEJclcEp8iQVJNuYtUNyiMTZpnPO8S0ammXZu6Td94wAIljA4U=
"],
Association["Book" -> 7, "Theorem" -> 26] -> CompressedData["
1:eJzdj+EJgFAIhO/pebZGKzXCW6BZ2ygNgv73I+jzUDkOwXXu2xwAjm7/YAES
kCB3RbBEhqSedBO7btAemTDLfJ4hyuplXKrcJ9+84QSAAAN8
"],
Association["Book" -> 7, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGDWBnYGBjY2BjZmZjZWdnBWJ2djY2NjDNzMTGDoIc
HOxgwAASA9FMTEAC1QwmVhCDEYwYWFgGxCuUAADCiQPI
"],
Association["Book" -> 7, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGE2BjY2BjZmZjZWUBIhYWVjY2NhDNwszExgKCMMAA
EmNh4WRgYmJnRzaAhQEoBGIwghFQ3YD4gxIAAHIpA28=
"],
Association["Book" -> 7, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGESDPO8MsEACWtgJ8
"],
Association["Book" -> 7, "Theorem" -> 32] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGPBhmgQAAlbECew==
"],
Association["Book" -> 7, "Theorem" -> 33] -> CompressedData["
1:eJzdyYENgDAMA7Aky7a+wUucsAe4lY/oJiHBCWC1UaNu49gHAZwzfiUQpYTk
1myLZO2JDIe7b8gtdoWV5SGLNA+uwfv7CRdjZQNf
"],
Association["Book" -> 7, "Theorem" -> 34] -> CompressedData["
1:eJzdj7ENgFAQQuEO9N8YruQILuCsbqRfY2JvYeILoYBQMC3rvBDA1u1nVGZF
usp2kvRwQDY3j75BL6WEIuK5FnAFPAXpkxNv2AFslwNp
"],
Association["Book" -> 7, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 7, "Theorem" -> 36] -> CompressedData["
1:eJzdj8ENgDAUQuF/0HYMV3KELuCsblSrMfHuwcQXwgHCgaVtayOAfdjfyKyR
rtV2kvR0QBYXz77BKKWEIuI5FnAFPAXpkw9v6GOOA2A=
"],
Association["Book" -> 7, "Theorem" -> 37] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGHWCmqrIhBwCaZwKA
"],
Association["Book" -> 7, "Theorem" -> 38] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGKmAeaAfQCAAAl2oCfQ==
"],
Association["Book" -> 7, "Theorem" -> 39] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGIWBiZeXkZGVlZWFkZGQFAUZGDlYOVnZWGGAAYmYW
FmYGFiYmJmSdLEDNYAFGMGJgYRkQD1ACAFPWA1A=
"],
Association["Book" -> 8, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGI2BlAQNWIGADMRgZWVAAAxAzQ2kWZI1ADhMTMp+F
YagBADvWAzY=
"],
Association["Book" -> 8, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGJeBkY+Pk5ORmAwIOIGBmYmVnZWdhB7HZgYABiJnZ
2VkYWIAAWR87AwMTK4jBCARAClV2SAAAnxIDpQ==
"],
Association["Book" -> 8, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGJ2Bj5+Hh4mFkZGTlAQJGRhYOFg5WDi4ODk4OIGAA
YmZ2diYGFhYmJmRt7AwMTOwgBlAnKHBYWAbE9ZQAAKLzA6o=
"],
Association["Book" -> 8, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGKeBkY2NjYmRkZAXSbIyMHKwcrOxANisYMAAxMwsL
MwMLExMTsi4WBgaIACMYMbCwDIjjKQEARbsDQg==
"],
Association["Book" -> 8, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGK2BjY2VmZGRkZQMCRkZ2NiAEsllZgYgVLMnCwsTA
wsKIEgYsDAxMTCAGUCdIgoVlQNxOCQAAQCsDPQ==
"],
Association["Book" -> 8, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGLeDjYWNkZGTlBQJGRhYOEOTi4ODkAAIGIGZmZ2dh
YAECZD3sDAxM7CAGUCcocFBlhwQAAJCEA5g=
"],
Association["Book" -> 8, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGL+BhY2RkZOUFAkZGFg4Q5OLg4OQAAgYgZmZnZ2Fg
AQJkLewMDEzsIAZQJyhwUGWHBAAAgwIDig==
"],
Association["Book" -> 8, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGMWBjZGRk5QUCRkYWLiDk5ODg4uEAAgYgi5mdnYWB
BQiQdbAzMDCxgxhAnaDAQZUdEgAAf3kDhw==
"],
Association["Book" -> 8, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGM2ADAg4gYGZiZWdlZ2EHsdmBgAGImdnZWRhYgABZ
AzsDAxMriMEIBEAKVXZIAABl+QNq
"],
Association["Book" -> 8, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGNWBnZ2UGAlYWZhTAAKFYGJiYgBwkAOQwMSHzmRmG
GgAAA+IC+Q==
"],
Association["Book" -> 8, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGN2BnZQYCVhZmFMAAoVgYmJiAHCQA5DAxIfOZGYYa
AAD9LgLy
"],
Association["Book" -> 8, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGOWBlBgJWFmYUwAChWBiYmIAcJADkMDEh85kZhhoA
APaQAus=
"],
Association["Book" -> 8, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGO2AEAlYmRhTAAMFMDExACRTFDAxMjCia6exaygEA
urYCpg==
"],
Association["Book" -> 8, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGPeAV4GVkZOEAQS4ODk4OIGAAYmYgYmBhYWJCVsvB
wMDEDmIwAgGQYmEZECdTAgBfIQNk
"],
Association["Book" -> 8, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCKGP+AXYGRk4QBBLi4OTg4gYABiZnZ2ZgYWFiYmZKXs
DAxM7CAGIxAAKRaWAXExJQAAVC0DWA==
"],
Association["Book" -> 8, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAOBlZGThAEEuDg5ODiBgAGJmIGJgYWFiQlbJwcDA
xA5iMAIBkGJhGRAHUwIARB4DRw==
"],
Association["Book" -> 8, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAmBkZOEAQS4uDk4OIGAAYmZ2dmYGFhYmJmSF7AwM
TOwQHYygwGFhGRD3UgIAN2sDOQ==
"],
Association["Book" -> 8, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGBGBiRAEMEMzEwASUQFbHCFKKzB96IQQAsmACnQ==
"], Association["Book" -> 8, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGBmBGAVAuCwMTE5CDrIwBKISijc7upBwAAN5lAtE=
"], Association["Book" -> 8, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGCGDhYuFkgQEGIGZmYWFiYGFiRAkDFgYGJiYQgxGM
gOoGxLGUAAD1qgLs
"],
Association["Book" -> 8, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGCmDhY+Hm5ODh4eLk5GTg5eJk5uFhZmBhYWJCVsTD
wMDEBWIwAgFIE8uAuJUSAABP2QNX
"],
Association["Book" -> 8, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGDGDhZIEBBiBmZmFhYmBhYkQJAxYGBiYmEIMRjIDq
BsSplAAA6PYC3g==
"],
Association["Book" -> 8, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGDmDh5uTg4eHi5ORk4OXiZObhYWZgYWFiQlbCw8DA
xAViMAIBSAvLgLiUEgAAP5cDRQ==
"],
Association["Book" -> 8, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGEGBhZYEABiBmZmFhYmBhYkQJAxYGBiYmEIMRjIDq
BsShlAAA3igC0g==
"],
Association["Book" -> 8, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGEuDg4OHh5OLiYuDj5GLm5WVmYGFhYkJWwMvAwMQD
YjACAZBiYRkQd1ICADfGAz0=
"],
Association["Book" -> 8, "Theorem" -> 26] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGFODg4OAEYgZOTg5mTk4mBhYWJiZkeU4GBiZ2EIMR
CIAUC8uAOJMSAAAQHQMO
"],
Association["Book" -> 8, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGFuDk5AACBiBm5uBgYmBhYUQJAw4GBiZ2EIORESzB
wjIgrqQEAAAEIgMA
"],
Association["Book" -> 9, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGGODjAAIGTg4OZi4uFgYWIECW5WJgYOIEMRiBAEih
yg4JAAAOWwMN
"],
Association["Book" -> 9, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGGuAAAgZODg5mTk4WBhYgQJbkZGBg4gQxGIEASKHK
DgkAAP+OAvw=
"],
Association["Book" -> 9, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGHODh4Wbg4uVh5uZmYmBhYUQJA24GBiYOEIORESzB
wjIgTqQEAAAIPQMG
"],
Association["Book" -> 9, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGHhDgY+Dj4WHm5WViYGFhRAkDXgYGJh4Qg5ERLMHC
MiAupAQAAA5GAw4=
"],
Association["Book" -> 9, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGIOBj4OPhYeblZWJgYWFECQNeBgYmHhCDkREswcIy
IA6kBAAAAGYC/g==
"],
Association["Book" -> 9, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGJODi4WHm4GBiYGFhRAkDDgYGJg4Qg5ERLMHCMiDO
owQAAOGpAtk=
"],
Association["Book" -> 9, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGJuDiZObjZ2ZgYWFiQhbmZ2Bg4gUxGIEASLGwDIjr
KAEA60YC5g==
"],
Association["Book" -> 9, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGKOBh5uJiYmBhYUQJAy4GBiZ2EIORESzBwjIgjqME
AADTBALI
"],
Association["Book" -> 9, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGKmDmZWdiYGFhRAkDdgYGJnYQg5ERLMHCMiBuowQA
AMaSArk=
"],
Association["Book" -> 9, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGLhBgZmBhYWJCEWJgYOIDMRiBAEixsAyIyygBAM8v
AsU=
"],
Association["Book" -> 9, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGMGBmYGFhYkIOBCEGBiY+EIMRCIAUC8vAuIwCAADE
JAK4
"],
Association["Book" -> 9, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGNGBiYmdH5rOAhEAMRjBiYGEZEGdRAgCwogKe
"],
Association["Book" -> 9, "Theorem" -> 15] -> CompressedData["
1:eJzlkIENwzAIBEllAjzEO3SljJAFOms3CthKInWFnjDPA5Ylv4/PfixE9K30
1zAvv3/wuit3as2IkLibWZ3JKsMn2fSh65j6zHOrV1TnvogRF/1yyNdSSEVi
I1UKYQRYOCzMWERyJKzKog9ZY+uAtXIwlJzbDAij
"],
Association["Book" -> 9, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGNmBjYUHmAjlMTMh8FoahBgCr8AKY
"],
Association["Book" -> 9, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGOGBhQeExMDAx4ZQdEgAApwQCkg==
"],
Association["Book" -> 9, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGOuBE5rAwMDAxgRiMYMTAwjIgbqIEAACpQQKV
"],
Association["Book" -> 9, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARJgYWBgYgIxGMGIgYVlgB1EOgAAofECjA==
"],
Association["Book" -> 9, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQMjI4RkHA7hAQCZkQKA
"],
Association["Book" -> 9, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARQMk8AAAJWpAns=
"],
Association["Book" -> 9, "Theorem" -> 23] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQwwMTENtBOoAACZgAKA
"],
Association["Book" -> 9, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQgwMg6XsAAAlz0CfQ==
"],
Association["Book" -> 9, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARgwDpewAACWcwJ8
"],
Association["Book" -> 9, "Theorem" -> 26] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQQMl7AAAJWqAns=
"],
Association["Book" -> 9, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARwwMQ20C6gAAJf0An4=
"],
Association["Book" -> 9, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQIwD7QDqAAAly4CfQ==
"],
Association["Book" -> 9, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 32] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGASpg4gORjEAApFhYBtg1pAMAqUoClg==
"],
Association["Book" -> 9, "Theorem" -> 33] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 34] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 9, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARpgRmIzMQ2YM8gFAJnpAoE=
"],
Association["Book" -> 9, "Theorem" -> 36] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGATbACARAioVloB1CMgAAnVgChg==
"],
Association["Book" -> 10, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGASZgHMIBAwCWWQJ8
"],
Association["Book" -> 10, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGARbANNAOIB8AAJZYAnw=
"],
Association["Book" -> 10, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQ7ANtAOIA8AAJksAoA=
"],
Association["Book" -> 10, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAXbAzsLAwDrQjiADAACgSgKK
"],
Association["Book" -> 10, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAQ7AwsDAOtBuIAMAAJtCAoM=
"],
Association["Book" -> 10, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 9] -> CompressedData["
1:eJztjcENAjEMBH0Ske1dx748EG9aooRrgFrpiASQeNEB81jJs1r5etxvxyYi
jxV/fnI+bVuJmAEITqrG2PfMVOXMpXLKulS5LwO+fS4UlZhHJbNeuFfGx3CV
6WtCzGeqKtpaQEwltBH0pogwUzPrbk3HUMYXi4AzUKeewc4gOp5sEQo6
"],
Association["Book" -> 10, "Theorem" -> 10] -> CompressedData["
1:eJztjssNAlEIRZlkXvhcHszbuLclS5gGrNWOBDVxZQeexU04QOB63m/nRkSP
jj+/2bctiUTM4Cgy1zqOiGBGZasomZdM1TaGt5/RQ5ZhVWQg8oVqhn8Muhna
K7C6xczEY7iRMDkPGHSwuYuwiEyVwWsx/Iu4m8It9xmOWT/a1Cdc2goj
"],
Association["Book" -> 10, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGAT7AM9AOIBkAAJ06AoY=
"],
Association["Book" -> 10, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 14] -> CompressedData["
1:eJztjesNAkEIhDGRGxjYvcQObMkSrgFrtSPZXR8/bcAvYQLDBK7H/XacROQx
5M8vto0MrvKF6ug4DC5sOk6+pUJBD5+ZV8qMbh+nljXNVX0BIFDNFIVcoK1l
KrKnGcysuwH7jsgvPrV3nls0j+rq7hOxRAjb
"],
Association["Book" -> 10, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 10, "Theorem" -> 17] -> CompressedData["
1:eJztjdsNAkEIRdnEXeZygdiCLVnCNmCtdiTDRP20AU8Iz5NwOx/3cxOR50x/
fnJ1D5Ag3rjPnuwlaRXRV668pASyN2y1JAMCH6Putsx6YmZiemSIQkJ3d8eu
UZ+oU9GabKiOLxgjIzNx6amo8gLS+wjR
"],
Association["Book" -> 10, "Theorem" -> 18] -> CompressedData["
1:eJztjdsNAkEIRdnEXeZygR5syRK2ga3VjmSYqJ824AnheRLu5/U4NxF5zvTn
N+4BEsQb99mTvSStIvrKlZeUQPaGrZZkQOBj1N2WWT/MTEyPDFFI6O7u2DXq
E3UqWpMN1fEFY2RkJm49FVVeyCsIwQ==
"],
Association["Book" -> 10, "Theorem" -> 19] -> CompressedData["
1:eJztjcsNAzEIRIkUGwZjLGsrSEspYRvYWrej4I+UawrIOyAz84Rf5/U+H0R0
j/HnB46mCyxyHq8Z7ELS7JaxtOwKx3S2JaKQnWCUsQ2O+CJSUs5eSUCNk5kh
cXUrhUOpHJsps3yBSG/euz7nQZQa4wOv0Qi0
"],
Association["Book" -> 10, "Theorem" -> 20] -> CompressedData["
1:eJztjcsNAzEIRIkUGwZjLEvbQFpKCdvA1rodBX+kXFNA3gGZmSf8Oq/3+SCi
e4w/v9B0gUXO4zWDXUia3TKWll3hmM62RBSyE4wytsERP0RKytkrCahxMjMk
rm6lcCiVYzNlli8Q6c171+c8iFJjfACjbAii
"],
Association["Book" -> 10, "Theorem" -> 21] -> CompressedData["
1:eJztjesNgDAIhDGx5VFLdQRXcoQu4KxuJLQ+/jqAH8klx11grftWBwA4XH4+
IR3uxOhq1qZDoQV3oZVUWD1/WkTCdG3YQ3PO3B+AYNQMxLBgyHnigFmnlNAq
JgFFEOmFiUrRUmRsBzm5nJV3CIE=
"],
Association["Book" -> 10, "Theorem" -> 22] -> CompressedData["
1:eJztjO0JgjEQgytY7jN922sXcCVHeBdwVjfyioJ/HcAHLhxJyO183M9LKeW5
5c9vRMzVmjs2ZjN1zbmwGnAALNvpEaljfEoNhhUNC29YsoyZTmDsEII+xrDc
F6FCtaoWogKqaiqV1D0DZoZwpd7J/Au7K/KOK1p+5iqQF2ieClw=
"],
Association["Book" -> 10, "Theorem" -> 23] -> CompressedData["
1:eJztjLsNAkEMRBcJy5/12LvcBaS0RAnXALXSEV4ISCmAJ2uCNyPfjsf9OLXW
niv+/Mh1zAgzLMxm5Swwwr1OdZmxbZVx+YwQa7QHJvyNapTbyuyYq4RizMys
98zcmMisEbfOJGZKbO4iLCKuQpzJ3b+IOyIgeUaH9aoU+gJJdAoi
"],
Association["Book" -> 10, "Theorem" -> 24] -> CompressedData["
1:eJztjMsNAjEMRIOE5U88drK7DdASJWwD1EpHOHDgSgE8WXN4M/LtfNzPS2vt
ueLPr4wZYYaF2aycBUa416kuM/a9MrbPCLFGR2DC36hGub3MgblKKMbMzPrO
zI2JzBpx60xipsTmLsIi4irEmdz9i7gjApJXdFivSqEvOcwKCg==
"],
Association["Book" -> 10, "Theorem" -> 25] -> CompressedData["
1:eJztjN0NAkEIhNdEwj97CxVcS5ZwDVirHcn64qsFOCFfyMDMeT0f122M8dr4
62dVhKqIi6tWsypLsr0elu1kZnMdDe+ncPXK8Op9iyXcOhaevvZxR9Za1uXM
OBDAbACORCAVBrQwIiQiYwKcE9W+4g/jmPeuElUTdn4DLR4KAQ==
"],
Association["Book" -> 10, "Theorem" -> 26] -> CompressedData["
1:eJztjMsNAjEMRINE5PFnrIQlKzjSEiVsA9RKR2S1F44UwDvY1huNH9vruZ1K
Ke99/PkdMxy4D4C3Me5cM9MyVXfTloXkpc+TnB6JsSRXHjUNw3Q0EL6HDLTe
+3X+FtECkWCBFmq1MJUaGu5VVSla5674QoCWvXU/U81dPYz2Afe/CWA=
"],
Association["Book" -> 10, "Theorem" -> 27] -> CompressedData["
1:eJztjTEOwlAMQz8SX2nyEzulrcTKlThCL8BZuREpCzN73xAlsWU/9tdzv7TW
3sc4+YN7OEDFGFkzk6nc5gMz1icQVCKhQJk2DmSsTHw9s9pCq4CVYB5iXcEl
rKJFpEnvZq1ru0mPcO9i7tOkBVRFq2L4jxLrrKYrHLWHD+oHP4EKRg==
"],
Association["Book" -> 10, "Theorem" -> 28] -> CompressedData["
1:eJztjUESAkEIA8cqp1gYSNjV8e6XfMJ+wLf6I1kvnr3bhxSQFLnvz8d+aq29
DvnzC+ERVIyRpZlM5VwPzFiXQLlEQoEK3TiQMZn4ZFa1Kw3gJJiHWVvwElaf
RaRJ72ata9ukR7h3Mfdl0QKqolUx/EuZtVbTGY6awwf1DTDxCjE=
"],
Association["Book" -> 10, "Theorem" -> 29] -> CompressedData["
1:eJztjLERAkEMA80MHvtsWf9D8DktUcI3QK10hI8LiMnZQMHK1v18Ps6LiLxm
/PmJY99JqmZnNswgi4wxTeXynGhX3X9yEREMog24dMyXjB42MzFVQNTkZloF
qIFwN3fncLNts8SXAQTQu9e+7aIYFW/gBQly
"],
Association["Book" -> 10, "Theorem" -> 30] -> CompressedData["
1:eJztjLENAlEMQ4NE5FziWCc2YCVGuAWYlY3I5wpqel7h4jnx/Xg+jouZvVb8
+Y19l+RekzWoUmopsUzX6bXwqab/5ElmKsUx1KlzvVTOLgCDO2kOu8G7SQfF
CESEtgAkFL9sZCZn9zq3U7Sy8w3QtglW
"],
Association["Book" -> 10, "Theorem" -> 31] -> CompressedData["
1:eJztjDEOQjEMQ4tEiJrGTtWRjStxhH8BzsqNcGFgZucpciLHye143I9Ta+25
5c+PXFmMmNIpatZaquglBwXp2OMnFOrk5Hqzna4QCQ5qqUJVpd6aeXMzoGlY
bshMczAvFxfsW+gjv0Qm+tD9mQNaAIF4ARq0CfI=
"],
Association["Book" -> 10, "Theorem" -> 32] -> CompressedData["
1:eJztjMENQjEMQ4tEftQ0dqpuwEqM8BdgVjbChQNn7jxFTuQ4uZ2P+3lprT23
/PkVFiOmdIqatZYqeslBQTr2+AmFOjm53mynK0SCg1qqUFWpr2be3AxoGpYb
MtMczONwwb6FPvJLZKIP3V85oAUQiBcKjgnY
"],
Association["Book" -> 10, "Theorem" -> 33] -> CompressedData["
1:eJztjEsOwjAMRI2EXcefpkosUthxJY7QC3BWboSzYt09bzHyaJ78PN6v4wIA
nxl/TtOHSH30qEmGe7gL1qFhbiPCbPSIntJdYnMfNYUJs+9l3ruHzfHGKW9W
8ikiAhKVAqjQFnSzmlWMiJhZlBcyI7Uf2bWUdV2vIhqa9Na+MjQKMQ==
"],
Association["Book" -> 10, "Theorem" -> 34] -> CompressedData["
1:eJztzLENQkEMA9BDIrnLJXEC5EsIKlZihL8As7IRHxpqel5hybLk2/q4r7vW
2vMdf79biBLXyrQ8WwAGDElcygNxLou81nKiqZiVoZGFjzEAKaQGyt5jjHJP
t+2TiBoxizTSduzkZrHVaczcexftwu6s9sVmQ8Qc+zknVHQeEC8N1AnN
"],
Association["Book" -> 10, "Theorem" -> 35] -> CompressedData["
1:eJztzTEOwkAMBMBDwo59Xm9OBHFp+RJPyAd4Kz/ikoaeOlOs5LVkP7f3a7uU
Uj57nP4gAi4dw4I5855pDkZnm/e+jeiL1GBd0YLoeXAjfeVo2op9SXskGnCc
lCKq7kWi3CZJYB5jhaqaWQ2bNFMDPwqEO5nXOl6FRzTyC+x2CZw=
"],
Association["Book" -> 10, "Theorem" -> 36] -> CompressedData["
1:eJztjNENw0AIQ4lUZMxx1SkbdKWMkAU6azcKXNXmP995EjYGya/9ve2LiHxK
bq6wNpItYZvWvNcl96kl7IMc8/LNpHsO/4xfimxMEwOii5kE1MMVGgxSAeQL
aqawk9y9P7P0UcnpZQdL/AfT
"],
Association["Book" -> 10, "Theorem" -> 37] -> CompressedData["
1:eJztjNENw0AIQ4lUZMxx0a2QlTpCFsis3ahwUZv/fOdJ2Bgkb/vx3hcR+ZQ8
3KKRbAnbtOa9LrlPLeE6yDEvZybdc/hn/FJkYZoYEF3MJKAertBgkAogX1Az
hV3k7n3N0lclp5d9AUGeB8I=
"],
Association["Book" -> 10, "Theorem" -> 38] -> CompressedData["
1:eJztjEsOwjAMRINE5PFnHKWlgS1X4gi9AGflRqSsWLPmLcajN5Lv+/Oxn0op
ryP+/AbAcR2DW2ZaptptmmVdSS59VnJ6JLY1OYgPGobpaCD8GBlYeu+X+U9E
C0SCBVpCq4Wp1NBwr6pK0TpvxRcCtOyt+Zlq7uphtDev8wjp
"],
Association["Book" -> 10, "Theorem" -> 39] -> CompressedData["
1:eJztzE0OwkAIBeAxEcrwMzQz1LbuvJJH6AU8qzeSrty79lsQXnjhcbyex6WU
8j7H349GeBruZmHG4HcJNV1HqO4jYjD7zststnoWTkS21SWXzRY9jzfK8qw1
3wFAAcRaC0jpE5iqZ2RFRCJioQlVUfQrs9TaWrsyS0gavX8A9vYJ0Q==
"],
Association["Book" -> 10, "Theorem" -> 40] -> CompressedData["
1:eJztzMEJQkEMBNAVTHazSSZRI3wED7ZkCb8Ba7Ujv168e/YdBoaBua2P+7pr
rT3f8feryrRcLAADhiQu5YFYyiKvdT7RVMzK0MjCxxiAFFIDZe8xRrmn2/ZG
RI2YRRppO3Zys9jqNGbuvYt2YXdW+2KzIWKO/ZwTKjoPiBfaFwl3
"],
Association["Book" -> 10, "Theorem" -> 41] -> CompressedData["
1:eJztzEEOQjEIBFBMpC0w0GoT3XwXXskj/At4Vm8kdeXatS+EZCCZ+/587Aci
eq319zOkie4+3ZvAsMXoMTcMxe0ym2poYFjg2j9EPCwir3ru6xkCx4BlGTMT
l6JKLCTMrTFW5FpzqlktrGD5ksHllJVHiJpJNI94A6VYCNQ=
"],
Association["Book" -> 10, "Theorem" -> 42] -> CompressedData["
1:eJztjDEOwkAQAw+J09m7602OJCBKvsQT8gHeyo84qKipmcK2bMm3/XHfD6WU
51v+/M62XnXJTMskN0Dzskg69RGl0SOxLamz8IFhGJ0Mgr9HBebe+zq+WmNB
a6EClmC1MLYaDPdKUo11eMUXDZiyT92PornTw2QvjvAIsQ==
"],
Association["Book" -> 10, "Theorem" -> 43] -> CompressedData["
1:eJztjMsNwkAQQxeJ1Xg+nmSzJIgjLVFCGqBWOmLDiTtX3sG2bMn3/fnYT6WU
1yF/fmC98ZqZlqm2AZx7J7m0EcnRI7H25EZ80DCMjgbCj5GBubV2GVciWiAS
LNASWi1MpYaGe1VVitbhFV8IMGWbmp+p5q4eRnsDhG4Inw==
"],
Association["Book" -> 10, "Theorem" -> 44] -> CompressedData["
1:eJztjLsNwzAQQxUgwvE+PEGWod4rZQQvkFmzUeRU6dPmFSRBAjzO5+O8lVJe
l/z5hcmZmZapNgFuY5Dc+ork6pHYR3ISHzQMq6OB8GtkYOu97+tJRAtEggVa
QquFqdTQcK+qStG6vOILAVr21vxONXf1MNobdzMIhw==
"],
Association["Book" -> 10, "Theorem" -> 45] -> CompressedData["
1:eJztjDsOAjEQQ4NEFHtmPErYT8+VOMJegLNyI7JU9LS8wrZsyffj+TgupZTX
KX9+QntmWia5AerLIuk2ZpRmj8S2pHbhA8MwOxkEP0cF+hhjnUetsaC1UAGL
WC2MrQbDvZJUY51e8UUDeo4+/CqaOz1M9gZo2ghx
"],
Association["Book" -> 10, "Theorem" -> 46] -> CompressedData["
1:eJztjDsOwkAMRI2EN/7OJspSpeJKHCEX4KzcCC8VPS2vGM/TSL6fz8d5IaLX
jD+/sXVgB0TD15HoOEZ0P8ZtFwuYlWAd9kHU4HWjAnOEWuaao/4wM3FrZsRB
yizCPpWXpbq4SWML1i9KUrdMv4aau7ok8AZvTwhm
"],
Association["Book" -> 10, "Theorem" -> 47] -> CompressedData["
1:eJztjLsNAkEQQxeJ1Xg+nrth4XJaooRrgFrpiD0iclJeYFu25Pv+fOyn1trr
kD8/kpmWqbYBXMcgeakZydkjcRvJjfigYZgdDYQfIwNrVV3njYg2iAQbtIV2
C1PpoeHeVZWifXrHFwIsWUv5mWru6mG0N1XQCE0=
"],
Association["Book" -> 10, "Theorem" -> 48] -> CompressedData["
1:eJztzLsVwkAMRFFxDkIafRevG6AlSnAD1EpH2BBQACk3eMEEc9se9+1ERM8j
f79ap6/TrKGVlY2uoVpVZg7DyLVHfSAcQFbsux3pQPaS2F+YhUQkghi0gOEs
wuGsynhjNmPB10V15HXOPDci3SKt/AVPiAhK
"],
Association["Book" -> 10, "Theorem" -> 49] -> CompressedData["
1:eJztjDsOAkEMQ4PEaOL8Fle7LVfiCHsBzsqNyFDR0/IiWbEc534+H+dFRF5L
/vzMzmOHE6iNrCpSUQtHgbwVa/sAN/SYt+oK+6IrjH4CqNgYkWKQnCMs0BZh
NtDMdr3qF1M1nEG7JjQdHp72BmMTCGE=
"],
Association["Book" -> 10, "Theorem" -> 50] -> CompressedData["
1:eJztjDsOAkEMQ4PEaOL8FlfQciWOsBfYs+6NyFDR0/IiWbEc57kfr/0iIueS
P7/D+wNOoDayqkhFLRwF8las7QPc0GPeqivsi64w+gegYmNEikFyjrBAW4TZ
QDPb9apfTNVwBu2a0HR4eNobVmcISg==
"],
Association["Book" -> 10, "Theorem" -> 51] -> CompressedData["
1:eJztjMENw1AIQ6lUBNh8UEboSh0hC3TWbJTQSxbose9g2Zbs1/557w8ROUb+
/IDuCFYVOEqumoAuXKGL1V8i7oZjK2ZCXBdmJqaaEDdJU4Khhkx3c/cVrrZt
xrzxTAQT/VyVXExixQlAMwhT
"],
Association["Book" -> 10, "Theorem" -> 52] -> CompressedData["
1:eJztjMsNAkEMQ4PEaOL8Fp/2TEuUsA1srdsRGU4UwJEXyYrlOM/jfB03EbmW
/PkFO5xAbWRVkYpaOArko1jbB7ihx7xVV9gXXWH0B0DFxogUg+QcYYG2CLOB
ZrbrVb+YquEM2j2h6fDwtDdAFAgh
"],
Association["Book" -> 10, "Theorem" -> 53] -> CompressedData["
1:eJztjN0NwkAMg4PU08X5az0CKzFCF2BWNiLXpw7AI18kK5bjPM/363yIyGfJ
n58AJ1A7WVWkohaOAnkUa7+AG3rMW3WFfdEVxnoAFRsjUgySc4QF2iLMBprZ
rle9MVXDGbQtoenw8LQvM64ICg==
"],
Association["Book" -> 10, "Theorem" -> 54] -> CompressedData["
1:eJztjNENw0AIQ4mUOzAGRboNslJGyAKdtRsV+pMF+llLfhgkfN6v695E5N34
6zdiAmA2j0Yt4QhklsGvFvvi7iDQsWa9JOtf1QRmkVJh2QjGgBVVp6p6eTqm
2qNhdnis8J3WlaxWfAD28Qdw
"],
Association["Book" -> 10, "Theorem" -> 55] -> CompressedData["
1:eJztjNsNAlEIRDGRwAxzNxorsCVL2Aas1Y6E9cMG/PQkHCbhcd+fj/1kZq/R
nx9RaDTmEaGN2CARag+riAI5xgzx2bz1eTfLCC3LtBWeooeLqvKIQJcTHvml
87W58EzMy+PZG+hNB1o=
"],
Association["Book" -> 10, "Theorem" -> 56] -> CompressedData["
1:eJzti8ENAjEQA4NEtPbuOlEuXAG0RAnXALXSETleFMCTediWLd+P5+O4lFJe
p/z5FYC2OSVtY0WpNUfDPpt24QPTsTo5hDhHJbYxxm29zVhglipgSVZPp9Vk
RlSSMtblFV8Y0NvoPa6iRzDS5W8VSQfV
"],
Association["Book" -> 10, "Theorem" -> 57] -> CompressedData["
1:eJzty80NwjAMBWAjYde/SdUktBxZiRG6ALOyES6XLsCR7/DkJ9uP/fXcLwDw
PuLvZ2x4+NqHH9Gbar3rmCPW2uOLOTYZOWwx/FjeOI9nl3xGREAiEUCDZcJw
r1nViYiZ1XgidzI/ZTeRUspV1bql1pYPXs0Iwg==
"],
Association["Book" -> 10, "Theorem" -> 58] -> CompressedData["
1:eJzty7sNAkEMBFAjYe/6b2BXuuQCWqKEa4Ba6Yg7Ehog5AUjjUZz356P7QQA
ryP+fmd6RizTMtY5byhaMiq1asRH75E8orRi2DFGH+7ltn8REZCIGVDh2tDN
cq9iRNRaY21M7qT2RWad2TzOIpLKKpfIN0YBCG4=
"],
Association["Book" -> 10, "Theorem" -> 59] -> CompressedData["
1:eJztjEsKAjEQRFuwkvQnlYwDIgyz8EoeYS7gWb2RiSsP4NJH0/Cq6bofz8dx
EpHXXH9+CHvjukW32K9rMaMxujNu7YNqpZMjtUubR2rU6OHjFYAgJTOBigKl
IKYi5zHZPSdYQL8YUnUZledQc1eWSr4BHxMH3w==
"],
Association["Book" -> 10, "Theorem" -> 60] -> CompressedData["
1:eJzti8sNwzAMQ1VbMS1RsVCgC3SljpAFMms2qt1b7z32geCBn+dxvo6biFzL
/vySTJKZALlzOAZGBpPjg8PBWS23VRJ4zJzzWSsEpQBSuwBba96KAqGqZgad
8q7bN2H3CNN9rq2xe/gbyk8Gvg==
"],
Association["Book" -> 10, "Theorem" -> 61] -> CompressedData["
1:eJzti8sNAjEQQweJ0Xg+TjawFEBLlLANUCsdkXCiAI68gy092ffj+ThOIvJa
8een7CTbFeDqQMO4NW6MD6jAdFw+V7Cwjd73eVR1gVlR4HJxnVs3La9MdXea
q1YqvjCg9zFGnumR6ZnBeAPzKgeZ
"],
Association["Book" -> 10, "Theorem" -> 62] -> CompressedData["
1:eJzti8sNAjEQQweJUTwfJ5rVijstbQnbwNZKRyScKIAj72BLT/bzvI7zJiKv
FX9+C8n+ALja0VF7Z9E/IB3TcflYwcRWY+zzp2qC1pICk810bq1pWkaombGZ
aobiiwaMUVVxp3mERTj9DesnB4o=
"],
Association["Book" -> 10, "Theorem" -> 63] -> CompressedData["
1:eJzti8sNAjEQQwcJJxlPJh9tVoIjLVHCNkCtdETCiQL2yJNl6cny43g9j4uI
vFf9OZmx51J9jC3RSbbq97bzS1LSyOqdLGu8KXNu2eYNgCAEUqCiQEqwpYhx
JprFAHPoD1Ncuxe7mnIzLanX/gHuxQeG
"],
Association["Book" -> 10, "Theorem" -> 64] -> CompressedData["
1:eJzti8sRwkAMQ5cZtLHlT5JhOXKgJUpIA9RKR3g5UQBH3kHWG43vx/NxnFpr
rxl/fs3w1W7jehF6kiXrNvhBlGl1vSLnmMqILUZ9AWjonWzwpoAIbCqWpboY
pYMO/aIkdI+wsyvN1CQy3+QvB18=
"],
Association["Book" -> 10, "Theorem" -> 65] -> CompressedData["
1:eJztjMENAjEMBI3EJrG98eVAunvxoCVKuAaolY5weFEAT0aWpVnLez+ej+Mk
Iq+5/vwcDuNtuzazsODw4L58UO3hEZnaZZnHUHYOej4BEJRiJlBRoDVwKmrN
qe61wAj9IqXrmpVnqrlrtB7xBuoJB3U=
"],
Association["Book" -> 10, "Theorem" -> 66] -> CompressedData["
1:eJzti9ENwkAMQw+JXG0nOeh1gq7ECF2AWdmIlC8G4JMn2bJkez+ej+PSWnud
9uf33IHMHEMYFcIz9cFTENxL8LP0QM5t8/qYsS2k1CpMGt1AiAZ0krHQutjx
RVUj17nqGrV05k2hN73vBxc=
"],
Association["Book" -> 10, "Theorem" -> 67] -> CompressedData["
1:eJzty8sNAkEMA9AgEcXOZ6JhK6AlStgGqJWOmOFEA9x4Bx8s+34+H+dFRF47
/n4AqGU4BvoY1eUfSMfqavexoxKzu8e6qFJgliWg3KhrS9NkRijJMqpmKL4Y
0D3njGsREYzw8jfBYQcv
"],
Association["Book" -> 10, "Theorem" -> 68] -> CompressedData["
1:eJzti8sNwkAMRI2EHX/Gmyi7C+FIS5SQBqiVjthwoQJuvMNonkZz35+P/URE
ryP+/ILaWnWfb96XzCtaflDNzfooW3Yc40UbsMDGg5mJRcyIg9aJE5iHOkRE
VT10EkACX4aHWSnl7B4tLKIu6xsCYwgD
"],
Association["Book" -> 10, "Theorem" -> 69] -> CompressedData["
1:eJzty8sNwkAMBFAjYXv934BTQFqihDRArXREwoUKuPEOI41Gs+3Px34BgNcZ
fz/R6x3VUnuW1ez8GCNTOqdVtp9jjY6Y4ccBEQGJRAANbozhXkdVJyJmFmOh
CDL/Ivch4pFXVU0T0yXrDeP4B6Y=
"],
Association["Book" -> 10, "Theorem" -> 70] -> CompressedData["
1:eJztjMsNwkAMRB2J2V1/dhJAIue0lBLSALXSEV5OaSA3nixLb2zNdrz3YxKR
z1h/ruH1bGY0xuKMdf6h2ulkpvaYx5EaPZbw/AcgKMVMoKJAa4ihqDWnutcC
C+iJlK73rLyFmruydfILxDIHJg==
"],
Association["Book" -> 10, "Theorem" -> 71] -> CompressedData["
1:eJztytENwjAMBFAjcUl85zitWgZgJUboAszKRqSIFfjj6XzSSb4fz8dxMbPX
WX8/sjVyJ5euEbfx4S6Jk5KDG5nOiCX2+Q7AUAppcHOgNcQ5UetMlWoBA/7F
eXN0X3vqGk7Js/XMN7RLBwI=
"],
Association["Book" -> 10, "Theorem" -> 72] -> CompressedData["
1:eJztzNENwjAMBFBzTmPnYiVB6gKs1BG6QGdlIww/TMAfTyd/nE5+nNdx3kTk
+T5/v2LG3cg1Jtf8cGc0zskYHFzGnkXacw1AoOomqFKx1YquaoZSMsWtKEg0
fiGC7c7eyzALb77l1xePgAZn
"],
Association["Book" -> 10, "Theorem" -> 73] -> CompressedData["
1:eJztjLENgEAMA4MEJPZjpB+BlRiBBZiVjUhomICOKxydYnk7zv0YzOyq+PmM
DnS0BrTMggSEolXkn48pyySNPq+yCJNPkjC5loX06ngawz1eEEH1HB3LmGN5
bpDmBpg=
"],
Association["Book" -> 10, "Theorem" -> 74] -> CompressedData["
1:eJztjdsJgFAMQyt4bRKsoBu4kiPcBZzVjWw/xAn881AKeUD2fh59MLOr3s93
kBslUvkLgMxjOazwUdnN2OTTEgZYeIsINo95lrw6nkpwxwsBxZoDY6kcSQM3
gOAGcQ==
"],
Association["Book" -> 10, "Theorem" -> 75] -> CompressedData["
1:eJztyssNwmAMA+AgEaXJn9iF8hBHVmKELsCsbETKhQm48R2sWM59fT7WnYi8
tvj7IQ6wzvOM5cPjwgB4JXi4bWOguNSpX81MTDVC1OVoWpWpFpnT5A3u5qSP
/OqxKwp7DPRdOehv23YHxA==
"],
Association["Book" -> 10, "Theorem" -> 76] -> CompressedData["
1:eJztyssNwkAMBFAjYcef8W60WHzEiZYoIQ1QKx2RcEkF3HiH0Yw0j+X1XA5E
9N7i75e85sxLr/xSzZtt/ZqFfvc6awEzbH0yM7GIGXHQmDiBvk6HiKiqh06S
KYGdAGHWWju6R4VFnMb4AMOHB38=
"],
Association["Book" -> 10, "Theorem" -> 77] -> CompressedData["
1:eJztjdEJgEAMQyt4Ng1WECdwJUe4BZzVjUx/dAL/fJRA0kD2fh59MLOr5OdT
goygtAAidFGJ2B6not5Gn5Y0wNJbZkbznGfSq+NyhDteAmCuGhjLaUQBbnES
Bk4=
"],
Association["Book" -> 10, "Theorem" -> 78] -> CompressedData["
1:eJztyrENAkEMRFEjYZ+9M7ZXBJAcAS1RwjVArXTEQUIFZLzgSyPNbXvct4OI
PN/5+6050bzkR3h3rNXoXoke1/JzcjL2n6qKmkWIQk6LJtn7HDQzdx/wxTIN
/DISEVV1xEAjgNn1Aq/+B0M=
"],
Association["Book" -> 10, "Theorem" -> 79] -> CompressedData["
1:eJztyrENQkEMg+EgEcVO4tM7QKJmJUZ4CzArG3GIhgXo+ArrL3zbH/f9YGbP
9/z92HnoKnx0IjGUEGoF1NjmnJd1i6AhomWgiZ6dDG92lZNU0H0lvgQwx9xO
dRSzipWpfAGEdAau
"],
Association["Book" -> 10, "Theorem" -> 80] -> CompressedData["
1:eJztissNwlAQAxeJ1dr7yctDSJxpKSWkgdRKR2w40QA3RvYcLD/3Y9svIvI6
9efXLPUo/4B0OJbqIk5VYp1j3PulSoFZloByo/aXpsmMUJJlVI2evzBgHXPO
uBYZ0fHyN3+DBqE=
"],
Association["Book" -> 10, "Theorem" -> 81] -> CompressedData["
1:eJztzMsRg0AMA1AzE2HLa2OyVJCWKIEGqJWO+FxSQW55B40OGn22fd0GETnu
+Pu5mqs/GEUyMzjRi84KZi3ZrhGgoqoRAkon2GCKcJiBD9xV+TWazfleer6u
u2we6VM7AYiXBro=
"],
Association["Book" -> 10, "Theorem" -> 82] -> CompressedData["
1:eJztytENgzAQA9BDqpOc75JwAvW/KzECCzArGzX0iwX465NlyZI/+7Htk4ic
V/09b1n5U5Szkb0G2WoPvpXus6/jA0CQEilQUaAU+DWR80g2ywl06M0YVaM2
e7lyMW0lenwBdLAGhQ==
"],
Association["Book" -> 10, "Theorem" -> 83] -> CompressedData["
1:eJztyrENAgEMQ9EgEcV2ErgcLMBKjHALMCsbcYiGCah4xZcL37bHfTuY2fOd
vx9ofJQgnFpopHBBF5aZue6XCBoiqg20la4Sw4uV6SQ76L5PfAlgOc+seWwq
kym1XmnUBnQ=
"],
Association["Book" -> 10, "Theorem" -> 84] -> CompressedData["
1:eJztjNEJwzAQQ69Q2dadfe5Bf/vRlTpCFsis2aiXkBnylSchEAh9l/W3PERk
2+PmCuYBOdzCXU3nVI9PsI/+6u9cABCUoiqgEGgNY6+oNV3NaoF2UFMnyD9G
Xj6dakZvw+MPeDsGig==
"],
Association["Book" -> 10, "Theorem" -> 85] -> CompressedData["
1:eJztyrsNhEAMBFAjnfHfi0XAprRECTRArXTEEl0HF92TZjTB7Od1nBMA3G/9
/UTfet9ElvSsWrKy3pmSbVjHAZGAEFWBCJTQ2ARJ1eeZmNmFkVoj8y8eiVCt
T1iYmYeGPJLKBvk=
"],
Association["Book" -> 10, "Theorem" -> 86] -> CompressedData["
1:eJztycsNwkAQA9BBYuL5b0Y5JFdaooQ0QK10xOZEB5x4ki1Lfpyv53kjovdV
f7+xH8euulZU91pdfc3SGtM2f2YQmM0IIAO7uDLMYlkgIqHCGAMeXzKTadb3
9HT3SEv9AIjyBuE=
"],
Association["Book" -> 10, "Theorem" -> 87] -> CompressedData["
1:eJztycsNwkAQA9BBYuL5b0a57JWWKCENUCsdsTnRASeeZMuSH+fred6I6H3V
34/MOVX3iureq6uvWVpjOdbNDAKzGQFkYBdXhllsG0QkVBhjwONLVjLN+p6e
7h5pqR9//wbL
"],
Association["Book" -> 10, "Theorem" -> 88] -> CompressedData["
1:eJztycsNwkAQA9BBYuL5b0Y5wDUtpYQ0QK10xOZEB5x4ki1L3s/Xcd6I6H3V
3688H6prRXWv1dXXLK0xbfNlBoHZjAAysIsrwyyWBSISKowx4PElM5lmfU9P
d4+01A918gay
"],
Association["Book" -> 10, "Theorem" -> 89] -> CompressedData["
1:eJztybsNw0AMA1AZsEz9z0KK1FkpI3iBzJqNfK6yQSo/gAQBvo7P+1iI6HvV
7W+eqntFde/V1dcsrTE95skMArMZAWRgF1eGWWwbRCRUGGPA40dmMs16TU93
j7TUE2xiBpo=
"],
Association["Book" -> 10, "Theorem" -> 90] -> CompressedData["
1:eJztycsNg0AQA9BByuD5LyMqSEspgQZSazpiOdEBpzzJliW/j+/nWIjod9Xf
c1S3iureqquvWVpj2ufHDAKzGQFkYBdXhlmsK0QkVBhjwOMmM5lm/UpPd4+0
1BNjTwaD
"],
Association["Book" -> 10, "Theorem" -> 91] -> CompressedData["
1:eJztycENgDAMA8Ag0caOkx8LsBIjsACzshGFDxvw4iRblrzux7ZPZnbe9ftQ
KTJuCsaYrFBVaVzuMAJZ9oyWykYk0727e4z0YHe8GrAwl4xZBEWJ5AU/kwXi
"],
Association["Book" -> 10, "Theorem" -> 92] -> CompressedData["
1:eJztjLENgDAMBI1EZF/iJAImYCVGYAFmZSOckgWouOKK/9fv53Wck4jcQz9f
4hR6dxptiI0SEE1KKgruoiYrKZcM6u5mRuRKslpN7cXCsm51LjnGjEMeRYEG
EA==
"],
Association["Book" -> 10, "Theorem" -> 93] -> CompressedData["
1:eJzti8sJgEAMBSMYssnmp9iALVnCNmCtdmQ82YEn5zDwGN4+zmNMAHA9+vmU
lIzY0rPUs5YtuVgFIgJCFAFkWAnNVJFEtTUunJk4gru+VKzp5rN3V61HD74B
YqoGog==
"],
Association["Book" -> 10, "Theorem" -> 94] -> CompressedData["
1:eJztyMsNg0AMhGFHwsaP8YI2G4S40VJK2AZSazoCTukgJ77DL83s/fPuDyL6
Xrn9l7XMXLNh2rwt+gJm2PkzM7GIGXFQHTmB6ZwOEVFVDx0lUwI/AoRZKWVw
jxYW8az1AFdSBnk=
"],
Association["Book" -> 10, "Theorem" -> 95] -> CompressedData["
1:eJztytENgDAIBFBMrPQoUKsTuJIjdAFndSPplxv45UvuEsgd/Tr7RET3qN/H
YKaoiNqBhhI83iJCwosbMWjjpKpIbK6lMAKPy5jzCzm31Vu1WSBjY5EHPxAG
Ag==
"],
Association["Book" -> 10, "Theorem" -> 96] -> CompressedData["
1:eJztyLENg1AMhGFHio397p6NKNJEFKzECG8BZs1GQJUNUuUrfuluG8c+HiLy
ufP3a1nIehPV1vRX58y4XlUVNYsQhSyTdrKu2Whm7t7gk/Vu4JeRiMjMJxoK
AcyVJ0g6BkI=
"],
Association["Book" -> 10, "Theorem" -> 97] -> CompressedData["
1:eJztycERgzAQQ9FlJjvatSXbARqgJUqgAWqlI8gpHeSUd/gHaTvO/ZjM7Prk
7+eWpkW9aZaK5nfv6zMCMLiT5rAKj1LSQTICEcEMxxio/EpS5Gj9papSnyuV
N0YXBkE=
"],
Association["Book" -> 10, "Theorem" -> 98] -> CompressedData["
1:eJztycERg0AMQ1FnJh7Zu9LikDRAS5RAA6k1HQVOdMCJd/gHadm+6/Yws9+R
2/WG3pqGZqlpflV99g2AwZ00h3V4tJYOkhGICGY4qtB5SlJkjemprtb3K5V/
P8sGMA==
"],
Association["Book" -> 10, "Theorem" -> 99] -> CompressedData["
1:eJztybsRgEAIBFCckeHg+JyfxNCWLOEasFY7EiNLMPEFO+yy9/PoAwBcT/w+
0DymLWoLcYvF1pyICAhRBJBhJjRTRRLVUjg5M3EEV33lM6ubj149b9MafANC
pAZK
"],
Association["Book" -> 10, "Theorem" -> 100] -> CompressedData["
1:eJztyLsNhEAMhGEjYePHeA8tCwEZLVECDVArHcFFV8IlfMEvzWzHuR8dEV3f
vP4hZ+Tqy6INGGHPw8zEImbEQXXgBD7PdIiIqnroIJkS+BEgzEopvXu0sIip
1hs11QYd
"],
Association["Book" -> 10, "Theorem" -> 101] -> CompressedData["
1:eJztycENgDAMA8AgEdlJmxIQC7ASI7AAs7IR5cUIfDhZftjbce7HICLXU79P
xNxiibDIOXPtAwCBqrsopEDpbgr3SoJkNSoyUeqLPa2xTmOU8NIvC7sBLKsF
7Q==
"],
Association["Book" -> 10, "Theorem" -> 102] -> CompressedData["
1:eJztx7ENgEAMBEEjYWP/3fsRARkBLVECDVArHQERJZAwwUq77se2dyJyPvl9
g2hlSZ8rR8b9qipqFiEKmQatZLu30MzcvcAHq9XAl5GIyMweBQ0BjC0vJgwF
4g==
"],
Association["Book" -> 10, "Theorem" -> 103] -> CompressedData["
1:eJztx8ENgDAMQ9EgETltnFSCCViJEboAs7IRhQsjcOEdvuytH3ufROS88/sI
3cNrxLoudVwAAlVSFLJAI0gFk2YwsywGtAbnqzzNzNmd1ccqUS4j6gXn
"],
Association["Book" -> 10, "Theorem" -> 104] -> CompressedData["
1:eJztybsNgEAMA9AgEfmSy0cCFmAlRrgFmJWNCBUj0PAKy5b3cR5jIqLrid9X
skdqeK6+1QJAYFYlFlrA7mYMNWtNSohAMqXbq86a4TFHj+puPeUGI9IF8Q==
"],
Association["Book" -> 10, "Theorem" -> 105] -> CompressedData["
1:eJztx7sNgDAMRVEjYePPS0AhomclRsgCzMpGhIoRaDjFle7ezqMNRHQ9+X3G
66YVmGF9mJlYxIw4qEycgNTXISKq6qGTpCSBlwBhlnMe3aOGRaxLuQEXSwXB
"],
Association["Book" -> 10, "Theorem" -> 106] -> CompressedData["
1:eJztissJgEAQQ0dwzQdHsARbsoRtwFrtyJ2TJXjxHUJeyNGvs08RcVf8fIdE
FR7ddhjLlkFGomWmGnJdbdQHw0yALyKdu625zPIY+AAF5gU4
"],
Association["Book" -> 10, "Theorem" -> 107] -> CompressedData["
1:eJztx7ENgDAMRFEjYcfO2Q6ioGclRsgCzMpGhIoRaHjF193ez6NPRHQ9+X0o
dQtf3MZkZmIRM2LQWjjc27jVRURVK7RIhMBf4g6zzJxR0WDA0vIGDE8FlQ==
"],
Association["Book" -> 10, "Theorem" -> 108] -> CompressedData["
1:eJzth8ENgDAMA4OEm8ZNKypYgJUYoQswKxuRTsEH62z5znFfYxGRZ86fL2N0
3/yIB0CQEikwMSBn+FSoBlqKJtBhxoCcDanWa+Pqxr1Yy33rL/ssBUM=
"],
Association["Book" -> 10, "Theorem" -> 109] -> CompressedData["
1:eJztytEJgDAMBNAIhtylqdA6QVdyhC7grG5k/HQCf3xw4Tgy5nnMRUSu5/w+
xZKYRdXEyAgxSKd6cdIiAgBzNypqheGlsfW9rsXzmdwyN/7wBUc=
"],
Association["Book" -> 10, "Theorem" -> 110] -> CompressedData["
1:eJztx8ERgDAIRFGcEQJZwEw6sCVLSAPWakfGkyV48R3+zu7jPMZCRNeT37fC
m9tcZiYWMSMG9cLhvs1bXURUtUKLRAj8Je4wy8wVFQkDWvYb/ioFaw==
"],
Association["Book" -> 10, "Theorem" -> 111] -> CompressedData["
1:eJztxcENgDAMQ9HQpjFOokqMwEqM0AWYlY0AcWICLjx92evYtzGJyHHP72O9
97iuVghKAaTOAjQzt6JgqipJ6FN7Sy6Z1LDmtAhPPwHe7QSG
"],
Association["Book" -> 10, "Theorem" -> 112] -> CompressedData["
1:eJztxcENgCAQRNE1cRzYARINMV5tyRJowFrtSDxagRff4f+9nUcbzOx68vva
uuVegEbA3SBbgBgxgZ5AUpJToZ/hLae5Vo05Bk9eipJu9Y4FLg==
"],
Association["Book" -> 10, "Theorem" -> 113] -> CompressedData["
1:eJztxbENgDAQBMFH4jj/n40EskRMS5TgBqiVjjAhFZAwwe7ezqMNZnY9+X1u
Kz0AjUCEQbYC7pjAyCApKajUz/RW8lKrxuIpss+zsm7uhwUW
"],
Association["Book" -> 10, "Theorem" -> 114] -> CompressedData["
1:eJztxckNgDAQQ9FBwjizRQKlAVqihDRArXREOFIBF5707b2fR59E5Hrm970c
ARQCZgKXDVDFAlqApLsbvYxnectYW/M5tVhorRZ2A+eYBP0=
"],
Association["Book" -> 10, "Theorem" -> 115] -> CompressedData["
1:eJztysENgDAMQ9EgUZw4SauOwEqM0AWYlY0oJ1bgwDt8yZL3cR5jEZHrye8b
SAqx1RQ1aSgRYQVZwx1mlpgrCOjLVHurvXOlcX48Z27wIgUV
"],
Association["Book" -> 11, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAAjHh4pAEAlWgCfA==
"],
Association["Book" -> 11, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweADlMQLAJUeAns=
"],
Association["Book" -> 11, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaABjEgk2QAAlWYCfA==
"],
Association["Book" -> 11, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAB3BwM7Bxs7KwMnKwMHGysHBwcrECKlZOTE0iC
AAeUhgMgnwMEWFkgfHYQAQDQOwQW
"],
Association["Book" -> 11, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWABHAzsHGzsrAycrAwcbGwcHBysbGysrJycnEAS
BNigNBwA+RwgwMoC4bODCADMswQI
"],
Association["Book" -> 11, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAB3BxAwMDBysDBycbOwcrKwcbOzsnJycbKysoO
4bEiAxCPA6iMnQWiAiwNAM7LBBU=
"],
Association["Book" -> 11, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSADFEYKAJUhAns=
"],
Association["Book" -> 11, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSACbGwcHAxcrAwcHGwcrBysrKzs7FycnKwgBpgA
k3AA4nEAVbGzsIF5YGkAyekEAA==
"],
Association["Book" -> 11, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWACvOysDKwcDKzcbOwcrOy8nKysXGxsHKysrOzs
rNwcIBIVAIU4OFhZgBJs7BBZAMu1BBE=
"],
Association["Book" -> 11, "Theorem" -> 10] -> CompressedData["
1:eJztycENQFAYBOFfYnZXiB60pITXgFp1xIuTDhx8h7nM1o69DVV19vw+xRQu
Zjl4nUBSAJslvW8hCeM95Odex8gEAg==
"],
Association["Book" -> 11, "Theorem" -> 11] -> CompressedData["
1:eJztx8EJgEAMRNEIhsxMgtiCLVnCNrC12pHxZAsefIcP/xjzHIuZXU9+37Kb
wyTPFD22ikZS0QdF4EWglFVaKUCsLm7XfgSY
"],
Association["Book" -> 11, "Theorem" -> 12] -> CompressedData["
1:eJztx7ENgEAMBEEjYfnu7OBboCVK+AaolY4wES0Q/AQr7TGvc25mdr9Z/sZh
kmeKHqOikVT0QRH4EChllXYKEKuLB9PiBIo=
"],
Association["Book" -> 11, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 11, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaADrAwcrGwc7BysrKzs7JwcIBorYAdisCwLgs8K
AL5vA8k=
"],
Association["Book" -> 11, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAEnNysXBxcnFxcXBysrKwgGsTkBAJuTjTABcQs
HFxAxZzcQCUcANIZBIg=
"],
Association["Book" -> 11, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"],
Association["Book" -> 11, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAE7Ky8vDycrOy8fDzc3OycnJxAAsjjZWfnQABO
Dg5+fj5+fi4WLk4ukBpeIAEA07sEow==
"],
Association["Book" -> 11, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAEbOwcrOycHOzsXGxs7KysrOzsrJxAGsSEAyAH
qIiDg52FjZ2dDayGlRUAvbED1w==
"],
Association["Book" -> 11, "Theorem" -> 19] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAEbGxsrCAAo4kFALVAA5g=
"],
Association["Book" -> 11, "Theorem" -> 20] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAFPHycrKwcHBzs7Kzs7OwgCshjZedAA1xAzAJi
cHJygigAwwgEJA==
"],
Association["Book" -> 11, "Theorem" -> 21] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAFvJycHEDAyckOBFwggoMDhJEBNxcPNzcHC4jJ
xcnFBaQAxMoEPQ==
"],
Association["Book" -> 11, "Theorem" -> 22] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAFnKysHBwc7Oys7OzsIArIY2XnQAOcQMwCZnCC
mBwAvXAECQ==
"],
Association["Book" -> 11, "Theorem" -> 23] -> CompressedData["
1:eJzth8sNgFAQAtfE/bE0YUuW8BqwVjsSu/DgECZwrOtcm5ndr36+i0dNuEdm
dqcHGBQzqlJAoUnsRXZr6T7DVgRa
"],
Association["Book" -> 11, "Theorem" -> 24] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAGnKysPGxsHKysrBzsrLwcrOzsrKiAg5WDg4OV
hZWdg40dSABFALXIA7U=
"],
Association["Book" -> 11, "Theorem" -> 25] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAG3Jw8bGw8nJycPFyc3DwgxIECQEI8HCycXEBp
IBMoAgDDUwRJ
"],
Association["Book" -> 11, "Theorem" -> 26] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAGPOxAwMnJycXOycoOJNk5EICTg4OHi5uHh4uF
i5uDk5uThwsoCAC9FgQk
"],
Association["Book" -> 11, "Theorem" -> 27] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAGPOzs7JycnHzsnKzsQJIDCXBycPDw8PEIcrFw
83JxcnPy8gEVAgC97wQ9
"],
Association["Book" -> 11, "Theorem" -> 28] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwSAHnJysOAAHEIEAKwuEzw4iAK2LA4A=
"],
Association["Book" -> 11, "Theorem" -> 29] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwWAH/KwQwM6KBoACHCDAyoKkAACtLwN+
"],
Association["Book" -> 11, "Theorem" -> 30] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwaAHrBDAzooGgAIcIMDKgqQAAKp9A28=
"],
Association["Book" -> 11, "Theorem" -> 31] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGweAH3NzcPFzcrEJcvLzcHCiAEwS4WLg4uTm5ubh5
gBwAuoUEGw==
"],
Association["Book" -> 11, "Theorem" -> 32] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAAQrzcHEJsXBxc3LzcCMABRJzcHBxcLJxcPJwg
EU4uTgC88gQ5
"],
Association["Book" -> 11, "Theorem" -> 33] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAAvNyc4my8HJzcfDwIwMHNzcfFzcHBwcLDxcXJ
zcPNzcnFCQC85QRC
"],
Association["Book" -> 11, "Theorem" -> 34] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAA3JxCbBwcnNx8PAjAwc3NwcXNwcfBwsPNxcnN
w83NycUJALk5BCw=
"],
Association["Book" -> 11, "Theorem" -> 35] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAAHNysnBzcnMiAg4ODk5sXyGDh4OAGyvHwcHBy
AACxagPj
"],
Association["Book" -> 11, "Theorem" -> 36] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRABnBzsnNxc3EiAg5ubk5uPn5OThYeTj5OTm5eT
k4sTALQTBAs=
"],
Association["Book" -> 11, "Theorem" -> 37] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVABbLwcnNx8PAjAwc3Nx8XNwcHBwsPFxcnNw83N
ycUJALQXBAo=
"],
Association["Book" -> 11, "Theorem" -> 38] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZABbKzsrOyogBUoxMrKwsrBygrmsbICAKZqA14=
"],
Association["Book" -> 11, "Theorem" -> 39] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdABXLy83BwogBMEuFi4OLk5ubm4eYAcAKx5A8I=
"], Association["Book" -> 12, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRACwuw8SICDh4eLl4+Pi4uFl4+Xk4+bl4eTixMA
sgMEDg==
"],
Association["Book" -> 12, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAC7DxIgIuHh5OLi5+fi4WHm4eDj5sXyOUEAK8q
A/U=
"],
Association["Book" -> 12, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZACvFwIwAEiOIGYhZuTn5Obm5uPg4MDAKrpA8M=
"], Association["Book" -> 12, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdACgoKCAgIC/AL8/PwcfHxcnFx8XBwsPJxcnNzc
3LxACgCwzwQA
"],
Association["Book" -> 12, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRADEpISIuLiouJi4hzCwlzcvHxcHCycQMDNy83N
ycUJALbaBEA=
"],
Association["Book" -> 12, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVADoqJCoqIiQMghJMTFzcvHxcHCCQTcvNzcnFyc
ALG3BBI=
"],
Association["Book" -> 12, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZADEiKioiJAyCEszMXNy8fFwcIJBNy83NycXJwA
r/cEBA==
"],
Association["Book" -> 12, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdADIiAgKsIhLs7FzcvHxcHCCQTcQMDJxQkArYMD
7w==
"],
Association["Book" -> 12, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAEIuKC4hLiHIJCXNy8fFycLJxAwM3Lzc3JxQkA
q2cD3A==
"],
Association["Book" -> 12, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAEkqKSkpIcfEJc3Lx8XBwsnEDADQScXJwAqgED
zQ==
"],
Association["Book" -> 12, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAEorKyshx8/FzcvHxcHCycQMANBJxcnACoUgO9
"],
Association["Book" -> 12, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAEIsLCHCIiXNy8fFxcLJxAwA0EnFycAKScA5g=
"],
Association["Book" -> 12, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAFsrIcfPxc3Lx8XBwsnEDADQScXJwAo40Diw==
"],
Association["Book" -> 12, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAFshx8/FzcvHxcHCycQMANBJxcnACg8gNu
"],
Association["Book" -> 12, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAFHHz8XNy8fFwcLJxAwA0EnFycAJ50A1E=
"],
Association["Book" -> 12, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAFHBxc3FxAwMLFxcHBCQQcHBwAnE0DKw==
"],
Association["Book" -> 12, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAGUpycXDw8XCy83BycPNzcQB4nAJ1vA0Y=
"],
Association["Book" -> 12, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAGnJxcPDxcLLzcHJw83NxAHicAm4EDLA==
"],
Association["Book" -> 13, "Theorem" -> 1] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAG3IJiwlwsvNxcnJyc3PxAAgCccAM/
"],
Association["Book" -> 13, "Theorem" -> 2] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAGgvz8XCxcnFyc3EAIBACa1QMg
"],
Association["Book" -> 13, "Theorem" -> 3] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwRAHXFycLBxAwMXJxQmkAJjbAvk=
"],
Association["Book" -> 13, "Theorem" -> 4] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwVAHwlwsvNxcnJyc3PxAAgCZWwMN
"],
Association["Book" -> 13, "Theorem" -> 5] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwZAHXCy83FycnJzc/EACAJhRAvo=
"],
Association["Book" -> 13, "Theorem" -> 6] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwdAHLLzcvNzc3Dw8XLycAJgYAvw=
"],
Association["Book" -> 13, "Theorem" -> 7] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTAArAgAAJYsArE=
"],
Association["Book" -> 13, "Theorem" -> 8] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXAAHKycnGxcvJxcnACWqALS
"],
Association["Book" -> 13, "Theorem" -> 9] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbAA/Jz8PNzcnFycAJb9At8=
"],
Association["Book" -> 13, "Theorem" -> 10] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfAAnNy83LycXJwAlmgCzw==
"],
Association["Book" -> 13, "Theorem" -> 11] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTABPGwcnMJ8QgCWDQLQ
"],
Association["Book" -> 13, "Theorem" -> 12] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXABXHxcnFycAJXEArg=
"],
Association["Book" -> 13, "Theorem" -> 13] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbAB3LycXJwAlYUCrg==
"],
Association["Book" -> 13, "Theorem" -> 14] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfAB3BycHACVQAKe
"],
Association["Book" -> 13, "Theorem" -> 15] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwTACnJycAJUYApU=
"],
Association["Book" -> 13, "Theorem" -> 16] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwXACfGIAlRQCng==
"],
Association["Book" -> 13, "Theorem" -> 17] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwbAC/ACU8QKJ
"],
Association["Book" -> 13, "Theorem" -> 18] -> CompressedData["
1:eJxTTMoPSmJkYGC4CCJGwfACAJTiAno=
"]},
SelectWithContents->True,
Selectable->False]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"dataA", "=",
RowBox[{
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "[", "\"\<Book\>\"", "]"}],
"\[Rule]", " ",
RowBox[{"N", "[",
RowBox[{"Max", "[",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "]"}], "]"}]}], "&"}], "/@",
"resDepth"}]}], ",", "vals", ",", "acc", ",", "xval"}], "}"}],
",", "\[IndentingNewLine]",
RowBox[{
RowBox[{"vals", "=",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}]}], ";",
RowBox[{"acc", "=",
RowBox[{"Association", "[",
RowBox[{"MapIndexed", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"First", "[", "#2", "]"}], "\[Rule]", " ", "#1"}],
"&"}], ",",
RowBox[{"Accumulate", "[",
RowBox[{"Values", "[",
RowBox[{"CountsBy", "[",
RowBox[{"dataA", ",", "First"}], "]"}], "]"}], "]"}]}],
"]"}], "]"}]}], ";", "\[IndentingNewLine]",
RowBox[{"xval", "=",
RowBox[{"Association", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "-",
RowBox[{
RowBox[{"vals", "[",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}], "/", "2"}]}],
")"}]}], "&"}], "/@",
RowBox[{"Normal", "[", "acc", "]"}]}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"Show", "[",
RowBox[{"{",
RowBox[{
RowBox[{"ListLinePlot", "[",
RowBox[{
RowBox[{"Values", "[", "dataA", "]"}], ",",
RowBox[{"Axes", "\[Rule]",
RowBox[{"{",
RowBox[{"False", ",", "True"}], "}"}]}], ",",
RowBox[{"Filling", "\[Rule]", "Axis"}], ",",
RowBox[{"Frame", "\[Rule]", " ", "True"}], ",",
RowBox[{"FrameLabel", "\[Rule]",
RowBox[{"{",
RowBox[{
"\"\<theorems by book\>\"", ",",
"\"\<maximum depth reduction\>\""}], "}"}]}], ",",
RowBox[{"FrameTicks", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"True", ",", "False"}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], ",",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"{",
RowBox[{"0", ",", "0"}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Normal", "[", "xval", "]"}]}], ",", "False"}],
"}"}]}], "}"}]}], ",",
RowBox[{"ColorFunctionScaling", "\[Rule]", "False"}], ",",
RowBox[{"ColorFunction", "\[Rule]", " ",
RowBox[{"Function", "[",
RowBox[{
RowBox[{"{",
RowBox[{"x", ",", "y"}], "}"}], ",",
RowBox[{"Piecewise", "[",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "6", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "6", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "10", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "10", "]"}]}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"bookColorIntense", "[", "13", "]"}], ",",
RowBox[{"x", "\[LessEqual]",
RowBox[{"acc", "[", "13", "]"}]}]}], "}"}]}], "}"}],
"]"}]}], "]"}]}]}], " ", "]"}], ",",
RowBox[{"Graphics", "[",
RowBox[{"{",
RowBox[{
RowBox[{"GrayLevel", "[", "0.5", "]"}], ",",
RowBox[{"Line", "[",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"#", ",",
RowBox[{"-", "5"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{"#", ",", "32"}], "}"}]}], "}"}], "&"}], "/@",
RowBox[{"Values", "[", "acc", "]"}]}], "]"}]}], "}"}],
"]"}]}], "}"}], "]"}]}]}], "]"}]], "Input"]
}, Open ]]
|
Formalizing Euclid
Everything we’ve discussed so far is basically derived from the original text of Euclid’s Elements. But what if we look instead at the pure “mathematical content” of Euclid? We’ve now got a way to represent this in the Wolfram Language. Consider Euclid’s 3.16. It asserts that:
|
✕
Style[
Text[
Style[Entity["GeometricScene", "EuclidBook3Proposition16"][
"Statement"], RGBColor["#777777"],
FontSize -> 14]]]
|
Well, we can now give a “computational translation” of this:

✕
Entity["GeometricScene", "EuclidBook3Proposition16"]["Scene"] |
And this is all we need to say to define that theorem in Euclid. Given the definition of the Wolfram Language, this is completely self-contained, and ready to be understood by both computers and humans. And from this form, we can now for example compute a random instance of the theorem:

✕
RandomInstance[%] |
As another example, here’s Euclid’s 4.2:
|
✕
Style[
Text[
Style[Entity["GeometricScene", "EuclidBook4Proposition2"][
"Statement"], RGBColor["#777777"],
FontSize -> 14]]]
|
This is now asking for a construction—or, effectively, stating the theorem that it’s possible to do such a construction with ruler and compass. And again we can give a computable version of this in the Wolfram Language, including the construction:

✕
Entity["GeometricScene", "EuclidBook4Proposition2"]["Scene"] |

✕
RandomInstance[%] |
It’s interesting to see, though, how the computable versions of theorems compare to their textual ones. Here are length comparisons for 2D geometry theorems:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; GraphicsRow[{Module[{res =
ToExpression[
First[StringSplit[
StringReplace[#[[1]], {"Euclid book" -> "",
"proposition" -> ""}]]]] -> ByteCount[#[[2]]] & /@
EntityValue[
EntityClass["GeometricScene", "EuclidsElements"], {"Name",
"Statement"}], vals, acc, xval},
vals = CountsBy[res, First];
acc = Association[
MapThread[#2 -> #1 &, {Accumulate[Values[CountsBy[res, First]]],
Keys[CountsBy[res, First]]}]];
xval =
Association[#[[1]] -> (#[[2]] - vals[#[[1]]]/2) & /@
Normal[acc]];
Labeled[
Show[{ListLinePlot[Values[res], Axes -> {False, True},
Filling -> Axis, Frame -> True,
FrameTicks -> {{False,
False}, {{#[[2]], #[[1]], {0, 0}} & /@ Normal[xval],
False}}, ColorFunctionScaling -> False,
ColorFunction ->
Function[{x, y},
Piecewise[{{bookColorIntense[6],
x <= acc[6]}, {bookColorIntense[13], x <= acc[13]}}]],
ImageSize -> {300, 200} ,
FrameLabel -> {None, "character length"}],
Graphics[{GrayLevel[0.5],
Line[{{#, -1100}, {#, 15000}} & /@ Values[acc]]}]}],
Style["textual", 11, GrayLevel[.4]]]],
Module[{res =
ToExpression[
First[StringSplit[
StringReplace[#[[1]], {"Euclid book" -> "",
"proposition" -> ""}]]]] -> LeafCount[#[[2]]] & /@
EntityValue[
EntityClass["GeometricScene", "EuclidsElements"], {"Name",
"Scene"}], vals, acc, xval},
vals = CountsBy[res, First];
acc = Association[
MapThread[#2 -> #1 &, {Accumulate[Values[CountsBy[res, First]]],
Keys[CountsBy[res, First]]}]];
xval =
Association[#[[1]] -> (#[[2]] - vals[#[[1]]]/2) & /@ Normal[acc]];
Labeled[
Show[{ListLinePlot[Values[res], Axes -> {False, True},
Filling -> Axis, Frame -> True,
FrameLabel -> {None, "expression length"},
FrameTicks -> {{False,
False}, {{#[[2]], #[[1]], {0, 0}} & /@ Normal[xval],
False}}, ColorFunctionScaling -> False,
ColorFunction ->
Function[{x, y},
Piecewise[{{bookColorIntense[6],
x <= acc[6]}, {bookColorIntense[13], x <= acc[13]}}]],
ImageSize -> {300, 200}],
Graphics[{GrayLevel[0.5],
Line[{{#, -5}, {#, 300}} & /@ Values[acc]]}]}],
Style["symbolic", 11, GrayLevel[.4]]]]},
ImageSize -> {650, Automatic}]
|
And we see that there is indeed at least some correlation between the lengths of textual and symbolic representations of theorems (the accumulation of points on the left is associated with constructions, where the text just says what’s wanted, and the symbolic form also says how to do it):

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; Module[{dataA =
GroupBy[ToExpression[First[StringSplit[Last[#], "."]]] ->
Callout[Take[#, 2], Last[#]] & /@
Transpose[{ByteCount /@
EntityValue[EntityClass["GeometricScene", "EuclidsElements"],
"HeathsStatement"],
LeafCount /@
EntityValue[EntityClass["GeometricScene", "EuclidsElements"],
"Scene"],
StringJoin[Riffle[StringSplit[#][[{3, 5}]], "."]] & /@
EntityValue[EntityClass["GeometricScene", "EuclidsElements"],
"Name"]}], First -> Last]},
ListPlot[Values[dataA],
PlotStyle -> Table[bookColorIntense[i], {i, Keys[dataA]}],
Frame -> True,
FrameLabel -> {Style["textual", GrayLevel[.5]],
Style["symbolic", GrayLevel[.5]]} ]]
|
In the Wolfram Language representation we’ve just been discussing, there’s a built-in Wolfram Language meaning to things like CircleThrough and PlanarAngle—and we can in a sense do general computations with these.
But at some level we can view what Euclid did as something purely formal. Yes, he talks about lines and planes. But we can think of these things just as formal constructs, without any externally known properties. Many centuries after Euclid, this became a much more familiar way to think about mathematics. And in the Wolfram Language we capture it with AxiomaticTheory and related functions.
For example, we can ask for an axiom system for Boolean algebra, or group theory:

✕
AxiomaticTheory["BooleanAxioms"] |

✕
AxiomaticTheory["GroupAxioms"] |
What does the ⊗ mean? We’re not saying. We’re just formally defining certain properties it’s supposed to have. In the case of Boolean algebra, we can interpret it as And. In the case of group theory, it’s group multiplication—though we’re not saying what particular group it’s for. And, yes, we could as well write the group theory axioms for example as:
|
✕
AxiomaticTheory[{"GroupAxioms", <|"Multiplication" -> f,
"Inverse" -> c, "Identity" -> e|>}]
|
OK, so can we do something similar for Euclid’s geometry? It’s more complicated, but thanks particularly to work by David Hilbert and Alfred Tarski in the first half of the 1900s, we can—and here’s a version of the result:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"geometryall", "=",
RowBox[{"{",
RowBox[{
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{"x", ",", " ", "y", ",", " ", "z"}], "}"}], ",", " ",
RowBox[{"implies", "[",
RowBox[{
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"x", ",", "y"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"z", ",", "z"}], "]"}]}], "]"}], ",",
RowBox[{"congruent", "[",
RowBox[{"x", ",", "y"}], "]"}]}], "]"}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{
"x", ",", " ", "y", ",", " ", "z", ",", " ", "u", ",", " ",
"v", ",", "w"}], "}"}], ",", " ",
RowBox[{"implies", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"x", ",", "y"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"z", ",", "u"}], "]"}]}], "]"}], ",",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"x", ",", "y"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"v", ",", "w"}], "]"}]}], "]"}]}], "]"}], ",",
" ",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"z", ",", "u"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"v", ",", "w"}], "]"}]}], "]"}]}], "]"}]}], "]"}],
",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{"x", ",", " ", "y", ",", " ", "z"}], "}"}], ",", " ",
RowBox[{"implies", "[",
RowBox[{
RowBox[{"between", "[",
RowBox[{"x", ",", "y", ",", "z"}], "]"}], ",",
RowBox[{"equal", "[",
RowBox[{"x", ",", "y"}], "]"}]}], "]"}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{
"x", ",", " ", "y", ",", " ", "z", ",", " ", "u", ",", " ",
"v"}], "}"}], ",", " ",
RowBox[{"implies", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"between", "[",
RowBox[{"x", ",", "u", ",", "z"}], "]"}], ",",
RowBox[{"between", "[",
RowBox[{"y", ",", "v", ",", "z"}], "]"}]}], "]"}], ",",
RowBox[{"Exists", "[",
RowBox[{"a", ",",
RowBox[{"and", "[",
RowBox[{
RowBox[{"between", "[",
RowBox[{"u", ",", "a", ",", "y"}], "]"}], ",",
RowBox[{"between", "[",
RowBox[{"v", ",", "a", ",", "x"}], "]"}]}], "]"}]}],
"]"}]}], "]"}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{
"x", ",", " ", "y", ",", " ", "z", ",", " ", "u", ",", " ",
"v"}], "}"}], ",", " ",
RowBox[{"implies", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"x", ",", "u"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"x", ",", "v"}], "]"}]}], "]"}], ",",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"y", ",", "u"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"y", ",", "v"}], "]"}]}], "]"}]}], "]"}],
",",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"z", ",", "u"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"z", ",", "v"}], "]"}]}], "]"}]}], "]"}], ",",
RowBox[{"not", "[",
RowBox[{"equal", "[",
RowBox[{"u", ",", "v"}], "]"}], "]"}]}], "]"}], ",",
RowBox[{"or", "[",
RowBox[{
RowBox[{"or", "[",
RowBox[{
RowBox[{"between", "[",
RowBox[{"x", ",", "y", ",", "z"}], "]"}], ",",
RowBox[{"between", "[",
RowBox[{"y", ",", "z", ",", "x"}], "]"}]}], "]"}], ",",
RowBox[{"between", "[",
RowBox[{"z", ",", "x", ",", "y"}], "]"}]}], "]"}]}],
"]"}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{
"x", ",", " ", "y", ",", " ", "z", ",", " ", "u", ",", " ",
"v", ",", " ", "w"}], "}"}], ",", " ",
RowBox[{"implies", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"between", "[",
RowBox[{"x", ",", "y", ",", "w"}], "]"}], ",",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"x", ",", "y"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"y", ",", "w"}], "]"}]}], "]"}]}], "]"}],
",",
RowBox[{"and", "[",
RowBox[{
RowBox[{"between", "[",
RowBox[{"x", ",", "u", ",", "v"}], "]"}], ",",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"x", ",", "u"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"u", ",", "v"}], "]"}]}], "]"}]}], "]"}]}],
"]"}], ",",
RowBox[{"and", "[",
RowBox[{
RowBox[{"between", "[",
RowBox[{"y", ",", "u", ",", "z"}], "]"}], ",",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"y", ",", "u"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"z", ",", "u"}], "]"}]}], "]"}]}], "]"}]}],
"]"}], ",",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"y", ",", "z"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"v", ",", "w"}], "]"}]}], "]"}]}], "]"}]}], "]"}],
",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{
"x", ",", " ", "y", ",", " ", "z", ",", " ", "a", ",", " ",
"b", ",", " ", "c", ",", " ", "u", ",", " ", "v"}], "}"}],
",", " ",
RowBox[{"implies", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"not", "[",
RowBox[{"equal", "[",
RowBox[{"x", ",", "y"}], "]"}], "]"}], ",",
RowBox[{"between", "[",
RowBox[{"x", ",", "y", ",", "z"}], "]"}]}], "]"}],
",",
RowBox[{"between", "[",
RowBox[{"a", ",", "b", ",", "c"}], "]"}]}], "]"}],
",",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"x", ",", "y"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"a", ",", "b"}], "]"}]}], "]"}]}], "]"}],
",",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"y", ",", "z"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"b", ",", "c"}], "]"}]}], "]"}]}], "]"}],
",",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"x", ",", "u"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"a", ",", "v"}], "]"}]}], "]"}]}], "]"}], ",",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"y", ",", "u"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"b", ",", "v"}], "]"}]}], "]"}]}], "]"}], ",",
RowBox[{"congruent", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"z", ",", "u"}], "]"}], ",",
RowBox[{"line", "[",
RowBox[{"c", ",", "v"}], "]"}]}], "]"}]}], "]"}]}], "]"}],
",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{"x", ",", " ", "y"}], "}"}], ",", " ",
RowBox[{"implies", "[",
RowBox[{
RowBox[{"equal", "[",
RowBox[{"x", ",", "y"}], "]"}], ",",
RowBox[{"equal", "[",
RowBox[{"y", ",", "x"}], "]"}]}], "]"}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{"x", ",", "y", ",", "z"}], "}"}], ",",
RowBox[{"implies", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"equal", "[",
RowBox[{"x", ",", "y"}], "]"}], ",",
RowBox[{"equal", "[",
RowBox[{"y", ",", "z"}], "]"}]}], "]"}], ",",
RowBox[{"equal", "[",
RowBox[{"x", ",", "z"}], "]"}]}], "]"}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{"x", ",",
RowBox[{"equal", "[",
RowBox[{"x", ",", "x"}], "]"}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{"a", ",", "b"}], "}"}], ",",
RowBox[{
RowBox[{"and", "[",
RowBox[{"a", ",", "b"}], "]"}], "\[Equal]",
RowBox[{"and", "[",
RowBox[{"b", ",", "a"}], "]"}]}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{"a", ",", "b"}], "}"}], ",",
RowBox[{
RowBox[{"or", "[",
RowBox[{"a", ",", "b"}], "]"}], "\[Equal]",
RowBox[{"or", "[",
RowBox[{"b", ",", "a"}], "]"}]}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{"a", ",", "b"}], "}"}], ",",
RowBox[{
RowBox[{"and", "[",
RowBox[{"a", ",",
RowBox[{"or", "[",
RowBox[{"b", ",",
RowBox[{"not", "[", "b", "]"}]}], "]"}]}], "]"}],
"\[Equal]", "a"}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{"a", ",", "b"}], "}"}], ",",
RowBox[{
RowBox[{"or", "[",
RowBox[{"a", ",",
RowBox[{"and", "[",
RowBox[{"b", ",",
RowBox[{"not", "[", "b", "]"}]}], "]"}]}], "]"}],
"\[Equal]", "a"}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{"a", ",", "b", ",", "c"}], "}"}], ",",
RowBox[{
RowBox[{"and", "[",
RowBox[{"a", ",",
RowBox[{"or", "[",
RowBox[{"b", ",", "c"}], "]"}]}], "]"}], "\[Equal]",
RowBox[{"or", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{"a", ",", "b"}], "]"}], ",",
RowBox[{"and", "[",
RowBox[{"a", ",", "c"}], "]"}]}], "]"}]}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{"a", ",", "b", ",", "c"}], "}"}], ",",
RowBox[{
RowBox[{"or", "[",
RowBox[{"a", ",",
RowBox[{"and", "[",
RowBox[{"b", ",", "c"}], "]"}]}], "]"}], "\[Equal]",
RowBox[{"and", "[",
RowBox[{
RowBox[{"or", "[",
RowBox[{"a", ",", "b"}], "]"}], ",",
RowBox[{"or", "[",
RowBox[{"a", ",", "c"}], "]"}]}], "]"}]}]}], "]"}], ",",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{"a", ",", "b"}], "}"}], ",",
RowBox[{
RowBox[{"implies", "[",
RowBox[{"a", ",", "b"}], "]"}], "\[Equal]",
RowBox[{"or", "[",
RowBox[{
RowBox[{"not", "[", "a", "]"}], ",", "b"}], "]"}]}]}],
"]"}], ",",
RowBox[{"HoldForm", "[",
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{
"\[Alpha]", ",", " ", "\[Beta]", ",", " ", "y", ",", " ",
"z"}], "}"}], ",", " ",
RowBox[{"implies", "[",
RowBox[{
RowBox[{"Exists", "[",
RowBox[{"x", ",", " ",
RowBox[{"implies", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"\[Alpha]", "[", "y", "]"}], ",", " ",
RowBox[{"\[Beta]", "[", "z", "]"}]}], "]"}], ",", " ",
RowBox[{"between", "[",
RowBox[{"x", ",", " ", "y", ",", " ", "z"}], "]"}]}],
"]"}]}], "]"}], ",", " ",
RowBox[{"Exists", "[",
RowBox[{"u", ",", " ",
RowBox[{"implies", "[",
RowBox[{
RowBox[{"and", "[",
RowBox[{
RowBox[{"\[Alpha]", "[", "y", "]"}], ",", " ",
RowBox[{"\[Beta]", "[", "z", "]"}]}], "]"}], ",", " ",
RowBox[{"between", "[",
RowBox[{"y", ",", " ", "u", ",", " ", "z"}], "]"}]}],
"]"}]}], "]"}]}], "]"}]}], "]"}], "]"}]}], "}"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"geometry", "=",
RowBox[{"Most", "[", "geometryall", "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Column", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"Style", "[",
RowBox[{"#", ",", "Smaller"}], "]"}], "&"}], "/@",
"geometryall"}], ",",
RowBox[{"Frame", "\[Rule]", "All"}], ",",
RowBox[{"FrameStyle", "\[Rule]", "LightGray"}]}], "]"}]], "Input"]
}, Open ]]
|
Once again, this is all just a collection of formal statements. The fact that we’re calling an operator between is just for our convenience and understanding. All we can really say for sure is that this is some ternary operator; any properties it has have to be defined by the axioms.
To get to this formalization of Euclid, quite a bit of tightening up had to be done. Euclid’s theorems often had implicit assumptions, and it sometimes wasn’t even clear exactly what their logical structure was supposed to be. But the mathematical content is presumably the same, and indeed some of Euclid’s axioms (like CN1) say basically exactly the same as these. (An important addition to what Euclid explicitly said is the last axiom above, which states Euclid’s implicit assumption—that I now believe to be incorrect for the physical universe—that space is continuous. Unlike other axioms, which just make statements “true for all values of ...”, this axiom makes a statement “true for all functions ...”.)
So what can we do with these axioms? Well, in principle we can prove any theorem in Euclidean geometry. Appending to the axioms (that we refer to—ignoring the last axiom—as geometry) an assertion that we can interpret as saying that if a point y is between x and z and between x and w, then either z is between y and w or w is between y and z:

✕
FindEquationalProof[or[between[y, z, w], between[y, w, z]], Append[geometry, and[between[x, y, z], between[x, y, w]]]] |
Here’s a graph representing this proof:
![%[“ProofGraph”]](https://content.wolfram.com/sites/43/2020/09/sw0921img155.png)
✕
%["ProofGraph"] |
The axioms (including the “setup assertion”) are at the top—and the proof, with all its various intermediate lemmas, establishes that our “hypothesis” (represented by a little purple diamond on the left) eventually leads to “true” at the bottom.
As a more complicated example, we can look at Euclid’s very first theorem, 1.1, which asserts that there’s a ruler-and-compass way to construct an equilateral triangle on any line segment. In the Wolfram Language, the construction is:

✕
Entity["GeometricScene", "EuclidBook1Proposition1"]["Scene"] |

✕
RandomInstance[%] |
And now we can write this directly in terms of our low-level constructs. First we need a definition of what circles are (Euclid has this as Definition 1.15)—basically saying that two circles centered at a that go through b and c are equal if the lines from a to b and a to c are congruent:
|
✕
circles = \!\(
\*SubscriptBox[\(\[ForAll]\), \({a, b, c}\)]\(implies[
equal[circle[a, b], circle[a, c]],
congruent[line[a, b], line[a, c]]]\)\)
|
We’ll call this definition circles. We’re going to do a construction that involves having circles that overlap, as specified by the assertions:
|
✕
{equal[circle[a, b], circle[a, c]], equal[circle[b, a], circle[b, c]]}
|
And then our goal is to show that we get an equilateral triangle, for which the following is true:
|
✕
and[congruent[line[a, b], line[a, c]], congruent[line[b, a], line[b, c]]] |
Putting this all together we can prove Euclid’s 1.1:

✕
FindEquationalProof[
and[congruent[line[a, b], line[a, c]],
congruent[line[b, a], line[b, c]]], Join[geometry, {\!\(
\*SubscriptBox[\(\[ForAll]\), \({a, b, c}\)]\(implies[
equal[circle[a, b], circle[a, c]],
congruent[line[a, b], line[a, c]]]\)\)}, {equal[circle[a, b],
circle[a, c]], equal[circle[b, a], circle[b, c]]}]]
|
And, yes, it took 272 steps—and here’s a graphical representation of the proof that got generated, with all its intermediate lemmas:
![%[ProofGraph]](https://content.wolfram.com/sites/43/2020/09/sw0921img163.png)
✕
%["ProofGraph"] |
We can go on and prove Euclid’s 1.2 as well, all the way from the lowest-level axioms. This time it takes us 330 steps, with proof graph:

✕
CloudGet["https://wolfr.am/POgPyWJt"];
FindEquationalProof[congruent[line[a, l], line[b, c]],
Join[geometry, {\!\(
\*SubscriptBox[\(\[ForAll]\), \({a, b, c}\)]\(implies[
equal[circle[a, b], circle[a, c]],
congruent[line[a, b], line[a, c]]]\)\)}, {equal[circle[a, b],
circle[a, d]], equal[circle[b, a], circle[b, d]],
and[between[a, d, e], between[b, d, f]],
and[equal[circle[b, c], circle[b, g]],
equal[circle[b, c], circle[b, h]]],
and[equal[circle[d, g], circle[d, k]],
equal[circle[d, g], circle[d, l]]]}], "ProofGraph"]
|
These graphs are conceptually similar to, but concretely rather different from, our “empirical metamathematics” graphs above. There are differences at the level of how interdependence of theorems is defined. But, more important, this graph is generated by automated theorem proving methods; the intermediate theorems (or lemmas) it involves are produced “on the fly” for the convenience of the computer, not because they help in any way to explain the proof to a human. In our empirical metamathematics on Euclid’s Elements, however, we’re dealing with the theorems that Euclid chose to define, and that have served as a basis for explaining his proofs to humans for more than two thousand years.
By the way, if our goal is simply to find out what’s true in geometry—rather than to write out step-by-step proofs—then we now know how to do that. Essentially it involves turning geometric assertions into algebraic ones—and then systematically solving the polynomial equations and inequalities that result. It can be computationally expensive, but in the Wolfram Language we now have one master function, CylindricalDecomposition, that ultimately does the job. And, yes, given Gödel's theorem, one might wonder whether this kind of finite procedure for solving any Euclid-style geometry problem was even possible. But it turns out that—unlike arithmetic, for which Gödel’s theorem was originally proved—Euclid-style geometry, like basic logic, is decidable, in the sense that there is ultimately a finite procedure for deciding whether any given statement is true or not. In principle, this procedure could be based on theorem proving from the axioms, but CylindricalDecomposition effectively leverages a tower of more sophisticated mathematics to provide a much more efficient approach.
All Possible Theorems
From the axioms of geometry one can in principle derive an infinite number of true theorems—of which Euclid picked just 465 to include in his Elements. But why these theorems, and not others? Given a precise symbolic representation of geometry—as in the axioms above—one can just start enumerating true theorems.
One way to do this is to use a multiway system, with the axioms defining transformation rules that one can apply in all possible ways. In effect this is like constructing every possible proof, and seeing what gets proved. Needless to say, the network that gets produced quickly becomes extremely large—even if its structure is interesting for our attempt to find a “bulk theory of metamathematics”.
Here’s an example of doing it, not for the full geometry axioms above, but for basic logic (which is actually part of the axiom system we’ve used for geometry). We can either start with expressions, or with statements. Here we start with the expression x∧y, and then progressively find all expressions equal to it. Here’s the first, rather pedantic step:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"BooleanDisplay", "[", "expr_", "]"}], ":=",
RowBox[{"With", "[",
RowBox[{
RowBox[{"{",
RowBox[{"symbs", "=",
RowBox[{"Union", "[",
RowBox[{"Level", "[",
RowBox[{"expr", ",",
RowBox[{"{",
RowBox[{"-", "1"}], "}"}]}], "]"}], "]"}]}], "}"}], ",",
RowBox[{"expr", "/.",
RowBox[{"Thread", "[",
RowBox[{
RowBox[{
RowBox[{"(",
RowBox[{"#", "\[Rule]",
RowBox[{"Take", "[",
RowBox[{
RowBox[{"Alphabet", "[", "\"\<Greek\>\"", "]"}], ",",
RowBox[{"Length", "[", "#", "]"}]}], "]"}]}], ")"}],
"&"}], "[",
RowBox[{"Select", "[",
RowBox[{"symbs", ",",
RowBox[{
RowBox[{"StringContainsQ", "[",
RowBox[{
RowBox[{"SymbolName", "[", "#", "]"}], ",", "\"\<$\>\""}],
"]"}], "&"}]}], "]"}], "]"}], "]"}]}]}], "]"}]}]], "Input"],
Cell[BoxData[
RowBox[{"Graph", "[",
RowBox[{
RowBox[{
RowBox[{
"ResourceFunction", "[", "\"\<MultiwayOperatorSystem\>\"", "]"}],
"[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"And", "[",
RowBox[{"a_", ",", "b_"}], "]"}], "\[RuleDelayed]",
RowBox[{"And", "[",
RowBox[{"b", ",", "a"}], "]"}]}], ",",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a_", ",", "b_"}], "]"}], "\[RuleDelayed]",
RowBox[{"Or", "[",
RowBox[{"b", ",", "a"}], "]"}]}], ",",
RowBox[{
RowBox[{"And", "[",
RowBox[{"a_", ",",
RowBox[{"Or", "[",
RowBox[{"b_", ",",
RowBox[{"Not", "[", "b_", "]"}]}], "]"}]}], "]"}],
"\[RuleDelayed]", "a"}], ",",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a_", ",",
RowBox[{"And", "[",
RowBox[{"b_", ",",
RowBox[{"Not", "[", "b_", "]"}]}], "]"}]}], "]"}],
"\[RuleDelayed]", "a"}], ",",
RowBox[{"a_", "\[RuleDelayed]",
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{", "b", "}"}], ",",
RowBox[{"And", "[",
RowBox[{"a", ",",
RowBox[{"Or", "[",
RowBox[{"b", ",",
RowBox[{"Not", "[", "b", "]"}]}], "]"}]}], "]"}]}],
"]"}]}], ",",
RowBox[{"a_", "\[RuleDelayed]",
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{", "b", "}"}], ",",
RowBox[{"Or", "[",
RowBox[{"a", ",",
RowBox[{"And", "[",
RowBox[{"b", ",",
RowBox[{"Not", "[", "b", "]"}]}], "]"}]}], "]"}]}],
"]"}]}], ",",
RowBox[{
RowBox[{"And", "[",
RowBox[{"a_", ",",
RowBox[{"Or", "[",
RowBox[{"b_", ",", "c_"}], "]"}]}], "]"}],
"\[RuleDelayed]",
RowBox[{"Or", "[",
RowBox[{
RowBox[{"And", "[",
RowBox[{"a", ",", "b"}], "]"}], ",",
RowBox[{"And", "[",
RowBox[{"a", ",", "c"}], "]"}]}], "]"}]}], ",",
RowBox[{
RowBox[{"Or", "[",
RowBox[{
RowBox[{"And", "[",
RowBox[{"a_", ",", "b_"}], "]"}], ",",
RowBox[{"And", "[",
RowBox[{"a_", ",", "c_"}], "]"}]}], "]"}],
"\[RuleDelayed]",
RowBox[{"And", "[",
RowBox[{"a", ",",
RowBox[{"Or", "[",
RowBox[{"b", ",", "c"}], "]"}]}], "]"}]}], ",",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a_", ",",
RowBox[{"And", "[",
RowBox[{"b_", ",", "c_"}], "]"}]}], "]"}],
"\[RuleDelayed]",
RowBox[{"And", "[",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a", ",", "b"}], "]"}], ",",
RowBox[{"Or", "[",
RowBox[{"a", ",", "c"}], "]"}]}], "]"}]}], ",",
RowBox[{
RowBox[{"And", "[",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a_", ",", "b_"}], "]"}], ",",
RowBox[{"Or", "[",
RowBox[{"a_", ",", "c_"}], "]"}]}], "]"}],
"\[RuleDelayed]",
RowBox[{"Or", "[",
RowBox[{"a", ",",
RowBox[{"And", "[",
RowBox[{"b", ",", "c"}], "]"}]}], "]"}]}]}], "}"}], ",",
RowBox[{"And", "[",
RowBox[{"x", ",", "y"}], "]"}], ",", "1", ",",
"\"\<StatesGraph\>\"", ",",
RowBox[{"\"\<StateRenderingFunction\>\"", "\[RuleDelayed]",
RowBox[{"(",
RowBox[{
RowBox[{"Inset", "[",
RowBox[{
RowBox[{"Framed", "[",
RowBox[{
RowBox[{"Style", "[",
RowBox[{
RowBox[{"TraditionalForm", "[",
RowBox[{"BooleanDisplay", "[",
RowBox[{"ToExpression", "[", "#2", "]"}], "]"}],
"]"}], ",", "Black"}], "]"}], ",",
RowBox[{"Background", "\[Rule]",
RowBox[{"Directive", "[",
RowBox[{
RowBox[{"Opacity", "[", "0.5`", "]"}], ",",
InterpretationBox[
ButtonBox[
TooltipBox[
GraphicsBox[{
{GrayLevel[0], RectangleBox[{0, 0}]},
{GrayLevel[0], RectangleBox[{1, -1}]},
{RGBColor[0.73925, 0.79406, 0.935],
RectangleBox[{0, -1}, {2, 1}]}},
AspectRatio->1,
DefaultBaseStyle->"ColorSwatchGraphics",
Frame->True,
FrameStyle->RGBColor[
0.49283333333333335`, 0.5293733333333334,
0.6233333333333334],
FrameTicks->None,
ImageSize->
Dynamic[{
Automatic,
1.35 (CurrentValue["FontCapHeight"]/
AbsoluteCurrentValue[Magnification])}],
PlotRangePadding->None],
StyleBox[
RowBox[{"RGBColor", "[",
RowBox[{
"0.73925`", ",", "0.79406`", ",", "0.935`"}],
"]"}], NumberMarks -> False]],
Appearance->None,
BaseStyle->{},
BaselinePosition->Baseline,
ButtonFunction:>
With[{Typeset`box$ = EvaluationBox[]},
If[
Not[
AbsoluteCurrentValue["Deployed"]],
SelectionMove[Typeset`box$, All, Expression];
FrontEnd`Private`$ColorSelectorInitialAlpha = 1;
FrontEnd`Private`$ColorSelectorInitialColor =
RGBColor[0.73925, 0.79406, 0.935];
FrontEnd`Private`$ColorSelectorUseMakeBoxes =
True; MathLink`CallFrontEnd[
FrontEnd`AttachCell[Typeset`box$,
FrontEndResource["RGBColorValueSelector"], {
0, {Left, Bottom}}, {Left, Top},
"ClosingActions" -> {
"SelectionDeparture", "ParentChanged",
"EvaluatorQuit"}]]]],
DefaultBaseStyle->{},
Evaluator->Automatic,
Method->"Preemptive"],
RGBColor[0.73925, 0.79406, 0.935],
Editable->False,
Selectable->False]}], "]"}]}], ",",
RowBox[{"FrameStyle", "\[Rule]",
RowBox[{"GrayLevel", "[", ".7", "]"}]}], ",",
RowBox[{"RoundingRadius", "\[Rule]", "4"}], ",",
RowBox[{"FrameMargins", "\[Rule]", "2"}]}], "]"}], ",",
"#"}], "]"}], "&"}], ")"}]}]}], "]"}], ",",
RowBox[{
"GraphLayout", "\[Rule]", "\"\<SpringElectricalEmbedding\>\""}],
",",
RowBox[{"EdgeStyle", "->",
RowBox[{
RowBox[{
RowBox[{
"ResourceFunction", "[",
"\"\<WolframPhysicsProjectStyleData\>\"", "]"}], "[",
"\"\<StatesGraph\>\"", "]"}], "[", "\"\<EdgeStyle\>\"",
"]"}]}]}], "]"}]], "Input"]
}, Open ]]
|
And here’s the second step:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"BooleanDisplay", "[", "expr_", "]"}], ":=",
RowBox[{"With", "[",
RowBox[{
RowBox[{"{",
RowBox[{"symbs", "=",
RowBox[{"Union", "[",
RowBox[{"Level", "[",
RowBox[{"expr", ",",
RowBox[{"{",
RowBox[{"-", "1"}], "}"}]}], "]"}], "]"}]}], "}"}], ",",
RowBox[{"expr", "/.",
RowBox[{"Thread", "[",
RowBox[{
RowBox[{
RowBox[{"(",
RowBox[{"#", "\[Rule]",
RowBox[{"Take", "[",
RowBox[{
RowBox[{"Alphabet", "[", "\"\<Greek\>\"", "]"}], ",",
RowBox[{"Length", "[", "#", "]"}]}], "]"}]}], ")"}],
"&"}], "[",
RowBox[{"Select", "[",
RowBox[{"symbs", ",",
RowBox[{
RowBox[{"StringContainsQ", "[",
RowBox[{
RowBox[{"SymbolName", "[", "#", "]"}], ",", "\"\<$\>\""}],
"]"}], "&"}]}], "]"}], "]"}], "]"}]}]}], "]"}]}]], "Input"],
Cell[BoxData[
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
"ResourceFunction", "[", "\"\<MultiwayOperatorSystem\>\"", "]"}],
"[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"And", "[",
RowBox[{"a_", ",", "b_"}], "]"}], "\[RuleDelayed]",
RowBox[{"And", "[",
RowBox[{"b", ",", "a"}], "]"}]}], ",",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a_", ",", "b_"}], "]"}], "\[RuleDelayed]",
RowBox[{"Or", "[",
RowBox[{"b", ",", "a"}], "]"}]}], ",",
RowBox[{
RowBox[{"And", "[",
RowBox[{"a_", ",",
RowBox[{"Or", "[",
RowBox[{"b_", ",",
RowBox[{"Not", "[", "b_", "]"}]}], "]"}]}], "]"}],
"\[RuleDelayed]", "a"}], ",",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a_", ",",
RowBox[{"And", "[",
RowBox[{"b_", ",",
RowBox[{"Not", "[", "b_", "]"}]}], "]"}]}], "]"}],
"\[RuleDelayed]", "a"}], ",",
RowBox[{"a_", "\[RuleDelayed]",
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{", "b", "}"}], ",",
RowBox[{"And", "[",
RowBox[{"a", ",",
RowBox[{"Or", "[",
RowBox[{"b", ",",
RowBox[{"Not", "[", "b", "]"}]}], "]"}]}], "]"}]}],
"]"}]}], ",",
RowBox[{"a_", "\[RuleDelayed]",
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{", "b", "}"}], ",",
RowBox[{"Or", "[",
RowBox[{"a", ",",
RowBox[{"And", "[",
RowBox[{"b", ",",
RowBox[{"Not", "[", "b", "]"}]}], "]"}]}], "]"}]}],
"]"}]}], ",",
RowBox[{
RowBox[{"And", "[",
RowBox[{"a_", ",",
RowBox[{"Or", "[",
RowBox[{"b_", ",", "c_"}], "]"}]}], "]"}],
"\[RuleDelayed]",
RowBox[{"Or", "[",
RowBox[{
RowBox[{"And", "[",
RowBox[{"a", ",", "b"}], "]"}], ",",
RowBox[{"And", "[",
RowBox[{"a", ",", "c"}], "]"}]}], "]"}]}], ",",
RowBox[{
RowBox[{"Or", "[",
RowBox[{
RowBox[{"And", "[",
RowBox[{"a_", ",", "b_"}], "]"}], ",",
RowBox[{"And", "[",
RowBox[{"a_", ",", "c_"}], "]"}]}], "]"}],
"\[RuleDelayed]",
RowBox[{"And", "[",
RowBox[{"a", ",",
RowBox[{"Or", "[",
RowBox[{"b", ",", "c"}], "]"}]}], "]"}]}], ",",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a_", ",",
RowBox[{"And", "[",
RowBox[{"b_", ",", "c_"}], "]"}]}], "]"}],
"\[RuleDelayed]",
RowBox[{"And", "[",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a", ",", "b"}], "]"}], ",",
RowBox[{"Or", "[",
RowBox[{"a", ",", "c"}], "]"}]}], "]"}]}], ",",
RowBox[{
RowBox[{"And", "[",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a_", ",", "b_"}], "]"}], ",",
RowBox[{"Or", "[",
RowBox[{"a_", ",", "c_"}], "]"}]}], "]"}],
"\[RuleDelayed]",
RowBox[{"Or", "[",
RowBox[{"a", ",",
RowBox[{"And", "[",
RowBox[{"b", ",", "c"}], "]"}]}], "]"}]}]}], "}"}], ",",
RowBox[{"And", "[",
RowBox[{"x", ",", "y"}], "]"}], ",", "2", ",",
"\"\<StatesGraphStructure\>\"", ",",
RowBox[{"\"\<StateRenderingFunction\>\"", "\[RuleDelayed]",
RowBox[{"(",
RowBox[{
RowBox[{"Inset", "[",
RowBox[{
RowBox[{"Style", "[",
RowBox[{
RowBox[{"TraditionalForm", "[",
RowBox[{"BooleanDisplay", "[",
RowBox[{"ToExpression", "[", "#2", "]"}], "]"}], "]"}],
",", "Black"}], "]"}], ",", "#", ",",
RowBox[{"Background", "\[Rule]",
RowBox[{
RowBox[{
RowBox[{
"ResourceFunction", "[",
"\"\<WolframPhysicsProjectStyleData\>\"", "]"}], "[",
"\"\<StatesGraph\>\"", "]"}], "[", "\"\<VertexStyle\>\"",
"]"}]}]}], "]"}], "&"}], ")"}]}], ",",
RowBox[{"EdgeStyle", "->",
RowBox[{
RowBox[{
RowBox[{
"ResourceFunction", "[",
"\"\<WolframPhysicsProjectStyleData\>\"", "]"}], "[",
"\"\<StatesGraph\>\"", "]"}], "[", "\"\<EdgeStyle\>\"",
"]"}]}], ",",
RowBox[{"ImageSize", "\[Rule]", " ", "300"}]}], "]"}], ",",
RowBox[{"Graph", "[",
RowBox[{
RowBox[{
RowBox[{
"ResourceFunction", "[", "\"\<MultiwayOperatorSystem\>\"",
"]"}], "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"And", "[",
RowBox[{"a_", ",", "b_"}], "]"}], "\[RuleDelayed]",
RowBox[{"And", "[",
RowBox[{"b", ",", "a"}], "]"}]}], ",",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a_", ",", "b_"}], "]"}], "\[RuleDelayed]",
RowBox[{"Or", "[",
RowBox[{"b", ",", "a"}], "]"}]}], ",",
RowBox[{
RowBox[{"And", "[",
RowBox[{"a_", ",",
RowBox[{"Or", "[",
RowBox[{"b_", ",",
RowBox[{"Not", "[", "b_", "]"}]}], "]"}]}], "]"}],
"\[RuleDelayed]", "a"}], ",",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a_", ",",
RowBox[{"And", "[",
RowBox[{"b_", ",",
RowBox[{"Not", "[", "b_", "]"}]}], "]"}]}], "]"}],
"\[RuleDelayed]", "a"}], ",",
RowBox[{"a_", "\[RuleDelayed]",
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{", "b", "}"}], ",",
RowBox[{"And", "[",
RowBox[{"a", ",",
RowBox[{"Or", "[",
RowBox[{"b", ",",
RowBox[{"Not", "[", "b", "]"}]}], "]"}]}], "]"}]}],
"]"}]}], ",",
RowBox[{"a_", "\[RuleDelayed]",
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{", "b", "}"}], ",",
RowBox[{"Or", "[",
RowBox[{"a", ",",
RowBox[{"And", "[",
RowBox[{"b", ",",
RowBox[{"Not", "[", "b", "]"}]}], "]"}]}], "]"}]}],
"]"}]}], ",",
RowBox[{
RowBox[{"And", "[",
RowBox[{"a_", ",",
RowBox[{"Or", "[",
RowBox[{"b_", ",", "c_"}], "]"}]}], "]"}],
"\[RuleDelayed]",
RowBox[{"Or", "[",
RowBox[{
RowBox[{"And", "[",
RowBox[{"a", ",", "b"}], "]"}], ",",
RowBox[{"And", "[",
RowBox[{"a", ",", "c"}], "]"}]}], "]"}]}], ",",
RowBox[{
RowBox[{"Or", "[",
RowBox[{
RowBox[{"And", "[",
RowBox[{"a_", ",", "b_"}], "]"}], ",",
RowBox[{"And", "[",
RowBox[{"a_", ",", "c_"}], "]"}]}], "]"}],
"\[RuleDelayed]",
RowBox[{"And", "[",
RowBox[{"a", ",",
RowBox[{"Or", "[",
RowBox[{"b", ",", "c"}], "]"}]}], "]"}]}], ",",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a_", ",",
RowBox[{"And", "[",
RowBox[{"b_", ",", "c_"}], "]"}]}], "]"}],
"\[RuleDelayed]",
RowBox[{"And", "[",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a", ",", "b"}], "]"}], ",",
RowBox[{"Or", "[",
RowBox[{"a", ",", "c"}], "]"}]}], "]"}]}], ",",
RowBox[{
RowBox[{"And", "[",
RowBox[{
RowBox[{"Or", "[",
RowBox[{"a_", ",", "b_"}], "]"}], ",",
RowBox[{"Or", "[",
RowBox[{"a_", ",", "c_"}], "]"}]}], "]"}],
"\[RuleDelayed]",
RowBox[{"Or", "[",
RowBox[{"a", ",",
RowBox[{"And", "[",
RowBox[{"b", ",", "c"}], "]"}]}], "]"}]}]}], "}"}], ",",
RowBox[{"And", "[",
RowBox[{"x", ",", "y"}], "]"}], ",", "2", ",",
"\"\<StatesGraph\>\"", ",",
RowBox[{"\"\<StateRenderingFunction\>\"", "\[RuleDelayed]",
RowBox[{"(",
RowBox[{
RowBox[{"Inset", "[",
RowBox[{
RowBox[{"Framed", "[",
RowBox[{
RowBox[{"Style", "[",
RowBox[{
RowBox[{"TraditionalForm", "[",
RowBox[{"BooleanDisplay", "[",
RowBox[{"ToExpression", "[", "#2", "]"}], "]"}],
"]"}], ",", "Black"}], "]"}], ",",
RowBox[{"Background", "\[Rule]",
RowBox[{"Directive", "[",
RowBox[{
RowBox[{"Opacity", "[", "0.5`", "]"}], ",",
InterpretationBox[
ButtonBox[
TooltipBox[
GraphicsBox[{
{GrayLevel[0], RectangleBox[{0, 0}]},
{GrayLevel[0], RectangleBox[{1, -1}]},
{RGBColor[0.73925, 0.79406, 0.935],
RectangleBox[{0, -1}, {2, 1}]}},
AspectRatio->1,
DefaultBaseStyle->"ColorSwatchGraphics",
Frame->True,
FrameStyle->RGBColor[
0.49283333333333335`, 0.5293733333333334,
0.6233333333333334],
FrameTicks->None,
ImageSize->
Dynamic[{
Automatic,
1.35 (CurrentValue["FontCapHeight"]/
AbsoluteCurrentValue[Magnification])}],
PlotRangePadding->None],
StyleBox[
RowBox[{"RGBColor", "[",
RowBox[{
"0.73925`", ",", "0.79406`", ",", "0.935`"}],
"]"}], NumberMarks -> False]],
Appearance->None,
BaseStyle->{},
BaselinePosition->Baseline,
ButtonFunction:>
With[{Typeset`box$ = EvaluationBox[]},
If[
Not[
AbsoluteCurrentValue["Deployed"]],
SelectionMove[Typeset`box$, All, Expression];
FrontEnd`Private`$ColorSelectorInitialAlpha = 1;
FrontEnd`Private`$ColorSelectorInitialColor =
RGBColor[0.73925, 0.79406, 0.935];
FrontEnd`Private`$ColorSelectorUseMakeBoxes =
True; MathLink`CallFrontEnd[
FrontEnd`AttachCell[Typeset`box$,
FrontEndResource["RGBColorValueSelector"], {
0, {Left, Bottom}}, {Left, Top},
"ClosingActions" -> {
"SelectionDeparture", "ParentChanged",
"EvaluatorQuit"}]]]],
DefaultBaseStyle->{},
Evaluator->Automatic,
Method->"Preemptive"],
RGBColor[0.73925, 0.79406, 0.935],
Editable->False,
Selectable->False]}], "]"}]}], ",",
RowBox[{"FrameStyle", "\[Rule]",
RowBox[{"GrayLevel", "[", ".7", "]"}]}], ",",
RowBox[{"RoundingRadius", "\[Rule]", "4"}], ",",
RowBox[{"FrameMargins", "\[Rule]", "2"}]}], "]"}], ",",
"#"}], "]"}], "&"}], ")"}]}], ",",
RowBox[{"PlotRange", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"5.2", ",", "7.3"}], "}"}], ",",
RowBox[{"{",
RowBox[{"4", ",", "5.5"}], "}"}]}], "}"}]}]}], "]"}], ",",
RowBox[{"ImageSize", "\[Rule]", " ", "550"}], ",",
RowBox[{"EdgeStyle", "\[Rule]",
RowBox[{"Directive", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{
"ResourceFunction", "[",
"\"\<WolframPhysicsProjectStyleData\>\"", "]"}], "[",
"\"\<StatesGraph\>\"", "]"}], "[", "\"\<EdgeStyle\>\"",
"]"}], ",",
RowBox[{"Arrowheads", "[", "Medium", "]"}]}], "]"}]}]}],
"]"}]}], "}"}]], "Input"]
}, Open ]]
|
Every path in this graph is a proof that its endpoint expressions are equal. And while eventually this approach will give us every possible theorem (in this case about equalities involving x∧y), it’ll obviously take a while, generating huge numbers of long and uninteresting results on its way to anything interesting.
As a different approach, we can consider just enumerating short possible statements, then picking out ones that we determine are true. In principle we could determine truth by explicitly proving theorems using the axioms (and, yes, if there was undecidability we wouldn’t always be able to do this). But in practice for the case of basic logic that we’re using as an example here, we can basically just explicitly construct truth tables to find out what’s true and what’s not.
Here are some statements in logic, sorted in increasing order of complexity (as measured by depth and number of symbols):

✕
CloudGet["https://wolfr.am/PO7vasDF"];
(LogicFormat /@ (all43 =
Take[Select[FindAllAON[4, 3], LowestQ[#, {a, b, c}] &], 100])) //
TraditionalForm[Style[#, 14]] &
|
Many (like a=b) are very obviously not true, at least not for all possible values of each variable. But—essentially by using truth tables—we can readily pick out ones that are always true:

✕
CloudGet["https://wolfr.am/PO7vasDF"]; (LogicFormat /@ (all43 =
Take[Select[FindAllAON[4, 3], LowestQ[#, {a, b, c}] &], 100])) //
TraditionalForm[
Style[#,
14]] &; (LogicFormat /@ (If[MemberQ[data53, #],
Framed[#,
Background ->
Lighter[RGBColor[1., 0.8549019607843137, 0.59], .6],
FrameStyle -> RGBColor["#efcabd"], RoundingRadius -> 3,
FrameMargins -> Tiny],
Framed[#, FrameMargins -> Tiny, FrameStyle -> None]] & /@
all43)) // TraditionalForm[Style[#, 14]] &
|
OK, so now we can get a list of true theorems:

✕
CloudGet["https://wolfr.am/PO7vasDF"];
Framed[LogicFormat[#],
Background -> Lighter[RGBColor[1., 0.8549019607843137, 0.59], .6],
FrameStyle -> RGBColor["#efcabd"], RoundingRadius -> 3,
FrameMargins -> None] & /@ Take[data53, 60] //
TraditionalForm[Style[#, 14]] &
|
Some are “interesting”. Others seem repetitive, overly complicated, or otherwise not terribly interesting. But if we want to “channel Euclid” we somehow have to decide which are the interesting theorems that we’re going to write down. And although Euclid himself didn’t explicitly discuss logic, we can look at textbooks of logic from the last couple of centuries—and we find that there’s a very consistent set of theorems that they end up picking out from the list, and giving names to:
One might assume that these named theorems were just the result of historical convention. But when I was writing A New Kind of Science I discovered something quite surprising. With all the theorems written out in “order of complexity”, I tried seeing which theorems I could prove just from theorems earlier in the list. Many were easy to prove. But some simply couldn’t be proved. And it turned out that these were essentially precisely the “named theorems”:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PO7vasDF\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{
RowBox[{"LogicFormat", "/@",
RowBox[{"(",
RowBox[{"interesting", "=",
RowBox[{"First", "/@",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"a", "==",
RowBox[{"a", "\[Wedge]", "a"}]}], ",",
"\"\<idempotent law for and\>\""}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"a", "==",
RowBox[{"a", "\[Vee]", "a"}]}], ",",
"\"\<idempotent law for or\>\""}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"a", "\[Wedge]", "b"}], "==",
RowBox[{"b", "\[Wedge]", "a"}]}], ",",
"\"\<commutativity for and\>\""}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"a", "\[Vee]", "b"}], "==",
RowBox[{"b", "\[Vee]", "a"}]}], ",",
"\"\<commutativity for or\>\""}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"a", "==",
RowBox[{"\[Square]",
RowBox[{"\[Square]", "a"}]}]}], ",",
"\"\<law of double negation\>\""}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"\[Square]", "a"}], "\[Wedge]", "a"}], "==",
RowBox[{
RowBox[{"\[Square]", "b"}], "\[Wedge]", "b"}]}], ",",
"\"\<definition of false (law of noncontradiction)\>\""}],
"}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"\[Square]", "a"}], "\[Vee]", "a"}], "==",
RowBox[{
RowBox[{"\[Square]", "b"}], "\[Vee]", "b"}]}], ",",
"\"\<definition of true (law of excluded middle)\>\""}],
"}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"\[Square]",
RowBox[{"(",
RowBox[{"a", "\[Vee]", "b"}], ")"}]}], "==",
RowBox[{
RowBox[{"\[Square]", "a"}], "\[Wedge]",
RowBox[{"\[Square]", "b"}]}]}], ",",
"\"\<de Morgan law\>\""}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"\[Square]",
RowBox[{"(",
RowBox[{"a", "\[Wedge]", "b"}], ")"}]}], "==",
RowBox[{
RowBox[{"\[Square]", "a"}], "\[Vee]",
RowBox[{"\[Square]", "b"}]}]}], ",",
"\"\<de Morgan law\>\""}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"a", "==",
RowBox[{"a", "\[Wedge]",
RowBox[{"(",
RowBox[{"a", "\[Vee]", "b"}], ")"}]}]}], ",",
"\"\<absorption law\>\""}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"a", "==",
RowBox[{"a", "\[Vee]",
RowBox[{"a", "\[Wedge]", "b"}]}]}], ",",
"\"\<absorption law\>\""}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"(",
RowBox[{"a", "\[Wedge]", "b"}], ")"}], "\[Wedge]",
"c"}], "==",
RowBox[{"a", "\[Wedge]",
RowBox[{"(",
RowBox[{"b", "\[Wedge]", "c"}], ")"}]}]}], ",",
"\"\<associativity of and\>\""}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"(",
RowBox[{"a", "\[Vee]", "b"}], ")"}], "\[Vee]", "c"}], "==",
RowBox[{"a", "\[Vee]",
RowBox[{"(",
RowBox[{"b", "\[Vee]", "c"}], ")"}]}]}], ",",
"\"\<associativity of or\>\""}], "}"}]}], "}"}]}]}],
")"}]}], "//",
RowBox[{"(",
RowBox[{
RowBox[{"TraditionalForm", "[",
RowBox[{"Style", "[",
RowBox[{"#", ",", "15"}], "]"}], "]"}], "&"}], ")"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"provable", "=",
RowBox[{"ParallelTable", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"data53", "[",
RowBox[{"[", "i", "]"}], "]"}], ",",
RowBox[{"FindEquationalProof", "[",
RowBox[{
RowBox[{"data53", "[",
RowBox[{"[", "i", "]"}], "]"}], ",",
RowBox[{
RowBox[{
RowBox[{"ForAll", "[",
RowBox[{
RowBox[{"{",
RowBox[{"a", ",", "b", ",", "c"}], "}"}], ",", "#"}],
"]"}], "&"}], "/@",
RowBox[{"Take", "[",
RowBox[{"data53", ",",
RowBox[{"i", "-", "1"}]}], "]"}]}]}], "]"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{"i", ",", "2", ",", "100"}], "}"}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"Head", "[",
RowBox[{"Last", "[", "#", "]"}], "]"}], "===", "Failure"}],
",",
RowBox[{"Framed", "[",
RowBox[{
RowBox[{"TraditionalForm", "[",
RowBox[{"LogicFormat", "[",
RowBox[{"First", "[", "#", "]"}], "]"}], "]"}], ",",
RowBox[{"Background", "\[Rule]",
InterpretationBox[
ButtonBox[
TooltipBox[
GraphicsBox[{
{GrayLevel[0], RectangleBox[{0, 0}]},
{GrayLevel[0], RectangleBox[{1, -1}]},
{RGBColor[1., 0.7803921568627451, 0.6823529411764706],
RectangleBox[{0, -1}, {2, 1}]}},
AspectRatio->1,
DefaultBaseStyle->"ColorSwatchGraphics",
Frame->True,
FrameStyle->RGBColor[
0.6666666666666667, 0.5202614379084968,
0.4549019607843138],
FrameTicks->None,
ImageSize->
Dynamic[{
Automatic,
1.35 (CurrentValue["FontCapHeight"]/
AbsoluteCurrentValue[Magnification])}],
PlotRangePadding->None],
StyleBox[
RowBox[{"RGBColor", "[",
RowBox[{
"1.`", ",", "0.7803921568627451`", ",",
"0.6823529411764706`"}], "]"}], NumberMarks ->
False]],
Appearance->None,
BaseStyle->{},
BaselinePosition->Baseline,
ButtonFunction:>With[{Typeset`box$ = EvaluationBox[]},
If[
Not[
AbsoluteCurrentValue["Deployed"]],
SelectionMove[Typeset`box$, All, Expression];
FrontEnd`Private`$ColorSelectorInitialAlpha = 1;
FrontEnd`Private`$ColorSelectorInitialColor =
RGBColor[1., 0.7803921568627451, 0.6823529411764706];
FrontEnd`Private`$ColorSelectorUseMakeBoxes = True;
MathLink`CallFrontEnd[
FrontEnd`AttachCell[Typeset`box$,
FrontEndResource["RGBColorValueSelector"], {
0, {Left, Bottom}}, {Left, Top},
"ClosingActions" -> {
"SelectionDeparture", "ParentChanged",
"EvaluatorQuit"}]]]],
DefaultBaseStyle->{},
Evaluator->Automatic,
Method->"Preemptive"],
RGBColor[1., 0.7803921568627451, 0.6823529411764706],
Editable->False,
Selectable->False]}], ",",
RowBox[{"FrameStyle", "\[Rule]",
RowBox[{"RGBColor", "[", "\"\<#f7c5b2\>\"", "]"}]}], ",",
RowBox[{"RoundingRadius", "\[Rule]", "3"}], ",",
RowBox[{"FrameMargins", "\[Rule]", "None"}]}], "]"}], ",",
RowBox[{"Graph", "[",
RowBox[{
RowBox[{
RowBox[{"Last", "[", "#", "]"}], "[", "\"\<ProofGraph\>\"",
"]"}], ",",
RowBox[{"VertexLabels", "\[Rule]", "None"}], ",",
RowBox[{"ImageSize", "\[Rule]",
RowBox[{"{",
RowBox[{"Automatic", ",", "50"}], "}"}]}]}], "]"}]}], "]"}],
"&"}], "/@",
RowBox[{"Take", "[",
RowBox[{"provable", ",", "70"}], "]"}]}], "//",
"TraditionalForm"}]], "Input"]
}, Open ]]
|
In other words, the “named theorems” are basically the simplest statements of new facts about logic, that can’t be established from “simpler facts”. Eventually as one’s going through the list of theorems, one will have accumulated enough to fill out what can serve as full axioms for logic—so that then all subsequent theorems can be proved from “existing facts”.
Now of course the setup we’ve just used relies on the idea that one’s separately got a list of true theorems. To do something more like Euclid, we’d have to pick certain theorems to serve as axioms, then derive all others from these.
Back in 2000 I figured out the very simplest possible axiom system for logic, written in terms of Nand, just the single axiom:
|
✕
AxiomaticTheory[
"WolframAxioms"] /. {\[FormalA] -> a, \[FormalB] ->
b, \[FormalC] -> c} // (TraditionalForm[Style[#, 18]] &)
|
So now writing And, Or and Not in terms of Nand according to
|
✕
LogicFormat /@ {Square[a] == a\[CenterDot]a,
Wedge[a, b] == (a\[CenterDot]b)\[CenterDot](a\[CenterDot]b),
Vee[a, b] == (a\[CenterDot]a)\[CenterDot](b\[CenterDot]b)} // \
(TraditionalForm[Style[#, 18]] &)
|
we can, for example, derive the notable theorems of logic from my axiom. FindEquationalProof gives automated proofs of these theorems, though most of them involve quite a few steps (the — indicates a theorem that is trivially true after substituting the forms for And, Or and Not):

✕
CloudGet["https://wolfr.am/PKWTJ8gE"];
Row[Grid[#, Frame -> All,
Background -> {{RGBColor[1., 0.8549019607843137, 0.59], None},
None}] & /@
Partition[
Transpose@{TraditionalForm[LogicFormat[#]] & /@ (Last /@
Flatten[Values[
notableTheorems /. {OverBar -> Square, CirclePlus -> Vee,
CircleTimes -> Wedge}]]), {54, 54, 103, 102, 54, 95, 92,
132, 143, 91, 328, 274, 958, 1502,
Style["\[LongDash]", LightGray], 56, 131, 130, 120, 103}}, 5],
Spacer[2]] // TraditionalForm
|
The longer cases here involve first proving the lemma a·b = b·a which takes 102 steps. Including this lemma as an axiom, the minimal axiom system (as I also found in 2000) is:
|
✕
AxiomaticTheory[
"WolframCommutativeAxioms"] /. {\[FormalA] -> a, \[FormalB] ->
b, \[FormalC] -> c} // (TraditionalForm[Style[#, 16]] &)
|
And with this axiom system FindEquationalProof succeeds in finding shorter proofs for the notable theorems of logic, even though now the definitions for And, Or and Not are just treated as theorems:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PKXzCFkk\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{
RowBox[{"#", "[", "\"\<ProofLength\>\"", "]"}], " ", "&"}], " ", "/@",
" ", "notableProofs"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"Row", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"Grid", "[",
RowBox[{"#", ",",
RowBox[{"Frame", "\[Rule]", "All"}], ",",
RowBox[{"Background", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
InterpretationBox[
ButtonBox[
TooltipBox[
GraphicsBox[{
{GrayLevel[0], RectangleBox[{0, 0}]},
{GrayLevel[0], RectangleBox[{1, -1}]},
{RGBColor[1., 0.8549019607843137, 0.59],
RectangleBox[{0, -1}, {2, 1}]}},
AspectRatio->1,
DefaultBaseStyle->"ColorSwatchGraphics",
Frame->True,
FrameStyle->RGBColor[
0.6666666666666667, 0.5699346405228758,
0.3933333333333333],
FrameTicks->None,
ImageSize->
Dynamic[{
Automatic,
1.35 (CurrentValue["FontCapHeight"]/
AbsoluteCurrentValue[Magnification])}],
PlotRangePadding->None],
StyleBox[
RowBox[{"RGBColor", "[",
RowBox[{
"1.`", ",", "0.8549019607843137`", ",", "0.59`"}],
"]"}], NumberMarks -> False]],
Appearance->None,
BaseStyle->{},
BaselinePosition->Baseline,
ButtonFunction:>
With[{Typeset`box$ = EvaluationBox[]},
If[
Not[
AbsoluteCurrentValue["Deployed"]],
SelectionMove[Typeset`box$, All, Expression];
FrontEnd`Private`$ColorSelectorInitialAlpha = 1;
FrontEnd`Private`$ColorSelectorInitialColor =
RGBColor[1., 0.8549019607843137, 0.59];
FrontEnd`Private`$ColorSelectorUseMakeBoxes = True;
MathLink`CallFrontEnd[
FrontEnd`AttachCell[Typeset`box$,
FrontEndResource["RGBColorValueSelector"], {
0, {Left, Bottom}}, {Left, Top},
"ClosingActions" -> {
"SelectionDeparture", "ParentChanged",
"EvaluatorQuit"}]]]],
DefaultBaseStyle->{},
Evaluator->Automatic,
Method->"Preemptive"],
RGBColor[1., 0.8549019607843137, 0.59],
Editable->False,
Selectable->False], ",", "None"}], "}"}], ",", "None"}],
"}"}]}]}], "]"}], "&"}], "/@",
RowBox[{"Partition", "[",
RowBox[{
RowBox[{"Transpose", "@",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"TraditionalForm", "[",
RowBox[{"LogicFormat", "[", "#", "]"}], "]"}], "&"}], "/@",
RowBox[{"(",
RowBox[{"Last", "/@",
RowBox[{"Flatten", "[",
RowBox[{"Values", "[",
RowBox[{"notableTheorems", "/.",
RowBox[{"{",
RowBox[{
RowBox[{"OverBar", "\[Rule]", "Square"}], ",",
RowBox[{"CirclePlus", "\[Rule]", "Vee"}], ",",
RowBox[{"CircleTimes", "\[Rule]", "Wedge"}]}],
"}"}]}], "]"}], "]"}]}], ")"}]}], ",",
RowBox[{"{",
RowBox[{
"21", ",", "15", ",", "8", ",", "9", ",", "17", ",", "130",
",", "119", ",", "9", ",", "28", ",", "43", ",", "32",
",", "26", ",", "20", ",", "249", ",", "239", ",", "89",
",", "129", ",", "129", ",", "328", ",", "338"}], "}"}]}],
"}"}]}], ",", "5"}], "]"}]}], ",",
RowBox[{"Spacer", "[", "2", "]"}]}], "]"}], "//",
"TraditionalForm"}]], "Input"]
}, Open ]]
|
Actually looking at these proofs is not terribly illuminating; they certainly don’t have the same kind of “explanatory feel” as Euclid. But combining the graphs for all these proofs is more interesting, because it shows us the common lemmas that were used in these proofs, and effectively defines a network of interdependencies between theorems:

✕
CloudGet["https://wolfr.am/PKXzCFkk"];
Show[Graph[dependencyNetworkSimplified,
GraphLayout -> "LayeredDigraphEmbedding",
EdgeStyle -> GrayLevel[.5, .5],
VertexStyle -> (# ->
Which[MemberQ[conclusion, #],
Directive[RGBColor[221/255, 17/255, 0], EdgeForm[]],
MemberQ[standingPropositions, Sort[#]], Hue[
0.8238095238095239, 0.4, 0.9647058823529412],
MemberQ[viaLemmaPropositions, Sort[#]], Hue[
0.8238095238095239, 0.9, 0.9647058823529412],
MemberQ[axiomsList, #], Hue[0.11309523809523807`, 0.84, 1.],
MemberQ[lemmas, #], {EdgeForm[Opacity[.75]], Opacity[.5]}] & /@
VertexList[dependencyNetwork]),
VertexSize -> (# ->
Which[MemberQ[conclusion, #], 2,
MemberQ[standingPropositions, Sort[#]], .4 Sqrt[LeafCount[#]],
MemberQ[viaLemmaPropositions,
Sort[#]], .4 Sqrt[LeafCount[#]],
MemberQ[axiomsList, #], .4 Sqrt[LeafCount[#]],
MemberQ[lemmas, #], .4 Sqrt[LeafCount[#]]] & /@
VertexList[dependencyNetwork]),
VertexLabels -> (# ->
Which[MemberQ[conclusion, #], None,
MemberQ[standingPropositions, Sort[#]], LogicFormat[#],
MemberQ[viaLemmaPropositions, Sort[#]],
LogicFormat[# /. {x1 -> a, x2 -> b, x3 -> c}],
MemberQ[axiomsList, #],
LogicFormat[# /. {x1 -> a, x2 -> b, x3 -> c}],
MemberQ[lemmas, #], None] & /@
VertexList[dependencyNetwork]), AspectRatio -> 1/2],
Editable -> True]
|
There are 361 lemmas (i.e. automatically generated intermediate theorems) here. It’s a fair number, given that we’re only proving 20 theorems—but it’s definitely much less than the total of 1978 that would be involved in proving each of the theorems separately.
In our graph here—like in our Euclid theorem-dependency graphs above—the axioms are shown (in yellow) at the top. The “notable theorems” that we’re proving are shown in pink. But the structure of the graph is a little different from our earlier Euclid theorem-dependency graphs, and this alternative layout makes it clearer:

✕
CloudGet["https://wolfr.am/PKXzCFkk"];
Show[Graph[dependencyNetworkSimplified,
GraphLayout -> "SpringElectricalEmbedding",
EdgeStyle -> GrayLevel[.5, .5],
VertexStyle -> (# ->
Which[MemberQ[conclusion, #],
Directive[RGBColor[221/255, 17/255, 0], EdgeForm[]],
MemberQ[standingPropositions, Sort[#]], Hue[
0.8238095238095239, 0.4, 0.9647058823529412],
MemberQ[viaLemmaPropositions, Sort[#]], Hue[
0.8238095238095239, 0.9, 0.9647058823529412],
MemberQ[axiomsList, #], Hue[0.11309523809523807`, 0.84, 1.],
MemberQ[lemmas, #], {EdgeForm[Opacity[.75]], Opacity[.3]}] & /@
VertexList[dependencyNetwork]),
VertexSize -> (# ->
Which[MemberQ[conclusion, #], 2,
MemberQ[standingPropositions, Sort[#]], .4 Sqrt[LeafCount[#]],
MemberQ[viaLemmaPropositions,
Sort[#]], .4 Sqrt[LeafCount[#]],
MemberQ[axiomsList, #], .4 Sqrt[LeafCount[#]],
MemberQ[lemmas, #], .4 Sqrt[LeafCount[#]]] & /@
VertexList[dependencyNetwork]),
VertexLabels -> (# ->
Which[MemberQ[conclusion, #], None,
MemberQ[standingPropositions, Sort[#]], LogicFormat[#],
MemberQ[viaLemmaPropositions, Sort[#]],
LogicFormat[# /. {x1 -> a, x2 -> b, x3 -> c}],
MemberQ[axiomsList, #],
LogicFormat[# /. {x1 -> a, x2 -> b, x3 -> c}],
MemberQ[lemmas, #], None] & /@
VertexList[dependencyNetwork]), AspectRatio -> 1],
Editable -> True]
|
In Euclid, a given theorem is proved on the basis of other theorems, and ultimately on the basis of axioms. But here the automated theorem-proving process creates lemmas that ultimately allow one to show that the theorems one’s trying to prove are equivalent to “true” (i.e. to a tautology)—shown as a red node.
We can ask other questions, such as how long the lemmas are. Here are the distributions of lengths of the final notable theorems, and of the intermediate lemmas used to prove them:

✕
CloudGet["https://wolfr.am/PKXzCFkk"];
{Labeled[Histogram[LeafCount /@ propositions, {1},
PlotRange -> {{0, 25}, {0, 6}}, Frame -> True],
Style["notable theorems", FontFamily -> "Source Sans Pro",
FontSize -> 12]],
Labeled[Histogram[LeafCount /@ lemmas, {1},
PlotRange -> {{0, 25}, {0, Automatic}}, Frame -> True],
Style["intermediate lemmas", FontFamily -> "Source Sans Pro",
FontSize -> 12]]}
|
We get something slightly more in the spirit of Euclid if we elide the lemmas, and just find the implied effective dependency graph between notable theorems:

✕
CloudGet["https://wolfr.am/PKXzCFkk"]; dependencies = {};
Module[{proofObject = #},
Module[{theorem = #},
If[MemberQ[
If[Length[#] >= 1,
Sort[#], #] & /@ (Normal[
proofObject["ProofDataset"][[All, 1]][[
Values]]] /. {x1 -> \[FormalA], x2 -> \[FormalB],
x3 -> \[FormalC]}), theorem],
dependencies =
Append[dependencies,
DirectedEdge[theorem,
Last[proofObject["Theorem"]]]]]] & /@ (Last /@
toProve)] & /@ notableProofs; SimpleGraph[dependencies,
AspectRatio -> 1/2,
VertexLabels -> (# -> LogicFormat[#] & /@ VertexList[dependencies]),
VertexStyle -> Hue[0.8238095238095239, 0.4, 0.9647058823529412],
VertexSize -> .4,
EdgeStyle -> Directive[Arrowheads[.01], GrayLevel[.5, .5]]]
|
Transitive reduction then gives:

✕
CloudGet["https://wolfr.am/PKXzCFkk"]; dependencies = {};
Module[{proofObject = #},
Module[{theorem = #},
If[MemberQ[
If[Length[#] >= 1,
Sort[#], #] & /@ (Normal[
proofObject["ProofDataset"][[All, 1]][[
Values]]] /. {x1 -> \[FormalA], x2 -> \[FormalB],
x3 -> \[FormalC]}), theorem],
dependencies =
Append[dependencies,
DirectedEdge[theorem,
Last[proofObject["Theorem"]]]]]] & /@ (Last /@
toProve)] & /@ notableProofs; \
TransitiveReductionGraph[dependencies,
VertexLabels -> (# -> LogicFormat[#] & /@ VertexList[dependencies]),
VertexStyle -> Hue[0.8238095238095239, 0.4, 0.9647058823529412],
VertexSize -> .15, AspectRatio -> 1/3,
EdgeStyle -> Directive[Arrowheads[.02], GrayLevel[.5, .5]]]
|
By omitting intermediate lemmas, we’re in a sense just getting a shadow of the dependencies of the notable theorems, in the “environment” defined by our particular choice of axioms. But with this setup, it’s interesting to see the distributive law be the “hardest theorem”—kind of the metamathematical analog of Euclid’s 13.18 about the Platonic solids.
OK, but what we’re doing so far with logic is still fundamentally a bit different from how most of Euclid works. Because what Euclid typically does is to say something like “imagine such-and-such a geometrical setup; then the following theorem will be true about it”. And the analog of that for logic would be to take axioms of logic, then append some logical assertion, and ask if with the axioms and this assertion some particular statement is true. In other words, there are some statements—like the axioms—that will be true in “pure logic”, but there are more statements that will be true with particular setups (or, in the case of logic, particular possible values for variables).
For example, in “pure logic” a∨bb∨b is not necessarily true (i.e. it is not a tautology). But if we assert that a(a∧b) is true, then this implies the following possible choices for a and b

✕
SatisfiabilityInstances[a == (a \[And] b), {a, b}, All]
|
and in all these cases a∨bb∨b is true. So, in a Euclid tradition, we could say “imagine a setup where a(a∧b); then we can prove from the axioms of logic the theorem that a(a∧b)”.
Above we looked at which statements in logic are true for all values of variables:

✕
CloudGet["https://wolfr.am/PO7vasDF"]; (LogicFormat /@ (all43 =
Take[Select[FindAllAON[4, 3], LowestQ[#, {a, b, c}] &], 100])) //
TraditionalForm[Style[#, 14]] &;
(LogicFormat /@ (If[MemberQ[data53, #],
Framed[#,
Background ->
Lighter[RGBColor[1., 0.8549019607843137, 0.59], .6],
FrameStyle -> RGBColor["#efcabd"], RoundingRadius -> 3,
FrameMargins -> Tiny],
Framed[#, FrameMargins -> Tiny, FrameStyle -> None]] & /@
Take[all43, 50])) // TraditionalForm[Style[#, 14]] &
|
Now let’s look at the ones that aren’t always true. If we assume that some particular one of these statements is true, we can see which other statements it implies are true:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PO7vasDF\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{
RowBox[{"(",
RowBox[{"LogicFormat", "/@",
RowBox[{"(",
RowBox[{"all43", "=",
RowBox[{"Take", "[",
RowBox[{
RowBox[{"Select", "[",
RowBox[{
RowBox[{"FindAllAON", "[",
RowBox[{"4", ",", "3"}], "]"}], ",",
RowBox[{
RowBox[{"LowestQ", "[",
RowBox[{"#", ",",
RowBox[{"{",
RowBox[{"a", ",", "b", ",", "c"}], "}"}]}], "]"}],
"&"}]}], "]"}], ",", "100"}], "]"}]}], ")"}]}], ")"}], "//",
RowBox[{
RowBox[{"TraditionalForm", "[",
RowBox[{"Style", "[",
RowBox[{"#", ",", "14"}], "]"}], "]"}], "&"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"CheckTrue", "[",
RowBox[{"expr_", ",", "reps_"}], "]"}], ":=",
RowBox[{"TrueQ", "[",
RowBox[{
RowBox[{
RowBox[{"Length", "[", "reps", "]"}], ">", "0"}], "&&",
RowBox[{"AllTrue", "[",
RowBox[{"reps", ",",
RowBox[{
RowBox[{"expr", "/.", "#"}], "&"}]}], "]"}]}],
"]"}]}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"FindSats", "[", "expr_", "]"}], ":=",
RowBox[{"With", "[",
RowBox[{
RowBox[{"{",
RowBox[{"vars", "=",
RowBox[{"Union", "[",
RowBox[{"Level", "[",
RowBox[{"expr", ",",
RowBox[{"{",
RowBox[{"-", "1"}], "}"}]}], "]"}], "]"}]}], "}"}], ",",
RowBox[{"Thread", "/@",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"vars", "\[Rule]", "#"}], "&"}], "/@",
RowBox[{"SatisfiabilityInstances", "[",
RowBox[{"expr", ",", "vars", ",", "All"}], "]"}]}], ")"}]}]}],
"]"}]}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"uxx", "=",
RowBox[{"Cases", "[",
RowBox[{
RowBox[{"(",
RowBox[{
RowBox[{"Complement", "[",
RowBox[{
RowBox[{"Take", "[",
RowBox[{"all43", ",", "30"}], "]"}], ",", "data53"}], "]"}],
"/.",
RowBox[{"{",
RowBox[{
RowBox[{"Vee", "\[Rule]", "Or"}], ",",
RowBox[{"Wedge", "\[Rule]", "And"}], ",",
RowBox[{"Square", "\[Rule]", "Not"}]}], "}"}]}], ")"}], ",",
"_Equal"}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"TraditionalForm", "[",
RowBox[{"Grid", "[",
RowBox[{
RowBox[{
RowBox[{"Function", "[",
RowBox[{"u", ",",
RowBox[{"{",
RowBox[{"u", ",",
RowBox[{"Select", "[",
RowBox[{"uxx", ",",
RowBox[{
RowBox[{"CheckTrue", "[",
RowBox[{"#", ",",
RowBox[{"FindSats", "[", "u", "]"}]}], "]"}], "&"}]}],
"]"}]}], "}"}]}], "]"}], "/@",
RowBox[{"Take", "[",
RowBox[{"uxx", ",", "18"}], "]"}]}], ",",
RowBox[{"Alignment", "\[Rule]", "Left"}], ",",
RowBox[{"Dividers", "\[Rule]", " ",
RowBox[{"{",
RowBox[{
RowBox[{"2", "\[Rule]", " ",
RowBox[{"GrayLevel", "[", "0.7", "]"}]}], ",",
RowBox[{
RowBox[{
RowBox[{"#", "\[Rule]", " ",
RowBox[{"GrayLevel", "[", "0.7", "]"}]}], "&"}], "/@",
RowBox[{"Range", "[",
RowBox[{"2", ",", "18"}], "]"}]}]}], "}"}]}], ",",
RowBox[{"Frame", "\[Rule]", "True"}]}], "]"}], "]"}]], "Input"]
}, Open ]]
|
Or on a larger scale, with a black dot when one statement implies another:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PO7vasDF\>\"", "]"}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"CheckTrue", "[",
RowBox[{"expr_", ",", "reps_"}], "]"}], ":=",
RowBox[{"TrueQ", "[",
RowBox[{
RowBox[{
RowBox[{"Length", "[", "reps", "]"}], ">", "0"}], "&&",
RowBox[{"AllTrue", "[",
RowBox[{"reps", ",",
RowBox[{
RowBox[{"expr", "/.", "#"}], "&"}]}], "]"}]}],
"]"}]}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"FindSats", "[", "expr_", "]"}], ":=",
RowBox[{"With", "[",
RowBox[{
RowBox[{"{",
RowBox[{"vars", "=",
RowBox[{"Union", "[",
RowBox[{"Level", "[",
RowBox[{"expr", ",",
RowBox[{"{",
RowBox[{"-", "1"}], "}"}]}], "]"}], "]"}]}], "}"}], ",",
RowBox[{"Thread", "/@",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"vars", "\[Rule]", "#"}], "&"}], "/@",
RowBox[{"SatisfiabilityInstances", "[",
RowBox[{"expr", ",", "vars", ",", "All"}], "]"}]}], ")"}]}]}],
"]"}]}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"all43p", "=",
RowBox[{"Select", "[",
RowBox[{
RowBox[{"FindAllAON", "[",
RowBox[{"4", ",", "3"}], "]"}], ",",
RowBox[{
RowBox[{"LowestQ", "[",
RowBox[{"#", ",",
RowBox[{"{",
RowBox[{"a", ",", "b", ",", "c"}], "}"}]}], "]"}], "&"}]}],
"]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"uxxp", "=",
RowBox[{"Cases", "[",
RowBox[{
RowBox[{"(",
RowBox[{
RowBox[{"Complement", "[",
RowBox[{"all43p", ",", "data53"}], "]"}], "/.",
RowBox[{"{",
RowBox[{
RowBox[{"Vee", "\[Rule]", "Or"}], ",",
RowBox[{"Wedge", "\[Rule]", "And"}], ",",
RowBox[{"Square", "\[Rule]", "Not"}]}], "}"}]}], ")"}], ",",
"_Equal"}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"uxxpr", "=",
RowBox[{"FindSats", "/@", "uxxp"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"ArrayPlot", "[",
RowBox[{"Boole", "[",
RowBox[{"Outer", "[",
RowBox[{"CheckTrue", ",", "uxxp", ",", "uxxpr", ",", "1"}], "]"}],
"]"}], "]"}]], "Input"]
}, Open ]]
|
For each of these theorems we can in principle construct a proof, using the axioms:

✕
FindEquationalProof[(a\[CirclePlus]b) == (b\[CirclePlus]b), Append[AxiomaticTheory["BooleanAxioms"], a == (a\[CircleTimes]b)], "ProofGraph"] |
And now we could go through and find out which theorems are useful in proving other theorems—and in principle this would allow us to build up a theorem dependency network. But there are undoubtedly many ways to do this, and so we’d need additional criteria to find ones that have whatever attributes would make us say “that might have been how someone like Euclid would have done it”.
OK, so could one look at geometry the same way? Basically, yes. Using the formalization we had above in terms of line, between, congruent, etc. we can again start by just enumerating possible statements. Unlike for logic, many of them won’t even make “structural sense”; for example they might contain line[congruent[...],...], but it makes no sense to have a line whose endpoint is a truth value. But we can certainly get a list of “structurally meaningful” statements.
And then we can ask which are “tautologically true”—though it’s in practice considerably harder to do this than for logic (the best known methods involve all sorts of elaborate algebraic computations, which Mathematica can certainly do, but which quickly become quite unwieldy). And after that, we can proceed like Euclid, and start saying “assert this, then you can prove this”. And, yes, it’s nice that after 2000+ years, we can finally imagine automating the process of producing generalizations of Euclid’s Elements. Though this just makes it more obvious that part of what Euclid did was in a sense a matter of art—picking in some kind of aesthetic way which possible sequence of theorems would best “tell his story” of geometry.
Math beyond Euclid
We’ve looked here at some of the empirical metamathematics of what Euclid did on geometry more than 2000 years ago. But what about more recent mathematics, and all those other areas of mathematics that have now been studied? In the history of mathematics, there have been perhaps 5 million research papers published, as well as probably hundreds of thousands of textbooks (though few quite as systematic as Euclid).
And, yes, in modern times almost all mathematics that’s published is on the web in some form. A few years ago we scraped arXiv and identified about 2 million things described as theorems there (the most popular being the central limit theorem, the implicit function theorem and Fubini’s theorem); we also scraped as much as we could of the visible web and found about 30 million theorems there. No doubt many were duplicates (though it’s hard—and in principle undecidable!—which they are). But it’s a reasonable estimate that there are a few million distinct theorems for which proofs have been published in the history of human mathematics.
It’s a remarkable piece of encapsulated intellectual achievement—perhaps the largest coherent such one produced by our species. And I’ve long been interested in seeing just what it would take to make it computable, and to bring it into the whole computational knowledge framework we have in the Wolfram Language. A few years ago I hoped that we could mobilize the mathematics community to help make this happen. But formalization is hard work, and it’s not at the center of what most mathematicians aspire to. Still, we’ve at least been slowly working—much as we have for Euclid-style geometry—to define the elements of computational language needed to represent theorems in various areas of mathematics.
For example, in the area of point-set topology, we have under development things like

✕
If[PacletFind["PureMath"] === {},
PacletInstall[First[PacletFindRemote["PureMath"]]]]
Needs["PureMath`"]
Entity["TopologyConcept", "IsHausdorff"]["Output"] // InputForm
|
which in traditional mathematical notation becomes:

✕
TraditionalForm[%] |
So far we have encoded in computable form 742 “topology concepts”, and 1687 theorems about them. Here are the connections recorded between concepts (dropping the concept of “topological spaces” that a third of all concepts are connected to, and labeling concepts with high betweenness centrality):

✕
Cell[CellGroupData[{
Cell[BoxData[{
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"PacletFind", "[", "\"\<PureMath\>\"", "]"}], "===",
RowBox[{"{", "}"}]}], ",",
RowBox[{"PacletInstall", "[",
RowBox[{"First", "[",
RowBox[{"PacletFindRemote", "[", "\"\<PureMath\>\"", "]"}],
"]"}], "]"}]}], "]"}], "\n",
RowBox[{"Needs", "[", "\"\<PureMath`\>\"", "]"}]}], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"edges", "[", "type_", "]"}], ":=",
RowBox[{"Join", "@@",
RowBox[{"KeyValueMap", "[",
RowBox[{
RowBox[{"Thread", "@*", "DirectedEdge"}], ",",
RowBox[{"EntityValue", "[",
RowBox[{
"type", ",", "\"\<ReferencedEntities\>\"", ",",
"\"\<EntityAssociation\>\""}], "]"}]}], "]"}]}]}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"graph", "[", "args___", "]"}], ":=",
RowBox[{"Graph", "[",
RowBox[{"args", ",",
RowBox[{"VertexSize", "\[Rule]", "0.5"}], ",",
RowBox[{"EdgeStyle", "\[Rule]",
RowBox[{"Directive", "[",
RowBox[{
RowBox[{"GrayLevel", "[",
RowBox[{".5", ",", ".5"}], "]"}], ",",
RowBox[{"Arrowheads", "[", ".02", "]"}]}], "]"}]}]}],
"]"}]}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"select", "[",
RowBox[{"g_Graph", ",", "centrality_", ",", "crit_"}], "]"}], ":=",
RowBox[{"Graph", "[",
RowBox[{"g", ",",
RowBox[{"VertexStyle", "\[Rule]", "Orange"}], ",",
RowBox[{"VertexSize", "\[Rule]", "2"}], ",",
RowBox[{"VertexLabels", "\[Rule]",
RowBox[{"MapThread", "[",
RowBox[{
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"crit", "[", "#2", "]"}], "&&",
RowBox[{
RowBox[{"StringLength", "[",
RowBox[{"ToString", "[",
RowBox[{"CommonName", "[", "#", "]"}], "]"}], "]"}],
"<", "20"}]}], ",",
RowBox[{"#", "\[Rule]",
RowBox[{"Placed", "[",
RowBox[{
RowBox[{"Style", "[",
RowBox[{
RowBox[{"CommonName", "[", "#", "]"}], ",",
RowBox[{"Background", "\[Rule]", "White"}]}], "]"}],
",", "Left"}], "]"}]}], ",",
RowBox[{"#", "\[Rule]", "None"}]}], "]"}], "&"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"VertexList", "[", "g", "]"}], ",",
RowBox[{"centrality", "[", "g", "]"}]}], "}"}]}], "]"}]}]}],
"]"}]}]], "Input"],
Cell[BoxData[
RowBox[{"Show", "[",
RowBox[{
RowBox[{"First", "[",
RowBox[{"WeaklyConnectedGraphComponents", "[",
RowBox[{"select", "[",
RowBox[{
RowBox[{"VertexDelete", "[",
RowBox[{
RowBox[{"graph", "[",
RowBox[{"edges", "[", "\"\<TopologyConcept\>\"", "]"}],
"]"}], ",",
TemplateBox[{"\"topological spaces\"",
RowBox[{"Entity", "[",
RowBox[{"\"Category\"", ",", "\"Top\""}], "]"}],
"\"Entity[\\\"Category\\\", \\\"Top\\\"]\"",
"\"category\""},
"Entity"]}], "]"}], ",", "BetweennessCentrality", ",",
RowBox[{"GreaterThan", "[", "0", "]"}]}], "]"}], "]"}], "]"}],
",", " ",
RowBox[{"Editable", " ", "\[Rule]", " ", "True"}]}],
"]"}]], "Input"]
}, Open ]]
|
And here is the graph of what theorem references what in its description:

✕
Cell[CellGroupData[{
Cell[BoxData[{
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"PacletFind", "[", "\"\<PureMath\>\"", "]"}], "===",
RowBox[{"{", "}"}]}], ",",
RowBox[{"PacletInstall", "[",
RowBox[{"First", "[",
RowBox[{"PacletFindRemote", "[", "\"\<PureMath\>\"", "]"}],
"]"}], "]"}]}], "]"}], "\n",
RowBox[{"Needs", "[", "\"\<PureMath`\>\"", "]"}]}], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"edges", "[", "type_", "]"}], ":=",
RowBox[{"Join", "@@",
RowBox[{"KeyValueMap", "[",
RowBox[{
RowBox[{"Thread", "@*", "DirectedEdge"}], ",",
RowBox[{"EntityValue", "[",
RowBox[{
"type", ",", "\"\<ReferencedEntities\>\"", ",",
"\"\<EntityAssociation\>\""}], "]"}]}], "]"}]}]}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"graph", "[", "args___", "]"}], ":=",
RowBox[{"Graph", "[",
RowBox[{"args", ",",
RowBox[{"VertexSize", "\[Rule]", "0.5"}], ",",
RowBox[{"EdgeStyle", "\[Rule]",
RowBox[{"Directive", "[",
RowBox[{
RowBox[{"GrayLevel", "[",
RowBox[{".5", ",", ".5"}], "]"}], ",",
RowBox[{"Arrowheads", "[", ".02", "]"}]}], "]"}]}]}],
"]"}]}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"select", "[",
RowBox[{"g_Graph", ",", "centrality_", ",", "crit_"}], "]"}], ":=",
RowBox[{"Graph", "[",
RowBox[{"g", ",",
RowBox[{"VertexStyle", "\[Rule]", "Orange"}], ",",
RowBox[{"VertexSize", "\[Rule]", "2"}], ",",
RowBox[{"VertexLabels", "\[Rule]",
RowBox[{"MapThread", "[",
RowBox[{
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"crit", "[", "#2", "]"}], "&&",
RowBox[{
RowBox[{"StringLength", "[",
RowBox[{"ToString", "[",
RowBox[{"CommonName", "[", "#", "]"}], "]"}], "]"}],
"<", "100"}]}], ",",
RowBox[{"#", "\[Rule]",
RowBox[{"Placed", "[",
RowBox[{
RowBox[{"Style", "[",
RowBox[{
RowBox[{"CommonName", "[", "#", "]"}], ",",
RowBox[{"Background", "\[Rule]", "White"}]}], "]"}],
",", "Left"}], "]"}]}], ",",
RowBox[{"#", "\[Rule]", "None"}]}], "]"}], "&"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"VertexList", "[", "g", "]"}], ",",
RowBox[{"centrality", "[", "g", "]"}]}], "}"}]}], "]"}]}]}],
"]"}]}]], "Input"],
Cell[BoxData[
RowBox[{"Show", "[",
RowBox[{
RowBox[{"First", "[",
RowBox[{"WeaklyConnectedGraphComponents", "[",
RowBox[{"select", "[",
RowBox[{
RowBox[{"VertexDelete", "[",
RowBox[{
RowBox[{"graph", "[",
RowBox[{"edges", "[", "\"\<TopologyTheorem\>\"", "]"}],
"]"}], ",",
TemplateBox[{"\"topological spaces\"",
RowBox[{"Entity", "[",
RowBox[{"\"Category\"", ",", "\"Top\""}], "]"}],
"\"Entity[\\\"Category\\\", \\\"Top\\\"]\"",
"\"category\""},
"Entity"]}], "]"}], ",",
RowBox[{"BetweennessCentrality", "@*", "UndirectedGraph"}],
",",
RowBox[{
RowBox[{"#", "<", "0.0001"}], "&"}]}], "]"}], "]"}], "]"}],
",", " ",
RowBox[{"Editable", " ", "\[Rule]", " ", "True"}]}],
"]"}]], "Input"]
}, Open ]]
|
We haven’t encoded proofs for these theorems, so we can’t yet make the kind of theorem dependency graph that we did for Euclid. But we do have the dependency graph for 76 properties of topological spaces:

✕
Cell[CellGroupData[{
Cell[BoxData[{
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"PacletFind", "[", "\"\<PureMath\>\"", "]"}], "===",
RowBox[{"{", "}"}]}], ",",
RowBox[{"PacletInstall", "[",
RowBox[{"First", "[",
RowBox[{"PacletFindRemote", "[", "\"\<PureMath\>\"", "]"}],
"]"}], "]"}]}], "]"}], "\n",
RowBox[{"Needs", "[", "\"\<PureMath`\>\"", "]"}]}], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{
RowBox[{"aggregate", "[", "axioms_List", "]"}], ":=",
RowBox[{"Union", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "1"}], "]"}], "]"}], "\[Implies]",
RowBox[{"Union", "@",
RowBox[{"Flatten", "[",
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"All", ",", "2"}], "]"}], "]"}], "]"}]}]}], "&"}],
"/@",
RowBox[{"GatherBy", "[",
RowBox[{"axioms", ",", "First"}], "]"}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"propertyOntology", "=",
RowBox[{
RowBox[{
RowBox[{"Map", "[",
RowBox[{
RowBox[{
RowBox[{"EntityValue", "[",
RowBox[{"#", ",", "\"\<PropertyRelations\>\""}], "]"}],
"&"}], ",",
RowBox[{"{",
RowBox[{
"\"\<TopologyConcept\>\"", ",", "\"\<TopologyTheorem\>\""}],
"}"}]}], "]"}], "//", "Flatten"}], "//", "DeleteMissing"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"preprocessedOntology", "=",
RowBox[{"aggregate", "@",
RowBox[{"Fold", "[",
RowBox[{
RowBox[{
RowBox[{"Union", "@",
RowBox[{"Flatten", "@",
RowBox[{"Replace", "[",
RowBox[{"#1", ",", "#2", ",", "1"}], "]"}]}]}], "&"}], ",",
"propertyOntology", ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"a_", "\[Equivalent]", "b_"}], "\[RuleDelayed]",
RowBox[{"{",
RowBox[{
RowBox[{"a", "\[Implies]", "b"}], ",",
RowBox[{"b", "\[Implies]", "a"}]}], "}"}]}], ",",
RowBox[{
RowBox[{"a_", "\[Implies]", "e_Equivalent"}],
"\[RuleDelayed]",
RowBox[{
RowBox[{"(",
RowBox[{
RowBox[{"a", "\[Implies]", "#"}], "&"}], ")"}], "/@",
RowBox[{"Subsets", "[",
RowBox[{"e", ",",
RowBox[{"{", "2", "}"}]}], "]"}]}]}], ",",
RowBox[{
RowBox[{"a_", "\[Implies]",
RowBox[{"b_", "\[Equivalent]", "c_"}]}], "\[RuleDelayed]",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"a", "&&", "b"}], "\[Implies]", "c"}], ",",
RowBox[{
RowBox[{"a", "&&", "c"}], "\[Implies]", "b"}]}], "}"}]}],
",",
RowBox[{
RowBox[{
RowBox[{"d_", "&&",
RowBox[{"(",
RowBox[{"a_", "||", "b_"}], ")"}]}], "\[Implies]", "c_"}],
"\[RuleDelayed]",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"d", "&&", "a"}], "\[Implies]", "c"}], ",",
RowBox[{
RowBox[{"d", "&&", "b"}], "\[Implies]", "c"}]}], "}"}]}],
",",
RowBox[{
RowBox[{"a_", "\[Implies]", "b_"}], "\[RuleDelayed]",
RowBox[{"{",
RowBox[{
RowBox[{"a", "\[Implies]", "b"}], ",",
RowBox[{
RowBox[{"LogicalExpand", "[",
RowBox[{"!", "b"}], "]"}], "\[Implies]",
RowBox[{"LogicalExpand", "[",
RowBox[{"!", "a"}], "]"}]}]}], "}"}]}], ",",
RowBox[{
RowBox[{"d_Or", "\[Implies]", "c_"}], "\[RuleDelayed]",
RowBox[{
RowBox[{"(",
RowBox[{
RowBox[{"#", "\[Implies]", "c"}], "&"}], ")"}], "/@",
RowBox[{"List", "@@", "d"}]}]}], ",",
RowBox[{
RowBox[{"a_", "\[Implies]", "d_Or"}], "\[RuleDelayed]",
RowBox[{"With", "[",
RowBox[{
RowBox[{"{",
RowBox[{"s", "=",
RowBox[{"List", "@@", "d"}]}], "}"}], ",",
RowBox[{
RowBox[{
RowBox[{"Implies", "[",
RowBox[{
RowBox[{"a", "&&",
RowBox[{"And", "@@",
RowBox[{"(",
RowBox[{"Not", "/@",
RowBox[{"Complement", "[",
RowBox[{"s", ",",
RowBox[{"{", "#", "}"}]}], "]"}]}], ")"}]}]}],
",", "#"}], "]"}], "&"}], "/@", "s"}]}], "]"}]}], ",",
RowBox[{
RowBox[{"a_", "\[Implies]", "b_"}], "\[RuleDelayed]",
RowBox[{"Implies", "[",
RowBox[{
RowBox[{"Union", "@",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{"{", "a", "}"}], "/.", " ",
RowBox[{"And", "\[Rule]", "List"}]}], "]"}]}], ",",
RowBox[{"Union", "@",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{"{", "b", "}"}], "/.", " ",
RowBox[{"And", "\[Rule]", "List"}]}], "]"}]}]}],
"]"}]}]}], "}"}]}], "]"}]}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"nodes", "=",
RowBox[{"CanonicalName", "/@",
RowBox[{"EntityProperties", "@",
RowBox[{"EntityPropertyClass", "[",
RowBox[{
"\"\<TopologicalSpace\>\"", ",",
"\"\<TopologicalProperties\>\""}], "]"}]}]}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{
RowBox[{"deduce", "[", "known_List", "]"}], ":=",
RowBox[{"If", "[",
RowBox[{
RowBox[{"SatisfiableQ", "[",
RowBox[{"And", "@@", "known"}], "]"}], ",",
RowBox[{"Union", "[",
RowBox[{"known", ",",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{"Cases", "[",
RowBox[{"preprocessedOntology", ",",
RowBox[{"x_", "/;",
RowBox[{"SubsetQ", "[",
RowBox[{"known", ",",
RowBox[{"First", "@", "x"}]}], "]"}]}]}], "]"}], "[",
RowBox[{"[",
RowBox[{"All", ",", "2"}], "]"}], "]"}], "]"}]}], "]"}],
",",
RowBox[{"{", "False", "}"}]}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"edges", "=",
RowBox[{"Cases", "[",
RowBox[{
RowBox[{"Union", "@@",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"Thread", "[",
RowBox[{"#", "\[DirectedEdge]",
RowBox[{"FixedPoint", "[",
RowBox[{"deduce", ",",
RowBox[{"{", "#", "}"}]}], "]"}]}], "]"}], "&"}], "/@",
"nodes"}], ")"}]}], ",",
RowBox[{
RowBox[{"a_String", "\[DirectedEdge]", "b_String"}], "/;",
RowBox[{"a", "\[NotEqual]", "b"}]}]}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Show", "[",
RowBox[{
RowBox[{"With", "[",
RowBox[{
RowBox[{"{",
RowBox[{"g", "=",
RowBox[{"TransitiveReductionGraph", "@",
RowBox[{"Graph", "[",
RowBox[{"nodes", ",", "edges", ",",
RowBox[{
"GraphLayout", "\[Rule]",
"\"\<LayeredDigraphEmbedding\>\""}]}], "]"}]}]}], "}"}],
",",
RowBox[{"Graph", "[",
RowBox[{"g", ",",
RowBox[{"VertexLabels", "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", "\[Rule]",
RowBox[{"CommonName", "[",
RowBox[{"EntityProperty", "[",
RowBox[{"\"\<TopologicalSpace\>\"", ",", "#"}], "]"}],
"]"}]}], "&"}], "/@",
RowBox[{"VertexList", "[", "g", "]"}]}], ")"}]}], ",", " ",
RowBox[{"EdgeStyle", " ", "\[Rule]", " ",
RowBox[{"GrayLevel", "[",
RowBox[{"0.5", ",", " ", "0.5"}], "]"}]}], ",", " ",
RowBox[{"AspectRatio", "\[Rule]", " ", "0.8"}], ",", " ",
RowBox[{"VertexStyle", " ", "\[Rule]", " ", "Orange"}]}],
"]"}]}], "]"}], ",", " ",
RowBox[{"Editable", " ", "\[Rule]", " ", "True"}]}],
"]"}]], "Input"]
}, Open ]]
|
The longest path here (along with a similar one starting with ![]() ) is 14 steps:
) is 14 steps:

✕
Cell[CellGroupData[{Cell[BoxData[{
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"PacletFind", "[", "\"\<PureMath\>\"", "]"}], "===",
RowBox[{"{", "}"}]}], ",",
RowBox[{"PacletInstall", "[",
RowBox[{"First", "[",
RowBox[{"PacletFindRemote", "[", "\"\<PureMath\>\"", "]"}],
"]"}], "]"}]}], "]"}], "\n",
RowBox[{"Needs", "[", "\"\<PureMath`\>\"", "]"}]}], "Input"],
Cell[BoxData[
RowBox[{"Row", "[",
RowBox[{"Riffle", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"EntityProperty", "[",
RowBox[{"\"\<TopologicalSpace\>\"", ",", "#"}], "]"}], "&"}], "/@",
RowBox[{"{",
RowBox[{
"\"\<IsSurface\>\"", ",", "\"\<IsManifold\>\"", ",",
"\"\<IsCompletelyMetrizable\>\"", ",", "\"\<IsMetrizable\>\"",
",", "\"\<IsPerfectlyNormal\>\"", ",",
"\"\<IsCompletelyNormal\>\"", ",", "\"\<IsNormal\>\"", ",",
"\"\<IsCompletelyRegular\>\"", ",", "\"\<IsRegular\>\"", ",",
"\"\<IsSemiregular\>\"", ",", "\"\<IsHausdorff\>\"", ",",
"\"\<IsLocallyHausdorff\>\"", ",", "\"\<IsT1\>\"", ",",
"\"\<IsT0\>\""}], "}"}]}], ",", "\"\< \[RightArrow] \>\""}],
"]"}], "]"}]], "Input"]
}, Open ]]
|
(And, yes, this isn’t particularly profound; it’s just an indication of what it looks like to make specific definitions in topology computable.)
So far, what we’ve discussed is being able to represent pure mathematical ideas and results in a high-level computable way, understandable to both humans and computers. But what if we want to just formalize everything, from the ground up, explicitly deriving and validating every theorem from the lowest-level foundations? Over the past few decades there have been a number of large-scale projects—like Mizar, Coq, Isabelle, HOL, Metamath, Lean—that have tried to do this (nowadays often in connection with creating “proof assistants”).
Ultimately each project defines a certain “machine code” for mathematics. And yes, even though people might think that “mathematics is a universal language”, if one’s really going to give full, precise, formal specifications there are all sorts of choices to be made. Should things be based on set theory, type theory, higher-order logic, calculus of constructions, etc.? Should the law of excluded middle be assumed? The axiom of choice? What if one’s axiomatic structure seems great, but implies a few silly results, like 1/0 = 0? There’s no perfect solution, but each of these projects has made a certain set of choices.
And the good news here is that for our purposes in doing large-scale empirical metamathematics—as in doing mathematics in the way mathematicians usually do it—it doesn’t seem like the choices will matter much. But what’s important for us is that these projects have accumulated tens of thousands of theorems (well, OK, some are “throwaway lemmas” or simple rearrangements), and that starting from axioms (or what amount to axioms), they’ve reached decently far into quite a few areas of mathematics.
Looking at them is a bit of a different experience from looking at Euclid. While the Elements has the feel of a “narrative textbook” (albeit from a different age), formalized mathematics projects tend to seem more like software codebases, with their theorem dependency graphs being more like function call graphs. But they still provide fascinating metamathematical corpuses, and there's undoubtedly lots about empirical metamathematics that one can learn from them.
Here I’m going to look at two examples: the Lean mathlib collection, which includes about 36,000 theorems (and 16,000 definitions) and the Metamath set.mm (“set theory”) collection, which has about 44,000 theorems (and 1500 definitions).
To get a sense of what’s in these collections, we can start by drawing interdependence graphs for the theorems they contain in different areas of mathematics. Just like for Euclid, we make the size of each node represent the number of theorems in a particular area, and the thickness of each edge represent the fraction of theorems from one area that directly reference another in their proof.
Leaving out theorems that effectively just do structural manipulation, rather than representing mathematical content (as well as “self-loop” connections within a single domain) here’s the interdependence graph for Lean:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"leanAssoc", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL39QRbE\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanGraph", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL3LfaQ4\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanDomains", " ", "=", " ",
RowBox[{"Union", "[",
RowBox[{"Values", "[", "leanAssoc", "]"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanInfrastructure", " ", "=", " ",
RowBox[{"{",
RowBox[{
"\"\<init\>\"", ",", " ", "\"\<system\>\"", ",", " ",
"\"\<tactic\>\"", ",", " ", "\"\<data\>\"", ",", " ",
"\"\<meta\>\"", ",", " ", "\"\<control\>\"", ",", " ",
"\"\<computability\>\""}], "}"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanColors", " ", "=", " ",
RowBox[{"Merge", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"AssociationThread", "[",
RowBox[{
RowBox[{"Complement", "[",
RowBox[{"leanDomains", ",", " ", "leanInfrastructure"}],
"]"}], " ", "\[Rule]", " ",
RowBox[{"Take", "[",
RowBox[{
RowBox[{"ColorData", "[",
RowBox[{"54", ",", " ", "\"\<ColorList\>\""}], "]"}], ",",
" ",
RowBox[{"Length", "[",
RowBox[{"Complement", "[",
RowBox[{"leanDomains", ",", " ", "leanInfrastructure"}],
"]"}], "]"}]}], "]"}]}], "]"}], ",", " ",
RowBox[{"AssociationThread", "[",
RowBox[{
"leanInfrastructure", " ", "\[Rule]", " ", "LightGray"}],
"]"}]}], "}"}], ",", " ", "Identity"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanDomainWeights", " ", "=", " ",
RowBox[{"Tally", "[",
RowBox[{"Values", "[", "leanAssoc", "]"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanEdgeWeights", " ", "=", " ",
RowBox[{"Tally", "[",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"leanAssoc", "[",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}], ",", " ",
RowBox[{"leanAssoc", "[",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "]"}]}], "}"}], " ", "&"}],
" ", "/@", " ",
RowBox[{"EdgeList", "[", "leanGraph", "]"}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanEdgesOutSimple", " ", "=", " ",
RowBox[{"Append", "[",
RowBox[{
RowBox[{"Merge", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"AssociationThread", "[",
RowBox[{
RowBox[{"{",
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", " ", "1", ",", " ", "1"}], "]"}],
"]"}], "}"}], "\[Rule]", " ",
RowBox[{"Total", "[",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "]"}]}], "]"}], " ",
"&"}], " ", "/@", " ",
RowBox[{"(",
RowBox[{"Transpose", " ", "/@", " ",
RowBox[{"GatherBy", "[",
RowBox[{
RowBox[{"Select", "[",
RowBox[{"leanEdgeWeights", ",", " ",
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", " ", "1"}], "]"}], "]"}], " ",
"\[NotEqual]", " ",
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", " ", "2"}], "]"}], "]"}]}], " ",
"&"}]}], "]"}], ",", " ",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", " ", "1"}], "]"}], "]"}], " ",
"&"}]}], "]"}]}], ")"}]}], ",", " ", "Identity"}], "]"}],
",", " ",
RowBox[{"\"\<init\>\"", " ", "\[Rule]", " ",
RowBox[{"{", "3493", "}"}]}]}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanNormalizedEdgeWeights", " ", "=", " ",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"DirectedEdge", "[",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", " ", "1"}], "]"}], "]"}], ",", " ",
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", " ", "2"}], "]"}], "]"}]}], "]"}], " ",
"\[Rule]", " ",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "/", " ",
RowBox[{"Flatten", "[",
RowBox[{"leanEdgesOutSimple", "[",
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "1"}], "]"}], "]"}], "]"}], "]"}]}]}],
" ", "&"}], " ", "/@", " ", "leanEdgeWeights"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{
RowBox[{"diskedLine", "[",
RowBox[{"{",
RowBox[{"line_", ",", "radii_"}], "}"}], "]"}], ":=",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"RegionIntersection", "[",
RowBox[{
RowBox[{"Line", "[", "line", "]"}], ",",
RowBox[{"Circle", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"radii", "[",
RowBox[{"[", "1", "]"}], "]"}]}], "]"}]}], "]"}], "[",
RowBox[{"[",
RowBox[{"1", ",", "1"}], "]"}], "]"}], ",",
"\[IndentingNewLine]",
RowBox[{
RowBox[{"RegionIntersection", "[",
RowBox[{
RowBox[{"Line", "[", "line", "]"}], ",",
RowBox[{"Circle", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"[", "2", "]"}], "]"}], ",",
RowBox[{"radii", "[",
RowBox[{"[", "2", "]"}], "]"}]}], "]"}]}], "]"}], "[",
RowBox[{"[",
RowBox[{"1", ",", "1"}], "]"}], "]"}]}], "}"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{
RowBox[{"weightedArrow", "[",
RowBox[{"line_", ",", "weight_"}], "]"}], ":=", " ",
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
"len", ",", "start", ",", "end", ",", "angle", ",", " ",
"thick", ",", " ", "rec", ",", " ", "mid"}], "}"}], ",",
"\[IndentingNewLine]",
RowBox[{
RowBox[{"start", "=",
RowBox[{"line", "[",
RowBox[{"[", "1", "]"}], "]"}]}], ";", " ",
RowBox[{"end", "=",
RowBox[{"line", "[",
RowBox[{"[", "2", "]"}], "]"}]}], ";", " ",
RowBox[{"mid", "=",
RowBox[{"Mean", "[", "line", "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"len", "=",
RowBox[{"EuclideanDistance", "[",
RowBox[{"start", ",", "end"}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"angle", "=",
RowBox[{"Arg", "[",
RowBox[{
RowBox[{"(",
RowBox[{"start", "-", "end"}], ")"}], ".",
RowBox[{"{",
RowBox[{"1", ",", "I"}], "}"}]}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"thick", "=",
RowBox[{"weight", "/", "len"}]}], ";", "\[IndentingNewLine]",
RowBox[{"rec", "=", " ",
RowBox[{
RowBox[{
RowBox[{"#", "+", "mid"}], "&"}], "/@",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"RotationMatrix", "[", "angle", "]"}], ".", "#"}],
"&"}], "/@",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"-", "len"}], "/", "2"}], ",",
RowBox[{
RowBox[{"-", " ", "thick"}], "/", "2"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"len", "/", "2"}], ",",
RowBox[{
RowBox[{"-", " ", "thick"}], "/", "2"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"len", "/", "2"}], ",", " ",
RowBox[{"thick", "/", "2"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"-", "len"}], "/", "2"}], ",", " ",
RowBox[{"thick", "/", "2"}]}], "}"}]}], "}"}]}],
")"}]}]}], ";", "\[IndentingNewLine]",
RowBox[{"Polygon", "[", "rec", "]"}]}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"VertexDelete", "[",
RowBox[{
RowBox[{"SimpleGraph", "[",
RowBox[{"Graph", "[",
RowBox[{"leanDomains", ",", " ",
RowBox[{"First", " ", "/@", " ", "leanNormalizedEdgeWeights"}],
",", " ",
RowBox[{"EdgeStyle", "\[Rule]",
RowBox[{"Thread", "[",
RowBox[{
RowBox[{"First", "/@", "leanNormalizedEdgeWeights"}], " ",
"\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"AbsoluteThickness", "[",
RowBox[{"20",
RowBox[{
RowBox[{"Last", "[", "#", "]"}], "[",
RowBox[{"[", "1", "]"}], "]"}]}], "]"}], ",",
RowBox[{"Arrowheads", "[",
RowBox[{
RowBox[{
RowBox[{"Last", "[", "#", "]"}], "[",
RowBox[{"[", "1", "]"}], "]"}], "/", "4"}], "]"}],
",", " ",
RowBox[{"GrayLevel", "[",
RowBox[{"0.5", ",", " ", "0.5"}], "]"}]}], "}"}],
"&"}], "/@", "leanNormalizedEdgeWeights"}], ")"}]}],
"]"}]}], ",", " ",
RowBox[{"VertexSize", "\[Rule]",
RowBox[{"Thread", "[",
RowBox[{
RowBox[{"First", "/@", "leanDomainWeights"}], " ", "\[Rule]",
" ",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"Sqrt", "[", "#", "]"}], "/", "90"}], "&"}], "/@",
RowBox[{"(",
RowBox[{"Last", "/@", "leanDomainWeights"}], ")"}]}],
")"}]}], "]"}]}], ",", " ",
RowBox[{"VertexStyle", " ", "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", " ", "\[Rule]", " ",
RowBox[{"{",
RowBox[{"Lighter", " ", "/@", " ",
RowBox[{"leanColors", "[", "#", "]"}]}], "}"}]}], " ",
"&"}], " ", "/@", " ", "leanDomains"}], ")"}]}], ",", " ",
RowBox[{"VertexLabels", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{
"\"\<algebra\>\"", " ", "\[Rule]", " ", "\"\<algebra\>\""}],
",",
RowBox[{
"\"\<algebraic_geometry\>\"", " ", "\[Rule]", " ",
"\"\<algebraic geometry\>\""}], ",",
RowBox[{
"\"\<analysis\>\"", " ", "\[Rule]", " ",
"\"\<analysis\>\""}], ",",
RowBox[{
"\"\<category_theory\>\"", " ", "\[Rule]", " ",
"\"\<category theory\>\""}], ",",
RowBox[{
"\"\<combinatorics\>\"", " ", "\[Rule]", " ",
"\"\<combinatorics\>\""}], ",",
RowBox[{
"\"\<computability\>\"", " ", "\[Rule]", " ",
"\"\<computability\>\""}], ",",
RowBox[{
"\"\<control\>\"", " ", "\[Rule]", " ", "\"\<control\>\""}],
",",
RowBox[{
"\"\<data\>\"", " ", "\[Rule]", " ", "\"\<data\>\""}], ",",
RowBox[{
"\"\<dynamics\>\"", " ", "\[Rule]", " ",
"\"\<dynamics\>\""}], ",",
RowBox[{
"\"\<geometry\>\"", " ", "\[Rule]", " ",
"\"\<geometry\>\""}], ",",
RowBox[{
"\"\<init\>\"", " ", "\[Rule]", " ", "\"\<init\>\""}], ",",
RowBox[{
"\"\<logic\>\"", " ", "\[Rule]", " ", "\"\<logic\>\""}], ",",
RowBox[{
"\"\<meta\>\"", " ", "\[Rule]", " ", "\"\<meta\>\""}], ",",
RowBox[{
"\"\<number_theory\>\"", " ", "\[Rule]", " ",
"\"\<number theory\>\""}], ",",
RowBox[{
"\"\<order\>\"", " ", "\[Rule]", " ",
"\"\<order theory\>\""}], ",",
RowBox[{
"\"\<set_theory\>\"", " ", "\[Rule]", " ",
"\"\<set theory\>\""}], ",",
RowBox[{
"\"\<system\>\"", " ", "\[Rule]", " ", "\"\<system\>\""}],
",",
RowBox[{
"\"\<tactic\>\"", " ", "\[Rule]", " ", "\"\<tactic\>\""}],
",",
RowBox[{
"\"\<topology\>\"", " ", "\[Rule]", " ",
"\"\<topology\>\""}]}], "}"}]}], ",", " ",
RowBox[{
"GraphLayout", " ", "\[Rule]", " ",
"\"\<SpringElectricalEmbedding\>\""}], ",", " ",
RowBox[{"PerformanceGoal", "\[Rule]", "\"\<Quality\>\""}], ",",
" ",
RowBox[{"AspectRatio", "\[Rule]",
RowBox[{"1", "/", "4"}]}]}], "]"}], "]"}], ",", " ",
RowBox[{"{",
RowBox[{
"\"\<init\>\"", ",", " ", "\"\<system\>\"", ",", " ",
"\"\<tactic\>\"", ",", " ", "\"\<data\>\"", ",", " ",
"\"\<meta\>\"", ",", " ", "\"\<control\>\"", ",", " ",
"\"\<computability\>\""}], "}"}], ",", " ",
RowBox[{"AspectRatio", "\[Rule]", " ", "1"}]}], "]"}]], "Input"]
}, Open ]]
|
And here’s the corresponding one for Metamath:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"extensibleStructures", " ", "=", " ",
RowBox[{"{",
RowBox[{
"\"\<df-struct\>\"", ",", "\"\<df-ndx\>\"", ",",
"\"\<df-slot\>\"", ",", "\"\<df-base\>\"", ",",
"\"\<df-base\>\"", ",", "\"\<df-sets\>\"", ",",
"\"\<df-ress\>\"", ",", "\"\<brstruct\>\"", ",",
"\"\<isstruct2\>\"", ",", "\"\<isstruct\>\"", ",",
"\"\<structcnvcnv\>\"", ",", "\"\<structfun\>\"", ",",
"\"\<structfn\>\"", ",", "\"\<slotfn\>\"", ",",
"\"\<strfvnd\>\"", ",", "\"\<wunndx\>\"", ",", "\"\<strfvn\>\"",
",", "\"\<strfvn\>\"", ",", "\"\<strfvss\>\"", ",",
"\"\<wunstr\>\"", ",", "\"\<ndxarg\>\"", ",", "\"\<ndxid\>\"",
",", "\"\<ndxid\>\"", ",", "\"\<strndxid\>\"", ",",
"\"\<reldmsets\>\"", ",", "\"\<setsvalg\>\"", ",",
"\"\<setsval\>\"", ",", "\"\<setsval\>\"", ",",
"\"\<setsidvald\>\"", ",", "\"\<fvsetsid\>\"", ",",
"\"\<fsets\>\"", ",", "\"\<wunsets\>\"", ",", "\"\<setsres\>\"",
",", "\"\<setsres\>\"", ",", "\"\<setsabs\>\"", ",",
"\"\<setscom\>\"", ",", "\"\<setscom\>\"", ",", "\"\<strfvd\>\"",
",", "\"\<strfv2d\>\"", ",", "\"\<strfv2\>\"", ",",
"\"\<strfv\>\"", ",", "\"\<strfv\>\"", ",", "\"\<strfv3\>\"",
",", "\"\<strssd\>\"", ",", "\"\<strssd\>\"", ",",
"\"\<strss\>\"", ",", "\"\<strss\>\"", ",", "\"\<str0\>\"", ",",
"\"\<str0\>\"", ",", "\"\<base0\>\"", ",", "\"\<strfvi\>\"",
",", "\"\<setsid\>\"", ",", "\"\<setsid\>\"", ",",
"\"\<setsnid\>\"", ",", "\"\<setsnid\>\"", ",",
"\"\<sbcie2s\>\"", ",", "\"\<sbcie3s\>\"", ",",
"\"\<baseval\>\"", ",", "\"\<baseid\>\"", ",", "\"\<elbasfv\>\"",
",", "\"\<elbasov\>\"", ",", "\"\<strov2rcl\>\"", ",",
"\"\<strov2rcl\>\"", ",", "\"\<basendx\>\"", ",",
"\"\<reldmress\>\"", ",", "\"\<ressval\>\"", ",",
"\"\<ressid2\>\"", ",", "\"\<ressval2\>\"", ",",
"\"\<ressbas\>\"", ",", "\"\<ressbas2\>\"", ",",
"\"\<ressbasss\>\"", ",", "\"\<ressbasss\>\"", ",",
"\"\<resslem\>\"", ",", "\"\<resslem\>\"", ",", "\"\<ress0\>\"",
",", "\"\<ress0\>\"", ",", "\"\<ressid\>\"", ",",
"\"\<ressinbas\>\"", ",", "\"\<ressval3d\>\"", ",",
"\"\<ressress\>\"", ",", "\"\<ressress\>\"", ",",
"\"\<ressabs\>\"", ",", "\"\<wunress\>\"", ",",
"\"\<df-rest\>\"", ",", "\"\<df-rest\>\"", ",",
"\"\<df-topn\>\"", ",", "\"\<restfn\>\"", ",", "\"\<topnfn\>\"",
",", "\"\<restval\>\"", ",", "\"\<restval\>\"", ",",
"\"\<elrest\>\"", ",", "\"\<elrest\>\"", ",", "\"\<elrestr\>\"",
",", "\"\<elrestr\>\"", ",", "\"\<0rest\>\"", ",",
"\"\<restid2\>\"", ",", "\"\<restsspw\>\"", ",",
"\"\<firest\>\"", ",", "\"\<restid\>\"", ",", "\"\<restid\>\"",
",", "\"\<topnval\>\"", ",", "\"\<topnid\>\"", ",",
"\"\<topnpropd\>\"", ",", "\"\<df-0g\>\"", ",",
"\"\<df-gsum\>\"", ",", "\"\<df-gsum\>\"", ",",
"\"\<df-gsum\>\"", ",", "\"\<df-topgen\>\"", ",",
"\"\<df-pt\>\"", ",", "\"\<df-prds\>\"", ",", "\"\<df-prds\>\"",
",", "\"\<reldmprds\>\"", ",", "\"\<reldmprds\>\"", ",",
"\"\<df-pws\>\"", ",", "\"\<prdsbasex\>\"", ",",
"\"\<imasvalstr\>\"", ",", "\"\<imasvalstr\>\"", ",",
"\"\<imasvalstr\>\"", ",", "\"\<prdsvalstr\>\"", ",",
"\"\<prdsvalstr\>\"", ",", "\"\<prdsvalstr\>\"", ",",
"\"\<prdsvallem\>\"", ",", "\"\<prdsvallem\>\"", ",",
"\"\<prdsval\>\"", ",", "\"\<prdsval\>\"", ",",
"\"\<prdsval\>\"", ",", "\"\<prdssca\>\"", ",",
"\"\<prdssca\>\"", ",", "\"\<prdssca\>\"", ",",
"\"\<prdsbas\>\"", ",", "\"\<prdsbas\>\"", ",",
"\"\<prdsbas\>\"", ",", "\"\<prdsplusg\>\"", ",",
"\"\<prdsplusg\>\"", ",", "\"\<prdsplusg\>\"", ",",
"\"\<prdsmulr\>\"", ",", "\"\<prdsmulr\>\"", ",",
"\"\<prdsmulr\>\"", ",", "\"\<prdsvsca\>\"", ",",
"\"\<prdsvsca\>\"", ",", "\"\<prdsvsca\>\"", ",",
"\"\<prdsip\>\"", ",", "\"\<prdsle\>\"", ",", "\"\<prdsle\>\"",
",", "\"\<prdsless\>\"", ",", "\"\<prdsds\>\"", ",",
"\"\<prdsds\>\"", ",", "\"\<prdsdsfn\>\"", ",",
"\"\<prdstset\>\"", ",", "\"\<prdstset\>\"", ",",
"\"\<prdshom\>\"", ",", "\"\<prdshom\>\"", ",", "\"\<prdsco\>\"",
",", "\"\<prdsco\>\"", ",", "\"\<prdsbas2\>\"", ",",
"\"\<prdsbas2\>\"", ",", "\"\<prdsbasmpt\>\"", ",",
"\"\<prdsbasfn\>\"", ",", "\"\<prdsbasprj\>\"", ",",
"\"\<prdsplusgval\>\"", ",", "\"\<prdsplusgval\>\"", ",",
"\"\<prdsplusgfval\>\"", ",", "\"\<prdsmulrval\>\"", ",",
"\"\<prdsmulrfval\>\"", ",", "\"\<prdsleval\>\"", ",",
"\"\<prdsdsval\>\"", ",", "\"\<prdsvscaval\>\"", ",",
"\"\<prdsvscafval\>\"", ",", "\"\<prdsbas3\>\"", ",",
"\"\<prdsbasmpt2\>\"", ",", "\"\<prdsbasmpt2\>\"", ",",
"\"\<prdsbascl\>\"", ",", "\"\<prdsdsval2\>\"", ",",
"\"\<prdsdsval3\>\"", ",", "\"\<pwsval\>\"", ",",
"\"\<pwsbas\>\"", ",", "\"\<pwselbasb\>\"", ",",
"\"\<pwselbas\>\"", ",", "\"\<pwselbas\>\"", ",",
"\"\<pwsplusgval\>\"", ",", "\"\<pwsmulrval\>\"", ",",
"\"\<pwsle\>\"", ",", "\"\<pwsleval\>\"", ",",
"\"\<pwsvscafval\>\"", ",", "\"\<pwsvscaval\>\"", ",",
"\"\<pwssca\>\"", ",", "\"\<pwsdiagel\>\"", ",",
"\"\<pwssnf1o\>\"", ",", "\"\<df-ordt\>\"", ",",
"\"\<df-xrs\>\"", ",", "\"\<df-qtop\>\"", ",", "\"\<df-imas\>\"",
",", "\"\<df-qus\>\"", ",", "\"\<df-xps\>\"", ",",
"\"\<imasval\>\"", ",", "\"\<imasval\>\"", ",",
"\"\<imasval\>\"", ",", "\"\<imasbas\>\"", ",",
"\"\<imasbas\>\"", ",", "\"\<imasbas\>\"", ",", "\"\<imasds\>\"",
",", "\"\<imasds\>\"", ",", "\"\<imasds\>\"", ",",
"\"\<imasdsfn\>\"", ",", "\"\<imasdsval\>\"", ",",
"\"\<imasdsval2\>\"", ",", "\"\<imasplusg\>\"", ",",
"\"\<imasplusg\>\"", ",", "\"\<imasplusg\>\"", ",",
"\"\<imasmulr\>\"", ",", "\"\<imasmulr\>\"", ",",
"\"\<imasmulr\>\"", ",", "\"\<imassca\>\"", ",",
"\"\<imassca\>\"", ",", "\"\<imasvsca\>\"", ",",
"\"\<imasvsca\>\"", ",", "\"\<imasip\>\"", ",",
"\"\<imastset\>\"", ",", "\"\<imasle\>\"", ",",
"\"\<f1ocpbllem\>\"", ",", "\"\<f1ocpbl\>\"", ",",
"\"\<f1ovscpbl\>\"", ",", "\"\<f1olecpbl\>\"", ",",
"\"\<imasaddfnlem\>\"", ",", "\"\<imasaddvallem\>\"", ",",
"\"\<imasaddflem\>\"", ",", "\"\<imasaddfn\>\"", ",",
"\"\<imasaddfn\>\"", ",", "\"\<imasaddval\>\"", ",",
"\"\<imasaddf\>\"", ",", "\"\<imasmulfn\>\"", ",",
"\"\<imasmulval\>\"", ",", "\"\<imasmulf\>\"", ",",
"\"\<imasvscafn\>\"", ",", "\"\<imasvscaval\>\"", ",",
"\"\<imasvscaf\>\"", ",", "\"\<imasless\>\"", ",",
"\"\<imasleval\>\"", ",", "\"\<qusval\>\"", ",",
"\"\<quslem\>\"", ",", "\"\<qusin\>\"", ",", "\"\<qusbas\>\"",
",", "\"\<quss\>\"", ",", "\"\<divsfval\>\"", ",",
"\"\<divsfval\>\"", ",", "\"\<ercpbllem\>\"", ",",
"\"\<ercpbl\>\"", ",", "\"\<ercpbl\>\"", ",", "\"\<erlecpbl\>\"",
",", "\"\<erlecpbl\>\"", ",", "\"\<qusaddvallem\>\"", ",",
"\"\<qusaddflem\>\"", ",", "\"\<qusaddval\>\"", ",",
"\"\<qusaddf\>\"", ",", "\"\<qusmulval\>\"", ",",
"\"\<qusmulf\>\"", ",", "\"\<xpsc\>\"", ",", "\"\<xpscg\>\"",
",", "\"\<xpscfn\>\"", ",", "\"\<xpsc0\>\"", ",",
"\"\<xpsc1\>\"", ",", "\"\<xpscfv\>\"", ",", "\"\<xpsfrnel\>\"",
",", "\"\<xpsfeq\>\"", ",", "\"\<xpsfrnel2\>\"", ",",
"\"\<xpscf\>\"", ",", "\"\<xpsfval\>\"", ",", "\"\<xpsff1o\>\"",
",", "\"\<xpsfrn\>\"", ",", "\"\<xpsfrn2\>\"", ",",
"\"\<xpsff1o2\>\"", ",", "\"\<xpsval\>\"", ",", "\"\<xpslem\>\"",
",", "\"\<xpsbas\>\"", ",", "\"\<xpsaddlem\>\"", ",",
"\"\<xpsadd\>\"", ",", "\"\<xpsmul\>\"", ",", "\"\<xpssca\>\"",
",", "\"\<xpsvsca\>\"", ",", "\"\<xpsless\>\"", ",",
"\"\<xpsle\>\"", ",", "\"\<df-plusg\>\"", ",",
"\"\<df-plusg\>\"", ",", "\"\<df-mulr\>\"", ",",
"\"\<df-mulr\>\"", ",", "\"\<df-starv\>\"", ",",
"\"\<df-starv\>\"", ",", "\"\<df-sca\>\"", ",", "\"\<df-sca\>\"",
",", "\"\<df-vsca\>\"", ",", "\"\<df-vsca\>\"", ",",
"\"\<df-ip\>\"", ",", "\"\<df-ip\>\"", ",", "\"\<df-tset\>\"",
",", "\"\<df-tset\>\"", ",", "\"\<df-ple\>\"", ",",
"\"\<df-ple\>\"", ",", "\"\<df-ocomp\>\"", ",",
"\"\<df-ocomp\>\"", ",", "\"\<df-ds\>\"", ",", "\"\<df-ds\>\"",
",", "\"\<df-unif\>\"", ",", "\"\<df-hom\>\"", ",",
"\"\<df-cco\>\"", ",", "\"\<strlemor0\>\"", ",",
"\"\<strlemor1\>\"", ",", "\"\<strlemor1\>\"", ",",
"\"\<strlemor2\>\"", ",", "\"\<strlemor2\>\"", ",",
"\"\<strlemor3\>\"", ",", "\"\<strlemor3\>\"", ",",
"\"\<strleun\>\"", ",", "\"\<strle1\>\"", ",", "\"\<strle2\>\"",
",", "\"\<strle3\>\"", ",", "\"\<plusgndx\>\"", ",",
"\"\<plusgid\>\"", ",", "\"\<1strstr\>\"", ",",
"\"\<1strbas\>\"", ",", "\"\<1strwunbndx\>\"", ",",
"\"\<1strwun\>\"", ",", "\"\<2strstr\>\"", ",",
"\"\<2strbas\>\"", ",", "\"\<2strop\>\"", ",", "\"\<grpstr\>\"",
",", "\"\<grpstr\>\"", ",", "\"\<grpbase\>\"", ",",
"\"\<grpbase\>\"", ",", "\"\<grpplusg\>\"", ",",
"\"\<grpplusg\>\"", ",", "\"\<ressplusg\>\"", ",",
"\"\<grpbasex\>\"", ",", "\"\<grpplusgx\>\"", ",",
"\"\<mulrndx\>\"", ",", "\"\<mulrid\>\"", ",", "\"\<rngstr\>\"",
",", "\"\<rngstr\>\"", ",", "\"\<rngbase\>\"", ",",
"\"\<rngbase\>\"", ",", "\"\<rngplusg\>\"", ",",
"\"\<rngplusg\>\"", ",", "\"\<rngmulr\>\"", ",",
"\"\<rngmulr\>\"", ",", "\"\<starvndx\>\"", ",",
"\"\<starvid\>\"", ",", "\"\<ressmulr\>\"", ",",
"\"\<ressstarv\>\"", ",", "\"\<srngfn\>\"", ",",
"\"\<srngfn\>\"", ",", "\"\<srngbase\>\"", ",",
"\"\<srngbase\>\"", ",", "\"\<srngplusg\>\"", ",",
"\"\<srngmulr\>\"", ",", "\"\<srnginvl\>\"", ",",
"\"\<scandx\>\"", ",", "\"\<scaid\>\"", ",", "\"\<vscandx\>\"",
",", "\"\<vscaid\>\"", ",", "\"\<vscaid\>\"", ",",
"\"\<lmodstr\>\"", ",", "\"\<lmodstr\>\"", ",",
"\"\<lmodbase\>\"", ",", "\"\<lmodbase\>\"", ",",
"\"\<lmodplusg\>\"", ",", "\"\<lmodplusg\>\"", ",",
"\"\<lmodsca\>\"", ",", "\"\<lmodsca\>\"", ",",
"\"\<lmodvsca\>\"", ",", "\"\<lmodvsca\>\"", ",",
"\"\<ipndx\>\"", ",", "\"\<ipid\>\"", ",", "\"\<ipsstr\>\"",
",", "\"\<ipsstr\>\"", ",", "\"\<ipsstr\>\"", ",",
"\"\<ipsbase\>\"", ",", "\"\<ipsbase\>\"", ",",
"\"\<ipsbase\>\"", ",", "\"\<ipsaddg\>\"", ",",
"\"\<ipsaddg\>\"", ",", "\"\<ipsaddg\>\"", ",",
"\"\<ipsmulr\>\"", ",", "\"\<ipsmulr\>\"", ",",
"\"\<ipsmulr\>\"", ",", "\"\<ipssca\>\"", ",", "\"\<ipssca\>\"",
",", "\"\<ipssca\>\"", ",", "\"\<ipsvsca\>\"", ",",
"\"\<ipsvsca\>\"", ",", "\"\<ipsvsca\>\"", ",", "\"\<ipsip\>\"",
",", "\"\<ipsip\>\"", ",", "\"\<ipsip\>\"", ",",
"\"\<resssca\>\"", ",", "\"\<ressvsca\>\"", ",",
"\"\<ressip\>\"", ",", "\"\<phlstr\>\"", ",", "\"\<phlstr\>\"",
",", "\"\<phlbase\>\"", ",", "\"\<phlbase\>\"", ",",
"\"\<phlplusg\>\"", ",", "\"\<phlplusg\>\"", ",",
"\"\<phlsca\>\"", ",", "\"\<phlsca\>\"", ",", "\"\<phlvsca\>\"",
",", "\"\<phlvsca\>\"", ",", "\"\<phlip\>\"", ",",
"\"\<phlip\>\"", ",", "\"\<tsetndx\>\"", ",", "\"\<tsetid\>\"",
",", "\"\<topgrpstr\>\"", ",", "\"\<topgrpbas\>\"", ",",
"\"\<topgrpplusg\>\"", ",", "\"\<topgrptset\>\"", ",",
"\"\<resstset\>\"", ",", "\"\<plendx\>\"", ",", "\"\<pleid\>\"",
",", "\"\<otpsstr\>\"", ",", "\"\<otpsbas\>\"", ",",
"\"\<otpstset\>\"", ",", "\"\<otpsle\>\"", ",", "\"\<ressle\>\"",
",", "\"\<ocndx\>\"", ",", "\"\<ocid\>\"", ",", "\"\<dsndx\>\"",
",", "\"\<dsid\>\"", ",", "\"\<unifndx\>\"", ",",
"\"\<unifid\>\"", ",", "\"\<odrngstr\>\"", ",",
"\"\<odrngbas\>\"", ",", "\"\<odrngplusg\>\"", ",",
"\"\<odrngmulr\>\"", ",", "\"\<odrngtset\>\"", ",",
"\"\<odrngle\>\"", ",", "\"\<odrngds\>\"", ",", "\"\<ressds\>\"",
",", "\"\<homndx\>\"", ",", "\"\<homid\>\"", ",",
"\"\<ccondx\>\"", ",", "\"\<ccoid\>\"", ",", "\"\<resshom\>\"",
",", "\"\<ressco\>\"", ",", "\"\<slotsbhcdif\>\""}], "}"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathGraph", " ", "=", " ",
RowBox[{"EdgeDelete", "[",
RowBox[{
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PLbmdhRv\>\"", "]"}], ",",
" ",
RowBox[{"Select", "[",
RowBox[{
RowBox[{"EdgeList", "[",
RowBox[{
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PLbmdhRv\>\"", "]"}],
";"}], "]"}], ",", " ",
RowBox[{
RowBox[{"MemberQ", "[",
RowBox[{"extensibleStructures", ",", " ",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}]}], "]"}], " ", "&"}]}],
"]"}]}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{
RowBox[{"metamathAssoc", " ", "=", " ",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PLborw8R\>\"", "]"}]}],
";"}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathDomains", " ", "=", " ",
RowBox[{"Union", "[",
RowBox[{"Values", "[", "metamathAssoc", "]"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathInfrastructure", " ", "=", " ",
RowBox[{"{",
RowBox[{
"\"\<SUPPLEMENTARY MATERIAL (USER'S MATHBOXES)\>\"", ",", " ",
"\"\<GUIDES AND MISCELLANEA\>\""}], "}"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathColors", " ", "=", " ",
RowBox[{"Merge", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"AssociationThread", "[",
RowBox[{
RowBox[{"Complement", "[",
RowBox[{
"metamathDomains", ",", " ", "metamathInfrastructure"}],
"]"}], " ", "\[Rule]", " ",
RowBox[{"Take", "[",
RowBox[{
RowBox[{"ColorData", "[",
RowBox[{"54", ",", " ", "\"\<ColorList\>\""}], "]"}], ",",
" ",
RowBox[{"Length", "[",
RowBox[{"Complement", "[",
RowBox[{
"metamathDomains", ",", " ", "metamathInfrastructure"}],
"]"}], "]"}]}], "]"}]}], "]"}], ",", " ",
RowBox[{"AssociationThread", "[",
RowBox[{
"metamathInfrastructure", " ", "\[Rule]", " ", "LightGray"}],
"]"}]}], "}"}], ",", " ", "Identity"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathDomainWeights", " ", "=", " ",
RowBox[{"Tally", "[",
RowBox[{"Values", "[", "metamathAssoc", "]"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathEdgeWeights", " ", "=", " ",
RowBox[{"Tally", "[",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"metamathAssoc", "[",
RowBox[{"#", "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}], ",", " ",
RowBox[{"metamathAssoc", "[",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "]"}]}], "}"}], " ", "&"}],
" ", "/@", " ",
RowBox[{"EdgeList", "[", "metamathGraph", "]"}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathEdgesOutSimple", " ", "=", " ",
RowBox[{"Append", "[",
RowBox[{
RowBox[{"Merge", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"AssociationThread", "[",
RowBox[{
RowBox[{"{",
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", " ", "1", ",", " ", "1"}], "]"}],
"]"}], "}"}], "\[Rule]", " ",
RowBox[{"Total", "[",
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "]"}]}], "]"}], " ",
"&"}], " ", "/@", " ",
RowBox[{"(",
RowBox[{"Transpose", " ", "/@", " ",
RowBox[{"GatherBy", "[",
RowBox[{
RowBox[{"Select", "[",
RowBox[{"metamathEdgeWeights", ",", " ",
RowBox[{
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", " ", "1"}], "]"}], "]"}], " ",
"\[NotEqual]", " ",
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", " ", "2"}], "]"}], "]"}]}], " ",
"&"}]}], "]"}], ",", " ",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", " ", "1"}], "]"}], "]"}], " ",
"&"}]}], "]"}]}], ")"}]}], ",", " ", "Identity"}], "]"}],
",", " ",
RowBox[{
"\"\<CLASSICAL FIRST-ORDER LOGIC WITH EQUALITY\>\"", " ",
"\[Rule]", " ",
RowBox[{"{", "7649", "}"}]}]}], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathNormalizedEdgeWeights", " ", "=", " ",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"DirectedEdge", "[",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", " ", "1"}], "]"}], "]"}], ",", " ",
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", " ", "2"}], "]"}], "]"}]}], "]"}], " ",
"\[Rule]", " ",
RowBox[{
RowBox[{"#", "[",
RowBox[{"[", "2", "]"}], "]"}], "/", " ",
RowBox[{"Flatten", "[",
RowBox[{"metamathEdgesOutSimple", "[",
RowBox[{"#", "[",
RowBox[{"[",
RowBox[{"1", ",", "1"}], "]"}], "]"}], "]"}], "]"}]}]}],
" ", "&"}], " ", "/@", " ", "metamathEdgeWeights"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{
RowBox[{"diskedLine", "[",
RowBox[{"{",
RowBox[{"line_", ",", "radii_"}], "}"}], "]"}], ":=",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"RegionIntersection", "[",
RowBox[{
RowBox[{"Line", "[", "line", "]"}], ",",
RowBox[{"Circle", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"[", "1", "]"}], "]"}], ",",
RowBox[{"radii", "[",
RowBox[{"[", "1", "]"}], "]"}]}], "]"}]}], "]"}], "[",
RowBox[{"[",
RowBox[{"1", ",", "1"}], "]"}], "]"}], ",",
"\[IndentingNewLine]",
RowBox[{
RowBox[{"RegionIntersection", "[",
RowBox[{
RowBox[{"Line", "[", "line", "]"}], ",",
RowBox[{"Circle", "[",
RowBox[{
RowBox[{"line", "[",
RowBox[{"[", "2", "]"}], "]"}], ",",
RowBox[{"radii", "[",
RowBox[{"[", "2", "]"}], "]"}]}], "]"}]}], "]"}], "[",
RowBox[{"[",
RowBox[{"1", ",", "1"}], "]"}], "]"}]}], "}"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{
RowBox[{"weightedArrow", "[",
RowBox[{"line_", ",", "weight_"}], "]"}], ":=", " ",
RowBox[{"Module", "[",
RowBox[{
RowBox[{"{",
RowBox[{
"len", ",", "start", ",", "end", ",", "angle", ",", " ",
"thick", ",", " ", "rec", ",", " ", "mid"}], "}"}], ",",
"\[IndentingNewLine]",
RowBox[{
RowBox[{"start", "=",
RowBox[{"line", "[",
RowBox[{"[", "1", "]"}], "]"}]}], ";", " ",
RowBox[{"end", "=",
RowBox[{"line", "[",
RowBox[{"[", "2", "]"}], "]"}]}], ";", " ",
RowBox[{"mid", "=",
RowBox[{"Mean", "[", "line", "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"len", "=",
RowBox[{"EuclideanDistance", "[",
RowBox[{"start", ",", "end"}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"angle", "=",
RowBox[{"Arg", "[",
RowBox[{
RowBox[{"(",
RowBox[{"start", "-", "end"}], ")"}], ".",
RowBox[{"{",
RowBox[{"1", ",", "I"}], "}"}]}], "]"}]}], ";",
"\[IndentingNewLine]",
RowBox[{"thick", "=",
RowBox[{"weight", "/", "len"}]}], ";", "\[IndentingNewLine]",
RowBox[{"rec", "=", " ",
RowBox[{
RowBox[{
RowBox[{"#", "+", "mid"}], "&"}], "/@",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"RotationMatrix", "[", "angle", "]"}], ".", "#"}],
"&"}], "/@",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"-", "len"}], "/", "2"}], ",",
RowBox[{
RowBox[{"-", " ", "thick"}], "/", "2"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"len", "/", "2"}], ",",
RowBox[{
RowBox[{"-", " ", "thick"}], "/", "2"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"len", "/", "2"}], ",", " ",
RowBox[{"thick", "/", "2"}]}], "}"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"-", "len"}], "/", "2"}], ",", " ",
RowBox[{"thick", "/", "2"}]}], "}"}]}], "}"}]}],
")"}]}]}], ";", "\[IndentingNewLine]",
RowBox[{"Polygon", "[", "rec", "]"}]}]}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"Show", "[",
RowBox[{
RowBox[{"VertexDelete", "[",
RowBox[{
RowBox[{"SimpleGraph", "[",
RowBox[{"Graph", "[",
RowBox[{"metamathDomains", ",", " ",
RowBox[{
"First", " ", "/@", " ", "metamathNormalizedEdgeWeights"}],
",", " ",
RowBox[{"EdgeStyle", "\[Rule]",
RowBox[{"Thread", "[",
RowBox[{
RowBox[{"First", "/@", "metamathNormalizedEdgeWeights"}],
" ", "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"AbsoluteThickness", "[",
RowBox[{"175",
RowBox[{
RowBox[{"Last", "[", "#", "]"}], "[",
RowBox[{"[", "1", "]"}], "]"}]}], "]"}], ",",
RowBox[{"Arrowheads", "[",
RowBox[{
RowBox[{"Last", "[", "#", "]"}], "[",
RowBox[{"[", "1", "]"}], "]"}], "]"}], ",", " ",
RowBox[{"GrayLevel", "[",
RowBox[{"0.5", ",", " ", "0.5"}], "]"}]}], "}"}],
"&"}], "/@", "metamathNormalizedEdgeWeights"}], ")"}]}],
"]"}]}], ",", " ",
RowBox[{"VertexSize", "\[Rule]",
RowBox[{"Thread", "[",
RowBox[{
RowBox[{"First", "/@", "metamathDomainWeights"}], " ",
"\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"Sqrt", "[", "#", "]"}], "/", "70"}], "&"}], "/@",
RowBox[{"(",
RowBox[{"Last", "/@", " ", "metamathDomainWeights"}],
")"}]}], ")"}]}], "]"}]}], ",", " ",
RowBox[{"VertexStyle", " ", "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", " ", "\[Rule]", " ",
RowBox[{"{",
RowBox[{"Lighter", " ", "/@", " ",
RowBox[{"metamathColors", "[", "#", "]"}]}], "}"}]}],
" ", "&"}], " ", "/@", " ", "metamathDomains"}], ")"}]}],
",", " ",
RowBox[{"VertexLabels", "\[Rule]",
RowBox[{"{",
RowBox[{
RowBox[{
"\"\<BASIC ALGEBRAIC STRUCTURES\>\"", " ", "\[Rule]", " ",
"\"\<algebraic structures\>\""}], ",",
RowBox[{
"\"\<BASIC CATEGORY THEORY\>\"", " ", "\[Rule]", " ",
"\"\<category theory\>\""}], ",",
RowBox[{
"\"\<BASIC LINEAR ALGEBRA\>\"", " ", "\[Rule]", " ",
"\"\<linear algebra\>\""}], ",",
RowBox[{
"\"\<BASIC ORDER THEORY\>\"", " ", "\[Rule]", " ",
"\"\<order theory\>\""}], ",",
RowBox[{
"\"\<BASIC REAL AND COMPLEX ANALYSIS\>\"", " ", "\[Rule]",
" ", "\"\<real and complex analysis\>\""}], ",",
RowBox[{
"\"\<BASIC REAL AND COMPLEX FUNCTIONS\>\"", " ", "\[Rule]",
" ", "\"\<real and complex functions\>\""}], ",",
RowBox[{
"\"\<BASIC STRUCTURES\>\"", " ", "\[Rule]", " ",
"\"\<basic structures\>\""}], ",",
RowBox[{
"\"\<BASIC TOPOLOGY\>\"", " ", "\[Rule]", " ",
"\"\<topology\>\""}], ",",
RowBox[{
"\"\<CLASSICAL FIRST-ORDER LOGIC WITH EQUALITY\>\"", " ",
"\[Rule]", " ", "\"\<logic\>\""}], ",",
RowBox[{
"\"\<ELEMENTARY GEOMETRY\>\"", " ", "\[Rule]", " ",
"\"\<geometry\>\""}], ",",
RowBox[{
"\"\<ELEMENTARY NUMBER THEORY\>\"", " ", "\[Rule]", " ",
"\"\<number theory\>\""}], ",",
RowBox[{
"\"\<GRAPH THEORY\>\"", " ", "\[Rule]", " ",
"\"\<graph theory\>\""}], ",",
RowBox[{
"\"\<GUIDES AND MISCELLANEA\>\"", " ", "\[Rule]", " ",
"\"\<miscellaneous\>\""}], ",",
RowBox[{
"\"\<REAL AND COMPLEX NUMBERS\>\"", " ", "\[Rule]", " ",
"\"\<real and complex numbers\>\""}], ",",
RowBox[{
"\"\<SUPPLEMENTARY MATERIAL (USER'S MATHBOXES)\>\"", " ",
"\[Rule]", " ", "\"\<supplementary material\>\""}], ",",
RowBox[{
"\"\<TG (TARSKI-GROTHENDIECK) SET THEORY\>\"", " ",
"\[Rule]", " ", "\"\<TG set theory\>\""}], ",",
RowBox[{
"\"\<ZFC (ZERMELO-FRAENKEL WITH CHOICE) SET THEORY\>\"",
" ", "\[Rule]", " ", "\"\<ZFC set theory\>\""}], ",",
RowBox[{
"\"\<ZF (ZERMELO-FRAENKEL) SET THEORY\>\"", " ", "\[Rule]",
" ", "\"\<ZF set theory\>\""}]}], "}"}]}], ",", " ",
RowBox[{
"GraphLayout", " ", "\[Rule]", " ",
"\"\<SpringElectricalEmbedding\>\""}], ",", " ",
RowBox[{"PerformanceGoal", "\[Rule]", "\"\<Quality\>\""}],
",", " ",
RowBox[{"AspectRatio", "\[Rule]", "1"}]}], "]"}], "]"}], ",",
" ",
RowBox[{"{",
RowBox[{
"\"\<SUPPLEMENTARY MATERIAL (USER'S MATHBOXES)\>\"", ",", " ",
"\"\<TG (TARSKI-GROTHENDIECK) SET THEORY\>\"", ",",
"\"\<ZFC (ZERMELO-FRAENKEL WITH CHOICE) SET THEORY\>\"", ",",
"\"\<ZF (ZERMELO-FRAENKEL) SET THEORY\>\"", ",", " ",
"\"\<CLASSICAL FIRST-ORDER LOGIC WITH EQUALITY\>\"", ",", " ",
"\"\<GUIDES AND MISCELLANEA\>\"", ",", " ",
"\"\<REAL AND COMPLEX NUMBERS\>\""}], "}"}]}], "]"}], ",", " ",
RowBox[{"Editable", " ", "\[Rule]", " ", "True"}]}],
"]"}]], "Input"]
}, Open ]]
|
It’s somewhat interesting to see how central algebra ends up being in both cases, and how comparatively “off on the side” category theory is. But it’s clear that much of what one’s seeing in these graphs is a reflection of the particular user communities of these systems, with some important pieces of modern mathematics (like the applications of algebraic geometry to number theory) notably missing.
But, OK, how do individual theorems work in these systems? As an example, let’s consider the Pythagorean theorem. In Euclid, this is 1.47, and here’s the first level of its dependency graph:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; EuclidGraphLarge[ Subgraph[euc, VertexOutComponent[euc, <|"Book" -> 1, "Theorem" -> 47|>, 1]]] |
Here’s the full graph involving a total of 39 elements (including, by the way, all 10 of the axioms), and having “depth” 20:

✕
CloudGet["https://wolfr.am/PJKo9Lnq"]; EuclidGraphLarge[ Subgraph[euc, VertexOutComponent[euc, <|"Book" -> 1, "Theorem" -> 47|>]], VertexSize -> 1.7] |
In Lean’s mathlib, the theorem is called euclidean_geometry.dist_square_eq _dist _square _add _dist _square _iff _angle _eq _pi _div _two—and its stated proof directly involves 7 other theorems:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"leanAssoc", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL39QRbE\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanGraph", " ", "=", " ",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL3LfaQ4\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanDomains", " ", "=", " ",
RowBox[{"Union", "[",
RowBox[{"Values", "[", "leanAssoc", "]"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanInfrastructure", " ", "=", " ",
RowBox[{"{",
RowBox[{
"\"\<init\>\"", ",", " ", "\"\<system\>\"", ",", " ",
"\"\<tactic\>\"", ",", " ", "\"\<data\>\"", ",", " ",
"\"\<meta\>\"", ",", " ", "\"\<control\>\"", ",", " ",
"\"\<computability\>\""}], "}"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanColors", " ", "=", " ",
RowBox[{"Merge", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"AssociationThread", "[",
RowBox[{
RowBox[{"Complement", "[",
RowBox[{"leanDomains", ",", " ", "leanInfrastructure"}],
"]"}], " ", "\[Rule]", " ",
RowBox[{"Take", "[",
RowBox[{
RowBox[{"ColorData", "[",
RowBox[{"54", ",", " ", "\"\<ColorList\>\""}], "]"}], ",",
" ",
RowBox[{"Length", "[",
RowBox[{"Complement", "[",
RowBox[{"leanDomains", ",", " ", "leanInfrastructure"}],
"]"}], "]"}]}], "]"}]}], "]"}], ",", " ",
RowBox[{"AssociationThread", "[",
RowBox[{
"leanInfrastructure", " ", "\[Rule]", " ", "LightGray"}],
"]"}]}], "}"}], ",", " ", "Identity"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"Column", "[",
RowBox[{
RowBox[{"Rest", "[",
RowBox[{"VertexOutComponent", "[",
RowBox[{
"leanGraph", ",",
"\"\<euclidean_geometry.dist_square_eq_dist_square_add_dist_\
square_iff_angle_eq_pi_div_two\>\"", ",", "1"}], "]"}], "]"}], ",",
RowBox[{"Frame", "\[Rule]", "All"}], ",",
RowBox[{"FrameStyle", "->",
RowBox[{"GrayLevel", "[", ".7", "]"}]}], ",", " ",
RowBox[{"With", "[",
RowBox[{
RowBox[{"{",
RowBox[{"leanA", "=",
RowBox[{
RowBox[{
RowBox[{"leanAssoc", "[", "#", "]"}], " ", "&"}], " ", "/@",
" ",
RowBox[{"Rest", "[",
RowBox[{"VertexOutComponent", "[",
RowBox[{
"leanGraph", ",",
"\"\<euclidean_geometry.dist_square_eq_dist_square_add_\
dist_square_iff_angle_eq_pi_div_two\>\"", ",", "1"}], "]"}],
"]"}]}]}], "}"}], ",",
RowBox[{"Background", " ", "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"Lighter", "[",
RowBox[{"#", ",", "0.5"}], "]"}], "&"}], " ", "/@", " ",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{
RowBox[{"leanColors", "[", "#", "]"}], " ", "&"}], " ", "/@",
"leanA"}], "]"}]}], ")"}]}]}], "]"}]}], "]"}]], "Input"]
}, Open ]]
|
Going 3 steps, the theorem dependency graph looks like (where “init” and “tactic” basically refer to structure rather than mathematical content):

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"leanAssoc", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL39QRbE\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanGraph", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL3LfaQ4\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanDomains", " ", "=", " ",
RowBox[{"Union", "[",
RowBox[{"Values", "[", "leanAssoc", "]"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanInfrastructure", " ", "=", " ",
RowBox[{"{",
RowBox[{
"\"\<init\>\"", ",", " ", "\"\<system\>\"", ",", " ",
"\"\<tactic\>\"", ",", " ", "\"\<data\>\"", ",", " ",
"\"\<meta\>\"", ",", " ", "\"\<control\>\"", ",", " ",
"\"\<computability\>\""}], "}"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanColors", " ", "=", " ",
RowBox[{"Merge", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"AssociationThread", "[",
RowBox[{
RowBox[{"Complement", "[",
RowBox[{"leanDomains", ",", " ", "leanInfrastructure"}],
"]"}], " ", "\[Rule]", " ",
RowBox[{"Take", "[",
RowBox[{
RowBox[{"ColorData", "[",
RowBox[{"54", ",", " ", "\"\<ColorList\>\""}], "]"}], ",",
" ",
RowBox[{"Length", "[",
RowBox[{"Complement", "[",
RowBox[{"leanDomains", ",", " ", "leanInfrastructure"}],
"]"}], "]"}]}], "]"}]}], "]"}], ",", " ",
RowBox[{"AssociationThread", "[",
RowBox[{
"leanInfrastructure", " ", "\[Rule]", " ", "LightGray"}],
"]"}]}], "}"}], ",", " ", "Identity"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"Legended", "[",
RowBox[{
RowBox[{"Subgraph", "[",
RowBox[{"leanGraph", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{
"leanGraph", ",",
"\"\<euclidean_geometry.dist_square_eq_dist_square_add_dist_\
square_iff_angle_eq_pi_div_two\>\"", ",", "3"}], "]"}], ",",
RowBox[{
"GraphLayout", "\[Rule]", "\"\<LayeredDigraphEmbedding\>\""}],
",",
RowBox[{"AspectRatio", "\[Rule]",
RowBox[{"1", "/", "3"}]}], ",", " ",
RowBox[{"EdgeStyle", "\[Rule]", " ",
RowBox[{"GrayLevel", "[",
RowBox[{"0.5", ",", " ", "0.5"}], "]"}]}], ",", " ",
RowBox[{"VertexStyle", " ", "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", " ", "\[Rule]", " ",
RowBox[{"{",
RowBox[{"Lighter", " ", "/@", " ",
RowBox[{"leanColors", "[",
RowBox[{"leanAssoc", "[", "#", "]"}], "]"}]}], "}"}]}],
" ", "&"}], " ", "/@", " ",
RowBox[{"VertexList", "[", "leanGraph", "]"}]}], ")"}]}], ",",
" ",
RowBox[{"VertexSize", " ", "\[Rule]", " ", "0.75"}]}], "]"}],
",", " ",
RowBox[{"SwatchLegend", "[",
RowBox[{
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{
RowBox[{"Lighter", " ", "/@", " ",
RowBox[{"leanColors", "[", "#", "]"}]}], " ", "&"}], " ", "/@",
" ",
RowBox[{"{",
RowBox[{
"\"\<algebra\>\"", ",", "\"\<analysis\>\"", ",",
"\"\<geometry\>\"", ",", "\"\<init\>\"", ",",
"\"\<tactic\>\"", ",", "\"\<topology\>\""}], "}"}]}], "]"}],
",", " ",
RowBox[{"{",
RowBox[{
"\"\<algebra\>\"", ",", "\"\<analysis\>\"", ",",
"\"\<geometry\>\"", ",", "\"\<init\>\"", ",", "\"\<tactic\>\"",
",", "\"\<topology\>\""}], "}"}]}], "]"}]}], "]"}]], "Input"]
}, Open ]]
|
The full graph involves a total of 2850 elements (and has “depth” 84), and after transitive reduction has the form:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"leanGraph", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL3LfaQ4\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanAssoc", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL39QRbE\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanColors", " ", "=", " ",
RowBox[{"Merge", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"AssociationThread", "[",
RowBox[{
RowBox[{"Complement", "[",
RowBox[{"leanDomains", ",", " ", "leanInfrastructure"}],
"]"}], " ", "\[Rule]", " ",
RowBox[{"Take", "[",
RowBox[{
RowBox[{"ColorData", "[",
RowBox[{"54", ",", " ", "\"\<ColorList\>\""}], "]"}], ",",
" ",
RowBox[{"Length", "[",
RowBox[{"Complement", "[",
RowBox[{"leanDomains", ",", " ", "leanInfrastructure"}],
"]"}], "]"}]}], "]"}]}], "]"}], ",", " ",
RowBox[{"AssociationThread", "[",
RowBox[{
"leanInfrastructure", " ", "\[Rule]", " ", "LightGray"}],
"]"}]}], "}"}], ",", " ", "Identity"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"Graph", "[",
RowBox[{
RowBox[{"TransitiveReductionGraph", "[",
RowBox[{"Subgraph", "[",
RowBox[{"leanGraph", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{
"leanGraph", ",",
"\"\<euclidean_geometry.dist_square_eq_dist_square_add_dist_\
square_iff_angle_eq_pi_div_two\>\""}], "]"}]}], "]"}], "]"}], ",",
RowBox[{
"GraphLayout", "\[Rule]", "\"\<LayeredDigraphEmbedding\>\""}], ",",
RowBox[{"AspectRatio", "\[Rule]",
RowBox[{"1", "/", "2"}]}], ",", " ",
RowBox[{"EdgeStyle", "\[Rule]", " ",
RowBox[{"GrayLevel", "[",
RowBox[{"0.5", ",", " ", "0.5"}], "]"}]}], ",", " ",
RowBox[{"VertexStyle", " ", "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", " ", "\[Rule]", " ",
RowBox[{"{",
RowBox[{"Lighter", " ", "/@", " ",
RowBox[{"leanColors", "[",
RowBox[{"leanAssoc", "[", "#", "]"}], "]"}]}], "}"}]}],
" ", "&"}], " ", "/@", " ",
RowBox[{"VertexList", "[", "leanGraph", "]"}]}], ")"}]}], ",",
" ",
RowBox[{"VertexSize", " ", "\[Rule]", " ", "0.75"}]}],
"]"}]], "Input"]
}, Open ]]
|
And, yes, this is considerably more complicated than Euclid’s version—but presumably that’s what happens if you insist on full formalization. Of the 2850 theorems used, 1503 are basically structural. The remainder bring mathematical content from different areas, and it’s notable in the picture above that different parts of the proof seem to “concentrate” on different areas. Curiously, theorems from geometry (which is basically all Euclid used) occupy only a tiny sliver of the pie chart of all theorems used:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"leanAssoc", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL39QRbE\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanGraph", " ", "=", " ",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL3LfaQ4\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanDomains", " ", "=", " ",
RowBox[{"Union", "[",
RowBox[{"Values", "[", "leanAssoc", "]"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanInfrastructure", " ", "=", " ",
RowBox[{"{",
RowBox[{
"\"\<init\>\"", ",", " ", "\"\<system\>\"", ",", " ",
"\"\<tactic\>\"", ",", " ", "\"\<data\>\"", ",", " ",
"\"\<meta\>\"", ",", " ", "\"\<control\>\"", ",", " ",
"\"\<computability\>\""}], "}"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanColors", " ", "=", " ",
RowBox[{"Merge", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"AssociationThread", "[",
RowBox[{
RowBox[{"Complement", "[",
RowBox[{"leanDomains", ",", " ", "leanInfrastructure"}],
"]"}], " ", "\[Rule]", " ",
RowBox[{"Take", "[",
RowBox[{
RowBox[{"ColorData", "[",
RowBox[{"54", ",", " ", "\"\<ColorList\>\""}], "]"}], ",",
" ",
RowBox[{"Length", "[",
RowBox[{"Complement", "[",
RowBox[{"leanDomains", ",", " ", "leanInfrastructure"}],
"]"}], "]"}]}], "]"}]}], "]"}], ",", " ",
RowBox[{"AssociationThread", "[",
RowBox[{
"leanInfrastructure", " ", "\[Rule]", " ", "LightGray"}],
"]"}]}], "}"}], ",", " ", "Identity"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"leanPythagoreanAntecedents", " ", "=", " ",
RowBox[{"Reverse", "[",
RowBox[{"KeyDrop", "[",
RowBox[{
RowBox[{"Counts", "[",
RowBox[{
RowBox[{
RowBox[{"leanAssoc", "[", "#", "]"}], " ", "&"}], " ", "/@",
" ",
RowBox[{"VertexList", "[",
RowBox[{"TransitiveReductionGraph", "[",
RowBox[{"Subgraph", "[",
RowBox[{"leanGraph", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{
"leanGraph", ",",
"\"\<euclidean_geometry.dist_square_eq_dist_square_add_\
dist_square_iff_angle_eq_pi_div_two\>\""}], "]"}]}], "]"}], "]"}],
"]"}]}], "]"}], ",", " ", "leanInfrastructure"}], "]"}],
"]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"PieChart", "[",
RowBox[{"leanPythagoreanAntecedents", ",",
RowBox[{"ChartLabels", "\[Rule]",
RowBox[{"Placed", "[",
RowBox[{
RowBox[{"Join", "[",
RowBox[{
RowBox[{"{", "\"\<order theory\>\"", "}"}], ",", " ",
RowBox[{"Rest", "[",
RowBox[{"Keys", "[", "leanPythagoreanAntecedents", "]"}],
"]"}]}], "]"}], ",", " ", "\"\<RadialCallout\>\""}], "]"}]}],
",",
RowBox[{"ImagePadding", "\[Rule]", "15"}], ",",
RowBox[{"ChartStyle", "\[Rule]",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"Lighter", "[",
RowBox[{
RowBox[{"First", "[",
RowBox[{"leanColors", "[", "#", "]"}], "]"}], ",", ".2"}],
"]"}], "&"}], "/@",
RowBox[{"Keys", "[", "leanPythagoreanAntecedents", "]"}]}],
")"}]}]}], "]"}]], "Input"]
}, Open ]]
|
The Metamath set.mm version of the Pythagorean theorem is called pythag, and its proof directly depends on 26 other theorems:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"metamathGraph", " ", "=", " ",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PLbmdhRv\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathAssoc", " ", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PLborw8R\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathDomains", " ", "=", " ",
RowBox[{"Union", "[",
RowBox[{"Values", "[", "metamathAssoc", "]"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathInfrastructure", " ", "=", " ",
RowBox[{"{",
RowBox[{
"\"\<SUPPLEMENTARY MATERIAL (USER'S MATHBOXES)\>\"", ",", " ",
"\"\<GUIDES AND MISCELLANEA\>\""}], "}"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathColors", " ", "=", " ",
RowBox[{"Merge", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"AssociationThread", "[",
RowBox[{
RowBox[{"Complement", "[",
RowBox[{
"metamathDomains", ",", " ", "metamathInfrastructure"}],
"]"}], " ", "\[Rule]", " ",
RowBox[{"Take", "[",
RowBox[{
RowBox[{"ColorData", "[",
RowBox[{"54", ",", " ", "\"\<ColorList\>\""}], "]"}], ",",
" ",
RowBox[{"Length", "[",
RowBox[{"Complement", "[",
RowBox[{
"metamathDomains", ",", " ", "metamathInfrastructure"}],
"]"}], "]"}]}], "]"}]}], "]"}], ",", " ",
RowBox[{"AssociationThread", "[",
RowBox[{
"metamathInfrastructure", " ", "\[Rule]", " ", "LightGray"}],
"]"}]}], "}"}], ",", " ", "Identity"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathPythagoreanColors", " ", "=", " ",
RowBox[{"Lighter", " ", "/@", " ",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{
RowBox[{"metamathColors", "[", "#", "]"}], " ", "&"}], " ", "/@",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"metamathAssoc", "[", "#", "]"}], " ", "&"}], " ", "/@",
" ",
RowBox[{"Rest", "[",
RowBox[{"VertexOutComponent", "[",
RowBox[{"metamathGraph", ",", "\"\<pythag\>\"", ",", "1"}],
"]"}], "]"}]}], ")"}]}], "]"}]}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"Grid", "[",
RowBox[{
RowBox[{"Partition", "[",
RowBox[{
RowBox[{"Rest", "[",
RowBox[{"VertexOutComponent", "[",
RowBox[{"metamathGraph", ",", "\"\<pythag\>\"", ",", "1"}],
"]"}], "]"}], ",", " ",
RowBox[{"UpTo", "[", "6", "]"}]}], "]"}], ",",
RowBox[{"Frame", "\[Rule]",
RowBox[{"{",
RowBox[{"All", ",", "All", ",",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{"5", ",", "3"}], "}"}], "\[Rule]", "False"}], ",",
RowBox[{
RowBox[{"{",
RowBox[{"5", ",", "4"}], "}"}], "\[Rule]", "False"}], ",",
RowBox[{
RowBox[{"{",
RowBox[{"5", ",", "5"}], "}"}], "\[Rule]", "False"}], ",",
RowBox[{
RowBox[{"{",
RowBox[{"5", ",", "6"}], "}"}], "\[Rule]", "False"}], ",",
RowBox[{
RowBox[{"{",
RowBox[{"5", ",", "2"}], "}"}], "\[Rule]", "True"}], ",",
RowBox[{
RowBox[{"{",
RowBox[{"4", ",", "3"}], "}"}], "\[Rule]", "True"}], ",",
RowBox[{
RowBox[{"{",
RowBox[{"4", ",", "4"}], "}"}], "\[Rule]", "True"}], ",",
RowBox[{
RowBox[{"{",
RowBox[{"4", ",", "5"}], "}"}], "\[Rule]", "True"}], ",",
RowBox[{
RowBox[{"{",
RowBox[{"4", ",", "6"}], "}"}], "\[Rule]", "True"}]}],
"}"}]}], "}"}]}], ",",
RowBox[{"FrameStyle", "->",
RowBox[{"GrayLevel", "[", ".7", "]"}]}], ",", " ",
RowBox[{"Background", " ", "\[Rule]", " ",
RowBox[{"{",
RowBox[{"None", ",", " ", "None", ",", " ",
RowBox[{"{",
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{"1", ",", " ", "1"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "1", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"1", ",", " ", "2"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "2", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"1", ",", " ", "3"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "3", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"1", ",", " ", "4"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "4", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"1", ",", " ", "5"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "5", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"1", ",", " ", "6"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "6", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"2", ",", " ", "1"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "7", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"2", ",", " ", "2"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "8", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"2", ",", " ", "3"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "9", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"2", ",", " ", "4"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "10", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"2", ",", " ", "5"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "11", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"2", ",", " ", "6"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "12", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"3", ",", " ", "1"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "13", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"3", ",", " ", "2"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "14", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"3", ",", " ", "3"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "15", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"3", ",", " ", "4"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "16", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"3", ",", " ", "5"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "17", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"3", ",", " ", "6"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "18", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"4", ",", " ", "1"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "19", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"4", ",", " ", "2"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "20", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"4", ",", " ", "3"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "21", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"4", ",", " ", "4"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "22", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"4", ",", " ", "5"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "23", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"4", ",", " ", "6"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "24", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"5", ",", " ", "1"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "25", "]"}], "]"}]}], ",", " ",
RowBox[{
RowBox[{"{",
RowBox[{"5", ",", " ", "2"}], "}"}], " ", "\[Rule]", " ",
RowBox[{"metamathPythagoreanColors", "[",
RowBox[{"[", "26", "]"}], "]"}]}]}], "}"}]}], "}"}]}]}],
"]"}]], "Input"]
}, Open ]]
|
After 1 step, the theorem dependency graph is:

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"metamathGraph", " ", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PLbmdhRv\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathAssoc", " ", "=", " ",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PLborw8R\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathDomains", " ", "=", " ",
RowBox[{"Union", "[",
RowBox[{"Values", "[", "metamathAssoc", "]"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathInfrastructure", " ", "=", " ",
RowBox[{"{",
RowBox[{
"\"\<SUPPLEMENTARY MATERIAL (USER'S MATHBOXES)\>\"", ",", " ",
"\"\<GUIDES AND MISCELLANEA\>\""}], "}"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathColors", " ", "=", " ",
RowBox[{"Merge", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"AssociationThread", "[",
RowBox[{
RowBox[{"Complement", "[",
RowBox[{
"metamathDomains", ",", " ", "metamathInfrastructure"}],
"]"}], " ", "\[Rule]", " ",
RowBox[{"Take", "[",
RowBox[{
RowBox[{"ColorData", "[",
RowBox[{"54", ",", " ", "\"\<ColorList\>\""}], "]"}], ",",
" ",
RowBox[{"Length", "[",
RowBox[{"Complement", "[",
RowBox[{
"metamathDomains", ",", " ", "metamathInfrastructure"}],
"]"}], "]"}]}], "]"}]}], "]"}], ",", " ",
RowBox[{"AssociationThread", "[",
RowBox[{
"metamathInfrastructure", " ", "\[Rule]", " ", "LightGray"}],
"]"}]}], "}"}], ",", " ", "Identity"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"Legended", "[",
RowBox[{
RowBox[{"Subgraph", "[",
RowBox[{"metamathGraph", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{"metamathGraph", ",", "\"\<pythag\>\"", ",", "1"}],
"]"}], ",",
RowBox[{
"GraphLayout", "\[Rule]", "\"\<LayeredDigraphEmbedding\>\""}],
",",
RowBox[{"AspectRatio", "\[Rule]",
RowBox[{"1", "/", "2"}]}], ",", " ",
RowBox[{"VertexLabels", " ", "\[Rule]", " ", "None"}], ",", " ",
RowBox[{"EdgeStyle", "\[Rule]", " ",
RowBox[{"GrayLevel", "[",
RowBox[{"0.5", ",", " ", "0.5"}], "]"}]}], ",", " ",
RowBox[{"VertexStyle", " ", "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", " ", "\[Rule]", " ",
RowBox[{"{",
RowBox[{"Lighter", " ", "/@", " ",
RowBox[{"metamathColors", "[",
RowBox[{"metamathAssoc", "[", "#", "]"}], "]"}]}],
"}"}]}], " ", "&"}], " ", "/@", " ",
RowBox[{"VertexList", "[", "metamathGraph", "]"}]}], ")"}]}],
",", " ",
RowBox[{"VertexSize", " ", "\[Rule]", " ", "0.75"}]}], "]"}],
",", " ",
RowBox[{"SwatchLegend", "[",
RowBox[{
RowBox[{"Lighter", " ", "/@", " ",
RowBox[{"Flatten", "[",
RowBox[{
RowBox[{
RowBox[{"metamathColors", "[", "#", "]"}], " ", "&"}], " ", "/@",
" ",
RowBox[{"{",
RowBox[{
"\"\<BASIC REAL AND COMPLEX FUNCTIONS\>\"", ",",
"\"\<CLASSICAL FIRST-ORDER LOGIC WITH EQUALITY\>\"", ",",
"\"\<REAL AND COMPLEX NUMBERS\>\"", ",",
"\"\<ZF (ZERMELO-FRAENKEL) SET THEORY\>\""}], "}"}]}],
"]"}]}], ",", " ",
RowBox[{"{",
RowBox[{
"\"\<real and complex functions\>\"", ",",
"\"\<classical first-order logic with equality\>\"", ",",
"\"\<real and complex numbers\>\"", ",", " ",
"\"\<ZF (Zermelo-Frankel) set theory\>\""}], "}"}]}], "]"}]}],
"]"}]], "Input"]
}, Open ]]
|
The full graph involves 7099 elements—and has depth 270. In other words, to get from the Pythagorean theorem all the way to the axioms can take as many as 270 steps.

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"metamathGraph", " ", "=", " ",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PLbmdhRv\>\"", "]"}]}],
";"}]], "Input",
Cell[BoxData[
RowBox[{
RowBox[{"metamathAssoc", " ", "=", " ",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PLborw8R\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathDomains", " ", "=", " ",
RowBox[{"Union", "[",
RowBox[{"Values", "[", "metamathAssoc", "]"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathInfrastructure", " ", "=", " ",
RowBox[{"{",
RowBox[{
"\"\<SUPPLEMENTARY MATERIAL (USER'S MATHBOXES)\>\"", ",", " ",
"\"\<GUIDES AND MISCELLANEA\>\""}], "}"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathColors", " ", "=", " ",
RowBox[{"Merge", "[",
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"AssociationThread", "[",
RowBox[{
RowBox[{"Complement", "[",
RowBox[{
"metamathDomains", ",", " ", "metamathInfrastructure"}],
"]"}], " ", "\[Rule]", " ",
RowBox[{"Take", "[",
RowBox[{
RowBox[{"ColorData", "[",
RowBox[{"54", ",", " ", "\"\<ColorList\>\""}], "]"}], ",",
" ",
RowBox[{"Length", "[",
RowBox[{"Complement", "[",
RowBox[{
"metamathDomains", ",", " ", "metamathInfrastructure"}],
"]"}], "]"}]}], "]"}]}], "]"}], ",", " ",
RowBox[{"AssociationThread", "[",
RowBox[{
"metamathInfrastructure", " ", "\[Rule]", " ", "LightGray"}],
"]"}]}], "}"}], ",", " ", "Identity"}], "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"Graph", "[",
RowBox[{
RowBox[{"TransitiveReductionGraph", "[",
RowBox[{"Subgraph", "[",
RowBox[{"metamathGraph", ",",
RowBox[{"VertexOutComponent", "[",
RowBox[{"metamathGraph", ",", "\"\<pythag\>\""}], "]"}]}],
"]"}], "]"}], ",",
RowBox[{
"GraphLayout", "\[Rule]", "\"\<LayeredDigraphEmbedding\>\""}], ",",
RowBox[{"AspectRatio", "\[Rule]",
RowBox[{"1", "/", "2"}]}], ",", " ",
RowBox[{"EdgeStyle", "\[Rule]", " ",
RowBox[{"GrayLevel", "[",
RowBox[{"0.5", ",", " ", "0.5"}], "]"}]}], ",", " ",
RowBox[{"VertexStyle", " ", "\[Rule]", " ",
RowBox[{"(",
RowBox[{
RowBox[{
RowBox[{"#", " ", "\[Rule]", " ",
RowBox[{"{",
RowBox[{"Lighter", " ", "/@", " ",
RowBox[{"metamathColors", "[",
RowBox[{"metamathAssoc", "[", "#", "]"}], "]"}]}], "}"}]}],
" ", "&"}], " ", "/@", " ",
RowBox[{"VertexList", "[", "metamathGraph", "]"}]}], ")"}]}],
",", " ",
RowBox[{"VertexSize", " ", "\[Rule]", " ", "0.75"}]}],
"]"}]], "Input"]
}, Open ]]
|
Given the complete Lean or Metamath corpuses, we can start doing the same kind of empirical metamathematics we did for Euclid’s Elements—except now the higher level of formalization that’s being used potentially allows us to go much further.
As a very simple example, here’s the distribution of numbers of theorems directly referenced in the proof of each theorem in Lean, Metamath and Euclid:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"leanGraph", " ", "=", " ",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL3LfaQ4\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathGraph", " ", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PLbmdhRv\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"euc", "=",
RowBox[{"ResourceData", "[",
TagBox["\"\<Theorem Network from Euclid's Elements\>\"",
#& ,
BoxID ->
"ResourceTag-Theorem Network from Euclid's Elements-Input",
AutoDelete->True], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{"GraphicsRow", "[",
RowBox[{
RowBox[{
RowBox[{"Histogram", "[",
RowBox[{
RowBox[{"Last", "[", "#", "]"}], ",",
RowBox[{"Frame", "\[Rule]", "True"}], ",",
RowBox[{"ImageSize", "\[Rule]", "250"}], ",",
RowBox[{"Epilog", "\[Rule]",
RowBox[{"Text", "[",
RowBox[{
RowBox[{"Style", "[",
RowBox[{
RowBox[{"First", "[", "#", "]"}], ",",
RowBox[{"Directive", "[",
RowBox[{
RowBox[{"FontSize", "\[Rule]", "12"}], ",",
RowBox[{"GrayLevel", "[", "0.25", "]"}], ",",
RowBox[{
"FontFamily", "\[Rule]", "\"\<Source Sans Pro\>\""}]}],
"]"}]}], "]"}], ",",
RowBox[{"Scaled", "[",
RowBox[{"{",
RowBox[{"1", ",", "1"}], "}"}], "]"}], ",",
RowBox[{"{",
RowBox[{"1.5", ",", "1.4"}], "}"}]}], "]"}]}]}], "]"}],
"&"}], "/@",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"\"\<Lean\>\"", ",",
RowBox[{"VertexOutDegree", "[", "leanGraph", "]"}]}], "}"}],
",",
RowBox[{"{",
RowBox[{"\"\<Metamath\>\"", ",",
RowBox[{"VertexOutDegree", "[", "metamathGraph", "]"}]}],
"}"}], ",",
RowBox[{"{",
RowBox[{"\"\<Euclid\>\"", ",",
RowBox[{"VertexOutDegree", "[", "euc", "]"}]}], "}"}]}],
"}"}]}], "]"}]], "Input"]
}, Open ]]
|
The differences presumably reflect different “hierarchical modularity conventions” in Lean and Metamath (and Euclid). But it’s interesting to note, for example, that in all three cases, the Pythagorean theorem is “above average” in terms of number of theorems referenced in its proof:

✕
Grid[{{"", "Lean", "Metamath", "Euclid"}, {"", 7, 26, 8},
Style[#, GrayLevel[0.4]] & /@ {"mean", 4.9, 18.7, 4.3}},
Frame -> All, FrameStyle -> Gray]
|
What are the most popular theorems used in proofs? In terms of direct references, here are the top-5 lists:

✕
Cell[CellGroupData[{
Cell[BoxData[
RowBox[{
RowBox[{"leanGraph", " ", "=", " ",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL3LfaQ4\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathGraph", " ", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PLbmdhRv\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"CloudGet", "[", "\"\<https://wolfr.am/PJKo9Lnq\>\"", "]"}],
";",
RowBox[{"Text", "[",
RowBox[{"MapIndexed", "[",
RowBox[{
RowBox[{
RowBox[{"Labeled", "[",
RowBox[{
RowBox[{
RowBox[{"Function", "[",
RowBox[{"u", ",",
RowBox[{"Grid", "[",
RowBox[{
RowBox[{"Take", "[",
RowBox[{
RowBox[{"ReverseSortBy", "[",
RowBox[{
RowBox[{
RowBox[{
RowBox[{"{",
RowBox[{
RowBox[{"If", "[",
RowBox[{
RowBox[{
RowBox[{"Head", "[", "#", "]"}], "===",
"Association"}], ",",
RowBox[{"EuclidVertexName", "[", "#", "]"}], ",",
"#"}], "]"}], ",",
RowBox[{"VertexInDegree", "[",
RowBox[{"u", ",", "#"}], "]"}]}], "}"}], "&"}], "/@",
" ",
RowBox[{"VertexList", "[", "u", "]"}]}], ",",
"Last"}], "]"}], ",", " ", "5"}], "]"}], ",",
RowBox[{"Frame", "\[Rule]", "All"}]}], "]"}]}], "]"}],
"[",
RowBox[{"Last", "[", "#", "]"}], "]"}], ",",
RowBox[{"First", "[", "#", "]"}]}], "]"}], "&"}], ",",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{"\"\<Lean\>\"", ",", "leanGraph"}], "}"}], ",",
RowBox[{"{",
RowBox[{"\"\<Metamath\>\"", ",", "metamathGraph"}], "}"}],
",",
RowBox[{"{",
RowBox[{"\"\<Euclid\>\"", ",", "euc"}], "}"}]}], "}"}]}],
"]"}], "]"}]}]], "Input"]
}, Open ]]
|
Not surprisingly, for Lean and Metamath these are quite “structural”. For Lean, congr_arg is the “congruency” statement that if a=b then f(a)=f(b); congr is a variant that says if a=b and f=g then f(a)=g(b); eq.trans is the transitivity statement if a=b and b=c then a=c (Euclid’s CN1); eq.symm is the statement if a=b then b=a; etc. For Metamath, syl is “transitive syllogism”: if x⇒y and y⇒z then x⇒z; eqid is about reflexity of equality; etc. In Euclid, these kinds of low-level results—if they are even stated at all—tend to be “many levels down” in the hierarchy of theorems, leaving the single most popular theorem, 10.11, to be one about proportion and rationality.
If one looks at all theorems directly and indirectly referenced by a given theorem, the distribution of total numbers of theorems is as follows (with Lean showing the most obviously exponential decay):

✕
Cell[CellGroupData[{Cell[BoxData[
RowBox[{
RowBox[{"leanGraph", " ", "=", " ",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PL3LfaQ4\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"metamathGraph", " ", "=",
RowBox[{
"CloudGet", "[", "\"\<https://wolfr.am/PLbmdhRv\>\"", "]"}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"euc", "=",
RowBox[{"ResourceData", "[",
TagBox["\"\<Theorem Network from Euclid's Elements\>\"",
#& ,
BoxID ->
"ResourceTag-Theorem Network from Euclid's Elements-Input",
AutoDelete->True], "]"}]}], ";"}]], "Input"],
Cell[BoxData[
RowBox[{
RowBox[{"outcs", "=",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"u", ",",
RowBox[{
RowBox[{
RowBox[{"Length", "[",
RowBox[{"VertexOutComponent", "[",
RowBox[{"u", ",", "#"}], "]"}], "]"}], "&"}], "/@",
RowBox[{"VertexList", "[", "u", "]"}]}]}], "]"}], "/@",
RowBox[{"{",
RowBox[{"leanGraph", ",", "metamathGraph"}], "}"}]}]}],
";"}]], "Input"],
Cell[BoxData[
RowBox[{"GraphicsRow", "[",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"u", ",",
RowBox[{"Histogram", "[",
RowBox[{
RowBox[{"Last", "[", "u", "]"}], ",", "50", ",",
RowBox[{"{",
RowBox[{"\"\<Log\>\"", ",", "\"\<Count\>\""}], "}"}], ",",
RowBox[{"PlotRange", "\[Rule]", "All"}], ",",
RowBox[{"Frame", "\[Rule]", "True"}], ",",
RowBox[{"ImageSize", "\[Rule]", "250"}], ",",
RowBox[{"Epilog", "\[Rule]",
RowBox[{"Text", "[",
RowBox[{
RowBox[{"Style", "[",
RowBox[{
RowBox[{"First", "[", "u", "]"}], ",",
RowBox[{"Directive", "[",
RowBox[{
RowBox[{"FontSize", "\[Rule]", "12"}], ",",
RowBox[{"GrayLevel", "[", "0.25", "]"}], ",",
RowBox[{
"FontFamily", "\[Rule]", "\"\<Source Sans Pro\>\""}]}],
"]"}]}], "]"}], ",",
RowBox[{"Scaled", "[",
RowBox[{"{",
RowBox[{"1", ",", "1"}], "}"}], "]"}], ",",
RowBox[{"{",
RowBox[{"1.5", ",", "1.4"}], "}"}]}], "]"}]}]}], "]"}]}],
"]"}], "/@",
RowBox[{"Transpose", "[",
RowBox[{"{",
RowBox[{
RowBox[{"{",
RowBox[{
"\"\<Lean\>\"", ",", "\"\<Metamath\>\"", ",",
"\"\<Euclid\>\""}], "}"}], ",",
RowBox[{"Append", "[",
RowBox[{"outcs", ",",
RowBox[{
RowBox[{"Function", "[",
RowBox[{"u", ",",
RowBox[{
RowBox[{
RowBox[{"Length", "[",
RowBox[{"VertexOutComponent", "[",
RowBox[{"u", ",", "#"}], "]"}], "]"}], "&"}], "/@",
RowBox[{"VertexList", "[", "u", "]"}]}]}], "]"}], "[",
"euc", "]"}]}], "]"}]}], "}"}], "]"}]}], "]"}]], "Input"]
}, Open ]]
|
What about the overall structure of the Lean and Metamath dependency graphs? We can ask about effective dimension, about causal invariance, about “event horizons”, and much more. But right now I’ll leave that for another time...
The Future of Empirical Metamathematics
I don’t think empirical metamathematics has been much of a thing in the past. In fact, looking on the web as I write this, I’m surprised to see that essentially all references to the actual term “empirical metamathematics” seem to point directly or indirectly to that one note of mine on the subject in A New Kind of Science.
But as I hope this piece has made clear, there’s a lot that can be done in empirical metamathematics. In everything I’ve written here, I haven’t started analyzing questions like how one can recognize a powerful or a surprising theorem. And I’ve barely scratched the surface even of the empirical metamathematics that can be done on Euclid’s Elements from 2000 years ago.
But what kind of a thing is empirical metamathematics? Assuming one’s looking at theorems and proofs constructed by humans rather than by automated systems, it’s about analyzing large-scale human output—a bit like doing data science on literary texts, or on things like websites or legal corpuses. But it’s different. Because ultimately the theorems and proofs that are the subject of empirical metamathematics are derived not from features of the world, but from a formal system that defines some area of mathematics.
With computational language the goal is to be able to describe anything in formalized, computational terms. But in empirical metamathematics, things are in a sense “born formalized”. Whatever the actual presentation of theorems and proofs may be there, their “true form” is ultimately something grounded in the formal structure of the mathematics being used.
Of course there is also a strong human element to the raw material of empirical metamathematics. It is (at least for now) humans who have chosen which of the infinite number of possible theorems should be considered interesting, and worthy of presentation. And at least traditionally, when humans write proofs, they usually do it less as a way to certify correctness, and more as a form of exposition: to explain to other humans why a particular theorem is true, and what structure it fits into.
In a sense, empirical metamathematics is a quite desiccated way to look at mathematics, in which all the elegant conceptual structure of its content has been removed. But if we’re to make a “science of metamathematics”, it’s almost inevitable that we have to think this way. Part of what we need to do is to understand some of the human aesthetics of mathematics, and in effect to see to deduce laws by which it may operate.
In this piece I’ve mostly concentrated on doing fairly straightforward graph-oriented data science, primarily on Euclid’s Elements. But in moving forward with empirical metamathematics a key question is what kind of model one should be trying to fit one’s observations into.
And this comes back to my current motivation for studying empirical metamathematics: as a window onto a general “bulk” theory of metamathematics—and as the foundation for a science not just of how we humans have explored metamathematical space, but of what fundamentally is out there in metamathematical space, and what its overall structure may be.
No doubt there are already clues in what I’ve done here, but probably only after we have the general theory will we have the paradigm that’s needed to identify them. But even without this, there’s much to do in studying empirical metamathematics for its own sake—and of better characterizing the remarkable human achievement that is mathematics.
And for now, it’s interesting to be able to look at something as old as Euclid’s Elements and to realize what new perspectives modern computational thinking can give us about it. Euclid was a pioneer in the notion of building everything up from formal rules—and the seeds he sowed played an important role in leading us to the modern computational paradigm. So it’s something of a thrill to be able to come back two thousand years later and see that paradigm—now all grown up—applied not only to something like the fundamental theory of physics, but also to what Euclid did all those years ago.
Thanks
For help with various aspects of the content of this piece I’d like to thank Peter Barendse, Ian Ford, Jonathan Gorard, Rob Lewis, Jose Martin-Garcia, Norm Megill, James Mulnix, Nik Murzin, Mano Namuduri, Ed Pegg, Michael Trott, and Xiaofan Zhang, as well as Sushma Kini and Jessica Wong, and for past discussions about related topics, also Bruno Buchberger, Dana Scott and the various participants of our 2016 workshop on the Semantic Representation of Mathematical Knowledge.
Note Added
As I was working on this piece, I couldn’t help wondering whether—in 2300 years—anyone else had worked on the empirical metamathematics of Euclid before. Turns out (as Don Knuth pointed out to me) at least one other person did—more than 400 years ago.
The person in question was Thomas Harriot (1560–1621).
The only thing Thomas Harriot published in his lifetime was the book A Briefe and True Report of the New Found Land of Virginia, based on a trip that he made to America in 1585. But his papers show that he did all sorts of math and science (including inventing the · notation for multiplication, < and >, as well as drawing pictures of the Moon through a telescope before Galileo, etc.). He seems to have had a well-ahead-of-his-time interest in discrete mathematics, apparently making Venn diagrams a couple of centuries before Venn
doing various enumerations of structures
as well as various repeated computations (but no cellular automata, so far as I can tell!):
And he seems to have made a detailed study of Euclid’s Elements, listing in detail (as I did) what theorems are used in each proof (this is for Book 1):
But then, in his “moment of empirical metamathematics” he lists out the full dependency table for theorems in Book 1, having computed what we’d now call the transitive closure:

It’s easy for us to reproduce this now, and, yes, he did make a few mistakes:
Studying the empirical metamathematics of Euclid seems (to me) like an obvious thing to do, and it’s good to know I’m not the first one doing it. And actually I’m now wondering if someone actually already did it not “just” 400 years ago, but perhaps 2000 (or more) years ago...