Humanizing Multicomputational Processes

Multicomputation is one of the core ideas of the Wolfram Physics Project—and in particular is at the heart of our emerging understanding of quantum mechanics. But how can one get an intuition for what is initially the rather abstract idea of multicomputation? A good approach, I believe, is to see it in action in familiar systems and situations. And I explore here what seems like a particularly good example: games and puzzles.

One might not imagine that something as everyday as well-known games and puzzles would have any connection to the formalism for something like quantum mechanics. But the idea of multicomputation provides a link. And indeed one can view the very possibility of being able to have “interesting” games and puzzles as being related to a core phenomenon of multicomputation: multicomputational irreducibility.

In an ordinary computational system each state of the system has a unique successor, and ultimately there is a single thread of time that defines a process of computation. But in a multicomputational system the key idea is that states can have multiple successors—and tracing their behavior defines a whole multiway graph of branching and merging threads of time. And the point is that this is directly related to how one can think about typical games and puzzles.

Given a particular state of a game or puzzle, a player must typically decide what to do next. And where the idea of multicomputation comes in is that there are usually several choices that they can make. In any particular instance of the game, they’ll make a particular choice. But the point of the multicomputational paradigm is to look globally at the consequences of all possible choices—and to produce a multiway graph that represents them.

The notion of making what we call a multiway graph has actually existed—usually under the name of “game graphs”—for games and puzzles for a bit more than a hundred years. But with the multicomputational paradigm there are now some more general concepts that can be applied to these constructs. And in turn understanding the relation to games and puzzles has the potential to provide a new level of intuition and familiarity about multiway graphs.

My particular goal here is to investigate—fairly systematically—a sequence of well-known games and puzzles using the general methods we’ve been developing for studying multicomputational systems. As is typical in investigations that connect with everyday things, we’ll encounter all sorts of specific details. And while these may not immediately seem relevant to larger-scale discussions, they are important in our effort to provide a realistic and relatable picture of actual games and puzzles—and in allowing the connections we make with multicomputation to be on a solid foundation.

It’s worth mentioning that the possibility of relating games and puzzles to physics is basically something that wouldn’t make sense without our Physics Project. For games and puzzles are normally at some fundamental level discrete—especially in the way that they involve discrete branching of possibilities. And if one assumes physics is fundamentally continuous, there’s no reason to expect a connection. But a key idea of our Physics Project is that the physical world is at the lowest level discrete—like games and puzzles. And what’s more, our Physics Project posits that physics—like games and puzzles—has discrete possibilities to explore.

At the outset each of the games and puzzles I discuss here may seem rather different in their structure and operation. But what we’ll see is that when viewed in a multicomputational way, there is remarkable—and almost monotonous—uniformity across our different examples. I won’t comment too much on the significance of what we see until the end, when I’ll begin to discuss how various important multicomputational phenomena may play out in the context of games and puzzles. And how the very difficulty of conceptualizing multicomputation in straightforward human terms is what fundamentally leads to the engaging character of games and puzzles.

Tic-Tac-Toe

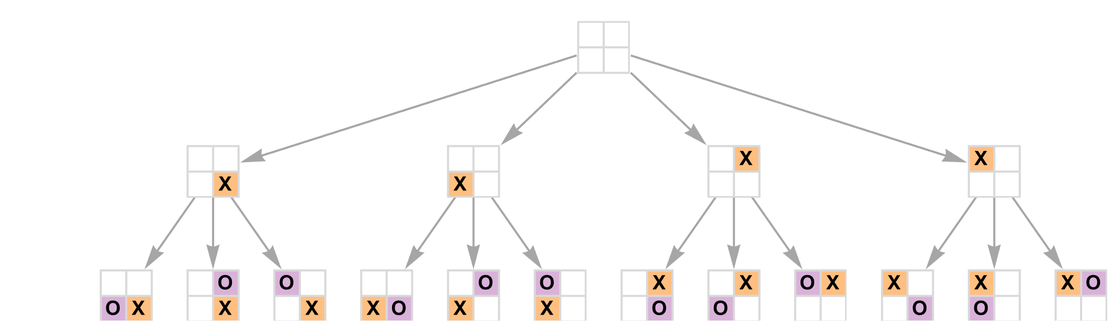
Consider a simplified version of tic-tac-toe (AKA “noughts and crosses”) played on a 2×2 board. Assume X plays first. Then one can represent the possible moves by the graph:

&#10005

On the next turn one gets:

&#10005

So far this graph is a simple tree. But if we play another turn we’ll see that different branches can merge, and “playing until the board is full” we get a multiway graph—or “game graph”—of the form:

&#10005

Every path through this graph represents a possible complete game:

&#10005

In our setup so far, the total number of board configurations that can ever be reached in any game (i.e. the total number of nodes in the graph) is 35, while the total number of possible complete games (i.e. the number of possible paths from the root of the graph) is 24.

If one renders the graph in 3D one can see that it has a very regular structure:

&#10005

And now if we define “winning” 2×2 tic-tac-toe as having two identical elements in a horizontal row, then we can annotate the multiway graph to indicate wins—removing cases where the “game is already over”:

&#10005

Much of the core structure of the multiway graph is actually already evident even in the seemingly trivial case of “one-player tic-tac-toe”, in which one is simply progressively filling in squares on the board:

&#10005

But what makes this not completely trivial is the existence of distinct paths that lead to equivalent states. Rendered differently the graph (which has 2⁴ = 16 nodes and 4! = 24 “game paths”) has an obvious 4D hypercube form (where now we have dropped the explicit X’s in each cell):

&#10005

For a 3×3 board the graph is a 9D hypercube with 2⁹ = 512 nodes and 9! = 362880 “game paths”, or in “move-layered” form:

&#10005

This basic structure is already visible in “1-player 1D tic-tac-toe” in which the multiway graph for a “length-n” board just corresponds to an n-dimensional hypercube:

&#10005

The total number of distinct board configurations in this case is just 2ⁿ, and the number of distinct “games” is n!. At move t the number of distinct board configurations (i.e. states) is Binomial[n, t].

With 2 players the graphs become slightly more complicated:

&#10005

The total number of states in these graphs is

&#10005

which is asymptotically . (Note that for n = 4 the result is the same as for the 2×2 board discussed above.) At move t the number of distinct states is given by

&#10005

&#10005

OK, so what about standard 2-player 3×3 tic-tac-toe? Its multiway graph begins:

&#10005

After 2 steps (i.e. one move by X and one by O) the graph is still a tree (with the initial state now at the center):

&#10005

After 3 steps there is starting to be merging:

&#10005

And continuing for all 9 moves the full layered graph—with 6046 states—is:

&#10005

At the level of this graph, the results are exactly the same as for a 2-player 1D version with a total of 9 squares. But for actual 2D 3×3 tic-tac-toe there is an additional element to the story: the concept of winning a game, and thereby terminating it. With the usual rules, a game is considered won when a player gets a horizontal, vertical or diagonal line of three squares, as in for example:

&#10005

Whenever a “win state” such as these is reached, the game is considered over, so that subsequent states in the multiway graph are pruned, and what was previously a 6046-node graph becomes a 5478-node graph

&#10005

with examples of the 568 pruned states including (where the “win” that terminated the game is marked):

&#10005

Wins can occur at different steps: anywhere from 5 to 9. The total numbers of distinct wins are as follows

&#10005

(yielding 626 wins at any step for X and 316 for O).

One can’t explicitly tell that a game has ended in a draw until every square has been filled in—and there are ultimately only 16 final “draw configurations” that can be reached:

&#10005

We can annotate the full (“game-over-pruned”) multiway graph, indicating win and draw states:

&#10005

To study this further, let’s start by looking at a subgraph that includes only “end games” starting with a board that already has 4 squares filled in:

&#10005

We see here that from our initial board

&#10005

it’s possible to get a final win for both X and O:

&#10005

But in many of these cases the outcome is already basically determined a step or more before the actual win occurs—in the sense that unless a given player “makes a mistake” they will always be able to force a win.

So, for example, if it is X’s turn and the state is

&#10005

then X is guaranteed to win if they play as follows:

&#10005

We can represent the “pre-forcing” of wins by coloring subgraphs (or in effect “light cones”) in the multiway graph:

&#10005

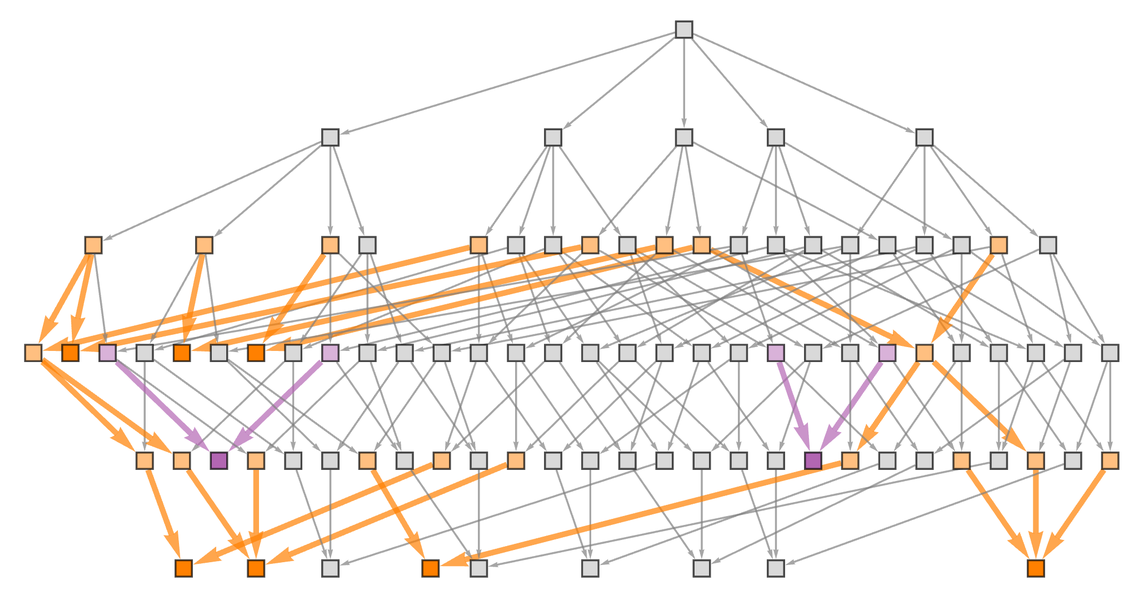
At the very beginning of the game, when X makes the first move, nothing is yet forced. But after just one move, it’s already possible to get to configurations where X can always force a win:

&#10005

Starting from a state obtained after 1 step, we can see that after 2 steps there are configurations where O can force a win:

&#10005

Going to more moves leads to more “forced-win” configurations:

&#10005

Annotating the whole multiway graph we get:

&#10005

We can think of this graph as a representation of the “solution” to the game: given any state the coloring in the graph tells us which player can force a win from that state, and the graph defines what moves they can make to do so.

Here’s a summary of possible game states at each move:

&#10005

&#10005

Here we’re just counting the number of possible states of various kinds at each step. But is there a way to think about these states as somehow being laid out in “game state space”? Branchial graphs provide a potential way to do this. The basic branchial graph at a particular step is obtained by joining pairs of states that share a common ancestor on the step before. For the case of 2-player 2×2 tic-tac-toe the branchial graphs we get on successive steps are as follows:

&#10005

Things get more complicated for ordinary 3×3 tic-tac-toe. But since the multiway graph for the first two steps is a pure tree, the branchial graphs at these steps still have a rather trivial structure:

&#10005

In general the number of connected components on successive steps is as follows

&#10005

and these are broken down across different graph structures as follows:

&#10005

Here in more detail are the forms of some typical components of branchial graphs achieved at particular steps:

&#10005

Within the branchial graph at a particular step, there can be different numbers of wins in different components:

&#10005

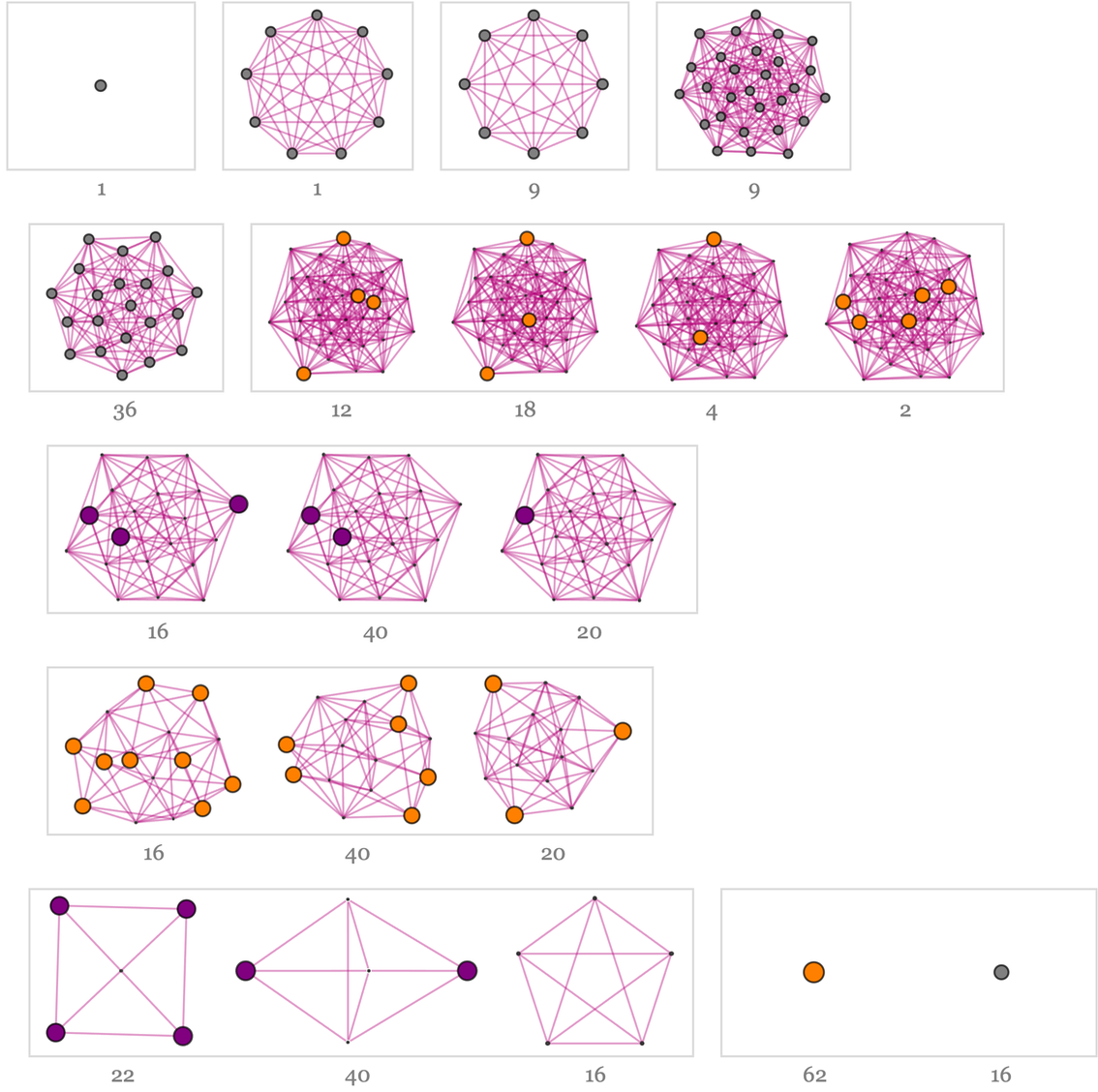
It’s notable that the wins are quite broadly distributed across branchial graphs. And this is in a sense why tic-tac-toe is not (more) trivial. If just by knowing what component of the branchial graph one was in one could immediately know the outcome, there would be even less “suspense” in the game. But with broad distribution across branchial space, “knowing roughly where you are” doesn’t help much in determining whether you’re going to win.

So far we’ve always been talking about what states can be reached, but not “how often” they’re reached. Imagine that rather than playing a specific game, we instead at each step just make every possible move with equal probability. The setup for tic-tac-toe is symmetrical enough that for most of the game the probability of every possible configuration at a given step is equal. But as soon as there start to be “wins”, and there is a “cone” of “game-over-pruned” states, then the remaining states no longer have equal probabilities.

For standard 3×3 tic-tac-toe this happens after 7 moves, where there are two classes of states, that occur with slightly different probabilities:

&#10005

At the end of the game, there are several classes of final states with different probabilities:

&#10005

And what this means for the probabilities of different outcomes of the game is as follows:

&#10005

Not surprisingly, the player who plays first has an advantage in winning. Perhaps more surprising is that in this kind of “strategyless” play, ties are comparatively uncommon—even though if one player actively tries to block the other, they often force a tie.

We’ve looked at “classic tic-tac-toe” and a few specific variants. But there are ultimately all sorts of possible variants. And a convenient general way to represent the “board” for any tic-tac-toe-like game is just to give a “flattened” list of values—with 0 representing a blank position, and i representing a symbol added by player i.

In standard “2D representation” one might have a board like

&#10005

which in flattened form would be:

&#10005

Typical winning patterns can then be represented

&#10005

where in each case we have framed the relevant “winning symbols”, and then given their positions in the flattened list. In ordinary tic-tac-toe it’s clear that the positions of “winning symbols” must always form an arithmetic progression. And it seems as if a good way to generalize tic-tac-toe is always to define a win for i to be associated with the presence of i symbols at positions that form an arithmetic progression of a certain length s. For ordinary tic-tac-toe s = 3, but for generalizations it could have other values.

Consider now the case of a length-5 list (i.e. 5-position “1D board”). The complete multiway graph is as follows, with “winning states” that contain arithmetic progressions of length s = 3 highlighted:

&#10005

In a more symmetrical rendering this is:

&#10005

Here’s the analogous result for a 7-position board, and 2 players:

&#10005

For each size of board n, we can compute the total number of winning states for any given player, as well as the total number of states altogether. The result when winning is based on arithmetic progressions of length 3 (i.e. s = 3) is:

&#10005

The 2-player n = 9 (= 3×3) case here is similar to ordinary tic-tac-toe, but not the same. In particular, states like

&#10005

are considered wins for X in the flattened setup, but not in ordinary tic-tac-toe.

If we increase the length of progression needed in order to declare a win, say to s = 4, we get:

&#10005

The total number of game states is unchanged, but—as expected—there are “fewer ways to win”.

But let’s say we have boards that are completely filled in. For small board sizes there may well not be an arithmetic progression of positions for any player—so that the game has to be considered a tie—as we see in this n = 5 case:

&#10005

But it is a result related to Ramsey theory that it turns out that for n ≥ 9, it’s inevitable that there will be an “arithmetic progression win” for at least one of the players—so that there is never a tie—as these examples illustrate:

&#10005

 

Walks and Their Multiway Graphs

A game like tic-tac-toe effectively involves at each step moving to one of several possible new board configurations—which we can think of as being at different “places” in “game state space”. But what if instead of board configurations we just consider our states to be positions on a lattice such as

&#10005

and then we look at possible walks, that at each step can, in this case, go one unit in any of 4 directions?

Starting at a particular point, the multiway graph after 1 step is just

&#10005

where we have laid out this graph so that the “states” are placed at their geometrical positions on the lattice.

After 2 steps we get:

&#10005

And in general the structure of the multiway graph just “recapitulates” the structure of the lattice:

&#10005

We can think of the paths in the multiway graph as representing all possible random walks of a certain length in the lattice. We can lay the graph out in 3D, with the vertical position representing the first step at which a given point can be reached:

&#10005

We can also lay out the graph more like we laid out multiway graphs for tic-tac-toe:

&#10005

One feature of these “random-walk” multiway graphs is that they contain loops, that record the possibility of “returning to places one’s already been”. And this is different from what happens for example in tic-tac-toe, in which at each step one is just adding an element to the board, and it’s never possible to go back.

But we can set up a similar “never-go-back rule” for walks, by considering “self-avoiding walks” in which any point that’s been visited can never be visited again. Let’s consider first the very trivial lattice:

&#10005

Now indicate the “current place we’ve reached” by a red dot, and the places we’ve visited before by blue dots—and start from one corner:

&#10005

There are only two possible walks here, one going clockwise, the other counterclockwise. Allowing one to start in each possible position yields a slightly more complicated multiway graph:

&#10005

With a 2×3 grid we get

&#10005

while with a 3×3 grid we get:

&#10005

Starting in the center, and with a different layout for the multiway graph, we get:

&#10005

Note the presence of large “holes”, in which paths on each side basically “get to the same place” in “opposite ways”. Note that of the 2304 possible ways to have 1 red dot and up to 8 blue ones, this actual multiway graph reaches only 57. (Starting from the corner reaches 75 and from all possible initial positions 438.)

With a 4×4 lattice (starting the walker in the corner) the multiway graph has the form

&#10005

or in an alternative layout

&#10005

where now 1677 states out of 524,288 are eventually visited, and the number of new states visited at each step (i.e. the number of nodes in successive layers in the graph) is:

&#10005

For a 5×5 grid 89,961 states are reached, distributed across steps according to:

&#10005

(For a grid with n vertices, there are a total of n 2^n–1 possible states, but the number actually reached is always much smaller.)

In talking about walks, an obvious question to ask is about mazes. Consider the maze:

&#10005

As far as traversing this maze is concerned, it is equivalent to “walking” on the graph

&#10005

which in another embedding is just

&#10005

But just as before, the multiway graph that represents all possible walks essentially just “recapitulates” this graph. And that means that “solving” the maze can in a sense equally be thought of as finding a path directly in the maze graph, or in the multiway graph:

&#10005

 

The Icosian Game & Some Relatives

Our discussion of self-avoiding walks turns out to be immediately related to the “Icosian game” of William Rowan Hamilton from 1857 (which is somewhat related to the early computer game Hunt the Wumpus):

The object of the “game” (or, more properly, puzzle) is to find a path (yes, a Hamiltonian path) around the icosahedron graph that visits every node (and returns back to where it started from). And once again we can construct a multiway graph that represents all possible sequences of “moves” in the game.

Let’s start with the simpler case of an underlying tetrahedron graph:

&#10005

From this we get the multiway graph:

&#10005

The “combined multiway graph” from all possible starting positions on the tetrahedron graph gives a truncated cuboctahedron multiway graph:

&#10005

And following this graph we see that from any initial state it’s always possible to reach a state where every node in the tetrahedron graph has been visited. In fact, because the tetrahedron graph is a complete graph it’s even guaranteed that the last node in the sequence will be “adjacent” to the starting node—so that one has formed a Hamiltonian cycle and solved the puzzle.

Things are less trivial for the cube graph:

&#10005

The multiway graph (starting from a particular state) in this case is:

&#10005

Now there are 13 configurations where no further moves are possible:

&#10005

In some of these, one’s effectively “boxed in” with no adjacent node to visit. In others, all the nodes have been filled in. But only 3 ultimately achieve a true Hamiltonian cycle that ends adjacent to the starting node:

&#10005

It turns out that one can reach each of these states through 4 distinct paths from the root of the multiway graph. An example of such a path is:

&#10005

We can summarize this path as a Hamiltonian circuit of the original cube graph:

&#10005

In the multiway graph, the 12 “winning paths” are

&#10005

In a different rendering this becomes

&#10005

and keeping only “winning paths” the subgraph of the multiway graph has the symmetrical form:

&#10005

The actual Hamiltonian circuits through the underlying cube graph corresponding to these winning paths are:

&#10005

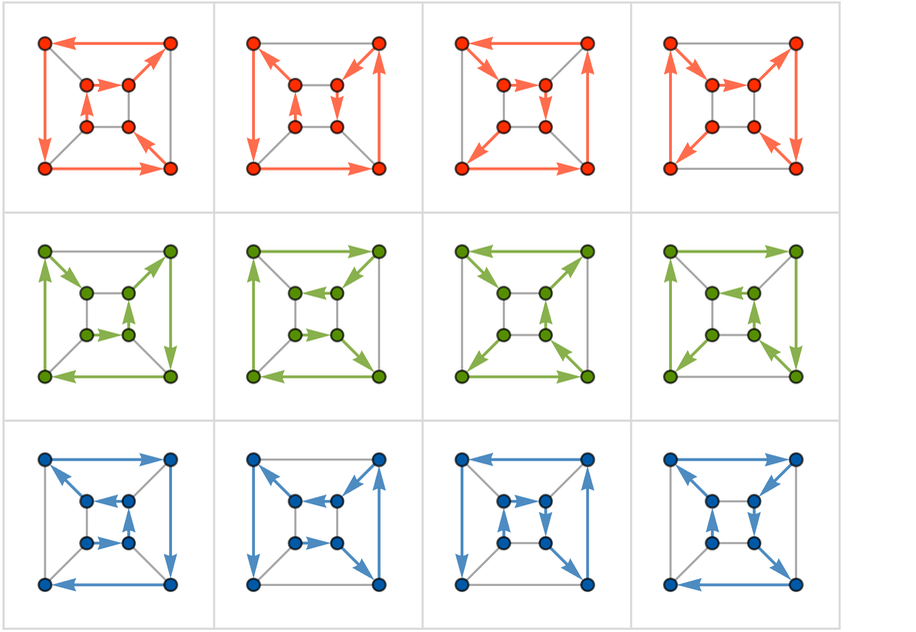
For the dodecahedral graph (i.e. the original Icosian game), the multiway graph is larger and more complicated. It begins

&#10005

and has its first merge after 11 steps (and 529 in all), and ends up with a total of 11,093 nodes—of which 2446 are “end states” where no further move is possible. This shows the number of end (below) and non-end (above) states at each successive step:

&#10005

The successive fractions of “on-track-to-succeed” states are as follows, indicating that the puzzle is in a sense harder at the beginning than at the end:

&#10005

There are 13 “end states” which fill in every position of the underlying dodecahedral graph, with 3 of these corresponding to Hamiltonian cycles:

&#10005

The total number of paths from the root of the multiway graph leading to end states (in effect the total number of ways to try to solve the puzzle) is 3120. Of these, 60 lead to the 3 Hamiltonian cycle end states. An example of one of these “winning paths” is:

&#10005

Examples of underlying Hamiltonian cycles corresponding to each of the 3 Hamiltonian cycle end states are:

&#10005

And this now shows all 60 paths through the multiway graph that reach Hamiltonian cycle end states—and thus correspond to solutions to the puzzle:

&#10005

In effect, solving the puzzle consists in successfully finding these paths out of all the possibilities in the multiway graph. In practice, though—much as in theorem-proving, for example—there are considerably more efficient ways to find “winning paths” than to look directly at all possibilities in the multiway graph (e.g. FindHamiltonianCycle in Wolfram Language). But for our purpose of understanding games and puzzles in a multicomputational framework, it’s useful to see how solutions to this puzzle lay out in the multiway graph.

The Icosian game from Hamilton was what launched the idea of Hamiltonian cycles on graphs. But already in 1736 Leonhard Euler had discussed what are now called Eulerian cycles in connection with the puzzle of the Bridges of Königsberg. In modern terms, we can state the puzzle as the problem of finding a path that visits once and only once all the edges in the graph (in which the “double bridges” from the original puzzle have been disambiguated by extra nodes):

&#10005

We can create a multiway graph that represents all possible paths starting from a particular vertex:

&#10005

But now we see that the end states here are

&#10005

and since none of them have visited every edge, there is no Eulerian circuit here. To completely resolve the puzzle we need to make a multiway graph in which we start from all possible underlying vertices. The result is a disconnected multiway graph whose end states again never visit every edge in the underlying graph (as one can tell from the fact that the number of “levels” in each subgraph is less than 10):

&#10005

 

The Geography Game

In the Geography Game one has a collection of words (say place names) and then one attempts to “string the words together”, with the last letter of one word being the same as the first letter of the next. The game typically ends when nobody can come up with a word that works and hasn’t been used before.

Usually in practice the game is played with multiple players. But one can perfectly well consider a version with just one player. And as an example let’s take our “words” to be the abbreviations for the states in the US. Then we can make a graph of what can follow what:

&#10005

Let’s at first ignore the question of whether a state has “already been used”. Then, starting, say, from Massachusetts (MA), we can construct the beginning of a multiway graph that gives us all possible sequences:

&#10005

After 10 steps the graph is

&#10005

or in a different rendering:

&#10005

This shows the total number of paths as a function of length through this graph, assuming one doesn’t allow any state to be repeated:

&#10005

The maximum length of path is 23—and there are 256 such paths, 88 ending with TX and 168 ending with AZ. A few sample such paths are

&#10005

and all these paths can be represented by what amounts to a finite state machine:

&#10005

By the way, the starting state that leads to the longest path is MN—which achieves length 24 in 2336 different ways, with possible endings being AZ, DE, KY and TX. A few samples are:

&#10005

Drawing these paths in the first few steps of the multiway graph starting from MN we get:

&#10005

 

Groups and (Simplified) Rubik’s Cubes

We’ve talked about puzzles that effectively involve walks on graphs. A particularly famous example of a puzzle that can be thought about in this way is the Rubik’s Cube. The graph in question is then the Cayley graph for the group formed by the transformations that can be applied to the cube.

As a very simple analog, we can consider the symmetry group of the square, D₄, based on the operations of reflection and 90° rotation. We generate the Cayley graph just like a multiway graph: by applying each operation at each step. And in this example the Cayley graph is:

&#10005

This graph is small enough that it is straightforward to see how to get from any configuration to any other. But while this Cayley graph has 8 nodes and maximum path length from any one node to any other of 3, the Cayley graph for the Rubik’s Cube has nodes and a maximum shortest path length of 20.

To get some sense of the structure of an object like this, we can consider the very simplified case of a “2×2×2 cube”—colored only on its corners—in which each face can be rotated by 90°:

&#10005

The first step in the multiway graph—starting from the configuration above—is then (note that the edges in the graph are not directed, since the underlying transformations are always reversible):

&#10005

Going another step gives:

&#10005

The complete multiway graph (which is also the Cayley graph for the group—which turns out to be S₈—generated by the transformations) has 8! = 40,320 nodes (and 483,840 edges). Starting from a state (i.e. node in the Cayley graph) the number of new states reached at successive steps is:

&#10005

The maximum shortest paths in the graph consist of 8 steps; an example is:

&#10005

Between these particular two endpoints there are actually 3216 “geodesic” paths—which spread out quite far in the multiway graph

&#10005

Picking out only geodesic paths we see there are many ways to get from one configuration of the cube to one of its “antipodes”:

&#10005

 

Peg Solitaire

Whereas something like tic-tac-toe involves progressively filling in a board, a large class of puzzles that have been used since at least the 1600s involve basically removing pegs from a board. The typical rules involve pegs being able to jump over a single intermediate peg into a hole, with the intermediate peg then being removed. The goal is to end up with just a single peg on the board.

Here’s a very simple example based on a T arrangement of pegs:

&#10005

In this case, there’s only one way to “solve the puzzle”. But in general there’s a multiway graph:

&#10005

A more complicated example is the “Tricky Triangle” (AKA the “Cracker Barrel puzzle”). Its multiway graph begins:

&#10005

After another couple of steps it becomes:

&#10005

There are a total of 3016 states in the final multiway graph, of which 118 are “dead-end” configurations from which no further moves are possible. The “earliest” of these dead-end configurations are:

&#10005

There are just 4 “winning states” that can be reached, and the “end games” that lead to them are:

&#10005

Starting from the initial configuration, the number of possible states reached at each step is given as follows, where the states that can lead to winning configurations is shown in yellow:

&#10005

This shows the complete multiway graph, with “winning paths” highlighted:

&#10005

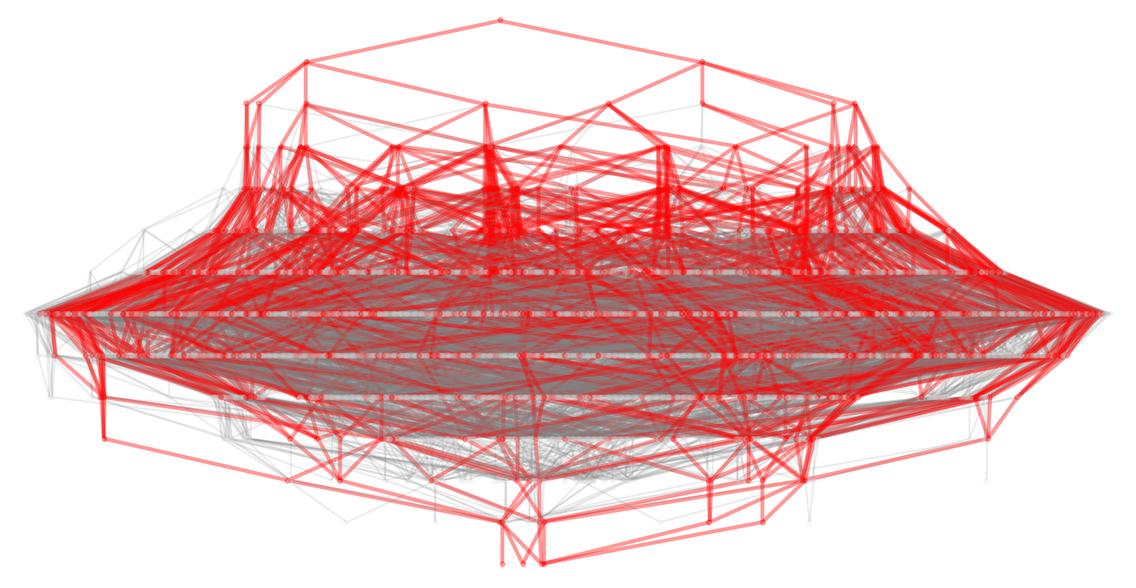
At successive steps, the fraction of states that can lead to a winning state is as follows:

&#10005

The branchial graphs are highly connected, implying that in a sense the puzzle remains “well mixed” and “unpredictable” until the very end:

&#10005

 

Checkers

Peg solitaire is a one-player “game”. Checkers (AKA draughts) is a two-player game with a somewhat similar setup. “Black” and “red” pieces move diagonally in different directions on a board, “taking” each other by jumping over when they are adjacent.

Let’s consider the rather minimal example of a 4×4 board. The basic set of possible moves for “black” and “red” is defined by the graphs (note that a 4×4 board is too small to support “multiple jumps”):

&#10005

With this setup we can immediately start to generate a multiway graph, based on alternating black and red moves:

&#10005

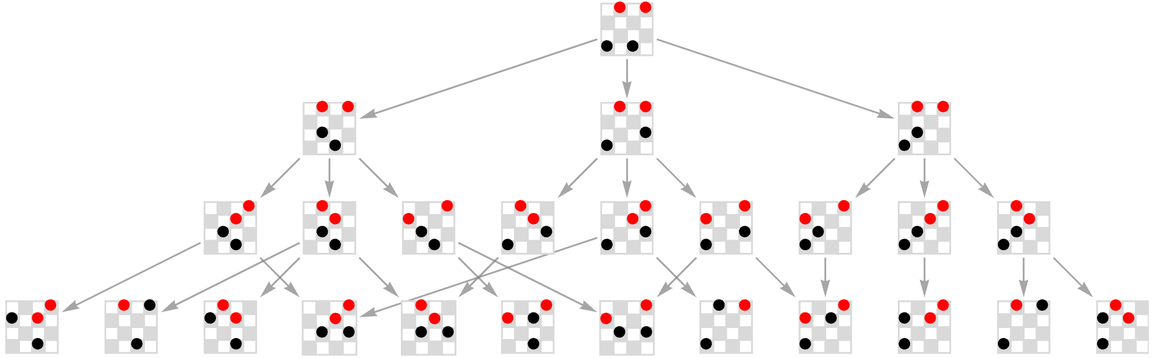
With the rules as defined so far, the full 161-node multiway graph is:

&#10005

It’s not completely clear what it means to “win” in this simple 4×4 case. But one possibility is to say that it happens when the other player can’t do anything at their next move. This corresponds to “dead ends” in the multiway graph. There are 26 of these, of which only 3 occur when it is red’s move next, and the rest all occur when it is black’s move:

&#10005

As before, any particular checkers game corresponds to a path in the multiway graph from the root to one of these end states. If we look at branchial graphs in this case, we find that they have many disconnected pieces, indicating that there are many largely independent “game paths” for this simple game—so there is not much “mixing” of outcomes:

&#10005

&#10005

The rules we’ve used so far don’t account for what amounts to the second level of rules for checkers: the fact that when a piece reaches the other side of the board it becomes a “king” that’s allowed to move backwards as well as forwards. Even with a single piece and single player this already generates a multiway graph—notably now with loops:

&#10005

or in an alternative layout (with explicitly undirected edges):

&#10005

With two pieces (and two players taking turns) the “kings” multiway graph begins:

&#10005

With this initial configuration, but without backward motion, the whole multiway graph is just:

&#10005

The full “kings” multiway graph in this case also only has 62 nodes—but includes all sorts of loops (though with this few pieces and black playing first it’s inevitable that any win will be for black):

&#10005

What about the ordinary + kings multiway graph from our original initial conditions? The combined graph has 161 nodes from the “pre-king” phase, and 4302 from the “post-king” phase—giving the final form:

&#10005

 

(Very Simplified) Go

The full game of Go is sophisticated and its multiway graph in any realistic case is far too big for us to generate at all explicitly (though one can certainly wonder if there are meaningful “continuum limit” results). However, to get some flavor of Go we can consider a vastly simplified version in which black and white “stones” are progressively placed on nodes of a graph, and the game is considered “won” if one player has successfully surrounded a connected collection of the other player’s stones.

Imagine that we start with a blank “board” consisting of a 2×2 square of positions, then on a sequence of “turns” add black and white stones in all possible ways. The resulting multiway graph is:

&#10005

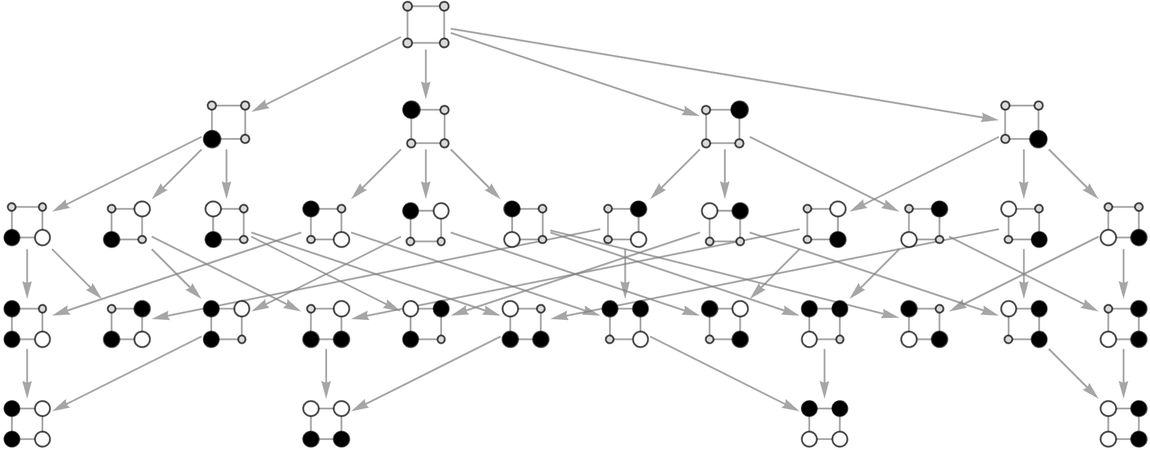
Every state that has no successor here is a win for either black or white. The “black wins” (with the surrounded stone highlighted) are

&#10005

while the “white wins” are:

&#10005

At this level what we have is basically equivalent to 2×2 tic-tac-toe, albeit with a “diagonal” win condition. With a 3×2 “board”, the first two steps in the multiway graph are:

&#10005

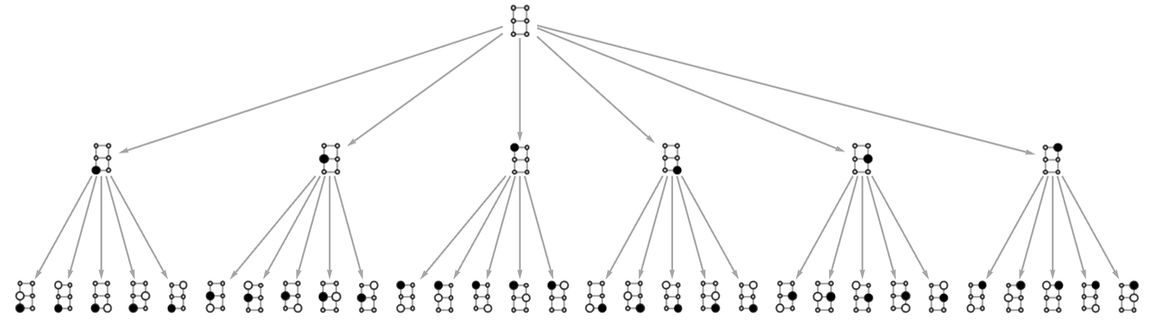
The final multiway graph is:

&#10005

The graph has 235 nodes, of which 24 are wins for white, and 34 for black:

&#10005

The successive branchial graphs in this case are (with wins for black and white indicated):

&#10005

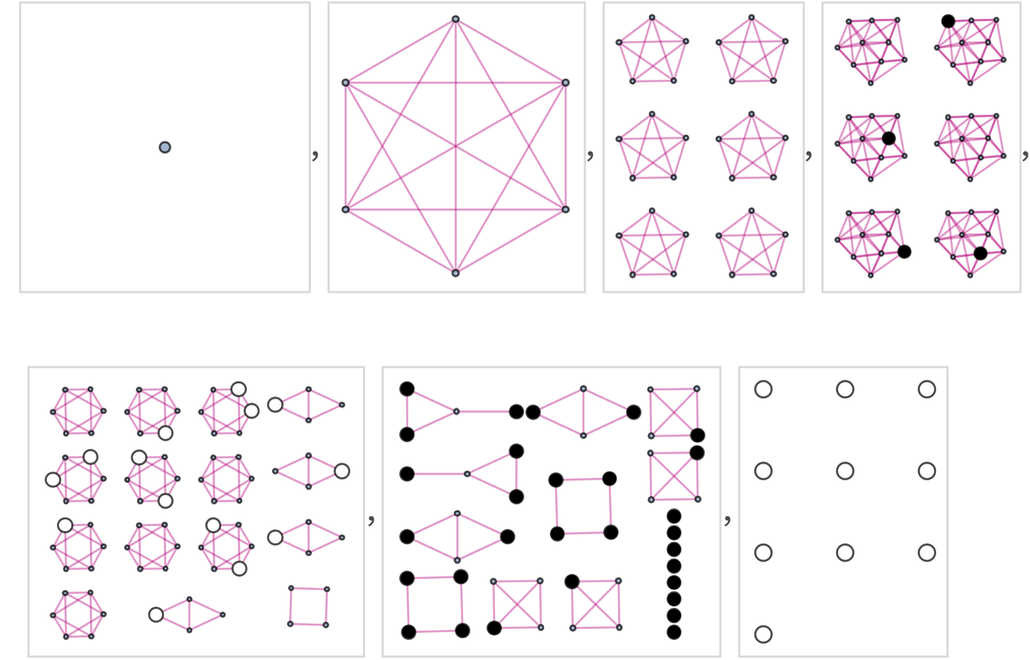
For a 3×3 “board” the multiway graph has 5172 states, with 604 being wins for white and 684 being wins for black.

Nim

As another example of a simple game, we’ll now consider Nim. In Nim, there are k piles of objects, and at each step p players alternate in removing as many objects as they want from whatever single pile they choose. The loser of the game is the player who is forced to have 0 objects in all the piles.

Starting off with 2 piles each containing 2 objects, one can construct a multiway graph for the game:

&#10005

With 3 piles this becomes:

&#10005

These graphs show all the different possible moves that relate different configurations of the piles. However, they do not indicate which player moves when. Adding this we get in the 22 case

&#10005

and in the 222 case:

&#10005

Even though these graphs look somewhat complicated, it turns out there is a very straightforward criterion for when a particular state has the property that its “opponent” can force a lose: just take the list of numbers and see if Apply[BitXor, list] is 0. Highlighting when this occurs we get:

&#10005

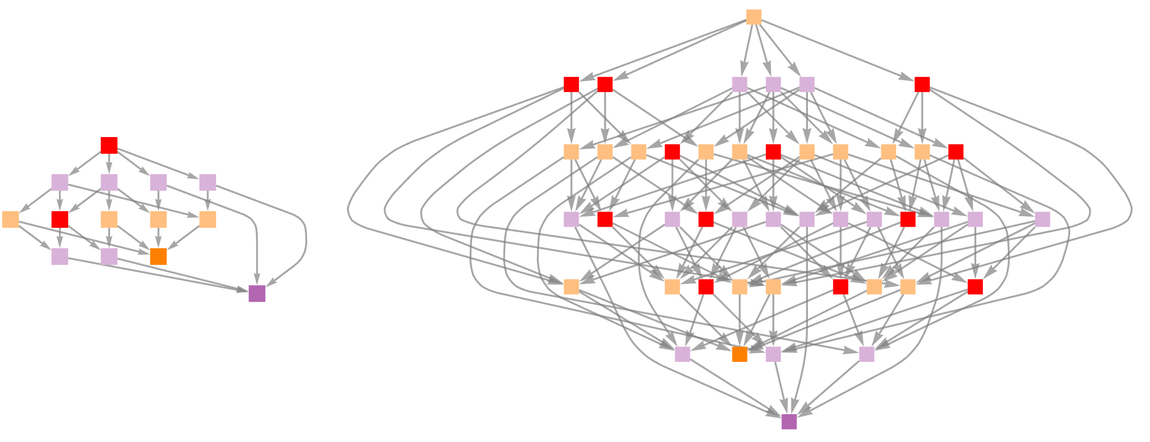
It turns that for Nim, the sequence of branchial graphs we get have a rather regular structure. In the 22 case, with the same highlighting as before, we get:

&#10005

In the 222 case the sequence of branchial graphs becomes:

&#10005

Here are results for some other cases:

&#10005

 

Sliding Block Puzzles

They go under many names—with many different kinds of theming. But many puzzles are ultimately sliding block puzzles. A simple example might ask to go from

&#10005

by sliding blocks into the empty (darker) square. A solution to this is:

&#10005

One can use a multiway graph to represent all possible transformations:

&#10005

(Note that only 12 of the 4! = 24 possible configurations of the blocks appear here; a configuration like cannot be reached.)

Since blocks can always be “slid both ways” every edge in a sliding-block-puzzle multiway graph has an inverse—so going forward we’ll just draw these multiway graphs as undirected.

Here are some simple cases:

&#10005

&#10005

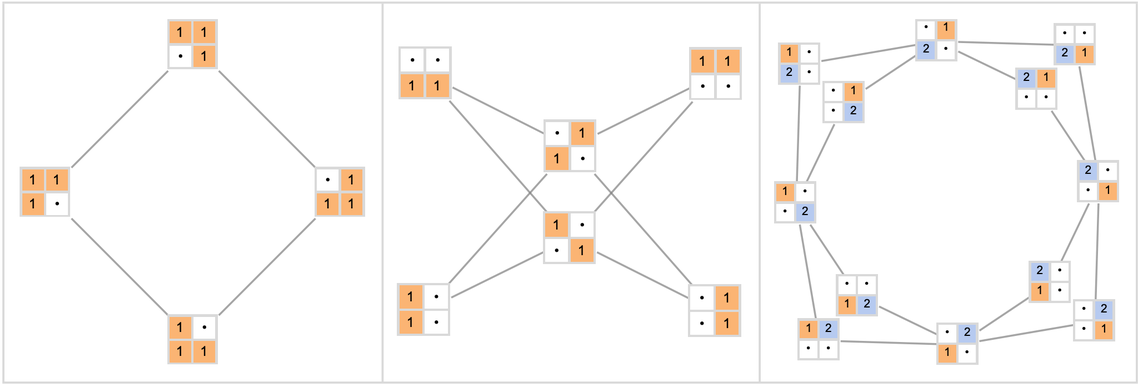
With a 3×2 board, things quickly get more complicated:

&#10005

Rendered in 3D this becomes:

&#10005

When all the blocks are distinct, one tends to get multiway graphs with a kind of spherical structure:

&#10005

(Note that in the first three cases here, it’s possible to reach all 30, 120, 360 conceivable arrangements of the blocks, while in the last case one can only reach “even permutations” of the blocks, or 360 of the 720 conceivable arrangements.)

This shows how one gets from to :

&#10005

With many identical blocks one tends to build up a simple lattice:

&#10005

Making one block different basically just “adds decoration”:

&#10005

As the number of “1” and “2” blocks becomes closer to equal, the structure fills in:

&#10005

Adding a third type of block rapidly leads to a very complicated structure:

&#10005

This summarizes a few of the graphs obtained:

&#10005

&#10005

 

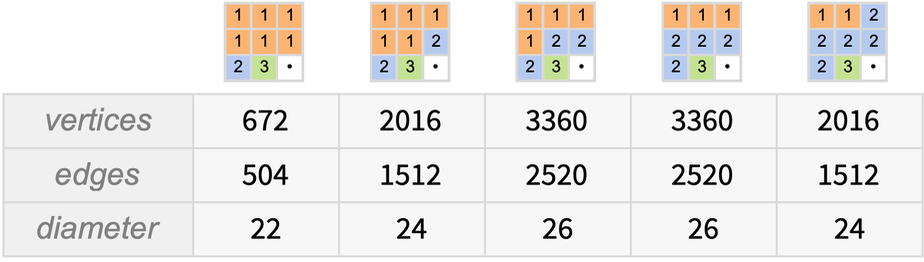
Towers of Hanoi, etc.

Another well-known puzzle is the Towers of Hanoi. And once again we can construct a multiway graph for it. Starting with all disks on the left peg the first step in the multiway graph is:

&#10005

Going two steps we get:

&#10005

The complete multiway graph is then (showing undirected edges in place of pairs of directed edges):

&#10005

It is rather easy to see how the recursive structure of this multiway graph builds up. Here’s the “base case” of 2 disks (and 3 pegs):

&#10005

And as each disk is added, the number of nodes in the multiway graph increases by a factor of 3—yielding for example with 4 disks (and still 3 pegs):

&#10005

With 4 pegs, things at first look more complicated, even with 2 disks:

&#10005

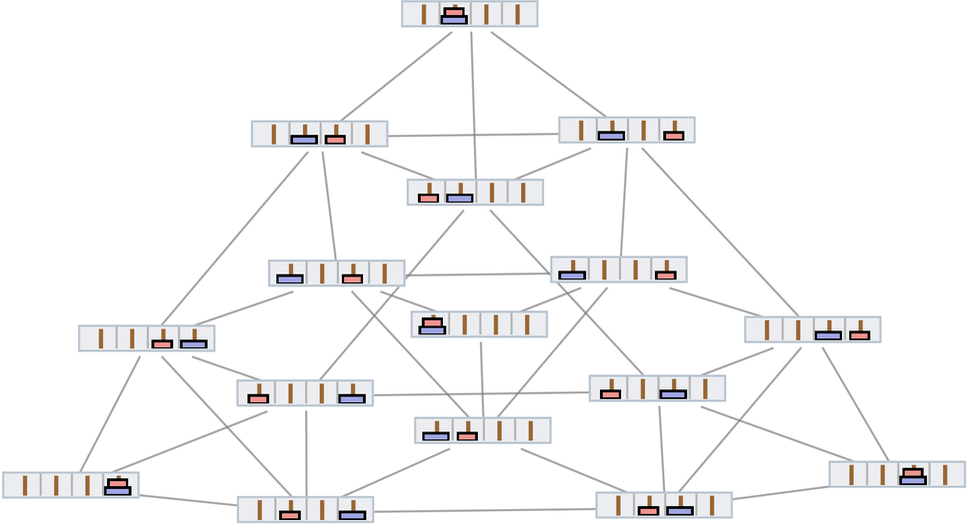
In a 3D rendering, more structure begins to emerge:

&#10005

And here are the results for 3, 4 and 5 disks—with the “points of the ears” corresponding to states where all the disks are on a single peg:

&#10005

With 3 pegs, the shortest “solution to the puzzle”—of moving all disks from one peg to another—goes along the “side” of the multiway graph, and for n pegs is of length 2ⁿ – 1:

&#10005

With 4 pegs, there is no longer a unique “geodesic path”:

&#10005

(And the sequence of path lengths for successive numbers of pegs is

&#10005

or a little below for a large number of pegs n.)

What about branchial graphs? For the standard 3-disk 3-peg case we have

&#10005

where successive “time slices” are assumed to be obtained by looking at successive vertical levels in the rendering of the multiway graph above.

For 4 disks one essentially gets “more of the same”:

&#10005

With 4 pegs things become slightly more complicated:

&#10005

And the trend continues for 5 pegs:

&#10005

 

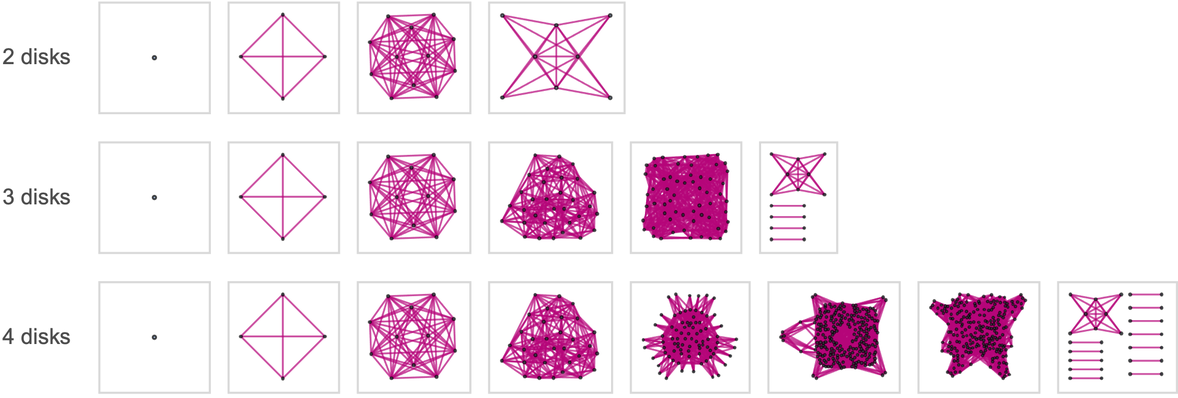
Multicomputational Implications & Interpretation

We’ve now gone through many examples of games and puzzles. And in each case we’ve explored the multiway graphs that encapsulate the whole spectrum of their possible behavior. So what do we conclude? The most obvious point is that when games and puzzles seem to us difficult—and potentially “interesting”—it’s some kind of reflection of apparent complexity in the multiway graph. Or, put another way, it’s when we find the multiway graph somehow “difficult to decode” that we get a rich and engaging game or puzzle.

In any particular instance of playing a game we’re basically following a specific path (that in analogy to physics we can call a “timelike path”) through the multiway graph (or “game graph”) for the game. And at some level we might just make the global statement that the game graph represents all such paths. But what the multicomputational paradigm suggests is that there are also more local statements that we can usefully make. In particular, at every step along a timelike path we can look “transversally” in the multiway graph, and see the “instantaneous branchial graph” that represents the “entanglement” of our path with “nearby paths”.

Figuring out “what move to make next” is then in a sense about deciding in “what direction” in branchial space to go. And what makes a game difficult is that we can’t readily predict what happens as we “travel through branchial space”. There’s a certain analogy here to the concept of computational irreducibility. Going from one state to another along some timelike path, computational irreducibility implies that even though we may know the underlying rules, we can’t readily predict their consequences—because it can require an irreducible amount of computation to figure out what their consequences will be after many steps.

Predicting “across branchial space” is a related, but slightly different phenomenon, that one can describe as “multicomputational irreducibility”. It’s not about the difficulty of working out a particular path of computation, but instead about the difficulty of seeing how many entangled paths interact.

When one plays a game, it’s common to talk about “how many moves ahead one can see”. And in our terms here, this is basically about asking how “far out in branchial space” we can readily get. As computationally bounded entities, we have a certain “reach” in branchial space. And the game is “difficult for us” if that reach isn’t sufficient to be able to get to something like a “winning position”.

There’s another point here, though. What counts as “winning” in a game is typically reaching some particular places or regions in the multiway graph. But the definition of these places or regions is typically something very computationally bounded (“just see if there’s a line of X’s”, etc.). It’s a certain “observation” of the system, that extracts just a particular (computationally bounded) sampling of the complete state. And then what’s key is that this sampling doesn’t manage to “decode the multicomputational irreducibility”.

There’s an analogy here to thermodynamics. The fact that in thermodynamics we perceive “heat” and “entropy increase” is a consequence of the fact that our (coarse-grained) measurements can’t “decode” the computationally irreducible process that leads to the particular states generated in the system. Similarly, the fact we perceive it to be “hard to figure out how to win a game” is a consequence of the fact that our criterion for winning isn’t able to “look inside the playing of the game” and “decode what’s going on” to the point where it’s in effect just selecting one particular, straightforward path. Instead it’s a question of going through the multicomputationally irreducible process of playing the game, and in effect “seeing where it lands” relative to the observation of winning.

There’s also an analogy here to quantum mechanics. Tracing through many possible paths of playing a game is like following many threads of history in quantum mechanics, and the criterion of winning is like a quantum measurement that selects certain threads. In our Physics Project we imagine that we as observers are extended in branchial space, “knitting together” different threads of history through our belief in our own single thread of experience. In games, the analog of our belief in a single thread of experience is presumably in effect that “all that matters is who wins or loses; it doesn’t matter how the game is played inside”.

To make a closer analogy with quantum mechanics one can start thinking about combining different chunks of “multiway game play”, and trying to work out a calculus for how those chunks fit together.

The games we’ve discussed here are all in a sense pure “games of skill”. But in games where there’s also an element of chance we can think of this as causing what is otherwise a single path in the multiway graph to “fuzz out” into a bundle of paths, and what is otherwise a single point in branchial space to become a whole extended region.

In studying different specific games and puzzles, we’ve often had to look at rather simplified cases in order to get multiway graphs of manageable size. But if we look at very large multiway graphs, are there perhaps overall regularities that will emerge? Is there potentially some kind of “continuum limit” for game graphs?

It’ll almost inevitably be the case that if we look in “enough detail” we’ll see all sorts of multicomputational irreducibility in action. But in our Physics Project—and indeed in the multicomputational paradigm in general—a key issue is that relevant observers don’t see that level of detail. And much like the emergence of thermodynamics or the gas laws from underlying molecular dynamics, the very existence of underlying computational irreducibility inevitably leads to simple laws for what the observer can perceive.

So what is the analog of “the observer” for a game? For at least some purposes it can be thought of as basically the “win” criteria. So now the question arises: if we look only at these criteria, can we derive the analog of “laws of physics”, insensitive to all the multicomputationally irreducible details underneath?

There’s much more to figure out about this, but perhaps one place to start is to look at the large-scale structure of branchial space—and the multiway graph—in various games. And one basic impression in many different games is that—while the character of branchial graphs may change between “different stages” in the game—across a single branchial graph there tends to be a certain uniformity. If one looks at the details there may be plenty of multicomputational irreducibility. But at some kind of “perceptible level” different parts of the graph may seem similar. And this suggests that the “local impression of the game” will tend to be similar at a particular stage even when quite different moves have been made, that take one to quite different parts of the “game space” defined by the branchial graph.

But while there may be similarity between different parts of the branchial graph, what we’ve seen is that in some games and puzzles the branchial graph breaks up into multiple disconnected regions. And what this reflects is the presence of distinct “conserved sectors” in a game—regions of game space that players can get into, but are then stuck with (at least for a certain time), much as in spacetime event horizons can prevent transport between different regions of physical space.

Another (related) effect that we notice in some games and puzzles but not others is large “holes” in the multiway graph: places where between two points in the graph there are multiple “distant” paths. When the multiway graph is densely connected, there’ll typically always be a way to “fix any mistake” by rerouting through nearby paths. But when there is a hole it is a sign that one can end up getting “committed” to one course of action rather than another, and it will be many steps before it’s possible to get to the same place as the other course of action would have reached.

If we assume that at some level all we ultimately “observe” in the multiway graph is the kind of coarse-graining that corresponds to assessing winning or losing then inevitably we’ll be dealing with a distribution of possible paths. Without “holes” these paths can be close together, and may seem obviously similar. But when there’s a hole there can be different paths that are far apart. And the fact there can be distant paths that are “part of the same distribution” can then potentially be thought of as something like a quantum superposition effect.

Are there analogs of general relativity and the path integral in games? To formulate this with clarity we’d have to define more carefully the character of “game space”. Presumably there’ll be the analog of a causal graph. And presumably there’ll also be an analog of energy in game space, associated with the “density of activity” at different places in game space. Then the analog of the phenomenon of gravity will be something like that the best game plays (i.e. the geodesic paths through the game graph) will tend to be deflected by the presence of high densities of activity. In other words, if there are lots of things to do when a game is in a certain state, good game plays will tend to be “pulled towards that state”. And at some level this isn’t surprising: when there’s high density of activity in the game graph, there will tend to be more options about what to do, so it’s more likely that one will be able to “do a good game play” if one goes through there.

So far we didn’t explicitly talk about strategies for games. But in our multicomputational framework a strategy has a fairly definite interpretation: it is a place in rulial space, where in effect one’s assuming a certain set of rules about how to construct the multiway graph. In other words, given a strategy one is choosing some edges in the multiway graph (or some possible events in the associated multiway causal graph), and dropping others.

In general it can be hard to talk about the “space of possible strategies”—because it’s like talking about the “space of possible programs”. But this is precisely what rulial space lets us talk about. What exact “geometry” the “space of strategies” has will depend on how we choose to coordinatize rulial space. But once again there will tend to be a certain level of coarse-graining achieved by looking only at the kinds of things one discusses in game theory—and at this level we can expect that all sorts of standard “structural” game-theoretic results will generically hold.

Personal Notes

Even as a kid I was never particularly into playing games or doing puzzles. And maybe it’s a sign I was always a bit too much of a scientist. Because just picking specific moves always seemed to me too arbitrary. To get my interest I needed a bigger picture, more of a coherent intellectual story. But now, in a sense, that’s just what the multicomputational approach to games and puzzles that I discuss here is bringing to us. Yes, it’s very “humanizing” to be able think about making particular moves. But the multicomputational approach immediately gives one a coherent global view that, at least to me, is intellectually much more satisfying.

The explorations I’ve discussed here can be thought of as originating from a single note in A New Kind of Science. In Chapter 5 of A New Kind of Science I had a section where I first introduced multiway systems. And as the very last note for that section I discussed “Game systems”:

&#10005

I did the research for this in the 1990s—and indeed I now find a notebook from 1998 about tic-tac-toe with some of the same results derived here

&#10005

together with a curious-looking graphical representation of the tic-tac-toe game graph:

&#10005

But back at that time I didn’t conclude much from the game graphs I generated; they just seemed large and complicated. Twenty years passed and I didn’t think much more about this. But then in 2017 my son Christopher was playing with a puzzle called Rush Hour:

And perhaps in a sign of familial tendency he decided to construct its game graph—coming up with what to me seemed like a very surprising result:

&#10005

At the time I didn’t try to understand the structure one has here—but I still “filed this away” as evidence that game graphs can have “visible large-scale structure”.

A couple of years later—in late 2019—our Physics Project was underway and we’d realized that there are deep relations between quantum mechanics and multiway graphs. Quantum mechanics had always seemed like something mysterious—the abstract result of pure mathematical formalism. But seeing the connection to multiway systems began to suggest that one might actually be able to “understand quantum mechanics” as something that could “mechanically arise” from some concrete underlying structure.

I started to think about finding ways to explain quantum mechanics at an intuitive level. And for that I needed a familiar analogy: something everyday that one could connect to multiway systems. I immediately thought about games. And in September 2020 I decided to take a look at games to explore this analogy in more detail. I quickly analyzed games like tic-tac-toe and Nim—as well as simple sliding block puzzles and the Towers of Hanoi. But I wanted to explore more games and puzzles. And I had other projects to do, so the multicomputational analysis of games and puzzles got set aside. The Towers of Hanoi reappeared earlier this year, when I used it as an example of generating a proof-like multiway graph, in connection with my study of the physicalization of metamathematics. And finally, a few weeks ago I decided it was time to write down what I knew so far about games and puzzles—and produce what’s here.

Thanks

Thanks to Brad Klee and Ed Pegg for extensive help in the final stages of the analysis given here—as well as to Christopher Wolfram for inspiration in 2017, and help in 2020.