AIs and Alien Minds

How do alien minds perceive the world? It’s an old and oft-debated question in philosophy. And it now turns out to also be a question that rises to prominence in connection with the concept of the ruliad that’s emerged from our Wolfram Physics Project.

I’ve wondered about alien minds for a long time—and tried all sorts of ways to imagine what it might be like to see things from their point of view. But in the past I’ve never really had a way to build my intuition about it. That is, until now. So, what’s changed? It’s AI. Because in AI we finally have an accessible form of alien mind.

We typically go to a lot of trouble to train our AIs to produce results that are like we humans would do. But what if we take a human-aligned AI, and modify it? Well, then we get something that’s in effect an alien AI—an AI aligned not with us humans, but with an alien mind.

So how can we see what such an alien AI—or alien mind—is “thinking”? A convenient way is to try to capture its “mental imagery”: the image it forms in its “mind’s eye”. Let’s say we use a typical generative AI to go from a description in human language—like “a cat in a party hat”—to a generated image:

It’s exactly the kind of image we’d expect—which isn’t surprising, because it comes from a generative AI that’s trained to “do as we would”. But now let’s imagine taking the neural net that implements this generative AI, and modifying its insides—say by resetting weights that appear in its neural net.

By doing this we’re in effect going from a human-aligned neural net to some kind of “alien” one. But this “alien” neural net will still produce some kind of image—because that’s what a neural net like this does. But what will the image be? Well, in effect, it’s showing us the mental imagery of the “alien mind” associated with the modified neural net.

But what does it actually look like? Well, here’s a sequence obtained by progressively modifying the neural net—in effect making it “progressively more alien”:

At the beginning it’s still a very recognizable picture of “a cat in a party hat”. But it soon becomes more and more alien: the mental image in effect diverges further from the human one—until it no longer “looks like a cat”, and in the end looks, at least to us, rather random.

There are many details of how this works that we’ll be discussing below. But what’s important is that—by studying the effects of changing the neural net—we now have a systematic “experimental” platform for probing at least one kind of “alien mind”. We can think of what we’re doing as a kind of “artificial neuroscience”, probing not actual human brains, but neural net analogs of them.

And we’ll see many parallels to neuroscience experiments. For example, we’ll often be “knocking out” particular parts of our “neural net brain”, a little like how injuries such as strokes can knock out parts of a human brain. But we know that when a human brain suffers a stroke, this can lead to phenomena like “hemispatial neglect”, in which a stroke victim asked to draw a clock will end up drawing just one side of the clock—a little like the pictures of cats “degrade” when parts of the “neural net brain” are knocked out.

Of course, there are many differences between real brains and artificial neural nets. But most of the core phenomena we’ll observe here seem robust and fundamental enough that we can expect them to span very different kinds of “brains”—human, artificial and alien. And the result is that we can begin to build up intuition about what the worlds of different—and alien—minds can be like.

Generating Images with AIs

How does an AI manage to create a picture, say of a cat in a party hat? Well, the AI has to be trained on “what makes a reasonable picture”—and how to determine what a picture is of. Then in some sense what the AI does is to start generating “reasonable” pictures at random, in effect continually checking what the picture it’s generating seems to be “of”, and tweaking it to guide it towards being a picture of what one wants.

So what counts as a “reasonable picture”? If one looks at billions of pictures—say on the web—there are lots of regularities. For example, the pixels aren’t random; nearby ones are usually highly correlated. If there’s a face, it’s usually more or less symmetrical. It’s more common to have blue at the top of a picture, and green at the bottom. And so on. And the important technological point is that it turns out to be possible to use a neural network to capture regularities in images, and to generate random images that exhibit them.

Here are some examples of “random images” generated in this way:

And the idea is that these images—while each is “random” in its specifics—will in general follow the “statistics” of the billions of images from the web on which the neural network has been “trained”. We’ll be talking more about images like these later. But for now suffice it to say that while some may just look like abstract patterns, others seem to contain things like landscapes, human forms, etc. And what’s notable is that none just look like “random arrays of pixels”; they all show some kind of “structure”. And, yes, given that they’ve been trained from pictures on the web, it’s not too surprising that the “structure” sometimes includes things like human forms.

But, OK, let’s say we specifically want a picture of a cat in a party hat. From all of the almost infinitely large number of possible “well-structured” random images we might generate, how do we get one that’s of a cat in a party hat? Well, a first question is: how would we know if we’ve succeeded? As humans, we could just look and see what our image is of. But it turns out we can also train a neural net to do this (and, no, it doesn’t always get it exactly right):

How is the neural net trained? The basic idea is to take billions of images—say from the web—for which corresponding captions have been provided. Then one progressively tweaks the parameters of the neural net to make it reproduce these captions when it’s fed the corresponding images. But the critical point is the neural net turns out to do more: it also successfully produces “reasonable” captions for images it’s never seen before. What does “reasonable” mean? Operationally, it means captions that are similar to what we humans might assign. And, yes, it’s far from obvious that a computationally constructed neural net will behave at all like us humans, and the fact that it does is presumably telling us fundamental things about how human brains work.

But for now what’s important is that we can use this captioning capability to progressively guide images we produce towards what we want. Start from “pure randomness”. Then try to “structure the randomness” to make a “reasonable” picture, but at every step see in effect “what the caption would be”. And try to “go in a direction” that “leads towards” a picture with the caption we want. Or, in other words, progressively try to get to a picture that’s of what we want.

The way this is set up in practice, one starts from an array of random pixels, then iteratively forms the picture one wants:

Different initial arrays lead to different final pictures—though if everything works correctly, the final pictures will all be of “what one asked for”, in this case a cat in a party hat (and, yes, there are a few “glitches”):

We don’t know how mental images are formed in human brains. But it seems conceivable that the process is not too different. And that in effect as we’re trying to “conjure up a reasonable image”, we’re continually checking if it’s aligned with what we want—so that, for example, if our checking process is impaired we can end up with a different image, as in hemispatial neglect.

The Notion of Interconcept Space

That everything can ultimately be represented in terms of digital data is foundational to the whole computational paradigm. But the effectiveness of neural nets relies on the slightly different idea that it’s useful to treat at least many kinds of things as being characterized by arrays of real numbers. In the end one might extract from a neural net that’s giving captions to images the word “cat”. But inside the neural net it’ll operate with arrays of numbers that correspond in some fairly abstract way to the image you’ve given, and the textual caption it’ll finally produce.

And in general neural nets can typically be thought of as associating “feature vectors” with things—whether those things are images, text, or anything else. But whereas words like “cat” and “dog” are discrete, the feature vectors associated with them just contain collections of real numbers. And this means that we can think of a whole space of possibilities, with “cat” and “dog” just corresponding to two specific points.

So what’s out there in that space of possibilities? For the feature vectors we typically deal with in practice the space is many-thousand-dimensional. But we can for example look at the (nominally straight) line from the “dog point” to the “cat point” in this space, and even generate sample images of what comes between:

And, yes, if we want to, we can keep going “beyond cat”—and pretty soon things start becoming quite weird:

We can also do things like look at the line from a plane to a cat—and, yes, there’s strange stuff in there (wings hat ears?):

What about elsewhere? For example, what happens “around” our standard “cat in a party hat”? With the particular setup we’re using, there’s a 2304-dimensional space of possibilities. But as an example, we look at what we get on a particular 2D plane through the “standard cat” point:

Our “standard cat” is in the middle. But as we move away from the “standard cat” point, progressively weirder things happen. For a while there are recognizable (if perhaps demonic) cats to be seen. But soon there isn’t much “catness” in evidence—though sometimes hats do remain (in what we might characterize as an “all hat, no cat” situation, reminiscent of the Texan “all hat, no cattle”).

How about if we pick other planes through the standard cat point? All sorts of images appear:

But the fundamental story is always the same: there’s a kind of “cat island”, beyond which there are weird and only vaguely cat-related images—encircled by an “ocean” of what seem like purely abstract patterns with no obvious cat connection. And in general the picture that emerges is that in the immense space of possible “statistically reasonable” images, there are islands dotted around that correspond to “linguistically describable concepts”—like cats in party hats.

The islands normally seem to be roughly “spherical”, in the sense that they extend about the same nominal distance in every direction. But relative to the whole space, each island is absolutely tiny—something like perhaps a fraction 2^–2000 ≈ 10^–600 of the volume of the whole space. And between these islands there lie huge expanses of what we might call “interconcept space”.

What’s out there in interconcept space? It’s full of images that are “statistically reasonable” based on the images we humans have put on the web, etc.—but aren’t of things we humans have come up with words for. It’s as if in developing our civilization—and our human language—we’ve “colonized” only certain small islands in the space of all possible concepts, leaving vast amounts of interconcept space unexplored.

What’s out there is pretty weird—and sometimes a bit disturbing. Here’s what we see zooming in on the same (randomly chosen) plane around “cat island” as above:

What are all these things? In a sense, words fail us. They’re things on the shores of interconcept space, where human experience has not (yet) taken us, and for which human language has not been developed.

What if we venture further out into interconcept space—and for example just sample points in the space at random? It’s just like we already saw above: we’ll get images that are somehow “statistically typical” of what we humans have put on the web, etc., and on which our AI was trained. Here are a few more examples:

And, yes, we can pick out at least two basic classes of images: ones that seem like “pure abstract textures”, and ones that seem “representational”, and remind us of real-world scenes from human experience. There are intermediate cases—like “textures” with structures that seem like they might “represent something”, and “representational-seeming” images where we just can’t place what they might be representing.

But when we do see recognizable “real-world-inspired” images they’re a curious reflection of the concepts—and general imagery—that we humans find “interesting enough to put on the web”. We’re not dealing here with some kind of “arbitrary interconcept space”; we’re dealing with “human-aligned” interconcept space that’s in a sense anchored to human concepts, but extends between and around them. And, yes, viewed in these terms it becomes quite unsurprising that in the interconcept space we’re sampling, there are so many images that remind us of human forms and common human situations.

But just what were the images that the AI saw, from which it formed this model of interconcept space? There were a few billion of them, “foraged” from the web. Like things on the web in general, it’s a motley collection; here’s a random sample:

Some can be thought of as capturing aspects of “life as it is”, but many are more aspirational, coming from staged and often promotionally oriented photography. And, yes, there are lots of Net-a-Porter-style “clothing-without-heads” images. There are also lots of images of “things”—like food, etc. But somehow when we sample randomly in interconcept space it’s the human forms that most distinctively stand out, conceivably because “things” are not particularly consistent in their structure, but human forms always have a certain consistency of “head-body-arms, etc.” structure.

It’s notable, though, that even the most real-world-like images we find by randomly sampling interconcept space seem to typically be “painterly” and “artistic” rather than “photorealistic” and “photographic”. It’s a different story close to “concept points”—like on cat island. There more photographic forms are common, though as we go away from the “actual concept point”, there’s a tendency towards either a rather toy-like appearance, or something more like an illustration.

By the way, even the most “photographic” images the AI generates won’t be anything that comes directly from the training set. Because—as we’ll discuss later—the AI is not set up to directly store images; instead its training process in effect “grinds up” images to extract their “statistical properties”. And while “statistical features” of the original images will show up in what the AI generates, any detailed arrangement of pixels in them is overwhelmingly unlikely to do so.

But, OK, what happens if we start not at a “describable concept” (like “a cat in a party hat”), but just at a random point in interconcept space? Here are the kinds of things we see:

The images often seem to be a bit more diverse than those around “known concept points” (like our “cat point” above). And occasionally there’ll be a “flash” of something “representationally familiar” (perhaps like a human form) that’ll show up. But most of the time we won’t be able to say “what these images are of”. They’re of things that are somehow “statistically” like what we’ve seen, but they’re not things that are familiar enough that we’ve—at least so far—developed a way to describe them, say with words.

The Images of Interconcept Space

There’s something strangely familiar—yet unfamiliar—to many of the images in interconcept space. It’s fairly common to see pictures that seem like they’re of people:

But they’re “not quite right”. And for us as humans, being particularly attuned to faces, it’s the faces that tend to seem the most wrong—even though other parts are “wrong” as well.

And perhaps in commentary on our nature as a social species (or maybe it’s as a social media species), there’s a great tendency to see pairs or larger groups of people:

There’s also a strange preponderance of torso-only pictures—presumably the result of “fashion shots” in the training data (and, yes, with some rather wild “fashion statements”):

People are by far the most common identifiable elements. But one does sometimes see other things too:

Then there are some landscape-type scenes:

Some look fairly photographically literal, but others build up the impression of landscapes from more abstract elements:

Occasionally there are cityscape-like pictures:

And—still more rarely—indoor-like scenes:

Then there are pictures that look like they’re “exteriors” of some kind:

It’s common to see images built up from lines or dots or otherwise “impressionistically formed”:

And then there are lots of images of that seem like they’re trying to be “of something”, but it’s not at all clear what that “thing” is, and whether indeed it’s something we humans would recognize, or whether instead it’s something somehow “fundamentally alien”:

It’s also quite common to see what look more like “pure patterns”—that don’t really seem like they’re “trying to be things”, but more come across like “decorative textures”:

But probably the single most common type of images are somewhat uniform textures, formed by repeating various simple elements, though usually with “dislocations” of various kinds:

Across interconcept space there’s tremendous variety to the images we see. Many have a certain artistic quality to them—and a feeling that they are some kind of “mindful interpretation” of a perhaps mundane thing in the world, or a simple, essentially mathematical pattern. And to some extent the “mind” involved is a collective version of our human one, reflected in a neural net that has “experienced” some of the many images humans have put on the web, etc. But in some ways the mind is also a more alien one, formed from the computational structure of the neural net, with its particular features, and no doubt in some ways computationally irreducible behavior.

And indeed there are some motifs that show up repeatedly that are presumably reflections of features of the underlying structure of the neural net. The “granulated” appearance, with alternation between light and dark, for example, is presumably a consequence of the dynamics of the convolutional parts of the neural net—and analogous to the results of what amounts to iterated blurring and sharpening with a certain effective pixel scale (reminiscent, for example, of video feedback):

Making Minds Alien

We can think of what we’ve done so far as exploring what a mind trained from human-like experiences can “imagine” by generalizing from those experiences. But what might a different kind of mind imagine?

As a very rough approximation, we can think of just taking the trained “mind” we’ve created, and explicitly modifying it, then seeing what it now “imagines”. Or, more specifically, we can take the neural net we have been using, and start making changes to it, and seeing what effect that has on the images it produces.

We’ll discuss later the details of how the network is set up, but suffice it to say here that it involves 391 distinct internal modules, involving altogether nearly a billion numerical weights. When the network is trained, those numerical weights are carefully tuned to achieve the results we want. But what if we just change them? We’ll still (normally) get a network that can generate images. But in some sense it’ll be “thinking differently”—so potentially the images will be different.

So as a very coarse first experiment—reminiscent of many that are done in biology—let’s just “knock out” each successive module in turn, setting all its weights to zero. If we ask the resulting network to generate a picture of “a cat in a party hat”, here’s what we now get:

Let’s look at these results in a bit more detail. In quite a few cases, zeroing out a single module doesn’t make much of a difference; for example, it might basically only change the facial expression of the cat:

But it can also more fundamentally change the cat (and its hat):

It can change the configuration or position of the cat (and, yes, some of those paws are not anatomically correct):

Zeroing out other modules can in effect change the “rendering” of the cat:

But in other cases things can get much more mixed up, and difficult for us to parse:

Sometimes there’s clearly a cat there, but its presentation is at best odd:

And sometimes we get images that have definite structure, but don’t seem to have anything to do with cats:

Then there are cases where we basically just get “noise”, albeit with things superimposed:

But—much like in neurophysiology—there are some modules (like the very first and last ones in our original list) where zeroing them out basically makes the system not work at all, and just generate “pure random noise”.

As we’ll discuss below, the whole neural net that we’re using has a fairly complex internal structure—for example, with a few fundamentally different kinds of modules. But here’s a sample of what happens if one zeros out modules at different places in the network—and what we see is that for the most part there’s no obvious correlation between where the module is, and what effect zeroing it out will have:

So far, we’ve just looked at what happens if we zero out a single module at a time. Here are some randomly chosen examples of what happens if one zeros out successively more modules (one might call this a “HAL experiment” in remembrance of the fate of the fictional HAL AI in the movie 2001):

And basically once the “catness” of the images is lost, things become more and more alien from there on out, ending either in apparent randomness, or sometimes barren “zeroness”.

Rather than zeroing out modules, we can instead randomize the weights in them (perhaps a bit like the effect of a tumor rather than a stroke in a brain)—but the results are usually at least qualitatively similar:

Something else we can do is just to progressively mix randomness uniformly into every weight in the network (perhaps a bit like globally “drugging” a brain). Here are three examples where in each case 0%, 1%, 2%, … of randomness was added—all “fading away” in a very similar way:

And similarly, we can progressively scale down towards zero (in 1% increments: 100%, 99%, 98%, …) all the weights in the network:

Or we can progressively increase the numerical values of the weights—eventually in some sense “blowing the mind” of the network (and going a bit “psychedelic” in the process):

Minds in Rulial Space

We can think of what we’ve done so far as exploring some of the “natural history” of what’s out there in generative AI space—or as providing a small taste of at least one approximation to the kind of mental imagery one might encounter in alien minds. But how does this fit into a more general picture of alien minds and what they might be like?

With the concept of the ruliad we finally have a principled way to talk about alien minds—at least at a theoretical level. And the key point is that any alien mind—or, for that matter, any mind—can be thought of as “observing” or sampling the ruliad from its own particular point of view, or in effect, its own position in rulial space.

The ruliad is defined to be the entangled limit of all possible computations: a unique object with an inevitable structure. And the idea is that anything—whether one interprets it as a phenomenon or an observer—must be part of the ruliad. The key to our Physics Project is then that “observers like us” have certain general characteristics. We are computationally bounded, with “finite minds” and limited sensory input. And we have a certain coherence that comes from our belief in our persistence in time, and our consistent thread of experience. And what we then discover in our Physics Project is the rather remarkable result that from these characteristics and the general properties of the ruliad alone it’s essentially inevitable that we must perceive the universe to exhibit the fundamental physical laws it does, in particular the three big theories of twentieth-century physics: general relativity, quantum mechanics and statistical mechanics.

But what about more detailed aspects of what we perceive? Well, that will depend on more detailed aspects of us as observers, and of how our minds are set up. And in a sense, each different possible mind can be thought of as existing in a certain place in rulial space. Different human minds are mostly close in rulial space, animal minds further away, and more alien minds still further. But how can we characterize what these minds are “thinking about”, or how these minds “perceive things”?

From inside our own minds we can form a sense of what we perceive. But we don’t really have good ways to reliably probe what another mind perceives. But what about what another mind imagines? Well, that’s where what we’ve been doing here comes in. Because with generative AI we’ve got a mechanism for exposing the “mental imagery” of an “AI mind”.

We could consider doing this with words and text, say with an LLM. But for us humans images have a certain fluidity that text does not. Our eyes and brains can perfectly well “see” and absorb images even if we don’t “understand” them. But it’s very difficult for us to absorb text that we don’t “understand”; it usually tends to seem just like a kind of “word soup”.

But, OK, so we generate “mental imagery” from “minds” that have been “made alien” by various modifications. How come we humans can understand anything such minds make? Well, it’s bit like one person being able to understand the thoughts of another. Their brains—and minds—are built differently. And their “internal view” of things will inevitably be different. But the crucial idea—that’s for example central to language—is that it’s possible to “package up” thoughts into something that can be “transported” to another mind. Whatever some particular internal thought might be, by the time we can express it with words in a language, it’s possible to communicate it to another mind that will “unpack” it into different internal thoughts.

It’s a nontrivial fact of physics that “pure motion” in physical space is possible; in other words, that an “object” can be moved “without change” from one place in physical space to another. And now, in a sense, we’re asking about pure motion in rulial space: can we move something “without change” from one mind at one place in rulial space to another mind at another place? In physical space, things like particles—as well as things like black holes—are the fundamental elements that are imagined to move without change. So what’s now the analog in rulial space? It seems to be concepts—as often, for example, represented by words.

So what does that mean for our exploration of generative AI “alien minds”? We can ask whether when we move from one potentially alien mind to another concepts are preserved. We don’t have a perfect proxy for this (though we could make a better one by appropriately training neural net classifiers). But as a first approximation this is like asking whether as we “change the mind”—or move in rulial space—we can still recognize the “concept” the mind produces. Or, in other words, if we start with a “mind” that’s generating a cat in a party hat, will we still recognize the concepts of cat or hat in what a “modified mind” produces?

And what we’ve seen is that sometimes we do, and sometimes we don’t. And for example when we looked at “cat island” we saw a certain boundary beyond which we could no longer recognize “catness” in the image that was produced. And by studying things like cat island (and particularly its analogs when not just the “prompt” but also the underlying neural net is changed) it should be possible to map out how far concepts “extend” across alien minds.

It’s also possible to think about a kind of inverse question: just what is the extent of a mind in rulial space? Or, in other words, what range of points of view, ultimately about the ruliad, can it hold? Will it be “narrow-minded”, able to think only in particular ways, with particular concepts? Or will it be more “broad-minded”, encompassing more ways of thinking, with more concepts?

In a sense the whole arc of the intellectual development of our civilization can be thought of as corresponding to an expansion in rulial space: with us progressively being able to think in new ways, and about new things. And as we expand in rulial space, we are in effect encompassing more of what we previously would have had to consider the domain of an alien mind.

When we look at images produced by generative AI away from the specifics of human experience—say in interconcept space, or with modified rules of generation—we may at first be able to make little from them. Like inkblots or arrangements of stars we’ll often find ourselves wanting to say that what we see looks like this or that thing we know.

But the real question is whether we can devise some way of describing what we see that allows us to build thoughts on what we see, or “reason” about it. And what’s very typical is that we manage to do this when we come up with a general “symbolic description” of what we see, say captured with words in natural language (or, now, computational language). Before we have those words, or that symbolic description, we’ll tend just not to absorb what we see.

And so, for example, even though nested patterns have always existed in nature, and were even explicitly created by mosaic artisans in the early 1200s, they seem to have never been systematically noticed or discussed at all until the latter part of the 20th century, when finally the framework of “fractals” was developed for talking about them.

And so it may be with many of the forms we’ve seen here. As of today, we have no name for them, no systematic framework for thinking about them, and no reason to view them as important. But particularly if the things we do repeatedly show us such forms, we’ll eventually come up with names for them, and start incorporating them into the domain that our minds cover.

And in a sense what we’ve done here can be thought of as showing us a preview of what’s out there in rulial space, in what’s currently the domain of alien minds. In the general exploration of ruliology, and the investigation of what arbitrary simple programs in the computational universe do, we’re able to jump far across the ruliad. But it’s typical that what we see is not something we can connect to things we’re familiar with. In what we’re doing here, we’re moving only much smaller distances in rulial space. We’re starting from generative AI that’s closely aligned with current human development—having been trained from images that we humans have put on the web, etc. But then we’re making small changes to our “AI mind”, and looking at what it now generates.

What we see is often surprising. But it’s still close enough to where we “currently are” in rulial space that we can—at least to some extent—absorb and reason about what we’re seeing. Still, the images often don’t “make sense” to us. And, yes, quite possibly the AI has invented something that has a rich and “meaningful” inner structure. But it’s just that we don’t (yet) have a way to talk about it—and if we did, it would immediately “make perfect sense” to us.

So if we see something we don’t understand, can we just “train a translator”? At some level the answer must be yes. Because the Principle of Computational Equivalence implies that ultimately there’s a fundamental uniformity to the ruliad. But the problem is that the translator is likely to have to do an irreducible amount of computational work. And so it won’t be implementable by a “mind like ours”. Still, even though we can’t create a “general translator” we can expect that certain features of what we see will still be translatable—in effect by exploiting certain pockets of computational reducibility that must necessarily exist even when the system as a whole is full of computational irreducibility. And operationally what this means in our case is that the AI may in effect have found certain regularities or patterns that we don’t happen to have noticed but that are useful in exploring further from the “current human point” in rulial space.

It’s very challenging to get an intuitive understanding of what rulial space is like. But the approach we’ve taken here is for me a promising first effort in “humanizing” rulial space, and seeing just how we might be able to relate to what is so far the domain of alien minds.

Appendix: How Does the Generative AI Work?

In the main part of this piece, we’ve mostly just talked about what generative AI does, not how it works inside. Here I’ll go a little deeper into what’s inside the particular type of generative AI system that I’ve used in my explorations. It’s a method called stable diffusion, and its operation is in many ways both clever and surprising. As it’s implemented today it’s steeped in fairly complicated engineering details. To what extent these will ultimately be necessary isn’t clear. But in any case here I’ll mostly concentrate on general principles, and on giving a broad outline of how generative AI can be used to produce images.

The Distribution of Typical Images

At the core of generative AI is the ability to produce things of some particular type that “follow the patterns of” known things of that type. So, for example, large language models (LLMs) are intended to produce text that “follows the patterns” of text written by humans, say on the web. And generative AI systems for images are similarly intended to produce images that “follow the patterns” of images put on the web, etc.

But what kinds of patterns exist in typical images, say on the web? Here are some examples of “typical images”—scaled down to 32×32 pixels and taken from a standard set of 60,000 images:

And as a very first thing, we can ask what colors show up in these images. They’re not uniform in RGB space:

But what about the positions of different colors? Adjusting to accentuate color differences, the “average image” turns out to have a curious “HAL’s eye” look (presumably with blue for sky at the top, and brown for earth at the bottom):

But just picking pixels separately—even with the color distribution inferred from actual images—won’t produce images that in any way look “natural” or “realistic”:

And the immediate issue is that the pixels aren’t really independent; most pixels in most images are correlated in color with nearby pixels. And in a first approximation one can capture this for example by fitting the list of colors of all the pixels to a multivariate Gaussian distribution with a covariance matrix that represents their correlation. Sampling from this distribution gives images like these—that indeed look somehow “statistically natural”, even if there isn’t appropriate detailed structure in them:

So, OK, how can one do better? The basic idea is to use neural nets, which can in effect encode detailed long-range connections between pixels. In some way it’s similar to what’s done in LLMs like ChatGPT—where one has to deal with long-range connections between words in text. But for images it’s structurally a bit more difficult, because in some sense one has to “consistently fit together 2D patches” rather than just progressively extend a 1D sequence.

And the typical way this is done at first seems a bit bizarre. The basic idea is to start with a random array of pixels—corresponding in effect to “pure noise”—and then progressively to “reduce the noise” to end up with a “reasonable image” that follows the patterns of typical images, all the while guided by some prompt that says what one wants the “reasonable image” to be of.

Attractors and Inverse Diffusion

How does one go from randomness to definite “reasonable” things? The key is to use the notion of attractors. In a very simple case, one might have a system—like this “mechanical” example—where from any “randomly chosen” initial condition one also evolves to one of (here) two definite (fixed-point) attractors:

One has something similar in a neural net that’s for example trained to recognize digits:

Regardless of exactly how each digit is written, or noise that gets added to it, the network will take this input and evolve to an attractor corresponding to a digit.

Sometimes there can be lots of attractors. Like in this (“class 2”) cellular automaton evolving down the page, many different initial conditions can lead to the same attractor, but there are many possible attractors, corresponding to different final patterns of stripes:

The same can be true for example in 2D cellular automata, where now the attractors can be thought of as being different “images” with structure determined by the cellular automaton rule:

But what if one wants to arrange to have particular images as attractors? Here’s where the somewhat surprising idea of “stable diffusion” can be used. Imagine we start with two possible images, and , and then in a series of steps progressively add noise to them:

Here’s the bizarre thing we now want to do: train a neural net to take the image we get at a particular step, and “go backwards”, removing noise from it. The neural net we’ll use for this is somewhat complicated, with “convolutional” pieces that basically operate on blocks of nearby pixels, and “transformers” that get applied with certain weights to more distant pixels. Schematically in Wolfram Language the network looks at a high level like this:

And roughly what it’s doing is to make an informationally compressed version of each image, and then to expand it again (through what is usually called a “U-net” neural net). We start with an untrained version of this network (say just randomly initialized). Then we feed it a couple of million examples of noisy pictures of and , and the denoised outputs we want in each case.

Then if we take the trained neural net and successively apply it, for example, to a “noised ”, the net will “correctly” determine that the “denoised” version is a “pure ”:

But what if we apply this network to pure noise? The network has been set up to always eventually evolve either to the “” attractor or the “” attractor. But which it “chooses” in a particular case will depend on the details of the initial noise—so in effect the network will seem to be picking at random to “fish” either “” or “” out of the noise:

How does this apply to our original goal of generating images “like” those found for example on the web? Well, instead of just training our “denoising” (or “inverse diffusion”) network on a couple of “target” images, let’s imagine we train it on billions of images from the web. And let’s also assume that our network isn’t big enough to store all those images in any kind of explicit way.

In the abstract it’s not clear what the network will do. But the remarkable empirical fact is that it seems to manage to successfully generate (“from noise”) images that “follow the general patterns” of the images it was trained from. There isn’t any clear way to “formally validate” this success. It’s really just a matter of human perception: to us the images (generally) “look right”.

It could be that with a different (alien?) system of perception we’d immediately see “something wrong” with the images. But for purposes of human perception, the neural net seems to give “reasonable-looking” images—perhaps not least because the neural net operates at least approximately like our brains and our processes of perception seem to operate.

Injecting a Prompt

We’ve described how a denoising neural net seems to be able to start from some configuration of random noise and generate a “reasonable-looking” image. And from any particular configuration of noise, a given neural net will always generate the same image. But there’s no way to tell what that image will be of; it’s just something to empirically explore, as we did above.

But what if we want to “guide” the neural net to generate an image that we’d describe as being of a definite thing, like “a cat in a party hat”? We could imagine “continually checking” whether the image we’re generating would be recognized by a neural net as being of what we wanted. And conceptually that’s what we can do. But we also need a way to “redirect” the image generation if it’s “not going in the right direction”. And a convenient way to do this is to mix a “description of what we want” right into the denoising training process. In particular, if we’re training to “recover an ”, mix a description of the “” right alongside the image of the “”.

And here we can make use of a key feature of neural nets: that ultimately they operate on arrays of (real) numbers. So whether they’re dealing with images composed of pixels, or text composed of words, all these things eventually have to be “ground up” into arrays of real numbers. And when a neural net is trained, what it’s ultimately “learning” is just how to appropriately transform these “disembodied” arrays of numbers.

There’s a fairly natural way to generate an array of numbers from an image: just take the triples of red, green and blue intensity values for each pixel. (Yes, we could pick a different detailed representation, but it’s not likely to matter—because the neural net can always effectively “learn a conversion”.) But what about a textual description, like “a cat in a party hat”?

We need to find a way to encode text as an array of numbers. And actually LLMs face the same issue, and we can solve it in basically the same way here as LLMs do. In the end what we want is to derive from any piece of text a “feature vector” consisting of an array of numbers that provide some kind of representation of the “effective meaning” of the text, or at least the “effective meaning” relevant to describing images.

Let’s say we train a neural net to reproduce associations between images and captions, as found for example on the web. If we feed this neural net an image, it’ll try to generate a caption for the image. If we feed the neural net a caption, it’s not realistic for it to generate a whole image. But we can look at the innards of the neural net and see the array of numbers it derived from the caption—and then use this as our feature vector. And the idea is that because captions that “mean the same thing” should be associated in the training set with “the same kind of images”, they should have similar feature vectors.

So now let’s say we want to generate a picture of a cat in a party hat. First we find the feature vector associated with the text “a cat in a party hat”. Then this is what we keep mixing in at each stage of denoising to guide the denoising process, and end up with an image that the image captioning network will identify as “a cat in a party hat”.

The Latent Space “Trick”

The most direct way to do “denoising” is to operate directly on the pixels in an image. But it turns out there’s a considerably more efficient approach, which operates not on pixels but on “features” of the image—or, more specifically, on a feature vector which describes an image.

In a “raw image” presented in terms of pixels, there’s a lot of redundancy—which is why, for example, image formats like JPEG and PNG manage to compress raw images so much without even noticeably modifying them for purposes of typical human perception. But with neural nets it’s possible to do much greater compression, particularly if all we want to do is to preserve the “meaning” of an image, without worrying about its precise details.

And in fact as part of training a neural net to associate images with captions, we can derive a “latent representation” of images, or in effect a feature vector that captures the “important features” of the image. And then we can do everything we’ve discussed so far directly on this latent representation—decoding it only at the end into the actual pixel representation of the image.

So what does it look like to build up the latent representation of an image? With the particular setup we’re using here, it turns out that the feature vector in the latent representation still preserves the basic spatial arrangement of the image. The “latent pixels” are much coarser than the “visible” ones, and happen to be characterized by 4 numbers rather than the 3 for RGB. But we can decode things to see the “denoising” process happening in terms of “latent pixels”:

And then we can take the latent representation we get, and once again use a trained neural net to fill in a “decoding” of this in terms of actual pixels, getting out our final generated image.

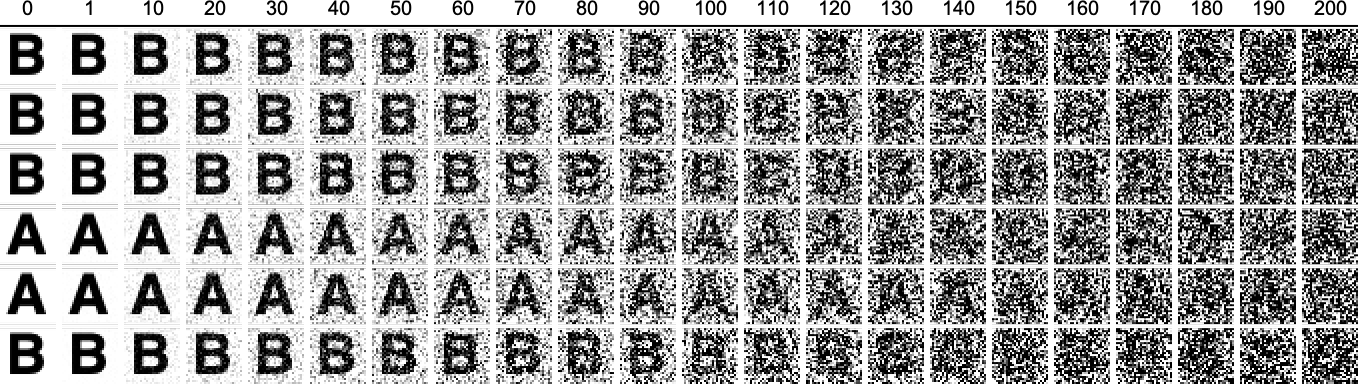
An Analogy in Simple Programs

Generative AI systems work by having attractors that are carefully constructed through training so that they correspond to “reasonable outputs”. A large part of what we’ve done above is to study what happens to these attractors when we change the internal parameters of the system (neural net weights, etc.). What we’ve seen has been complicated, and, indeed, often quite “alien looking”. But is there perhaps a simpler setup in which we can see similar core phenomena?

By the time we’re thinking about creating attractors for realistic images, etc. it’s inevitable that things are going to be complicated. But what if we look at systems with much simpler setups? For example, consider a dynamical system whose state is characterized just by a single number—such as an iterated map on the interval, like x a x (1 – x).

Starting from a uniform array of possible x values, we can show down the page which values of x are achieved at successive iterations:

For a = 2.9, the system evolves from any initial value to a single attractor, which consists of a single fixed final value. But if we change the “internal parameter” a to 3.1, we now get two distinct final values. And at the “bifurcation point” a = 3 there’s a sudden change from one to two distinct final values. And indeed in our generative AI system it’s fairly common to see similar discontinuous changes in behavior even when an internal parameter is continuously changed.

As another example—slightly closer to image generation—consider (as above) a 1D cellular automaton that exhibits class 2 behavior, and evolves from any initial state to some fixed final state that one can think of as an attractor for the system:

Which attractor one reaches depends on the initial condition one starts from. But—in analogy to our generative AI system—we can think of all the attractors as being “reasonable outputs” for the system. But now what happens if we change the parameters of the system, or in this case, the cellular automaton rule? In particular, what will happen to the attractors? It’s like what we did above in changing weights in a neural net—but a lot simpler.

The particular rule we’re using here has 4 possible colors for each cell, and is defined by just 64 discrete values from 0 to 3. So let’s say we randomly change just one of those values at a time. Here are some examples of what we get, always starting from the same initial condition as in the first picture above:

With a couple of exceptions these seem to produce results that are at least “roughly similar” to what we got without changing the rule. In analogy to what we did above, the cat might have changed, but it’s still more or less a cat. But let’s now try “progressive randomization”, where we modify successively more values in the definition of the rule. For a while we again get “roughly similar” results, but then—much like in our cat examples above—things eventually “fall apart” and we get “much more random” results:

One important difference between “stable diffusion” and cellular automata is that while in cellular automata, the evolution can lead to continued change forever, in stable diffusion there’s an annealing process used that always makes successive steps “progressively smaller”—and essentially forces a fixed point to be reached.

But notwithstanding this, we can try to get a closer analogy to image generation by looking (again as above) at 2D cellular automata. Here’s an example of the (not-too-exciting-as-images) “final states” reached from three different initial states in a particular rule:

And here’s what happens if one progressively changes the rule:

At first one still gets “reasonable-according-to-the-original-rule” final states. But if one changes the rule further, things get “more alien”, until they look to us quite random.

In changing the rule, one is in effect “moving in rulial space”. And by looking at how this works in cellular automata, one can get a certain amount of intuition. (Changes to the rule in a cellular automaton seem a bit like “changes to the genotype” in biology—with the behavior of the cellular automaton representing the corresponding “phenotype”.) But seeing how “rulial motion” works in a generative AI that’s been trained on “human-style input” gives a more accessible and humanized picture of what’s going on, even if it seems still further out of reach in terms of any kind of traditional explicit formalization.

Thanks

This project is the first I’ve been able to do with our new Wolfram Institute. I thank our Fourmilab Fellow Nik Murzin and Ruliad Fellow Richard Assar for help. I also thank Jeff Arle, Nicolò Monti, Philip Rosedale and the Wolfram Research Machine Learning Group.