
Delivering from Our R&D Pipeline
In 2020 it was Versions 12.1 and 12.2; in 2021 Versions 12.3 and 13.0. In late June this year it was Version 13.1. And now we’re releasing Version 13.2. We continue to have a huge pipeline of R&D, some short term, some medium term, some long term (like decade-plus). Our goal is to deliver timely snapshots of where we’re at—so people can start using what we’ve built as quickly as possible.
Version 13.2 is—by our standards—a fairly small release, that mostly concentrates on rounding out areas that have been under development for a long time, as well as adding “polish” to a range of existing capabilities. But it’s also got some “surprise” new dramatic efficiency improvements, and it’s got some first hints of major new areas that we have under development—particularly related to astronomy and celestial mechanics.
But even though I’m calling it a “small release”, Version 13.2 still introduces completely new functions into the Wolfram Language, 41 of them—as well as substantially enhancing 64 existing functions. And, as usual, we’ve put a lot of effort into coherently designing those functions, so they fit into the tightly integrated framework we’ve been building for the past 35 years. For the past several years we’ve been following the principle of open code development (does anyone else do this yet?)—opening up our core software design meetings as livestreams. During the Version 13.2 cycle we’ve done about 61 hours of design livestreams—getting all sorts of great real-time feedback from the community (thanks, everyone!). And, yes, we’re holding steady at an overall average of one hour of livestreamed design time per new function, and a little less than half that per enhanced function.
Introducing Astro Computation
Astronomy has been a driving force for computation for more than 2000 years (from the Antikythera device on)… and in Version 13.2 it’s coming to Wolfram Language in a big way. Yes, the Wolfram Language (and Wolfram|Alpha) have had astronomical data for well over a decade. But what’s new now is astronomical computation fully integrated into the system. In many ways, our astro computation capabilities are modeled on our geo computation ones. But astro is substantially more complicated. Mountains don’t move (at least perceptibly), but planets certainly do. Relativity also isn’t important in geography, but it is in astronomy. And on the Earth, latitude and longitude are good standard ways to describe where things are. But in astronomy—especially with everything moving—describing where things are is much more complicated. Oh, and there’s the question of where things “are,” versus where things appear to be—because of effects ranging from light-propagation delays to refraction in the Earth’s atmosphere.
The key function for representing where astronomical things are is AstroPosition. Here’s where Mars is now:

What does that output mean? It’s very “here and now” oriented. By default, it’s telling me the azimuth (angle from north) and altitude (angle above the horizon) for Mars from where Here says I am, at the time specified by Now. How can I get a less “personal” representation of “where Mars is”? Because if even I just reevaluate my previous input now, I’ll get a slightly different answer, just because of the rotation of the Earth:

One thing to do is to use equatorial coordinates, that are based on a frame centered at the center of the Earth but not rotating with the Earth. (One direction is defined by the rotation axis of the Earth, the other by where the Sun is at the time of the spring equinox.) The result is the “astronomer-friendly” right ascension/declination position of Mars:

And maybe that’s good enough for a terrestrial astronomer. But what if you want to specify the position of Mars in a way that doesn’t refer to the Earth? Then you can use the now-standard ICRS frame, which is centered at the center of mass of the Solar System:

Often in astronomy the question is basically “which direction should I point my telescope in?”, and that’s something one wants to specify in spherical coordinates. But particularly if one’s “out and about in the Solar System” (say thinking about a spacecraft), it’s more useful to be able to give actual Cartesian coordinates for where one is:

And here are the raw coordinates (by default in astronomical units):
AstroPosition is backed by lots of computation, and in particular by ephemeris data that covers all planets and their moons, together with other substantial bodies in the Solar System:

By the way, particularly the first time you ask for the position of an obscure object, there may be some delay while the necessary ephemeris gets downloaded. The main ephemerides we use give data for the period 2000–2050. But we also have access to other ephemerides that cover much longer periods. So, for example, we can tell where Ganymede was when Galileo first observed it:

We also have position data for more than 100,000 stars, galaxies, pulsars and other objects—with many more coming soon:

Things get complicated very quickly. Here’s the position of Venus seen from Mars, using a frame centered at the center of Mars:

If we pick a particular point on Mars, then we can get the result in azimuth-altitude coordinates relative to the Martian horizon:

Another complication is that if you’re looking at something from the surface of the Earth, you’re looking through the atmosphere, and the atmosphere refracts light, making the position of the object look different. By default, AstroPosition takes account of this when you use coordinates based on the horizon. But you can switch it off, and then the results will be different—and, for example, for the Sun at sunset, substantially different:


And then there’s the speed of light, and relativity, to think about. Let’s say we want to know where Neptune “is” now. Well, do we mean where Neptune “actually is”, or do we mean “where we observe Neptune to be” based on light from Neptune coming to us? For frames referring to observations from Earth, we’re normally concerned with the case where we include the “light time” effect—and, yes, it does make a difference:

OK, so AstroPosition—which is the analog of GeoPosition—gives us a way to represent where things are, astronomically. The next important function to discuss is AstroDistance—the analog of GeoDistance.
This gives the current distance between Venus and Mars:

This is the current distance from where we are (according to Here) and the position of the Viking 2 lander on Mars:

This is the distance from Here to the star τ Ceti:

To be more precise, AstroDistance really tells us the distance from a certain object, to an observer, at a certain local time for the observer (and, yes, the fact that it’s local time matters because of light delays):

And, yes, things are quite precise. Here’s the distance to the Apollo 11 landing site on the Moon, computed 5 times with a 1-second pause in between, and shown to 10-digit precision:

This plots the distance to Mars for every day in the next 10 years:

Another function is AstroAngularSeparation, which gives the angular separation between two objects as seen from a given position. Here’s the result from Jupiter and Saturn (seen from the Earth) over a 20-year span:

The Beginnings of Astro Graphics
In addition to being able to compute astronomical things, Version 13.2 includes first steps in visualizing astronomical things. There’ll be more on this in subsequent versions. But Version 13.2 already has some powerful capabilities.
As a first example, here’s a part of the sky around Betelgeuse as seen right now from where I am:

Zooming out, one can see more of the sky:

There are lots of options for how things should be rendered. Here we’re seeing a realistic image of the sky, with grid lines superimposed, aligned with the equator of the Earth:

And here we’re seeing a more whimsical interpretation:

Just like for maps of the Earth, projections matter. Here’s a Lambert azimuthal projection of the whole sky:

The blue line shows the orientation of the Earth’s equator, the yellow line shows the plane of the ecliptic (which is basically the plane of the Solar System), and the red line shows the plane of our galaxy (which is where we see the Milky Way).
If we want to know what we actually “see in the sky” we need a stereographic projection (in this case centered on the south direction):

There’s a lot of detail in the astronomical data and computations we have (and even more will be coming soon). So, for example, if we zoom in on Jupiter we can see the positions of its moons (though their disks are too small to be rendered here):

It’s fun to see how this corresponds to Galileo’s original observation of these moons more than 400 years ago. This is from Galileo:
The old typesetting does cause a little trouble:

But the astronomical computation is more timeless. Here are the computed positions of the moons of Jupiter from when Galileo said he saw them, in Padua:

And, yes, the results agree!
By the way, here’s another computation that could be verified soon. This is the time of maximum eclipse for an upcoming solar eclipse:

And here’s what it will look like from a particular location right at that time:

Dates, Times and Units: There’s Always More to Do
Dates are complicated. Even without any of the issues of relativity that we have to deal with for astronomy, it’s surprisingly difficult to consistently “name” times. What time zone are you talking about? What calendar system will you use? And so on. Oh, and then what granularity of time are you talking about? A day? A week? A month (whatever that means)? A second? An instantaneous moment (or perhaps a single elementary time from our Physics Project)?
These issues arise in what one might imagine would be trivial functions: the new RandomDate and RandomTime in Version 13.2. If you don’t say otherwise, RandomDate will give an instantaneous moment of time, in your current time zone, with your default calendar system, etc.—randomly picked within the current year:

But let’s say you want a random date in June 1988. You can do that by giving the date object that represents that month:

OK, but let’s say you don’t want an instant of time then, but instead you want a whole day. The new option DateGranularity allows this:

You can ask for a random time in the next 6 hours:

Or 10 random times:

You can also ask for a random date within some interval—or collection of intervals—of dates:

And, needless to say, we correctly sample uniformly over any collection of intervals:

Another area of almost arbitrary complexity is units. And over the course of many years we’ve systematically solved problem after problem in supporting basically every kind of unit that’s in use (now more than 5000 base types). But one holdout has involved temperature. In physics textbooks, it’s traditional to carefully distinguish absolute temperatures, measured in kelvins, from temperature scales, like degrees Celsius or Fahrenheit. And that’s important, because while absolute temperatures can be added, subtracted, multiplied etc. just like other units, temperature scales on their own cannot. (Multiplying by 0° C to get 0 for something like an amount of heat would be very wrong.) On the other hand, differences in temperature—even measured in Celsius—can be multiplied. How can all this be untangled?
In previous versions we had a whole different kind of unit (or, more precisely, different physical quantity dimension) for temperature differences (much as mass and time have different dimensions). But now we’ve got a better solution. We’ve basically introduced new units—but still “temperature-dimensioned” ones—that represent temperature differences. And we’ve introduced a new notation (a little Δ subscript) to indicate them:

If you take a difference between two temperatures, the result will have temperature-difference units:

But if you convert this to an absolute temperature, it’ll just be in ordinary temperature units:
And with this unscrambled, it’s actually possible to do arbitrary arithmetic even on temperatures measured on any temperature scale—though the results also come back as absolute temperatures:
It’s worth understanding that an absolute temperature can be converted either to a temperature scale value, or a temperature scale difference:

All of this means that you can now use temperatures on any scale in formulas, and they’ll just work:

Dramatically Faster Polynomial Operations
Almost any algebraic computation ends up somehow involving polynomials. And polynomials have been a well-optimized part of Mathematica and the Wolfram Language since the beginning. And in fact, little has needed to be updated in the fundamental operations we do with them in more than a quarter of a century. But now in Version 13.2—thanks to new algorithms and new data structures, and new ways to use modern computer hardware—we’re updating some core polynomial operations, and making them dramatically faster. And, by the way, we’re getting some new polynomial functionality as well.
Here is a product of two polynomials, expanded out:

Factoring polynomials like this is pretty much instantaneous, and has been ever since Version 1:

But now let’s make this bigger:
There are 999 terms in the expanded polynomial:
Factoring this isn’t an easy computation, and in Version 13.1 takes about 19 seconds:

✕
|
But now, in Version 13.2, the same computation takes 0.3 seconds—nearly 60 times faster:
It’s pretty rare that anything gets 60x faster. But this is one of those cases, and in fact for still larger polynomials, the ratio will steadily increase further. But is this just something that’s only relevant for obscure, big polynomials? Well, no. Not least because it turns out that big polynomials show up “under the hood” in all sorts of important places. For example, the innocuous-seeming object

can be manipulated as an algebraic number, but with minimal polynomial:

In addition to factoring, Version 13.2 also dramatically increases the efficiency of polynomial resultants, GCDs, discriminants, etc. And all of this makes possible a transformative update to polynomial linear algebra, i.e. operations on matrices whose elements are (univariate) polynomials.
Here’s a matrix of polynomials:
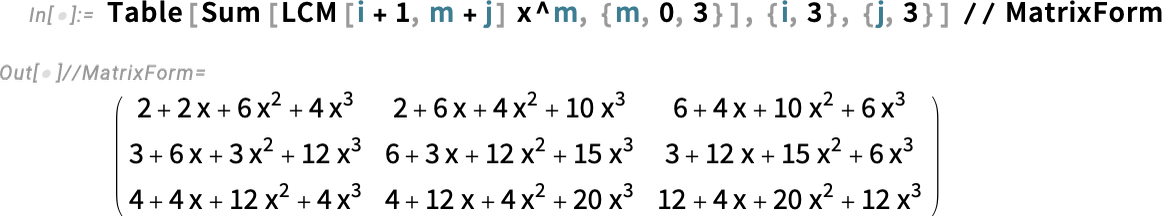
And here’s a power of the matrix:

And the determinant of this:
In Version 13.1 this didn’t look nearly as nice; the result comes out unexpanded as:
![]()

Both size and speed are dramatically improved in Version 13.2. Here’s a larger case—where in 13.1 the computation takes more than an hour, and the result has a staggering leaf count of 178 billion

✕
|
but in Version 13.2 it’s 13,000 times faster, and 60 million times smaller:

Polynomial linear algebra is used “under the hood” in a remarkable range of areas, particularly in handling linear differential equations, difference equations, and their symbolic solutions. And in Version 13.2, not only polynomial MatrixPower and Det, but also LinearSolve, Inverse, RowReduce, MatrixRank and NullSpace have been dramatically sped up.
In addition to the dramatic speed improvements, Version 13.2 also adds a polynomial feature for which I, for one, happen to have been waiting for more than 30 years: multivariate polynomial factoring over finite fields:

Indeed, looking in our archives I find many requests stretching back to at least 1990—from quite a range of people—for this capability, even though, charmingly, a 1991 internal note states:

✕
|
Yup, that was right. But 31 years later, in Version 13.2, it’s done!
Integrating External Neural Nets
The Wolfram Language has had integrated neural net technology since 2015. Sometimes this is automatically used inside other Wolfram Language functions, like ImageIdentify, SpeechRecognize or Classify. But you can also build your own neural nets using the symbolic specification language with functions like NetChain and NetGraph—and the Wolfram Neural Net Repository provides a continually updated source of neural nets that you can immediately use, and modify, in the Wolfram Language.
But what if there’s a neural net out there that you just want to run from within the Wolfram Language, but don’t need to have represented in modifiable (or trainable) symbolic Wolfram Language form—like you might run an external program executable? In Version 13.2 there’s a new construct NetExternalObject that allows you to run trained neural nets “from the wild” in the same integrated framework used for actual Wolfram-Language-specified neural nets.
NetExternalObject so far supports neural nets that have been defined in the ONNX neural net exchange format, which can easily be generated from frameworks like PyTorch, TensorFlow, Keras, etc. (as well as from Wolfram Language). One can get a NetExternalObject just by importing an .onnx file. Here’s an example from the web:

If we “open up” the summary for this object we see what basic tensor structure of input and output it deals with:

But to actually use this network we have to set up encoders and decoders suitable for the actual operation of this particular network—with the particular encoding of images that it expects:


Now we just have to run the encoder, the external network and the decoder—to get (in this case) a cartoonized Mount Rushmore:

Often the “wrapper code” for the NetExternalObject will be a bit more complicated than in this case. But the built-in NetEncoder and NetDecoder functions typically provide a very good start, and in general the symbolic structure of the Wolfram Language (and its integrated ability to represent images, video, audio, etc.) makes the process of importing typical neural nets “from the wild” surprisingly straightforward. And once imported, such neural nets can be used directly, or as components of other functions, anywhere in the Wolfram Language.
Displaying Large Trees, and Making More
We first introduced trees as a fundamental structure in Version 12.3, and we’ve been enhancing them ever since. In Version 13.1 we added many options for determining how trees are displayed, but in Version 13.2 we’re adding another, very important one: the ability to elide large subtrees.
Here’s a size-200 random tree with every branch shown:

And here’s the same tree with every node being told to display a maximum of 3 children:

And, actually, tree elision is convenient enough that in Version 13.2 we’re doing it by default for any node that has more than 10 children—and we’ve introduced the global $MaxDisplayedChildren to determine what that default limit should be.
Another new tree feature in Version 13.2 is the ability to create trees from your file system. Here’s a tree that goes down 3 directory levels from my Wolfram Desktop installation directory:

Calculus & Its Generalizations
Is there still more to do in calculus? Yes! Sometimes the goal is, for example, to solve more differential equations. And sometimes it’s to solve existing ones better. The point is that there may be many different possible forms that can be given for a symbolic solution. And often the forms that are easiest to generate aren’t the ones that are most useful or convenient for subsequent computation, or the easiest for a human to understand.
In Version 13.2 we’ve made dramatic progress in improving the form of solutions that we give for the most kinds of differential equations, and systems of differential equations.
Here’s an example. In Version 13.1 this is an equation we could solve symbolically, but the solution we give is long and complicated:

✕
|
But now, in 13.2, we immediately give a much more compact and useful form of the solution:

The simplification is often even more dramatic for systems of differential equations. And our new algorithms cover a full range of differential equations with constant coefficients—which are what go by the name LTI (linear time-invariant) systems in engineering, and are used quite universally to represent electrical, mechanical, chemical, etc. systems.
In addition to streamlining “everyday calculus”, we’re also pushing on some frontiers of calculus, like fractional calculus. In Version 13.1 we introduced symbolic fractional differentiation, with functions like FractionalD. In Version 13.2 we now also have numerical fractional differentiation, with functions like NFractionalD, here shown getting the ½th derivative of Sin[x]:

In Version 13.1 we introduced symbolic solutions of fractional differential equations with constant coefficients; now in Version 13.2 we’re extending this to asymptotic solutions of fractional differential equations with both constant and polynomial coefficients. Here’s an Airy-like differential equation, but generalized to the fractional case with a Caputo fractional derivative:

Analysis of Cluster Analysis
The Wolfram Language has had basic built-in support for cluster analysis since the mid-2000s. But in more recent times—with increased sophistication from machine learning—we’ve been adding more and more sophisticated forms of cluster analysis. But it’s one thing to do cluster analysis; it’s another to analyze the cluster analysis one’s done, to try to better understand what it means, how to optimize it, etc. In Version 13.2 we’re both adding the function ClusteringMeasurements to do this, as well as adding more options for cluster analysis, and enhancing the automation we have for method and parameter selection.
Let’s say we do cluster analysis on some data, asking for a sequence of different numbers of clusters:

Which is the “best” number of clusters? One measure of this is to compute the “silhouette score” for each possible clustering, and that’s something that ClusteringMeasurements can now do:

As is fairly typical in statistics-related areas, there are lots of different scores and criteria one can use—ClusteringMeasurements supports a wide variety of them.
Chess as Computable Data
Our goal with Wolfram Language is to make as much as possible computable. Version 13.2 adds yet another domain—chess—supporting import of the FEN and PGN chess formats:

PGN files typically contain many games, each represented as a list of FEN strings. This counts the number of games in a particular PGN file:
Here’s the first game in the file:

Given this, we can now use Wolfram Language’s video capabilities to make a video of the game:

Controlling Runaway Computations
Back in 1979 when I started building SMP—the forerunner to the Wolfram Language—I did something that to some people seemed very bold, perhaps even reckless: I set up the system to fundamentally do “infinite evaluation”, that is, to continue using whatever definitions had been given until nothing more could be done. In other words, the process of evaluation would always go on until a fixed point was reached. “But what happens if x doesn’t have a value, and you say
However, if you type x = x + 1 the system clearly has to do something. And in a sense the purest thing to do would just be to continue computing forever. But 34 years ago that led to a rather disastrous problem on actual computers—and in fact still does today. Because in general this kind of repeated evaluation is a recursive process, that ultimately has to be implemented using the call stack set up for every instance of a program by the operating system. But the way operating systems work (still!) is to allocate only a fixed amount of memory for the stack—and if this is overrun, the operating system will simply make your program crash (or, in earlier times, the operating system itself might crash). And this meant that ever since Version 1, we’ve needed to have a limit in place on infinite evaluation. In early versions we tried to give the “result of the computation so far”, wrapped in Hold. Back in Version 10, we started just returning a held version of the original expression:

But even this is in a sense not safe. Because with other infinite definitions in place, one can end up with a situation where even trying to return the held form triggers additional infinite computational processes.
In recent times, particularly with our exploration of multicomputation, we’ve decided to revisit the question of how to limit infinite computations. At some theoretical level, one might imagine explicitly representing infinite computations using things like transfinite numbers. But that’s fraught with difficulty, and manifest undecidability (“Is this infinite computation output really the same as that one?”, etc.) But in Version 13.2, as the beginning of a new, “purely symbolic” approach to “runaway computation” we’re introducing the construct TerminatedEvaluation—that just symbolically represents, as it says, a terminated computation.
So here’s what now happens with x = x + 1:

A notable feature of this is that it’s “independently encapsulated”: the termination of one part of a computation doesn’t affect others, so that, for example, we get:
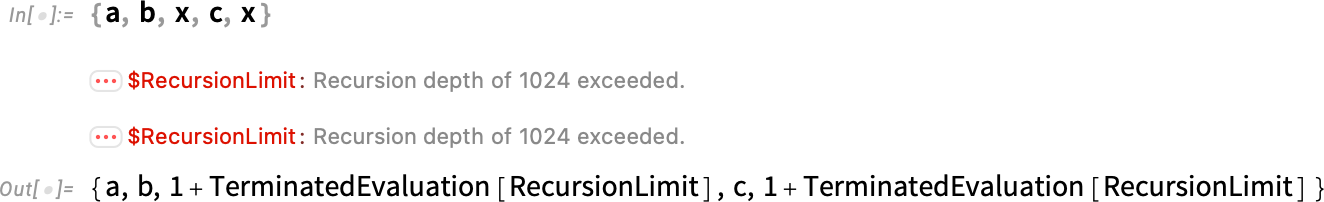
There’s a complicated relation between terminated evaluations and lazy evaluation, and we’re working on some interesting and potentially powerful new capabilities in this area. But for now, TerminatedEvaluation is an important construct for improving the “safety” of the system in the corner case of runaway computations. And introducing it has allowed us to fix what seemed for many years like “theoretically unfixable” issues around complex runaway computations.
TerminatedEvaluation is what you run into if you hit system-wide “guard rails” like $RecursionLimit. But in Version 13.2 we’ve also tightened up the handling of explicitly requested aborts—by adding the new option PropagateAborts to CheckAbort. Once an abort has been generated—either directly by using Abort[ ], or as the result of something like TimeConstrained[ ] or MemoryConstrained[ ]—there’s a question of how far that abort should propagate. By default, it’ll propagate all the way up, so your whole computation will end up being aborted. But ever since Version 2 (in 1991) we’ve had the function CheckAbort, which checks for aborts in the expression it’s given, then stops further propagation of the abort.
But there was always a lot of trickiness around the question of things like TimeConstrained[ ]. Should aborts generated by these be propagated the same way as Abort[ ] aborts or not? In Version 13.2 we’ve now cleaned all of this up, with an explicit option PropagateAborts for CheckAbort. With PropagateAborts→True all aborts are propagated, whether initiated by Abort[ ] or TimeConstrained[ ] or whatever. PropagateAborts→False propagates no aborts. But there’s also PropagateAborts→Automatic, which propagates aborts from TimeConstrained[ ] etc., but not from Abort[ ].
Yet Another Little List Function
In our never-ending process of extending and polishing the Wolfram Language we’re constantly on the lookout for “lumps of computational work” that people repeatedly want to do, and for which we can create functions with easy-to-understand names. These days we often prototype such functions in the Wolfram Function Repository, then further streamline their design, and eventually implement them in the permanent core Wolfram Language. In Version 13.2 just two new basic list-manipulation functions came out of this process: PositionLargest and PositionSmallest.
We’ve had the function Position since Version 1, as well as Max. But something I’ve often found myself needing to do over the years is to combine these to answer the question: “Where is the max of that list?” Of course it’s not hard to do this in the Wolfram Language—Position[list, Max[list]] basically does it. But there are some edge cases and extensions to think about, and it’s convenient just to have one function to do this. And, what’s more, now that we have functions like TakeLargest, there’s an obvious, consistent name for the function: PositionLargest. (And by “obvious”, I mean obvious after you hear it; the archive of our livestreamed design review meetings will reveal that—as is so often the case—it actually took us quite a while to settle on the “obvious”.)
Here’s PositionLargest and in action:
And, yes, it has to return a list, to deal with “ties”:
Graphics, Image, Graph, …? Tell It from the Frame Color
Everything in the Wolfram Language is a symbolic expression. But different symbolic expressions are displayed differently, which is, of course, very useful. So, for example, a graph isn’t displayed in the raw symbolic form
|
✕
|
but rather as a graph:

✕
|
But let’s say you’ve got a whole collection of visual objects in a notebook. How can you tell what they “really are”? Well, you can click them, and then see what color their borders are. It’s subtle, but I’ve found one quickly gets used to noticing at least the kinds of objects one commonly uses. And in Version 13.2 we’ve made some additional distinctions, notably between images and graphics.
So, yes, the object above is a Graph—and you can tell that because it has a purple border when you click it:

✕
|
This is a Graphics object, which you can tell because it’s got an orange border:

✕
|
And here, now, is an Image object, with a light blue border:

✕
|
For some things, color hints just don’t work, because people can’t remember which color means what. But for some reason, adding color borders to visual objects seems to work very well; it provides the right level of hinting, and the fact that one often sees the color when it’s obvious what the object is helps cement a memory of the color.
In case you’re wondering, there are some others already in use for borders—and more to come. Trees are green (though, yes, ours by default grow down). Meshes are brown:

✕
|
Brighter, Better Syntax Coloring
How do we make it as easy as possible to type correct Wolfram Language code? This is a question we’ve been working on for years, gradually inventing more and more mechanisms and solutions. In Version 13.2 we’ve made some small tweaks to a mechanism that’s actually been in the system for many years, but the changes we’ve made have a substantial effect on the experience of typing code.
One of the big challenges is that code is typed “linearly”—essentially (apart from 2D constructs) from left to right. But (just like in natural languages like English) the meaning is defined by a more hierarchical tree structure. And one of the issues is to know how something you typed fits into the tree structure.
Something like this is visually obvious quite locally in the “linear” code you typed. But sometimes what defines the tree structure is quite far away. For example, you might have a function with several arguments that are each large expressions. And when you’re looking at one of the arguments it may not be obvious what the overall function is. And part of what we’re now emphasizing more strongly in Version 13.2 is dynamic highlighting that shows you “what function you’re in”.
It’s highlighting that appears when you click. So, for example, this is the highlighting you get clicking at several different positions in a simple expression:

Here’s an example “from the wild” showing you that if you type at the position of the cursor, you’ll be adding an argument to the ContourPlot function:

✕
|
But now let’s click in a different place:

✕
|
Here’s a smaller example:
|
✕
|
Notice that we’re highlighting both the enclosing grouping {…} and the enclosing function head.
We’ve had the basic capability for this kind of highlighting for nearly a decade. But in Version 13.2 we’re making it much bolder, and we’ve subtly tweaked what highlighting shows up when. This may seem like a detail, but I, for example, have found it quite transformative in the way that I actually type code.
In the past I often found myself multiclicking to figure out the structure of the code. But now I just have to click and the highlighting is bright enough to be immediately obvious, even if it’s quite far away in the linear rendering of the code.
It’s also important that the highlighting colors for function heads and for grouping constructs are now much more distinct. In the past, they were both shades of green, which were hard to distinguish and understand. With the Version 13.2 colors one quickly gets used to how things are set up, and it’s easy to get a sense of the structure of an expression. And having these two colors (as opposed to more, or fewer) seems to be about right in terms of giving information, but not giving so much that it’s hard to assimilate.
User Interface Conveniences
We first introduced the notebook interface in Version 1 back in 1988. And already in that version we had many of the current features of notebooks—like cells and cell groups, cell styles, etc. But over the past 34 years we’ve been continuing to tweak and polish the notebook interface to make it ever smoother to use.
In Version 13.2 we have some minor but convenient additions. We’ve had the Divide Cell menu item (cmdshiftD) for more than 30 years. And the way it’s always worked is that you click where you want a cell to be divided. Meanwhile, we’ve always had the ability to put multiple Wolfram Language inputs into a single cell. And while sometimes it’s convenient to type code that way, or import it from elsewhere like that, it makes better use of all our notebook and cell capabilities if each independent input is in its own cell. And now in Version 13.2 Divide Cell can make it like that, analyzing multiline inputs to divide them between complete inputs that occur on different lines:

✕
|
Similarly, if you’re dealing with text instead of code, Divide Cell will now divide at explicit line breaks—that might correspond to paragraphs.
In a completely different area, Version 13.1 added a new default toolbar for notebooks, and in Version 13.2 we’re beginning the process of steadily adding features to this toolbar. The main obvious feature that’s been added is a new interactive tool for changing frames in cells. It’s part of the Cell Appearance item in the toolbar:

✕
|
Just click a side of the frame style widget and you’ll get a tool to edit that frame style—and you’ll immediately see any changes reflected in the notebook:

✕
|
If you want to edit all the sides, you can lock the settings together with:
|
✕
|
Cell frames have always been a useful mechanism for delineating, highlighting or otherwise annotating cells in notebooks. But in the past it’s been comparatively difficult to customize them beyond what’s in the stylesheet you’re using. With the new toolbar feature in Version 13.2 we’ve made it very easy to work with cell frames, making it realistic for custom cell frames to become a routine part of notebook content.
Mixing Compiled and Evaluated Code
We’ve worked hard to have code you write in the Wolfram Language immediately run efficiently. But by taking the extra one-time effort to invoke the Wolfram Language compiler—telling it more details about how you expect to use your code— you can often make your code run more efficiently, and sometimes dramatically so. In Version 13.2 we’ve been continuing the process of streamlining the workflow for using the compiler, and for unifying code that’s set up for compilation, and code that’s not.
The primary work you have to do in order to make the best use of the Wolfram Language compiler is in specifying types. One of the important features of the Wolfram Language in general is that a symbol x can just as well be an integer, a list of complex numbers or a symbolic representation of a graph. But the main way the compiler adds efficiency is by being able to assume that x is, say, always going to be an integer that fits into a 64-bit computer word.
The Wolfram Language compiler has a sophisticated symbolic language for specifying types. Thus, for example
is a symbolic specification for the type of a function that takes two 64-bit integers as input, and returns a single one. TypeSpecifier[ ... ] is a symbolic construct that doesn’t evaluate on its own, and can be used and manipulated symbolically. And it’s the same story with Typed[ ... ], which allows you to annotate an expression to say what type it should be assumed to be.
But what if you want to write code which can either be evaluated in the ordinary way, or fed to the compiler? Constructs like Typed[ ... ] are for permanent annotation. In Version 13.2 we’ve added TypeHint which allows you to give a hint that can be used by the compiler, but will be ignored in ordinary evaluation.
This compiles a function assuming that its argument x is an 8-bit integer:

By default, the 100 here is assumed to be represented as a 64-bit integer. But with a type hint, we can say that it too should be represented as an 8-bit integer:

150 doesn’t fit in an 8-bit integer, so the compiled code can’t be used:

But what’s relevant here is that the function we compiled can be used not only for compilation, but also in ordinary evaluation, where the TypeHint effectively just “evaporates”:
As the compiler develops, it’s going to be able to do more and more type inferencing on its own. But it’ll always be able to get further if the user gives it some hints. For example, if x is a 64-bit integer, what type should be assumed for xx? There are certainly values of x for which xx won’t fit in a 64-bit integer. But the user might know those won’t show up. And so they can give a type hint that says that the xx should be assumed to fit in a 64-bit integer, and this will allow the compiler to do much more with it.
It’s worth pointing out that there are always going to be limitations to type inferencing, because, in a sense, inferring types requires proving theorems, and there can be theorems that have arbitrarily long proofs, or no proofs at all in a certain axiomatic system. For example, imagine asking whether the type of a zero of the Riemann zeta function has a certain imaginary part. To answer this, the type inferencer would have to solve the Riemann hypothesis. But if the user just wanted to assume the Riemann hypothesis, they could—at least in principle—use TypeHint.
TypeHint is a wrapper that means something to the compiler, but “evaporates” in ordinary evaluation. Version 13.2 adds IfCompiled, which lets you explicitly delineate code that should be used with the compiler, and code that should be used in ordinary evaluation. This is useful when, for example, ordinary evaluation can use a sophisticated built-in Wolfram Language function, but compiled code will be more efficient if it effectively builds up similar functionality from lower-level primitives.
In its simplest form FunctionCompile lets you take an explicit pure function and make a compiled version of it. But what if you have a function where you’ve already assigned downvalues to it, like:
Now in Version 13.2 you can use the new DownValuesFunction wrapper to give a function like this to FunctionCompile:
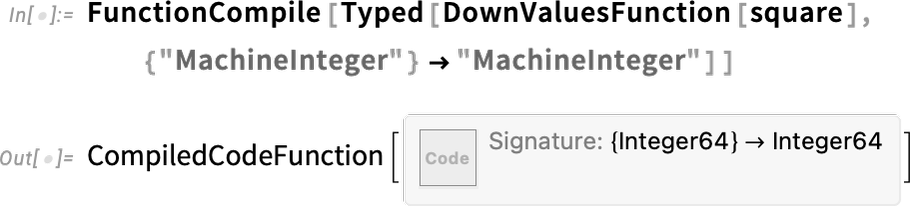
This is important because it lets you set up a whole network of definitions using := etc., then have them automatically be fed to the compiler. In general, you can use DownValuesFunction as a wrapper to tag any use of a function you’ve defined elsewhere. It’s somewhat analogous to the KernelFunction wrapper that you can use to tag built-in functions, and specify what types you want to assume for them in code that you’re feeding to the compiler.
Packaging Large-Scale Compiled Code
Let’s say you’re building a substantial piece of functionality that might include compiled Wolfram Language code, external libraries, etc. In Version 13.2 we’ve added capabilities to make it easy to “package up” such functionality, and for example deploy it as a distributable paclet.
As an example of what can be done, this installs a paclet called GEOSLink that includes the GEOS external library and compiler-based functionality to access this:

Now that the paclet is installed, we can use a file from it to set up a whole collection of functions that are defined in the paclet:
Given the code in the paclet we can now just start calling functions that use the GEOS library:
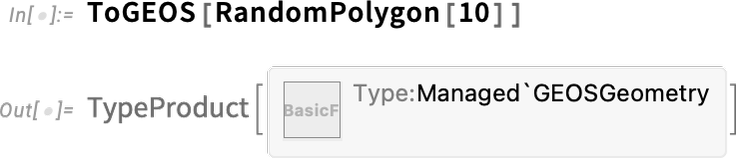
It’s quite nontrivial that this “just works”. Because for it to work, the system has to have been told to load and initialize the GEOS library, as well as convert the Wolfram Language polygon geometry to a form suitable for GEOS. The returned result is also nontrivial: it’s essentially a handle to data that’s inside the GEOS library, but being memory-managed by the Wolfram Language system. Now we can take this result, and call a GEOS library function on it, using the Wolfram Language binding that’s been defined for that function:
This gets the result “back from GEOS” into pure Wolfram Language form:

How does all this work? This goes to the directory for the installed GEOSLink paclet on my system:

✕
|
There’s a subdirectory called LibraryResources that contains dynamic libraries suitable for my computer system:

✕
|
The libgeos libraries are the raw external GEOS libraries “from the wild”. The GEOSLink library is a library that was built by the Wolfram Language compiler from Wolfram Language code that defines the “glue” for interfacing between the GEOS library and the Wolfram Language:

✕
|
What is all this? It’s all based on new functionality in Version 13.2. And ultimately what it’s doing is to create a CompiledComponent construct (which is a new thing in Version 13.2). A CompiledComponent construct represents a bundle of compilable functionality with elements like "Declarations", "InstalledFunctions", "LibraryFunctions", "LoadingEpilogs" and "ExternalLibraries". And in a typical case—like the one shown here—one creates (or adds to) a CompiledComponent using DeclareCompiledComponent.
Here’s an example of part of what’s added by DeclareCompiledComponent:

✕
|
First there’s a declaration of an external (in this case GEOS) library function, giving its type signature. Then there’s a declaration of a compilable Wolfram Language function GEOSUnion that directly calls the GEOSUnion function in the external library, defining it to take a certain memory-managed data structure as input, and return a similarly memory-managed object as output.
From this source code, all you do to build an actual library is use BuildCompiledComponent. And given this library you can start calling external GEOS functions directly from top-level Wolfram Language code, as we did above.
But the CompiledComponent object does something else as well. It also sets up everything you need to be able to write compilable code that calls the same functions as you can within the built library.
The bottom line is that with all the new functionality in Version 13.2 it’s become dramatically easier to integrate compiled code, external libraries etc. and to make them conveniently distributable. It’s a fairly remarkable simplification of what was previously a time-consuming and complex software engineering challenge. And it’s good example of how powerful it can be to set up symbolic specifications in the Wolfram Language and then use our compiler technology to automatically create and deploy code defined by them.
And More…
In addition to all the things we’ve discussed, there are other updates and enhancements that have arrived in the six months since Version 13.1 was released. A notable example is that there have been no fewer than 241 new functions added to the Wolfram Function Repository during that time, providing specific add-on functionality in a whole range of areas:
But within the core Wolfram Language itself, Version 13.2 also adds lots of little new capabilities, that polish and round out existing functionality. Here are some examples:
Parallelize now supports automatic parallelization of a variety of new functions, particularly related to associations.
Blurring now joins DropShadowing as a 2D graphics effect.
MeshRegion, etc. can now store vertex coloring and vertex normals to allow enhanced visualization of regions.
RandomInstance does much better at quickly finding non-degenerate examples of geometric scenes that satisfy specified constraints.
ImageStitch now supports stitching images onto spherical and cylindrical canvases.
Functions like Definition and Clear that operate on symbols now consistently handle lists and string patterns.
FindShortestTour has a direct way to return individual features of the result, rather than always packaging them together in a list.
PersistentSymbol and LocalSymbol now allow reassignment of parts using functions like AppendTo.
SystemModelMeasurements now gives diagnostics such as rise time and overshoot for SystemModel control systems.
Import of OSM (OpenStreetMap) and GXF geo formats are now supported.




