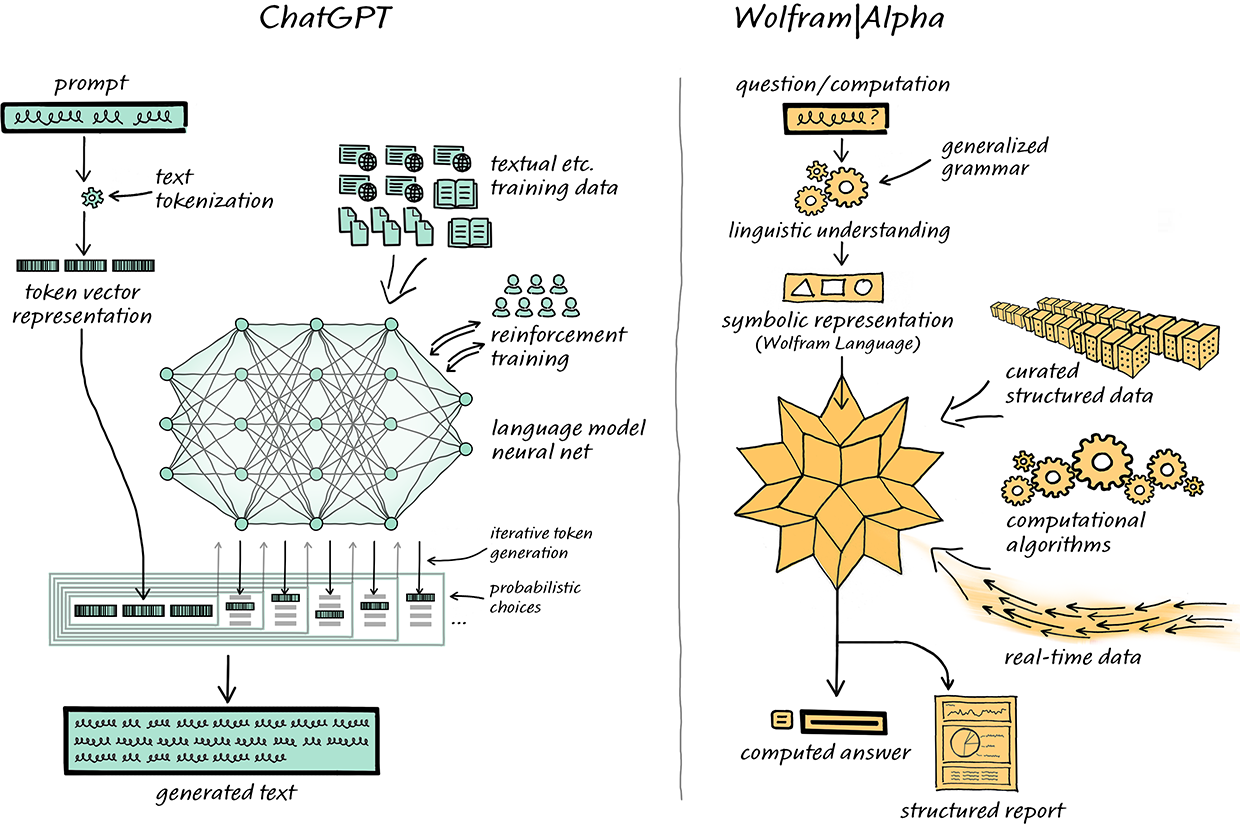
It’s Just Adding One Word at a Time
That ChatGPT can automatically generate something that reads even superficially like human-written text is remarkable, and unexpected. But how does it do it? And why does it work? My purpose here is to give a rough outline of what’s going on inside ChatGPT—and then to explore why it is that it can do so well in producing what we might consider to be meaningful text. I should say at the outset that I’m going to focus on the big picture of what’s going on—and while I’ll mention some engineering details, I won’t get deeply into them. (And the essence of what I’ll say applies just as well to other current “large language models” [LLMs] as to ChatGPT.)
The first thing to explain is that what ChatGPT is always fundamentally trying to do is to produce a “reasonable continuation” of whatever text it’s got so far, where by “reasonable” we mean “what one might expect someone to write after seeing what people have written on billions of webpages, etc.” Continue reading