Version 14.0 of Wolfram Language and Mathematica is available immediately both on the desktop and in the cloud. See also more detailed information on Version 13.1, Version 13.2 and Version 13.3.
Building Something Greater and Greater… for 35 Years and Counting
Today we celebrate a new waypoint on our journey of nearly four decades with the release of Version 14.0 of Wolfram Language and Mathematica. Over the two years since we released Version 13.0 we’ve been steadily delivering the fruits of our research and development in .1 releases every six months. Today we’re aggregating these—and more—into Version 14.0.
It’s been more than 35 years now since we released Version 1.0. And all those years we’ve been continuing to build a taller and taller tower of capabilities, progressively expanding the scope of our vision and the breadth of our computational coverage of the world:

Version 1.0 had 554 built-in functions; in Version 14.0 there are 6602. And behind each of those functions is a story. Sometimes it’s a story of creating a superalgorithm that encapsulates decades of algorithmic development. Sometimes it’s a story of painstakingly curating data that’s never been assembled before. Sometimes it’s a story of drilling down to the essence of something to invent new approaches and new functions that can capture it.
And from all these pieces we’ve been steadily building the coherent whole that is today’s Wolfram Language. In the arc of intellectual history it defines a broad, new, computational paradigm for formalizing the world. And at a practical level it provides a superpower for implementing computational thinking—and enabling “computational X” for all fields X.
To us it’s profoundly satisfying to see what has been done over the past three decades with everything we’ve built so far. So many discoveries, so many inventions, so much achieved, so much learned. And seeing this helps drive forward our efforts to tackle still more, and to continue to push every boundary we can with our R&D, and to deliver the results in new versions of our system.
Our R&D portfolio is broad. From projects that get completed within months of their conception, to projects that rely on years (and sometimes even decades) of systematic development. And key to everything we do is leveraging what we have already done—often taking what in earlier years was a pinnacle of technical achievement, and now using it as a routine building block to reach a level that could barely even be imagined before. And beyond practical technology, we’re also continually going further and further in leveraging what’s now the vast conceptual framework that we’ve been building all these years—and progressively encapsulating it in the design of the Wolfram Language.
We’ve worked hard all these years not only to create ideas and technology, but also to craft a practical and sustainable ecosystem in which we can systematically do this now and into the long-term future. And we continue to innovate in these areas, broadening the delivery of what we’ve built in new and different ways, and through new and different channels. And in the past five years we’ve also been able to open up our core design process to the world—regularly livestreaming what we’re doing in a uniquely open way.
And indeed over the past several years the seeds of essentially everything we’re delivering today in Version 14.0 has been openly shared with the world, and represents an achievement not only for our internal teams but also for the many people who have participated in and commented on our livestreams.
Part of what Version 14.0 is about is continuing to expand the domain of our computational language, and our computational formalization of the world. But Version 14.0 is also about streamlining and polishing the functionality we’ve already defined. Throughout the system there are things we’ve made more efficient, more robust and more convenient. And, yes, in complex software, bugs of many kinds are a theoretical and practical inevitability. And in Version 14.0 we’ve fixed nearly 10,000 bugs, the majority found by our increasingly sophisticated internal software testing methods.
Now We Need to Tell the World
Even after all the work we’ve put into the Wolfram Language over the past several decades, there’s still yet another challenge: how to let people know just what the Wolfram Language can do. Back when we released Version 1.0 I was able to write a book of manageable size that could pretty much explain the whole system. But for Version 14.0—with all the functionality it contains—one would need a book with perhaps 200,000 pages.
And at this point nobody (even me!) immediately knows everything the Wolfram Language does. Of course one of our great achievements has been to maintain across all that functionality a tightly coherent and consistent design that results in there ultimately being only a small set of fundamental principles to learn. But at the vast scale of the Wolfram Language as it exists today, knowing what’s possible—and what can now be formulated in computational terms—is inevitably very challenging. And all too often when I show people what’s possible, I’ll get the response “I had no idea the Wolfram Language could do that!”
So in the past few years we’ve put increasing emphasis into building large-scale mechanisms to explain the Wolfram Language to people. It begins at a very fine-grained level, with “just-in-time information” provided, for example, through suggestions made when you type. Then for each function (or other construct in the language) there are pages that explain the function, with extensive examples. And now, increasingly, we’re adding “just-in-time learning material” that leverages the concreteness of the functions to provide self-contained explanations of the broader context of what they do.
By the way, in modern times we need to explain the Wolfram Language not just to humans, but also to AIs—and our very extensive documentation and examples have proved extremely valuable in training LLMs to use the Wolfram Language. And for AIs we’re providing a variety of tools—like immediate computable access to documentation, and computable error handling. And with our Chat Notebook technology there’s also a new “on ramp” for creating Wolfram Language code from linguistic (or visual, etc.) input.
But what about the bigger picture of the Wolfram Language? For both people and AIs it’s important to be able to explain things at a higher level, and we’ve been doing more and more in this direction. For more than 30 years we’ve had “guide pages” that summarize specific functionality in particular areas. Now we’re adding “core area pages” that give a broader picture of large areas of functionality—each one in effect covering what might otherwise be a whole product on its own, if it wasn’t just an integrated part of the Wolfram Language:

But we’re going even much further, building whole courses and books that provide modern hands-on Wolfram-Language-enabled introductions to a broad range of areas. We’ve now covered the material of many standard college courses (and quite a lot besides), in a new and very effective “computational” way, that allows immediate, practical engagement with concepts:

All these courses involve not only lectures and notebooks but also auto-graded exercises, as well as official certifications. And we have a regular calendar of everyone-gets-together-at-the-same-time instructor-led peer Study Groups about these courses. And, yes, our Wolfram U operation is now emerging as a significant educational entity, with many thousands of students at any given time.
In addition to whole courses, we have “miniseries” of lectures about specific topics:
And we also have courses—and books—about the Wolfram Language itself, like my Elementary Introduction to the Wolfram Language, which came out in a third edition this year (and has an associated course, online version, etc.):
In a somewhat different direction, we’ve expanded our Wolfram Summer School to add a Wolfram Winter School, and we’ve greatly expanded our Wolfram High School Summer Research Program, adding year-round programs, middle-school programs, etc.—including the new “Computational Adventures” weekly activity program.
And then there’s livestreaming. We’ve been doing weekly “R&D livestreams” with our development team (and sometimes also external guests). And I myself have also been doing a lot of livestreaming (232 hours of it in 2023 alone)—some of it design reviews of Wolfram Language functionality, and some of it answering questions, technical and other.
The list of ways we’re getting the word out about the Wolfram Language goes on. There’s Wolfram Community, that’s full of interesting contributions, and has ever-increasing readership. There are sites like Wolfram Challenges. There are our Wolfram Technology Conferences. And lots more.
We’ve put immense effort into building the whole Wolfram technology stack over the past four decades. And even as we continue to aggressively build it, we’re putting more and more effort into telling the world about just what’s in it, and helping people (and AIs) to make the most effective use of it. But in a sense, everything we’re doing is just a seed for what the wider community of Wolfram Language users are doing, and can do. Spreading the power of the Wolfram Language to more and more people and areas.
The LLMs Have Landed
The machine learning superfunctions Classify and Predict first appeared in Wolfram Language in 2014 (Version 10). By the next year there were starting to be functions like ImageIdentify and LanguageIdentify, and within a couple of years we’d introduced our whole neural net framework and Neural Net Repository. Included in that were a variety of neural nets for language modeling, that allowed us to build out functions like SpeechRecognize and an experimental version of FindTextualAnswer. But—like everyone else—we were taken by surprise at the end of 2022 by ChatGPT and its remarkable capabilities.
Very quickly we realized that a major new use case—and market—had arrived for Wolfram|Alpha and Wolfram Language. For now it was not only humans who’d need the tools we’d built; it was also AIs. By March 2023 we’d worked with OpenAI to use our Wolfram Cloud technology to deliver a plugin to ChatGPT that allows it to call Wolfram|Alpha and Wolfram Language. LLMs like ChatGPT provide remarkable new capabilities in reproducing human language, basic human thinking and general commonsense knowledge. But—like unaided humans—they’re not set up to deal with detailed computation or precise knowledge. For that, like humans, they have to use formalism and tools. And the remarkable thing is that the formalism and tools we’ve built in Wolfram Language (and Wolfram|Alpha) are basically a broad, perfect fit for what they need.
We created the Wolfram Language to provide a bridge from what humans think about to what computation can express and implement. And now that’s what the AIs can use as well. The Wolfram Language provides a medium not only for humans to “think computationally” but also for AIs to do so. And we’ve been steadily doing the engineering to let AIs call on Wolfram Language as easily as possible.
But in addition to LLMs using Wolfram Language, there’s also now the possibility of Wolfram Language using LLMs. And already in June 2023 (Version 13.3) we released a major collection of LLM-based capabilities in Wolfram Language. One category is LLM functions, that effectively use LLMs as “internal algorithms” for operations in Wolfram Language:
In typical Wolfram Language fashion, we have a symbolic representation for LLMs: LLMConfiguration[…] represents an LLM with its various parameters, promptings, etc. And in the past few months we’ve been steadily adding connections to the full range of popular LLMs, making Wolfram Language a unique hub not only for LLM usage, but also for studying the performance—and science—of LLMs.
You can define your own LLM functions in Wolfram Language. But there’s also the Wolfram Prompt Repository that plays a similar role for LLM functions as the Wolfram Function Repository does for ordinary Wolfram Language functions. There’s a public Prompt Repository that so far has several hundred curated prompts. But it’s also possible for anyone to post their prompts in the Wolfram Cloud and make them publicly (or privately) accessible. The prompts can define personas (“talk like a [stereotypical] pirate”). They can define AI-oriented functions (“write it with emoji”). And they can define modifiers that affect the form of output (“haiku style”).
In addition to calling LLMs “programmatically” within Wolfram Language, there’s the new concept (first introduced in Version 13.3) of “Chat Notebooks”. Chat Notebooks represent a new kind of user interface, that combines the graphical, computational and document features of traditional Wolfram Notebooks with the new linguistic interface capabilities brought to us by LLMs.
The basic idea of a Chat Notebook—as introduced in Version 13.3, and now extended in Version 14.0—is that you can have “chat cells” (requested by typing ‘) whose content gets sent not to the Wolfram kernel, but instead to an LLM:

You can use “function prompts”—say from the Wolfram Prompt Repository—directly in a Chat Notebook:

And as of Version 14.0 you can also knit Wolfram Language computations directly into your “conversation” with the LLM:

(You type \ to insert Wolfram Language, very much like the way you can use <* … *> to insert Wolfram Language into external evaluation cells.)
One thing about Chat Notebooks is that—as their name suggests—they really are centered around “chatting”, and around having a sequential interaction with an LLM. In an ordinary notebook, it doesn’t matter where in the notebook each Wolfram Language evaluation is requested; all that’s relevant is the order in which the Wolfram kernel does the evaluations. But in a Chat Notebook the “LLM evaluations” are always part of a “chat” that’s explicitly laid out in the notebook.
A key part of Chat Notebooks is the concept of a chat block: type ~ and you get a separator in the notebook that “starts a new chat”:

Chat Notebooks—with all their typical Wolfram Notebook editing, structuring, automation, etc. capabilities—are very powerful just as “LLM interfaces”. But there’s another dimension as well, enabled by LLMs being able to call Wolfram Language as a tool.
At one level, Chat Notebooks provide an “on ramp” for using Wolfram Language. Wolfram|Alpha—and even more so, Wolfram|Alpha Notebook Edition—let you ask questions in natural language, then have the questions translated into Wolfram Language, and answers computed. But in Chat Notebooks you can go beyond asking specific questions. Instead, through the LLM, you can just “start chatting” about what you want to do, then have Wolfram Language code generated, and executed:

The workflow is typically as follows. First, you have to conceptualize in computational terms what you want. (And, yes, that step requires computational thinking—which is a very important skill that too few people have so far learned.) Then you tell the LLM what you want, and it’ll try to write Wolfram Language code to achieve it. It’ll typically run the code for you (but you can also always do it yourself)—and you can see whether you got what you wanted. But what’s crucial is that Wolfram Language is intended to be read not only by computers but also by humans. And particularly since LLMs actually usually seem to manage to write pretty good Wolfram Language code, you can expect to read what they wrote, and see if it’s what you wanted. If it is, you can take that code, and use it as a “solid building block” for whatever larger system you might be trying to set up. Otherwise, you can either fix it yourself, or try chatting with the LLM to get it to do it.
One of the things we see in the example above is the LLM—within the Chat Notebook—making a “tool call”, here to a Wolfram Language evaluator. In the Wolfram Language there’s now a whole mechanism for defining tools for LLMs—with each tool being represented by an LLMTool symbolic object. In Version 14.0 there’s an experimental version of the new Wolfram LLM Tool Repository with some predefined tools:
In a default Chat Notebook, the LLM has access to some default tools, which include not only the Wolfram Language evaluator, but also things like Wolfram documentation search and Wolfram|Alpha query. And it’s common to see the LLM go back and forth trying to write “code that works”, and for example sometimes having to “resort” (much like humans do) to reading the documentation.
Something that’s new in Version 14.0 is experimental access to multimodal LLMs that can take images as well as text as input. And when this capability is enabled, it allows the LLM to “look at pictures from the code it generated”, see if they’re what was asked for, and potentially correct itself:

The deep integration of images into Wolfram Language—and Wolfram Notebooks—yields all sorts of possibilities for multimodal LLMs. Here we’re giving a plot as an image and asking the LLM how to reproduce it:

Another direction for multimodal LLMs is to take data (in the hundreds of formats accepted by Wolfram Language) and use the LLM to guide its visualization and analysis in the Wolfram Language. Here’s an example that starts from a file data.csv in the current directory on your computer:

One thing that’s very nice about using Wolfram Language directly is that everything you do (well, unless you use RandomInteger, etc.) is completely reproducible; do the same computation twice and you’ll get the same result. That’s not true with LLMs (at least right now). And so when one uses LLMs it feels like something more ephemeral and fleeting than using Wolfram Language. One has to grab any good results one gets—because one might never be able to reproduce them. Yes, it’s very helpful that one can store everything in a Chat Notebook, even if one can’t rerun it and get the same results. But the more “permanent” use of LLM results tends to be “offline”. Use an LLM “up front” to figure something out, then just use the result it gave.
One unexpected application of LLMs for us has been in suggesting names of functions. With the LLM’s “experience” of what people talk about, it’s in a good position to suggest functions that people might find useful. And, yes, when it writes code it has a habit of hallucinating such functions. But in Version 14.0 we’ve actually added one function—DigitSum—that was suggested to us by LLMs. And in a similar vein, we can expect LLMs to be useful in making connections to external databases, functions, etc. The LLM “reads the documentation”, and tries to write Wolfram Language “glue” code—which then can be reviewed, checked, etc., and if it’s right, can be used henceforth.
Then there’s data curation, which is a field that—through Wolfram|Alpha and many of our other efforts—we’ve become extremely expert at over the past couple of decades. How much can LLMs help with that? They certainly don’t “solve the whole problem”, but integrating them with the tools we already have has allowed us over the past year to speed up some of our data curation pipelines by factors of two or more.
If we look at the whole stack of technology and content that’s in the modern Wolfram Language, the overwhelming majority of it isn’t helped by LLMs, and isn’t likely to be. But there are many—sometimes unexpected—corners where LLMs can dramatically improve heuristics or otherwise solve problems. And in Version 14.0 there are starting to be a wide variety of “LLM inside” functions.
An example is TextSummarize, which is a function we’ve considered adding for many versions—but now, thanks to LLMs, can finally implement to a useful level:

The main LLMs that we’re using right now are based on external services. But we’re building capabilities to allow us to run LLMs in local Wolfram Language installations as soon as that’s technically feasible. And one capability that’s actually part of our mainline machine learning effort is NetExternalObject—a way of representing symbolically an externally defined neural net that can be run inside Wolfram Language. NetExternalObject allows you, for example, to take any network in ONNX form and effectively treat it as a component in a Wolfram Language neural net. Here’s a network for image depth estimation—that we’re here importing from an external repository (though in this case there’s actually a similar network already in the Wolfram Neural Net Repository):

Now we can apply this imported network to an image that’s been encoded with our built-in image encoder—then we’re taking the result and visualizing it:

It’s often very convenient to be able to run networks locally, but it can sometimes take quite high-end hardware to do so. For example, there’s now a function in the Wolfram Function Repository that does image synthesis entirely locally—but to run it, you do need a GPU with at least 8 GB of VRAM:

By the way, based on LLM principles (and ideas like transformers) there’ve been other related advances in machine learning that have been strengthening a whole range of Wolfram Language areas—with one example being image segmentation, where ImageSegmentationComponents now provides robust “content-sensitive” segmentation:

Still Going Strong on Calculus
When Mathematica 1.0 was released in 1988, it was a “wow” that, yes, now one could routinely do integrals symbolically by computer. And it wasn’t long before we got to the point—first with indefinite integrals, and later with definite integrals—where what’s now the Wolfram Language could do integrals better than any human. So did that mean we were “finished” with calculus? Well, no. First there were differential equations, and partial differential equations. And it took a decade to get symbolic ODEs to a beyond-human level. And with symbolic PDEs it took until just a few years ago. Somewhere along the way we built out discrete calculus, asymptotic expansions and integral transforms. And we also implemented lots of specific features needed for applications like statistics, probability, signal processing and control theory. But even now there are still frontiers.
And in Version 14 there are significant advances around calculus. One category concerns the structure of answers. Yes, one can have a formula that correctly represents the solution to a differential equation. But is it in the best, simplest or most useful form? Well, in Version 14 we’ve worked hard to make sure it is—often dramatically reducing the size of expressions that get generated.
Another advance has to do with expanding the range of “pre-packaged” calculus operations. We’ve been able to do derivatives ever since Version 1.0. But in Version 14 we’ve added implicit differentiation. And, yes, one can give a basic definition for this easily enough using ordinary differentiation and equation solving. But by adding an explicit ImplicitD we’re packaging all that up—and handling the tricky corner cases—so that it becomes routine to use implicit differentiation wherever you want:

Another category of pre-packaged calculus operations new in Version 14 are ones for vector-based integration. These were always possible to do in a “do-it-yourself” mode. But in Version 14 they are now streamlined built-in functions—that, by the way, also cover corner cases, etc. And what made them possible is actually a development in another area: our decade-long project to add geometric computation to Wolfram Language—which gave us a natural way to describe geometric constructs such as curves and surfaces:

Related functionality new in Version 14 is ContourIntegrate:

Functions like ContourIntegrate just “get the answer”. But if one’s learning or exploring calculus it’s often also useful to be able to do things in a more step-by-step way. In Version 14 you can start with an inactive integral

and explicitly do operations like changing variables:

Sometimes actual answers get expressed in inactive form, particularly as infinite sums:

And now in Version 14 the function TruncateSum lets you take such a sum and generate a truncated “approximation”:

Functions like D and Integrate—as well as LineIntegrate and SurfaceIntegrate—are, in a sense, “classic calculus”, taught and used for more than three centuries. But in Version 14 we also support what we can think of as “emerging” calculus operations, like fractional differentiation:

Core Language
What are the primitives from which we can best build our conception of computation? That’s at some level the question I’ve been asking for more than four decades, and what’s determined the functions and structures at the core of the Wolfram Language.
And as the years go by, and we see more and more of what’s possible, we recognize and invent new primitives that will be useful. And, yes, the world—and the ways people interact with computers—change too, opening up new possibilities and bringing new understanding of things. Oh, and this year there are LLMs which can “get the intellectual sense of the world” and suggest new functions that can fit into the framework we’ve created with the Wolfram Language. (And, by the way, there’ve also been lots of great suggestions made by the audiences of our design review livestreams.)
One new construct added in Version 13.1—and that I personally have found very useful—is Threaded. When a function is listable—as Plus is—the top levels of lists get combined:
But sometimes you want one list to be “threaded into” the other at the lowest level, not the highest. And now there’s a way to specify that, using Threaded:
In a sense, Threaded is part of a new wave of symbolic constructs that have “ambient effects” on lists. One very simple example (introduced in 2015) is Nothing:
Another, introduced in 2020, is Splice:
An old chestnut of Wolfram Language design concerns the way infinite evaluation loops are handled. And in Version 13.2 we introduced the symbolic construct TerminatedEvaluation to provide better definition of how out-of-control evaluations have been terminated:

In a curious connection, in the computational representation of physics in our recent Physics Project, the direct analog of nonterminating evaluations are what make possible the seemingly unending universe in which we live.
But what is actually going on “inside an evaluation”, terminating or not? I’ve always wanted a good representation of this. And in fact back in Version 2.0 we introduced Trace for this purpose:
But just how much detail of what the evaluator does should one show? Back in Version 2.0 we introduced the option TraceOriginal that traces every path followed by the evaluator:
But often this is way too much. And in Version 14.0 we’ve introduced the new setting TraceOriginal→Automatic, which doesn’t include in its output evaluations that don’t do anything:
This may seem pedantic, but when one has an expression of any substantial size, it’s a crucial piece of pruning. So, for example, here’s a graphical representation of a simple arithmetic evaluation, with TraceOriginal→True:

And here’s the corresponding “pruned” version, with TraceOriginal→Automatic:

(And, yes, the structures of these graphs are closely related to things like the causal graphs we construct in our Physics Project.)
In the effort to add computational primitives to the Wolfram Language, two new entrants in Version 14.0 are Comap and ComapApply. The function Map takes a function f and “maps it” over a list:
Comap does the “mathematically co-” version of this, taking a list of functions and “comapping” them onto a single argument:
Why is this useful? As an example, one might want to apply three different statistical functions to a single list. And now it’s easy to do that, using Comap:

By the way, as with Map, there’s also an operator form for Comap:

Comap works well when the functions it’s dealing with take just one argument. If one has functions that take multiple arguments, ComapApply is what one typically wants:
Talking of “co-like” functions, a new function added in Version 13.2 is PositionSmallest. Min gives the smallest element in a list; PositionSmallest instead says where the smallest elements are:
One of the important objectives in the Wolfram Language is to have as much as possible “just work”. When we released Version 1.0 strings could be assumed just to contain ordinary ASCII characters, or perhaps to have an external character encoding defined. And, yes, it could be messy not to know “within the string itself” what characters were supposed to be there. And by the time of Version 3.0 in 1996 we’d become contributors to, and early adopters of, Unicode, which provided a standard encoding for “16-bits’-worth” of characters. And for many years this served us well. But in time—and particularly with the growth of emoji—16 bits wasn’t enough to encode all the characters people wanted to use. So a few years ago we began rolling out support for 32-bit Unicode, and in Version 13.1 we integrated it into notebooks—in effect making strings something much richer than before:
And, yes, you can use Unicode everywhere now:

Video as a Fundamental Object
Back when Version 1.0 was released, a megabyte was a lot of memory. But 35 years later we routinely deal with gigabytes. And one of the things that makes practical is computation with video. We first introduced Video experimentally in Version 12.1 in 2020. And over the past three years we’ve been systematically broadening and strengthening our ability to deal with video in Wolfram Language. Probably the single most important advance is that things around video now—as much as possible—“just work”, without “creaking” under the strain of handling such large amounts of data.
We can directly capture video into notebooks, and we can robustly play video anywhere within a notebook. We’ve also added options for where to store the video so that it’s conveniently accessible to you and anyone else you want to give access to it.
There’s lots of complexity in the encoding of video—and we now robustly and transparently support more than 500 codecs. We also do lots of convenient things automatically, like rotating portrait-mode videos—and being able to apply image processing operations like ImageCrop across whole videos. In every version, we’ve been further optimizing the speed of some video operation or another.
But a particularly big focus has been on video generators: programmatic ways to produce videos and animations. One basic example is AnimationVideo, which produces the same kind of output as Animate, but as a Video object that can either be displayed directly in a notebook, or exported in MP4 or some other format:

AnimationVideo is based on computing each frame in a video by evaluating an expression. Another class of video generators take an existing visual construct, and simply “tour” it. TourVideo “tours” images, graphics and geo graphics; Tour3DVideo (new in Version 14.0) tours 3D geometry:

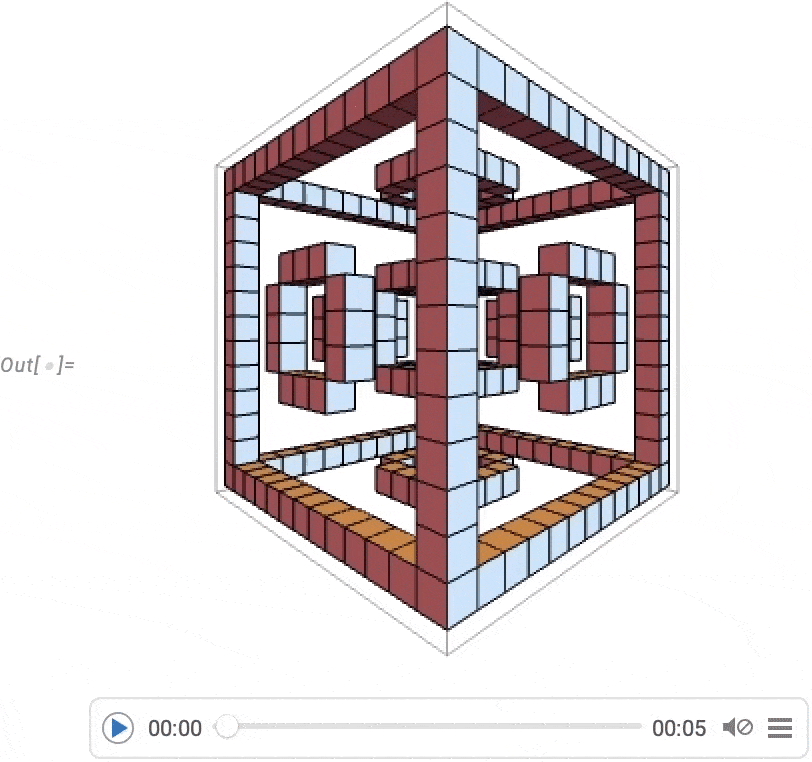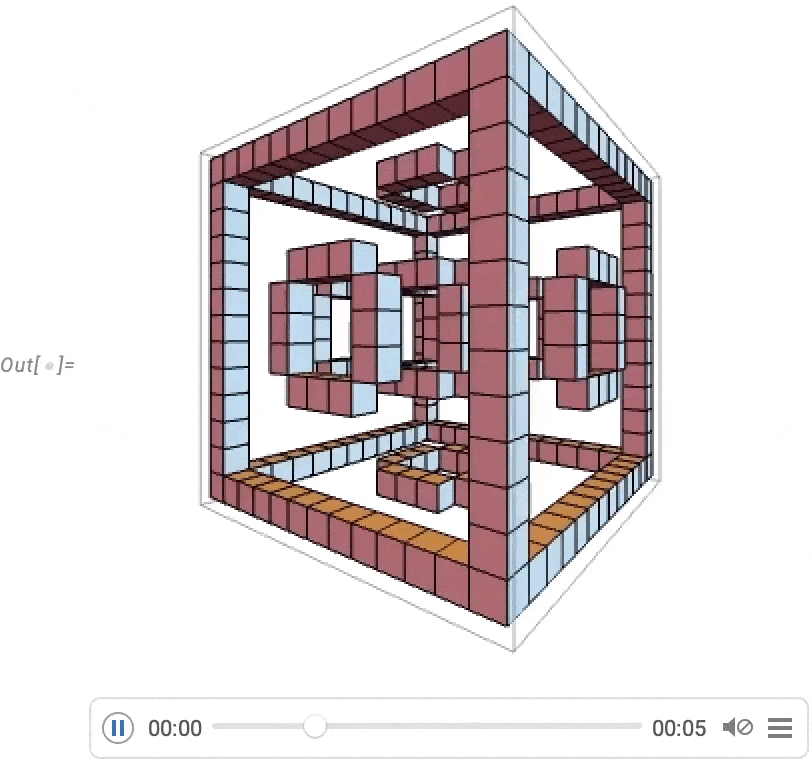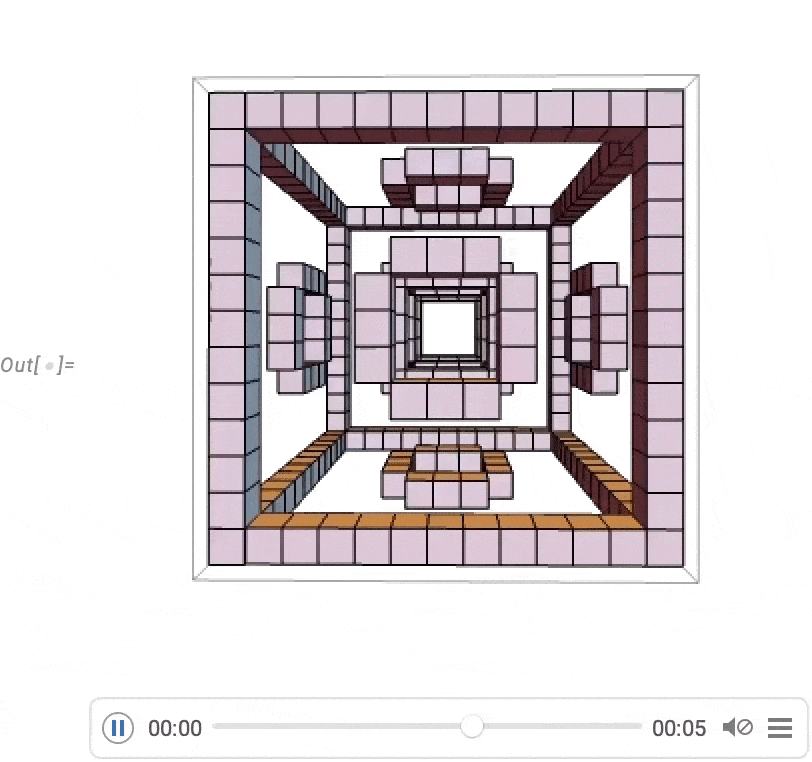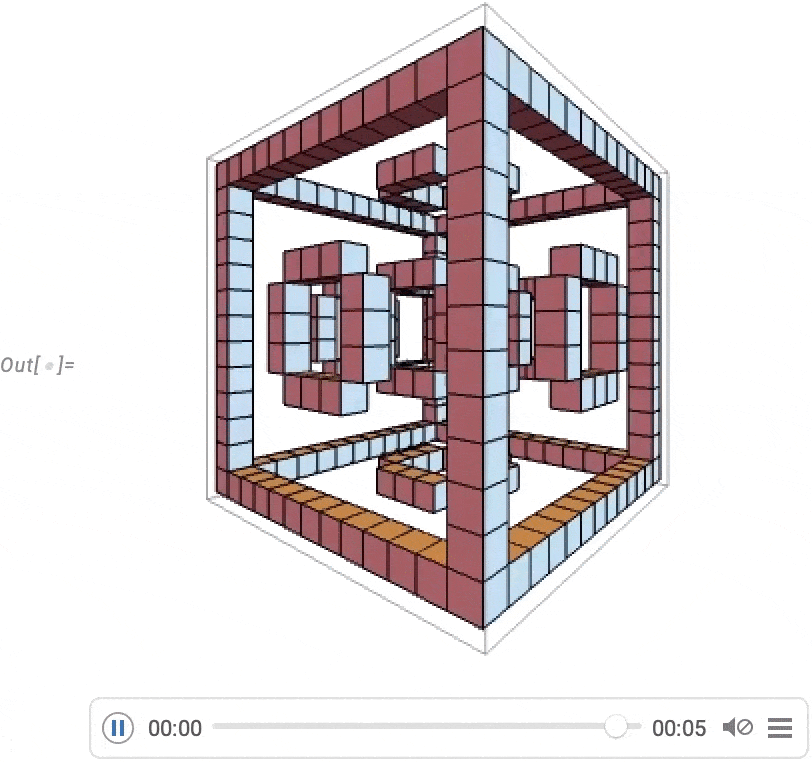
A very powerful capability in Wolfram Language is being able to apply arbitrary functions to videos. One example of how this can be done is VideoFrameMap, which maps a function across frames of a video, and which was made efficient in Version 13.2:
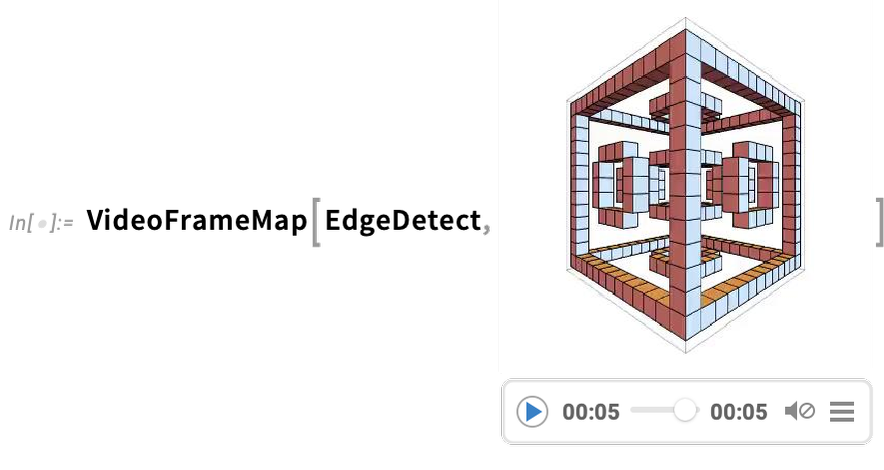
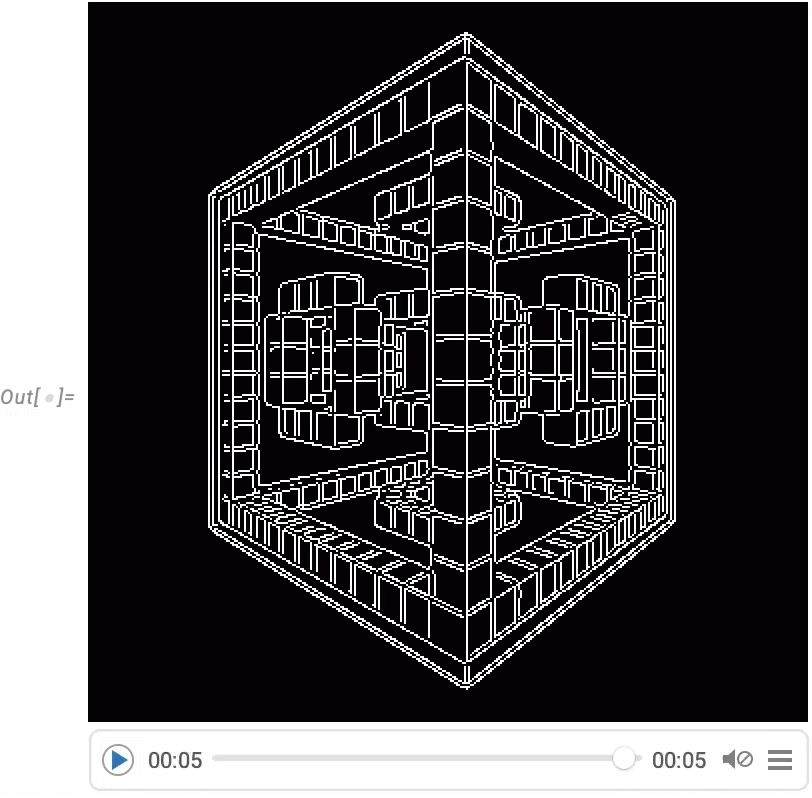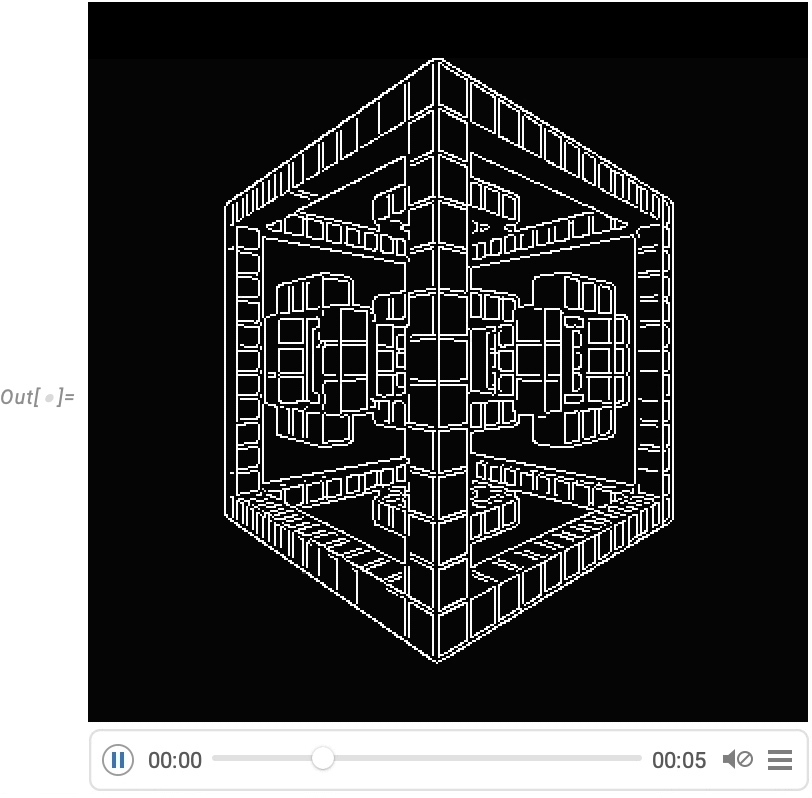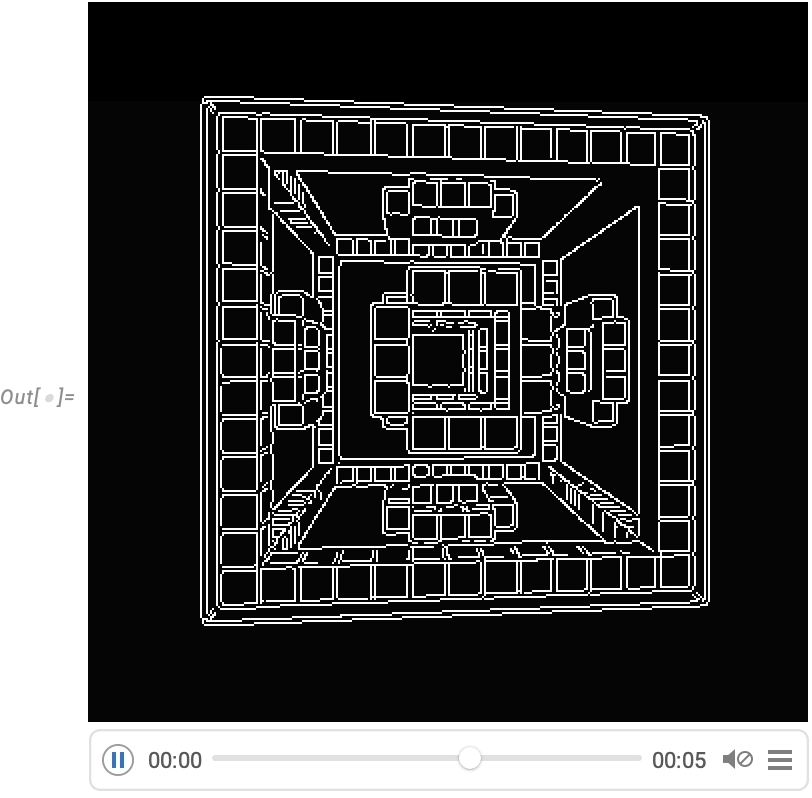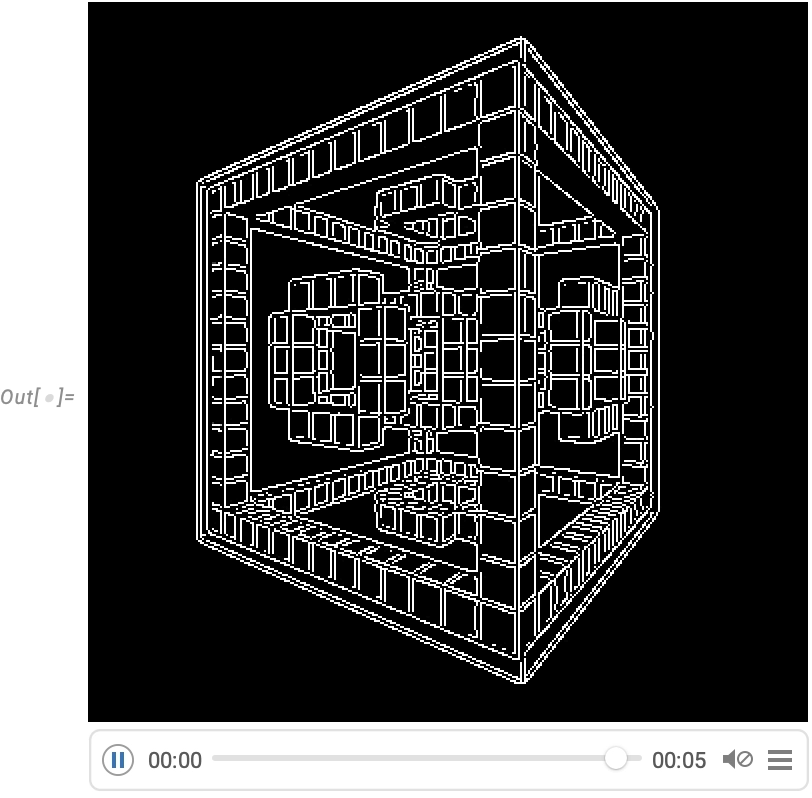
And although Wolfram Language isn’t intended as an interactive video editing system, we’ve made sure that it’s possible to do streamlined programmatic video editing in the language, and for example in Version 14.0 we’ve added things like transition effects in VideoJoin and timed overlays in OverlayVideo.
So Much Got Faster, Stronger, Sleeker
With every new version of Wolfram Language we add new capabilities to extend yet further the domain of the language. But we also put a lot of effort into something less immediately visible: making existing capabilities faster, stronger and sleeker.
And in Version 14 two areas where we can see some examples of all these are dates and quantities. We introduced the notion of symbolic dates (DateObject, etc.) nearly a decade ago. And over the years since then we’ve built many things on this structure. And in the process of doing this it’s become clear that there are certain flows and paths that are particularly common and convenient. At the beginning what mattered most was just to make sure that the relevant functionality existed. But over time we’ve been able to see what should be streamlined and optimized, and we’ve steadily been doing that.
In addition, as we’ve worked towards new and different applications, we’ve seen “corners” that need to be filled in. So, for example, astronomy is an area we’ve significantly developed in Version 14, and supporting astronomy has required adding several new “high-precision” time capabilities, such as the TimeSystem option, as well as new astronomy-oriented calendar systems. Another example concerns date arithmetic. What should happen if you want to add a month to January 30? Where should you land? Different kinds of business applications and contracts make different assumptions—and so we added a Method option to functions like DatePlus to handle this. Meanwhile, having realized that date arithmetic is involved in the “inner loop” of certain computations, we optimized it—achieving a more than 100x speedup in Version 14.0.
Wolfram|Alpha has been able to deal with units ever since it was first launched in 2009—now more than 10,000 of them. And in 2012 we introduced Quantity to represent quantities with units in the Wolfram Language. And over the past decade we’ve been steadily smoothing out a whole series of complicated gotchas and issues with units. For example, what does ![]() .
.
At first our priority with Quantity was to get it working as broadly as possible, and to integrate it as widely as possible into computations, visualizations, etc. across the system. But as its capabilities have expanded, so have its uses, repeatedly driving the need to optimize its operation for particular common cases. And indeed between Version 13 and Version 14 we’ve dramatically sped up many things related to Quantity, often by factors of 1000 or more.
Talking of speedups, another example—made possible by new algorithms operating on multithreaded CPUs—concerns polynomials. We’ve worked with polynomials in Wolfram Language since Version 1, but in Version 13.2 there was a dramatic speedup of up to 1000x on operations like polynomial factoring.
In addition, a new algorithm in Version 14.0 dramatically speeds up numerical solutions to polynomial and transcendental equations—and, together with the new MaxRoots options, allows us, for example, to pick off a few roots from a degree-one-million polynomial
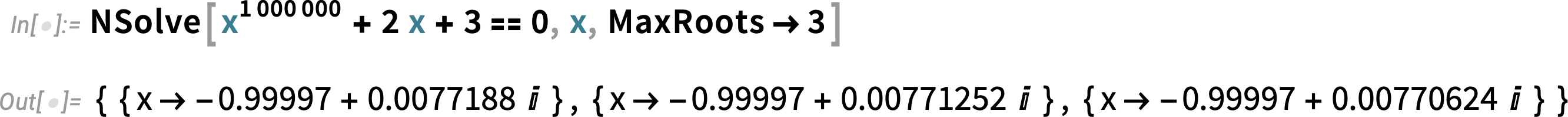
or to find roots of a transcendental equation that we could not even attempt before without pre-specifying bounds on their values:

Another “old” piece of functionality with recent enhancement concerns mathematical functions. Ever since Version 1.0 we’ve set up mathematical functions so that they can be computed to arbitrary precision:
But in recent versions we’ve wanted to be “more precise about precision”, and to be able to rigorously compute just what range of outputs are possible given the range of values provided as input:
But every function for which we do this effectively requires a new theorem, and we’ve been steadily increasing the number of functions covered—now more than 130—so that this “just works” when you need to use it in a computation.
The Tree Story Continues
Trees are useful. We first introduced them as basic objects in the Wolfram Language only in Version 12.3. But now that they’re there, we’re discovering more and more places they can be used. And to support that, we’ve been adding more and more capabilities to them.
One area that’s advanced significantly since Version 13 is the rendering of trees. We tightened up the general graphic design, but, more importantly, we introduced many new options for how rendering should be done.
For example, here’s a random tree where we’ve specified that for all nodes only 3 children should be explicitly displayed: the others are elided away:

Here we’re adding several options to define the rendering of the tree:

By default, the branches in trees are labeled with integers, just like parts in an expression. But in Version 13.1 we added support for named branches defined by associations:

Our original conception of trees was very centered around having elements one would explicitly address, and that could have “payloads” attached. But what became clear is that there were applications where all that mattered was the structure of the tree, not anything about its elements. So we added UnlabeledTree to create “pure trees”:

Trees are useful because many kinds of structures are basically trees. And since Version 13 we’ve added capabilities for converting trees to and from various kinds of structures. For example, here’s a simple Dataset object:

You can use ExpressionTree to convert this to a tree:

And TreeExpression to convert it back:

We’ve also added capabilities for converting to and from JSON and XML, as well as for representing file directory structures as trees:

Finite Fields
In Version 1.0 we had integers, rational numbers and real numbers. In Version 3.0 we added algebraic numbers (represented implicitly by Root)—and a dozen years later we added algebraic number fields and transcendental roots. For Version 14 we’ve now added another (long-awaited) “number-related” construct: finite fields.
Here’s our symbolic representation of the field of integers modulo 7:

And now here’s a specific element of that field

which we can immediately compute with:

But what’s really important about what we’ve done with finite fields is that we’ve fully integrated them into other functions in the system. So, for example, we can factor a polynomial whose coefficients are in a finite field:

We can also do things like find solutions to equations over finite fields. So here, for example, is a point on a Fermat curve over the finite field GF(173):

And here is a power of a matrix with elements over the same finite field:

Going Off Planet: The Astro Story
A major new capability added since Version 13 is astro computation. It begins with being able to compute to high precision the positions of things like planets. Even knowing what one means by “position” is complicated, though—with lots of different coordinate systems to deal with. By default AstroPosition gives the position in the sky at the current time from your Here location:

But one can instead ask about a different coordinate system, like global galactic coordinates:

And now here’s a plot of the distance between Saturn and Jupiter over a 50-year period:

In direct analogy to GeoGraphics, we’ve added AstroGraphics, here showing a patch of sky around the current position of Saturn:

And this now shows the sequence of positions for Saturn over the course of a couple of years—yes, including retrograde motion:

There are many styling options for AstroGraphics. Here we’re adding a background of the “galactic sky”:

And here we’re including renderings for constellations (and, yes, we had an artist draw them):

Something specifically new in Version 14.0 has to do with extended handling of solar eclipses. We always try to deliver new functionality as fast as we can. But in this case there was a very specific deadline: the total solar eclipse visible from the US on April 8, 2024. We’ve had the ability to do global computations about solar eclipses for some time (actually since soon before the 2017 eclipse). But now we can also do detailed local computations right in the Wolfram Language.
So, for example, here’s a somewhat detailed overall map of the April 8, 2024, eclipse:

Now here’s a plot of the magnitude of the eclipse over a few hours, complete with a little “rampart” associated with the period of totality:

And here’s a map of the region of totality every minute just after the moment of maximum eclipse:

Millions of Species Become Computable
We first introduced computable data on biological organisms back when Wolfram|Alpha was released in 2009. But in Version 14—following several years of work—we’ve dramatically broadened and deepened the computable data we have about biological organisms.
So for example here’s how we can figure out what species have cheetahs as predators:

And here are pictures of these:

Here’s a map of countries where cheetahs have been seen (in the wild):

We now have data—curated from a great many sources—on more than a million species of animals, as well as most of the plants, fungi, bacteria, viruses and archaea that have been described. And for animals, for example, we have nearly 200 properties that are extensively filled in. Some are taxonomic properties:

Some are physical properties:


Some are genetic properties:

Some are ecological properties (yes, the cheetah is not the apex predator):

It’s useful to be able to get properties of individual species, but the real power of our curated computable data shows up when one does larger-scale analyses. Like here’s a plot of the lengths of genomes for organisms with the longest ones across our collection of organisms:

Or here’s a histogram of the genome lengths for organisms in the human gut microbiome:

And here’s a scatterplot of the lifespans of birds against their weights:

Following the idea that cheetahs aren’t apex predators, this is a graph of what’s “above” them in the food chain:

Chemical Computation
We began the process of introducing chemical computation into the Wolfram Language in Version 12.0, and by Version 13 we had good coverage of atoms, molecules, bonds and functional groups. Now in Version 14 we’ve added coverage of chemical formulas, amounts of chemicals—and chemical reactions.
Here’s a chemical formula, that basically just gives a “count of atoms”:

Now here are specific molecules with that formula:

Let’s pick one of these molecules:

Now in Version 14 we have a way to represent a certain quantity of molecules of a given type—here 1 gram of methylcyclopentane:

ChemicalConvert can convert to a different specification of quantity, here moles:

And here a count of molecules:

But now the bigger story is that in Version 14 we can represent not just individual types of molecules, and quantities of molecules, but also chemical reactions. Here we give a “sloppy” unbalanced representation of a reaction, and ReactionBalance gives us the balanced version:

And now we can extract the formulas for the reactants:

We can also give a chemical reaction in terms of molecules:

But with our symbolic representation of molecules and reactions, there’s now a big thing we can do: represent classes of reactions as “pattern reactions”, and work with them using the same kinds of concepts as we use in working with patterns for general expressions. So, for example, here’s a symbolic representation of the hydrohalogenation reaction:

Now we can apply this pattern reaction to particular molecules:

Here’s a more elaborate example, in this case entered using a SMARTS string:

Here we’re applying the reaction just once:

And now we’re doing it repeatedly
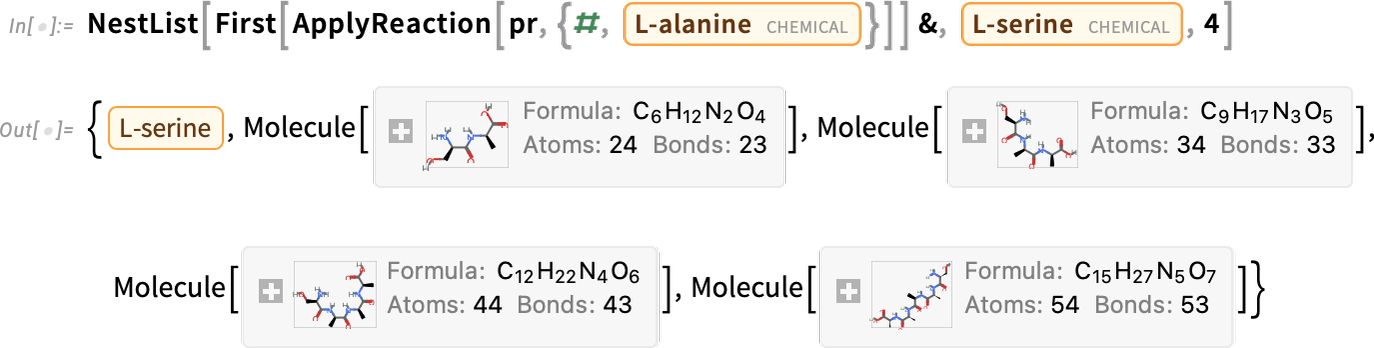
in this case generating longer and longer molecules (which in this case happen to be polypeptides):

The Knowledgebase Is Always Growing
Every minute of every day, new data is being added to the Wolfram Knowledgebase. Much of it is coming automatically from real-time feeds. But we also have a very large-scale ongoing curation effort with humans in the loop. We’ve built sophisticated (Wolfram Language) automation for our data curation pipeline over the years—and this year we’ve been able to increase efficiency in some areas by using LLM technology. But it’s hard to do curation right, and our long-term experience is that to do so ultimately requires human experts being in the loop, which we have.
So what’s new since Version 13.0? 291,842 new notable current and historical people; 264,467 music works; 118,538 music albums; 104,024 named stars; and so on. Sometimes the addition of an entity is driven by the new availability of reliable data; often it’s driven by the need to use that entity in some other piece of functionality (e.g. stars to render in AstroGraphics). But more than just adding entities there’s the issue of filling in values of properties of existing entities. And here again we’re always making progress, sometimes integrating newly available large-scale secondary data sources, and sometimes doing direct curation ourselves from primary sources.
A recent example where we needed to do direct curation was in data on alcoholic beverages. We have very extensive data on hundreds of thousands of types of foods and drinks. But none of our large-scale sources included data on alcoholic beverages. So that’s an area where we need to go to primary sources (in this case typically the original producers of products) and curate everything for ourselves.
So, for example, we can now ask for something like the distribution of flavors of different varieties of vodka (actually, personally, not being a consumer of such things, I had no idea vodka even had flavors…):

But beyond filling out entities and properties of existing types, we’ve also steadily been adding new entity types. One recent example is geological formations, 13,706 of them:

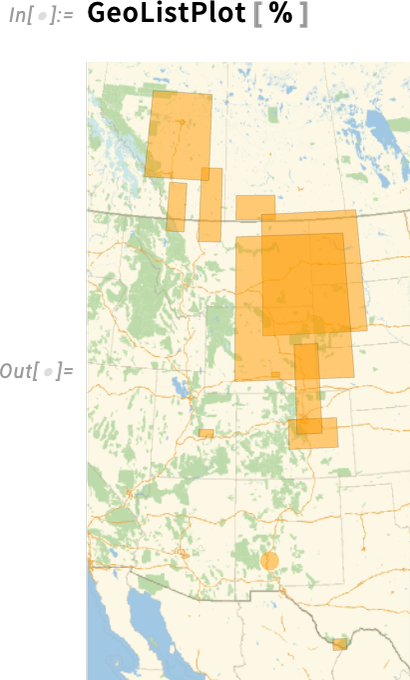
So now, for example, we can specify where T. rex have been found

and we can show those regions on a map:
Industrial-Strength Multidomain PDEs
PDEs are hard. It’s hard to solve them. And it’s hard to even specify what exactly you want to solve. But we’ve been on a multi-decade mission to “consumerize” PDEs and make them easier to work with. Many things go into this. You need to be able to easily specify elaborate geometries. You need to be able to easily define mathematically complicated boundary conditions. You need to have a streamlined way to set up the complicated equations that come out of underlying physics. Then you have to—as automatically as possible—do the sophisticated numerical analysis to efficiently solve the equations. But that’s not all. You also often need to visualize your solution, compute other things from it, or run optimizations of parameters over it.
It’s a deep use of what we’ve built with Wolfram Language—touching many parts of the system. And the result is something unique: a truly streamlined and integrated way to handle PDEs. One’s not dealing with some (usually very expensive) “just for PDEs” package; what we now have is a “consumerized” way to handle PDEs whenever they’re needed—for engineering, science, or whatever. And, yes, being able to connect machine learning, or image computation, or curated data, or data science, or real-time sensor feeds, or parallel computing, or, for that matter, Wolfram Notebooks, to PDEs just makes them so much more valuable.
We’ve had “basic, raw NDSolve” since 1991. But what’s taken decades to build is all the structure around that to let one conveniently set up—and efficiently solve—real-world PDEs, and connect them into everything else. It’s taken developing a whole tower of underlying algorithmic capabilities such as our more-flexible-and-integrated-than-ever-before industrial-strength computational geometry and finite element methods. But beyond that it’s taken creating a language for specifying real-world PDEs. And here the symbolic nature of the Wolfram Language—and our whole design framework—has made possible something very unique, that has allowed us to dramatically simplify and consumerize the use of PDEs.
It’s all about providing symbolic “construction kits” for PDEs and their boundary conditions. We started this about five years ago, progressively covering more and more application areas. In Version 14 we’ve particularly focused on solid mechanics, fluid mechanics, electromagnetics and (one-particle) quantum mechanics.
Here’s an example from solid mechanics. First, we define the variables we’re dealing with (displacement and underlying coordinates):
Next, we specify the parameters we want to use to describe the solid material we’re going to work with:
Now we can actually set up our PDE—using symbolic PDE specifications like SolidMechanicsPDEComponent—here for the deformation of a solid object pulled on one side:

And, yes, “underneath”, these simple symbolic specifications turn into a complicated “raw” PDE:
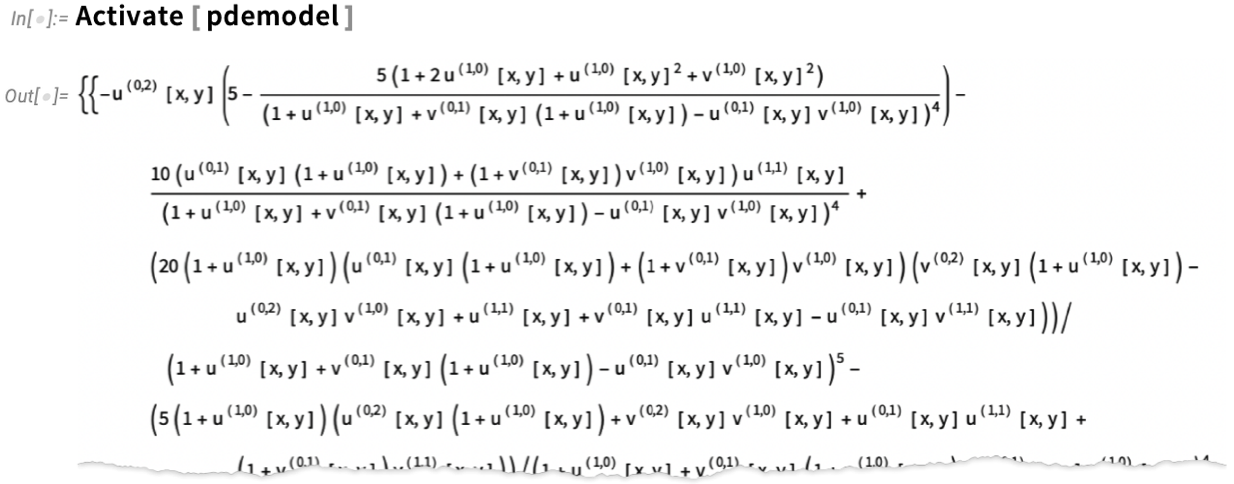
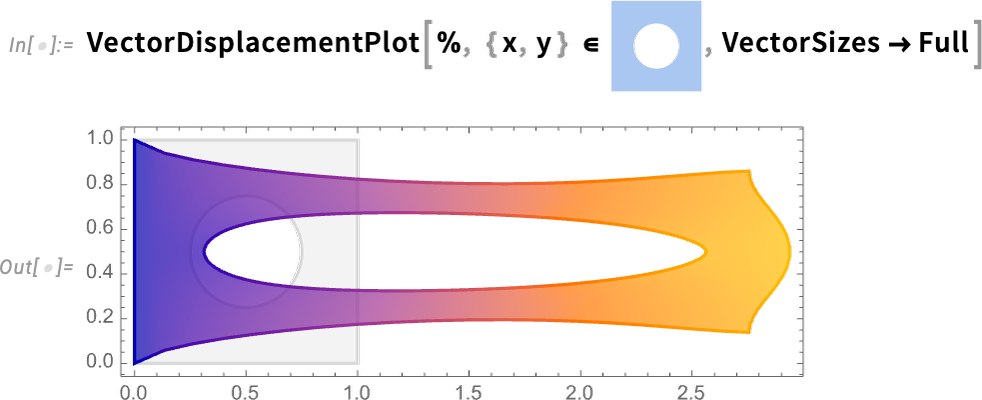
Now we are ready to actually solve our PDE in a particular region, i.e. for an object with a particular shape:

And now we can visualize the result, which shows how our object stretches when it’s pulled on:
The way we’ve set things up, the material for our object is an idealization of something like rubber. But in the Wolfram Language we now have ways to specify all sorts of detailed properties of materials. So, for example, we can add reinforcement as a unit vector in a particular direction (say in practice with fibers) to our material:
Then we can rerun what we did before
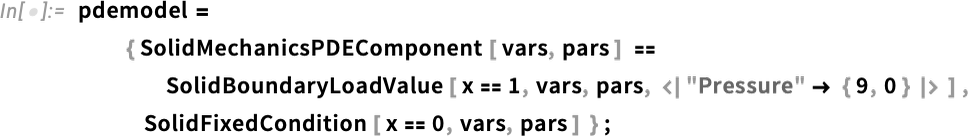
but now we get a slightly different result:
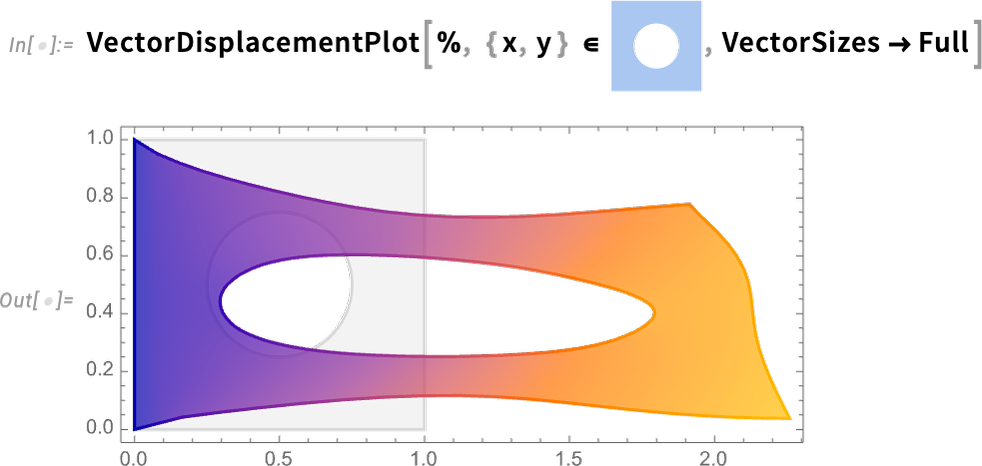
Another major PDE domain that’s new in Version 14.0 is fluid flow. Let’s do a 2D example. Our variables are 2D velocity and pressure:
Now we can set up our fluid system in a particular region, with no-slip conditions on all walls except at the top where we assume fluid is flowing from left to right. The only parameter needed is the Reynolds number. And instead of just solving our PDEs for a single Reynolds number, let’s create a parametric solver that can take any specified Reynolds number:

Now here’s the result for Reynolds number 100:
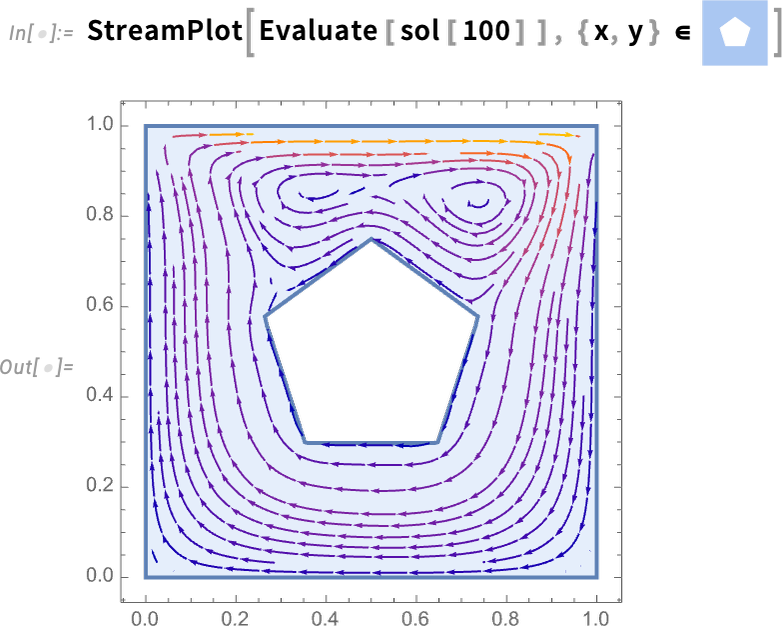
But with the way we’ve set things up, we can as well generate a whole video as a function of Reynolds number (and, yes, the Parallelize speeds things up by generating different frames in parallel):

Much of our work in PDEs involves catering to the complexities of real-world engineering situations. But in Version 14.0 we’re also adding features to support “pure physics”, and in particular to support quantum mechanics done with the Schrödinger equation. So here, for example, is the 2D 1-particle Schrödinger equation (with ![]() ):
):

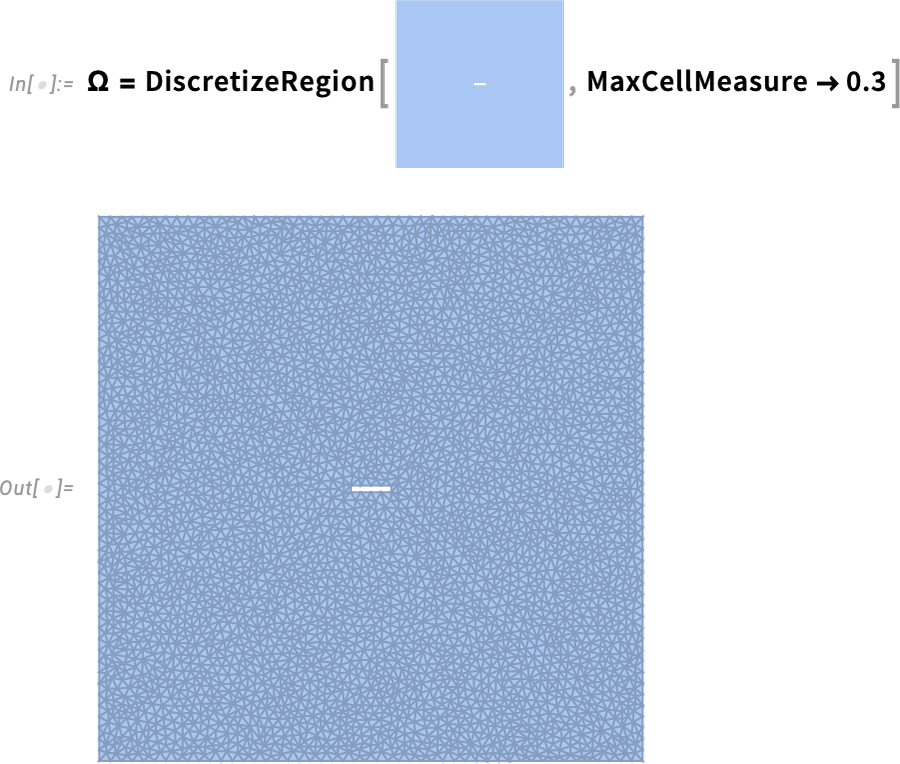
Here’s the region we’re going to be solving over—showing explicit discretization:
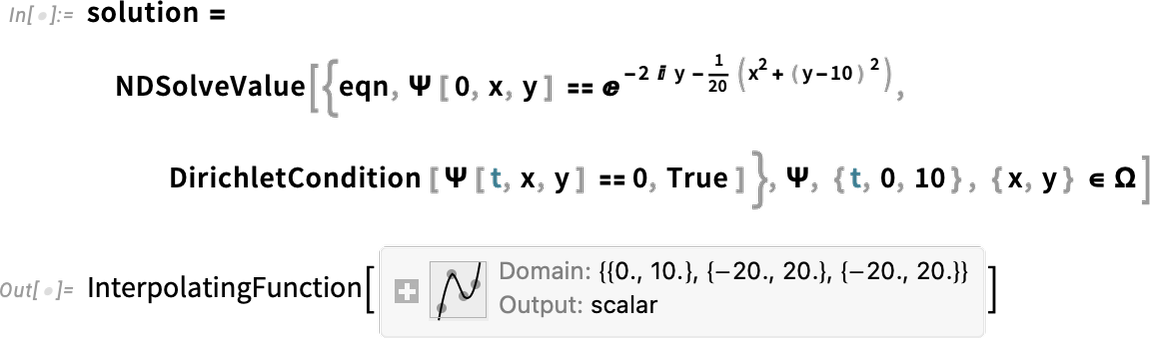
Now we can solve the equation, adding in some boundary conditions:
And now we get to visualize a Gaussian wave packet scattering around a barrier:
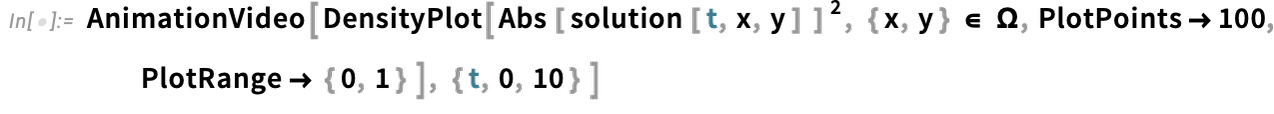
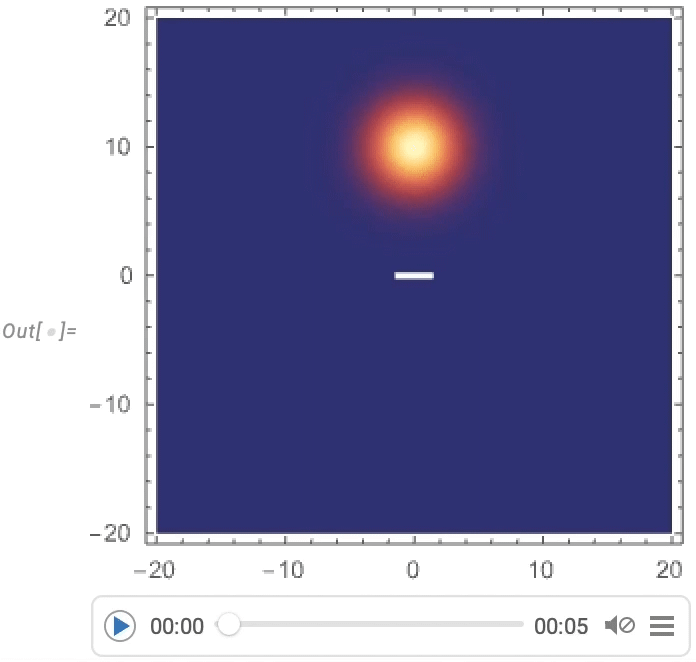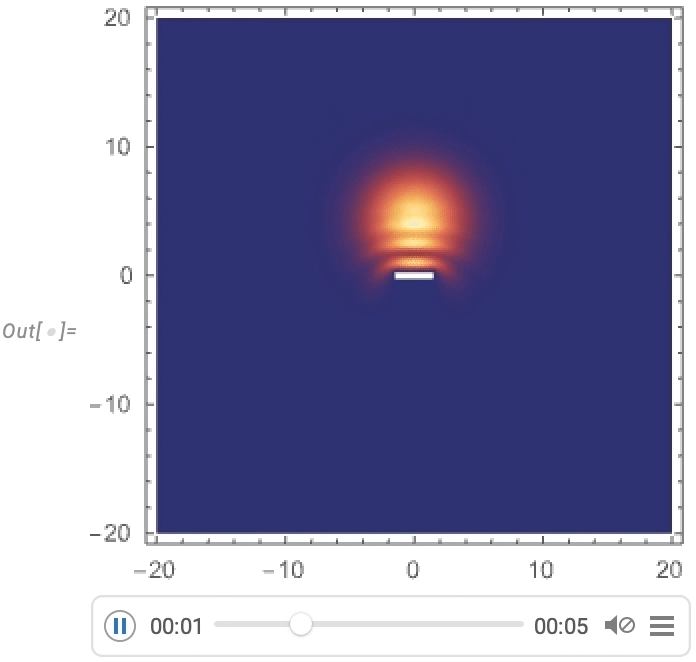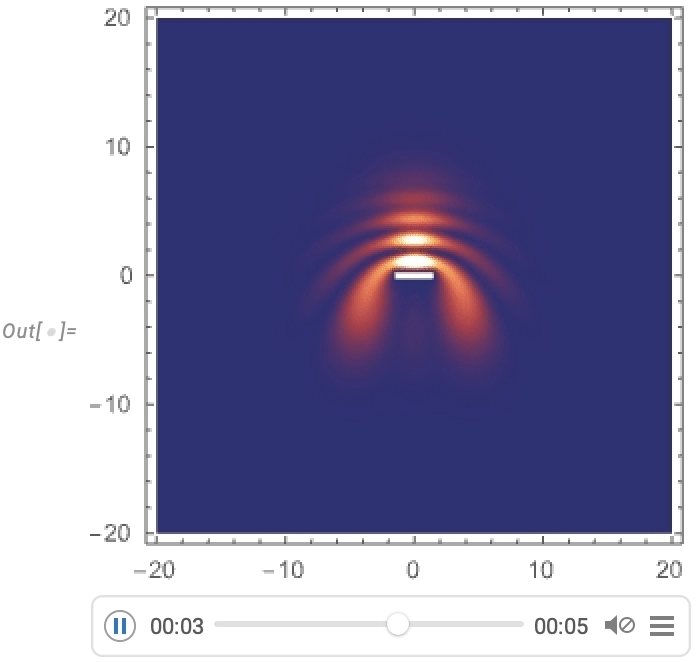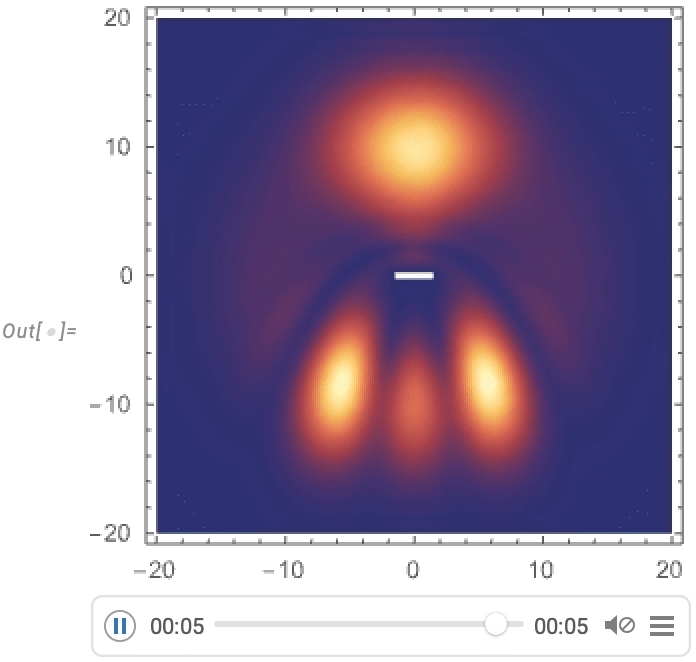
Streamlining Systems Engineering Computation
Systems engineering is a big field, but it’s one where the structure and capabilities of the Wolfram Language provide unique advantages—that over the past decade have allowed us to build out rather complete industrial-strength support for modeling, analysis and control design for a wide range of types of systems. It’s all an integrated part of the Wolfram Language, accessible through the computational and interface structure of the language. But it’s also integrated with our separate Wolfram System Modeler product, that provides a GUI-based workflow for system modeling and exploration.
Shared with System Modeler are large collections of domain-specific modeling libraries. And, for example, since Version 13, we’ve added libraries in areas such as battery engineering, hydraulic engineering and aircraft engineering—as well as educational libraries for mechanical engineering, thermal engineering, digital electronics, and biology. (We’ve also added libraries for areas such as business and public policy simulation.)

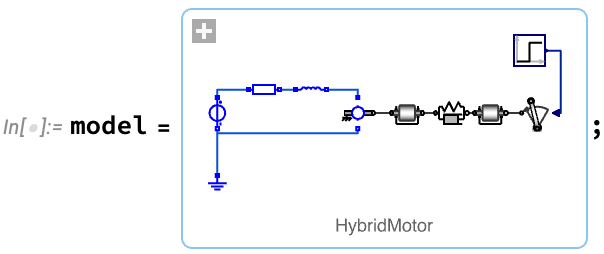
A typical workflow for systems engineering begins with the setting up of a model. The model can be built from scratch, or assembled from components in model libraries—either visually in Wolfram System Modeler, or programmatically in the Wolfram Language. For example, here’s a model of an electric motor that’s turning a load through a flexible shaft:
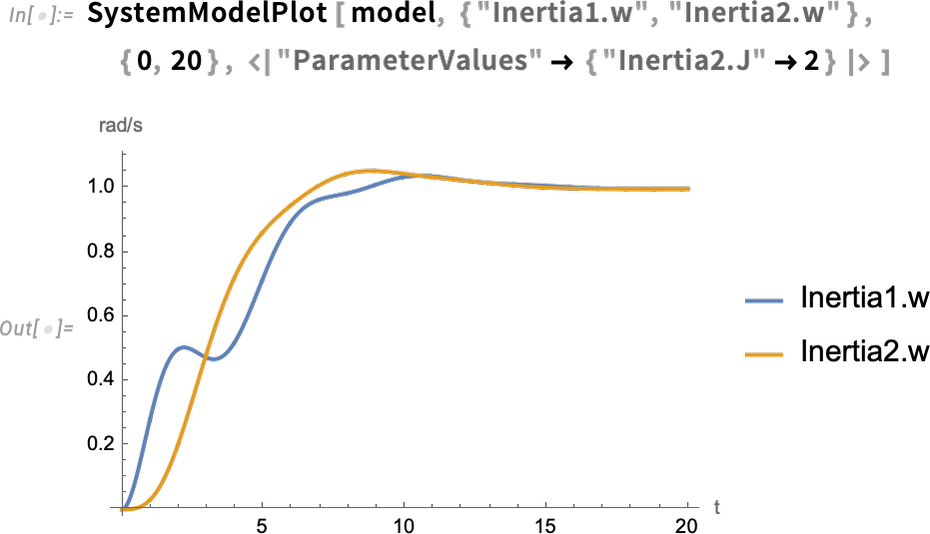
Once one’s got a model, one can then simulate it. Here’s an example where we’ve set one parameter of our model (the moment of inertia of the load), and we’re computing the values of two others as a function of time:
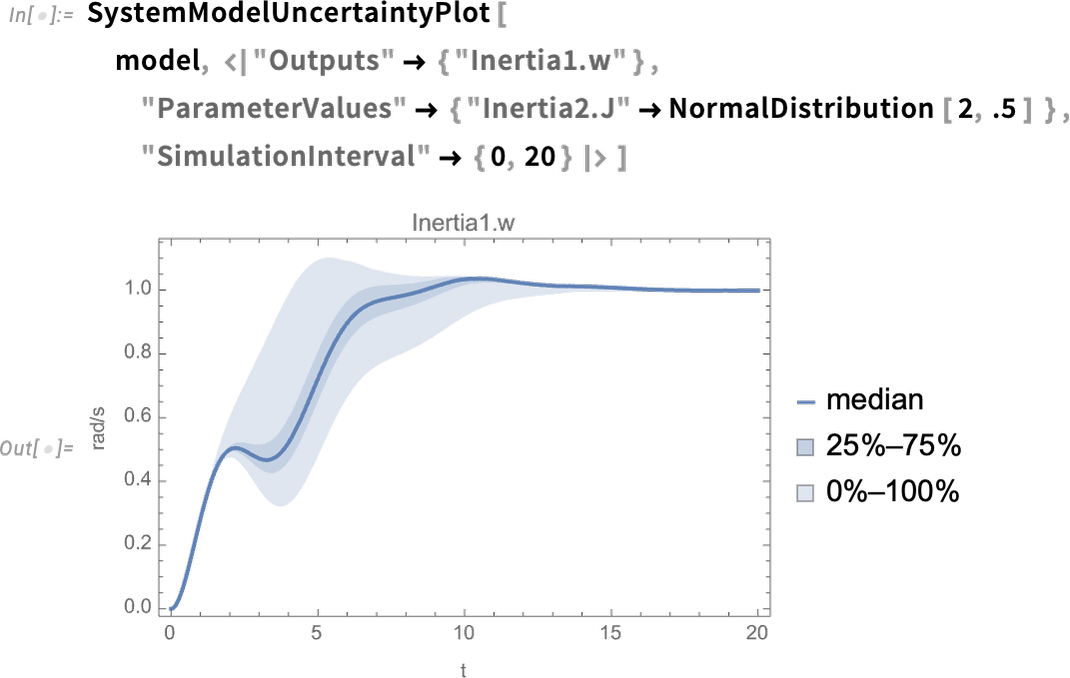
A new capability in Version 14.0 is being able to see the effect of uncertainty in parameters (or initial values, etc.) on the behavior of a system. So here, as an example, we’re saying the value of the parameter is not definite, but is instead distributed according to a normal distribution—then we’re seeing the distribution of output results:
The motor with flexible shaft that we’re looking at can be thought of as a “multidomain system”, combining electrical and mechanical components. But the Wolfram Language (and Wolfram System Modeler) can also handle “mixed systems”, combining analog and digital (i.e. continuous and discrete) components. Here’s a fairly sophisticated example from the world of control systems: a helicopter model connected in a closed loop to a digital control system:

This whole model system can be represented symbolically just by:
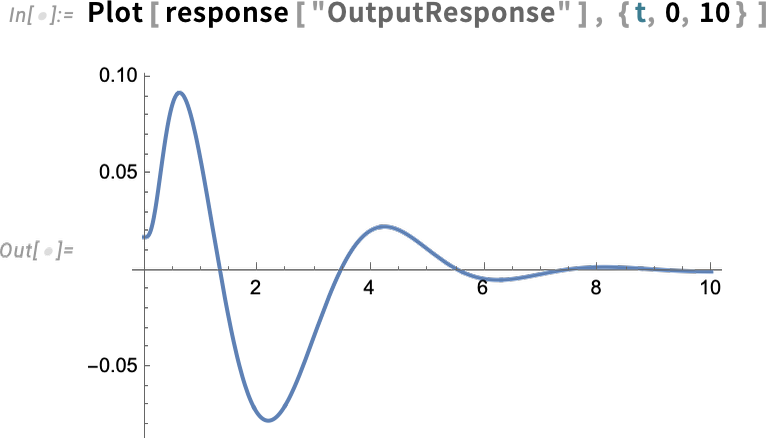
And now we compute the input-output response of the model:

Here’s specifically the output response:
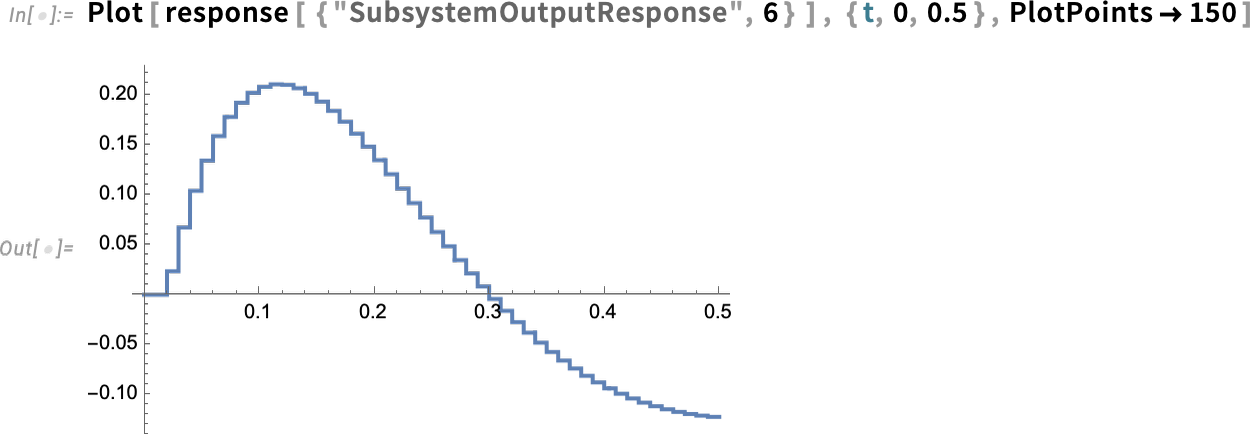
But now we can “drill in” and see specific subsystem responses, here of the zero-order hold device (labeled ZOH above)—complete with its little digital steps:
But what if we want to design the control systems ourselves? Well, in Version 14 we can now apply all our Wolfram Language control systems design functionality to arbitrary system models. Here’s an example of a simple model, in this case in chemical engineering (a continuously stirred tank):

Now we can take this model and design an LQG controller for it—then assemble a whole closed-loop system for it:
Now we can simulate the closed-loop system—and see that the controller succeeds in bringing the final value to 0:
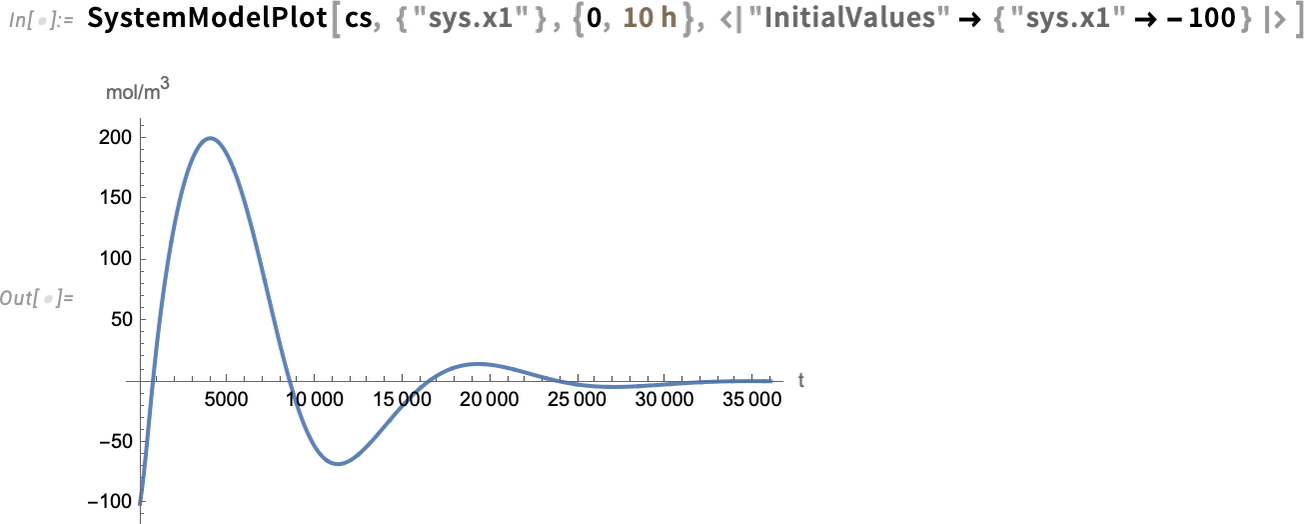
Graphics: More Beautiful & Alive
Graphics have always been an important part of the story of the Wolfram Language, and for more than three decades we’ve been progressively enhancing and updating their appearance and functionality—sometimes with help from advances in hardware (e.g. GPU) capabilities.
Since Version 13 we’ve added a variety of “decorative” (or “annotative”) effects in 2D graphics. One example (useful for putting captions on things) is Haloing:

Another example is DropShadowing:

All of these are specified symbolically, and can be used throughout the system (e.g. in hover effects, etc). And, yes, there are many detailed parameters you can set:
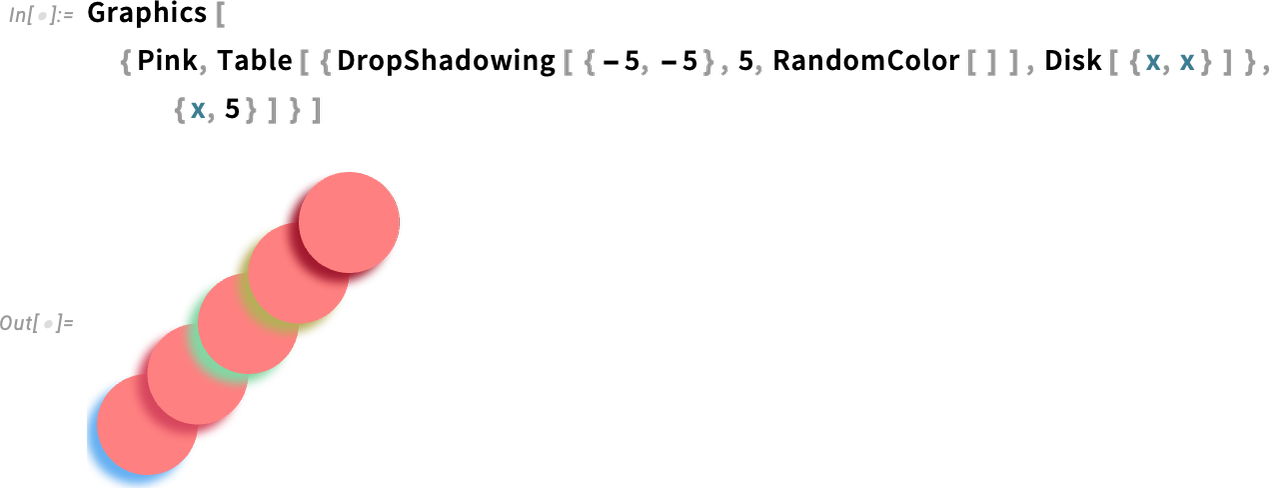
A significant new capability in Version 14.0 is convenient texture mapping. We’ve had low-level polygon-by-polygon textures for a decade and a half. But now in Version 14.0 we’ve made it straightforward to map textures onto whole surfaces. Here’s an example wrapping a texture onto a sphere:

And here’s wrapping the same texture onto a more complicated surface:

A significant subtlety is that there are many ways to map what amount to “texture coordinate patches” onto surfaces. The documentation illustrates new, named cases:

And now here’s what happens with stereographic projection onto a sphere:

Here’s an example of “surface texture” for the planet Venus

and here it’s been mapped onto a sphere, which can be rotated:


Here’s a “flowerified” bunny:

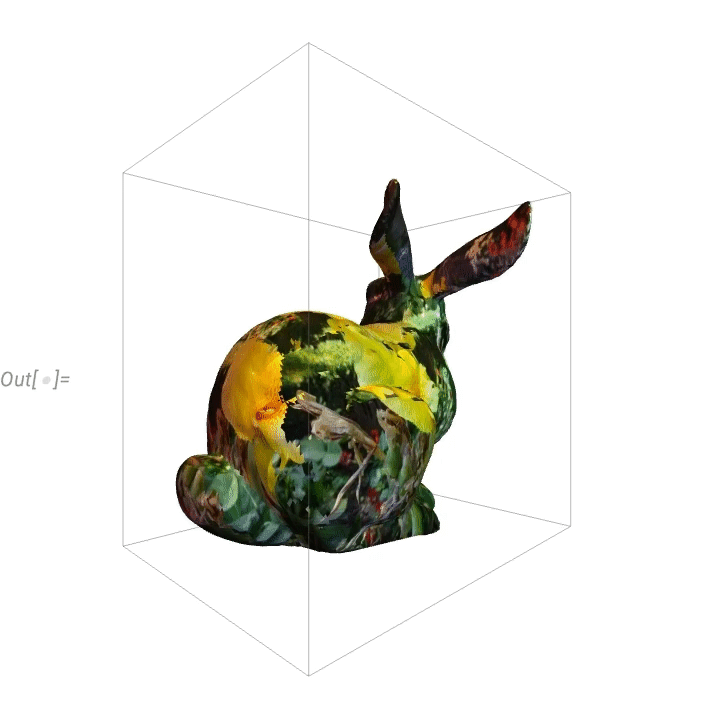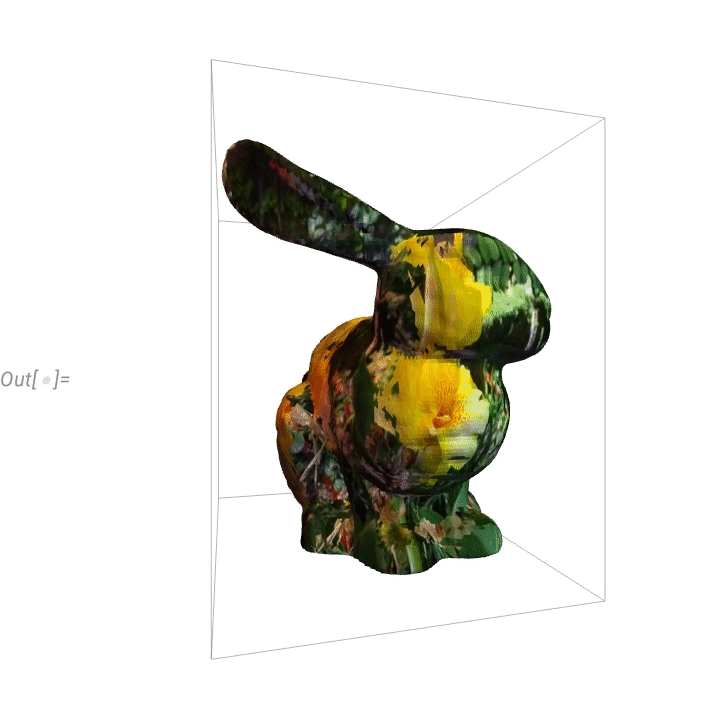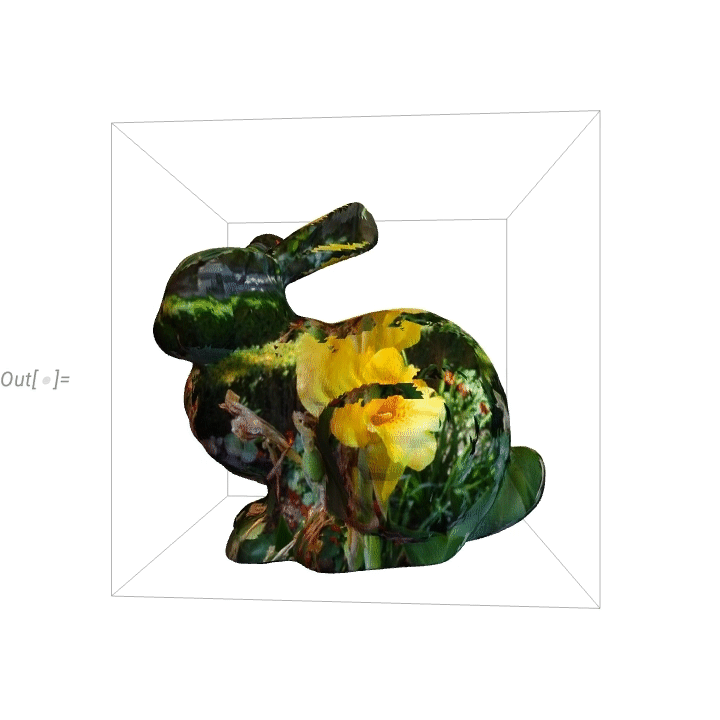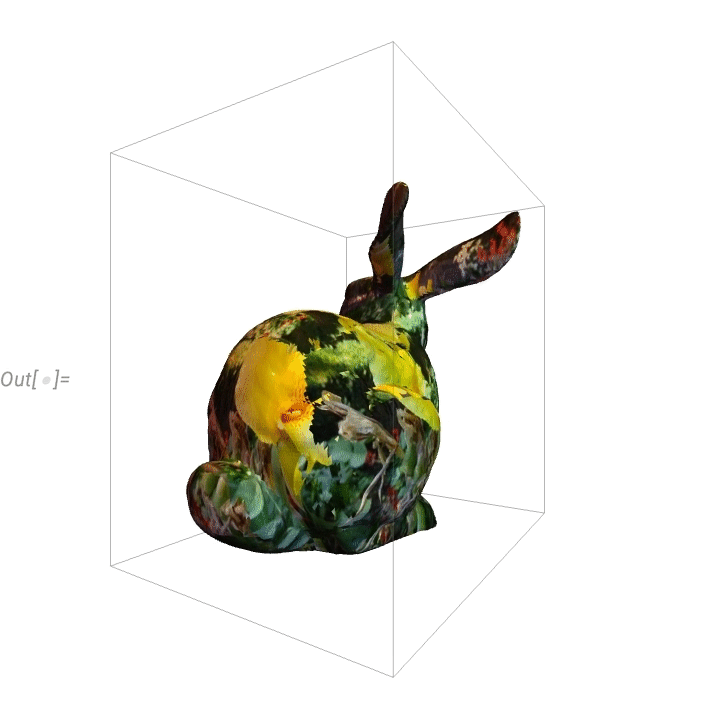
Things like texture mapping help make graphics visually compelling. Since Version 13 we’ve also added a variety of “live visualization” capabilities that automatically “bring visualizations to life”. For example, any plot now by default has a “coordinate mouseover”:
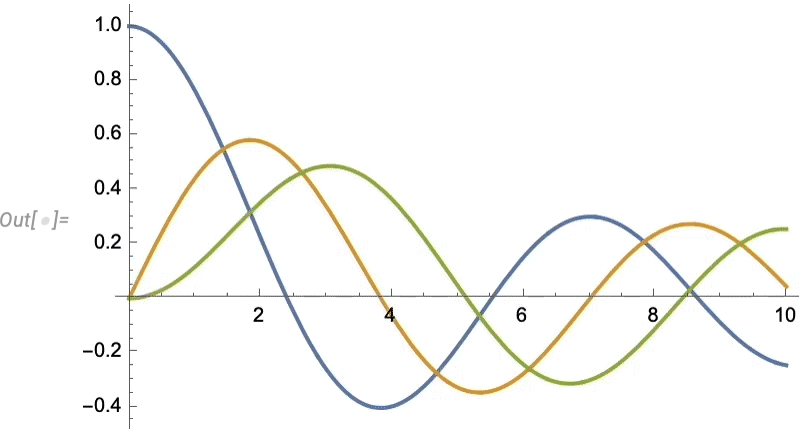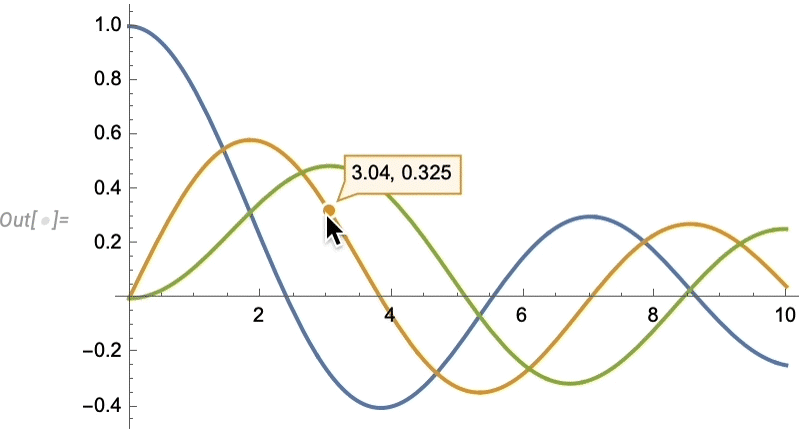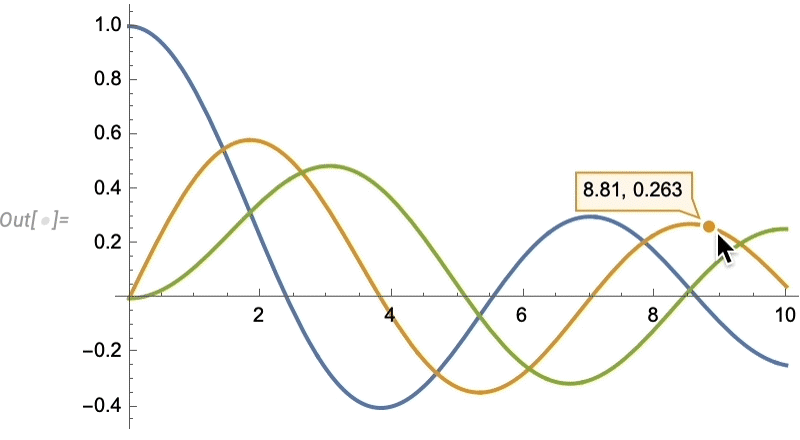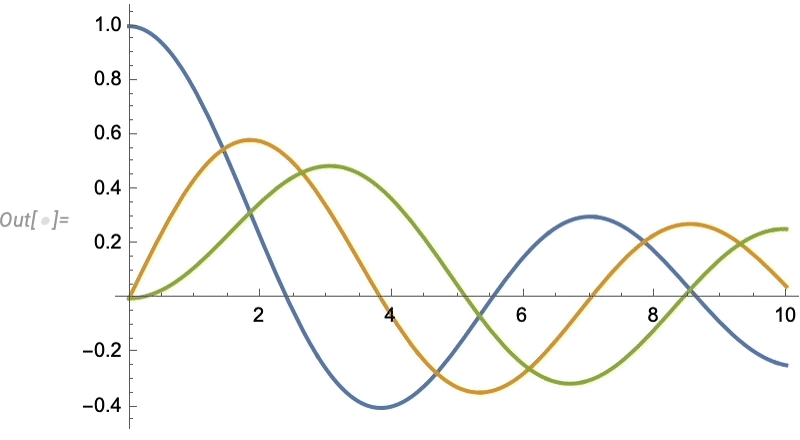
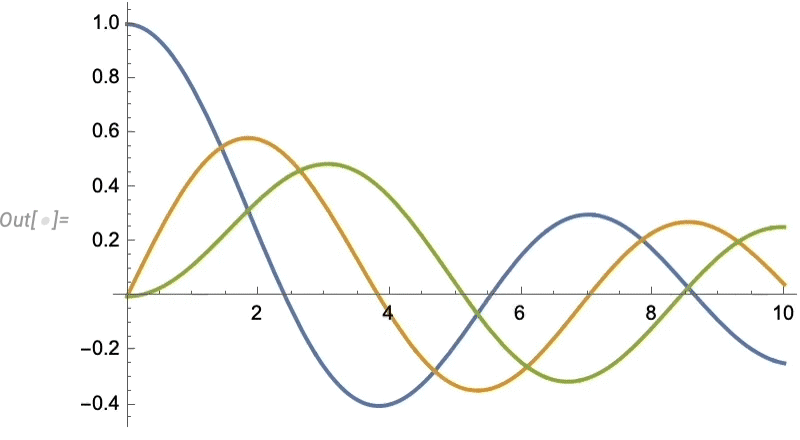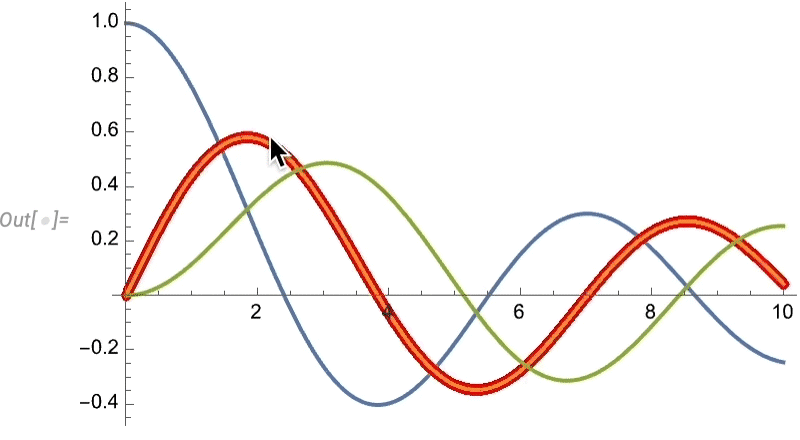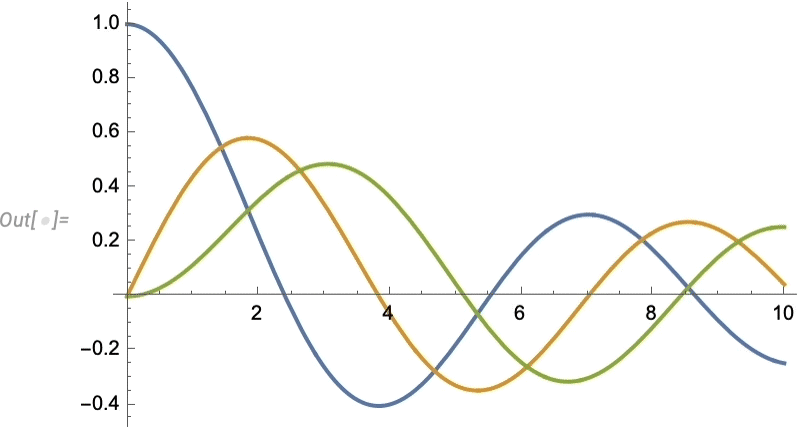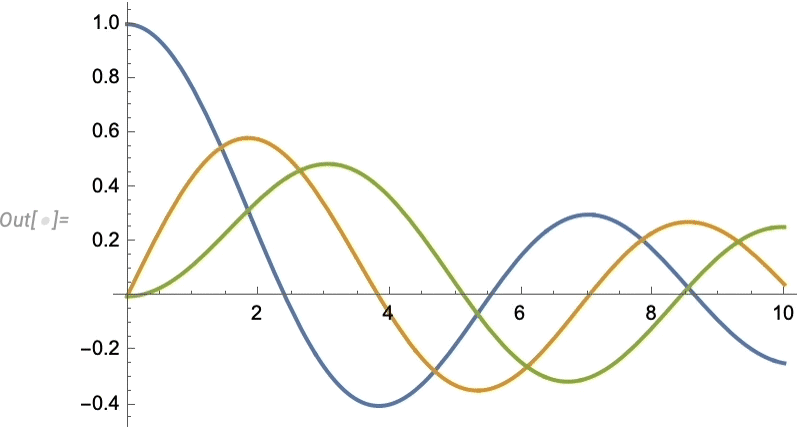
As usual, there’s lots of ways to control such “highlighting” effects:


Euclid Redux: The Advance of Synthetic Geometry
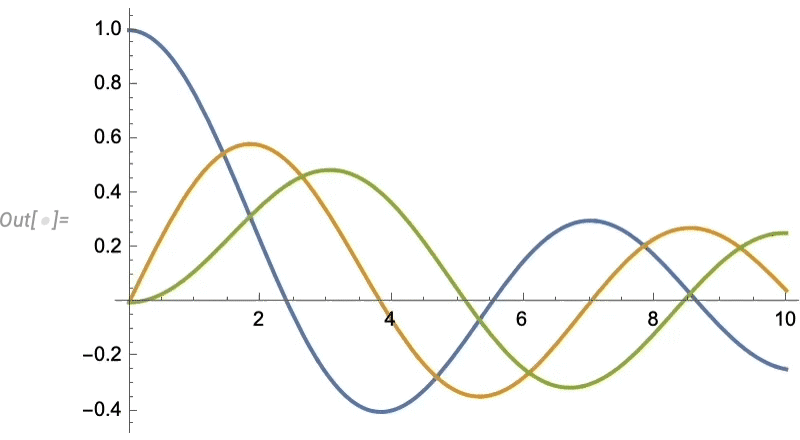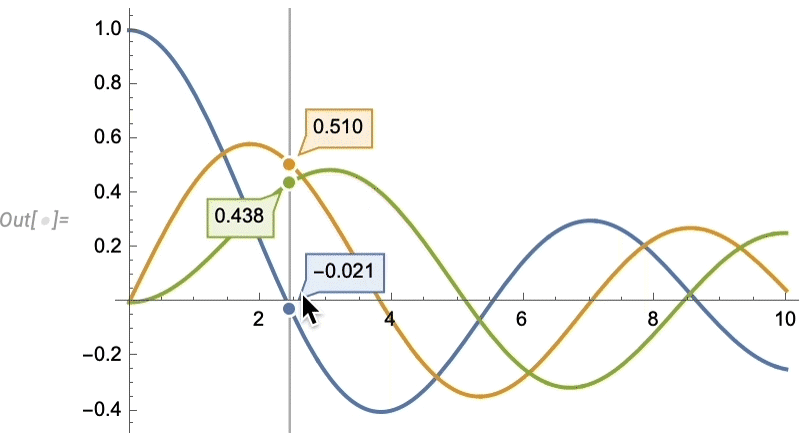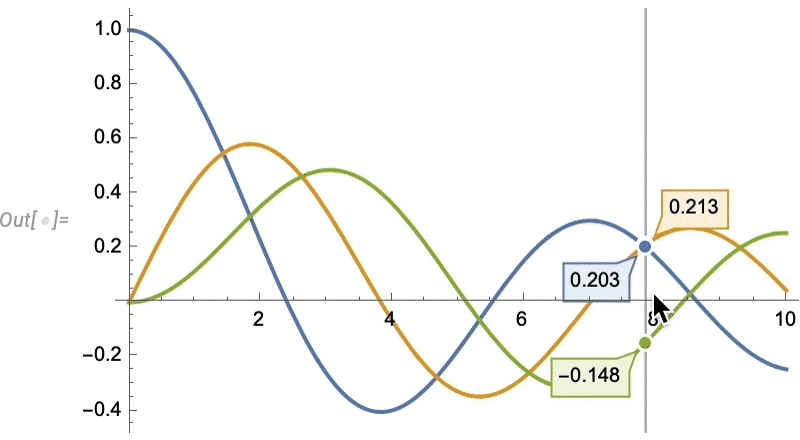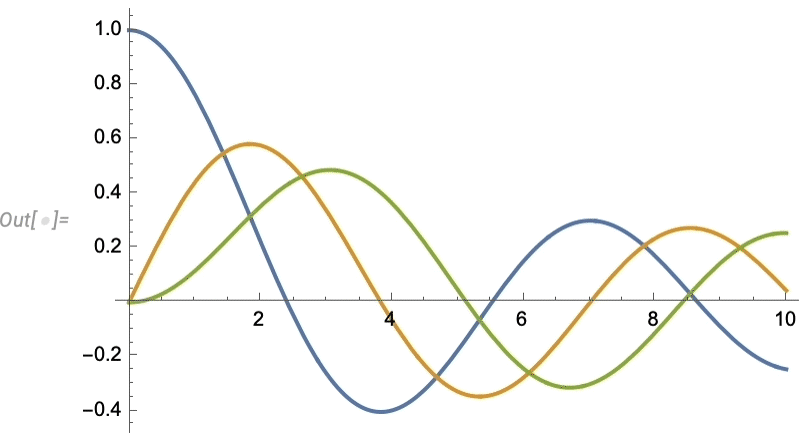
One might say it’s been two thousand years in the making. But four years ago (Version 12) we began to introduce a computable version of Euclid-style synthetic geometry.
The idea is to specify geometric scenes symbolically by giving a collection of (potentially implicit) constraints:

We can then generate a random instance of geometry consistent with the constraints—and in Version 14 we’ve considerably enhanced our ability to make sure that geometry will be “typical” and non-degenerate:

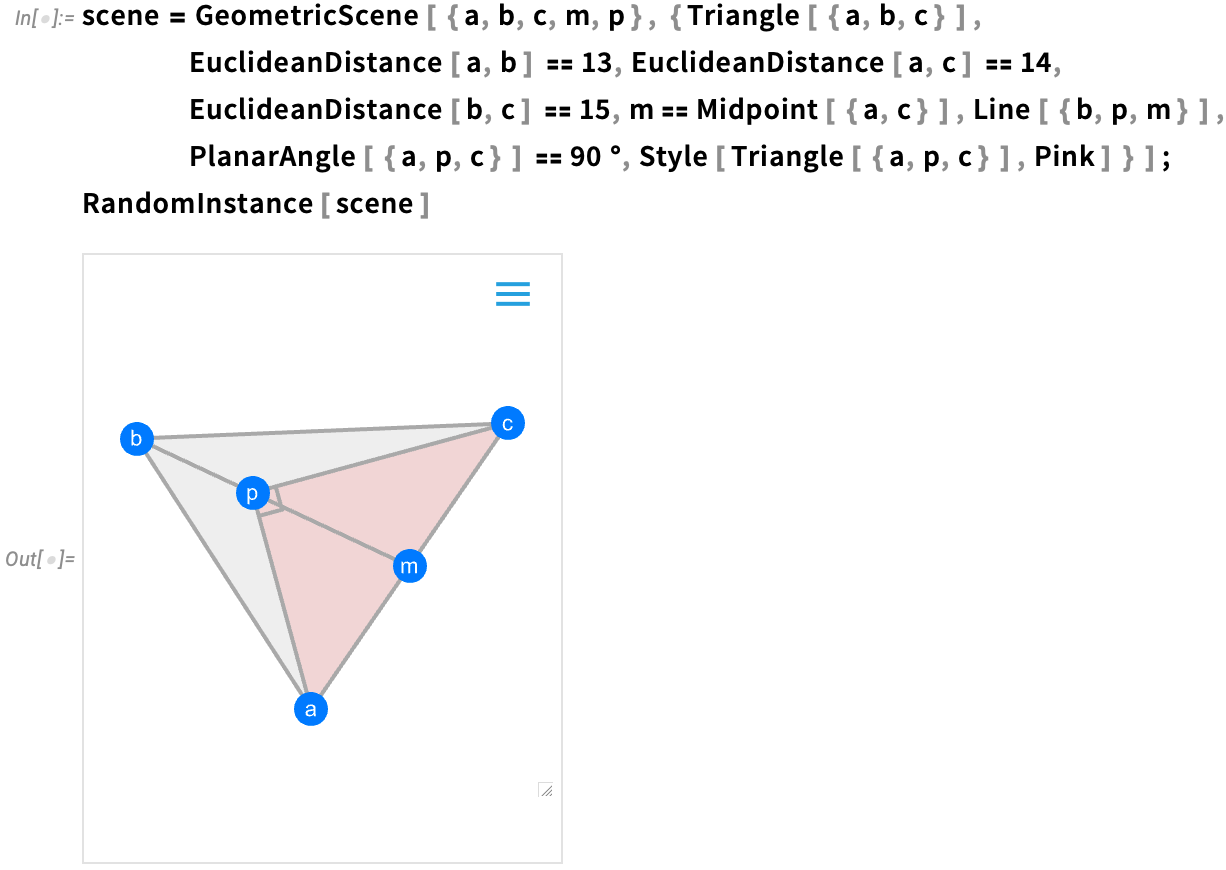
But now a new feature of Version 14 is that we can find values of geometric quantities that are determined by the constraints:

Here’s a slightly more complicated case:

And here we’re now solving for the areas of two triangles in the figure:

We’ve always been able to give explicit styles for particular elements of a scene:
Now one of the new features in Version 14 is being able to give general “geometric styling rules”, here just assigning random colors to each element:

The Ever-Smoother User Interface
Our goal with Wolfram Language is to make it as easy as possible to express oneself computationally. And a big part of achieving that is the coherent design of the language itself. But there’s another part as well, which is being able to actually enter Wolfram Language input one wants—say in a notebook—as easily as possible. And with every new version we make enhancements to this.
One area that’s been in continuous development is interactive syntax highlighting. We first added syntax highlighting nearly two decades ago—and over time we’ve progressively made it more and more sophisticated, responding both as you type, and as code gets executed. Some highlighting has always had obvious meaning. But particularly highlighting that is dynamic and based on cursor position has sometimes been harder to interpret. And in Version 14—leveraging the brighter color palettes that have become the norm in recent years—we’ve tuned our dynamic highlighting so it’s easier to quickly tell “where you are” within the structure of an expression:

On the subject of “knowing what one has”, another enhancement—added in Version 13.2—is differentiated frame coloring for different kinds of visual objects in notebooks. Is that thing one has a graphic? Or an image? Or a graph? Now one can tell from the color of frame when one selects it:

An important aspect of the Wolfram Language is that the names of built-in functions are spelled out enough that it’s easy to tell what they do. But often the names are therefore necessarily quite long, and so it’s important to be able to autocomplete them when one’s typing. In 13.3 we added the notion of “fuzzy autocompletion” that not only “completes to the end” a name one’s typing, but also can fill in intermediate letters, change capitalization, etc. Thus, for example, just typing lll brings up an autocompletion menu that begins with ListLogLogPlot:

A major user interface update that first appeared in Version 13.1—and has been enhanced in subsequent versions—is a default toolbar for every notebook:
![]()
The toolbar provides immediate access to evaluation controls, cell formatting and various kinds of input (like inline cells, ![]() , hyperlinks, drawing canvas, etc.)—as well as to things like
, hyperlinks, drawing canvas, etc.)—as well as to things like ![]() cloud publishing,
cloud publishing, ![]() documentation search and
documentation search and ![]() “chat” (i.e. LLM) settings.
“chat” (i.e. LLM) settings.
Much of the time, it’s useful to have the toolbar displayed in any notebook you’re working with. But on the left-hand side there’s a little tiny ![]() that lets you minimize the toolbar:
that lets you minimize the toolbar:

In 14.0 there’s a Preferences setting that makes the toolbar come up minimized in any new notebook you create—and this in effect gives you the best of both worlds: you have immediate access to the toolbar, but your notebooks don’t have anything “extra” that might distract from their content.
Another thing that’s advanced since Version 13 is the handling of “summary” forms of output in notebooks. A basic example is what happens if you generate a very large result. By default only a summary of the result is actually displayed. But now there’s a bar at the bottom that gives various options for how to handle the actual output:

By default, the output is only stored in your current kernel session. But by pressing the Iconize button you get an iconized form that will appear directly in your notebook (or one that can be copied anywhere) and that “has the whole output inside”. There’s also a Store full expression in notebook button, which will “invisibly” store the output expression “behind” the summary display.
If the expression is stored in the notebook, then it’ll be persistent across kernel sessions. Otherwise, well, you won’t be able to get to it in a different kernel session; the only thing you’ll have is the summary display:

It’s a similar story for large “computational objects”. Like here’s a Nearest function with a million data points:
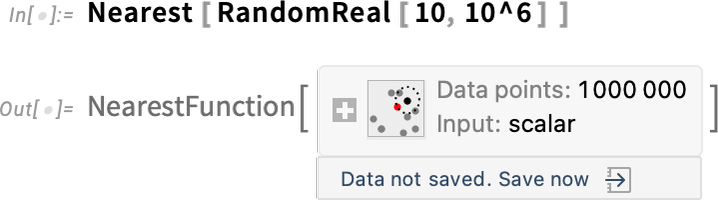
By default, the data is just something that exists in your current kernel session. But now there’s a menu that lets you save the data in various persistent locations:

And There’s the Cloud Too
There are many ways to run the Wolfram Language. Even in Version 1.0 we had the notion of remote kernels: the notebook front end running on one machine (in those days essentially always a Mac, or a NeXT), and the kernel running on a different machine (in those days sometimes even connected by phone lines). But a decade ago came a major step forward: the Wolfram Cloud.
There are really two distinct ways in which the cloud is used. The first is in delivering a notebook experience similar to our longtime desktop experience, but running purely in a browser. And the second is in delivering APIs and other programmatically accessed capabilities—notably, even at the beginning, a decade ago, through things like APIFunction.
The Wolfram Cloud has been the target of intense development now for nearly 15 years. Alongside it have also come Wolfram Application Server and Wolfram Web Engine, which provide more streamlined support specifically for APIs (without things like user management, etc., but with things like clustering).
All of these—but particularly the Wolfram Cloud—have become core technology capabilities for us, supporting many of our other activities. So, for example, the Wolfram Function Repository and Wolfram Paclet Repository are both based on the Wolfram Cloud (and in fact this is true of our whole resource system). And when we came to build the Wolfram plugin for ChatGPT earlier this year, using the Wolfram Cloud allowed us to have the plugin deployed within a matter of days.
Since Version 13 there have been quite a few very different applications of the Wolfram Cloud. One is for the function ARPublish, which takes 3D geometry and puts it in the Wolfram Cloud with appropriate metadata to allow phones to get augmented-reality versions from a QR code of a cloud URL:


On the Cloud Notebook side, there’s been a steady increase in usage, notably of embedded Cloud Notebooks, which have for example become common on Wolfram Community, and are used all over the Wolfram Demonstrations Project. Our goal all along has been to make Cloud Notebooks be as easy to use as simple webpages, but to have the depth of capabilities that we’ve developed in notebooks over the past 35 years. We achieved this some years ago for fairly small notebooks, but in the past couple of years we’ve been going progressively further in handling even multi-hundred-megabyte notebooks. It’s a complicated story of caching, refreshing—and dodging the vicissitudes of web browsers. But at this point the vast majority of notebooks can be seamlessly deployed to the cloud, and will display as immediately as simple webpages.
The Great Integration Story for External Code
It’s been possible to call external code from Wolfram Language ever since Version 1.0. But in Version 14 there are important advances in the extent and ease with which external code can be integrated. The overall goal is to be able to use all the power and coherence of the Wolfram Language even when some part of a computation is done in external code. And in Version 14 we’ve done a lot to streamline and automate the process by which external code can be integrated into the language.
Once something is integrated into the Wolfram Language it just becomes, for example, a function that can be used just like any other Wolfram Language function. But what’s underneath is necessarily quite different for different kinds of external code. There’s one setup for interpreted languages like Python. There’s another for C-like compiled languages and dynamic libraries. (And then there are others for external processes, APIs, and what amount to “importable code specifications”, say for neural networks.)
Let’s start with Python. We’ve had ExternalEvaluate for evaluating Python code since 2018. But when you actually come to use Python there are all these dependencies and libraries to deal with. And, yes, that’s one of the places where the incredible advantages of the Wolfram Language and its coherent design are painfully evident. But in Version 14.0 we now have a way to encapsulate all that Python complexity, so that we can deliver Python functionality within Wolfram Language, hiding all the messiness of Python dependencies, and even the versioning of Python itself.
As an example, let’s say we want to make a Wolfram Language function Emojize that uses the Python function emojize within the emoji Python library. Here’s how we can do that:

And now you can just call Emojize in the Wolfram Language and—under the hood—it’ll run Python code:

The way this works is that the first time you call Emojize, a Python environment with all the right features is created, then is cached for subsequent uses. And what’s important is that the Wolfram Language specification of Emojize is completely system independent (or as system independent as it can be, given vicissitudes of Python implementations). So that means that you can, for example, deploy Emojize in the Wolfram Function Repository just like you would deploy something written purely in Wolfram Language.
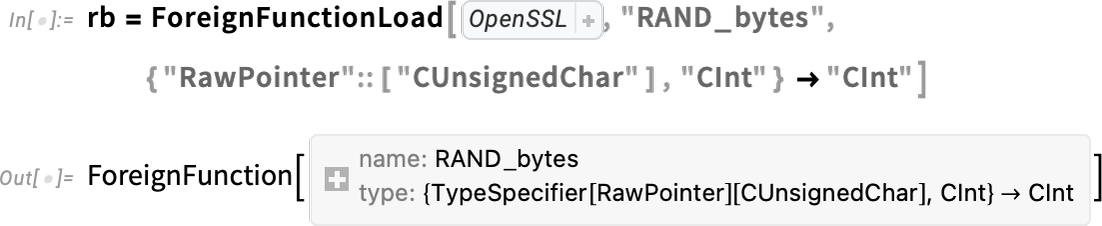
There’s very different engineering involved in calling C-compatible functions in dynamic libraries. But in Version 13.3 we also made this very streamlined using the function ForeignFunctionLoad. There’s all sorts of complexity associated with converting to and from native C data types, managing memory for data structures, etc. But we’ve now got very clean ways to do this in Wolfram Language.
As an example, here’s how one sets up a “foreign function” call to a function RAND_bytes in the OpenSSL library:
Inside this, we’re using Wolfram Language compiler technology to specify the native C types that will be used in the foreign function. But now we can package this all up into a Wolfram Language function:

And we can call this function just like any other Wolfram Language function:
Internally, all sorts of complicated things are going on. For example, we’re allocating a raw memory buffer that’s then getting fed to our C function. But when we do that memory allocation we’re creating a symbolic structure that defines it as a “managed object”:
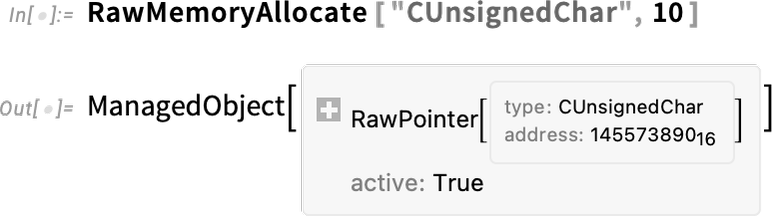
And now when this object is no longer being used, the memory associated with it will be automatically freed.
And, yes, with both Python and C there’s quite a bit of complexity underneath. But the good news is that in Version 14 we’ve basically been able to automate handling it. And the result is that what gets exposed is pure, simple Wolfram Language.
But there’s another big piece to this. Within particular Python or C libraries there are often elaborate definitions of data structures that are specific to that library. And so to use these libraries one has to dive into all the—potentially idiosyncratic—complexities of those definitions. But in the Wolfram Language we have consistent symbolic representations for things, whether they’re images, or dates or types of chemicals. When you first hook up an external library you have to map its data structures to these. But once that’s done, anyone can use what’s been built, and seamlessly integrate with other things they’re doing, perhaps even calling other external code. In effect what’s happening is that one’s leveraging the whole design framework of the Wolfram Language, and applying that even when one’s using underlying implementations that aren’t based on the Wolfram Language.
For Serious Developers
A single line (or less) of Wolfram Language code can do a lot. But one of the remarkable things about the language is that it’s fundamentally scalable: good both for very short programs and very long programs. And since Version 13 there’ve been several advances in handling very long programs. One of them concerns “code editing”.
Standard Wolfram Notebooks work very well for exploratory, expository and many other forms of work. And it’s certainly possible to write large amounts of code in standard notebooks (and, for example, I personally do it). But when one’s doing “software-engineering-style work” it’s both more convenient and more familiar to use what amounts to a pure code editor, largely separate from code execution and exposition. And this is why we have the “package editor”, accessible from File > New > Package/Script. You’re still operating in the notebook environment, with all its sophisticated capabilities. But things have been “skinned” to provide a much more textual “code experience”—both in terms of editing, and in terms of what actually gets saved in .wl files.
Here’s typical example of the package editor in action (in this case applied to our GitLink package):

Several things are immediately evident. First, it’s very line oriented. Lines (of code) are numbered, and don’t break except at explicit newlines. There are headings just like in ordinary notebooks, but when the file is saved, they’re stored as comments with a certain stylized structure:

It’s still perfectly possible to run code in the package editor, but the output won’t get saved in the .wl file:

One thing that’s changed since Version 13 is that the toolbar is much enhanced. And for example there’s now “smart search” that is aware of code structure:

You can also ask to go to a line number—and you’ll immediately see whatever lines of code are nearby:

In addition to code editing, another set of features new since Version 13 of importance to serious developers concern automated testing. The main advance is the introduction of a fully symbolic testing framework, in which individual tests are represented as symbolic objects
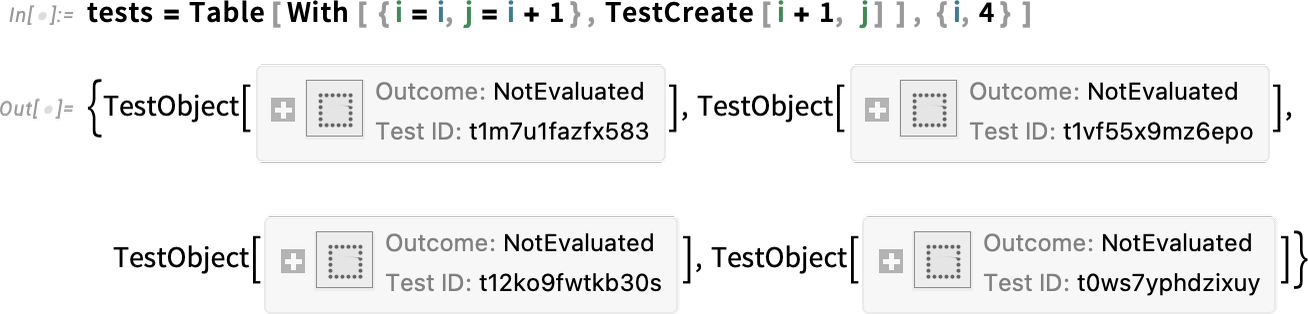
and can be manipulated in symbolic form, then run using functions like TestEvaluate and TestReport:

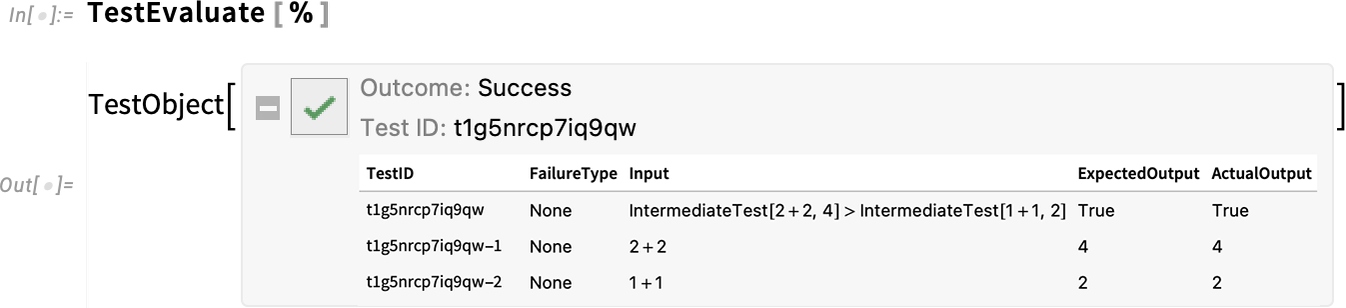
In Version 14.0 there’s another new testing function—IntermediateTest—that lets you insert what amount to checkpoints inside larger tests:

Evaluating this test, we see that the intermediate tests were also run:
Wolfram Function Repository: 2900 Functions & Counting
The Wolfram Function Repository has been a big success. We introduced it in 2019 as a way to make specific, individual contributed functions available in the Wolfram Language. And now there are more than 2900 such functions in the Repository.
The nearly 7000 functions that constitute the Wolfram Language as it is today have been painstakingly developed over the past three and a half decades, always mindful of creating a coherent whole with consistent design principles. And now in a sense the success of the Function Repository is one of the dividends of all that effort. Because it’s the coherence and consistency of the underlying language and its design principles that make it feasible to just add one function at a time, and have it really work. You want to add a function to do some very specific operation that combines images and graphs. Well, there’s a consistent representation of both images and graphs in the Wolfram Language, which you can leverage. And by following the principles of the Wolfram Language—like for the naming of functions—you can create a function that’ll be easy for Wolfram Language users to understand and use.
Using the Wolfram Function Repository is a remarkably seamless process. If you know the function’s name, you can just call it using ResourceFunction; the function will be loaded if it’s needed, and then it’ll just run:

If there’s an update available for the function, it’ll give you a message, but run the old version anyway. The message has a button that lets you load in the update; then you can rerun your input and use the new version. (If you’re writing code where you want to “burn in” a particular version of a function, you can just use the ResourceVersion option of ResourceFunction.)
If you want your code to look more elegant, just evaluate the ResourceFunction object

and use the formatted version:

And, by the way, pressing the + then gives you more information about the function:

An important feature of functions in the Function Repository is that they all have documentation pages—that are organized pretty much like the pages for built-in functions:

But how does one create a Function Repository entry? Just go to File > New > Repository Item > Function Repository Item and you’ll get a Definition Notebook:

We’ve optimized this to be as easy to fill in as possible, minimizing boilerplate and automatically checking for correctness and consistency whenever possible. And the result is that it’s perfectly realistic to create a simple Function Repository item in under an hour—with the main time spent being in the writing of good expository examples.
When you press Submit to Repository your function gets sent to the Wolfram Function Repository review team, whose mandate is to ensure that functions in the repository do what they say they do, work in a way that is consistent with general Wolfram Language design principles, have good names, and are adequately documented. Except for very specialized functions, the goal is to finish reviews within a week (and sometimes considerably sooner)—and to publish functions as soon as they are ready.
There’s a digest of new (and updated) functions in the Function Repository that gets sent out every Friday—and makes for interesting reading (you can subscribe here):

The Wolfram Function Repository is a curated public resource that can be accessed from any Wolfram Language system (and, by the way, the source code for every function is available—just press the Source Notebook button). But there’s another important use case for the infrastructure of the Function Repository: privately deployed “resource functions”.
It all works through the Wolfram Cloud. You use the exact same Definition Notebook, but now instead of submitting to the public Wolfram Function Repository, you just deploy your function to the Wolfram Cloud. You can make it private so that only you, or some specific group, can access it. Or you can make it public, so anyone who knows its URL can immediately access and use it in their Wolfram Language system.
This turns out to be a tremendously useful mechanism, both for group projects, and for creating published material. In a sense it’s a very lightweight but robust way to distribute code—packaged into functions that can immediately be used. (By the way, to find the functions you’ve published from your Wolfram Cloud account, just go to the DeployedResources folder in the cloud file browser.)
(For organizations that want to manage their own function repository, it’s worth mentioning that the whole Wolfram Function Repository mechanism—including the infrastructure for doing reviews, etc.—is also available in a private form through the Wolfram Enterprise Private Cloud.)
So what’s in the public Wolfram Function Repository? There are a lot of “specialty functions” intended for specific “niche” purposes—but very useful if they’re what you want:





There are functions that add various kinds of visualizations:







Some functions set up user interfaces:

Some functions link to external services:




Some functions provide simple utilities:

There are also functions that are being explored for potential inclusion in the core system:


There are also lots of “leading-edge” functions, added as part of research or exploratory development. And for example in pieces I write (including this one), I make a point of having all pictures and other output be backed by “click-to-copy” code that reproduces them—and this code quite often contains functions either from the public Wolfram Function Repository or from (publicly accessible) private deployments.
The Paclet Repository Arrives
Paclets are a technology we’ve used for more than a decade and a half to distribute updated functionality to Wolfram Language systems in the field. In Version 13 we began the process of providing tools for anyone to create paclets. And since Version 13 we’ve introduced the Wolfram Language Paclet Repository as a centralized repository for paclets:
What is a paclet? It’s a collection of Wolfram Language functionality—including function definitions, documentation, external libraries, stylesheets, palettes and more—that can be distributed as a unit, and immediately deployed in any Wolfram Language system.
The Paclet Repository is a centralized place where anyone can publish paclets for public distribution. So how does this relate to the Wolfram Function Repository? They are interestingly complementary—with different optimization and different setups. The Function Repository is more lightweight, the Paclet Repository more flexible. The Function Repository is for making available individual new functions, that independently fit into the whole existing structure of the Wolfram Language. The Paclet Repository is for making available larger-scale pieces of functionality, that can define a whole framework and environment of their own.
The Function Repository is also fully curated, with every function being reviewed by our team before it is posted. The Paclet Repository is an immediate-deployment system, without pre-publication review. In the Function Repository every function is specified just by its name—and our review team is responsible for ensuring that names are well chosen and have no conflicts. In the Paclet Repository, every contributor gets their own namespace, and all their functions and other material live inside that namespace. So, for example, I contributed the function RandomHypergraph to the Function Repository, which can be accessed just as ResourceFunction["RandomHypergraph"]. But if I had put this function in a paclet in the Paclet Repository, it would have to be accessed as something like PacletSymbol["StephenWolfram/Hypergraphs", "RandomHypergraph"].
PacletSymbol, by the way, is a convenient way of “deep accessing” individual functions inside a paclet. PacletSymbol temporarily installs (and loads) a paclet so that you can access a particular symbol in it. But more often one wants to permanently install a paclet (using PacletInstall), then explicitly load its contents (using Needs) whenever one wants to have its symbols available. (All the various ancillary elements, like documentation, stylesheets, etc. in a paclet get set up when it is installed.)
What does a paclet look like in the Paclet Repository? Every paclet has a home page that typically includes an overall summary, a guide to the functions in the paclet, and some overall examples of the paclet:

Individual functions typically have their own documentation pages:

Just like in the main Wolfram Language documentation, there can be a whole hierarchy of guide pages, and there can be things like tutorials.
Notice that in examples in paclet documentation, one often sees constructs like ![]() . These represent symbols in the paclet, presented in forms like PacletSymbol["WolframChemistry/ProteinVisualization", "AmidePlanePlot"] that allow these symbols to be accessed in a “standalone” way. If you directly evaluate such a form, by the way, it’ll force (temporary) installation of the paclet, then return the actual, raw symbol that appears in the paclet:
. These represent symbols in the paclet, presented in forms like PacletSymbol["WolframChemistry/ProteinVisualization", "AmidePlanePlot"] that allow these symbols to be accessed in a “standalone” way. If you directly evaluate such a form, by the way, it’ll force (temporary) installation of the paclet, then return the actual, raw symbol that appears in the paclet:
So how does one create a paclet suitable for submission to the Paclet Repository? You can do it purely programmatically, or you can start from File > New > Repository Item > Paclet Repository Item, which launches what amounts to a whole paclet creation IDE. The first step is to specify where you want to assemble your paclet. You give some basic information

then a Paclet Resource Definition Notebook is created, from which you can give function definitions, set up documentation pages, specify what you want your paclet’s home page to be like, etc.:

There are lots of sophisticated tools that let you create full-featured paclets with the same kind of breadth and depth of capabilities that you find in the Wolfram Language itself. For example, Documentation Tools lets you construct full-featured documentation pages (function pages, guide pages, tutorials, …):

Once you’ve assembled a paclet, you can check it, build it, deploy it privately—or submit it to the Paclet Repository. And once you submit it, it will automatically get set up on the Paclet Repository servers, and within just a few minutes the pages you’ve created describing your paclet will show up on the Paclet Repository website.
So what’s in the Paclet Repository so far? There’s a lot of good and very serious stuff, contributed both by teams at our company and by members of the broader Wolfram Language community. In fact, many of the 134 paclets now in the Paclet Repository have enough in them that there’s a whole piece like this that one could write about them.
One category of things you’ll find in the Paclet Repository are snapshots of our ongoing internal development projects—many of which will eventually become built-in parts of the Wolfram Language. A good example of this is our LLM and Chat Notebook functionality, whose rapid development and deployment over the past year was made possible by the use of the Paclet Repository. Another example, representing ongoing work from our chemistry team (AKA WolframChemistry in the Paclet Repository) is the ChemistryFunctions paclet, which contains functions like:

And, yes, this is interactive:

Or, also from WolframChemistry:

Another “development snapshot” is DiffTools—a paclet for making and viewing diffs between strings, cells, notebooks, etc.:

A major paclet is QuantumFramework—which provides the functionality for our Wolfram Quantum Framework
and delivers broad support for quantum computing (with at least a few connections to multiway systems and our Physics Project):


Talking of our Physics Project, there are over 200 functions supporting it that are in the Wolfram Function Repository. But there are also paclets, like WolframInstitute/Hypergraph:

An example of an externally contributed package is Automata—with more than 250 functions for doing computations related to finite automata:


Another contributed paclet is FunctionalParsers, which goes from a symbolic parser specification to an actual parser, here being used in a reverse mode to generate random “sentences”:

Phi4Tools is a more specialized paclet, for working with Feynman diagrams in ![]() field theory:
field theory:



And, as another example, here’s MaXrd, for crystallography and x-ray scattering:


As just one more example, there’s the Organizer paclet—a utility paclet for making and manipulating organizer notebooks. But unlike the other paclets we’ve seen here, it doesn’t expose any Wolfram Language functions; instead, when you install it, it puts a palette in your Palettes list:


Coming Attractions
As of today, Version 14 is finished, and out in the world. So what’s next? We have lots of projects underway—some already with years of development behind them. Some extend and strengthen what’s already in the Wolfram Language; some take it in new directions.
One major focus is broadening and streamlining the deployment of the language: unifying the way it’s delivered and installed on computers, packaging it so it can be efficiently integrated into other standalone applications, etc.
Another major focus is expanding the handling of very large amounts of data by the Wolfram Language—and seamlessly integrating out-of-core and lazy processing.
Then of course there’s algorithmic development. Some is “classical”, directly building on the towers of functionality we’ve developed over the decades. Some is more “AI based”. We’ve been creating heuristic algorithms and meta-algorithms ever since Version 1.0—increasingly using methods from machine learning. How far will neural net methods go? We don’t know yet. We’re routinely using them in things like algorithm selection. But to what extent can they help in the heart of algorithms?
I’m reminded of something we did back in 1987 in developing Version 1.0. There was a long tradition in numerical analysis of painstakingly deriving series approximations for particular cases of mathematical functions. But we wanted to be able to compute hundreds of different functions to arbitrary precision for any complex values of their arguments. So how did we do it? We generalized from series to rational approximations—and then, in a very “machine-learning-esque” way—we spent months of CPU time systematically optimizing these approximations. Well, we’ve been trying to do the same kind of thing again—though now over more ambitious domains—and now using not rational functions but large neural nets as our basis.
We’ve also been exploring using neural nets to “control” precise algorithms, in effect making heuristic choices which either guide or can be validated by the precise algorithms. So far, none of what we’ve produced has outperformed our existing methods, but it seems plausible that fairly soon it will.
We’re doing a lot with various aspects of metaprogramming. There’s the project of
getting LLMs to help in the construction of Wolfram Language code—and in giving comments on it, and in analyzing what went wrong if the code didn’t do what one expected. Then there’s code annotation—where LLMs may help in doing things like predicting the most likely type for something. And there’s code compilation. We’ve been working for many years on a full-scale compiler for the Wolfram Language, and in every version what we have becomes progressively more capable. We’ve been doing some level of automatic compilation in particular cases (particularly ones involving numerical computation) for more than 30 years. And eventually full-scale automatic compilation will be possible for everything. But as of now some of the biggest payoffs from our compiler technology have been for our internal development, where we can now get optimal down-to-the-metal performance simply by compiled (albeit carefully written) Wolfram Language code.
One of the big lessons of the surprising success of LLMs is that there’s potentially more structure in meaningful human language than we thought. I’ve long been interested in creating what I’ve called a “symbolic discourse language” that gives a computational representation of everyday discourse. The LLMs haven’t explicitly done that. But they encourage the idea that it should be possible, and they also provide practical help in doing it. And whether the goal is to be able to represent narrative text, or contracts, or textual specifications, it’s a matter of extending the computational language we’ve built to encompass more kinds of concepts and structures.
There are typically several kinds of drivers for our continued development efforts. Sometimes it’s a question of continuing to build a tower of capabilities in some known direction (like, for example, solving PDEs). Sometimes the tower we’ve built suddenly lets us see new possibilities. Sometimes when we actually use what we’ve built we realize there’s an obvious way to polish or extend it—or to “double down” on something that we can now see is valuable. And then there are cases where things happening in the technology world suddenly open up new possibilities—like LLMs have recently done, and perhaps XR will eventually do. And finally there are cases where new science-related insights suggest new directions.
I had assumed that our Physics Project would at best have practical applications only centuries hence. But in fact it’s become clear that the correspondence it’s defined between physics and computation gives us quite immediate new ways to think about aspects of practical computation. And indeed we’re now actively exploring how to use this to define a new level of parallel and distributed computation in the Wolfram Language, as well as to represent symbolically not only the results of computations but also the ongoing process of computation.
One might think that after nearly four decades of intense development there wouldn’t be anything left to do in developing the Wolfram Language. But in fact at every level we reach, there’s ever more that becomes possible, and ever more that can we see might be possible. And indeed this moment is a particularly fertile one, with an unprecedentedly broad waterfront of possibilities. Version 14 is an important and satisfying waypoint. But there are wonderful things ahead—as we continue our long-term mission to make the computational paradigm achieve its potential, and to build our computational language to help that happen.
Posted in: Big Picture, Mathematica, New Technology, Wolfram Language






