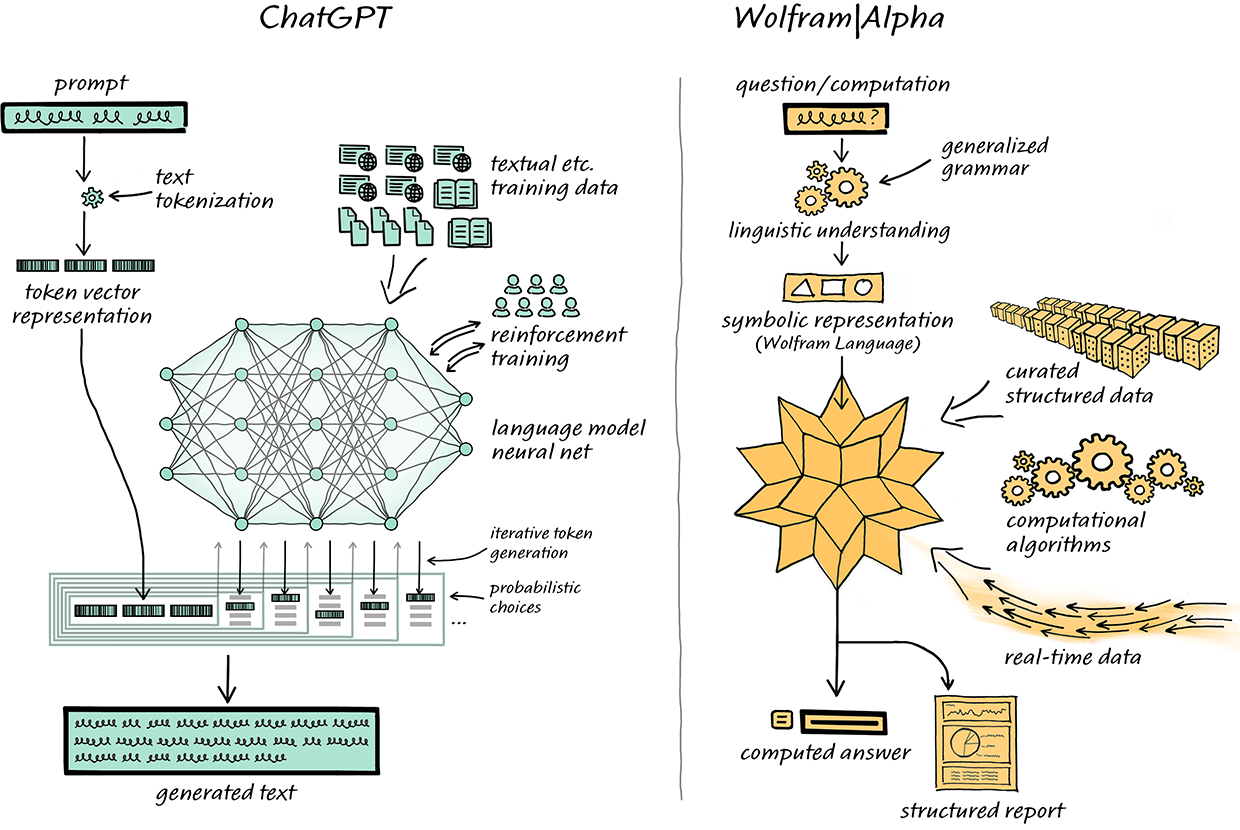
Since this was written, OpenAI has discontinued ChatGPT Plugins and launched custom GPTs. Find more information about the Wolfram GPT here: https://gpt.wolfram.com.
In Just Two and a Half Months…
Early in January I wrote about the possibility of connecting ChatGPT to Wolfram|Alpha. And today—just two and a half months later—I’m excited to announce that it’s happened! Thanks to some heroic software engineering by our team and by OpenAI, ChatGPT can now call on Wolfram|Alpha—and Wolfram Language as well—to give it what we might think of as “computational superpowers”. It’s still very early days for all of this, but it’s already very impressive—and one can begin to see how amazingly powerful (and perhaps even revolutionary) what we can call “
Back in January, I made the point that, as an LLM neural net, ChatGPT—for all its remarkable prowess in textually generating material “like” what it’s read from the web, etc.—can’t itself be expected to do actual nontrivial computations, or to systematically produce correct (rather than just “looks roughly right”) data, etc. But when it’s connected to the Wolfram plugin it can do these things. So here’s my (very simple) first example from January, but now done by ChatGPT with “Wolfram superpowers” installed: Continue reading