Won’t AI Eventually Be Able to Do Everything?

Particularly given its recent surprise successes, there’s a somewhat widespread belief that eventually AI will be able to “do everything”, or at least everything we currently do. So what about science? Over the centuries we humans have made incremental progress, gradually building up what’s now essentially the single largest intellectual edifice of our civilization. But despite all our efforts, there are still all sorts of scientific questions that remain. So can AI now come in and just solve all of them?

To this ultimate question we’re going to see that the answer is inevitably and firmly no. But that certainly doesn’t mean AI can’t importantly help the progress of science. At a very practical level, for example, LLMs provide a new kind of linguistic interface to the computational capabilities that we’ve spent so long building in the Wolfram Language. And through their knowledge of “conventional scientific wisdom” LLMs can often provide what amounts to very high-level “autocomplete” for filling in “conventional answers” or “conventional next steps” in scientific work. Continue reading

Version 14.0 of Wolfram Language and Mathematica is available immediately both on the desktop and in the cloud. See also more detailed information on Version 13.1, Version 13.2 and Version 13.3.

Building Something Greater and Greater… for 35 Years and Counting

Today we celebrate a new waypoint on our journey of nearly four decades with the release of Version 14.0 of Wolfram Language and Mathematica. Over the two years since we released Version 13.0 we’ve been steadily delivering the fruits of our research and development in .1 releases every six months. Today we’re aggregating these—and more—into Version 14.0.

It’s been more than 35 years now since we released Version 1.0. And all those years we’ve been continuing to build a taller and taller tower of capabilities, progressively expanding the scope of our vision and the breadth of our computational coverage of the world:

Continue reading

The Concept of the Observer

We call it perception. We call it measurement. We call it analysis. But in the end it’s about how we take the world as it is, and derive from it the impression of it that we have in our minds.

We might have thought that we could do science “purely objectively” without any reference to observers or their nature. But what we’ve discovered particularly dramatically in our Physics Project is that the nature of us as observers is critical even in determining the most fundamental laws we attribute to the universe.

But what ultimately does an observer—say like us—do? And how can we make a theoretical framework for it? Much as we have a general model for the process of computation—instantiated by something like a Turing machine—we’d like to have a general model for the process of observation: a general “observer theory”. Continue reading

The Importance of Multiway Systems

It’s all about systems where there can in effect be many possible paths of history. In a typical standard computational system like a cellular automaton, there’s always just one path, defined by evolution from one state to the next. But in a multiway system, there can be many possible next states—and thus many possible paths of history. Multiway systems have a central role in our Physics Project, particularly in connection with quantum mechanics. But what’s now emerging is that multiway systems in fact serve as a quite general foundation for a whole new “multicomputational” paradigm for modeling.

My objective here is twofold. First, I want to use multiway systems as minimal models for growth processes based on aggregation and tiling. And second, I want to use this concrete application as a way to develop further intuition about multiway systems in general. Elsewhere I have explored multiway systems for strings, multiway systems based on numbers, multiway Turing machines, multiway combinators, multiway expression evaluation and multiway systems based on games and puzzles. But in studying multiway systems for aggregation and tiling, we’ll be dealing with something that is immediately more physical and tangible. Continue reading

Transcript of a talk at TED AI on October 17, 2023, in San Francisco

Human language. Mathematics. Logic. These are all ways to formalize the world. And in our century there’s a new and yet more powerful one: computation.

And for nearly 50 years I’ve had the great privilege of building an ever taller tower of science and technology based on that idea of computation. And today I want to tell you some of what that’s led to.

There’s a lot to talk about—so I’m going to go quickly… sometimes with just a sentence summarizing what I’ve written a whole book about. Continue reading

An Unexpected Correspondence

Enter any expression and it’ll get evaluated:

And internally—say in the Wolfram Language—what’s going on is that the expression is progressively being transformed using all available rules until no more rules apply. Here the process can be represented like this:

We can think of the yellow boxes in this picture as corresponding to “evaluation events” that transform one “state of the expression” (represented by a blue box) to another, eventually reaching the “fixed point” 12.

And so far this may all seem very simple. But actually there are many surprisingly complicated and deep issues and questions. For example, to what extent can the evaluation events be applied in different orders, or in parallel? Does one always get the same answer? What about non-terminating sequences of events? And so on. Continue reading

Logic, Math and AI

In many ways the great quest of Doug Lenat’s life was an attempt to follow on directly from the work of Aristotle and Leibniz. For what Doug was fundamentally trying to do over the forty years he spent developing his CYC system was to use the framework of logic—in more or less the same form that Aristotle and Leibniz had it—to capture what happens in the world. It was a noble effort and an impressive example of long-term intellectual tenacity. And while I never managed to actually use CYC myself, I consider it a magnificent experiment—that if nothing else ultimately served to demonstrate the importance of building frameworks beyond logic alone in usefully representing and reasoning about the world. Continue reading

AIs and Alien Minds

How do alien minds perceive the world? It’s an old and oft-debated question in philosophy. And it now turns out to also be a question that rises to prominence in connection with the concept of the ruliad that’s emerged from our Wolfram Physics Project.

I’ve wondered about alien minds for a long time—and tried all sorts of ways to imagine what it might be like to see things from their point of view. But in the past I’ve never really had a way to build my intuition about it. That is, until now. So, what’s changed? It’s AI. Because in AI we finally have an accessible form of alien mind. Continue reading

The Leading Edge of 2023 Technology … and Beyond

Today we’re launching Version 13.3 of Wolfram Language and Mathematica—both available immediately on desktop and cloud. It’s only been 196 days since we released Version 13.2, but there’s a lot that’s new, not least a whole subsystem around LLMs.

Last Friday (June 23) we celebrated 35 years since Version 1.0 of Mathematica (and what’s now Wolfram Language). And to me it’s incredible how far we’ve come in these 35 years—yet how consistent we’ve been in our mission and goals, and how well we’ve been able to just keep building on the foundations we created all those years ago. Continue reading

This is part of an ongoing series about our LLM-related technology:ChatGPT Gets Its “Wolfram Superpowers”!Instant Plugins for ChatGPT: Introducing the Wolfram ChatGPT Plugin KitThe New World of LLM Functions: Integrating LLM Technology into the Wolfram LanguagePrompts for Work & Play: Launching the Wolfram Prompt RepositoryIntroducing Chat Notebooks: Integrating LLMs into the Notebook Paradigm

A New Kind of Notebook

We originally invented the concept of “Notebooks” back in 1987, for Version 1.0 of Mathematica. And over the past 36 years, Notebooks have proved to be an incredibly convenient medium in which to do—and publish—work (and indeed, I, for example, have created hundreds of thousands of them). And, yes, eventually the basic concepts of Notebooks were widely copied—though still not even with everything we had back in 1987!

Well, now there’s a new challenge and opportunity for Notebooks: integrating LLM functionality into them. It’s an interesting design problem, and I’m pretty pleased with what we’ve come up with. And today we’re introducing Chat Notebooks as a new kind of Notebook that supports LLM-based chat functionality. Continue reading

This is part of an ongoing series about our LLM-related technology:ChatGPT Gets Its “Wolfram Superpowers”!Instant Plugins for ChatGPT: Introducing the Wolfram ChatGPT Plugin KitThe New World of LLM Functions: Integrating LLM Technology into the Wolfram LanguagePrompts for Work & Play: Launching the Wolfram Prompt RepositoryIntroducing Chat Notebooks: Integrating LLMs into the Notebook Paradigm

Building Blocks of “LLM Programming”

Prompts are how one channels an LLM to do something. LLMs in a sense always have lots of “latent capability” (e.g. from their training on billions of webpages). But prompts—in a way that’s still scientifically mysterious—are what let one “engineer” what part of that capability to bring out. Continue reading

This is part of an ongoing series about our LLM-related technology:ChatGPT Gets Its “Wolfram Superpowers”!Instant Plugins for ChatGPT: Introducing the Wolfram ChatGPT Plugin KitThe New World of LLM Functions: Integrating LLM Technology into the Wolfram LanguagePrompts for Work & Play: Launching the Wolfram Prompt RepositoryIntroducing Chat Notebooks: Integrating LLMs into the Notebook Paradigm

Turning LLM Capabilities into Functions

So far, we mostly think of LLMs as things we interact directly with, say through chat interfaces. But what if we could take LLM functionality and “package it up” so that we can routinely use it as a component inside anything we’re doing? Well, that’s what our new LLMFunction is about. Continue reading

This is part of an ongoing series about our LLM-related technology:ChatGPT Gets Its “Wolfram Superpowers”!Instant Plugins for ChatGPT: Introducing the Wolfram ChatGPT Plugin KitThe New World of LLM Functions: Integrating LLM Technology into the Wolfram LanguagePrompts for Work & Play: Launching the Wolfram Prompt RepositoryIntroducing Chat Notebooks: Integrating LLMs into the Notebook Paradigm

Build a New Plugin in under a Minute…

A few weeks ago, in collaboration with OpenAI, we released the Wolfram plugin for ChatGPT, which lets ChatGPT use Wolfram Language and Wolfram|Alpha as tools, automatically called from within ChatGPT. One can think of this as adding broad “computational superpowers” to ChatGPT, giving access to all the general computational capabilities and computational knowledge in Wolfram Language and Wolfram|Alpha.

But what if you want to make your own special plugin, that does specific computations, or has access to data or services that are for example available only on your own computer or computer system? Well, today we’re releasing a first version of a kit for doing that. And building on our whole Wolfram Language tech stack, we’ve managed to make the whole process extremely easy—to the point where it’s now realistic to deploy at least a basic custom ChatGPT plugin in under a minute. Continue reading

This is part of an ongoing series about our LLM-related technology:ChatGPT Gets Its “Wolfram Superpowers”!Instant Plugins for ChatGPT: Introducing the Wolfram ChatGPT Plugin KitThe New World of LLM Functions: Integrating LLM Technology into the Wolfram LanguagePrompts for Work & Play: Launching the Wolfram Prompt RepositoryIntroducing Chat Notebooks: Integrating LLMs into the Notebook Paradigm

In Just Two and a Half Months…

Early in January I wrote about the possibility of connecting ChatGPT to Wolfram|Alpha. And today—just two and a half months later—I’m excited to announce that it’s happened! Thanks to some heroic software engineering by our team and by OpenAI, ChatGPT can now call on Wolfram|Alpha—and Wolfram Language as well—to give it what we might think of as “computational superpowers”. It’s still very early days for all of this, but it’s already very impressive—and one can begin to see how amazingly powerful (and perhaps even revolutionary) what we can call “ChatGPT + Wolfram” can be.

Back in January, I made the point that, as an LLM neural net, ChatGPT—for all its remarkable prowess in textually generating material “like” what it’s read from the web, etc.—can’t itself be expected to do actual nontrivial computations, or to systematically produce correct (rather than just “looks roughly right”) data, etc. But when it’s connected to the Wolfram plugin it can do these things. So here’s my (very simple) first example from January, but now done by ChatGPT with “Wolfram superpowers” installed: Continue reading

The Shock of ChatGPT

Just a few months ago writing an original essay seemed like something only a human could do. But then ChatGPT burst onto the scene. And suddenly we realized that an AI could write a passable human-like essay. So now it’s natural to wonder: How far will this go? What will AIs be able to do? And how will we humans fit in?

My goal here is to explore some of the science, technology—and philosophy—of what we can expect from AIs. I should say at the outset that this is a subject fraught with both intellectual and practical difficulty. And all I’ll be able to do here is give a snapshot of my current thinking—which will inevitably be incomplete—not least because, as I’ll discuss, trying to predict how history in an area like this will unfold is something that runs straight into an issue of basic science: the phenomenon of computational irreducibility. Continue reading

It’s Just Adding One Word at a Time

That ChatGPT can automatically generate something that reads even superficially like human-written text is remarkable, and unexpected. But how does it do it? And why does it work? My purpose here is to give a rough outline of what’s going on inside ChatGPT—and then to explore why it is that it can do so well in producing what we might consider to be meaningful text. I should say at the outset that I’m going to focus on the big picture of what’s going on—and while I’ll mention some engineering details, I won’t get deeply into them. (And the essence of what I’ll say applies just as well to other current “large language models” [LLMs] as to ChatGPT.)

The first thing to explain is that what ChatGPT is always fundamentally trying to do is to produce a “reasonable continuation” of whatever text it’s got so far, where by “reasonable” we mean “what one might expect someone to write after seeing what people have written on billions of webpages, etc.” Continue reading

The Mystery of the Second Law

Entropy increases. Mechanical work irreversibly turns into heat. The Second Law of thermodynamics is considered one of the great general principles of physical science. But 150 years after it was first introduced, there’s still something deeply mysterious about the Second Law. It almost seems like it’s going to be “provably true”. But one never quite gets there; it always seems to need something extra. Sometimes textbooks will gloss over everything; sometimes they’ll give some kind of “common-sense-but-outside-of-physics argument”. But the mystery of the Second Law has never gone away.

Why does the Second Law work? And does it even in fact always work, or is it actually sometimes violated? What does it really depend on? What would be needed to “prove it”?

For me personally the quest to understand the Second Law has been no less than a 50-year story. But back in the 1980s, as I began to explore the computational universe of simple programs, I discovered a fundamental phenomenon that was immediately reminiscent of the Second Law. And in the 1990s I started to map out just how this phenomenon might finally be able to demystify the Second Law. But it is only now—with ideas that have emerged from our Physics Project—that I think I can pull all the pieces together and finally be able to construct a proper framework to explain why—and to what extent—the Second Law is true. Continue reading

When I Was 12 Years Old…

I’ve been trying to understand the Second Law now for a bit more than 50 years.

It all started when I was 12 years old. Building on an earlier interest in space and spacecraft, I’d gotten very interested in physics, and was trying to read everything I could about it. There were several shelves of physics books at the local bookstore. But what I coveted most was the largest physics book collection there: a series of five plushly illustrated college textbooks. And as a kind of graduation gift when I finished (British) elementary school in June 1972 I arranged to get those books. And here they are, still on my bookshelf today, just a little faded, more than half a century later:

Continue reading

The Basic Arc of the Story

As I’ve explained elsewhere, I think I now finally understand the Second Law of thermodynamics. But it’s a new understanding, and to get to it I’ve had to overcome a certain amount of conventional wisdom about the Second Law that I at least have long taken for granted. And to check myself I’ve been keen to know just where this conventional wisdom came from, how it’s been validated, and what might have made it go astray.

And from this I’ve been led into a rather detailed examination of the origins and history of thermodynamics. All in all, it’s a fascinating story, that both explains what’s been believed about thermodynamics, and provides some powerful examples of the complicated dynamics of the development and acceptance of ideas. Continue reading

ChatGPT and Wolfram|Alpha

It’s always amazing when things suddenly “just work”. It happened to us with Wolfram|Alpha back in 2009. It happened with our Physics Project in 2020. And it’s happening now with OpenAI’s ChatGPT. Continue reading

Delivering from Our R&D Pipeline

In 2020 it was Versions 12.1 and 12.2; in 2021 Versions 12.3 and 13.0. In late June this year it was Version 13.1. And now we’re releasing Version 13.2. We continue to have a huge pipeline of R&D, some short term, some medium term, some long term (like decade-plus). Our goal is to deliver timely snapshots of where we’re at—so people can start using what we’ve built as quickly as possible. Continue reading

::[ ]

Threaded

MapApply

FeatureImpactPlot

IntegrateChangeVariables

ReconstructionMesh

VideoCapture

RootTree

ImplicitD

“ExprStruct”

ChemicalConvert

UniqueElements

ReplaceAt

TypeEvaluate

TreeLeafCount

QuestionSelector

IncludeSingularSolutions

KernelConfiguration

PhongShading

PatternReaction

FractionalD

OrdinalScale

DropShadowing

UnlabeledTree

FeatureValueDependencyPlot

CaputoD

BlockDiagonalMatrix

ModelPredictiveController

GeodesicPolyhedron

InertEvaluate

Until

TernaryListPlot

FromRawPointer

VideoScreenCapture

PermutationMatrix

FeatureValueImpactPlot

ApplyReaction

GraphJoin

TorusGraph

DSolveChangeVariables

CumulativeFeatureImpactPlot

TreeElementShape

LibraryFunctionDeclaration

SymmetricDifference

FlatShading

CircularArcThrough

GouraudShading

DiscreteInputOutputModel

EstimatedPointNormals

GraphProduct

NominalScale

QuestionGenerator

GraphSum

BuckyballGraph

ChemicalInstance

InertExpression

UpperTriangularMatrix

CreateTypeInstance

PlaybackSettings

DeleteElements

BlockUpperTriangularMatrix

CompilerCallback

BlockLowerTriangularMatrix

ToRawPointer

LocalEvaluate

LowerTriangularMatrix

UnmanageObject

TypeOf

DeleteAdjacentDuplicates

InfiniteLineThrough

$DefaultLocalKernels

TernaryPlotCorners

ForAllType

SameAs

ResidueSum

CompiledExpressionDeclaration

Cast

ParentEdgeStyle

TreeElementLabelFunction

TreeElementSizeFunction

ParentEdgeLabelStyle

ParentEdgeLabel

TreeElementSize

TreeElementLabelStyle

TreeElementCoordinates

VideoTransparency

TreeElementShapeFunction

ParentEdgeShapeFunction

ParentEdgeLabelFunction

TreeElementStyleFunction

ParentEdgeStyleFunction

🙀

The Epic Continues…

Last week it was 34 years since the original launch of Mathematica and what’s now the Wolfram Language. And through all those years we’ve energetically continued building further and further, adding ever more capabilities, and steadily extending the domain of the computational paradigm.

In recent years we’ve established something of a rhythm, delivering the fruits of our development efforts roughly twice a year. We released Version 13.0 on December 13, 2021. And now, roughly six months later, we’re releasing Version 13.1. As usual, even though it’s a “.1” release, it’s got a lot of new (and updated) functionality, some of which we’ve worked on for many years but finally now brought to fruition. Continue reading

The Nature of Alien Intelligence

“We’re going to launch lots of tiny spacecraft into interstellar space, have them discover alien intelligence, then bring back its technology to advance human technology by a million years”. I’ve heard some pretty wacky startup pitches over the years, but this might possibly be the all-time winner.

But as I thought about it, I realized that beyond the “absurdly extreme moonshot” character of this pitch, there’s some science that I’ve done that makes it clear that it’s also fundamentally philosophically confused. The nature of the confusion is interesting, however, and untangling it will give us an opportunity to illuminate some deep features of both intelligence and technology—and in the end suggest a way to think about the long-term trajectory of the very concept of technology and its relation to our universe.

Let’s start with a scenario. Let’s say one of the little spacecraft comes across a planet where it sees complicated swirling patterns:

&#10005

Continue reading

Humanizing Multicomputational Processes

Multicomputation is one of the core ideas of the Wolfram Physics Project—and in particular is at the heart of our emerging understanding of quantum mechanics. But how can one get an intuition for what is initially the rather abstract idea of multicomputation? A good approach, I believe, is to see it in action in familiar systems and situations. And I explore here what seems like a particularly good example: games and puzzles. Continue reading

From the Foundations Laid by A New Kind of Science

When A New Kind of Science was published twenty years ago I thought what it had to say was important. But what’s become increasingly clear—particularly in the last few years—is that it’s actually even much more important than I ever imagined. My original goal in A New Kind of Science was to take a step beyond the mathematical paradigm that had defined the state of the art in science for three centuries—and to introduce a new paradigm based on computation and on the exploration of the computational universe of possible programs. And already in A New Kind of Science one can see that there’s immense richness to what can be done with this new paradigm. Continue reading

I Think I Should Write a Quick Book…

In the end it’s about five and a half pounds of paper, 1280 pages, 973 illustrations and 583,313 words. And its creation took more than a decade of my life. Almost every day of my thirties, and a little beyond, I tenaciously worked on it. Figuring out more and more science. Developing new kinds of computational diagrams. Crafting an exposition that I wrote and rewrote to make as clear as possible. And painstakingly laying out page after page of what on May 14, 2002, would be published as A New Kind of Science.

I’ve written before (even in the book itself) about the intellectual journey involved in the creation of A New Kind of Science. But here I want to share some of the more practical “behind the scenes” journey of the making of what I and others usually now call simply “the NKS book”. Some of what I’ll talk about happened twenty years ago, some more like thirty years ago. And it’s been interesting to go back into my archives (and, yes, those backup tapes from 30 years ago were hard to read!) and relive some of what finally led to the delivery of the ideas and results of A New Kind of Science as truckloads of elegantly printed books with striking covers. Continue reading

Suddenly There’s Just So Much New Science to Do

Something remarkable has happened these past two years. For 45 years I’ve devoted myself to building a taller and taller tower of science and technology—which along the way has delivered many outputs of which I’m quite proud. But starting in 2020 with the unexpected breakthroughs of our Wolfram Physics Project we’ve jumped to a whole new level. And suddenly—yes, building on our multi-decade tower—it seems as if we’ve found a new paradigm that’s incredibly powerful, and that’s going to let us tackle an almost absurd range of longstanding questions in all sorts of areas of science.

Developing a fundamental theory of physics is certainly an ambitious place to start, and I’m happy to say that things seem to be going quite excellently there, not least in providing new foundations for many existing results and initiatives in physics. But the amazing (and to me very unexpected) thing is that we can take our new paradigm and also apply it to a huge range of other areas. Just a couple of weeks ago I published a 250-page treatise about its application to the “physicalization of metamathematics”—and to providing a very new view of the foundations of mathematics (with implications both for the question of what mathematics really is, and for the practical long-term future of mathematics). Continue reading

How Is It That Things Can Move?

It seems like the kind of question that might have been hotly debated by ancient philosophers, but would have been settled long ago: how is it that things can move? And indeed with the view of physical space that’s been almost universally adopted for the past two thousand years it’s basically a non-question. As crystallized by the likes of Euclid it’s been assumed that space is ultimately just a kind of “geometrical background” into which any physical thing can be put—and then moved around.

But in our Physics Project we’ve developed a fundamentally different view of space—in which space is not just a background, but has its own elaborate composition and structure. And in fact, we posit that space is in a sense everything that exists, and that all “things” are ultimately just features of the structure of space. We imagine that at the lowest level, space consists of large numbers of abstract “atoms of space” connected in a hypergraph that’s continually getting updated according to definite rules and that’s a huge version of something like this:

&#10005

Continue reading

1 | Mathematics and Physics Have the Same Foundations

One of the many surprising (and to me, unexpected) implications of our Physics Project is its suggestion of a very deep correspondence between the foundations of physics and mathematics. We might have imagined that physics would have certain laws, and mathematics would have certain theories, and that while they might be historically related, there wouldn’t be any fundamental formal correspondence between them.

But what our Physics Project suggests is that underneath everything we physically experience there is a single very general abstract structure—that we call the ruliad—and that our physical laws arise in an inexorable way from the particular samples we take of this structure. We can think of the ruliad as the entangled limit of all possible computations—or in effect a representation of all possible formal processes. And this then leads us to the idea that perhaps the ruliad might underlie not only physics but also mathematics—and that everything in mathematics, like everything in physics, might just be the result of sampling the ruliad. Continue reading

The March of Innovation Continues

Just a few weeks ago it was 1/3 of a century since Mathematica 1.0 was released. Today I’m excited to announce the latest results of our long-running R&D pipeline: Version 13 of Wolfram Language and Mathematica. (Yes, the 1, 3 theme—complete with the fact that it’s the 13th of the month today—is amusing, if coincidental.)

It’s 207 days—or a little over 6 months—since we released Version 12.3. And I’m pleased to say that in that short time an impressive amount of R&D has come to fruition: not only a total of 117 completely new functions, but also many hundreds of updated and upgraded functions, several thousand bug fixes and small enhancements, and a host of new ideas to make the system ever easier and smoother to use.

Every day, every week, every month for the past third of a century we’ve been pushing hard to add more to the vast integrated framework that is Mathematica and the Wolfram Language. And now we can see the results of all those individual ideas and projects and pieces of work: a steady drumbeat of innovation sustained now over the course of more than a third of a century:

&#10005

Continue reading

The Entangled Limit of Everything

I call it the ruliad. Think of it as the entangled limit of everything that is computationally possible: the result of following all possible computational rules in all possible ways. It’s yet another surprising construct that’s arisen from our Physics Project. And it’s one that I think has extremely deep implications—both in science and beyond.

In many ways, the ruliad is a strange and profoundly abstract thing. But it’s something very universal—a kind of ultimate limit of all abstraction and generalization. And it encapsulates not only all formal possibilities but also everything about our physical universe—and everything we experience can be thought of as sampling that part of the ruliad that corresponds to our particular way of perceiving and interpreting the universe.

We’re going to be able to say many things about the ruliad without engaging in all its technical details. (And—it should be said at the outset—we’re still only at the very beginning of nailing down those technical details and setting up the difficult mathematics and formalism they involve.) But to ground things here, let’s start with a slightly technical discussion of what the ruliad is. Continue reading

Mathematica 1.0 was launched on June 23, 1988. So (depending a little on how you do the computation) today is its one-third-century anniversary. And it’s wonderful to see how the tower of ideas and technology that we’ve worked so hard on for so long has grown in that third of a century—and how tall it’s become and how rapidly it still goes on growing.

In the past few years, I’ve come to have an ever-greater appreciation for just how unique what we’ve ended up building is, and just how fortunate our original choices of foundations and principles were. And even after a third of a century, what we have still seems like an artifact from the future—indeed ever more so with each passing year as it continues to grow and develop.

In the long view of intellectual history, this past one-third century will be seen as the time when the computational paradigm first took serious root, and when all its implications for “computational X” began to grow. And personally I feel very fortunate to have lived at the right time in history to have been able to be deeply involved with this and for what we have built to have made such a contribution to it. Continue reading

A Minimal Example of Multicomputation

Multicomputation is an important new paradigm, but one that can be quite difficult to understand. Here my goal is to discuss a minimal example: multiway systems based on numbers. Many general multicomputational phenomena will show up here in simple forms (though others will not). And the involvement of numbers will often allow us to make immediate use of traditional mathematical methods.

A multiway system can be described as taking each of its states and repeatedly replacing it according to some rule or rules with a collection of states, merging any states produced that are identical. In our Physics Project, the states are combinations of relations between elements, represented by hypergraphs. We’ve also often considered string substitution systems, in which the states are strings of characters. But here I’ll consider the case in which the states are numbers, and for now just single integers. Continue reading

This is the first of a series of pieces I’m planning in connection with the upcoming 20th anniversary of the publication of A New Kind of Science.

“There’s a Whole New Field to Build…”

For me the story began nearly 50 years ago—with what I saw as a great and fundamental mystery of science. We see all sorts of complexity in nature and elsewhere. But where does it come from? How is it made? There are so many examples. Snowflakes. Galaxies. Lifeforms. Turbulence. Do they all work differently? Or is there some common underlying cause? Some essential “phenomenon of complexity”?

It was 1980 when I began to seriously work on these questions. And at first I did so in the main scientific paradigm I knew: models based on mathematics and mathematical equations. I studied the approaches people had tried to use. Nonequilibrium thermodynamics. Synergetics. Nonlinear dynamics. Cybernetics. General systems theory. I imagined that the key question was: “Starting from disorder and randomness, how could spontaneous self-organization occur, to produce the complexity we see?” For somehow I assumed that complexity must be created as a kind of filtering of ubiquitous thermodynamic-like randomness in the world.

At first I didn’t get very far. I could write down equations and do math. But there wasn’t any real complexity in sight. But in a quirk of history that I now realize had tremendous significance, I had just spent a couple of years creating a big computer system that was ultimately a direct forerunner of our modern Wolfram Language. So for me it was obvious: if I couldn’t figure out things myself with math, I should use a computer. Continue reading

The Path to a New Paradigm

One might have thought it was already exciting enough for our Physics Project to be showing a path to a fundamental theory of physics and a fundamental description of how our physical universe works. But what I’ve increasingly been realizing is that actually it’s showing us something even bigger and deeper: a whole fundamentally new paradigm for making models and in general for doing theoretical science. And I fully expect that this new paradigm will give us ways to address a remarkable range of longstanding central problems in all sorts of areas of science—as well as suggesting whole new areas and new directions to pursue. Continue reading

Hiding in Plain Sight for a Century?

On December 7, 1920, Moses Schönfinkel introduced the S and K combinators—and in doing so provided the first explicit example of a system capable of what we now call universal computation. A hundred years later—as I prepared to celebrate the centenary of combinators—I decided it was time to try using modern computational methods to see what we could now learn about combinators. And in doing this, I got a surprise.

It’s already remarkable that S and K yield universal computation. But from my explorations I began to think that something even more remarkable might be true, and that in fact S alone might be sufficient to achieve universal computation. Or in other words, that just applying the rule

S f g x → f[x][g[x]]

over and over again might be all that’s needed to do any computation that can be done.

I don’t know for sure that this is true, though I’ve amassed empirical evidence that seems to point in this direction. And today I’m announcing a prize of $20,000 (yes, the “20” goes with the 1920 invention of combinators, and the 2020 making of my conjecture) for proving—or disproving—that the S combinator alone can support universal computation. Continue reading

Based on a talk at Numerous Numerosity: An interdisciplinary meeting on the notions of cardinality, ordinality and arithmetic across the sciences.

Everyone Has to Have Numbers… Don’t They?

The aliens arrive in a starship. Surely, one might think, to have all that technology they must have the idea of numbers. Or maybe one finds an uncontacted tribe deep in the jungle. Surely they too must have the idea of numbers. To us numbers seem so natural—and “obvious”—that it’s hard to imagine everyone wouldn’t have them. But if one digs a little deeper, it’s not so clear.

It’s said that there are human languages that have words for “one”, “a pair” and “many”, but no words for specific larger numbers. In our modern technological world that seems unthinkable. But imagine you’re out in the jungle, with your dogs. Each dog has particular characteristics, and most likely a particular name. Why should you ever think about them collectively, as all “just dogs”, amenable to being counted? Continue reading

Look What We Made in Five Months!

It’s hard to believe we’ve been doing this for 35 years, building a taller and taller tower of ideas and technology that allow us to reach ever further. In earlier times we used to release the results of efforts only every few years. But in recent times we’ve started doing incremental (“.1”) releases that deliver our latest R&D achievements—both fully fleshed out, and partly as “coming attractions”—much more frequently.

We released Version 12.2 on December 16, 2020. And today, just five months later, we’re releasing Version 12.3. There are some breakthroughs and major new directions in 12.3. But much of what’s in 12.3 is just about making Wolfram Language and Mathematica better, smoother and more convenient to use. Things are faster. More “But what about ___?” cases are handled. Big frameworks are more completely filled out. And there are lots of new conveniences.

There are also the first pieces of what will become large-scale structures in the future. Early functions—already highly useful in their own right—that will in future releases be pieces of major systemwide frameworks. Continue reading

In preparation for a conference entitled “Distributed Consensus with Cellular Automata & Related Systems” that we’re organizing with NKN (= “New Kind of Network”) I decided to explore the problem of distributed consensus using methods from A New Kind of Science (yes, NKN “rhymes” with NKS) as well as from the Wolfram Physics Project.

A Simple Example

&#10005 BlockRandom[SeedRandom[77]; Module[{pts = RandomPointConfiguration[HardcorePointProcess[0.09, 2, 2], Rectangle[{0, 0}, {40, 40}]]["Points"], clrs}, clrs = Table[ RandomChoice[{.65, .35} -> {Hue[0.15, 0.72, 1], Hue[ 0.98, 1, 0.8200000000000001]}], Length[pts]]; Graphics[{EdgeForm[Gray], Table[Style[Disk[pts[[n]]], clrs[[n]]], {n, Range[Length[pts]]}]}]]]

Consider a collection of “nodes”, each one of two possible colors. We want to determine the majority or “consensus” color of the nodes, i.e. which color is the more common among the nodes.

One obvious method to find this “majority” color is just sequentially to visit each node, and tally up all the colors. But it’s potentially much more efficient if we can use a distributed algorithm, where we’re running computations in parallel across the various nodes. Continue reading

See also:The Concept of the Ruliad (November 10, 2021)
(introducing the term “ruliad” for “rulial universe”)

What Is Formal, and What Is Actualized?

Why does the universe exist? Why is there something rather than nothing? These are old and fundamental questions that one might think would be firmly outside the realm of science. But to my surprise I’ve recently realized that our Physics Project may shed light on them, and perhaps even show us the way to answers.

We can view the ultimate goal of our Physics Project as being to find an abstract representation of what our universe does. But even if we find such a representation, the question still remains of why that representation is actualized: why what it represents is “actually happening”, with the actual stuff our universe is “made of”.

It’s one thing to say that we have a rule or program that can reproduce a representation of what our universe is doing. But it seems very different to say that the rule or program is “actually being run” and is “actually generating” the “physical reality” of our universe. Continue reading

How’s It Going?

When we launched the Wolfram Physics Project a year ago today, I was fairly certain that—to my great surprise—we’d finally found a path to a truly fundamental theory of physics, and it was beautiful. A year later it’s looking even better. We’ve been steadily understanding more and more about the structure and implications of our models—and they continue to fit beautifully with what we already know about physics, particularly connecting with some of the most elegant existing approaches, strengthening and extending them, and involving the communities that have developed them.

And if fundamental physics wasn’t enough, it’s also become clear that our models and formalism can be applied even beyond physics—suggesting major new approaches to several other fields, as well as allowing ideas and intuition from those fields to be brought to bear on understanding physics.

Needless to say, there is much hard work still to be done. But a year into the process I’m completely certain that we’re “climbing the right mountain”. And the view from where we are so far is already quite spectacular. Continue reading

Continue reading

For most big ideas in recorded intellectual history one can answer the question: “What became of the person who originated it?” But late last year I tried to answer that for Moses Schönfinkel, who sowed a seed for what’s probably the single biggest idea of the past century: abstract computation and its universality.

I managed to find out quite a lot about Moses Schönfinkel. But I couldn’t figure out what became of him. Still, I kept on digging. And it turns out I was able to find out more. So here’s an update…. Continue reading

“What about Consciousness?”

For years I’ve batted it away. I’ll be talking about my discoveries in the computational universe, and computational irreducibility, and my Principle of Computational Equivalence, and people will ask “So what does this mean about consciousness?” And I’ll say “that’s a slippery topic”. And I’ll start talking about the sequence: life, intelligence, consciousness.

I’ll ask “What is the abstract definition of life?” We know about the case of life on Earth, with all its RNA and proteins and other implementation details. But how do we generalize? What is life generally? And I’ll argue that it’s really just computational sophistication, which the Principle of Computational Equivalence says happens all over the place. Then I’ll talk about intelligence. And I’ll argue it’s the same kind of thing. We know the case of human intelligence. But if we generalize, it’s just computational sophistication—and it’s ubiquitous. And so it’s perfectly reasonable to say that “the weather has a mind of its own”; it just happens to be a mind whose details and “purposes” aren’t aligned with our existing human experience. Continue reading

“[Despite] Considerable Effort… [It Proved] Intractable”

In the early years of the twentieth century it looked as if—if only the right approach could be found—all of mathematics might somehow systematically be solved. In 1910 Whitehead and Russell had published their monumental Principia Mathematica showing (rather awkwardly) how all sorts of mathematics could be represented in terms of logic. But Emil Post wanted to go further. In what seems now like a rather modern idea (with certain similarities to the core structure of the Wolfram Language, and very much like the string multiway systems in our Physics Project), he wanted to represent the logic expressions of Principia Mathematica as strings of characters, and then have possible operations correspond to transformations on these strings.

In the summer of 1920 it was all going rather well, and Emil Post as a freshly minted math PhD from Columbia arrived in Princeton to take up a prestigious fellowship. But there was one final problem. Having converted everything to string transformations, Post needed to have a theory of what such transformations could do. Continue reading

It All Started with Feynman Diagrams

Any serious calculation in particle physics takes a lot of algebra. Maybe it doesn’t need to. But with the methods based on Feynman diagrams that we know so far, it does. And in fact it was these kinds of calculations that first led me to use computers for symbolic computation. That was in 1976, which by now is a long time ago. But actually the idea of doing Feynman diagram calculations by computer is even older. Continue reading

Yet Bigger than Ever Before

When we released Version 12.1 in March of this year, I was pleased to be able to say that with its 182 new functions it was the biggest .1 release we’d ever had. But just nine months later, we’ve got an even bigger .1 release! Version 12.2, launching today, has 228 completely new functions!

Continue reading

December 7, 1920

On Tuesday, December 7, 1920, the Göttingen Mathematics Society held its regular weekly meeting—at which a 32-year-old local mathematician named Moses Schönfinkel with no known previous mathematical publications gave a talk entitled “Elemente der Logik” (“Elements of Logic”).

A hundred years later what was presented in that talk still seems in many ways alien and futuristic—and for most people almost irreducibly abstract. But we now realize that that talk gave the first complete formalism for what is probably the single most important idea of this past century: the idea of universal computation. Continue reading

The Abstract Representation of Things

“In principle you could use combinators,” some footnote might say. But the implication tends to be “But you probably don’t want to.” And, yes, combinators are deeply abstract—and in many ways hard to understand. But tracing their history over the hundred years since they were invented, I’ve come to realize just how critical they’ve actually been to the development of our modern conception of computation—and indeed my own contributions to it. Continue reading

Ultimate Symbolic Abstraction

Before Turing machines, before lambda calculus—even before Gödel’s theorem—there were combinators. They were the very first abstract examples ever to be constructed of what we now know as universal computation—and they were first presented on December 7, 1920. In an alternative version of history our whole computing infrastructure might have been built on them. But as it is, for a century, they have remained for the most part a kind of curiosity—and a pinnacle of abstraction, and obscurity. Continue reading

In preparing my keynote at our 31st annual technology conference, I tried to collect some of my thoughts about our long-term mission and how I view the opportunities it is creating…

What I’ve Spent My Life On

I’ve been fortunate to live at a time in history when there’s a transformational intellectual development: the rise of computation and the computational paradigm. And I’ve devoted my adult life to doing what I can to make computation and the computational method achieve their potential, both intellectually and in the world at large. I’ve alternated (about five times so far) between doing this with basic science and with practical technology, each time building on what I’ve been able to do before.

The basic science has shown me the immense power and potential of what’s out there in the computational universe: the capability of even simple programs to generate behavior of immense complexity, including, I now believe, the fundamental physics of our whole universe. But how can we humans harness all that power and potential? How do we use the computational universe to achieve things we want: to take our human objectives and automate achieving them?

I’ve now spent four decades in an effort to build a bridge between what’s possible with computation, and what we humans care about and think about. It’s a story of technology, but it’s also a story of big and deep ideas. And the result has been the creation of the first and only full-scale computational language—that we now call the Wolfram Language. Continue reading

When the NASA Innovative Advanced Concepts Program asked me to keynote their annual conference I thought it would be a good excuse to spend some time on a question I’ve always wanted to explore…

Can You Build a Warp Drive?

“So you think you have a fundamental theory of physics. Well, then tell us if warp drive is possible!” Despite the hopes and assumptions of science fiction, real physics has for at least a century almost universally assumed that no genuine effect can ever propagate through physical space any faster than light. But is this actually true? We’re now in a position to analyze this in the context of our model for fundamental physics. And I’ll say at the outset that it’s a subtle and complicated question, and I don’t know the full answer yet.

But I increasingly suspect that going faster than light is not a physical impossibility; instead, in a sense, doing it is “just” an engineering problem. But it may well be an irreducibly hard engineering problem. And one that can’t be solved with the computational resources available to us in our universe. But it’s also conceivable that there may be some clever “engineering solution”, as there have been to so many seemingly insuperable engineering problems in the past. And that in fact there is a way to “move through space” faster than light. Continue reading

Towards a Science of Metamathematics

One of the many surprising things about our Wolfram Physics Project is that it seems to have implications even beyond physics. In our effort to develop a fundamental theory of physics it seems as if the tower of ideas and formalism that we’ve ended up inventing are actually quite general, and potentially applicable to all sorts of areas.

One area about which I’ve been particularly excited of late is metamathematics—where it’s looking as if it may be possible to use our formalism to make what might be thought of as a “bulk theory of metamathematics”.

Mathematics itself is about what we establish about mathematical systems. Metamathematics is about the infrastructure of how we get there—the structure of proofs, the network of theorems, and so on. And what I’m hoping is that we’re going to be able to make an overall theory of how that has to work: a formal theory of the large-scale structure of metamathematics—that, among other things, can make statements about the general properties of “metamathematical space”. Continue reading

And We’re Off and Running…

We recently wrapped up the four weeks of our first-ever “Physics track” Wolfram Summer School—and the results were spectacular! More than 30 projects potentially destined to turn into academic papers—reporting all kinds of progress on the Wolfram Physics Project.

When we launched the Wolfram Physics Project just three months ago one of the things I was looking forward to was seeing other people begin to seriously contribute to the project. Well, it turns out I didn’t have to wait long! Because—despite the pandemic and everything—things are already very much off and running!

Six weeks ago we made a list of questions we thought we were ready to explore in the Wolfram Physics Project. And in the past five weeks I’m excited to say that through projects at the Summer School lots of these are already well on their way to being answered. If we ever wondered whether there was a way for physicists (and physics students) to get involved in the project, we can now give a resounding answer, “yes”. Continue reading

Related livestreams
Related notebooks
Video work logs
Related tweets

Generalized Physics and the Theory of Computation

Let’s say we find a rule that reproduces physics. A big question would then be: “Why this rule, and not another?” I think there’s a very elegant potential answer to this question, that uses what we’re calling rule space relativity—and that essentially says that there isn’t just one rule: actually all possible rules are being used, but we’re basically picking a reference frame that makes us attribute what we see to some particular rule. In other words, our description of the universe is a sense of our making, and there can be many other—potentially utterly incoherent—descriptions, etc.

But so how does this work at a more formal level? This bulletin is going to explore one very simple case. And in doing so we’ll discover that what we’re exploring is potentially relevant not only for questions of “generalized physics”, but also for fundamental questions in the theory of computation. In essence, what we’ll be doing is to study the structure of spaces created by applying all possible rules, potentially, for example, allowing us to “geometrize” spaces of possible algorithms and their applications. Continue reading

Related livestreams
Related notebooks
Video work logs
Related tweets

The Structure and Pathologies of Spacetime

In our models, space emerges as the large-scale limit of our spatial hypergraph, while spacetime effectively emerges as the large-scale limit of the causal graph that represents causal relationships between updating events in the spatial hypergraph. An important result is that (subject to various assumptions) there is a continuum limit in which the emergent spacetime follows Einstein’s equations from general relativity.

And given this, it is natural to ask what happens in our models with some of the notable phenomena from general relativity, such as black holes, event horizons and spacetime singularities. I already discussed this to some extent in my technical introduction to our models. My purpose here is to go further, both in more completely understanding the correspondence with general relativity, and in seeing what additional or different phenomena arise in our models. Continue reading

First, Thank You!

We launched the Wolfram Physics Project two weeks ago, on April 14. And, in a word, wow! People might think that interest in fundamental science has waned. But the thousands of messages we’ve received tell a very different story. People really care! They’re excited. They’re enjoying understanding what we’ve figured out. They’re appreciating the elegance of it. They want to support the project. They want to get involved.

It’s tremendously encouraging—and motivating. I wanted this project to be something for the world—and something lots of people could participate in. And it’s working. Our livestreams—even very technical ones—have been exceptionally popular. We’ve had lots of physicists, mathematicians, computer scientists and others asking questions, making suggestions and offering help. We’ve had lots of students and others who tell us how eager they are to get into doing research on the project. And we’ve had lots of people who just want to tell us they appreciate what we’re doing. So, thank you!

Continue reading

I Never Expected This

It’s unexpected, surprising—and for me incredibly exciting. To be fair, at some level I’ve been working towards this for nearly 50 years. But it’s just in the last few months that it’s finally come together. And it’s much more wonderful, and beautiful, than I’d ever imagined.

In many ways it’s the ultimate question in natural science: How does our universe work? Is there a fundamental theory? An incredible amount has been figured out about physics over the past few hundred years. But even with everything that’s been done—and it’s very impressive—we still, after all this time, don’t have a truly fundamental theory of physics.

Back when I used do theoretical physics for a living, I must admit I didn’t think much about trying to find a fundamental theory; I was more concerned about what we could figure out based on the theories we had. And somehow I think I imagined that if there was a fundamental theory, it would inevitably be very complicated. Continue reading

“Someday…”

I’ve been saying it for decades: “Someday I’m going to mount a serious effort to find the fundamental theory of physics.” Well, I’m thrilled that today “someday” has come, and we’re launching the Wolfram Physics Project. And getting ready to launch this project over the past few months might be the single most intellectually exciting time I’ve ever had. So many things I’d wondered about for so long getting solved. So many exciting moments of “Surely it can’t be that simple?” And the dawning realization, “Oh my gosh, it’s actually going to work!”

Physics was my first great intellectual passion. And I got started young, publishing my first paper when I was 15. I was lucky enough to be involved in physics in one of its golden ages, in the late 1970s. Not that I was trying to find a fundamental theory of physics back then. Like essentially all physicists, I spent my time on the hard work of figuring out the consequences of the theories we already had.

But doing that got me progressively more involved with computers. And then I realized: computation is its own paradigm. There’s a whole way of thinking about the world using the idea of computation. And it’s very powerful, and fundamental. Maybe even more fundamental than physics can ever be. And so it was that I left physics, and began to explore the computational universe: in a sense the universe of all possible universes. Continue reading

We’re pleased that despite the coronavirus pandemic and its impact on so many people and businesses we’re still able to launch today as planned… (Thanks to our dedicated team and the fact that remote working has been part of our company for decades…)

The Biggest .1 Release Ever

It’s always an interesting time. We’re getting ready to wrap up a .1 version—to release the latest fruits of our research and development efforts. “Is it going to be a big release?”, I wonder. Of course, I know we’ve done a lot of work since we released Version 12.0 last April. All those design reviews (many livestreamed). All those new things we’ve built and figured out.

But then we start actually making the list for the new version. And—OMG—it goes on and on. Different teams are delivering on this or that project that started X years ago. A new function is being added for this. There’s some new innovation about that. Etc.

We started this journey a third of a century ago when we began the development of Version 1.0. And after all these years, it’s amazing how the energy of each new release seems to be ever greater.

And as we went on making the list for Version 12.1 we wondered, “Will it actually be our biggest .1 release ever?”. We finally got the answer: “Yes! And by a lot”.

Counting functions isn’t always the best measure, but it’s an indication. And in Version 12.1 there are a total of 182 completely new functions—as well as updates and enhancements to many hundreds more.

Continue reading

Wolfram Notebooks on the Web

We’ve been working towards it for many years, but now it’s finally here: an incredibly smooth workflow for publishing Wolfram Notebooks to the web—that makes possible a new level of interactive publishing and computation-enabled communication.

You create a Wolfram Notebook—using all the power of the Wolfram Language and the Wolfram Notebook system—on the desktop or in the cloud. Then you just press a button to publish it to the Wolfram Cloud—and immediately anyone anywhere can both read and interact with it on the web.

It’s an unprecedentedly easy way to get rich, interactive, computational content onto the web. And—together with the power of the Wolfram Language as a computational language—it promises to usher in a new era of computational communication, and to be a crucial driver for the development of “computational X” fields. Continue reading

Today my latest book is published: Adventures of a Computational Explorer.

From the preface:

“You work so hard… but what do you do for fun?” people will ask me. Well, the fact is that I’ve tried to set up my life so that the things I work on are things I find fun. Most of those things are aligned with big initiatives of mine, and with products and companies and scientific theories that I’ve built over decades. But sometimes I work on things that just come up, and that for one reason or another I find interesting and fun.

This book is a collection of pieces I’ve written over the past dozen years on some of these things, and the adventures I’ve had around them. Most of the pieces I wrote in response to some particular situation or event. Their topics are diverse. But it’s remarkable how connected they end up being. And at some level all of them reflect the paradigm for thinking that has defined much of my life.

It all centers around the idea of computation, and the generality of abstraction to which it leads. Whether I’m thinking about science, or technology, or philosophy, or art, the computational paradigm provides both an overall framework and specific facts that inform my thinking. And in a sense this book reflects the breadth of applicability of this computational paradigm. Continue reading

The Story of Rule 30

How can something that simple produce something that complex? It’s been nearly 40 years since I first saw rule 30—but it still amazes me. Long ago it became my personal all-time favorite science discovery, and over the years it’s changed my whole worldview and led me to all sorts of science, technology, philosophy and more.

But even after all these years, there are still many basic things we don’t know about rule 30. And I’ve decided that it’s now time to do what I can to stimulate the process of finding more of them out. So as of today, I am offering $30,000 in prizes for the answers to three basic questions about rule 30. Continue reading

The Next Big Step for Wolfram|Alpha

Wolfram|Alpha has been a huge hit with students. Whether in college or high school, Wolfram|Alpha has become a ubiquitous way for students to get answers. But it’s a one-shot process: a student enters the question they want to ask (say in math) and Wolfram|Alpha gives them the (usually richly contextualized) answer. It’s incredibly useful—especially when coupled with its step-by-step solution capabilities.

But what if one doesn’t want just a one-shot answer? What if one wants to build up (or work through) a whole computation? Well, that’s what we created Mathematica and its whole notebook interface to do. And for more than 30 years that’s how countless inventions and discoveries have been made around the world. It’s also how generations of higher-level students have been taught.

But what about students who aren’t ready to use Mathematica yet? What if we could take the power of Mathematica (and what’s now the Wolfram Language), but combine it with the ease of Wolfram|Alpha?

Well, that’s what we’ve done in Wolfram|Alpha Notebook Edition. Continue reading

How I Got the Book

In May 2017, I got an email from a former high-school teacher of mine named George Rutter: “I have a copy of Dirac’s big book in German (Die Prinzipien der Quantenmechanik) that was owned by Alan Turing, and following your book Idea Makers it seemed obvious that you were the right person to own this.” He explained that he’d got the book from another (by then deceased) former high-school teacher of mine, Norman Routledge, who I knew had been a friend of Alan Turing’s. George ended, “If you would like the book, I could give it to you the next time you are in England.”

A couple of years passed. But in March 2019 I was indeed in England, and arranged to meet George for breakfast at a small hotel in Oxford. We ate and chatted, and waited for the food to be cleared. Then the book moment arrived. George reached into his briefcase and pulled out a rather unassuming, typical mid-1900s academic volume. Continue reading

I’ve been reflecting recently on things I like to do. Of course I like creating things, figuring things out, and so on. But something else I like—that I don’t believe I’ve ever written about before—is mentoring. I’ve been doing it a shockingly long time: my first memories of it date from before I was 10 years old, 50 years ago. Somehow I always ended up being the one giving lots of advice—first to kids my own age, then also to ones somewhat younger, or older, and later to all sorts of people.

I was in England recently, and ran into someone I’d known as a kid nearly 50 years ago—and hadn’t seen since. He’s had a fascinating and successful career, but was kind enough to say that my interactions and advice to him nearly 50 years ago had really been important to him. Of course it’s nice to hear things like that—but as I reflect on it, I realize that mentoring is something I find fulfilling, whether or not I end up knowing that whatever seeds I’ve sown germinate (though, to be clear, I do find it fascinating to see what happens). Continue reading

(Artwork by Gunilla Feigenbaum)

Behind the Feigenbaum Constant

It’s called the Feigenbaum constant, and it’s about 4.6692016. And it shows up, quite universally, in certain kinds of mathematical—and physical—systems that can exhibit chaotic behavior.

Mitchell Feigenbaum, who died on June 30 at the age of 74, was the person who discovered it—back in 1975, by doing experimental mathematics on a pocket calculator.

It became a defining discovery in the history of chaos theory. But when it was first discovered, it was a surprising, almost bizarre result, that didn’t really connect with anything that had been studied before. Somehow, though, it’s fitting that it should have been Mitchell Feigenbaum—who I knew for nearly 40 years—who would discover it.

Trained in theoretical physics, and a connoisseur of its mathematical traditions, Mitchell always seemed to see himself as an outsider. He looked a bit like Beethoven—and projected a certain stylish sense of intellectual mystery. He would often make strong assertions, usually with a conspiratorial air, a twinkle in his eye, and a glass of wine or a cigarette in his hand. Continue reading

An Invitation to Washington

Three and a half weeks ago I got an email asking me if I’d testify at a hearing of the US Senate Commerce Committee’s Subcommittee on Communications, Technology, Innovation and the Internet. Given that the title of the hearing was “Optimizing for Engagement: Understanding the Use of Persuasive Technology on Internet Platforms” I wasn’t sure why I’d be relevant.

But then the email went on: “The hearing is intended to examine, among other things, whether algorithmic transparency or algorithmic explanation are policy options Congress should be considering.” That piqued my interest, because, yes, I have thought about “algorithmic transparency” and “algorithmic explanation”, and their implications for the deployment of artificial intelligence.

Generally I stay far away from anything to do with politics. But figuring out how the world should interact with AI is really important. So I decided that—even though it was logistically a bit difficult—I should do my civic duty and go to Washington and testify. Continue reading

The first workshop to define what is now the Santa Fe Institute took place on October 5–6, 1984. I was recently asked to give some reminiscences of the event, for a republication of a collection of papers derived from this and subsequent workshops.

It was a slightly dark room, decorated with Native American artifacts. Around it were tables arranged in a large rectangle, at which sat a couple dozen men (yes, all men), mostly in their sixties. The afternoon was wearing on, with many different people giving their various views about how to organize what amounted to a putative great new interdisciplinary university.

Here’s the original seating chart, together with a current view of the meeting room. (I’m only “Steve” to Americans currently over the age of 60…):

Continue reading

Someone from the House Permanent Select Committee on Intelligence recently contacted me about a hearing they’re having on the subject of deep fakes. I can’t attend the hearing, but the conversation got me thinking about the subject of deep fakes, and I made a few quick notes….

What You See May Not Be What Happened

The idea of modifying images is as old as photography. At first, it had to be done by hand (sometimes with airbrushing). By the 1990s, it was routinely being done with image manipulation software such as Photoshop. But it’s something of an art to get a convincing result, say for a person inserted into a scene. And if, for example, the lighting or shadows don’t agree, it’s easy to tell that what one has isn’t real.

What about videos? If one does motion capture, and spends enough effort, it’s perfectly possible to get quite convincing results—say for animating aliens, or for putting dead actors into movies. The way this works, at least in a first approximation, is for example to painstakingly pick out the keypoints on one face, and map them onto another.

What’s new in the past couple of years is that this process can basically be automated using machine learning. And, for example, there are now neural nets that are simply trained to do “face swapping”:

Continue reading

What the Wolfram Language Makes Possible

We’re on an exciting path these days with the Wolfram Language. Just three weeks ago we launched the Free Wolfram Engine for Developers to help people integrate the Wolfram Language into large-scale software projects. Now, today, we’re launching the Wolfram Function Repository to provide an organized platform for functions that are built to extend the Wolfram Language—and we’re opening up the Function Repository for anyone to contribute.

The Wolfram Function Repository is something that’s made possible by the unique nature of the Wolfram Language as not just a programming language, but a full-scale computational language. In a traditional programming language, adding significant new functionality typically involves building whole libraries, which may or may not work together. But in the Wolfram Language, there’s so much already built into the language that it’s possible to add significant functionality just by introducing individual new functions—which can immediately integrate into the coherent design of the whole language.

To get it started, we’ve already got 532 functions in the Wolfram Function Repository, in 26 categories:

Continue reading

First Encounters

In the mid-1970s, particle physics was hot. Quarks were in. Group theory was in. Field theory was in. And so much progress was being made that it seemed like the fundamental theory of physics might be close at hand.

Right in the middle of all this was Murray Gell-Mann—responsible for not one, but most of the leaps of intuition that had brought particle physics to where it was. There’d been other theories, but Murray’s—with their somewhat elaborate and abstract mathematics—were always the ones that seemed to carry the day.

It was the spring of 1978 and I was 18 years old. I’d been publishing papers on particle physics for a few years, and had gotten quite known around the international particle physics community (and, yes, it took decades to live down my teenage-particle-physicist persona). I was in England, but planned to soon go to graduate school in the US, and was choosing between Caltech and Princeton. And one weekend afternoon when I was about to go out, the phone rang. In those days, it was obvious if it was an international call. “This is Murray Gell-Mann”, the caller said, then launched into a monologue about why Caltech was the center of the universe for particle physics at the time.
Continue reading

Why Aren’t You Using Our Technology?

It happens far too often. I’ll be talking to a software developer, and they’ll be saying how great they think our technology is, and how it helped them so much in school, or in doing R&D. But then I’ll ask them, “So, are you using Wolfram Language and its computational intelligence in your production software system?” Sometimes the answer is yes. But too often, there’s an awkward silence, and then they’ll say, “Well, no. Could I?”

I want to make sure the answer to this can always be: “Yes, it’s easy!” And to help achieve that, we’re releasing today the Free Wolfram Engine for Developers. It’s a full engine for the Wolfram Language, that can be deployed on any system—and called from programs, languages, web servers, or anything.

The Wolfram Engine is the heart of all our products. It’s what implements the Wolfram Language, with all its computational intelligence, algorithms, knowledgebase, and so on. It’s what powers our desktop products (including Mathematica), as well as our cloud platform. It’s what’s inside Wolfram|Alpha—as well as an increasing number of major production systems out in the world. And as of today, we’re making it available for anyone to download, for free, to use in their software development projects.

Continue reading

The Wolfram|Alpha Story

Today it’s 10 years since we launched Wolfram|Alpha. At some level, Wolfram|Alpha is a never-ending project. But it’s had a great first 10 years. It was a unique and surprising achievement when it first arrived, and over its first decade it’s become ever stronger and more unique. It’s found its way into more and more of the fabric of the computational world, both realizing some of the long-term aspirations of artificial intelligence, and defining new directions for what one can expect to be possible. Oh, and by now, a significant fraction of a billion people have used it. And we’ve been able to keep it private and independent, and its main website has stayed free and without external advertising.
Continue reading

What Kind of a Thing Is the Wolfram Language?

I’ve sometimes found it a bit of a struggle to explain what the Wolfram Language really is. Yes, it’s a computer language—a programming language. And it does—in a uniquely productive way, I might add—what standard programming languages do. But that’s only a very small part of the story. And what I’ve finally come to realize is that one should actually think of the Wolfram Language as an entirely different—and new—kind of thing: what one can call a computational language.

So what is a computational language? It’s a language for expressing things in a computational way—and for capturing computational ways of thinking about things. It’s not just a language for telling computers what to do. It’s a language that both computers and humans can use to represent computational ways of thinking about things. It’s a language that puts into concrete form a computational view of everything. It’s a language that lets one use the computational paradigm as a framework for formulating and organizing one’s thoughts.

It’s only recently that I’ve begun to properly internalize just how broad the implications of having a computational language really are—even though, ironically, I’ve spent much of my life engaged precisely in the consuming task of building the world’s only large-scale computational language.
Continue reading

This is an edited transcript of a recent talk I gave at a blockchain conference, where I said I’d talk about “What will the world be like when computational intelligence and computational contracts are ubiquitous?”

We live in an interesting time today—a time when we’re just beginning to see the implications of what we might call “the force of computation”. In the end, it’s something that’s going to affect almost everything. And what’s going to happen is really a deep story about the interplay between the human condition, the achievements of human civilization—and the fundamental nature of this thing we call computation.

Continue reading

The Road to Version 12

Today we’re releasing Version 12 of Wolfram Language (and Mathematica) on desktop platforms, and in the Wolfram Cloud. We released Version 11.0 in August 2016, 11.1 in March 2017, 11.2 in September 2017 and 11.3 in March 2018. It’s a big jump from Version 11.3 to Version 12.0. Altogether there are 278 completely new functions, in perhaps 103 areas, together with thousands of different updates across the system:

Continue reading

Read Stephen Wolfram’s Reddit AMA about this essay »

The Pursuit of Productivity

I’m a person who’s only satisfied if I feel I’m being productive. I like figuring things out. I like making things. And I want to do as much of that as I can. And part of being able to do that is to have the best personal infrastructure I can. Over the years I’ve been steadily accumulating and implementing “personal infrastructure hacks” for myself. Some of them are, yes, quite nerdy. But they certainly help me be productive. And maybe in time more and more of them will become mainstream, as a few already have.

Now, of course, one giant “productivity hack” that I’ve been building for the world for a very long time is the whole technology stack around the Wolfram Language. And for me personally, another huge “productivity hack” is my company, which I started more than 32 years ago. Yes, it could (and should) be larger, and have more commercial reach. But as a nicely organized private company with about 800 people it’s an awfully efficient machine for turning ideas into real things, and for leveraging what skills I have to greatly amplify my personal productivity.

I could talk about how I lead my life, and how I like to balance doing leadership, doing creative work, interacting with people, and doing things that let me learn. I could talk about how I try to set things up so that what I’ve already built doesn’t keep me so busy I can’t start anything new. But instead what I’m going to focus on here is my more practical personal infrastructure: the technology and other things that help me live and work better, feel less busy, and be more productive every day. Continue reading

Spikeys Everywhere

We call it “Spikey”, and in my life today, it’s everywhere:

It comes from a 3D object—a polyhedron that’s called a rhombic hexecontahedron:

But what is its story, and how did we come to adopt it as our symbol?

Continue reading

A Discovery about Basic Logic

Logic is a foundation for many things. But what are the foundations of logic itself?

In symbolic logic, one introduces symbols like p and q to stand for statements (or “propositions”) like “this is an interesting essay”. Then one has certain “rules of logic”, like that, for any p and any q, NOT (p AND q) is the same as (NOT p) OR (NOT q).

But where do these “rules of logic” come from? Well, logic is a formal system. And, like Euclid’s geometry, it can be built on axioms. But what are the axioms? We might start with things like p AND q = q AND p, or NOT NOT p = p. But how many axioms does one need? And how simple can they be?

It was a nagging question for a long time. But at 8:31pm on Saturday, January 29, 2000, out on my computer screen popped a single axiom. I had already shown there couldn’t be anything simpler, but I soon established that this one little axiom was enough to generate all of logic:

&#10005 ((p·q)·r)·(p·((p·r)·p))==r

But how did I know it was correct? Well, because I had a computer prove it. And here’s the proof, as I printed it in 4-point type in A New Kind of Science (and it’s now available in the Wolfram Data Repository):

Continue reading

Technology for the Long Term

On June 23 we celebrate the 30th anniversary of the launch of Mathematica. Most software from 30 years ago is now long gone. But not Mathematica. In fact, it feels in many ways like even after 30 years, we’re really just getting started. Our mission has always been a big one: to make the world as computable as possible, and to add a layer of computational intelligence to everything.

Our first big application area was math (hence the name “Mathematica”). And we’ve kept pushing the frontiers of what’s possible with math. But over the past 30 years, we’ve been able to build on the framework that we defined in Mathematica 1.0 to create the whole edifice of computational capabilities that we now call the Wolfram Language—and that corresponds to Mathematica as it is today.

From when I first began to design Mathematica, my goal was to create a system that would stand the test of time, and would provide the foundation to fill out my vision for the future of computation. It’s exciting to see how well it’s all worked out. My original core concepts of language design continue to infuse everything we do. And over the years we’ve been able to just keep building and building on what’s already there, to create a taller and taller tower of carefully integrated capabilities.

It’s fun today to launch Mathematica 1.0 on an old computer, and compare it with today:

Continue reading

The more one does computational thinking, the better one gets at it. And today we’re launching the Wolfram Challenges site to give everyone a source of bite-sized computational thinking challenges based on the Wolfram Language. Use them to learn. Use them to stay sharp. Use them to prove how great you are.

The Challenges typically have the form: “Write a function to do X”. But because we’re using the Wolfram Language—with all its built-in computational intelligence—it’s easy to make the X be remarkably sophisticated.

The site has a range of levels of Challenges. Some are good for beginners, while others will require serious effort even for experienced programmers and computational thinkers. Typically each Challenge has at least some known solution that’s at most a few lines of Wolfram Language code. But what are those lines of code?

Continue reading

A Glimpse of the Future

It was 1968. I was 8 years old. The “space race” was in full swing. For the first time, a space probe had recently landed on another planet (Venus). And I was eagerly studying everything I could to do with space.

Then on April 3, 1968 (May 15 in the UK), the movie 2001: A Space Odyssey was released—and I was keen to see it. So in the early summer of 1968 there I was, the first time I’d ever been in an actual cinema (yes, it was called that in the UK). I’d been dropped off for a matinee, and was pretty much the only person in the theater. And to this day, I remember sitting in a plush seat and eagerly waiting for the curtain to go up, and the movie to begin.

It started with an impressive extraterrestrial sunrise. But then what was going on? Those weren’t space scenes. Those were landscapes, and animals. I was confused, and frankly a little bored. But just when I was getting concerned, there was a bone thrown in the air that morphed into a spacecraft, and pretty soon there was a rousing waltz—and a big space station turning majestically on the screen.

Continue reading

Not Entirely Fooling Around

What happens if you take four of today’s most popular buzzwords and string them together? Does the result mean anything? Given that today is April 1 (as well as being Easter Sunday), I thought it’d be fun to explore this. Think of it as an Easter egg… from which something interesting just might hatch. And to make it clear: while I’m fooling around in stringing the buzzwords together, the details of what I’ll say here are perfectly real.

Continue reading

The Release Pipeline

Last September we released Version 11.2 of the Wolfram Language and Mathematica—with all sorts of new functionality, including 100+ completely new functions. Version 11.2 was a big release. But today we’ve got a still bigger release: Version 11.3 that, among other things, includes nearly 120 completely new functions.

This June 23rd it’ll be 30 years since we released Version 1.0, and I’m very proud of the fact that we’ve now been able to maintain an accelerating rate of innovation and development for no less than three decades. Critical to this, of course, has been the fact that we use the Wolfram Language to develop the Wolfram Language—and indeed most of the things that we can now add in Version 11.3 are only possible because we’re making use of the huge stack of technology that we’ve been systematically building for more than 30 years.

We’ve always got a large pipeline of R&D underway, and our strategy for .1 versions is to use them to release everything that’s ready at a particular moment in time. Sometimes what’s in a .1 version may not completely fill out a new area, and some of the functions may be tagged as “experimental”. But our goal with .1 versions is to be able to deliver the latest fruits of our R&D efforts on as timely a basis as possible. Integer (.0) versions aim to be more systematic, and to provide full coverage of new areas, rounding out what has been delivered incrementally in .1 versions.

In addition to all the new functionality in 11.3, there’s a new element to our process. Starting a couple of months ago, we began livestreaming internal design review meetings that I held as we brought Version 11.3 to completion. So for those interested in “how the sausage is made”, there are now almost 122 hours of recorded meetings, from which you can find out exactly how some of the things you can now see released in Version 11.3 were originally invented. And in this post, I’m going to be linking to specific recorded livestreams relevant to features I’m discussing.

What’s New?

OK, so what’s new in Version 11.3? Well, a lot of things. And, by the way, Version 11.3 is available today on both desktop (Mac, Windows, Linux) and the Wolfram Cloud. (And yes, it takes extremely nontrivial software engineering, management and quality assurance to achieve simultaneous releases of this kind.) Continue reading

The Nature of the Problem

Let’s say we had a way to distribute beacons around our solar system (or beyond) that could survive for billions of years, recording what our civilization has achieved. What should they be like?

It’s easy to come up with what I consider to be sophomoric answers. But in reality I think this is a deep—and in some ways unsolvable—philosophical problem, that’s connected to fundamental issues about knowledge, communication and meaning.

Still, a friend of mine recently started a serious effort to build little quartz disks, etc., and have them hitch rides on spacecraft, to be deposited around the solar system. At first I argued that it was all a bit futile, but eventually I agreed to be an advisor to the project, and at least try to figure out what to do to the extent we can.

But, OK, so what’s the problem? Basically it’s about communicating meaning or knowledge outside of our current cultural and intellectual context. We just have to think about archaeology to know this is hard. What exactly was some arrangement of stones from a few thousand years ago for? Sometimes we can pretty much tell, because it’s close to something in our current culture. But a lot of the time it’s really hard to tell.
Continue reading

Catch a current livestream, or watch recorded livestreams here »

Thinking in Public

I’ve been CEOing Wolfram Research for more than 30 years now. But what does that actually entail? What do I end up doing on a typical day? I certainly work hard. But I think I’m not particularly typical of CEOs of tech companies our size. Because for me a large part of my time is spent on the front lines of figuring out how our products should be designed and architected, and what they should do.

Thirty years ago I mostly did this by myself. But nowadays I’m almost always working with groups of people from our 800 or so employees. I like to do things very interactively. And in fact, for the past 15 years or so I’ve spent much of my time doing what I often call “thinking in public”: solving problems and making decisions live in meetings with other people.

I’m often asked how this works, and what actually goes on in our meetings. And recently I realized: what better way to show (and perhaps educate) people than just to livestream lots of our actual meetings? So over the past couple of months, I’ve livestreamed over 40 hours of my internal meetings—in effect taking everyone behind the scenes in what I do and how our products are created. (Yes, the livestreams are also archived.)

Continue reading

A Powerful Way to Express Ideas

People are used to producing prose—and sometimes pictures—to express themselves. But in the modern age of computation, something new has become possible that I’d like to call the computational essay.

I’ve been working on building the technology to support computational essays for several decades, but it’s only very recently that I’ve realized just how central computational essays can be to both the way people learn, and the way they communicate facts and ideas. Professionals of the future will routinely deliver results and reports as computational essays. Educators will routinely explain concepts using computational essays. Students will routinely produce computational essays as homework for their classes.

Here’s a very simple example of a computational essay:

Continue reading

Is there a global theory for the shapes of fishes? It’s the kind of thing I might feel encouraged to ask by my explorations of simple programs and the forms they produce. But for most of the history of biology, it’s not the kind of thing anyone would ever have asked. With one notable exception: D’Arcy Wentworth Thompson.

And it’s now 100 years since D’Arcy Thompson published the first edition of his magnum opus On Growth and Form—and tried to use ideas from mathematics and physics to discuss global questions of biological growth and form. Probably the most famous pages of his book are the ones about fish shapes:

Continue reading

Our Latest R&D Output

I’m excited today to announce the latest output from our R&D pipeline: Version 11.2 of the Wolfram Language and Mathematica—available immediately on desktop (Mac, Windows, Linux) and cloud.

It was only this spring that we released Version 11.1. But after the summer we’re now ready for another impressive release—with all kinds of additions and enhancements, including 100+ entirely new functions:

Continue reading

The Summer Camp Was a Success!

How far can one get in teaching computational thinking to high-school students in two weeks? Judging by the results of this year’s Wolfram High-School Summer Camp the answer is: remarkably far.

I’ve been increasingly realizing what an immense and unique opportunity there now is to teach computational thinking with the whole stack of technology we’ve built up around the Wolfram Language. But it was a thrill to see just how well this seems to actually work with real high-school students—and to see the kinds of projects they managed to complete in only two weeks.

Continue reading

The Philosophy of Chemicals

“We’ve just got to decide: is a chemical like a city or like a number?” I spent my day yesterday—as I have for much of the past 30 years—designing new features of the Wolfram Language. And yesterday afternoon one of my meetings was a fast-paced discussion about how to extend the chemistry capabilities of the language.

At some level the problem we were discussing was quintessentially practical. But as so often turns out to be the case for things we do, it ultimately involves some deep intellectual issues. And to actually get the right answer—and to successfully design language features that will stand the test of time—we needed to plumb those depths, and talk about things that usually wouldn’t be considered outside of some kind of philosophy seminar.

Continue reading

A British Train Station

A week ago a new train station, named “Cambridge North”, opened in Cambridge, UK. Normally such an event would be far outside my sphere of awareness. (I think I last took a train to Cambridge in 1975.) But last week people started sending me pictures of the new train station, wondering if I could identify the pattern on it:

And, yes, it does indeed look a lot like patterns I’ve spent years studying—that come from simple programs in the computational universe. My first—and still favorite—examples of simple programs are one-dimensional cellular automata like this:

Continue reading

Starting now, in celebration of its 15th anniversary, A New Kind of Science will be freely available in its entirety, with high-resolution images, on the web or for download.

It’s now 15 years since I published my book A New Kind of Science—more than 25 since I started writing it, and more than 35 since I started working towards it. But with every passing year I feel I understand more about what the book is really about—and why it’s important. I wrote the book, as its title suggests, to contribute to the progress of science. But as the years have gone by, I’ve realized that the core of what’s in the book actually goes far beyond science—into many areas that will be increasingly important in defining our whole future. Continue reading

(An Elementary Introduction to the Wolfram Language is available in print, as an ebook, and free on the web—as well as in Wolfram Programming Lab in the Wolfram Open Cloud. There’s also now a free online hands-on course based on it.)

a book entitled An Elementary Introduction to the Wolfram Language—as part of my effort to teach computational thinking to the next generation. I just published the second edition of the book—with (among other things) a significantly extended section on modern machine learning.

I originally expected my book’s readers would be high schoolers and up. But it’s actually also found a significant audience among middle schoolers (11- to 14-year-olds). So the question now is: can one teach the core concepts of modern machine learning even to middle schoolers? Well, the interesting thing is that—thanks to the whole technology stack we’ve now got in the Wolfram Language—the answer seems to be “yes”! Continue reading

After a Decade, It’s Finally Here!

I’m pleased to announce that as of today, the Wolfram Data Repository is officially launched! It’s been a long road. I actually initiated the project a decade ago—but it’s only now, with all sorts of innovations in the Wolfram Language and its symbolic ways of representing data, as well as with the arrival of the Wolfram Cloud, that all the pieces are finally in place to make a true computable data repository that works the way I think it should.

Continue reading

A Minor Release That’s Not Minor

I’m pleased to announce the release today of Version 11.1 of the Wolfram Language (and Mathematica). As of now, Version 11.1 is what’s running in the Wolfram Cloud—and desktop versions are available for immediate download for Mac, Windows and Linux.

What’s new in Version 11.1? Well, actually a remarkable amount. Here’s a summary:

Continue reading

A Talk, a Performance… a Live Experiment

“In the next hour I’m going to try to make a new discovery in mathematics.” So I began a few days ago at two different hour-long Math Encounters events at the National Museum of Mathematics (“MoMath”) in New York City. I’ve been a trustee of the museum since before it opened in 2012, and I was looking forward to spending a couple of hours trying to “make some math” there with a couple of eclectic audiences from kids to retirees.

People usually assume that new discoveries aren’t things one can ever see being made in real time. But the wonderful thing about the computational tools I’ve spent decades building is that they make it so fast to implement ideas that it becomes realistic to make discoveries as a kind of real-time performance art. Continue reading

Note added 09/29/2021: Some information regarding Wolfram Cloud products described in this post may be outdated. Please visit https://www.wolfram.com/cloud to learn more.

Code for Everyone

Computational thinking needs to be an integral part of modern education—and today I’m excited to be able to launch another contribution to this goal: Wolfram|Alpha Open Code.

Every day, millions of students around the world use Wolfram|Alpha to compute answers. With Wolfram|Alpha Open Code they’ll now not just be able to get answers, but also be able to get code that lets them explore further and immediately apply computational thinking. Continue reading

[This post is about the movie Arrival; there are no movie spoilers here.]

Connecting with Hollywood

“It’s an interesting script” said someone on our PR team. It’s pretty common for us to get requests from movie-makers about showing our graphics or posters or books in movies. But the request this time was different: could we urgently help make realistic screen displays for a big Hollywood science fiction movie that was just about to start shooting?
Continue reading

Last week I gave a talk (and did a panel discussion) at a conference entitled “Ethics of Artificial Intelligence” held at the NYU Philosophy Department’s Center for Mind, Brain and Consciousness. Here’s the video and a transcript:

Thanks for inviting me here today.

You know, it’s funny to be here. My mother was a philosophy professor in Oxford. And when I was a kid I always said the one thing I’d never do was do or talk about philosophy. But, well, here I am. Continue reading

Leibniz’s Dream

Gottfried Leibniz—who died 300 years ago this November—worked on many things. But a theme that recurred throughout his life was the goal of turning human law into an exercise in computation. Of course, as we know, he didn’t succeed. But three centuries later, I think we’re finally ready to give it a serious try again. And I think it’s a really important thing to do—not just because it’ll enable all sorts of new societal opportunities and structures, but because I think it’s likely to be critical to the future of our civilization in its interaction with artificial intelligence.

Human law, almost by definition, dates from the very beginning of civilization—and undoubtedly it’s the first system of rules that humans ever systematically defined. Presumably it was a model for the axiomatic structure of mathematics as defined by the likes of Euclid. And when science came along, “natural laws” (as their name suggests) were at first viewed as conceptually similar to human laws, except that they were supposed to define constraints for the universe (or God) rather than for humans.

Over the past few centuries we’ve had amazing success formalizing mathematics and exact science. And out of this there’s a more general idea that’s emerged: the idea of computation. In computation, we’re dealing with arbitrary systems of rules—not necessarily ones that correspond to mathematical concepts we know, or features of the world we’ve identified. So now the question is: can we use the ideas of computation, in very much the way Leibniz imagined, to formalize human law? Continue reading

The Computational Future

Computational thinking is going to be a defining feature of the future—and it’s an incredibly important thing to be teaching to kids today. There’s always lots of discussion (and concern) about how to teach traditional mathematical thinking to kids. But looking to the future, this pales in comparison to the importance of teaching computational thinking. Yes, there’s a certain amount of traditional mathematical thinking that’s needed in everyday life, and in many careers. But computational thinking is going to be needed everywhere. And doing it well is going to be a key to success in almost all future careers.

Doctors, lawyers, teachers, farmers, whatever. The future of all these professions will be full of computational thinking. Whether it’s sensor-based medicine, computational contracts, education analytics or computational agriculture—success is going to rely on being able to do computational thinking well.

I’ve noticed an interesting trend. Pick any field X, from archeology to zoology. There either is now a “computational X” or there soon will be. And it’s widely viewed as the future of the field.

Continue reading

Note: There have been additional updates to Mathematica. Read about the updates in Version 11.1, Version 11.2 and Version 11.3

I’m thrilled today to announce the release of a major new version of Mathematica and the Wolfram Language: Version 11, available immediately for both desktop and cloud. Hundreds of us have been energetically working on building this for the past two years—and in fact I’ve personally put several thousand hours into it. I’m very excited about what’s in it; it’s a major step forward, with a lot of both breadth and depth—and with remarkably central relevance to many of today’s most prominent technology areas.

It’s been more than 28 years since Version 1 came out—and nearly 30 years since I started its development. And all that time I’ve been continuing to pursue a bold vision—and to build a taller and taller stack of technology. With most software, after a few years and a few versions, not a lot of important new stuff ever gets added. But with Mathematica and the Wolfram Language it’s been a completely different story: for three decades we’ve been taking major steps forward at every version, progressively conquering vast numbers of new areas. Continue reading

I spend most of my time trying to build the future with science and technology. But for many years now I’ve also had two other great interests: people and history. And today I’m excited to be publishing my first book that builds on these interests. It’s called Idea Makers, and its subtitle is Personal Perspectives on the Lives & Ideas of Some Notable People. It’s based on essays I’ve written over the past decade about a range of people—from ones I’ve personally known (like Richard Feynman and Steve Jobs) to ones who died long before I was born (like Ada Lovelace and Gottfried Leibniz).

Continue reading

The Most-Used Mathematical Algorithm Idea in History

An octillion. A billion billion billion. That’s a fairly conservative estimate of the number of times a cellphone or other device somewhere in the world has generated a bit using a maximum-length linear-feedback shift register sequence. It’s probably the single most-used mathematical algorithm idea in history. And the main originator of this idea was Solomon Golomb, who died on May 1—and whom I knew for 35 years.

Solomon Golomb’s classic book Shift Register Sequences, published in 1967—based on his work in the 1950s—went out of print long ago. But its content lives on in pretty much every modern communications system. Read the specifications for 3G, LTE, Wi-Fi, Bluetooth, or for that matter GPS, and you’ll find mentions of polynomials that determine the shift register sequences these systems use to encode the data they send. Solomon Golomb is the person who figured out how to construct all these polynomials.

He also was in charge when radar was first used to find the distance to Venus, and of working out how to encode images to be sent from Mars. He introduced the world to what he called polyominoes, which later inspired Tetris (“tetromino tennis”). He created and solved countless math and wordplay puzzles. And—as I learned about 20 years ago—he came very close to discovering my all-time-favorite rule 30 cellular automaton all the way back in 1959, the year I was born.
Continue reading

Fifty years ago today there was a six-year-old at a kindergarten (“nursery school” in British English) in Oxford, England who was walking under some trees and noticed that the patches of light under the trees didn’t look the same as usual. Curious, he looked up at the sun. It was bright, but he could see that one side of it seemed to be missing. And he realized that was why the patches of light looked odd.

He’d heard of eclipses. He didn’t really understand them. But he had the idea that that was what he was seeing. Excited, he told another kid about it. They hadn’t heard of eclipses. But he pointed out that the sun had a bite taken out of it. The other kid looked up. Perhaps the sun was too bright, but they looked away without noticing anything. Then the first kid tried another kid. And then another. None of them believed him about the eclipse and the bite taken out of the sun.

Of course, this is a story about me. And now I can find the eclipse by going to Wolfram|Alpha (or the Wolfram Language):

Continue reading

This week’s release of the movie The Man Who Knew Infinity (which I saw in rough form last fall through its mathematican-producers Manjul Bhargava and Ken Ono) leads me to write about its subject, Srinivasa Ramanujan…
 
 

Continue reading

Edited transcript of a talk given on March 4, 2016, at the Computer History Museum, Mountain View, California.

I normally spend my time trying to build the future. But I find history really interesting and informative, and I study it quite a lot. Usually it’s other people’s history. But the Computer History Museum asked me to talk today about my own history, and the history of technology I’ve built. So that’s what I’m going to do here. Continue reading

The Theory Works!

The equation that Albert Einstein wrote down for the gravitational field in 1915 is simple enough:

But working out its consequences is not. And in fact even after 100 years we’re still just at the beginning of the process.

Continue reading

Note added 07/31/20: Some information regarding Wolfram Cloud products described in this post may be outdated. Please visit https://www.wolfram.com/cloud to learn more.

It’s been very satisfying to see how successfully Wolfram|Alpha has democratized computational knowledge and how its effects have grown over the years. Now I want to do the same thing with knowledge-based programming—through the Wolfram Open Cloud.

Last week we released Wolfram Programming Lab as an environment for people to learn knowledge-based programming with the Wolfram Language. Today I’m pleased to announce that we’re making Wolfram Programming Lab available for free use on the web in the Wolfram Open Cloud.
Continue reading

I think it was 1979 when I first met Marvin Minsky, while I was still a teenager working on physics at Caltech. It was a weekend, and I’d arranged to see Richard Feynman to discuss some physics. But Feynman had another visitor that day as well, who didn’t just want to talk about physics, but instead enthusiastically brought up one unexpected topic after another.

That afternoon we were driving through Pasadena, California—and with no apparent concern to the actual process of driving, Feynman’s visitor was energetically pointing out all sorts of things an AI would have to figure if it was to be able to do the driving. I was a bit relieved when we arrived at our destination, but soon the visitor was on to another topic, talking about how brains work, and then saying that as soon as he’d finished his next book he’d be happy to let someone open up his brain and put electrodes inside, if they had a good plan to figure out how it worked.

Feynman often had eccentric visitors, but I was really wondering who this one was. It took a couple more encounters, but then I got to know that eccentric visitor as Marvin Minsky, pioneer of computation and AI—and was pleased to count him as a friend for more than three decades.
Continue reading

I’m excited today to be able to announce the launch of Wolfram Programming Lab—an environment for anyone to learn programming and computational thinking through the Wolfram Language. You can run Wolfram Programming Lab through a web browser, as well as natively on desktop systems (Mac, Windows, Linux).

Continue reading

(New York Public Library)

Ada Lovelace was born 200 years ago today. To some she is a great hero in the history of computing; to others an overestimated minor figure. I’ve been curious for a long time what the real story is. And in preparation for her bicentennial, I decided to try to solve what for me has always been the “mystery of Ada”.

It was much harder than I expected. Historians disagree. The personalities in the story are hard to read. The technology is difficult to understand. The whole story is entwined with the customs of 19th-century British high society. And there’s a surprising amount of misinformation and misinterpretation out there.

But after quite a bit of research—including going to see many original documents—I feel like I’ve finally gotten to know Ada Lovelace, and gotten a grasp on her story. In some ways it’s an ennobling and inspiring story; in some ways it’s frustrating and tragic.

It’s a complex story, and to understand it, we’ll have to start by going over quite a lot of facts and narrative.

Continue reading

An Elementary Introduction to the Wolfram Language is available in print, free on the web, etc.

I wasn’t sure if I was ever going to write another book. My last book—A New Kind of Science—took me more than a decade of intensely focused work, and is the largest personal project I’ve ever done.

But a little while ago, I realized there was another book I had to write: a book that would introduce people with no knowledge of programming to the Wolfram Language and the kind of computational thinking it allows.

The result is An Elementary Introduction to the Wolfram Language, published today in print, free on the web, etc. Continue reading

A hundred years ago today Albert Einstein published his General Theory of Relativity—a brilliant, elegant theory that has survived a century, and provides the only successful way we have of describing spacetime.

There are plenty of theoretical indications, though, that General Relativity isn’t the end of the story of spacetime. And in fact, much as I like General Relativity as an abstract theory, I’ve come to suspect it may actually have led us on a century-long detour in understanding the true nature of space and time.

I’ve been thinking about the physics of space and time for a little more than 40 years now. At the beginning, as a young theoretical physicist, I mostly just assumed Einstein’s whole mathematical setup of Special and General Relativity—and got on with my work in quantum field theory, cosmology, etc. on that basis.

But about 35 years ago, partly inspired by my experiences in creating technology, I began to think more deeply about fundamental issues in theoretical science—and started on my long journey to go beyond traditional mathematical equations and instead use computation and programs as basic models in science. Quite soon I made the basic discovery that even very simple programs can show immensely complex behavior—and over the years I discovered that all sorts of systems could finally be understood in terms of these kinds of programs.

Encouraged by this success, I then began to wonder if perhaps the things I’d found might be relevant to that ultimate of scientific questions: the fundamental theory of physics. Continue reading

Not many years ago, the idea of having a computer broadly answer questions asked in plain English seemed like science fiction. But when we released Wolfram|Alpha in 2009 one of the big surprises (not least to me!) was that we’d managed to make this actually work. And by now people routinely ask personal assistant systems—many powered by Wolfram|Alpha—zillions of questions in ordinary language every day.

It all works fairly well for quick questions, or short commands (though we’re always trying to make it better!). But what about more sophisticated things? What’s the best way to communicate more seriously with AIs? Continue reading

Today is the 200th anniversary of the birth of George Boole. In our modern digital world, we’re always hearing about “Boolean variables”—1 or 0, true or false. And one might think, “What a trivial idea! Why did someone even explicitly need to invent it?” But as is so often the case, there’s a deeper story—for Boolean variables were really just a side effect of an important intellectual advance that George Boole made.

When George Boole came onto the scene, the disciplines of logic and mathematics had developed quite separately for more than 2000 years. And George Boole’s great achievement was to show how to bring them together, through the concept of what’s now called Boolean algebra. And in doing so he effectively created the field of mathematical logic, and set the stage for the long series of developments that led for example to universal computation.

When George Boole invented Boolean algebra, his basic goal was to find a set of mathematical axioms that could reproduce the classical results of logic. His starting point was ordinary algebra, with variables like x and y, and operations like addition and multiplication.

At first, ordinary algebra seems a lot like logic. After all, p and q is the same as q and p, just as p×q = q×p. But if one looks in more detail, there are differences. Like p×p = p², but p and p is just p. Somewhat confusingly, Boole used the notation of standard algebra, but added special rules to create an axiom system that he then showed could reproduce all the usual results of logic.

Boole was rather informal in the way he described his axiom system. But within a few decades, it had been more precisely formalized, and over the course of the century that followed, a few progressively simpler forms of it were found. And then, as it happens, 15 years ago I ended up finishing this 150-year process, by finding—largely as a side effect of other science I was doing—the provably very simplest possible axiom system for logic, that actually happens to consist of just a single axiom.

Continue reading

“What is this a picture of?” Humans can usually answer such questions instantly, but in the past it’s always seemed out of reach for computers to do this. For nearly 40 years I’ve been sure computers would eventually get there—but I’ve wondered when.

I’ve built systems that give computers all sorts of intelligence, much of it far beyond the human level. And for a long time we’ve been integrating all that intelligence into the Wolfram Language.

Now I’m excited to be able to say that we’ve reached a milestone: there’s finally a function called ImageIdentify built into the Wolfram Language that lets you ask, “What is this a picture of?”—and get an answer.

And today we’re launching the Wolfram Language Image Identification Project on the web to let anyone easily take any picture (drag it from a web page, snap it on your phone, or load it from a file) and see what ImageIdentify thinks it is:

Continue reading

Note added 04/30/2018: Due to changes around Apple Watch and WatchKit, the Wolfram Cloud app does not currently support Apple Watch. The functionality described in this post remains available for other mobile devices.

My goal with the Wolfram Language is to take programming to a new level. And over the past year we’ve been rolling out ways to use and deploy the language in many places—desktop, cloud, mobile, embedded, etc. So what about wearables? And in particular, what about the Apple Watch? A few days ago I decided to explore what could be done. So I cleared my schedule for the day, and started writing code.

My idea was to write code with our standard Wolfram Programming Cloud, but instead of producing a web app or web API, to produce an app for the Apple Watch. And conveniently enough, a preliminary version of our Wolfram Cloud app just became available in the App Store—letting me deploy from the Wolfram Cloud to both mobile devices and the watch.

Continue reading

The Wolfram Cloud Needs to Be Perfect

The Wolfram Cloud is coming out of beta soon (yay!), and right now I’m spending much of my time working to make it as good as possible (and, by the way, it’s getting to be really great!). Mostly I concentrate on defining high-level function and strategy. But I like to understand things at every level, and as a CEO, one’s ultimately responsible for everything. And at the beginning of March I found myself diving deep into something I never expected…

Here’s the story. As a serious production system that lots of people will use to do things like run businesses, the Wolfram Cloud should be as fast as possible. Our metrics were saying that typical speeds were good, but subjectively when I used it something felt wrong. Sometimes it was plenty fast, but sometimes it seemed way too slow.

We’ve got excellent software engineers, but months were going by, and things didn’t seem to be changing. Meanwhile, we’d just released the Wolfram Data Drop. So I thought, why don’t I just run some tests myself, maybe collecting data in our nice new Wolfram Data Drop?

A great thing about the Wolfram Language is how friendly it is for busy people: even if you only have time to dash off a few lines of code, you can get real things done. And in this case, I only had to run three lines of code to find a problem.

First, I deployed a web API for a trivial Wolfram Language program to the Wolfram Cloud:

Continue reading

Last week I spoke at SXSW Interactive 2015 in Austin, Texas. Here’s a slightly edited transcript: Continue reading

Pictures from Pi Day now added »

This coming Saturday is “Pi Day of the Century”. The date 3/14/15 in month/day/year format is like the first digits of π=3.1415… And at 9:26:53.589… it’s a “super pi moment”.

Between Mathematica and Wolfram|Alpha, I’m pretty sure our company has delivered more π to the world than any other organization in history. So of course we have to do something special for Pi Day of the Century.

Continue reading

Where should data from the Internet of Things go? We’ve got great technology in the Wolfram Language for interpreting, visualizing, analyzing, querying and otherwise doing interesting things with it. But the question is, how should the data from all those connected devices and everything else actually get to where good things can be done with it? Today we’re launching what I think is a great solution: the Wolfram Data Drop.

When I first started thinking about the Data Drop, I viewed it mainly as a convenience—a means to get data from here to there. But now that we’ve built the Data Drop, I’ve realized it’s much more than that. And in fact, it’s a major step in our continuing efforts to integrate computation and the real world.

So what is the Wolfram Data Drop? At a functional level, it’s a universal accumulator of data, set up to get—and organize—data coming from sensors, devices, programs, or for that matter, humans or anything else. And to store this data in the cloud in a way that makes it completely seamless to compute with. Continue reading

In the Wolfram Language a little code can go a long way. And to use that fact to let everyone have some fun, today we’re introducing Tweet-a-Program.

Compose a tweet-length Wolfram Language program, and tweet it to @WolframTaP. Our Twitter bot will run your program in the Wolfram Cloud and tweet back the result.

Continue reading

It’s been many years in the making, and today I’m excited to announce the launch of Mathematica Online: a version of Mathematica that operates completely in the cloud—and is accessible just through any modern web browser.

In the past, using Mathematica has always involved first installing software on your computer. But as of today that’s no longer true. Instead, all you have to do is point a web browser at Mathematica Online, then log in, and immediately you can start to use Mathematica—with zero configuration.

Here’s what it looks like:

Continue reading

Every four years for more than a century there’s been an International Congress of Mathematicians (ICM) held somewhere in the world. In 1900 it was where David Hilbert announced his famous collection of math problems—and it’s remained the top single periodic gathering for the world’s research mathematicians.

This year the ICM is in Seoul, and I’m going to it today. I went to the ICM once before—in Kyoto in 1990. Mathematica was only two years old then, and mathematicians were just getting used to it. Plenty already used it extensively—but at the ICM there were also quite a few who said, “I do pure mathematics. How can Mathematica possibly help me?”

Continue reading

For as long as I can remember, my all-time favorite activity has been creating ideas and turning them into reality—a kind of “entrepreneurism of ideas”. And over the years—in science, technology and business—I think I’ve developed some pretty good tools and strategies for doing this, that I’ve increasingly realized would be good for a lot of other people (and organizations) too.

So how does one spread idea entrepreneurism—entrepreneurism centered on ideas rather than commercial enterprises? Somewhat unwittingly I think we’ve developed a rather good vehicle—that’s both a very successful educational program, and a fascinating annual adventure for me.

Twelve years ago my book A New Kind of Science had just come out, and we were inundated with people wanting to learn more, and get involved in research around it. We considered various alternatives, but eventually we decided to organize a summer school where we would systematically teach about our methodology, while mentoring each student to do a unique original project.

From the very beginning, the summer school was a big success. And over the years we’ve gradually improved and expanded it. It’s still the Wolfram Science Summer School—and its intellectual core is still A New Kind of Science. But today it has become a broader vehicle for passing on our tools and strategies for idea entrepreneurism.

This year’s summer school just ended last week. We had 63 students from 21 countries—with a fascinating array of backgrounds and interests. Most were in college or graduate school; a few were younger or older. And over the course of the three weeks of the summer school—with great energy and intellectual entrepreneurism—each student worked towards their own unique project.
Continue reading

We’ve got an incredible amount of new technology coming out this summer. Two weeks ago we launched Wolfram Programming Cloud. Today I’m pleased to announce the release of a major new version of Mathematica: Mathematica 10.

We released Mathematica 1 just over 26 years ago—on June 23, 1988. And ever since we’ve been systematically making Mathematica ever bigger, stronger, broader and deeper. But Mathematica 10—released today—represents the single biggest jump in new functionality in the entire history of Mathematica.
Continue reading

Twenty-six years ago today we launched Mathematica 1.0. And I am excited that today we have what I think is another historic moment: the launch of Wolfram Programming Cloud—the first in a sequence of products based on the new Wolfram Language.

My goal with the Wolfram Language in general—and Wolfram Programming Cloud in particular—is to redefine the process of programming, and to automate as much as possible, so that once a human can express what they want to do with sufficient clarity, all the details of how it is done should be handled automatically.

I’ve been working toward this for nearly 30 years, gradually building up the technology stack that is needed—at first in Mathematica, later also in Wolfram|Alpha, and now in definitive form in the Wolfram Language. The Wolfram Language, as I have explained elsewhere, is a new type of programming language: a knowledge-based language, whose philosophy is to build in as much knowledge about computation and about the world as possible—so that, among other things, as much as possible can be automated. Continue reading

Last weekend I gave a speech at this year’s graduation event for the Stanford Online High School (OHS) that one of my children has been attending. Here’s the transcript:

Thank you for inviting me to be part of this celebration today—and congratulations to this year’s OHS graduates.

You know, as it happens, I myself never officially graduated from high school, and this is actually the first high school graduation I’ve ever been to.

It’s been fun over the past three years—from a suitable parental distance of course—to see my daughter’s experiences at OHS. One day I’m sure everyone will know about online high schools—but you’ll be able to say, “Yes, I was there when that way of doing such-and-such a thing was first invented—at OHS.”

It’s great to see the OHS community—and to see so many long-term connections being formed independent of geography. And it’s also wonderful to see students with such a remarkable diversity of unique stories.

Of course, for the graduates here today, this is the beginning of a new chapter in their stories.

I suspect some of you already have very definite life plans. Many are still exploring. It’s worth remembering that there’s no “one right answer” to life. Different people are amazingly different in what they’ll consider an “‘A’ in life”. I think the first challenge is always to understand what you really like. Then you’ve got to know what’s out there to do in the world. And then you’ve got to solve the puzzle of fitting the two together. Continue reading

Two weeks ago I spoke at SXSW Interactive in Austin, TX. Here’s a slightly edited transcript (it’s the “speaker’s cut”, including some demos I had to abandon during the talk):

Well, I’ve got a lot planned for this hour.

Basically, I want to tell you a story that’s been unfolding for me for about the last 40 years, and that’s just coming to fruition in a really exciting way. And by just coming to fruition, I mean pretty much today. Because I’m planning to show you today a whole lot of technology that’s the result of that 40-year story—that I’ve never shown before, and that I think is going to be pretty important.

I always like to do live demos. But today I’m going to be pretty extreme. Showing you a lot of stuff that’s very very fresh. And I hope at least a decent fraction of it is going to work.

OK, here’s the big theme: taking computation seriously. Really understanding the idea of computation. And then building technology that lets one inject it everywhere—and then seeing what that means. Continue reading

We’re getting closer to the first official release of the Wolfram Language—so I am starting to demo it more publicly.

Here’s a short video demo I just made. It’s amazing to me how much of this is based on things I hadn’t even thought of just a few months ago. Knowledge-based programming is going to be much bigger than I imagined…

Connected devices are central to our long-term strategy of injecting sophisticated computation and knowledge into everything. With the Wolfram Language we now have a way to describe and compute about things in the world. Connected devices are what we need to measure and interface with those things.

In the end, we want every type of connected device to be seamlessly integrated with the Wolfram Language. And this will have all sorts of important consequences. But as we work toward this, there’s an obvious first step: we have to know what types of connected devices there actually are.

So to have a way to answer that question, today we’re launching the Wolfram Connected Devices Project—whose goal is to work with device manufacturers and the technical community to provide a definitive, curated, source of systematic knowledge about connected devices.

Continue reading

I have the good fortune of knowing many people, which means I end up sending out lots of holiday cards. For many years I used to send out physical cards. But last year, convenience, timeliness and ease of reply made me finally make the switch to e-cards.

I often like to write notes on the cards I send. And when I was sending out paper cards, that was straightforward to do. But what about with e-cards?

Well, it’d be easy to type messages and have them printed on the e-cards. But that seems awfully impersonal. And anyway, I rather like having at least one time each year when I do a bunch of actual writing by hand—not least so my handwriting doesn’t atrophy completely.

So there’s an obvious solution: handwritten e-cards. Which is exactly what I did this year:
Continue reading

Last week I wrote about our large-scale plan to use new technology we’re building to inject sophisticated computation and knowledge into everything. Today I’m pleased to announce a step in that direction: working with the Raspberry Pi Foundation, effective immediately there’s a pilot release of the Wolfram Language—as well as Mathematica—that will soon be bundled as part of the standard system software for every Raspberry Pi computer.

Continue reading

Computational knowledge. Symbolic programming. Algorithm automation. Dynamic interactivity. Natural language. Computable documents. The cloud. Connected devices. Symbolic ontology. Algorithm discovery. These are all things we’ve been energetically working on—mostly for years—in the context of Wolfram|Alpha, Mathematica, CDF and so on.

But recently something amazing has happened. We’ve figured out how to take all these threads, and all the technology we’ve built, to create something at a whole different level. The power of what is emerging continues to surprise me. But already I think it’s clear that it’s going to be profoundly important in the technological world, and beyond.

At some level it’s a vast unified web of technology that builds on what we’ve created over the past quarter century. At some level it’s an intellectual structure that actualizes a new computational view of the world. And at some level it’s a practical system and framework that’s going to be a fount of incredibly useful new services and products.

I have to admit I didn’t entirely see it coming. For years I have gradually understood more and more about what the paradigms we’ve created make possible. But what snuck up on me is a breathtaking new level of unification—that lets one begin to see that all the things we’ve achieved in the past 25+ years are just steps on a path to something much bigger and more important.

Continue reading

Today it’s exactly a quarter of a century since we launched Mathematica 1.0 on June 23, 1988. Much has come and gone in the world of computing since that time. But I’m pleased to say that through all of it Mathematica has just kept getting stronger and stronger. Continue reading

In a few weeks it’ll be 25 years ago: June 23, 1988—the day Mathematica was launched.

Late the night before we were still duplicating floppy disks and stuffing product boxes. But at noon on June 23 there I was at a conference center in Santa Clara starting up Mathematica in public for the first time:

Continue reading

I’ve been curious about Gottfried Leibniz for years, not least because he seems to have wanted to build something like Mathematica and Wolfram|Alpha, and perhaps A New Kind of Science as well—though three centuries too early. So when I took a trip recently to Germany, I was excited to be able to visit his archive in Hanover.

Leafing through his yellowed (but still robust enough for me to touch) pages of notes, I felt a certain connection—as I tried to imagine what he was thinking when he wrote them, and tried to relate what I saw in them to what we now know after three more centuries:

Continue reading

More than a million people have now used our Wolfram|Alpha Personal Analytics for Facebook. And as part of our latest update, in addition to collecting some anonymized statistics, we launched a Data Donor program that allows people to contribute detailed data to us for research purposes.

A few weeks ago we decided to start analyzing all this data. And I have to say that if nothing else it’s been a terrific example of the power of Mathematica and the Wolfram Language for doing data science.

We’d always planned to use the data we collect to enhance our Personal Analytics system. But I couldn’t resist also trying to do some basic science with it.

I’ve always been interested in people and the trajectories of their lives. But I’ve never been able to combine that with my interest in science. Until now. And it’s been quite a thrill over the past few weeks to see the results we’ve been able to get. Sometimes confirming impressions I’ve had; sometimes showing things I never would have guessed. And all along reminding me of phenomena I’ve studied scientifically in A New Kind of Science.

So what does the data look like? Here are the social networks of a few Data Donors—with clusters of friends given different colors. (Anyone can find their own network using Wolfram|Alpha—or the SocialMediaData function in Mathematica.)

Continue reading

Last week I gave a talk at SXSW 2013 in Austin about some of the things I’m thinking about these days—including quite a few that I’ve never talked publicly about before. Here’s a video, and a slightly edited transcript:

Well, this is a pretty exciting time for me. Because it turns out that a whole bunch of things that I’ve been working on for more than 30 years are all finally converging, in a very nice way. And what I’d like to do here today is tell you a bit about that, and about some things I’ve figured out recently—and about what it all means for our future.

This is going to be a bit of a wild talk in some ways. It’s going to go from pretty intellectual stuff about basic science and so on, to some really practical technology developments, with a few sneak peeks at things I’ve never shown before.

Let’s start from some science. And you know, a lot of what I’ll say today connects back to what I thought at first was a small discovery that I made about 30 years ago. Let me tell you the story.

I started out at a pretty young age as a physicist. Diligently doing physics pretty much the way it had been done for 300 years. Starting from this-or-that equation, and then doing the math to figure out predictions from it. That worked pretty well in some cases. But there were too many cases where it just didn’t work. So I got to wondering whether there might be some alternative; a different approach. Continue reading

At the core of Mathematica is a language. A very powerful symbolic language. Built up with great care over a quarter of a century—and now incorporating a huge swath of knowledge and computation.

Millions and millions of lines of code have been written in this language, for all sorts of purposes. And today—particularly with new large-scale deployment options made possible through the web and the cloud—the language is poised to expand dramatically in usage.

But there’s a problem. And it’s a problem that—embarrassingly enough—I’ve been thinking about for more than 20 years. The problem is: what should the language be called?

Usually on this blog when I discuss our activities as a company, I talk about progress we’ve made, or problems we’ve solved. But today I’m going to make an exception, and talk instead about a problem we haven’t solved, but need to solve.

You might say, “How hard can it be to come up with one name?” In my experience, some names are easy to come up with. But others are really really hard. And this is an example of a really really hard one. (And perhaps the very length of this post communicates some of that difficulty…)

Let’s start by talking a little about names in general. There are names like, say, “quark”, that are in effect just random words. And that have to get all their meaning “externally”, by having it explicitly described. But there are others, like “website” for example, that already give a sense of their meaning just from the words or word roots they contain.

I’ve named all sorts of things in my time. Science concepts. Technologies. Products. Mathematica functions. I’ve used different approaches in different cases. In a few cases, I’ve used “random words” (and have long had a Mathematica-based generator of ones that sound good). But much more often I’ve tried to start with a familiar word or words that capture the essence of what I’m naming. Continue reading

Richard Crandall liked to call himself a “computationalist”. For though he was trained in physics (and served for many years as a physics professor at Reed College), computation was at the center of his life. He used it in physics, in engineering, in mathematics, in biology… and in technology. He was a pioneer in experimental mathematics, and was associated for many years with Apple and with Steve Jobs, and was proud of having invented “at least 5 algorithms used in the iPhone”. He was also an extremely early adopter of Mathematica, and a well-known figure in the Mathematica community. And when he died just before Christmas at the age of 64 he was hard at work on his latest, rather different, project: an “intellectual biography” of Steve Jobs that I had suggested he call “Scientist to Mr. Jobs”.

I first met Richard Crandall in 1987, when I was developing Mathematica, and he was Chief Scientist at Steve Jobs’s company NeXT. Richard had pioneered using Pascal on Macintoshes to teach scientific computing. But as soon as he saw Mathematica, he immediately adopted it, and for a quarter of a century used it to produce a wonderful range of discoveries and inventions.

He also contributed greatly to Mathematica and its usage. Indeed, even before Mathematica 1.0 in 1988, he insisted on visiting our company to contribute his expertise in numerical evaluation of special functions (his favorites were polylogarithms and zeta-like functions). And then, after the NeXT computer was released, he wrote what may have been the first-ever Mathematica-based app: a “supercalculator” named Gourmet that he said “eats other calculators for breakfast”. A couple of years later he wrote a book entitled Mathematica for the Sciences, that pioneered the use of Mathematica programs as a form of exposition.

Over the years, I interacted with Richard about a great many things. Usually it would start with a “call me” message. And I would get on the phone, never knowing what to expect. And Richard would be talking about his latest result in number theory. Or the latest Apple GPU. Or his models of flu epidemiology. Or the importance of running Mathematica on iOS. Or a new way to multiply very long integers. Or his latest achievements in image processing. Or a way to reconstruct fractal brain geometries.
Continue reading

I was just in New York City for the grand opening of the National Museum of Mathematics. Yes, there is now a National Museum of Mathematics, right in downtown Manhattan. And it’s really good—a unique and wonderful place. Which I’m pleased to say I’ve been able to help in various ways in bringing into existence over the past 3 years.

Of all companies, ours is probably the one that has been most involved in bringing math to the world (Mathematica, Wolfram|Alpha, Wolfram Demonstrations Project, MathWorld, Computer-Based Math, Wolfram Foundation, …). And for a long time I’ve thought how nice it would be if there were a substantial, physical, “museum of mathematics” somewhere. But until recently I’d sort of assumed that if such a thing were going to exist, I’d have to be the one to make it happen.

A little more than 3 years ago, though, my older daughter picked out of my mail a curious folding geometrical object—which turned out to be an invitation to an event about the creation of a museum of mathematics. At first, it wasn’t clear what kind of museum this was supposed to be. But as soon as we arrived at the event, it started to be much clearer: this was “math as physical experience”. With the centerpiece of the event, for example, being a square-wheeled tricycle that one could ride on a cycloidal “road”—a mathematical possibility that, as it happens, was the subject of some early Mathematica demonstrations. Continue reading

There aren’t very many qualitatively different types of computer interfaces in use in the world today. But with the release of Mathematica 9 I think we have the first truly practical example of a new kind—the computed predictive interface.

If one’s dealing with a system that has a small fixed set of possible actions or inputs, one can typically build an interface out of elements like menus or forms. But if one has a more open-ended system, one typically has to define some kind of language. Usually this will be basically textual (as it is for the most part for Mathematica); sometimes it may be visual (as for Wolfram SystemModeler).

The challenge is then to make the language broad and powerful, while keeping it as easy as possible for humans to write and understand. And as a committed computer language designer for the past 30+ years, I have devoted an immense amount of effort to this.

But with Wolfram|Alpha I had a different idea. Don’t try to define the best possible artificial computer language, that humans then have to learn. Instead, use natural language, just like humans do among themselves, and then have the computer do its best to understand this. At first, it was not at all clear that such an approach was going to work. But one of the big things we’ve learned from Wolfram|Alpha is with enough effort (and enough built-in knowledge), it can. And indeed two years ago in Mathematica 8 we used what we’d done with Wolfram|Alpha to add to Mathematica the capability of taking free-form natural language input, and automatically generating from it precise Mathematica language code.

But let’s say one’s just got some output from Mathematica. What should one do next? One may know the appropriate Mathematica language input to give. Or at least one may be able to express what one wants to do in free-form natural language. But in both cases there’s a kind of creative act required: starting from nothing one has figure out what to say.

So can we make this easier? The answer, I think, is yes. And that’s what we’ve now done with the Predictive Interface in Mathematica 9.

The concept of the Predictive Interface is to take what you’ve done so far, and from it predict a few possibilities for what you’re likely to want to do next.

Continue reading

I’m excited to be able to announce that today we’re releasing Mathematica 9—and it’s big! A whole array of new ideas and new application areas… and major advances along a great many algorithmic frontiers.

Next year Mathematica will be 25 years old (and all sorts of festivities are planned!). And in that quarter century we’ve just been building and building. The core principles that we began with have been validated over and over again. And with them we’ve created a larger and larger stack of technology, that allows us to do more and more, and reach further and further.

From the beginning, our goal has been an ambitious one: to cover and automate every area of computational and algorithmic work. Having built the foundations of the Mathematica language, we started a quarter century ago attacking core areas of mathematics. And over the years since then, we have been expanding outward at an ever-increasing pace, conquering one area after another.

As with Wolfram|Alpha, we’ll never be finished. But as the years go by, the scope of what we’ve done becomes more and more immense. And with Mathematica 9 today we are taking yet another huge step.

So what’s new in Mathematica 9? Lots and lots of important things. An amazing range—something for almost everyone. And actually just the very size of it already represents an important challenge. Because as Mathematica grows bigger and bigger, it becomes more and more difficult for one to grasp everything that’s in it. Continue reading

This is an edited version of a short talk I gave last weekend at The Nantucket Project—a fascinatingly eclectic event held on an island that I happen to have been visiting every summer for the past dozen years.

Lots of things have happened in the world in the past 100 years. But I think in the long view of history one thing will end up standing out among all others: this has been the century when the idea of computation emerged.

We’ve seen all sorts of things “get computerized” over the last few decades—and by now a large fraction of people in the world have at least some form of computational device. But I think we’re still only at the very beginning of absorbing the implications of the idea of computation. And what I want to do here today is to talk about some things that are happening, and that I think are going to happen, as a result of the idea of computation.

I’ve been working on this stuff since I was teenager—which is now about a third of a century. And I think I’ve been steadily understanding more and more.

Our computational knowledge engine, Wolfram|Alpha, which was launched on the web about three years ago now, is one of the latest fruits of this understanding. Continue reading

I have four children, all with very different interests. My second-youngest, Christopher, age 13, has always liked technology. And last weekend he and I went to see the wild, wacky and creative technology (and other things) on display at the Maker Faire in New York.

I had told the organizers I could give a talk. But a week or so before the event, Christopher told me he thought what I planned to talk about wasn’t as interesting as it could be. And that actually he could give some demos that would be a lot more interesting and relevant.

Christopher has been an avid Mathematica user for years now. And he likes hooking Mathematica up to interesting devices—with two recent favorites being Arduino boards and quadricopter drones.

And so it was that last Sunday I walked onto a stage with him in front of a standing-room-only crowd of a little over 300 people, carrying a quadricopter. (I wasn’t trusted with the Arduino board.)

Christopher had told me that I shouldn’t talk too long—and that then I should hand over to him. He’d been working on his demo the night before, and earlier that morning. I suggested he should practice what he was going to say, but he’d have none of that. Instead, up to the last minute, he spent his time cleaning up code for the demo.

I must have given thousands of talks in my life, but the whole situation made me quite nervous. Would the Arduino board work? Would the quadricopter fly? What would Christopher do if it didn’t?

I don’t think my talk was particularly good. But then Christopher bounced onto the stage, and soon was typing raw Mathematica code in front of everyone—with me now safely off on the side (where I snapped this picture):

Continue reading

Note added: Since this blog was written, Facebook has modified their API to make much less information available about Facebook friends. While I think adding privacy controls is a good idea, what Facebook has done reduces the richness of the results that Wolfram|Alpha Personal Analytics can give for Facebook users.

Now of course most people haven’t been doing the kind of data collecting that I’ve been doing for the past couple of decades. But these days a lot of people do have a rich source of data about themselves: their Facebook histories.

And today I’m excited to announce that we’ve developed a first round of capabilities in Wolfram|Alpha to let anyone do personal analytics with Facebook data. Wolfram|Alpha knows about all kinds of knowledge domains; now it can know about you, and apply its powers of analysis to give you all sorts of personal analytics. And this is just the beginning; over the months to come, particularly as we see about how people use this, we’ll be adding more and more capabilities.

It’s pretty straightforward to get your personal analytics report: all you have to do is type “facebook report” into the standard Wolfram|Alpha website.

If you’re doing this for the first time, you’ll be prompted to authenticate the Wolfram Connection app in Facebook, and then sign in to Wolfram|Alpha (yes, it’s free). And as soon as you’ve done that, Wolfram|Alpha will immediately get to work generating a personal analytics report from the data it can get about you through Facebook.

Here’s the beginning of the report I get today when I do this:

Yes, it was my birthday yesterday. And yes, as my children are fond of pointing out, I’m getting quite ancient… Continue reading

The announcement early yesterday morning of experimental evidence for what’s presumably the Higgs particle brings a certain closure to a story I’ve watched (and sometimes been a part of) for nearly 40 years. In some ways I felt like a teenager again. Hearing about a new particle being discovered. And asking the same questions I would have asked at age 15. “What’s its mass?” “What decay channel?” “What total width?” “How many sigma?” “How many events?”

When I was a teenager in the 1970s, particle physics was my great interest. It felt like I had a personal connection to all those kinds of particles that were listed in the little book of particle properties I used to carry around with me. The pions and kaons and lambda particles and f mesons and so on. At some level, though, the whole picture was a mess. A hundred kinds of particles, with all sorts of detailed properties and relations. But there were theories. The quark model. Regge theory. Gauge theories. S-matrix theory. It wasn’t clear what theory was correct. Some theories seemed shallow and utilitarian; others seemed deep and philosophical. Some were clean but boring. Some seemed contrived. Some were mathematically sophisticated and elegant; others were not.

By the mid-1970s, though, those in the know had pretty much settled on what became the Standard Model. In a sense it was the most vanilla of the choices. It seemed a little contrived, but not very. It involved some somewhat sophisticated mathematics, but not the most elegant or deep mathematics. But it did have at least one notable feature: of all the candidate theories, it was the one that most extensively allowed explicit calculations to be made. They weren’t easy calculations—and in fact it was doing those calculations that got me started having computers to do calculations, and set me on the path that eventually led to Mathematica. But at the time I think the very difficulty of the calculations seemed to me and everyone else to make the theory more satisfying to work with, and more likely to be meaningful. Continue reading

(This is an updated version of what I wrote for Alan Turing’s 98th birthday.)

Today (June 23, 2012) would have been Alan Turing’s 100^th birthday—if he had not died in 1954, at the age of 41.

I never met Alan Turing; he died five years before I was born. But somehow I feel I know him well—not least because many of my own intellectual interests have had an almost eerie parallel with his.

And by a strange coincidence, Mathematica’s “birthday” (June 23, 1988) is aligned with Turing’s—so that today is also the celebration of Mathematica‘s 24^th birthday.

I think I first heard about Alan Turing when I was about eleven years old, right around the time I saw my first computer. Through a friend of my parents, I had gotten to know a rather eccentric old classics professor, who, knowing my interest in science, mentioned to me this “bright young chap named Turing” whom he had known during the Second World War.

One of the classics professor’s eccentricities was that whenever the word “ultra” came up in a Latin text, he would repeat it over and over again, and make comments about remembering it. At the time, I didn’t think much of it—though I did remember it. Only years later did I realize that “Ultra” was the codename for the British cryptanalysis effort at Bletchley Park during the war. In a very British way, the classics professor wanted to tell me something about it, without breaking any secrets. And presumably it was at Bletchley Park that he had met Alan Turing.

A few years later, I heard scattered mentions of Alan Turing in various British academic circles. I heard that he had done mysterious but important work in breaking German codes during the war. And I heard it claimed that after the war, he had been killed by British Intelligence. At the time, at least some of the British wartime cryptography effort was still secret, including Turing’s role in it. I wondered why. So I asked around, and started hearing that perhaps Turing had invented codes that were still being used. (In reality, the continued secrecy seems to have been intended to prevent it being known that certain codes had been broken—so other countries would continue to use them.)

I’m not sure where I next encountered Alan Turing. Probably it was when I decided to learn all I could about computer science—and saw all sorts of mentions of “Turing machines”. But I have a distinct memory from around 1979 of going to the library, and finding a little book about Alan Turing written by his mother, Sara Turing.

And gradually I built up quite a picture of Alan Turing and his work. And over the 30+ years that have followed, I have kept on running into Alan Turing, often in unexpected places.
Continue reading

Today I’m excited to be able to announce that our company is moving into yet another new area: large-scale system modeling. Last year, I wrote about our plans to initiate a new generation of large-scale system modeling. Now we are taking a major step in that direction with the release of Wolfram SystemModeler.

SystemModeler is a very general environment that handles modeling of systems with mechanical, electrical, thermal, chemical, biological, and other components, as well as combinations of different types of components. It’s based—like Mathematica—on the very general idea of representing everything in symbolic form.

In SystemModeler, a system is built from a hierarchy of connected components—often assembled interactively using SystemModeler‘s drag-and-drop interface. Internally, what SystemModeler does is to derive from its symbolic system description a large collection of differential-algebraic and other equations and event specifications—which it then solves using powerful built-in hybrid symbolic-numeric methods. The result of this is a fully computable representation of the system—that mirrors what an actual physical version of the system would do, but allows instant visualization, simulation, analysis, or whatever.

Here’s an example of SystemModeler in action—with a 2,685-equation dynamic model of an airplane being used to analyze the control loop for continuous descent landings:

Continue reading

(This is the third in a series of posts about A New Kind of Science. Previous posts have covered the original reaction to the book and what’s happened since it was published.)

Today ten years have passed since A New Kind of Science (“the NKS book”) was published. But in many ways the development that started with the book is still only just beginning. And over the next several decades I think its effects will inexorably become ever more obvious and important.

Indeed, even at an everyday level I expect that in time there will be all sorts of visible reminders of NKS all around us. Today we are continually exposed to technology and engineering that is directly descended from the development of the mathematical approach to science that began in earnest three centuries ago. Sometime hence I believe a large portion of our technology will instead come from NKS ideas. It will not be created incrementally from components whose behavior we can analyze with traditional mathematics and related methods. Rather it will in effect be “mined” by searching the abstract computational universe of possible simple programs.

And even at a visual level this will have obvious consequences. For today’s technological systems tend to be full of simple geometrical shapes (like beams and boxes) and simple patterns of behavior that we can readily understand and analyze. But when our technology comes from NKS and from mining the computational universe there will not be such obvious simplicity. Instead, even though the underlying rules will often be quite simple, the overall behavior that we see will often be in a sense irreducibly complex.

So as one small indication of what is to come—and as part of celebrating the first decade of A New Kind of Science—starting today, when Wolfram|Alpha is computing, it will no longer display a simple rotating geometric shape, but will instead run a simple program (currently, a 2D cellular automaton) from the computational universe found by searching for a system with the right kind of visually engaging behavior.

Continue reading

(This is the second of a series of posts related to next week’s tenth anniversary of A New Kind of Science. The previous post covered developments since the book was published; the next covers its future.)

“You’re destroying the heritage of mathematics back to ancient Greek times!” With great emotion, so said a distinguished mathematical physicist to me just after A New Kind of Science was published ten years ago. I explained that I didn’t write the book to destroy anything, and that actually I’d spent all those years working hard to add what I hoped was an important new chapter to human knowledge. And, by the way—as one might guess from the existence of Mathematica—I personally happen to be quite a fan of the tradition of mathematics.

He went on, though, explaining that surely the main points of the book must be wrong. And if they weren’t wrong, they must have been done before. The conversation went back and forth. I had known this person for years, and the depth of his emotion surprised me. After all, I was the one who had just spent a decade on the book. Why was he the one who was so worked up about it?

And then I realized: this is what a paradigm shift sounds like—up close and personal. Continue reading

(This is the first of a series of posts related to next week’s tenth anniversary of A New Kind of Science. The second covers what’s happened since it was published, and the third its future.)

On May 14, 2012, it’ll be 10 years since A New Kind of Science (“the NKS book”) was published.

After 20 years of research, and nearly 11 years writing the book, I’d taken most things about as far as I could at that time. And so when the book was finished, I mainly launched myself back into technology development. And inspired by my work on the NKS book, I’m happy to say that I’ve had a very fruitful decade (Mathematica reinvented, CDF, Wolfram|Alpha, etc.).

I’ve been doing little bits of NKS-oriented science here and there (notably at our annual Summer School). But mostly I’ve been busy with other things. And so it’s been other people who’ve been having the fun of moving the science of NKS forward. But almost every day I’ll hear about something that’s been being done with NKS. And as we approach the 10-year mark, I’ve been very curious to try to get at least a slightly more systematic view of what’s been going on.

A place to start is the academic literature, where there’s now an average of slightly over one new paper per day published citing the NKS book—with that number steadily increasing. The papers span all kinds of areas (here identified by journal fields):

Continue reading

Today marks an important milestone for Wolfram|Alpha, and for computational knowledge in general: for the first time, Wolfram|Alpha is now on average giving complete, successful responses to more than 90% of the queries entered on its website (and with “nearby” interpretations included, the fraction is closer to 95%).

I consider this an impressive achievement—the hard-won result of many years of progressively filling out the knowledge and linguistic capabilities of the system.

The picture below shows how the fraction of successful queries (in green) has increased relative to unsuccessful ones (red) since Wolfram|Alpha was launched in 2009. And from the log scale in the right-hand panel, we can see that there’s been a roughly exponential decrease in the failure rate, with a half-life of around 18 months. It seems to be a kind of Moore’s law for computational knowledge: the net effect of innumerable individual engineering achievements and new ideas is to give exponential improvement.

Continue reading

One day I’m sure everyone will routinely collect all sorts of data about themselves. But because I’ve been interested in data for a very long time, I started doing this long ago. I actually assumed lots of other people were doing it too, but apparently they were not. And so now I have what is probably one of the world’s largest collections of personal data.

Every day—in an effort at “self awareness”—I have automated systems send me a few emails about the day before. But even though I’ve been accumulating data for years—and always meant to analyze it—I’ve never actually gotten around to doing it. But with Mathematica and the automated data analysis capabilities we just released in Wolfram|Alpha Pro, I thought now would be a good time to finally try taking a look—and to use myself as an experimental subject for studying what one might call “personal analytics”.

Let’s start off talking about email. I have a complete archive of all my email going back to 1989—a year after Mathematica was released, and two years after I founded Wolfram Research. Here’s a plot with a dot showing the time of each of the third of a million emails I’ve sent since 1989:

Continue reading

It’s a sad but true fact that most data that’s generated or collected—even with considerable effort—never gets any kind of serious analysis. But in a sense that’s not surprising. Because doing data science has always been hard. And even expert data scientists usually have to spend lots of time wrangling code and data to do any particular analysis.

I myself have been using computers to work with data for more than a third of a century. And over that time my tools and methods have gradually evolved. But this week—with the release of Wolfram|Alpha Pro—something dramatic has happened, that will forever change the way I approach data.

The key idea is automation. The concept in Wolfram|Alpha Pro is that I should just be able to take my data in whatever raw form it arrives, and throw it into Wolfram|Alpha Pro. And then Wolfram|Alpha Pro should automatically do a whole bunch of analysis, and then give me a well-organized report about my data. And if my data isn’t too large, this should all happen in a few seconds.

And what’s amazing to me is that it actually works. I’ve got all kinds of data lying around: measurements, business reports, personal analytics, whatever. And I’ve been feeding it into Wolfram|Alpha Pro. And Wolfram|Alpha Pro has been showing me visualizations and coming up with analyses that tell me all kinds of useful things about the data.

Continue reading

Today I’m excited to be able to announce the launch of Wolfram|Alpha Pro—the biggest single step in the development of Wolfram|Alpha since its original introduction.

Over the two and a half years since we first launched, Wolfram|Alpha has been growing rapidly in content and capabilities. But today’s introduction of Wolfram|Alpha Pro in effect adds a whole new model for interacting with Wolfram|Alpha—and brings all sorts of fundamentally new and remarkable capabilities.

Starting today, everyone has access to Wolfram|Alpha Pro at wolframalpha.com. Unlike the “tourist” version of Wolfram|Alpha, though, you have to log in, and, yes, to get full capabilities there’s a subscription ($4.99/month, or $2.99/month for students). (Right now, you can try it for free with a trial subscription.)

So, what does Wolfram|Alpha Pro do?

Continue reading

There’s been very little change in top-level internet domains (like .com, .org, .us, etc.) for a long time. But a number of years ago I started thinking about the possibility of having a new .data top-level domain (TLD). And starting this week, there’ll finally be a period when it’s possible to apply to create such a thing.

It’s not at all clear what’s going to happen with new TLDs—or how people will end up feeling about them. Presumably there’ll be TLDs for places and communities and professions and categories of goods and events. A .data TLD would be a slightly different kind of thing. But along with some other interested parties, I’ve been exploring the possibility of creating such a thing. Continue reading

Last weekend I decided to have a short break from all the exciting technological things we’re doing… and to give a talk at the Singularity Summit in New York City about the implications of A New Kind of Science for the future, technological and otherwise. Here’s the transcript:

Well, what I wanted to do here was to have some fun—and talk about the future.

That’s something that’s kind of recreational for me. Because what I normally do is work in the trenches just trying to actually build the future… kind of one brick at a time—or at least one big project at a time.

I’ve been doing this now for a bit more than 30 years, and I guess I’ve built a fairly tall tower. From which it’s possible to do and see some pretty interesting things. Continue reading

Opening keynote of the Wolfram Mathematica Virtual Conference 2011, September 26–27.

Hi. I’m pleased to be with you. I’ve been asked to talk a bit about the background and vision of Mathematica.

You know, this month it’s exactly 25 years since I started building Mathematica. It’s been really exciting seeing Mathematica grow and prosper over the years. But I have to say that in just the last few years, something truly remarkable seems to have been happening. It feels like Mathematica is really coming of age. It’s in just the right place at the right time. And it’s making possible some fundamentally new and profoundly powerful things. Like Wolfram|Alpha, and CDF, and yet other things that we’ll have coming over the next year.

But let me start off at the beginning. How did Mathematica come to be in the first place? Here’s the personal story. Continue reading

I’m so sad this evening—as millions are—to hear of Steve Jobs’s death. Scattered over the last quarter century, I learned much from Steve Jobs, and was proud to consider him a friend. And indeed, he contributed in various ways to all three of my major life projects so far: Mathematica, A New Kind of Science and Wolfram|Alpha.

I first met Steve Jobs in 1987, when he was quietly building his first NeXT computer, and I was quietly building the first version of Mathematica. A mutual friend had made the introduction, and Steve Jobs wasted no time in saying that he was planning to make the definitive computer for higher education, and he wanted Mathematica to be part of it. I don’t now remember the details of our first meeting, but at the end of it, Steve gave me his business card, which tonight I found duly still sitting in my files:

Continue reading

Things with Wolfram|Alpha are going well. Really well. So well that I’m now incredibly keen to scale them up dramatically.

When I started the Wolfram|Alpha project, I was not even sure anything like it would be possible. But over the last two years we’ve proved that, yes, with the tower of technology we’ve created, one can in fact take large swaths of knowledge, make them computable, and deliver them for everyone to use.

From the outside, it’s easy to see that there’s been steady growth in the domains of knowledge that Wolfram|Alpha covers. And over the next few months there’ll be some big additions, notably in everyday and consumer areas. But to me what’s most dramatic is what’s happened on the inside. Because what we’ve done is to build a giant system of technology and management processes that allows us systematically to make any area of knowledge computable.

The catch is that it always takes effort. We rely on a huge tower of automation. But in every new area we tackle there are new issues, new opportunities—and new ways that resources and human effort have to be used.

I’m very pleased with how broad and deep the coverage we have already achieved is. But we have an immense to-do list, assembled not least from all the feedback we’ve received from users of Wolfram|Alpha. And the good news is that at this point it’s a straight shot: given enough effort, we can complete the to-do list. We have all the systems we need to scale the knowledge in Wolfram|Alpha up all the way. Continue reading

The precursors of what we’re trying to do with computable data in Wolfram|Alpha in many ways stretch back to the very dawn of human history—and in fact their development has been fascinatingly tied to the whole progress of civilization.

Last year we invited the leaders of today’s great data repositories to our Wolfram Data Summit—and as a conversation piece we assembled a timeline of the historical development of systematic data and computable knowledge.

This year, as we approach the Wolfram Data Summit 2011, we’ve taken the comments and suggestions we got, and we’re making available a five-feet-long (1.5 meters) printed poster of the timeline—as well as having the basic content on the web.

The story the timeline tells is a fascinating one: of how, in a multitude of steps, our civilization has systematized more and more areas of knowledge—collected the data associated with them, and gradually made them amenable to automation. Continue reading

Two weeks ago we made a major announcement: building on technology that we’ve been developing for more than 20 years, we released Computable Document Format (CDF). I think CDF is going to have a big effect on the way all sorts of things can be  communicated. Because for the first time it makes it practical to include live computation as a routine part of a document.

There are many important applications of CDF that we’ll no doubt be seeing over the months and years to come. But today I’m pleased to announce an experimental one from us: Wolfram|Alpha with CDF.

Starting today, as soon as you have the free CDF plugin installed (or if you have Mathematica 8 on your system) you can go to the top right-hand corner of the Wolfram|Alpha website, and set CDF on, with the result that Wolfram|Alpha will generate not just a static web page, but instead full CDF output—that you can directly interact and compute with. Continue reading

This week I’m giving a talk at a conference on Mathematics and Computation in Music (MCM 2011)… so I decided to collect some of my thoughts on such topics…

How difficult is it to generate human-like music? To pass the analog of the Turing test for music?

Though music typically has a certain formal structure—as the Pythagoreans noted 2500 years ago—it seems at its core somehow fundamentally human: a reflection of raw creativity that is almost a defining characteristic of human capabilities.

But what is that creativity? Is it something that requires the whole history of our biological and cultural evolution? Or can it exist just as well in systems that have nothing directly to do with humans?

In my work on A New Kind of Science, I studied the computational universe of possible programs—and found that even very simple programs can show amazingly rich and complex behavior, on a par, for example, with what one sees in nature. And through my Principle of Computational Equivalence I came to believe that there can be nothing that fundamentally distinguishes our human capabilities from all sorts of processes that occur in nature—or in very simple programs.

But what about music? Some people used their belief that “no simple program will ever create great music” to argue that there must be something wrong with my Principle of Computational Equivalence.

So I became curious: is there really something special and human about music? Or can it in fact be created perfectly well in an automatic, computational way?

Continue reading

I got started with science quite early in my life… with the result that I got my PhD (at Caltech, in physics) when I was 20 years old. Last weekend a young woman named Catherine Beni (whom I had met quite a few years ago) sent me mail saying she had just received her PhD from Caltech (in applied math)—also at the age of 20.

Needless to say, we were both curious who had the record for youngest Caltech PhD. Catherine said she was 20 years, 2 months and 12 days old when she did her PhD defense. Well, I knew I’d finished my PhD in November 1979—and I was born August 29, 1959. So that would also have made me around 20 years and 2 months old.

I quickly searched the OCR’ed archive that I have of my paper documents, and found this:

The month was confirmed, but frustratingly, no day was filled in. But then I remembered something about my PhD defense (the little talk that people give to officially get their theses signed off). In the middle of it, I was having a rather spirited discussion (about the second law of thermodynamics) with Richard Feynman, and suddenly the room started shaking—there was a minor earthquake.
Continue reading

Wolfram|Alpha, A New Kind of Science, and even Mathematica all have aspects that are philosophy projects. Each of them, in different ways, informs questions in philosophy—and are themselves informed by philosophical ideas and discoveries.

Indeed, the very fact that I decided Wolfram|Alpha might be a possible project was the result of what amounts to a philosophical realization that I learned from A New Kind of Science: there is no bright line that identifies “intelligence”; it is all just computation.

I don’t get to talk much about philosophy. But here is a recording of a keynote speech I was recently asked to give about “computing and philosophy”.

To mark the second anniversary of the launch of Wolfram|Alpha, I did an interactive webcast:

Here’s a transcript of my introduction:

[Note: here is what I wrote for Wolfram|Alpha’s first anniversary a year ago.]

So, as of today, Wolfram|Alpha has officially been out in the wild for two years.

And I’m happy to say, it’s doing really well.

You know, I’d been thinking about building Wolfram|Alpha for more than 30 years.

And I’ve been working to build the stack of ideas and technology to make it possible for nearly that long.

At the beginning, I was not really sure that Wolfram|Alpha was going to be possible at all.

And I think if I look a year ago from now my main conclusion was that after a year out in the wild, we’d proved that, yes, Wolfram|Alpha was indeed possible.

Well, now that we’re two years out, I think my conclusion is: Wolfram|Alpha is even a lot more important than I thought it was.

This effort to make all our knowledge computable is really something very fundamental, that’s sort of inevitably going to be needed just all over the place.

So what have we been up to this year?
Continue reading

In the last several weeks, I’ve given talks about innovation, mobile technology, mathematics and philosophy. Last week I gave a talk at the Bio–IT World conference in Boston.

At the beginning I covered many of my favorite topics: Wolfram|Alpha, Mathematica, A New Kind of Science. But then I turned more specifically to biomedicine, and talked about quite a few topics that I’ve never discussed in public before.

Here’s an edited transcript.

OK. Well. I’m going to talk about some pretty ambitious things here today.

Both in technology and in science.

I’m going to talk about what we can know, and what we can compute, in biomedicine.

And about how we can make use of that.

I’m going to talk both about some practical technology and some basic science that I’ve been involved in building, that tries to address those things.

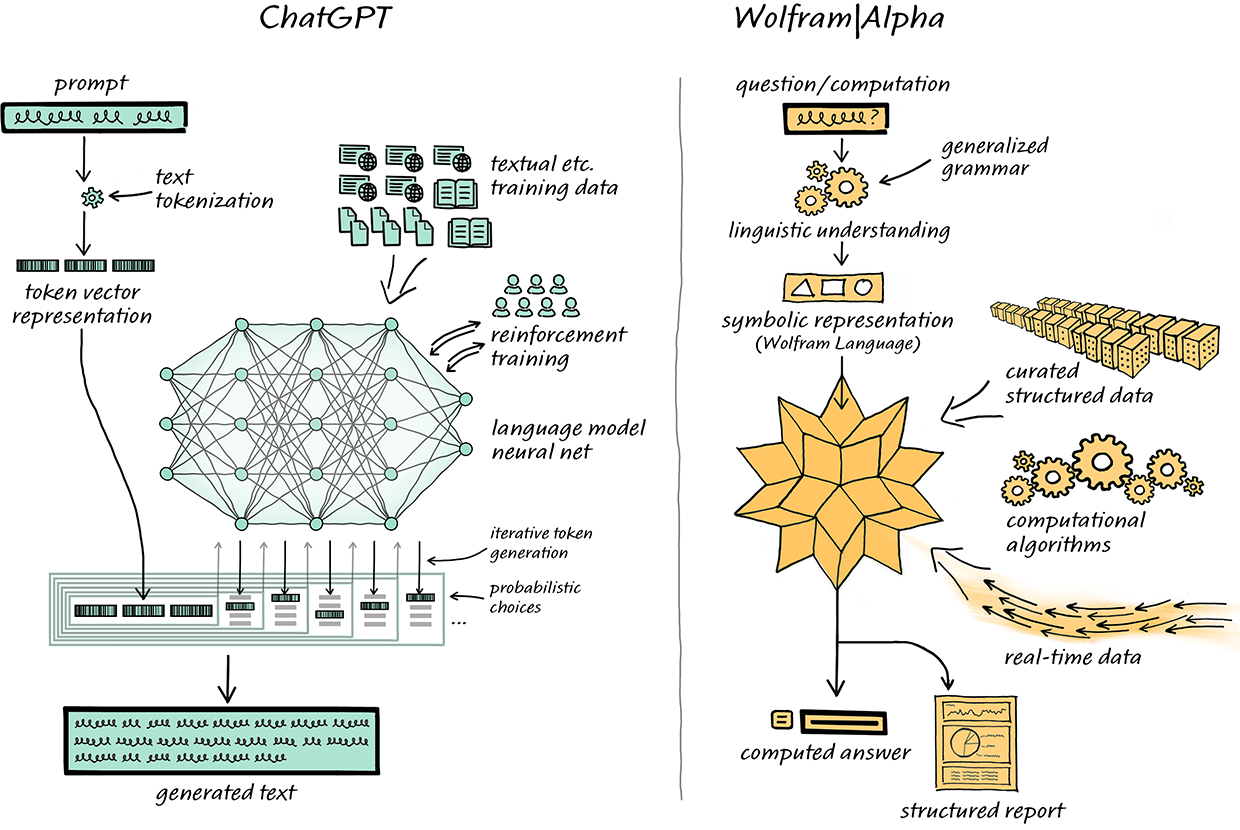
Many of you I hope will have seen and used Wolfram|Alpha, which has been off entertaining us in the background there.

Let me start with that.

You know–when computers, and I, were a lot younger, it used to be a common assumption that one day one would just be able to walk up to a computer and ask it anything.

And that if what one asked could somehow be answered on the basis of any knowledge that had been accumulated in our civilization, then the computer would be able to figure it out.

Well, 30 years ago I started wondering what it would take to actually do this.

And at first I have to say I thought the only possibility was to build a whole artificial intelligence—a whole brain-like thing that somehow thinks like a human.

And that seemed really hard.

But gradually I realized that actually, that might not be the right direction at all.

And that we might not want to build sort of the analog of a bird—but rather the analog of an airplane.

And that computation—and a bunch of ideas around it—might be the key.

Well, by that point I’d assembled a pretty big stack of technology and science, and organizational capability.

And a little more than five years ago I decided it was time to try a serious assault on the problem—of making the world’s knowledge computable.

Well, the result was Wolfram|Alpha. Which is a very long-term project.

But already gets used every day by millions of people, who manage effectively just to walk up to it and have it answer all kinds of things.
Continue reading

Over the past 25 years, we’ve been fortunate enough to make a mark in all sorts of areas of science and technology. Today I’m excited to announce that we’re in a position to tackle another major area: large-scale systems modeling.

It’s a huge and important area, long central to engineering, and increasingly central to fields like biomedicine. To do it right is also incredibly algorithmically demanding. But the exciting thing is that now we’ve finally assembled the technology stack that we need to do it—and we’re able to begin the process of making large-scale systems modeling an integrated core feature of Mathematica, accessible to a very broad range of users.

Lots of remarkable things will become possible. Using the methodology we’ve developed for Wolfram|Alpha, we’ll be curating not only data about systems and their components, but also complete dynamic models. Then we’ll have the tools to easily assemble models of almost arbitrary complexity—and to put them into algorithmic form so that they can be simulated, optimized, validated, visualized or manipulated by anything across the Mathematica system.

And then we’ll also be able to inject large-scale models into the Wolfram|Alpha system, and all its deployment channels.

So what does this mean? Here’s an example. Imagine that there’s a model for a new kind of car engine—probably involving thousands of individual components. The model is running in Mathematica, inside a Wolfram|Alpha server. Now imagine someone out in the field with a smartphone, wondering what will happen if they do a particular thing with an engine.

Well, with the technology we’re building, they should be able to just type (or say) into an app: “Compare the frequency spectrum for the crankshaft in gears 1 and 5”. Back on the server, Wolfram|Alpha technology will convert the natural language into a definite symbolic query. Then in Mathematica the model will be simulated and analyzed, and the results—quantitative, visual or otherwise—will be sent back to the user. Like a much more elaborate and customized version of what Wolfram|Alpha would do today with a question about a satellite position or a tide.

OK. So what needs to happen to make all this stuff possible? To begin with, how can Mathematica even represent something like a car—with all its various physical components, moving and running and acting on each other?
Continue reading

About a month before Wolfram|Alpha launched, I was on the phone with a group from IBM, talking about our vision for computable knowledge in Wolfram|Alpha. A few weeks later, the group announced that they were going to use what they had done in natural language processing to try to make a system to compete on Jeopardy.

I thought it was a brilliant way to showcase their work—and IBM’s capabilities in general. And now, a year and a half later, IBM has built an impressive level of anticipation for their upcoming Jeopardy television event. Whatever happens (and IBM’s system certainly should be able to win), one thing is clear: what IBM is doing will have an important effect in changing people’s expectations for how they might be able to interact with computers.

When Wolfram|Alpha was launched, people at first kept on referring to it as a “new search engine”—because basically keyword search was the only model they had for how they might find information on a large scale. But IBM’s project gives a terrific example of another model: question answering. And when people internalize this model, they’ll be coming a lot closer to realizing what’s possible with what we’re building in Wolfram|Alpha.

So what really is the relation between Wolfram|Alpha and the IBM Jeopardy project?

Continue reading

Wolfram|Alpha is making possible a whole new very interesting and very powerful kind of computing. And with the release today of version 2.0 of the Wolfram|Alpha API, it’s going to be considerably easier for a broad range of software developers to take advantage of it.

I’m happy to say that it seems as if Wolfram|Alpha is pretty useful to humans—for example through the wolframalpha.com website. But it also turns out that Wolfram|Alpha is extremely useful to programs. And in fact, even today, the number of requests coming to Wolfram|Alpha each second from programs often exceeds by some margin all the requests coming directly from humans.

The reason for this popularity is really pretty simple: Wolfram|Alpha completely changes the economics of a lot of programming. You see, these days a remarkable number of programs rely on having some kind of knowledge. And traditionally, the only way to get knowledge into a program was for the programmer to painstakingly put it there.

But with Wolfram|Alpha in the picture, it’s a different story. Because built into Wolfram|Alpha is already a huge amount of computable knowledge. And if a program is connected to Wolfram|Alpha, then it can immediately make use of all that knowledge.

Whether one’s building a website or a mobile app or desktop software or an enterprise application, the point is that one can use Wolfram|Alpha as a “knowledge-based computing” platform—so that having all sorts of computable knowledge becomes effectively free from an engineering point of view.

How does a program communicate with Wolfram|Alpha?  It uses the Wolfram|Alpha API. (These days, API is pretty much a term on its own, but it comes from “Application Program Interface”.)
Continue reading

Today we’re releasing the first three of a planned series of “course assistant” apps, built using Wolfram|Alpha technology.

The long-term goal is to have an assistant app for every major course, from elementary school to graduate school. And the good news is that Wolfram|Alpha has the breadth and depth of capabilities to make this possible—and not only in traditionally “computational” kinds of courses.

The concept of these apps is to make it as quick and easy as possible to access the particular capabilities of Wolfram|Alpha relevant for specific courses. Each app is organized according to the major curriculum units of a course. Then within each section of the app, there are parts that cover each of the particular types of problems relevant to that unit.
Continue reading

“Someone has to make the first great ebook publishing company; it might as well be us.” So I said a few weeks before the iPad was released this April. And a little while later Touch Press was formed. The iPad was released, and simultaneously, Touch Press’s first book The Elements was released. The book has been on the iPad bestseller list ever since—in addition to being featured in all sorts of iPad television commercials and the like.

Well, it’s good for a publishing company to have a successful first book.  But for me it’s been getting a little old telling people that I’m a partner in a new publishing company, but so far we’ve only published one book. So it’s exciting to be able to say that as of this week, Touch Press has a second book: Solar System.

Continue reading

A hundred years ago this month the first volume of Whitehead and Russell’s nearly-2000-page monumental work Principia Mathematica was published. A decade in the making, it contained page after page like the one below, devoted to showing how the truths of mathematics could be derived from logic.

Principia Mathematica is inspiring for the obvious effort put into it—and as someone who has spent much of their life engaged in very large intellectual projects, I feel a certain sympathy towards it. Continue reading

I love computer languages. In fact, I’ve spent roughly half my life nurturing one particular very rich computer language: Mathematica.

But do we really need computer languages to tell our computers what to do? Why can’t we just use natural human languages, like English, instead?

If you’d asked me a few years ago, I would have said it was hopeless. That perhaps one could make toy examples, but that ultimately natural language just wouldn’t be up to the task of creating useful programs.

But then along came Wolfram|Alpha. In which we’ve been able to make free-form linguistics work vastly better than I ever thought possible.

But still, in Wolfram|Alpha the input is essentially just set up to request knowledge—and Wolfram|Alpha responds by computing and presenting whatever knowledge is requested. But programming is different. It is not about generating static knowledge, but about generating programs that can take a range of inputs, and dynamically perform operations.

So the first question is: how might we represent these programs?

Continue reading

With the release of Mathematica 8 today, the single most dramatic change is that you don’t have to communicate with Mathematica in the Mathematica language any more: you can just use free-form English instead.

Wolfram|Alpha has pioneered the concept of specifying computations with free-form linguistic input. And with Mathematica 8, the powerful methods of Wolfram|Alpha become available within the Mathematica environment.

All one has to do is to type an = at the beginning of a line. Then what follows is taken as free-form linguistic input.

You don’t have to use precise Mathematica syntax. You can type things in just the way you think about them, in free-form English. But what happens is that Mathematica calls on Wolfram|Alpha to try to interpret your input, and turn it into precise Mathematica code.

Continue reading

Mathematica 8 is released today! It’s a huge and important release. With dramatic breakthroughs—and major broadening of the whole scope of Mathematica.

After 8 versions and 22 years most software systems have decayed to slow and lumbering development. But not Mathematica. In fact, with Mathematica it’s quite the opposite. As the years go by, Mathematica development is actually speeding up.

What has made that happen? Partly it’s our tenacious and broadening pursuit of ambitious long-term goals. But partly, it’s a remarkable reflection—and validation—of the core principles on which Mathematica has always been built.

Continue reading

Every year at our annual Wolfram Technology Conference I give a keynote speech about the state of our technology.

Here are the first two parts of the video from this year.

For nearly a quarter of a century, one of the responsibilities that I’ve taken most seriously is the shepherding of the design of Mathematica. Partly that has involved establishing foundational principles, and maintaining unity and consistency across the system. But at some point all the capabilities of Mathematica must get expressed in the individual built-in functions—like Table or NestList—that ultimately make up the system.

Each one of those functions encapsulates some piece of repeated computational work—often implemented by some deep tower of algorithms. And each one of those now 3000 or so functions requires a name.

We’re currently in the closing weeks of a (spectacular!) new version of Mathematica, and I spent part of last week doing final design reviews for some fascinating new areas of the system. And as part of those design reviews, we were confirming and tweaking some of the names we’re going to use for new functions.

The naming of functions is a strange and difficult art—a bit like an ultimately abstracted form of poetry. The goal is to take the concept and functionality of a function, and capture the essence of it in one, or two, or perhaps three, words (like Riffle, or DeleteCases, or FixedPointList)—chosen so that when someone sees those words, they immediately get the right idea about the function. In even the most succinct forms of ordinary poetry, you get at least a handful of words to communicate with. In function names, you typically get at most perhaps three.

Continue reading

Last week I gave a talk at the 2010 Emerging Technologies conference at MIT. I talked about many of my favorite topics, but with a particular orientation toward the future of the technology industry.

Here’s a transcript of the talk:

The Emerging Computation Revolution

When we look back on the history of technology, I think we’ll see that the greatest revolution of the 20th century was the arrival of the concept of computation.

And in these years today, I think we’re seeing something else happen: the emergence of a second set of revolutions made possible by the concept of computation.

And it’s those revolutions that I want to talk about here today.

Now, needless to say, I’m quite involved in these.  And for me it’s really been about a 30-year journey getting to the point we’re at today—slowly understanding what’s possible.

Well, behind me here I have one of the fruits of that—Wolfram|Alpha.

And I want to talk about that, and about the idea of knowledge-based computing that it’s making possible.

There’s a lot of knowledge in the world.  A lot of data that’s been systematically collected.  A lot of methods, models, algorithms, expertise that have been built up.

And ever since I was a kid I’ve wondered whether we could somehow make all of this computable. Whether we could somehow build something that’s a bit like those old science fiction computers.

So that we could just walk up to a machine, and immediately be able to answer any question that can be answered on the basis of the knowledge that our civilization has accumulated.

It’s an ambitious goal. And when I first thought about this nearly 40 years ago, it seemed very far off.

But every decade or so since then I’ve returned to this. And finally, earlier this past decade, I started to think that perhaps it wasn’t crazy to actually try to build something like this.

There were several things that made that possible.

Continue reading

Keynote talk given at the Wolfram Data Summit in Washington, DC on Thursday, September 9, 2010.

Well, I should start off by admitting one thing.

This Data Summit was my idea.

And I have to say that the #1 reason I wanted to have it was so I could have a chance to meet you all.

So… thanks for coming, and I hope I will have a chance to meet you-all!

Well, I’ve been a collector and an enthusiast of systematic data for about as long as I can remember.

But in the last few years, I’ve launched into what one might think of as the ultimate extreme data project.

It’s actually something I’ve been thinking about since I was a kid.

The idea is: take all the systematic knowledge—and data—that our civilization has accumulated, and somehow make it computable.

Make it so that given any specific question one wants to ask, one can just compute the answer on the basis of that knowledge and data.

Well, every so often I’d think about this again. And it’d always just seem too big and too difficult. And like it was at least decades in the future.

But two things happened in my life. Continue reading

I spent a decade of my life writing A New Kind of Science. Most of that time was devoted to discovering the science in the book. But another part was spent figuring out how to present the science in the best possible way—using words and pictures.

It took a lot of technology to do that presentation. On the software side, the biggest part was using Mathematica to create elaborate algorithmic diagrams—thousands of them. But then came the question of how to actually deliver everything. And back in 2002 when A New Kind of Science was published, the only real possibility was to print a book on paper, using the very best printing technology of the time.

The actual print production process was quite an adventure—going right to the edge of what was possible. But in the end we got many compliments on the object we produced. And from that time to this, that 5.5 lb (2.5 kg) lump of paper has been the definitive representation of my decade-plus of intellectual work.

But today I’m excited to be able to say that there’s something new and in some ways even better: a full version on the iPad.

Continue reading

I like to write.  And most days I actually do write a lot.  But most of it is not visible to the world at large.  Hundreds of internal emails and documents.  Pieces of content inside Wolfram|Alpha or Mathematica.  The occasional unsigned public webpage or other document.

My purpose in this blog is to have a visible outlet for a little more of what I do, and what I think about.

I’m constantly thinking about new things.  Coming up with new ideas. Getting new perspectives.  Thinking of new possible projects to do.

Usually I don’t talk much about things until or unless I’ve actually done something real with them.  Which can take years, and sometimes decades—if it happens at all.

But I’ve decided it’s time I started writing a little more about what I’m thinking about—rather than always waiting to have a complete, finished, project or product.

I’d also like to write about some of the things that happen in my life.  In some ways my life is delightfully simple and ordinary.  But in others I’ve chosen to make it pretty far out on the curve.

Some of the wildest and juiciest things that happen I won’t be able to write publicly about, typically because they’re someone’s corporate or personal secrets.  Or because, frankly, I don’t want to tell the world about some things I’m doing before I’m ready.

I’m a great believer in the value of history, not least because I think it’s the best way to have an informed view about the future.  I’ve also been a collector of stories—often as a participant.  Sometimes the stories aren’t appropriate for public consumption, at least at the time.  But I’ve now been around long enough that it’s beginning to be OK to tell pretty much any of the earlier ones.  So I hope to have a chance to do that on this blog.

There’s a lot that I could write—about all sorts of topics.  Some of it is timely; some of it I just think I should write down sometime.

I’ll enjoy writing whatever I end up writing.  But if people want to request particular topics, please contact me. I suspect there are a lot of things where I might have something interesting to say, but I’ve never realized it.  So ask me!

The creation of large data repositories has been a key historical indicator of social and intellectual development—and indeed perhaps one of the defining characteristics of the whole progress of civilization.

And through our work on Wolfram|Alpha—with its insatiable appetite for systematic data—we have gained a uniquely broad view of the many great data repositories that exist in the world today.

Some of these repositories are maintained by national or international agencies, some by companies and other organizations, and some by individuals. A few of the repositories are quite new, but many date back 40 or more years, and some well over a century. But there is one thing in common across essentially every great data repository: a core of diligent and committed people who have carefully shepherded its development.

Curiously, though, few of these people have ever met their counterparts in other domains of data. And in our work on Wolfram|Alpha we are almost certainly the first group ever to have had the pleasure of getting to know such a broad range of leaders of great data repositories.

And one of the things that we have discovered is that there is much in common in both the methods used and the issues faced by these data repositories. So as part of our contribution to the worldwide data community we have decided to sponsor a data summit to bring together for the first time the leaders of today’s great data repositories.

The Wolfram Data Summit 2010 will be held in Washington, DC on September 9–10.
Continue reading

Years ago I wondered if it would ever be possible to systematically make human knowledge computable. And today, one year after the official launch of Wolfram|Alpha, I think I can say for sure: it is possible.

It takes a stack of technology and ideas that I’ve been assembling for nearly 30 years. And in many ways it’s a profoundly difficult project. But this year has shown that it is possible.

Wolfram|Alpha is of course a very long-term undertaking. But much has been built, the direction is set, and things are moving with accelerating speed.

Over the past year, we’ve roughly doubled the amount that Wolfram|Alpha knows. We’ve doubled the number of domains it handles, and the number of algorithms it can use. And we’ve actually much more than doubled the amount of raw data in it.

Things seem to be scaling better and better. The more we put into Wolfram|Alpha, the easier it becomes to add still more. We’ve honed both our automated and human processes, progressively building on what Wolfram|Alpha already does.

When we launched Wolfram|Alpha a year ago, about 2/3 of all queries generated a response. Now over 90% do.

So, what are some of the things we’ve learned over the past year? Continue reading

(This post was originally published on the Wolfram|Alpha Blog.)

So what’s been happening with Wolfram|Alpha this summer? A lot!

At a first glance, the website looks pretty much as it did when it first launched—with the straightforward input field. But inside that simple exterior an incredible amount has happened. Our development organization has been buzzing with activity all summer. In fact, it’s clear from the metrics that the intensity is steadily rising, with things being added at an ever-increasing rate.

Wolfram|Alpha was always planned to be a very long-term project, and paced accordingly. We pushed very hard to get it launched before the summer so that we could spend the “quiet time” of our first summer steadily enhancing it, before more people start using it more intently in the fall.

Two really great things have happened as a result of actually getting Wolfram|Alpha launched. The first is that we’ve discovered that there’s a huge community of people out there who want to help the mission of Wolfram|Alpha. And we’re steadily ramping up our mechanisms for those people to contribute to the project. Continue reading

(This post was originally published on the Wolfram|Alpha Blog.)

It’s now a week since we officially launched Wolfram|Alpha into the world.

It’s been a great first week.

Approaching 100 million queries. Lots of compliments.

But for me the most striking thing is how many people want to help Wolfram|Alpha succeed.

Making the world’s knowledge computable is a huge undertaking.

And it’s wonderful to see all the help we’re being offered in doing it.

We’ve worked hard to construct a framework. But to realize the full promise of computable knowledge, we need a lot of input and support. Continue reading

(This post was originally published on the Wolfram|Alpha Blog.)

Starting later today, we’ll be launching Wolfram|Alpha (you can see the proceedings on a live webcast).

This is a proud moment for us and for the whole Mathematica community. (We hope the launch goes well!)

Wolfram|Alpha defines a new direction in computing—that would have simply not have been possible without Mathematica, and that in time will add some remarkable new dimensions to Mathematica itself.

In terms of technology, Wolfram|Alpha is a uniquely complex software system, which has been entirely developed and deployed with Mathematica and Mathematica technologies.
Continue reading

May 14, 2009 marks the 7^th anniversary of the publication of A New Kind of Science, and it has been my tradition on these anniversaries to write a short report on the progress of NKS.

It has been fascinating over the past few years to watch the progressive absorption of NKS methods and the NKS paradigm into countless different fields. Sometimes there’s visible mention of NKS, though often there is not.

There has been an inexorable growth in the use of the types of models pioneered in NKS. There has been steadily increasing use of the kinds of computational experiments and investigations introduced in NKS. And the NKS way of thinking about computation and in terms of computation has become steadily more widespread.
Continue reading

Some might say that Mathematica and A New Kind of Science are ambitious projects.

But in recent years I’ve been hard at work on a still more ambitious project—called Wolfram|Alpha.

And I’m excited to say that in just two months it’s going to be going live:

Continue reading

In the middle of last year, we finished our decade-long project to reinvent Mathematica, and we released Mathematica 6.

We introduced a great many highly visible innovations in Mathematica 6—like dynamic interactivity and computable data. But we were also building a quite unprecedented platform for developing software.

And even long before Mathematica 6 was released, we were already working on versions of Mathematica well beyond 6.

And something remarkable was happening. There’d been all sorts of areas we’d talked about someday being in Mathematica. But they’d always seemed far off.

Well, now, suddenly, lots of them seemed like they were within reach. It seemed as if everything we’d built into Mathematica was coming together to make a huge number of new things possible.

All over our company, efforts were starting up to build remarkable things.

It was crucial that over the years, we’d invested a huge amount in creating long-term systems for organizing our software development efforts. So we were able to take those remarkable things that were being built, and flow them into Mathematica.

And at some point, we realized we just couldn’t wait any longer. Even though Mathematica 6 had come out only last year, we had assembled so much new functionality that we just had to release Mathematica 7.

So 18 months after the release of Mathematica 6, I’m happy to be able to announce that today Mathematica 7 is released!

Continue reading

A few times a year they would arrive. Email dispatches from an adventurous explorer in the world of geometry. Sometimes with subject lines like “Phenomenal discoveries!!!” Usually with images attached. And stories of how Russell Towle had just used Mathematica to discover yet another strange and wonderful geometrical object.

Then, this August, another email arrived, this time from Russell Towle’s son: “… last night, my father died in a car accident”.

I first heard from Russell Towle thirteen years ago, when he wrote to me suggesting that Mathematica’s graphics language be extended to have primitives not just for polygons and cubes, but also for “polar zonohedra”.

I do not now recall, but I strongly suspect that at that time I had never heard of zonohedra. But Russell Towle’s letter included some intriguing pictures, and we wrote back encouragingly.

There soon emerged more information. That Russell Towle lived in a hexagonal house of his own design, in a remote part of the Sierra Nevada mountains of California. That he was a fan of Archimedes, and had learned Greek to be able to understand his work better. And that he was not only an independent mathematician, but also a musician and an accomplished local historian. Continue reading

Today is an important anniversary for me and our company.

Twenty years ago today—at noon (Pacific Time) on Thursday, June 23, 1988—Mathematica 1.0 was officially launched.

Much has changed in the world since then, particularly when it comes to computer technology.

ut I’m happy to be able to say that Mathematica still seems as modern today as it did back then when it was first released. And if you take almost any Mathematica 1.0 program from 20 years ago, it’ll run without change in the latest Mathematica 6.0 today.

From the beginning, I had planned Mathematica for the long term. I wanted to build a system that could capture the essence of computation, and apply it wherever that became possible.

I spent great effort to get the fundamentals right—and to build the system on principles that would endure.

And looking back over the past two decades it’s satisfying to see how well that has worked out. Continue reading

It’s not easy to make a big software system that really fits together. It’s incredibly important, though. Because it’s what makes the whole system more than just the sum of its parts. It’s what gives the system limitless possibilities—rather than just a bunch of specific features.

But it’s hard to achieve. It requires maintaining consistency and coherence across every area, over the course of many years. But I think it’s something we’ve been very successful at doing with Mathematica. And I think it’s actually one of the most crucial assets for the long-term future of Mathematica.

It’s also a part of things that I personally am deeply involved in.

Ever since we started developing it more than 21 years ago, I’ve been the chief architect and chief designer of Mathematica‘s core functionality. And particularly for Mathematica 6, there was a huge amount of design to do. Actually, I think much more even than for Mathematica 1.

In fact, I just realized that over the course of the decade during which were developing Mathematica 6—and accelerating greatly towards the end—I spent altogether about 10,000 hours doing what we call “design reviews” for Mathematica 6, trying to make all those new functions and pieces of functionality in Mathematica 6 be as clean and simple as possible, and all fit together.

At least the way I do it, doing software design is a lot like doing fundamental science.

In fundamental science, one starts from a bunch of phenomena, and then one tries to drill down to find out what’s underneath them—to try to find the root causes, the ultimate primitives, of what’s going on.

Well, in software design, one starts from a bunch of functionality, and then one needs to drill down to find out just what ultimate primitives one needs to support them.

In science, if one does a good job at finding the primitives, then one can have a very broad theory that covers not just the phenomena one started from, but lots of others too.

And in software design, it’s the same kind of thing.

If one does a good job at finding the primitives, then one can build a very broad system that gives one not just the functionality one was first thinking about, but lots more too.
Continue reading

Not a lot gets written in the general press about foundational issues in mathematics, but this afternoon I found myself talking to a journalist about the subject of certainty in mathematics.

It turned out to be a pretty interesting conversation, so I thought I’d write here about a few things that came up.

Mathematics likes to think of itself as a very certainty-based business. If you’ve “proved something mathematically”, then it’s supposed to just be true. No ifs or buts. Complete certainty.

But in practice that’s not quite how it works—at least the way mathematics has traditionally been done. Because in reality a mathematical proof of the kind people publish in papers is something much more social. It’s a vehicle for convincing other humans—one’s fellow mathematicians—that something is true.

There’ve been a few million mathematical proofs published over the past century or so. Essentially all of them are written in a kind of human-compatible mixture of mathematical formalism and ordinary natural language.

They’re intended for human consumption. For people to read, and process. The best of them aren’t just arguments for some particular theorem. Instead they’re expositions that illuminate some whole mathematical structure.

But inevitably they require effort to read. It’s not just a mechanical matter. Instead, every reader of every proof has to somehow map what the proof is saying into their particular patterns of thought. So that they can personally be convinced that the proof is true.

And of course, in practice, proofs written by humans have bugs. Somewhere between the imprecision of ordinary language, and the difficulty of really thinking through every possible eventuality, it’s almost inevitable that any long proof that’s been published isn’t perfect. And even with an army of people to check it, not every bug will be found.

So how do computers—and Mathematica change this picture?

Continue reading

(This post was originally posted on the NKS Forum.)

The following are some remarks that I made on the Foundations of Math (FOM) mailing list in connection with discussion of the Wolfram 2,3 Turing Machine Prize. Though much of what I say is well understood in the NKS community, I thought it might nevertheless be of interest here.

Several people forwarded me the thread on this mailing list about our 2,3 Turing machine prize.

I’m glad to see that it has stimulated discussion. Perhaps I can make a few general remarks.

What do we learn from simple universal Turing machines?

John McCarthy wrote:

In the 1950s I thought that the smallest possible (symbol-state product) universal Turing machine would tell something about the nature of computation. Unfortunately, it didn’t.

I suspect that what was imagined at that time was that by finding the smallest universal machines one would discover some “spark of computation”—some critical ingredient in the rules necessary to make universal computation possible. (At the time, it probably also still seemed that there might be a “spark of life” or a “spark of intelligence” that could be found in systems.)

I remember that when I first heard about universality in the Game of Life in the early 1970s, I didn’t think it particularly significant; it seemed like just a clever hack.

But a few decades later—after building up the whole framework in A New Kind of Science, I have a quite different view. Continue reading

(Main prize page: The Wolfram 2,3 Turing Machine Research Prize)

“And although it will no doubt be very difficult to prove, it seems likely that this Turing machine will in the end turn out to be universal.”

So I wrote on page 709 of A New Kind of Science (NKS).

I had searched the computational universe for the simplest possible universal Turing machine. And I had found a candidate—that my intuition told me was likely to be universal. But I was not sure.

And so as part of commemorating the fifth anniversary of A New Kind of Science on May 14 this year, we announced a $25,000 prize for determining whether or not that Turing machine is in fact universal.

I had no idea how long it would take before the prize was won. A month? A year? A decade? A century? Perhaps the question was even formally undecidable (say from the usual axioms of mathematics).

But today I am thrilled to be able to announce that after only five months the prize is won—and we have the answer: the Turing machine is in fact universal!

Alex Smith—a 20-year-old undergraduate from Birmingham, UK—has produced a 40-page proof.

I’m pleased that my intuition was correct. But more importantly, we now have another piece of evidence for the very general Principle of Computational Equivalence (PCE) that I introduced in A New Kind of Science.

We are also at the end of a quest that has spanned more than half a century to find the very simplest universal Turing machine.

Here it is. Just two states and three colors. And able to do any computation that can be done.

Continue reading

I don’t have much time for hobbies these days, but occasionally I get to indulge a bit. A few days ago I did a videoconference talking about one of my favorite hobbies: hunting for the fundamental laws of physics.

Physics was my first field (in fact, I became a card-carrying physicist when I was a teenager). And as it happens, the talk I just gave (for the European Network on Random Geometry) was organized by one of my old physics collaborators.

Physicists often like to think that they’re dealing with the most fundamental kinds of questions in science. But actually, what I realized back in 1981 or so is that there’s a whole layer underneath.

There’s not just our own physical universe to think about, but the whole universe of possible universes.

If one’s going to do theoretical science, one had better be dealing with some kind of definite rules. But the question is: what rules?

Nowadays we have a great way to parametrize possible rules: as possible computer programs. And I’ve built a whole science out of studying the universe of possible programs—and have discovered that even very simple ones can generate all sorts of rich and complex behavior.

Well, that’s turned out to be relevant in modeling all sorts of systems in the physical and biological and social sciences, and in discovering interesting technology, and so on.

But here’s my big hobby question: what about our physical universe? Could it be operating according to one of these simple rules? Continue reading

When I hear about something like Wednesday’s bridge collapse, I immediately wonder whether any of the science I’ve worked on can be of any help.

Bridge design is one of the classic—almost iconic—successes of traditional mathematical science.

And when I first talked about A New Kind of Science, a not uncommon reaction was precisely, “But can it help build better bridges?”

Well, as a matter of fact, I rather suspect it can.

Bridges have a long history. Early on, only a few types seem to have been used. But with the arrival of iron structures in the 1800s there was a kind of “Cambrian explosion” of different types of truss bridges:

But what is the very best bridge structure, say from the point of view of robustness? There’s a huge universe of possibilities. But so far, only a tiny corner has been explored—and that mostly in the 1800s. Continue reading

Our 2007 NKS Summer School started about two weeks ago, and one of my roles there was to show a little of how NKS is done.

In the past, it would have been pretty unrealistic to show this in any kind of live way. But with computer experiments, and especially with Mathematica, that’s changed. And now it’s actually possible to make real discoveries in real time in front of live audiences.

I’ve done a few dozen “live experiments” now (here is an account of one from 2005). My scheme is as follows. Sometime between a few hours and a few minutes before the live experiment, I come up with a topic that I’m pretty sure hasn’t been studied before. Then I make sure to avoid thinking about it until I’m actually in front of the live audience.

Then, once the experiment starts, I have a limited time to discover something. Just by running Mathematica. Preferably with a little help from the audience. And occasionally with a little help from references on the web.

Every live experiment is an adventure. And it seems like almost every time, at around the halfway point, things look bad. We’ve tried lots of things. We’ve opened lots of threads. But nothing’s coming together.

But then, somehow, things almost always manage to come together. And we manage to discover something. That’s often pretty interesting. (There are still papers coming out now based on the live experiment I did at our very first Summer School, back in 2003).

I usually make my first live experiment at each Summer School be a piece of “pure NKS”: an abstract investigation of some simple program out in the computational universe.

This year I decided to take a look at an “old chestnut” that I’d recently been reminded about: a simple program (though it wasn’t thought of that way then) that was actually first investigated all the way back in 1920. Continue reading

It is perhaps ironic that two weeks after releasing what is probably the single most complex computational system ever constructed, we are today announcing a prize for the very simplest of computational systems.

But today is the fifth anniversary of the publication of A New Kind of Science, and to commemorate this, we have decided to establish the first NKS prize.

The prize is related to a core objective of the basic science of NKS: to map out the abstract universe of possible computational systems.

We know from NKS that very simple programs can show immensely complex behavior. And in the NKS book I formulated the Principle of Computational Equivalence that gives an explanation for this discovery.

That principle has many predictions. And one of them is that the ability to do general-purpose computing—to be capable of universal computation—should be common even among systems with very simple rules.

Today’s CPUs have millions of components. But the Principle of Computational Equivalence implies that all kinds of vastly simpler systems should also support universal computation.

The NKS book already gives several dramatic examples. But the purpose of the prize is to determine the boundary of universal computation for a particularly classic type of computational system: Turing machines. Continue reading

New technology is often what has driven the creation of new science. And so it has been with Mathematica.

One of the main reasons I originally started building Mathematica was that I wanted to use it myself.

And having Mathematica was a bit like having one of the first telescopes: I could point it somewhere, and immediately see all sorts of new things that had never been seen before.

Much has been discovered with Mathematica in almost every area of science.

But my particular interest has been to create a new kind of science that is uniquely made possible by Mathematica: a science based on exploring the computational universe.

We are used to creating computer programs for particular purposes. But as a matter of basic science we can ask about the universe of all possible programs.

And with Mathematica it becomes easy to explore this.

A quarter of a century ago I had begun my exploration of the computational universe—and had glimpsed some remarkable phenomena.

Then, when Mathematica was built, I went back and started a systematic study of the computational universe.

The results were remarkable. Wherever I looked—even among the simplest of programs—I saw all sorts of complex and interesting behavior. And from what I found I could make progress on a remarkable range of longstanding questions across all sorts of areas.

For eleven years I worked to develop this. And finally, on May 14, 2002, I published what I had done in my book A New Kind of Science.

Today is the fifth anniversary of that event. Continue reading

Mathematica 1.0 was released on June 23, 1988—now nearly 19 years ago. And normally, after 19 years, pretty much all one expects from software products is slow growth and incremental updates.

But as in so many things, Mathematica today just became a big exception.

Some people have said that Mathematica 6.0 shouldn’t even be called “Mathematica” at all. That it’s something so qualitatively new and different that it should be given a completely different name.

Well, perhaps I’m just too sentimental. Or too steeped in history. Or too naive about branding. But to me there’s no choice. We owe it to all the foundations we’ve laid these past twenty years to still call what we’ve built today “Mathematica.”

Realistically, I think it took us ten years after Mathematica 1.0 just to realize what a powerful thing we had in Mathematica.

We’d always talked about “symbolic programming,” and how it let us unify a lot of different ideas and areas. But sometime around the mid-1990s it began to dawn on us just what an amazing thing symbolic programming actually is.

And we began to think that there might be a whole new level one could reach in computing if one really did everything one could with symbolic programming.

Well, that was an intellectual challenge we couldn’t resist. So about ten years ago, we embarked on seeing just what might be possible. Continue reading

(This post was originally published on the NKS Forum.)

Last Friday (April 28, 2006) would have been Kurt Gödel’s 100th birthday. I agreed to try to write something about it for publication in a newspaper … which had the dual misfeatures that (a) I had to compress what I was saying and (b) that it didn’t actually get done…

Still, I thought people on the Forum might find my draft interesting … so here it is. Please recognize that this wasn’t polished for final publication…

When Kurt Gödel was born—one hundred years ago today—the field of mathematics seemed almost complete. Two millennia of development had just been codified into a few axioms, from which it seemed one should be able almost mechanically to prove or disprove anything in mathematics—and, perhaps with some extension, in physics too.

Twenty-five years later things were proceeding apace, when at the end of a small academic conference, a quiet but ambitious fresh PhD involved with the Vienna Circle ventured that he had proved a theorem that this whole program must ultimately fail.

In the seventy-five years since then, what became known as Gödel’s theorem has been ascribed almost mystical significance, sowed the seeds for the computer revolution, and meanwhile been practically ignored by working mathematicians—and viewed as irrelevant for broader science.

The ideas behind Gödel’s theorem have, however, yet to run their course. And in fact I believe that today we are poised for a dramatic shift in science and technology for which its principles will be remarkably central.

Gödel’s original work was quite abstruse. He took the axioms of logic and arithmetic, and asked a seemingly paradoxical question: can one prove the statement “this statement is unprovable”? Continue reading

(This post was originally published on the NKS Forum.)

I sent the following today to our NKS mailing list:

—

Today [May 14, 2004] marks the second anniversary of the release of A New Kind of Science. And I’m very happy to be able to report that NKS is continuing to develop extremely well.

A wonderful community is forming around the ideas of NKS. The pace of research and applications is steadily building—with an average of about one new paper now appearing every day. NKS classes and courses are being taught. And several times each week we hear about an ambitious new initiative based on NKS—in technology, or art, or business or somewhere else.

We’re trying to do our part to help. Earlier this year we released the online version of the complete book. We launched the NKS Forum. We just sponsored the second annual conference: NKS 2004. And we’re working hard to make wolframscience.com the best possible reference source and meeting place for the NKS community.
Continue reading

(This post was originally published on the NKS Forum.)

At the NKS 2004 conference I did my now-traditional “live computer experiment”. This time the topic I picked came from a question someone asked at the minicourse before the conference: does increasing the “range” of a cellular automaton have a big effect on its behavior?

I decided to investigate a simple version of this question.

In an ordinary r=1 cellular automaton, the new color of a particular cell depends on the previous colors of cells with offsets -1, 0, 1. The question I asked was then: what happens if the offsets are larger?

In the simplest non-trivial cellular automata, the color of a cell depends on the previous colors of two cells. In the ordinary short-range case, the cells have offsets -1, 1. But now we can ask what happens if instead they have offsets -1, m. Continue reading

(This post was originally published on the NKS Forum.)

Today (December 28, 2003) would have been John von Neumann’s 100th birthday—if he had not died at age 53 in 1957. I’ve been interested in von Neumann for many years—not least because his work touched on some of my most favorite topics. He is mentioned in 12 separate places in my book—second in number only to Alan Turing, who appears 19 times.

I always feel that one can appreciate people’s work better if one understands the people themselves better. And from talking to many people who knew him, I think I’ve gradually built up a decent picture of John von Neumann as a man.

He would have been fun to meet. He knew a lot, was very quick, always impressed people, and was lively, social and funny. Continue reading

(This post was originally published on the NKS Forum.)

There’s a certain complexity to many of the characteristic forms used in Christmas images: snowflakes, Christmas trees, frost patterns, etc.

And as in so many other cases, it’s rather easy to capture the essence of these forms using very simple cellular automaton rules.

So that means it’s easy to use cellular automaton rules to make Christmas-like images.

Well, going through some of my archives recently, I was reminded that I did that almost exactly twenty years ago—for Christmas 1983. (The actual file date is November 22, 1983.) Continue reading